この記事では、古典制御工学の重要な基本である伝達関数について纏めます。
はじめに
最近、制御工学を学び始めたので、勉強した内容を記事に纏めることにしました。
この前、重要な数学的基礎であるラプラス変換についての記事を投稿しました。
今回は、古典制御工学における基本中の基本である伝達関数という概念について説明します。
伝達関数はラプラス変換を用いるため、まずは前回の記事を読むことをおすすめします。今回は、ラプラス変換の基本を既に理解していることを前提に話を進めます。
ただし、数式だけの説明よりも、実際にコードを実行して結果を見ていく方がイメージが掴みやすいはずなので、コードも掲載し、その使い方も説明します。
実装に関しては、制御工学ではMATLABが最も一般的ですが、近年は無料で使えるPythonも人気があるため、今回は誰でもすぐに実装できるようにPythonを使用します。
Pythonにはcontrolという制御工学のためのモジュールがあります。このモジュールはMATLABの使い方を参考にして作られているため、書き方はほぼ同じです。
インストールはpipで簡単に行えます。
pip install control
今回はこのモジュールを使用します。又、計算と可視化のためにnumpyとmatplotlibも使用します。
簡単な運動方程式からの伝達関数
伝達関数の由来を理解するために、よく使われる例から紹介します。
運動の法則により、質量$m$の物体に時間$t$の関数である力$f(t)$が加えられるとします。このとき、位置$x(t)$は以下のように変化します。
\ddot{x}(t) = \frac{d^2x(t)}{dt^2}= \frac{f(t)}{m}
これは位置$x(t)$と力$f(t)$の関係を示す微分方程式です。$\ddot{x}(t)$は$x(t)$の2階微分、つまり加速度です。
制御工学では解析のためにラプラス変換を行い、$X(s) = \mathcal{L}[x(t)]$、$F(s) = \mathcal{L}[f(t)]$とします。又ラプラス変換の重要な微分の性質
\mathcal{L}[\dot{x}(t)] = sX(s) - x(0)
を使用します。ここで$x(0)$は位置$x(t)$の$t=0$における初期値ですが、制御工学では通常すべての初期値を$0$に設定するため、
\mathcal{L}[\dot{x}(t)] = sX(s)
となります。そして、
\mathcal{L}[\ddot{x}(t)] = s^2X(s)
となります。つまり、微分は単に$s$を掛けるだけの簡単な操作になります。
したがって、例の微分方程式のラプラス変換は
\begin{align}
\mathcal{L}[\ddot{x}(t)] &= \mathcal{L}\left[\frac{f(t)}{m}\right] \\
s^2X(s) &= \frac{F(s)}{m} \\
X(s) &= \frac{1}{ms^2}F(s)
\end{align}
となります。これで、ラプラス変数$s$の空間における位置と力の関係を表す方程式が得られました。元の時間$t$の空間での表現と似ていますが、微分が単に$s$になることで、すっきりした形になります。
ここで、
G(s) = \frac{1}{ms^2}
とします。すると、
X(s) = G(s)F(s)
となります。
この$G(s)$が今回の主役である伝達関数です。
この例からわかるように、伝達関数は、ラプラス変数の空間において「ある入力とある出力の関係を掛け算で表す関数」です。ここでは入力$F(s)$、出力$X(s)$としていますが、これはさまざまなシステムに適用できます。
より一般的には、制御工学の業界では通常、入力を$U(s)$、出力を$Y(s)$と表すことが多いです。
Y(s) = G(s)U(s)
つまり、ある入力$U(s)$があり、伝達関数$G(s)$を通すことで、出力$Y(s)$が得られるということです。イメージとしては以下のようになります。
(これは制御工学の標準的なブロック線図ではなく、あくまでイメージです)
このように、ラプラス変換を行うことで、システムを単なる伝達関数の掛け算として表現できます。このため、この方法は制御工学において制御対象のシステムモデルを構築する際に一般的に用いられます。
伝達関数は、上記のような非常に単純なものから、より複雑なものまであります。
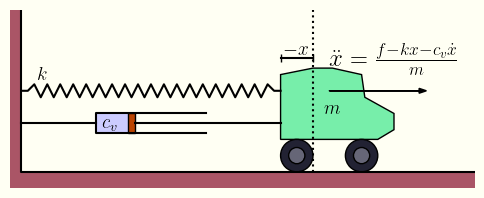
もう少し複雑な例として、制御工学の入門でよく扱われる「バネとダンパーが付いた車」のシステムを見てみましょう。
この図のように、車にバネが付いているため、加える力$f(t)$に加えて$-kx(t)$が働きます。ここで$x(t)$はバネの平衡点からの位置、$k$はバネ定数です。又、ダンパーも付いているため、ダンパーによる力$-c_v\dot{x}(t)$も働きます。ここで$c_v$は粘性減衰係数です。
したがって、運動方程式は以下のようになります。
\ddot{x}(t) = \frac{f(t) - kx(t) - c_v\dot{x}(t)}{m}
ここでラプラス変換を行い、伝達関数を導出します。
\begin{align}
\mathcal{L}[\ddot{x}(t)] &= \frac{\mathcal{L}[f(t)] - k\mathcal{L}[x(t)] - c_v\mathcal{L}[\dot{x}(t)]}{m} \\
s^2X(s) &= \frac{1}{m}F(s) - \frac{k}{m}X(s) - \frac{c_vs}{m}X(s) \\
s^2X(s) + \frac{c_vs}{m}X(s) + \frac{k}{m}X(s) &= \frac{1}{m}F(s) \\
X(s) &= \frac{1}{ms^2 + c_vs + k}F(s)
\end{align}
よって、以下の伝達関数が得られます。
G(s) = \frac{1}{ms^2 + c_vs + k}
伝達関数の一般的な形
以上のバネとダンパーは比較的に簡単な例ですが、要素を追加すると伝達関数が複雑になります。それでも、似たような形をしています。
実際、古典制御工学で扱うシステムは基本的に線型時不変系で、殆どが以下のような形で表現できます。
\begin{align}
& \frac{d^n}{dt^n}y(t) + a_{n-1}\frac{d^{n-1}}{dt^{n-1}}y(t) + \cdots + a_1\frac{d}{dt}y(t) + a_0y(t) \\
&= b_m\frac{d^m}{dt^m}u(t) + b_{m-1}\frac{d^{m-1}}{dt^{m-1}}u(t) + \cdots + b_1\frac{d}{dt}u(t) + b_0u(t)
\end{align}
それをラプラス変換を行います。
\begin{align}
& s^n Y(s) + a_{n-1}s^{n-1}Y(s) + \cdots + a_1 sY(s) + a_0 Y(s) \\
&= b_m s^m U(s) + b_{m-1}s^{m-1}U(s) + \cdots + b_1sU(s) + b_0U(s)
\end{align}
そうしたら、伝達関数はこのように表現できます。
\begin{align}
G(s) = \frac{Y(s)}{U(s)} &= \frac{b_m s^m + b_{m-1}s^{m-1} + \cdots + b_1s + b_0}{s^n + a_{n-1}s^{n-1} + \cdots + a_1 s + a_0}
\end{align}
ここで、$a_0$、$a_1$、…、$a_n$と$b_0$、$b_1$、…、$b_m$は定数です。つまり、伝達関数はさまざまな$s$の多項式からなる分子と分母で構成されます。
ここで$n$は分母の最高次数です。最高で$n$次を持つ伝達関数は「$n$次遅れ系」と呼ばれます。
例えば、上記の$F$と$X$の例は$s^2$を持つため、2次遅れ系となります。
この次数は、システムの性質を表す非常に重要な指標です。
又、$m$は分子の最高次数であり、通常は$m \le n$です。上記の例では$m=0$ですが、後で紹介するより複雑な例では$m > 0$となることもあります。
Pythonによる伝達関数の実装
伝達関数の一般的な形を理解したところで、次に実際にPythonで実装して使用してみます。
controlモジュールのtf関数(transfer functionの略)を使用して、以下のように伝達関数を作成します。
import control
bunshi = [7,5,6]
bunbo = [1,2,3,4]
G = control.tf(bunshi,bunbo)
print(G)
tf関数には、分子と分母の定数を最高次数から順にリストで渡します。printするとわかりやすく表示されます。
7 s^2 + 5 s + 6
---------------------
s^3 + 2 s^2 + 3 s + 4
forced_response関数を使用すると、ある伝達関数Gを持つシステムにおいて、時間tの関数である入力uに対する出力yを求めることができます。
y = control.forced_response(G,t,u).outputs
では、上記のバネとダンパーが付いた車の例を使用して、結果をグラフで描画してみましょう。
import numpy as np
import matplotlib.pyplot as plt
import control
k = 5000 # バネ定数
m = 1000 # 質量
c_v = 500 # 粘性摩擦係数
# 伝達関数
G = control.tf([1],[m,c_v,k])
t = np.linspace(0,20,2001) # 時間の配列
f = np.zeros(len(t)) # 入力の力の配列
f[t>1] = 2000 # 1秒経ったら力を入れる
# 出力の位置の計算
x = control.forced_response(G,t,f).outputs
plt.figure(figsize=[6,5],dpi=100,facecolor='#eeffdd')
plt.subplot(211)
plt.plot(t,f)
plt.ylabel(r'$f(t)$',size=14)
plt.grid(ls=':')
plt.subplot(212)
plt.plot(t,x)
plt.ylabel(r'$x(t)$',size=14)
plt.xlabel(r'$t$',size=14)
plt.grid(ls=':')
plt.show()
結果からわかるように、$t=0$からずっと力$f(t)=2000$を加え続けると、車は動き出し、バネの力によって引き戻されながら振動しますが、ダンパーがあるため、最終的には$f/k=2000/5000=0.4$に収束します。
パラメータと入力の力を変更して、異なる結果を見てみましょう。
k = 10000
m = 50
c_v = 200
t = np.linspace(0,16,2001)
f = np.zeros(len(t))
f[t>1] = 1000
f[t>5] = -500
f[t>10] = 2500-t[t>10]*200
このように、あるシステムの伝達関数を定義しておけば、入力を与えることで出力を求めることができます。
なお、ここでの出力の計算はPythonモジュール内で行われています。自分で実装したい場合、難しいことではありませんが、今回は重点ではなく別の話題となるため、割愛します。
次に、伝達関数がどのようなシステムに適用できるかを理解するために、さまざまな使用例を挙げていきます。
さまざまなシステムの伝達関数の例
運動の速度
上の例と同様に運動方程式を考えます。ただし、今回は位置$x(t)$ではなく、その微分である速度$v(t) = \dot{x}(t)$に注目します。すると、運動方程式は以下のようになります。
\dot{v}(t) = \frac{f(t)}{m}
そして、空気摩擦抵抗を考慮した走行する薄い中空円筒のシステムを考えます。運動方程式は以下のようになります。
\dot{v}(t) = \frac{f(t)-c_v v(t)}{m}
このように空気摩擦抵抗もダンパーの粘性摩擦力と同様に速度に比例し、係数$c_v$を持ちます。ダンパーほど強くはありませんが、ダンパーがなくても高速で移動する物体は空気によって減速されます。
実際に空気の抵抗を考えると、速度$v$に比例する空気摩擦抵抗以外に、速度の平方$v^2$に比例する空気圧力抵抗があります。$v^2$だと線形モデルを作れないので、今回は無視して、空気摩擦抵抗のみ考慮することになります。
現実では空気圧力抵抗の方が大きいので、このモデルは正確とは言いがたくて無理があります。ただしこのような薄い中空円筒の場合は走行方法では投影面積が小さいので、空気圧力抵抗よりも空気摩擦抵抗の方が目立ってきてこのモデルは合理的になります。
ラプラス変換すると、以下のようになります。
\begin{align}
\mathcal{L}[\dot{v}(t)] &= \frac{\mathcal{L}[f(t)]-c_v \mathcal{L}[v(t)]}{m} \\
sV(s) &= \frac{F(s)-c_vV(s)}{m} \\
V(s) &= \frac{1}{ms + c_v}F(s)
\end{align}
これにより、伝達関数が得られます。
G(s) = \frac{1}{ms + c_v}
これは1次遅れ系です。
Pythonで実装して挙動を確認します。
m = 400 # 質量
c_v = 8 # 粘性摩擦係数
G = control.tf([1],[m,c_v])
t = np.linspace(0,600,2001)
f = np.zeros(len(t))
f[(t>20)&(t<300)] = 5000
v = control.forced_response(G,t,f).outputs
plt.figure(figsize=[6,5],dpi=100,facecolor='#eeffdd')
plt.subplot(211)
plt.plot(t,f)
plt.ylabel(r'$f(t)$',size=14)
plt.grid(ls=':')
plt.subplot(212)
plt.plot(t,v)
plt.ylabel(r'$v(t)$',size=14)
plt.xlabel(r'$t$',size=14)
plt.grid(ls=':')
plt.show()
この結果の意味は想像しやすいと思います。一定の力を加えて加速しようとすると、最初はどんどん速くなりますが、空気の粘性によってやがてこれ以上速くならない状態になります。そして、力を抜くと次第に減速し、最終的には停止します。
水槽の水位
断面積$A$の水槽の底に穴が開いて水が抜けていく場合を考え、入力である水の流量$u(t)$と出力である水位$y(t)$のシステムを考えましょう。
この関係は以下の式で表せます。
A\dot{y}(t) = u(t) - By(t)
ここで$B$は定数で、$By(t)$は失われる水の流量を表します。これはパスカルの原理により、水位$y(t)$に比例します。
ラプラス変換すると、
\begin{align}
AsY(s) &= U(s) - BY(s) \\
Y(s) &= \frac{1}{As+B}U(s)
\end{align}
このような伝達関数が得られます。
\begin{align}
G(s) &= \frac{1}{As+B}
\end{align}
これは力と速度の伝達関数と同様の1次遅れ系です。関わる定数が異なるだけで、本質はほぼ同じです。
Pythonで実装して結果を確認すると、同様の挙動が見られます。
A = 20
B = 15
G = control.tf([1],[A,B])
t = np.linspace(0,30,2001)
u = np.zeros(len(t))
u[(t>2)&(t<15)] = 400
y = control.forced_response(G,t,u).outputs
plt.figure(figsize=[6,5],dpi=100,facecolor='#eeffdd')
plt.subplot(211)
plt.plot(t,u)
plt.ylabel(r'$u(t)$',size=14)
plt.grid(ls=':')
plt.subplot(212)
plt.plot(t,y)
plt.ylabel(r'$y(t)$',size=14)
plt.xlabel(r'$t$',size=14)
plt.grid(ls=':')
plt.show()
温度
加熱されている容器内の水のシステムにおいて、入力である熱流量$q(t)$と出力である室温との差の温度$y(t)$の伝達関数を考えます。
温度の変化は以下の微分方程式で表せます。
\dot{y}(t) = -ay(t) + \frac{1}{C}q(t)
ここで$C$は水の熱容量であり、温度変化に必要な熱流量を表します。又、環境温度による温度変化は、環境との温度差$y(t)$に比例し、$ay(t)$と表されます($a$は定数)。
水槽の例と同様にラプラス変換を行うと、伝達関数が得られます。
\begin{align}
sY(s) &= -aY(s) + \frac{1}{C}Q(s) \\
Y(s) &= \frac{1}{C(s+a)}Q(s)
\end{align}
G(s) = \frac{1}{C(s+a)}
Pythonで実装します。
C = 100
a = 0.1
G = control.tf([1],[C,C*a])
t = np.linspace(0,150,2001)
q = np.zeros(len(t))
q[(t>10)&(t<75)] = 400
y = control.forced_response(G,t,q).outputs
plt.figure(figsize=[6,5],dpi=100,facecolor='#eeffdd')
plt.subplot(211)
plt.plot(t,q)
plt.ylabel(r'$q(t)$',size=14)
plt.grid(ls=':')
plt.subplot(212)
plt.plot(t,y)
plt.ylabel(r'$y(t)$',size=14)
plt.xlabel(r'$t$',size=14)
plt.grid(ls=':')
plt.show()
RC回路
電気システムも制御工学の重要な応用分野です。
まずは簡単な例として、抵抗$R$とコンデンサー$C$のみからなる電気システム、つまりRC回路を考えます。入力電圧$v_{\text{in}}(t)$が与えられたとき、抵抗の電圧$v_R$とコンデンサーの電圧$v_C$がどのように変化するかを考えてみましょう。
各電圧の関係は以下のようになります。
v_{\text{in}}(t) = v_R(t) + v_C(t)
ここで電流$\iota(t)$が流れるとすると、抵抗の電圧は
v_R(t) = R\iota(t)
であり、コンデンサーの電圧は
v_C(t) = \frac{1}{C}\int_{0}^{t}\iota(\tau)d\tau
となります。これを微分すると、
\dot{v}_C(t) = \frac{dv_C(t)}{dt} = \frac{1}{C}\iota(\tau)
となります。
したがって、
v_R(t) = R\iota(t) = RC\dot{v}_C(t)
各電圧の関係式に$v_R(t)$を代入すると、以下のようになります。
\begin{align}
v_{\text{in}}(t) &= RC\dot{v}_C(t) + v_C(t) \\
v_C(t) &= v_{\text{in}}(t) - RC\dot{v}_C(t)
\end{align}
ここでラプラス変換を行います。
\begin{align}
V_C(s) &= V_{\text{in}}(s) - RCsV_C(s) \\
V_C(s) &= \frac{1}{RCs + 1}V_{\text{in}}(s)
\end{align}
これでコンデンサーの伝達関数が得られました。
G_C(s) = \frac{1}{RCs + 1}
又、コンデンサーの結果を用いて、抵抗の電圧も求めてみます。
\begin{align}
V_R(s) &= V_{\text{in}}(s) - V_C(s) \\
&= V_{\text{in}}(s) - \frac{1}{RCs + 1}V_{\text{in}}(s) \\
&= \frac{RCs}{RCs + 1}V_{\text{in}}(s)
\end{align}
これで抵抗の伝達関数も求められました。
G_C(s) = \frac{RCs}{RCs + 1}
コンデンサーの伝達関数と同じ分母を持つため、1次遅れ系となりますが、分子が$1$ではなくなっています。これまでの1次遅れ系とは少し異なることがわかります。
Pythonで実装して挙動を確認します。ただし、今回は入力と出力が同じ単位なので、すべて同じグラフに描画します。その方がわかりやすいです。
C = 0.05
R = 10
G_C = control.tf([1],[R*C,1])
G_R = control.tf([R*C,0],[R*C,1])
t = np.linspace(0,8,2001)
v_in = np.zeros(len(t))
v_in[(t>1)&(t<4)] = 100
v_C = control.forced_response(G_C,t,v_in).outputs
v_R = control.forced_response(G_R,t,v_in).outputs
plt.figure(figsize=[6,4],dpi=100,facecolor='#eeffdd')
plt.plot(t,v_in,'--',label=r'$v_\text{in}$',lw=2)
plt.plot(t,v_C,label='$v_C$',lw=1)
plt.plot(t,v_R,label='$v_R$',lw=1)
plt.ylabel(r'$v(t)$',size=14)
plt.xlabel(r'$t$',size=14)
plt.legend(fontsize=14)
plt.grid(ls=':')
plt.show()
$v_C$は今まで見てきた1次遅れ系と同じ挙動ですが、$v_R$はご存知の通り$v_{\text{in}}(t) - v_C(t)$であるため、このような形状になります。
つまり、電圧を印加すると、最初は殆どすべてが$v_R$に現れますが、時間の経過とともに次第に$v_C$に移行し、印加を止めた後も電圧は$v_C$に残り、同時に逆方向の$v_R$が発生します。
RLC回路
RC回路にインダクタンス$L$のコイルを加えたものをRLC回路と呼びます。
コイルの電圧は
v_L(t) = L\dot{\iota}(t) = L\frac{d\iota(t)}{dt}
となります。この場合、電圧の関係は以下のようになります。
v_{\text{in}}(t) = v_R(t) + v_L(t) + v_C(t)
よって、
\begin{align}
v_C(t) &= v_{\text{in}}(t) - v_R(t) - v_L(t) \\
v_C(t) &= v_{\text{in}}(t) - R\iota(t) - L\dot{\iota}(t) \\
v_C(t) &= v_{\text{in}}(t) - RC\dot{v}_{C}(t) - LC\ddot{v}_{C}(t)
\end{align}
ラプラス変換します。
\begin{align}
V_C(s) &= V_{\text{in}}(s) - RCsV_C(s) -LCs^2V_C(s) \\
V_C(s) &= \frac{1}{LCs^2 + RCs + 1}V_{\text{in}}(s)
\end{align}
このように、コンデンサーの伝達関数が得られます。
G_C(s) = \frac{1}{LCs^2 + RCs + 1}
これは2次遅れ系となります。
抵抗の伝達関数も同様に求められます。
\begin{align}
v_R(t) &= v_{\text{in}}(t) - \frac{1}{C}\int_{0}^{t}\iota(\tau)d\tau - L\dot{\iota}(t) \\
v_R(t) &= v_{\text{in}}(t) - \frac{1}{RC}\int_{0}^{t}v_R(\tau)d\tau - \frac{L}{R}\dot{v}_R(t) \\
V_R(s) &= V_{\text{in}}(s) - \frac{1}{RCs}V_R(s) - \frac{L}{R}sV_R(s) \\
\left(1 + \frac{1}{RCs} + \frac{L}{R}s\right)V_R(s) &= V_{\text{in}}(s) \\
V_R(s) &= \frac{RCs}{LCs^2 + RCs + 1}V_{\text{in}}(s)
\end{align}
G_R(s) = \frac{RCs}{LCs^2 + RCs + 1}
そして、コイルの伝達関数も以下のように求められます。
\begin{align}
V_L(s) &= V_{\text{in}}(s) - V_C(s) - V_R(s) \\
V_L(s) &= V_{\text{in}}(s) - \frac{1}{LCs^2 + RCs + 1}V_{\text{in}}(s) - \frac{RCs}{LCs^2 + RCs + 1}V_{\text{in}}(s) \\
V_L(s) &= \frac{LCs^2}{LCs^2 + RCs + 1}V_{\text{in}}(s)
\end{align}
G_L(s) = \frac{LCs^2}{LCs^2 + RCs + 1}
これで、興味深い関係が見えてきましたね。
RC回路と同様に実装して挙動を確認します。
C = 0.02
R = 1.6
L = 0.5
G_C = control.tf([1],[L*C,R*C,1])
G_R = control.tf([R*C,0],[L*C,R*C,1])
G_L = control.tf([L*C,0,0],[L*C,R*C,1])
t = np.linspace(0,8,2001)
v_in = np.zeros(len(t))
v_in[(t>1)&(t<4)] = 100
v_C = control.forced_response(G_C,t,v_in).outputs
v_R = control.forced_response(G_R,t,v_in).outputs
v_L = control.forced_response(G_L,t,v_in).outputs
plt.figure(figsize=[6,6],dpi=100,facecolor='#eeffdd')
plt.plot(t,v_in,'--',label=r'$v_\text{in}$',lw=2)
plt.plot(t,v_C,label='$v_C$',lw=1)
plt.plot(t,v_R,label='$v_R$',lw=1)
plt.plot(t,v_L,label='$v_L$',lw=1)
plt.ylabel(r'$v(t)$',size=14)
plt.xlabel(r'$t$',size=14)
plt.legend(fontsize=14)
plt.grid(ls=':')
plt.show()
2次遅れ系になると、このように振動が見られます。又、$v_C$、$v_R$、$v_L$はいずれも振動し、さらに位相関係も見られます。$v_L$は$v_R$より90°進んでおり、$v_R$は$v_C$より90°進んでいます。これは高校物理でも学んだRLC回路の性質ですね。
直流モーター
直流モーターは制御工学でよく扱われる対象です。電圧でモーターを制御し、トルクを利用してさまざまな動作が可能だからです。
直流モーターが接続された回路は以下のようになります。
RLC回路と比較すると、モーターがコンデンサーCの代わりに配置されていますね。ここで、モーターの電圧は以下のようになります。
v_M(t) = K_M\dot{\theta}(t)
$K_M$はモーターの逆起電力定数、$\theta(t)$はモーターの回転角度、その微分$\dot{\theta}(t)$はモーターの角速度です。
電流から発生するトルクは
\tau(t) = K_{\tau}\iota(t)
ここで$K_{\tau}$はモーターのトルク定数です。
トルクと角速度の関係は
J_c\ddot{\theta}(t) = \tau(t) - B\dot{\theta}(t)
$J_c$はモーターの慣性モーメント、$B$は回転に関する粘性摩擦係数です。これはモーターのブラシなどに起因します。
トルクを代入すると、以下のようになります。
J_c\ddot{\theta}(t) = K_{\tau}\iota(t) - B\dot{\theta}(t)
ここでラプラス変換を行います。
\begin{align}
J_c s^2\Theta(s) &= K_{\tau}I(s) - Bs\Theta(s) \\
I(s) &= \frac{J_c s^2\Theta(s) + Bs\Theta(s)}{K_{\tau}}
\end{align}
一方、電圧の関係は以下のようになります。
\begin{align}
v_{\text{in}}(t) &= v_R(t) + v_L(t) + v_M(t) \\
v_{\text{in}}(t) &= R \iota(t) + L\dot{\iota}(t) + K_M\dot{\theta}(t) \\
V_{\text{in}}(s) &= R I(s) + L s I(s) + K_M s \Theta(s)
\end{align}
$I(s)$の値を代入します。
\begin{align}
V_{\text{in}}(s) &= \frac{R}{K_{\tau}} (J_c s^2\Theta(s) + Bs\Theta(s)) + \frac{Ls}{K_{\tau}} (J_c s^2\Theta(s) + Bs\Theta(s)) + K_M s \Theta(s) \\
V_{\text{in}}(s) &= \left( \frac{RJ_c s^2}{K_{\tau}} + \frac{RBs}{K_{\tau}} + \frac{LJ_c s^3}{K_{\tau}} + \frac{LBs^2}{K_{\tau}} + K_Ms \right) \Theta(s) \\
\Theta(s) &= \frac{K_{\tau}}{LJ_cs^3 + (RJ_c+LB)s^2 + (RB+K_MK_{\tau})s}V_{\text{in}}(s)
\end{align}
このように、入力電圧$V_{\text{in}}$に対する3次遅れ系の伝達関数が得られました。
G_{\theta}(s) = \frac{K_{\tau}}{LJ_cs^3 + (RJ_c+LB)s^2 + (RB+K_MK_{\tau})s}
ただし、角速度$\omega = \dot{\theta}$に着目する場合は、以下のように2次遅れ系となります。
G_{\omega}(s) = sG_{\theta}(s) = \frac{K_{\tau}}{LJ_cs^2 + (RJ_c+LB)s + (RB+K_MK_{\tau})}
実装して挙動を確認します。
R = 0.8
L = 1.6
K_tau = 10
K_M = 4
B = 0.5
J_c = 0.2
G_omega = control.tf([K_tau],[L*J_c,R*J_c+L*B,R*B+K_M*K_tau])
G_theta = control.tf([1],[1,0])*G_omega
t = np.linspace(0,8,2001)
v_in = np.zeros(len(t))
v_in[(t>1)&(t<4)] = 100
omega = control.forced_response(G_omega,t,v_in).outputs
theta = control.forced_response(G_theta,t,v_in).outputs
plt.figure(figsize=[6,8],dpi=100,facecolor='#eeffdd')
plt.subplot(311)
plt.plot(t,v_in)
plt.ylabel(r'$v_{\text{in}}(t)$',size=14)
plt.grid(ls=':')
plt.subplot(312)
plt.plot(t,omega)
plt.ylabel(r'$\omega(t)$ [rad/s]',size=14)
plt.xlabel(r'$t$',size=14)
plt.grid(ls=':')
plt.subplot(313)
plt.plot(t,theta)
plt.ylabel(r'$\theta(t)$ [rad]',size=14)
plt.xlabel(r'$t$',size=14)
plt.grid(ls=':')
plt.show()
このように直流モーターに電圧を入力したら回ります。回転速度は、電圧を変えたばかりの時に振動がありますがやがて収束して安定になります。
伝達関数の結合
伝達関数でシステムを表現する利点として、「結合が可能であること」がよく挙げられます。つまり、
\begin{align}
V(s) = G_1(s)U(s) \\
W(s) = G_2(s)V(s) \\
Y(s) = G_3(s)W(s)
\end{align}
とした場合、
Y(s) = G_1(s)G_2(s)G_3(s)U(s)
となります。イメージとしては以下のようになります。
ここで、$V(s)$は$G_1(s)$の出力であり、$G_2(s)$の入力となります。同様に、$W(s)$は$G_2(s)$の出力であり、$G_3(s)$の入力です。
具体的な例として、先ほど紹介した直流モーターを車の動力源として考えてみましょう。
f(t) = c_M\omega(t)
ここで、$c_M$はモーターの角速度から力を生成する効率を表す定数です。これは角速度から力への伝達関数と見なすことができます。
G_{\omega \to f}(s) = c_M
モーターの角速度の伝達関数を$G_{v_{\text{in}} \to \omega}(s)$、車の運動の位置の伝達関数を$G_{f \to x}(s)$とすると、モーターの電圧から車の位置への伝達関数は以下のように得られます。
G_{v_{\text{in}} \to x}(s) = G_{v_{\text{in}} \to \omega}(s) G_{\omega \to f}(s) G_{f \to x}(s)
この伝達関数を用いることで、入力電圧$v_{\text{in}}(t)$から車の位置$x(t)$を求めることができます。
X(s) = G_{v_{\text{in}} \to x}(s)V_{\text{in}}(s)
非線形の線形化
これまでに挙げた例は全て線形システムです。実際、「線形システムしか扱えない」という点が伝達関数の限界としてよく指摘されます。非線形システムは基本的に伝達関数で表現できないため、適用範囲が限定されています。
しかしながら、非線形システムに対してもさまざまな工夫を施すことで、近似的に線形化して扱うことが可能です。
よく用いられる例として、振り子を取り上げます。以下のように振り子が吊るされている状況を考えます。
トルク$\tau(t)$が加えられる質量$m$の振り子の角度$\theta$に関する運動方程式は以下のようになります。
J\ddot{\theta} = -B\dot{\theta}(t) - mgl\sin(\theta(t)) + \tau(t)
ここで、$g$は重力加速度、$l$は棒の長さ、$B$は粘性摩擦係数です。$J$は慣性モーメントであり、振り子の質量が$l$に比べて小さい場合、$J \approx ml^2$と近似できます。
この方程式には$\sin(\theta(t))$が含まれているため非線形となり、ラプラス変換を行なってもこれまでのような伝達関数は得られません。
線形化するためには、テイラー展開が用いられます。
f(\theta) = f(0) + \frac{\dot{f}(0)}{1!}\theta + \frac{\ddot{f}(0)}{2!}\theta^2 + \frac{\dddot{f}(0)}{3!}\theta^3 + \cdots
ここで$f(\theta)= \sin\theta$なので、
\begin{align}
\sin(\theta) &= \sin(0) + \frac{\cos(0)}{1!}\theta - \frac{\sin(0)}{2!}\theta^2 - \frac{\cos(0)}{3!}\theta^3 + \cdots \\
&= 0 + \theta - \frac{1}{3!}\theta^3 - 0 + \cdots \\
&= \theta - \frac{1}{6}\theta^3 + \cdots
\end{align}
これを運動方程式に代入すると、
J\ddot{\theta}(t) = - B\dot{\theta}(t) - mgl\left(\theta(t)-\frac{\theta^3(t)}{6}+\cdots\right) + \tau(t)
$\theta(t)$が小さい時、$\theta^3(t)$以上は非常に小さいので、省略できます。すると、
J\ddot{\theta}(t) \approx - B\dot{\theta}(t) - mgl\theta(t) + \tau(t)
これで線形化されました。
通常通りラプラス変換を行うと、
\begin{align}
Js^2\Theta(s) &= - B s\Theta(s) - mgl\Theta(s) + T(s) \\
\Theta(s) &= \frac{1}{Js^2 + B s + mgl}T(s)
\end{align}
となり、伝達関数が得られます。
G(s) = \frac{1}{Js^2 + B s + mgl}
これは、バネとダンパーからなるシステムと同様の2次遅れ系です。
実装
B = 2
m = 5
g = 9.8
l = 1.2
J = m*l**2
G = control.tf([1],[J,B,m*g*l])
t = np.linspace(0,25,2001)
tau = np.zeros(len(t))
tau[(t>1)&(t<15)] = 2
theta = control.forced_response(G,t,tau).outputs
plt.figure(figsize=[6,5],dpi=100,facecolor='#eeffdd')
plt.subplot(211)
plt.plot(t,tau)
plt.ylabel(r'$\tau(t)$ [N/m]',size=14)
plt.grid(ls=':')
plt.subplot(212)
plt.plot(t,np.rad2deg(theta))
plt.ylabel(r'$\theta(t)$ [°]',size=14)
plt.xlabel(r'$t$',size=14)
plt.grid(ls=':')
plt.show()
纏め
今回は、古典制御工学の基本である伝達関数について説明しました。伝達関数は、ラプラス変換を用いてシステムの入出力関係を表す関数であり、微分方程式を簡単な代数方程式に変換することで解析を容易にします。
又、さまざまな物理システム(機械、流体、熱、電気)の伝達関数を導出し、Pythonを用いてその挙動をシミュレーションしました。これにより、伝達関数が実際のシステムの動的特性をどのように表現するかを確認できました。
参考
- 【伝達関数とは?】基本概念と利点を解説!システム解析の基礎を学ぶ
- 伝達関数とは?3つの利点と、初期値の考え方を具体例で解説!
- 伝達関数の4つの基本要素と、よくある伝達関数例まとめ
- 高次系の伝達関数とそのイメージ。2次系は1次系2つで表せない?
- 高次系の伝達関数例3選。倒立振子・DCサーボモータの運動方程式
- 【制御図鑑Ⅱ】古典制御・現代制御の主な手法15種類のまとめ
- 伝達関数とは何ぞや?
- 古典制御 - PID制御
pythonでの実装
- Pythonによる伝達関数の実装
- 【制御工学】Pythonによる伝達関数のグラフ化
- python-control を用いたfeedback制御の基礎
- pythonのcontrolライブラリの使用方法メモ
- RLC直列回路の伝達関数・状態空間モデルとPythonによるシミュレーション
- 【制御工学】制御工学シミュレーションのまとめ
- RC回路のシミュレーション
- 「はじめての制御工学」の図のシミュレーションについて
- Python で学ぶ 制御工学
書籍