はじめに

制御系を設計する場合、補償器やフィルタは連続時間の伝達関数として表現するのが一般的です。一方、シミュレーションやデータ処理において、離散信号に対して逐次的に伝達関数を適用する必要が生じることがあります。

そこで、この記事はPythonを使用して、連続時間の伝達関数を離散化して差分方程式（漸化式）に変換し、離散信号に対して適用するためのクラスを作成してみます。

この記事では以下のライブラリを使用します。

NumPy
SciPy
Matplotlib（評価用）
Python-Control（評価用）

伝達関数の離散化

連続時間の伝達関数は、scipy.signal.cont2discrete()で離散化することができます。
例えば、連続時間の伝達関数をサンプル時間Tsで離散化する場合は、以下のように記述します。
ここでnumとdenは、それぞれ伝達関数の分子係数と分母係数とします。

(num_d, den_d, Ts)  = cont2discrete((num, den), Ts, 'bilinear')

3番目の引数には離散化に使用するアルゴリズムを指定します。省略するとzoh（0次ホールド）となりますが、ここではbilinear（相一次変換）を使ってみました。

戻り値のうち、num_dとden_dはそれぞれ離散時間における伝達関数の分子係数と分母係数です（Tsは引数と同じくサンプリング周期です）。

差分方程式への変換

今更ですが、離散時間における伝達関数の一般系を次式のように定義します。

G_d(z) = \frac{Y(z)}{X(z)} = \frac{b_{n} z^n + b_{n-1} z^{n-1} + \cdots + b_{0}}{a_{n} z^n + a_{n-1} z^{n-1} + \cdots a_{0}}

ここで、num_dとden_dは以下に相当します。

変数	値
`num_d`	$\big[b_{n}, b_{n-1}, \cdots, b_{0}\big]$
`den_d`	$\big[a_{n}, a_{n-1}, \cdots, a_{0}\big]$

$G_d(z)$の分母と分子を$z^n$で割ると以下のようになります。

G_d(z) = \frac{Y(z)}{X(z)} = \frac{b_{n} + b_{n-1} z^{-1} + \cdots + b_{0} z^{-n}}{a_{n} + a_{n-1} z^{-1} + \cdots a_{0} z^{-n}}

これを

\begin{align}
& & (a_{n} + a_{n-1} z^{-1} + \cdots a_{0} z^{-n})Y(z) = (b_{n} + b_{n-1} z^{-1} + \cdots + b_{0} z^{-n})X(z) \\
& \Rightarrow & a_nY(z) = (b_{n} + b_{n-1} z^{-1} + \cdots + b_{0} z^{-n})X(z) - (a_{n-1} z^{-1} + \cdots a_{0} z^{-n}) Y(z) \\
& \Rightarrow & Y(z) = \frac{1}{a_n} \Big\{ (b_{n} + b_{n-1} z^{-1} + \cdots + b_{0} z^{-n})X(z) - (a_{n-1} z^{-1} + \cdots a_{0} z^{-n}) Y(z) \Big\}
\end{align}

と変形していけば、最後に差分方程式（漸化式）として

\begin{align}
y[k] = \frac{1}{a_n} & \big( b_n x[k] + b_{n-1} x[k-1]+\cdots b_0 x[k-n] \\
& - a_{n-1} y[k-1] - a_{n-1} y[k-2] - \cdots - a_0 y[k-n] \big)
\end{align}

が得られます。

クラスの実装

ここまで説明した伝達関数の離散化、および差分方程式による計算を、Pythonで一つのクラスとして実装した例を示します。

import numpy as np
from scipy.signal import cont2discrete

class DiscreteTransferFunction:
    def __init__(self, num, den, Ts):
        (self.num_d, self.den_d, Ts) = cont2discrete((num, den), Ts, 'bilinear')
        self.num_d = np.squeeze(self.num_d)
        self.den_d = np.squeeze(self.den_d)
        self.num_d = np.insert(self.num_d, 0, [0] * (len(self.den_d) - len(self.num_d)))

        self.x_d = np.zeros((len(self.num_d), 1))
        self.y_d = np.zeros((len(self.den_d), 1))
    
    def calc(self, x):
        self.x_d = np.insert(self.x_d, 0, x)[0:-1]
        self.y_d = np.insert(self.y_d, 0, 0)[0:-1]

        y = (np.dot(self.x_d, self.num_d) - np.dot(self.y_d, self.den_d)) / self.den_d[0]
        self.y_d[0] = y

        return y

コンストラクタでは、与えられた連続時間の伝達関数を離散化し、その次数に合わせて入出力信号（状態変数）であるx_dとy_dの初期化を行います。分子多項式の要素数（次数）が分母多項式よりも小さいと不都合が生じるため、必要に応じてnum_dの先頭を0埋めしています。

calc()関数では毎時刻の差分方程式を計算します。ここでは、入出力信号をx_d、y_dとしてそれぞれ以下のように定義し、num_dやden_dとの内積を計算する処理として、次数などが変わった場合もコードの修正を不要としています¹。

変数	値
`x_d`	$\Big[ x[k], x[k-1], \cdots, x[k-n] \Big]$
`y_d`	$\Big[ 0, y[k-1], \cdots, y[k-n] \Big]$

実行例

ここでは連続時間の伝達関数として、以下に示す2次のローパスフィルタを考えます。これを離散化して、1Hzの正弦波信号に適用してみましょう。

G(s) = \frac{\omega_c^2}{s^2 + 2\zeta\omega_cs + \omega_c^2} \quad (\omega_c =2\pi, \zeta = 1/\sqrt{2})

import matplotlib.pyplot as plt

...

# 伝達関数の定義と離散化
wc = 1 * 2 * np.pi
zeta = 1 / np.sqrt(2)

num = np.array([wc**2])
den = np.array([1, 2 * zeta * wc, wc**2])

Ts = 0.01
G_lpf = DiscreteTransferFunction(num, den, Ts)

# 変数の初期化
t = np.arange(0, 5, Ts)
x = np.sin(2 * np.pi * 10 * t)
y = np.zeros_like(x)

# シミュレーション
for k in range(len(x)):
    y[k] = G_lpf.calc(x[k])

# プロット
plt.figure()
plt.plot(t, x, label='Input')
plt.plot(t, y, label='Output')
plt.grid(True)
plt.legend()
plt.show()

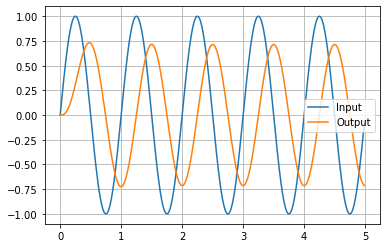
これを実行すると以下のグラフがプロットされます。今回のローパスフィルタでは、1Hzのゲインが-3dB（≒0.7倍）なので問題なさそうです。

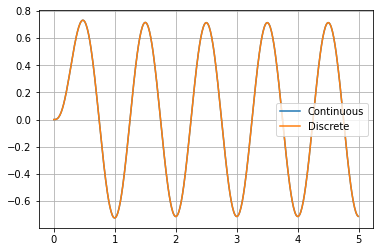
念のため、連続時間でのシミュレーション結果と比較してみましょう。

from control import tf
from control.matlab import lsim

...

G = tf(num, den)
(yc, tc, xc) = lsim(G, U=x, T=t)

plt.figure()
plt.plot(tc, yc, label='Continuous')
plt.plot(t, y, label='Discrete')
plt.grid(True)
plt.legend()
plt.show()

完全に一致していますね。

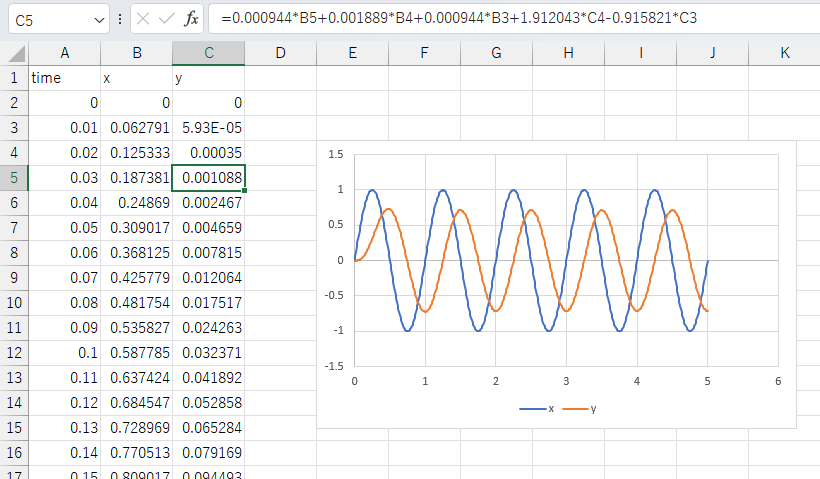
（おまけ）Excelでの計算

上で計算した差分方程式はExcelでも利用することができます。例えば、以下のコードを実行すればExcel用の数式が生成されます。

col_in = 'B'
col_out = 'C'
headerlines = 1

N = len(G_lpf.den_d)
for k in range(N):
    formula = ''
    baserow = headerlines + k + 1

    for i in range(N):
        if G_lpf.num_d[i] != 0 and (baserow - i) > headerlines:
            formula += '%+f*%s%d' % (G_lpf.num_d[i], col_in, baserow - i)
    
    for i in range(1, N):
        if baserow - i > headerlines:
            formula += '%+f*%s%d' % (-G_lpf.den_d[i], col_out, baserow - i)
    
    if formula == '':
        forlula = '0'
    
    print('%s%d =%s' % (col_out,baserow, formula))

print('%s%d以降: %s%dの数式をオートフィル' % (col_out, baserow + 1, col_out, baserow))

ここでは、（時刻がA列と仮定して）入力信号（col_in）をB列、出力信号（col_out）をC列に割り当て、1行目はヘッダ（header_lines）として2行目からデータを格納する設定としています。

先ほどと同じ2次のローパスフィルタの場合、このコードを実行すると以下のように数式が生成されます。

C2 =+0.000944*B2
C3 =+0.000944*B3+0.001889*B2+1.912043*C2
C4 =+0.000944*B4+0.001889*B3+0.000944*B2+1.912043*C3-0.915821*C2
C5以降: C4の数式をオートフィル

実際にExcelで使ってみると、Pythonと同様の結果が得られていることが分かります。
Officeしか使えない環境向けに、あらかじめデータ処理用のExcelファイルとして準備しておくと便利かもしれません。

おわりに

本記事では、Pythonで連続時間の伝達関数を離散化し、シミュレーション等で使用するための方法を紹介しました。少しニッチな内容かもしれませんが、組み込みソフトウェアの実装などにも応用できるため用途は幅広いかと思います。参考になれば幸いです。

ここではden_dをそのまま使用するため、y_dの先頭を0としています。 ↩

Pythonによる伝達関数の実装