概要
制御工学の勉強メモ。第2弾。
前回は、バネ・マス・ダンパ系の質点の運動方程式から、伝達関数/状態空間モデルを求めて、制御系のPythonライブラリ「Python Control Systems Library」を使ってシミュレーションをしました。
今回は、RLC直列回路を対象に、回路方程式から伝達関数/状態空間モデルを求めて、Pythonを使ってシミュレーションをしてみます。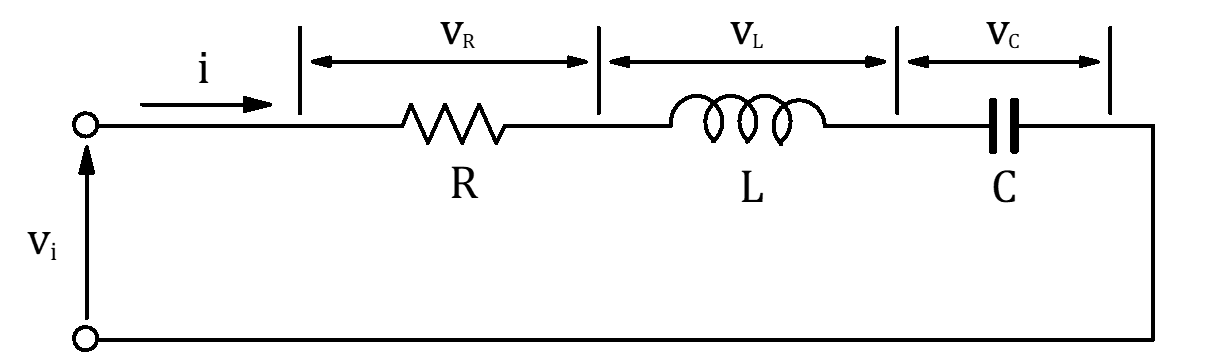
回路方程式
通常は、次のように 電流 $i(t)$ を使って回路方程式を立てます。
$$ v_{i}(t) = Ri(t) + L\frac{\mathrm{d}}{\mathrm{dt}}i(t) + \frac{1}{C}\int^{t}_{0} i(\tau),\mathrm{d} \tau$$
しかし、ここでは 前回の力学系との対応をとるために、次の関係を使って 電荷 $q(t)$ を使って回路方程式を書いていきます。
$$ i(t) = \frac{\mathrm{d}}{\mathrm{dt}}q(t)$$
電荷 $q(t)$ で回路方程式を書くと次のようになります。
$$ v_{i}(t) = R\frac{\mathrm{d}}{\mathrm{dt}}q(t) + L\frac{\mathrm{d}^2}{\mathrm{dt}^2}q(t) + \frac{1}{C}q(t) $$
微分をドット表記に変えて、式を整理します。
$$ L \ddot{q}(t) + R \dot{q}(t) + \frac{1}{C}q(t) = v_{i}(t) $$
これは、前回で示したバネ・マス・ダンパ系における1自由度の質点の運動方程式(下記)と、同じ形になっていることが分かります。
$$ m\ddot{y}(t) + c\dot{y}(t) + ky(t) = f(t)$$
伝達関数でシステムをモデル化
力学のモデルでは、力 $f(t)$ をシステムに対する入力、変位 $y(t)$ をシステムからの出力として伝達関数を求めました。
仮に、それに対応させれば、入力電圧 $v_i(t)$ をシステムに対する入力、電荷 $q(t)$ をシステムからの出力として伝達関数を求める形になるのですが、電荷 $q(t)$ を直接的に観測(計測)することは簡単ではありません。また、実際のところ、関心があるのは各素子の電圧になります。よって、電気回路の場合は、電圧を出力として伝達関数を求めます。
ここでは、入力電圧 $v_i(t)$ をシステムに対する入力 $u(t)$、コンデンサの両端電圧 $v_{C}(t)$ を、システムの出力 $y(t)$ とした伝達関数を求めていきます。
$$ 入力,,,u(t) = v_{i}(t) $$
$$ 出力,,,y(t) = v_{C}(t) = \frac{1}{C}q(t) $$
上記の出力を、$q(t)$ についての式にします。
$$ q(t) = Cy(t) $$
これを、先の回路方程式 $ L \ddot{q}(t) + R \dot{q}(t) + \frac{1}{C}q(t) = v_{i}(t)$ に代入すれば、次を得ます。
$$ LC \ddot{y}(t) + RC \dot{y}(t) + y(t) = u(t) $$
これをラプラス変換して、システムの伝達関数 $G(s)=Y(s)/U(s)$ を求めると次のようになります(この際、$\dot{y}(0)=0$ と $y(0)=0$ を仮定します)。
$$ LCs^2Y(s) + RCsY(s) + Y(s) = U(s)$$
$$ \big(LCs^2+ RC s + 1\big) Y(s) = U(s)$$
$$ G(s) = \frac{Y(s)}{U(s)} = \frac{1}{LC s^2 + RC s + 1}$$
なお、力学モデルでは、力を入力、変位を出力として、質量を $m$、減衰係数を $c$、バネ定数を $k$ とした伝達関数は次のようになりました。力学系も回路系も非常に似た形になっていることが分かります。
$$ G(s) = \frac{Y(s)}{F(s)} = \frac{1}{m s^2 + c s + k}$$
Pythonでモデル化・シミュレーション
Python の Python Control Systems Library を利用して、シミュレーションをします。伝達関数を設定してシステムをモデル化して、ステップ応答をシミュレーションします。
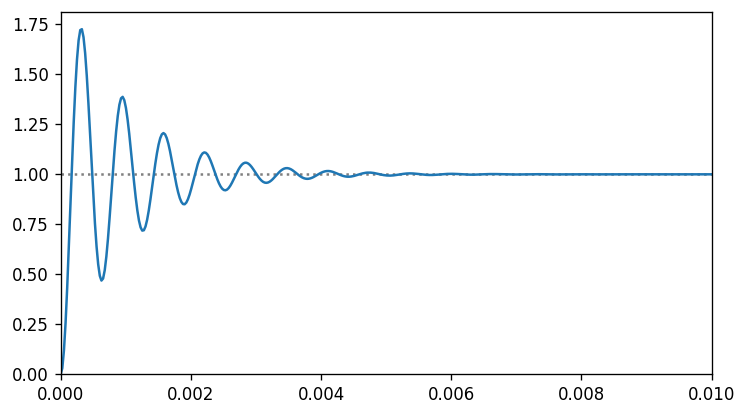
力学系では、質点に一瞬だけ力を加えたときの変位を観測するためにインパルス応答のシミュレーションをしましたが、電気回路では、入力電圧 $v_{i}(t)=1, (t\ge0)$ としたときのコンデンサ電圧 $v_{C}$ を観測するという設定のほうが自然なのでステップ応答をみていきます。
!pip install --upgrade sympy
!pip install slycot
!pip install control
import numpy as np
import control.matlab as ctrl
import matplotlib.pyplot as plt
R = 2 # 抵抗値
L = 1e-3 # インダクタンス
C = 10e-6 # 静電容量
sys = ctrl.tf((1),(L*C,R*C,1))
print(sys)
t_range = (0,0.01)
y, t = ctrl.step(sys, T=np.linspace(*t_range, 400))
plt.figure(figsize=(7,4),dpi=120,facecolor='white')
plt.hlines(1,*t_range,colors='gray',ls=':')
plt.plot(t,y)
plt.xlim(*t_range)
plt.ylim(bottom=0)
plt.show()
1
------------
s^2 + s + 10
入力電圧を $v_{i}(t)=1, (t\ge0)$ とすると、コンデンサ電圧 $v_{C}$ は、最初に振動して、最終的には $1,[\mathrm{V}]$ に落ち着くことが分かります。
状態空間モデルでモデル化
システムを、次のような状態空間モデル $\mathcal{P}$ として記述します。
\mathcal{P}\,:\,\left\{
\begin{array}{l}
\dot{\boldsymbol{x}} = \mathbf{A}\boldsymbol{x} + \mathbf{B}\boldsymbol{u}& 状態方程式\\
\boldsymbol{y} = \mathbf{C}\boldsymbol{x} + \mathbf{D}\boldsymbol{u}& 出力方程式(観測方程式)
\end{array}
\right.
準備として、回路方程式 $ LC \ddot{y}(t) + RC \dot{y}(t) + y(t) = u(t) $ を、 $\ddot{y}(t)=...$ に変形しておきます。
$$ \ddot{y}(t) = -\frac{1}{LC} y(t)- \frac{R}{L} \dot{y}(t) + \frac{1}{LC} u(t)$$
$x_1(t)=y(t)$、$x_2(t)=\dot{y}(t)$ として、状態 $\boldsymbol{x}=[x_1,,x_2]^T$ を定めます。
これより、$\dot{x}_1(t)=\dot{y}(t)=x_2$ となります。また、$\dot{x}_2(t)=-\frac{1}{LC} y(t)- \frac{R}{L} \dot{y}(t) + \frac{1}{LC} u(t)$ となります。
以上より、次の状態方程式を得ることができます。
\left[
\begin{array}{c}
\dot{x}_1 \\
\dot{x}_2
\end{array}
\right]
=\left[
\begin{array}{cc}
0 & 1 \\
-\frac{1}{LC} & -\frac{R}{L}
\end{array}
\right]
\left[
\begin{array}{c}
x_1 \\
x_2
\end{array}
\right]
+ \left[
\begin{array}{c}
0 \\
\frac{1}{LC}
\end{array}
\right] u
\dot{\boldsymbol{x}}
=\left[
\begin{array}{cc}
0 & 1 \\
-\frac{1}{LC} & -\frac{R}{L}
\end{array}
\right]
\boldsymbol{x} + \left[
\begin{array}{cc}
0 \\
\frac{1}{LC}
\end{array}
\right] u
$$\dot{\boldsymbol{x}}
=\mathbf{A}\boldsymbol{x} + \mathbf{B} u$$
また、次の出力方程式(観測方程式)を得る(コンデンサ電圧 $v_{C}$ に相当する状態 $x_1$ と、電流に相当する $Cx_2 (= C\dot{y}(t) = C\dot{v}_{C}(t) = C\big(\frac{1}{C}\dot{q}(t)\big)= \dot{q}(t) = i(t),) $ を観測する形)。
y = \left[
\begin{array}{cc}
1 & 0\\
0 & C\\
\end{array}
\right] \left[
\begin{array}{c}
x_1 \\
x_2
\end{array}
\right]
$$y
=\mathbf{C}\boldsymbol{x} + \mathbf{D} u$$
ただし、$\mathbf{D}=0$。
Pythonでモデル化・シミュレーション
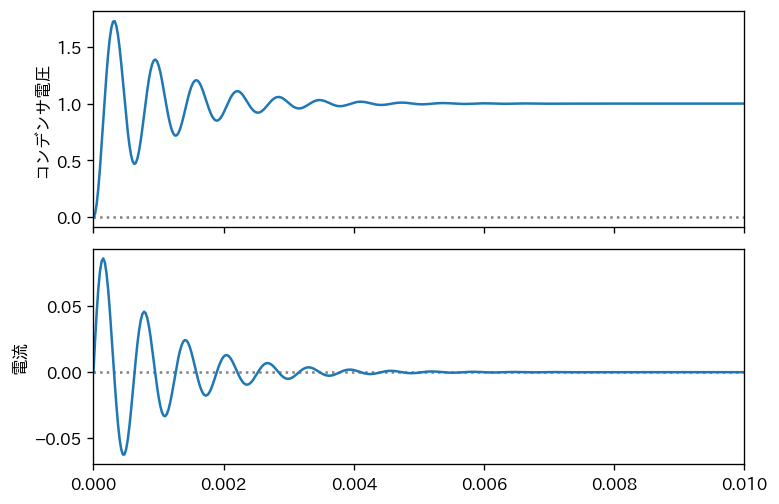
状態空間モデルで、ステップ応答をシミュレーションします。
!pip install japanize-matplotlib
import numpy as np
import control.matlab as ctrl
import matplotlib.pyplot as plt
import japanize_matplotlib
R = 2 # 抵抗値
L = 1e-3 # インダクタンス
C = 10e-6 # 静電容量
A = [[0,1],[-1/(L*C), -R/L]]
B = [[0],[1/(L*C)]]
C = [[1,0],[0,C]]
D = 0
sys = ctrl.ss(A,B,C,D)
# print(sys)
t_range = (0,0.01)
y, t = ctrl.step(sys, T=np.linspace(*t_range, 400))
fig, ax = plt.subplots(nrows=2, figsize=(7,5),dpi=120,sharex='col')
fig.patch.set_facecolor('white')
fig.subplots_adjust(hspace=0.1)
for i,s in enumerate(['コンデンサ電圧','電流']) :
ax[i].hlines(0,*t_range,colors='gray',ls=':')
ax[i].plot(t,y[:,i])
ax[i].set_ylabel(s)
ax[i].set_xlim(*t_range)
plt.show()