目的
-Feedback制御なんかをあまり理解していなかったので、纏めた。
-MATLABではなく、pythonで制御性の確認をしたかった。
1. プロセスモデル
1-1. 伝達関数の作り方① 定常ゲイン、時定数
1次遅れ系(First Order Lag)は化学プラントのプロセスでよく見る。
このプロセスを伝達関数にて記載すると
$$P(s) = \frac{K}{Ts + 1}e^{-Ls}$$
となる。ここで、
K:定常ゲイン(Steady-State gain),
T:時定数(Time Constant),
L:むだ時間(Dead Time)
である。
これを python-controlを用いて記述する。主にMATLABの関数が使えるので、
伝達関数についてはMATLABの公式ドキュメントを参考にできる。
また、python-controlの詳細はこちらから確認出来る。
例えば、$P(s) = \frac{10}{25s + 1}$をmatlab.tfを用いて記述してみると
from control import matlab
Kt = 10 #Steady-State gain
J = 25 #Time Constant
Cm = 4 #Dead time ここでは使用しない
num = [Kt] #分子の係数
dem = [J,1] #分母の係数
P = matlab.tf(num,dem)
print(P)
と表現される。
1-2. 伝達関数の作り方② むだ時間
状態方程式で表す場合、$\frac{K}{Ts + 1}$は簡単に状態方程式になるが、
$e^(-Ls)$は非線形の為、Pade近似が必要となる。
Pade近似とは
$$ e^{-Ts} = \frac{1-k_1s+k_2s^2+・・・±k_ns^n}{1+k_1s+k_2s^2+・・・+k_ns^n}$$
で表される。こちらもpython-controlのライブラリ内の関数であるmatlab.pdを用いることが出来る。
ここで、「pade近似の級数をどうすれば良いのか?」という疑問が上がる。
MATLABの公式ドキュメントによると、
制限
高次のパデ近似を計算すると、極が集積した伝達関数ができます。
そのような極設定は摂動にきわめて敏感になるため、次数が N>10 のパデ近似は避けてください。
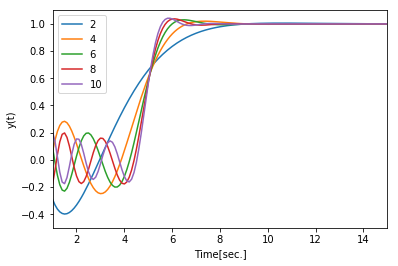
と記載が有る。pade近似について、step応答で遅れ時間がどのように表現されるかを確認する。
# pade近似を表現,前提として5秒のむだ時間を設定
# まずパデ近似の分子、分母を求める
num2, dem2 = matlab.pade(5,2)
num4, dem4 = matlab.pade(5,4)
num6, dem6 = matlab.pade(5,6)
num8, dem8 = matlab.pade(5,8)
num10, dem10 = matlab.pade(5,10)
# pade近似の分子、分母を伝達関数の形に変換
P2 = matlab.tf(num2,dem2)
P4 = matlab.tf(num4,dem4)
P6 = matlab.tf(num6,dem6)
P8 = matlab.tf(num8,dem8)
P10 = matlab.tf(num10,dem10)
# 最後にstep応答を行う
time= 100
t = np.linspace(0,time,1000)
y2,T = matlab.step(P2,t)
y4,T = matlab.step(P4,t)
y6,T = matlab.step(P6,t)
y8,T = matlab.step(P8,t)
y10,T = matlab.step(P10,t)
# 結果の表示
from matplotlib import pylab as plt
plt.plot(T, y2, label = "2")
plt.plot(T, y4, label = "4")
plt.plot(T, y6, label = "6")
plt.plot(T, y8, label = "8")
plt.plot(T, y10, label = "10")
plt.xlim((1,15))
plt.ylim((-0.50,1.1))
plt.xlabel("Time[sec.]")
plt.ylabel("y(t)")
plt.legend()
上のグラフの様に、級数が上がると、振動の周波数が上がり、振幅も抑えられていることが確認出来る。
ただ、個人的には、10次まで使うか?というと、あまり5次程度と10次異なるとはあまり思えないので、
今後は5次のpade近似を用いる。
2.PID Controller
PID制御については、こちらのページの11章 を参照のこと。
$$ K(s) = \frac{k_ps + k_i + k_d s^2}{s}$$
この式だと、各係数k, $k_i$,$k_d$は単位が異なる。そこで、単位をあわせる為、
$$k = k_p, T_i = \frac{k_p}{k_i}, T_d = \frac{k_d}{k_p}$$とすると、伝達関数は
$$K(s) = k[1 + \frac{1}{sT_i} + sT_d]$$
となる。
pidコントローラーをpython-controlで記述すると
K = 0.75 #Proprotional Gain
Ti = 8#Integral Time
Td = 2 #Derivarive Time
# 伝達関数用の係数に変換
kp = K
ki = kp/Ti
kd = Td * kp
num = [kd, kp, ki]
den = [1, 0]
C = matlab.tf(num, den)
print(C)
3. Feedback
Feedbackとは次のブロック線図で表されるものである。橋本伊織ら著の「プロセス制御工学」では、
・・・槽内温度の測定値に応じて調節弁開度を変化させるという結果から原因へ向かう信号の流れ、
すなわちフィードバックが存在する。
この様に、信号の伝達経路がフィードバックループによって閉じられている制御をフィードバック制御(Feedback Control)あるいは、閉ループ制御(Closed-loop Control)と呼ぶ。
「プロセス制御工学(p.4-5)」
ブロック図にて図示すると、以下の通りである(引用)
ここで、
r:設定値,e:偏差,C;コントローラー,G:プロセス,S:検出部,y:出力 となる。
上記のCはPIDコントローラーに当り、Gはプロセスモデルに当る。
簡易なFeedback制御であれば、Sは不要であり、これをpython-controlで記述する際は、
matlab.feedback(sys1,sys2,-1)を用いることになる。
ここでのsys1は上のC,Gに相当し、sys2はSに相当する。
今回、sys2は1としておいておく。また、最後の-1は負のフィードバックに相当し、通常は負である。
上記を以下にて記述する。
# プロセスモデルを作成する。
# 今回は上記のPの関数と、Pade近似の4次を用いて作成する。
G = P * P4
# feedback loopを作成する
sys = matlab.feedback(G*C,1,-1)
print(sys)
4.step応答(Step response)
化学プロセスにてプロセスモデルの応答性を見る時は、step応答を見るのが一般的である。(ボード線図やナイキスト線図はみたことがない)step応答の何が良いかというと、step応答から、PIDパラメーターのチューニングが出来るという利点がある。
そこで、まずstep応答について説明する。
4-1. 過渡応答(Transient response)の種類
伝達関数はプロセスや制御系の動特性解析を容易にしてくれる。入力の変化に対する出力の時間的変化を見る。この時間的変化は過渡応答(Transient Response) とも呼ばれ、とくに入力がステップ状に変化する場合の応答をステップ応答(Step Respose) インパルス上に変化する場合の応答をインパルス応答(Impulse Response) 、一定の速度で変化し続ける場合の応答をランプ応答(Ramp Response) と呼ぶ。 *「プロセス制御工学」橋本ら著 *
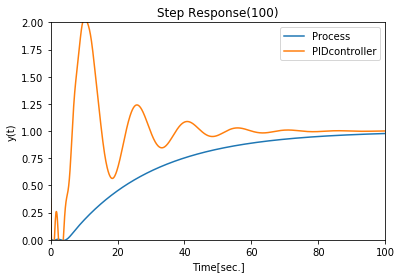
この中で、応答性を見る際によくやるのが、Step応答である。こちらもpython-control内のmatlab.step関数を用いて記述すると、
"""Step Response"""
time= 100 #step応答を算出する時間[分]
t = np.linspace(0,time,1000) #時間を指定する。
y1,T = matlab.step(G,t)
y2, T = matlab.step(sys,t)
y3 = y1/Kt #y軸のスケールをあわせる為、除する
plt.plot(T, y3, label = "Process")
plt.plot(T, y2, label = "PIDcontroller")
plt.title("Step Response(100)")
plt.xlim((0,time))
plt.ylim((0,2))
plt.xlabel("Time[sec.]")
plt.ylabel("y(t)")
plt.legend()
となる。