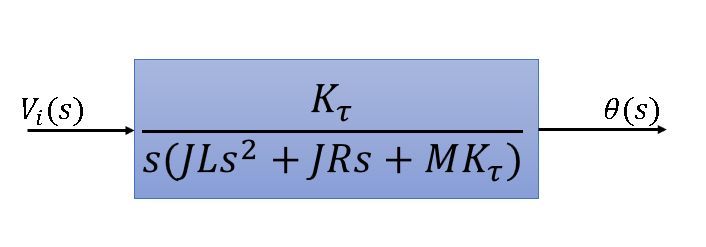これはAmusementCreators AdventCalendar2018の17日目の記事でした。間に合わなくてすみません。
AmusementCreatorsのkerochanです。今回も前回書いた記事の続きです。前回の記事で書いたことを前提にこの記事を書いているので、前回の記事を読まないと分からない部分があるかと思います。
前回の記事
今回の記事はPID制御について記述するが、その前に1つ知っているとシステムの理解に便利な図があるので紹介する。
ブロック線図
下図は、あるシステム(制御系)の入出力の流れを表現した図である。
この図をブロック線図といい、システムの入出力の流れをブロックという長方形を用いて表現した図である。基本的には下図のような矢印とブロックを用いて表現される。$G(s),U(s),X(s)$はそれぞれ伝達関数、入力、出力を表している。
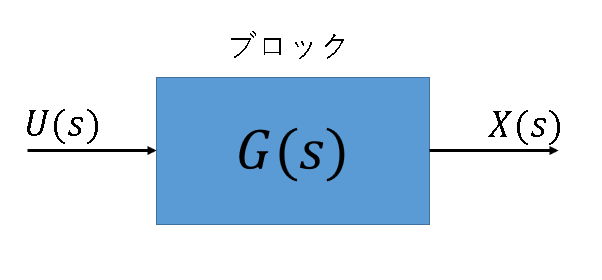
このブロック線図の表す意味は、$X(s) = G(s)U(s)$と等しい。つまり、システムのモデルの表現となっていることがわかる。モデル化されたシステムは基本的には数式で表現されるが、それでは入出力の関係や流れが即座に把握しにくい。そこで、そのモデルをブロック線図を用いて表現してやることで見ただけで入出力関係が明確に把握しやすくなる。さらに、逆にブロック線図の形からおおよそのシステムの動作も把握することができる。これらのことから、ブロック線図がシステムの表現法としてよい方法であるといえる。
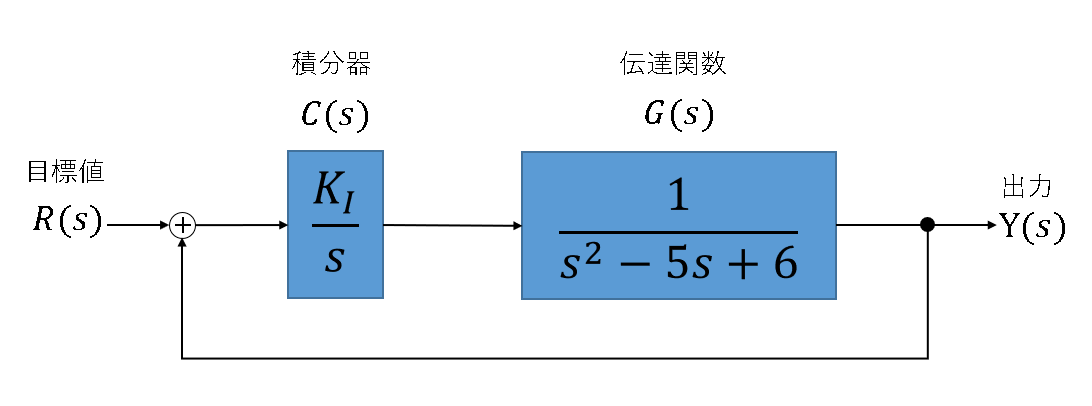
ちなみに、一番初めに示したブロック線図はI制御のブロック線図であり、不安定なシステム(伝達関数$G(s)$の極は共に正数)を積分器によってフィードバック制御している。これについては後に書く。
PID制御
PID制御とはフィードバック制御方法のひとつである。古典制御の発展の中で洗練され長く用いられてきた制御方法で、経験による情報が多く蓄積されているためコントローラのパラメータの調整がしやすく、現在産業界で広く用いられているかつ主力の制御方法となっている。
PID制御の「PID」はそれぞれ比例、積分、微分を表している。これらのことからわかるようにPID制御は比例、積分、微分を用いたフィードバック制御である。
以下、ロボットアームを例にとりPID制御について説明する。
ロボットアームの制御
ロボットアームは、人型ロボットから工場の生産ラインまで非常に広く用いられており、「モノを持ち運ぶ」目的を持つシステムの中で最もポピュラーなものであるといえるであろう。ロボットアームの目的は、「掴んだモノを所定の位置まで持ち運ぶこと」である。人間がモノを持ち運ぶ多くの場合はほこれを実現するためには「アームの位置を目標角度まで動かす」ことが最も重要な要素となる。仮にモノをしっかりと掴めたとしても、最終的な位置が目標角度から大きくずれてしまえば上の目的を実現できなくなるばかりか他のモノやシステムに損傷や誤作動を引きおこすことになる。例えば自動車の生産ラインであればアームがつかんだ部品が車体を傷つけてしまう可能性がある。このようなトラブルを起こさないためには、適切なアームの角度の制御および観測が必要となる。(観測の精度なども制御にとって重要な要素のひとつである)
一般的なロボットアームは人間の腕のようにいくつかの関節がありかつ先端にはモノを掴むことのできる手がついている。しかし、ここでは腕の角度の制御のみを考えたいため、ここでは下図のようなアームを考える。
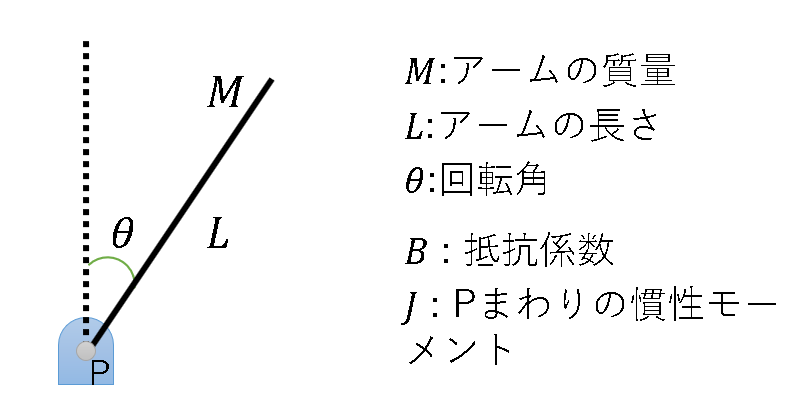
この例では、簡単のため回転による空気抵抗は無視できるとして$B=0$とし、アームにはたらく重力は考えないものとする。
また、回転軸はDCモーターの軸に接続されており、モーターの回転は損失なくアームに伝達されるとする。モーターの回路図を下に示す。
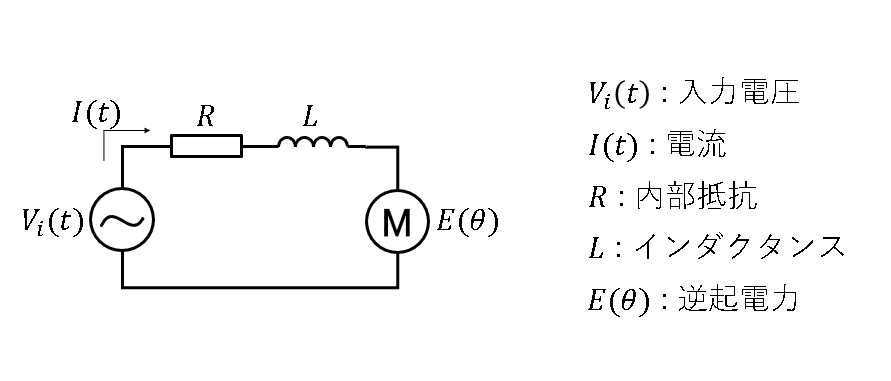
モーター本体はMマークの書かれた円形記号である。
伝達関数を求める
以下入力を$V_i(t)$、出力を$\theta(t)$としてこのシステムの伝達関数を求めてみる。
上の2枚の図から、下の4つの方程式が導かれる。
V_i(t) = R I(t) + L\frac{dI(t)}{dt} + E(\theta) \\
E(\theta) = M\frac{d\theta(t)}{dt} \\
\tau(t) = K_{\tau}I(t) \\
J\frac{d^2\theta}{dt^2} = \tau(t)
これらの方程式は上から
- モーターの回路方程式
- モーターによる逆起電力の式
- モーターのトルクと電流の関係式
- アームの運動方程式
を表している。ただし、$\tau(t)$はモーターのトルク(回転の勢い)、$M,K_\tau$は定数であり、$J, R, L,K_\tau > 0, M < 0$であるとする。さらに、$V_i(0)=0, \theta(0)=\dot{\theta}(0)=0$とする。
上の4式をラプラス変換した結果は下式のようになる。(第1,2式はまとめた)
V_i(s) = (R+Ls)I(s) + Ms\theta(s) \\
\tau(s) = K_{\tau}I(s) \\
Js^2 \theta(s) = \tau(s)
これらを入力と出力の関係式として整理すると下式となる。
\theta(s) = \frac{K_\tau}{s(JLs^2 + JRs + MK_\tau)}V_i(s)
よって伝達関数$G(s)$は下式となる。
G(s) = \frac{K_\tau}{s(JLs^2 + JRs + MK_\tau)}
極と安定性を検討する
求めた伝達関数の極は簡単に求めることができて、下のようになる。
s = 0, -\frac{R}{2L} \pm \frac{\sqrt{(JR)^2 - 4JLMT_\tau}}{2JL}
極に$s=0$が存在する場合、ラプラス逆変換によりその極に対応する項に定数値が現れる。$R,L > 0$よりすべての極の実部が正でないから、このシステムは安定であることがわかる。
なお、$D = (JR)^2 - 4JLMT_\tau$とすると常に$D\geq 0$であるから、$t\to \infty $で出力は必ず振動せずに収束する。
収束速度を検討する
このシステムは抵抗値やインダクタンスの値にかかわらず常に収束することがわかった。これはつまり、アームが目標角度を通り越して回転し続けることがないということである。収束速度についても、$-R/2L$の値を調べることで調べて検討するが可能である。
しかし、この収束速度について検討はできるが変更が難しい場合が多い。なぜなら、モーターの内部構成がわからないか、少なくともこちらで変更することができない場合が多いからである。
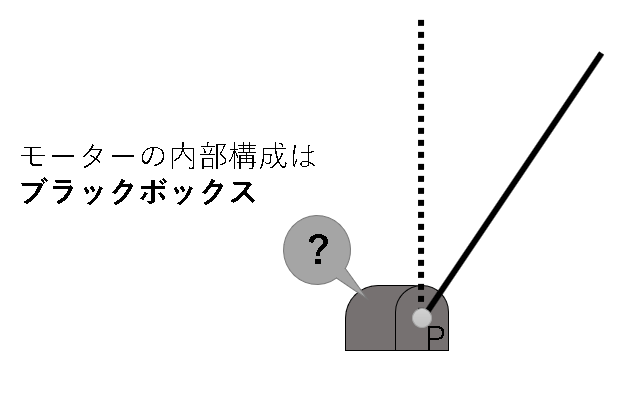
制御の方法はいくつかあるが、この例では記事の初めに紹介したPID制御を用いた制御を考える。
制御器と制御系
制御を行うための要素をコントローラ(制御器)といい、制御の対象となるシステムを制御対象という。また、コントローラと制御対象となっているシステム全体をまとめて制御系という。
コントローラとはいっても、結局は入力に対してある操作をしそれに応じた出力を行うだけであるからブロック線図で表現できる。例えば、この記事で一番初めに示したブロック線図の$C(s)$がコントローラに相当する。そしてPID制御ではこのコントローラの伝達関数の形がP、I、Dの各制御で決まっており、最適な応答となるように各コントローラのもつパラメータを変化させる。なお、一般的な入力に対する最適な応答を与えるようなパラメータを解析的に求めることは不可能であり実験と観察の繰り返しにより決めるものである。
また、出力を目標値へ収束させることが目的であるため、PID制御に限らずフィードバック制御におけるコントローラへの入力は目標値と出力の差となる。これを偏差という。この記事では偏差を「目標値 - 出力」と定義する。つまり、偏差が正ならば出力が目標値よりも小さく、負ならばその逆となる。もし出力が目標値に一致すれば入力が0となるためシステムは動作しない、つまり出力が目標値のままとなる。下図は、PID制御における制御系のブロック線図である。
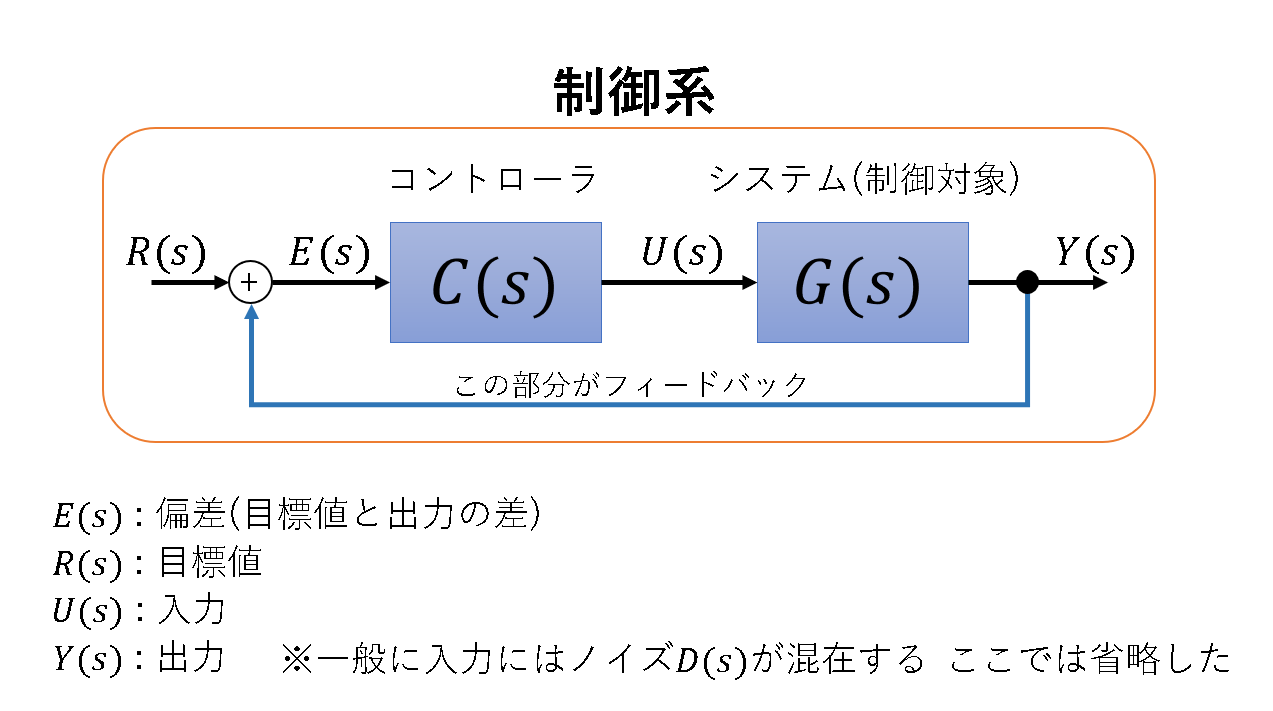
まずは各制御器が出力にどのような影響を与えるか簡単に紹介する。なお、以下の説明では$G(s)=1/(s+1), R(s)=1/s$であるとする。
P制御(比例制御)
P制御を担うコントローラ、比例器は次の伝達関数で表される。ただし$K_P$は定数(パラメータ)である。
C(s) = K_P
この式からも明らかなように、比例制御では偏差を定数($K_P$)倍した出力によってシステムを制御する。下図はシステム$G(s)$にP制御を施し、$K_P$を変化させたときの各パラメータに対する応答を表している。
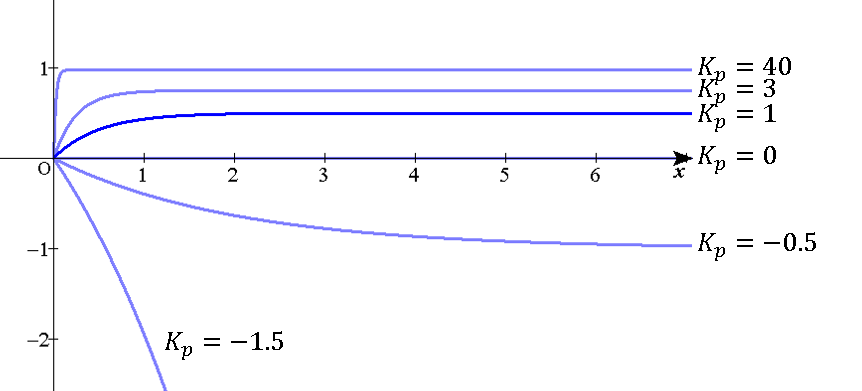
このグラフから、$K_P$の値によって定常値や収束速度が大きく変化していることがわかる。
ここで注目すべきはまず、$K_P=-1.5$のときの応答である。このとき応答は発散しているのだが、元のシステムでは極$s = -1 < 0$であり発散はしない。これはつまり、$K_p$の値によって制御系全体の極を決めることができるということあり、$K_P$は任意に決められることからそれはすなわち、うまく$K_P$を選べば元々不安定なシステムを制御系全体で見れば安定にすることができる、ということである。
前々回の記事で、制御によって不安定なシステムを安定にできると書いたが、これはまさに制御器のパラメータを適切に決めることと同じである。このことは他の制御(I,D制御)においても同じである。
では、P制御の問題点は何であろうか。上の図から容易に想像はできるが、それは定常値が目標値と一致しないということである。上図では目標値を1としているにもかかわらず、定常値はそれよりも小さい。$K_P = 40$では一致しているようにも見えるがわずかに差がある。これは、この制御系の定常値が$K_P/(K_P + 1)$であるため、有限な$K_P$では定常値は厳密に1とならないことによる。
この問題点は制御にとっては致命的で、もはやこれは制御とは呼べないものになっている。なぜなら、制御がそもそも「ある目的に適合するように」対象を操作することであり、P制御のみではある目的=目標値に一致させることに適合していないからである。よって、基本的にはP制御だけ用いることはなく、以下で説明するI制御と組み合わせることになる。
I制御(積分制御)
I制御を担うコントローラ、積分器は次の伝達関数で表される。ただし$K_I$はパラメータである。
C(s) = \frac{K_I}{s}
I制御では偏差を積分して$K_I$倍した出力によってシステムを制御する。下図はシステム$G(s)$にI制御を施し、$K_I$を変化させたときの各パラメータに対する応答を表している。
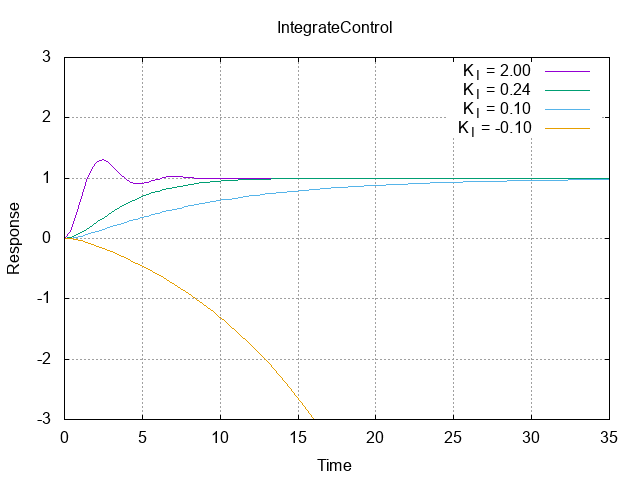
このグラフを見ると、P制御と同様にパラメータ$K_I$によって制御系全体の安定性が決まっていることがわかる。しかし、I制御ではP制御では見られなった振動が発生している。これは、式的には$K_I$を含む分母多項式が二次であることが原因である(この例では分母多項式は$s^2 + s + K_I$)。同様にグラフから、応答が収束する場合は必ず定常値が1、つまり目標値と一致している。P制御の項でI制御とともに用いると書いたのは、このグラフのようにI制御を用いることでほとんどの場合に、定常値を目標値に一致させることができるからである。これを聞くと、P制御の必要性がないと感じるかもしれないが、後述するがI制御のみでは目標値への収束が可能であるがそれとは別の問題点があるためP制御を用いる必要がある。
さて、I制御では偏差の積分を出力として制御すると書いたが、この積分がどのような意味を持つのかを考えてみる。
まず、下にシステム$G(s)$をI制御した時の偏差のグラフを示す。
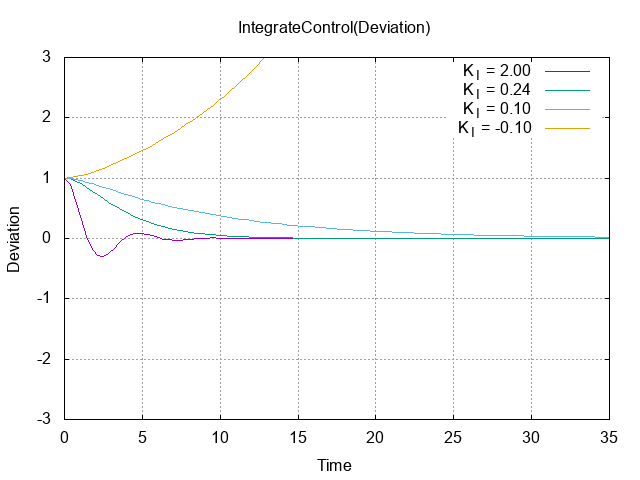
I制御における積分器の積分範囲は$[0,t]$である。つまり、時刻0からある時刻まで偏差を積分していることになる。この積分値は、上のグラフの時刻0から任意の時刻tまでの、偏差の関数とDivision=0で囲まれた領域の面積に等しい(ただし、Division>0の領域の面積は正、Division<0の領域の面積は負であるとする)。
次にシステムの入力を力、出力を位置とした場合(すなわち物体の運動)のI制御の動作の概略図を下に示す。ただし、$e(t)$は偏差を表す。
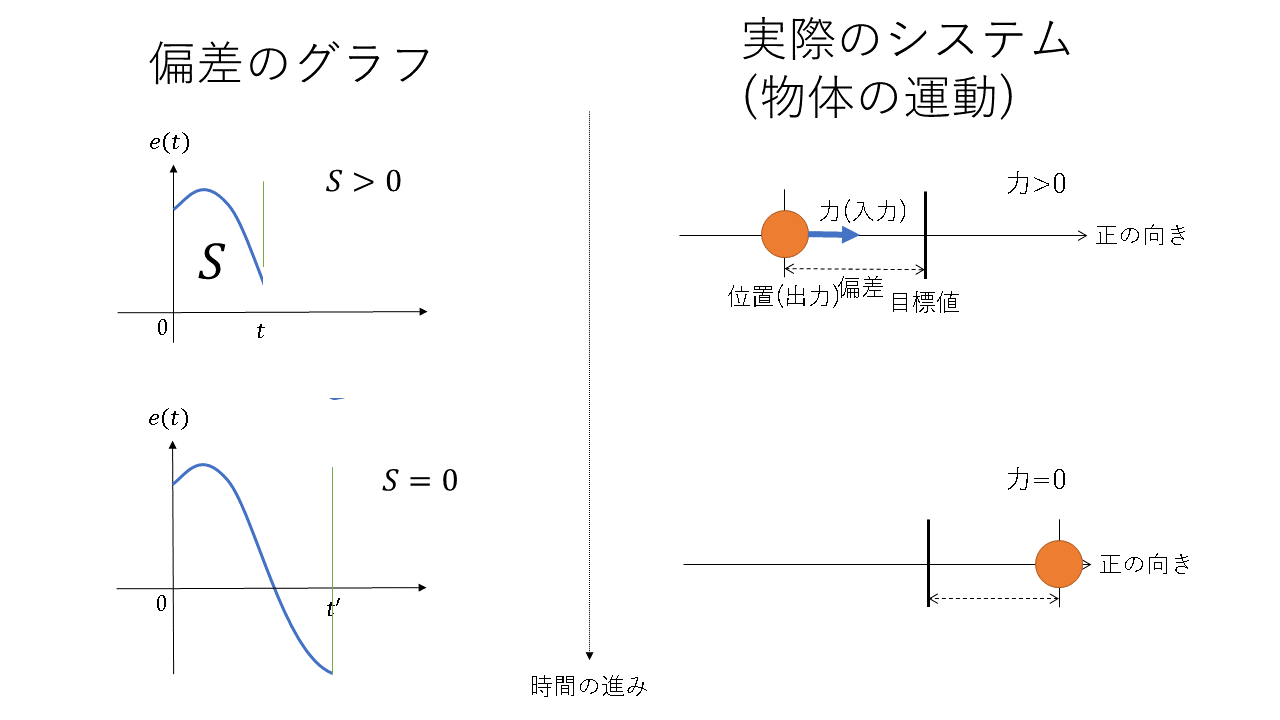
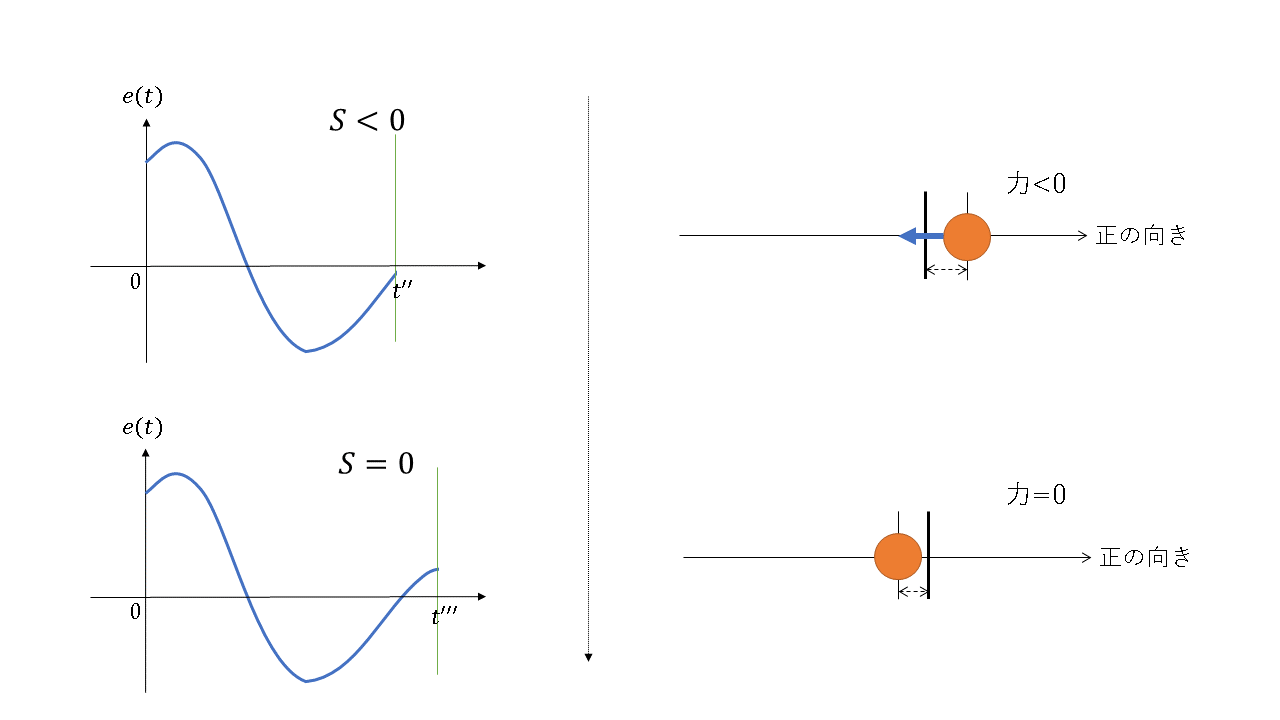
これを見ればI制御における積分の意味がよくわかるであろう。つまりこの積分は、適切なパラメータを設定すれば、時刻0からある時刻までの偏差情報を用いて目標値からのずれを小さくするような値を算出する役割があるということであり、I制御は過去の偏差情報を用いた制御方法といえる。
ここで、「適切なパラメータ」と書いたがその理由は、先に書いたように数式的に見れば極の値に影響するからであるが、次のように考えればその意味が分かりやすい。基本的には$K_I$が大きい程、積分により算出された出力が大きくなる、つまりより早く目標値に収束するようになるということを意味している($K_I=0.24$と$K_I = 0.1$の場合の応答を比較すればわかりやすい)。しかし、大きすぎる場合には上図のように目標値を超えてしまう可能性もありこれが応答の振動の原因となっている($K_I=2.0$で応答が振動していることがわかる)。逆に$K_I$が負の場合は、目標値に向かう方向とは逆向きの入力を与えることを意味するため、明らかに応答は発散する($K_I = -0.1$で応答が発散している)。
これらのことから、I制御の問題点は主に次の2つが挙げられる。
1つは、パラメータが大きすぎることで応答に振動が発生するということ。もう1つは、急激な偏差の変化を反映させることが難しいということである。前者の理由は上で示した。後者の理由はI制御が過去の偏差情報を利用しているため、変化が起こってから十分な時間が経過しなければ制御対象への入力にその変化の情報が反映されないからである。このことは下図を見ればよくわかるであろう。なお、このような急激な偏差の変化は外部からの大きなノイズによって起こりうる。
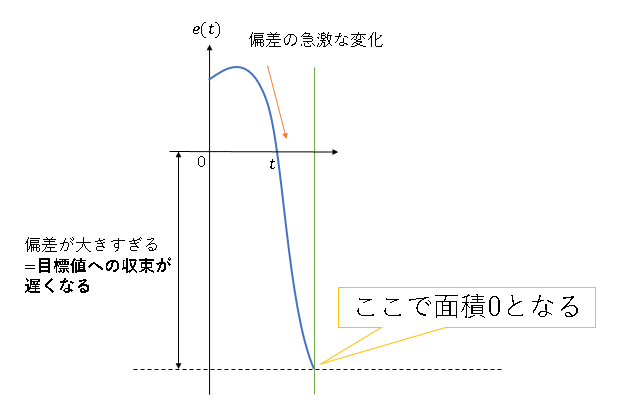
上の図を見ればわかるように、偏差の情報が反映されるまでに時間がかかるためその分目標値からのずれが増加する。それはつまり収束に時間がかかるということでもある。このことは、仮に大きなノイズがなかった場合にも、十分時間が経過していなければ積分器による制御対象への入力はあまり大きくならないということである。すなわち、I制御のみでは収束が遅いということである。先に書いたI制御とP制御を併用する理由は、I制御の目標値に収束するという機能は残しつつ、収束の遅さをP制御によって改善するためである。P制御が有効である理由は、パラメータの値によって応答の収束をかなり早くさせることができる($K_P = 40$のグラフが顕著である)ためである。
まとめると、I制御は応答を目標値へ収束させることはできるが、その速度は遅めでしかも急激な偏差の変化を即座に反映させることは困難と言える。収束の遅さはP制御を用いることで改善できるが、ノイズによる急激な偏差の変化を即座に反映させることはできない。一般のシステムでは大抵外乱が入るため、急激な偏差の変化は無視することができない。よって、これに対して適切な制御をしなければ性能の悪化につながることは容易に想像がつく。この問題点を改善するための「適切な制御」が次に紹介するD制御である。
D制御(微分制御)
D制御を担うコントローラ、微分器は次の伝達関数で表される。ただし$K_D$はパラメータである。
C(s) = K_D s
D制御では偏差を微分して$K_D$倍した出力によってシステムを制御する。下図はシステム$G(s)$にD制御を施し、$K_D$を変化させたときの各パラメータに対する応答を表している。
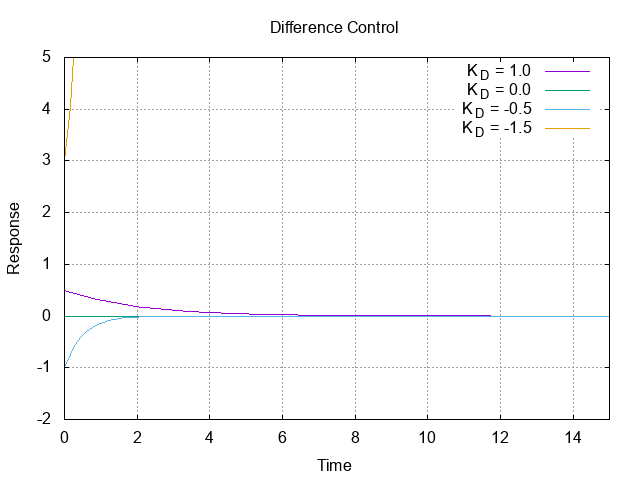
この図を見ると、P,I制御とは応答の形が大きく異なることがわかる。特に初期値が0でない点、定常値が0であるという点が顕著である。
D制御の物理的な意味はI制御と比較して考えるとわかりやすいと思う。偏差の微分とはある時刻における偏差の変化量であるから、偏差の増加量または減少量を$K_D$倍した値を制御対象の入力として制御していることになる。ここまで聞けば、I制御と組み合わせることがなぜ有効なのかがわかるであろう。I制御の問題点は、急激な偏差の変化に対して即座にその影響を出力に反映できないということであった。適切なパラメータを与えれば、D制御ではこの急激な変化に即座に反応して変化を抑えるような入力を制御対象に与える。つまり、適切なパラメータを与えればD制御は、I制御の問題点を補うような動作を行うということである。これがI制御とD制御を併用する理由である。ただし、I制御の場合と同様に、適切なパラメータを選ばなければ出力は発散してしまう($K_D = -1.5$の応答は正の方向に発散)ことには注意すべきである。さらに、このシステムの場合には表れないが、$K_D$の値によっては振動が発生するシステムも存在し得るため注意が必要である。このようになる理由は、I制御で振動する場合と同じように考えればよい。
ここまで、P,I,Dの各制御について説明したが、各制御方法にはいくつかの欠点が存在することもわかった。この欠点を補うために、基本的にはこの3つの制御方法を組み合わせて制御系を構築する。その際、比例器、積分器、微分器が互いに影響しないようにこれらのコントローラはブロック線図上では並列に組み合わされる。すなわち、PID制御でのコントローラは下のようなブロック線図で表される。
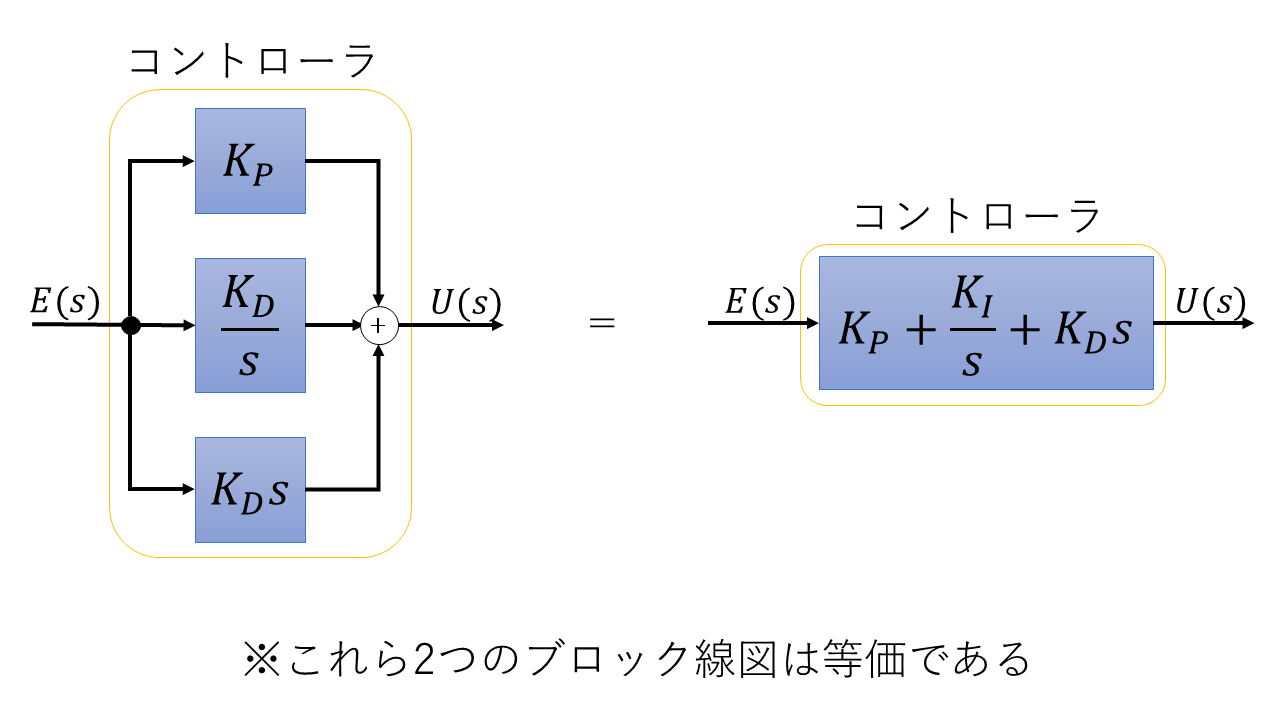
よって、コントローラの伝達関数$C(s)$は下式となる。
C(s) = K_P + \frac{K_I}{s} + K_D s = \frac{K_D s^2 + K_p s + K_I}{s}
PID制御の適用
さて、PID制御の説明に大きく文章量をとってしまったがやっとここで実際にシステムにPID制御を施してみる。
制御対象のシステムの伝達関数を下に再掲する。
G(s) = \frac{K_\tau}{s(JLs^2 + JRs + MK_\tau)}
このシステムにPID制御を施した場合の制御系のブロック線図は下図のようになる。ただし今回はノイズ$D(s)$は無視するものとする。
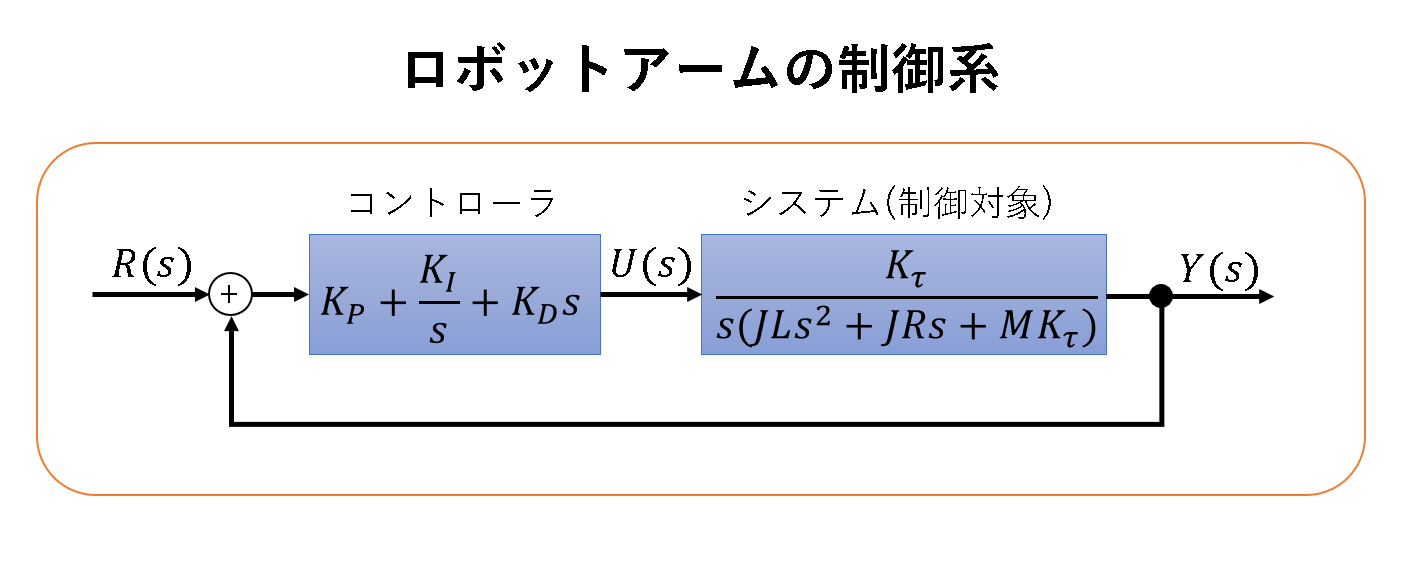
このような形で表されるブロック線図の目標値$R(s)$と出力$Y(s)$の関係は下式で表される。
Y(s) = \frac{C(s)G(s)}{1 + C(s)G(s)}R(s)
ここで$H(s)$を上式の伝達関数する。つまり、
H(s) = \frac{C(s)G(s)}{1 + C(s)G(s)}
とすと、出力が安定であるためには$H(s)$が安定であればよいことがわかる。($H(s)$が安定な時、この制御系は内部安定であるという)
$H(s)$の中身を計算すると下式となる。
H(s) = \frac{K_\tau(K_D s^2 + K_P s + K_I)}{JLs^4 + JRs^3 + K_\tau(M + K_D)s^2 + K_\tau K_P s + K_\tau K_I}
安定性を判別する場合、通常は分母多項式の極を求める必要があるが、上式のように分母多項式が複雑な場合は極を求めることが難しい。そこで今回は、極を求めなくとも分母多項式の係数だけで安定性を判別できる方法を用いて安定性を判別してみることにする。この方法をラウスの安定判別法といい、係数を用いた簡単な計算とラウス表と呼ばれる表を用いることで簡単に安定性の判別ができる、非常に優れた方法である。詳しい方法については下のURLを参考にしてほしい。そこまで難解な計算があるわけではないので比較的簡単に理解できると思う。(理論は理解が難しいが)
ラウスの安定判別法
この方法を用いてラウス表を作成すると下のようになる。
| 項 | |||
|---|---|---|---|
| $s^4$ | $JL$ | $K_\tau(M + K_D)$ | $K_\tau K_I$ |
| $s^3$ | $JR$ | $K_\tau K_P$ | 0 |
| $s^2$ | $K_\tau(M + K_D -LK_P/R)$ | $K_\tau K_I$ | 0 |
| $s^1$ | $K_\tau K_P - JRK_I / (M + K_D -LK_P/R)$ | 0 | 0 |
| $s^0$ | $K_\tau K_I$ | 0 | 0 |
制御系が安定であるには、元の分母多項式の係数がすべて正かつラウス列と呼ばれる数列の要素がすべて正である必要がある。
これを踏まえて、制御系が安定となるような各パラメータの範囲は下のようになる。
K_D > -M \\
K_P > 0 \\
K_I > 0 \\
M + K_D > \frac{L}{R} K_P \\
\frac{L}{R} K_\tau K_P^2 - K_\tau(M + K_D)K_P +JRK_I < 0
これを満たすようなパラメータを設定することで制御系は安定となる。ここで安定性が保証されたので、次は安定となる範囲で過渡特性や定常特性が最適となるようなパラメータを設定することが必要となる。これには、先に書いたように解析的に最適なパラメータを求めることはできない。そのため、実際にパラメータを設定しその応答を記録してパラメータごとの応答を比較する、というような方法で最適なパラメータを求めていく。ただし、PID制御に関する知識は非常に多いため最適なパラメータをある程度決めることができる方法がいくつか存在している。この記事ではその方法は示さないが、気になる人は各自調べてみてもよいかもしれない。
本来ならば上で書いたようなことをして最適なパラメータを求めるのだが、さすがにモーター内部の抵抗値やインダクタンスを調べられるような道具や場所がないため、大変申し訳ないがこの記事ではここで終わりとする。
まとめ
アドベントカレンダー遅れてごめんなさい。図を描いたり計算したりしてたら期日に間に合わなくなってしまいました。毎日コツコツ書かないとだめですね。。。
さて、これでやっと古典制御の話をだいぶおおざっぱですが書くことができました。。本当なら、実際のシステムを作って実験をして。。。としたかったんですけど、何分そこまで充実した設備はないので数式的な部分だけで済ませてしまいました。かなり急ぎ足で書いたので(特にD制御からあとの部分)、何を言っているのかわからない箇所、誤字・脱字など至らない部分があるかもしれませんが、もしそのような個所があればコメントなどで報告お願いします。この記事を読んでもし制御に興味を持ってくださる方がいればとても嬉しく思います。
参考文献
PID制御 - Wikipedia (https://ja.wikipedia.org/wiki/PID%E5%88%B6%E5%BE%A1)アクセス月日 2018年12月15日
ラウス・フルビッツの安定判別法 - Wikipedia(https://ja.wikipedia.org/wiki/%E3%83%A9%E3%82%A6%E3%82%B9%E3%83%BB%E3%83%95%E3%83%AB%E3%83%93%E3%83%83%E3%83%84%E3%81%AE%E5%AE%89%E5%AE%9A%E5%88%A4%E5%88%A5%E6%B3%95)アクセス月日 2018年12月19日
佐藤和也、平元和彦、平田研二『はじめての制御工学』講談社,2010年