これはAmusementCreators AdventCalendar2018の10日目の記事です。
AmusementCreatorsのkerochanです。今回は前回書いた記事の続きみたいなものです。前回の記事で書いたことを前提にこの記事を書いているので、前回の記事を読まないと分からない部分があるかと思います。
前回の記事
システムの極と安定性
今回の記事はシステムと極の安定性について書いてある。
伝達関数の極と零点
前の記事で、線形時不変なシステムは次の形でモデル化されることを示した。
\sum_{i=0}^n a_i \frac{d^i x(t)}{dt^i} = \sum_{i=0}^n b_i \frac{d^i u(t)}{dt^i}
この式において、$x(t)$を入力、$u(t)$を出力とし、$x(t)$のラプラス変換を$X(s)$、$u(t)$のラプラス変換を$U(s)$、
x(0) = 0, \frac{dx(0)}{dt} = 0, \cdots ,\frac{d^nx(0)}{dt^n} = 0 \\
u(0) = 0, \frac{du(0)}{dt} = 0, \cdots ,\frac{d^mu(0)}{dt^m} = 0
とすると、両辺をラプラス変換した結果は下のようになる。
X(s) = \frac{\sum_{i=0}^m b_is^i}{\sum_{i=0}^n a_is^i}U(s) \\
上式から、このシステムの伝達関数$G(s)$は、
G(s) = \frac{\sum_{i=0}^m b_is^i}{\sum_{i=0}^n a_is^i}
であることがわかる。
ここで、$G(s)$は有理関数でありその分母と分子は共に$s$に関する多項式になっている。$s$は複素数であることに注意しておきたい。この多項式をそれぞれ分母多項式、分子多項式といい、分母多項式の値が$0$になるような$s$をシステムの極といい、分子多項式の値が$0$になるような$s$をシステムの零点という。
極の値はシステムの安定性に大きく関係し、零点はシステムの収束の速さに大きく関係している。
極と安定性
極の値は安定性に大きく関係していると書いたが、そもそもシステムの安定性とは何か。
安定性とは、簡単に言えば**「あるシステムへの有限の入力に対し、出力が発散つまり無限大にならないこと」である。
そして、結論から言えば、システムが安定であるための条件は「伝達関数の全ての極の実部が負であること」**である。
たとえ実部が正であるような極が1つあっただけでも、そのシステムの出力は無限大に発散する、つまり不安定になる。
また、システムが安定であるような極であったとしても、極の値によって「どのくらい早く収束するか」や「振動するかしないか」などシステムの特性(性能)に大きく影響するため、極の値はシステムの制御にとって最も重要な指標といえる。
なお、零点は先に書いたようにシステムの安定性を決定する要因ではないが、システムの過渡特性に影響するためこれもまた制御では重要な指標であるといえる。
ステップ応答とインパルス応答
システムの特性を調べるために、入力としてインパルス関数と単位ステップ関数を入れた際の出力を用いることが多い。この出力を特別にインパルス応答、ステップ応答という。この二つの応答を調べることで、システムの大まかな特性を知ることができる。
インパルス関数と単位ステップ関数については下のリンクから各自調べてもらいたい。
単位ステップ関数、インパルス関数(ディラックのデルタ関数)
これらの関数の具体的なイメージとしては、単位ステップ関数は電灯のスイッチのON(=1)とOFF(=0)の切り替えを表しており、インパルス関数はハンマーなどで一瞬だけ物体を叩いた際に生じた力を表している、というようなものを考えてもらえればよい。
インパルス関数および単位ステップ関数のラプラス変換を$U_1(s), U_2(s)$とすると、それぞれ次のようになる。
U_1(s) = 1 \\
U_2(s) = \frac{1}{s}
よって、伝達関数$G(s)$で表されるようなシステムのインパルス応答とステップ応答、$X_1(s), X_2(s)$は次のようになる。
X_1(s) = G(s)U_1(s) = G(s) \\
X_2(s) = G(s)U_2(s) = \frac{G(s)}{s}
この式からわかるように、インパルス応答は伝達関数そのものであることがわかる。これは、仮にシステムの具体的なモデルがわからなくても、インパルス応答を見ることで、そのシステムの伝達関数がわかるということであり、これはすなわちシステムがどのようなモデルで表されるかを解析することと同じである。よって、インパルス応答はシステムのモデルの解析に非常に有用であることがわかる。
また、ステップ応答の形に関していくつかの指標が定量化されておりこれらの指標を慣習的に用いていることから、ステップ応答が具体的なシステムの特性をわかりやすい形で表現しているといえる。
例として、下に伝達関数$G(s) = 1/(s^2 + 8s + 16.25)$で表されるシステムのインパルス応答とステップ応答のグラフを示す。なお、この形の伝達関数で表されるシステムを二次遅れ系という。
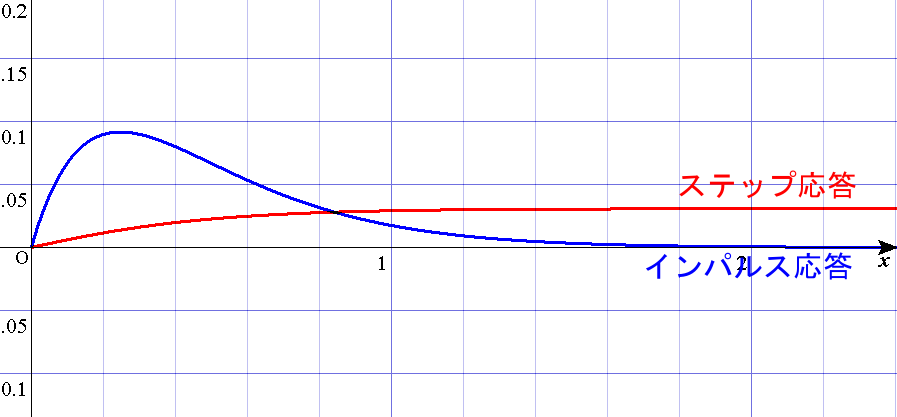
定常特性と過渡特性
十分に時間が経過した際のシステムの出力の収束性に関する特性を定常特性といい、その際もしも出力がある値に収束するならばその値を定常値という。
また、定常値に至るまでの出力の変化に関する特性を過渡特性という。
この2つの特性に関する指標はいくつかあり、例として下に2つ示す。
- 遅れ時間 : システムの速応性(収束の速さ)に関係。出力が定常値の50%になるまでの時間
- 行き過ぎ時間 : システムの減衰性(振動の収束の速さ)に関係。出力が応答の最大値となるまでの時間
これらの過渡特性は、先に書いたようにステップ応答によって解析できる。
制御によるシステムの性能改善
前回の記事で、システムは制御してこそ使用できると書いた。自動車であれば制御できて初めて安全に走行でき、電子機器であれば制御して初めて安定して動作可能になるのである。
制御をする目的は、上記のようにシステムの安全性を確保することだけではない。システムの性能を向上させることもその目的である。例えば、自転車を例に挙げて考えてみる。自転車も入力をペダルの回転速度、出力を位置とすればシステムであるといえる。
ここに、2台の自転車A,Bがあるとして、自転車Aは5秒間ある一定の速さでペダルをこぐことで目標値である時速10kmに達し、Bは10秒間こぐことでその速度に達するとする。この2つの自転車の性能を比較すると明らかにAの方が加速が早く、加速の面では性能が高いことがわかる。
しかし、仮に自転車Bのこぐ速度を2倍にすることで自転車Aと同じ時間で同じ時速に達することができるとすれば、それは形式的には自転車Aと自転車Bは同じ性能であるといえる。
これはまさに入力を制御することで性能を改善しているということである。(もっとも、自転車の場合は入力を加える原動力が人間であることから、この制御方法は手動制御にあたる。そのため、制御をしている側から見ても、外から自転車をこいでいる人を見ても性能が同じであるとか考えにくいかもしれないが)
上の例のように、コントローラ(上の例では入力を2倍するという動作)を用いて入力を制御し出力を目標値へ収束させる制御方法をフィードフォワード制御という。これとは別に、入力を出力の値と目標値との差としてそれをコントローラを通してシステムに入力し出力を目標値へ収束させる制御方法をフィードバック制御という。
簡単に言えば、前者は出力を使わない制御方法、後者は出力を用いる制御方法ということである(これは人間の行う制御方法であるともとれる)。
一般にシステムには外乱(システムへのカオス的な入力)が入るが、フィードフォワード制御ではこの外乱の影響が排除できないため、基本的にはフィードバック制御の方が多く用いられる。ただし、フィードフォワード制御の方が出力のセンシングが不要であるという点で設計コストが安く済むため、外乱がほとんどないような場面での制御にはフィードフォワード制御が適している。
まとめ
今回はシステムの極と安定性について書きました。本当はPID制御まで書きたかったのですが、これまた個人的な事情で書けなかった(投稿1日前に書き始めたせいですすみません)ので次回の記事に書きたいと思います。
この記事について何かおかしな点や疑問点等あればコメントをお願いします。
参考文献
よく使われる関数のラプラス変換
https://eleking.net/math/m-laplace/ml-function.htmlアクセス日時 2018/12/10 18:37
ディラックのデルタ関数-大人になってからの再学習
http://zellij.hatenablog.com/entry/20120613/p1 アクセス日時 2018/12/10 18:37
佐藤和也、平元和彦、平田研二『はじめての制御工学』講談社,2010年
佐藤和也、下本陽一、熊澤典良『はじめての現代制御理論』講談社,2012年