これはAmusementCreators AdventCalendar2018の3日目の記事です。
AmusementCreatorsのkerochanです。今回は工シスらしいことでも書こうかと思い、「システム」について書いてあります。
といっても、システムに関しては講義なので学習した程度で完全に理解しているわけではないので、もし何か誤りやおかしな解釈、わかりにくい点などがあればどんどん指摘してほしいです。
システムとは何か
私達は日常的に、そうでなくとも技術的な話し合いにおいてよく「システム」という単語を耳にしたり使ったりするが、そもそも「システム」とはどのようなものであろうか?
JISZ8115では、次のように定義されている。
所定の任務を達成するために, 選定され, 配列され, 互いに連係して動作する一連のアイテム (ハードウェア, ソフトウェア, 人間要素) の組合せ
簡単に言えば、ある目的を達成するために、互いに連携して動く複数の要素全体ということである。
この定義に照らし合わせれば、例えば「自動車」は、「人を移動させる」という目的の達成のために、「エンジン、タイヤ、ハンドルなど」の部品が「互いに動力や情報をやりとりして」動作しているためシステムである、と言える。
このように考えれば、飛行機や船舶などの乗り物類、ロボットアームや蒸気機関などの機械類、そしてパソコンや組み込みハードウェアなどの電子機器類などもシステムであると言えるであろう。世の中の様々なものがシステムなのである。
さて、システムが動作するためには何かしらの「信号」が必要である。そして、システムを用いる場合そのシステムによって何かしらの「結果」が生成される。先の例の自動車でも、「アクセルペダルを踏む」という「信号」がなければ自動車本体は動かない。また、自動車の目的が人を移動させる、ということであるから「位置」が「結果」となる。
この、「信号」と「結果」をそれぞれ「入力」と「出力」と呼ぶ。自動車であれば、上の例の場合、入力は「アクセルペダルを踏むこと」であり、出力は「位置」ということになる。
上のことを言い換えれば、「システムが動くためには適当な入力が必要であり、それにより出力が得られる」ということである。図で表せば下のようになる。

自動車の例では、上の図のシステムが「自動車」、入力が「アクセルペダルを踏むこと」、出力が「位置」ということになる。
システムの解析
システムを解析することは、そのシステムの安全性や性能の分析やそれによるシステムの最適化などに大きく貢献する。先に書いたように、システムは私達の生活の中で非常によく用いられるものである。そのため、システムの解析を行うことは、システムの不具合やそれに起因する人的、物的被害を抑えることにつながる。すなわち、システムを解析することは極めて重要なことである。
では、そのシステムの解析というのはどのように行えばよいのだろうか。
例えば、自動車と船舶と飛行機の三つのシステムでは、動作や内部の構造は大きく異なっている。そのため、この三つは全く別のシステムと考えられるかもしれない。しかし、これらのシステムは次のような共通点を持っている。
- 入力は「力」、出力は「位置」
つまり、これらのシステムは互いに全く異なるものだが、内部の構成を考えなければ同一の形式で表されるということである。
この「同一の形式」というのは、例えばこの三つのシステムの場合は下の運動方程式である。ただし、$m$は質量、$x$は変位、$f$は力であるとする。
m\frac{d^2 x}{dt^2} = f
システムの動作や内部構成は、物理現象と深い関わりがあるため上のような微分方程式の形で表されることが多い。このように、システムを数学的な数式に表すことをモデル化といい、モデル化されたシステムをあらわす数式を数学的モデルという。
システムをモデル化することで、システムを数学的に解析することができ、そのシステムの性能や特性の分析が容易になる。また、上の三つのシステムのように、異なるシステムを同一の形式のモデルにすることが可能となり、互いに異なるシステムであった場合も同じ手順でシステムを解析することができる(全てのシステムが同じモデルで表現されるわけではない)。
これがシステムをモデル化する利点であり、モデル化によりシステムの解析が容易になることがわかる。
システムの制御
システムの解析は、安全性などの面において非常に重要であると説明したが、もう一つ「制御」という面においても非常に重要である。
「制御」とは、JISZ8116で次のように定義されている。
ある目的に適合するように、対象となっているものに所要の操作を加えること
対象をシステムと考えれば、制御とは「ある目的を達成するように、システムにある操作を加えること」ということになる。
システムは制御されて初めて使えるようになるといっても過言ではない。例えば、自動車の場合アクセルペダルをずっと踏み続ける、ということはしないはずである。そんなことをすれば、他の自動車や建築物などに衝突し、人的物的被害を発生させうることになりかねない。確かに人を運ぶという目的は達成されたかもしれないが、その目標が「安全に」達成されたとはいいがたい。
私達は普通、現在の自動車の速度や位置(出力でもある)、あるいは他の自動車や建築物との距離などの情報からアクセルペダルを押したり放したりするはずである。これがまさに「制御」であり、制御により初めて「安全に」人を運ぶという目標が達成される。すなわち、システムと制御は密接な関係にあるということである。
制御では、入力を「操作量」、出力を「制御量」といい、制御するシステムのことを制御対象という。この場合は人間が目や耳で得た情報や制御量を元に操作量を変化させているため、手動制御と呼ばれる。これとは対照的に、近年話題の自動運転のように、機械やコンピュータなどが情報や制御量を元に操作量を変化させることを自動制御という。
さて、システムの解析は制御にとっても重要であると書いたが、その理由はシステムの性能によって制御を行った際のシステムの出力が変化するからである。例えば、自動車Aの2倍の質量を持つ自動車Bを考え、「ある時速以上になったらアクセルペダルを放す」という方法で制御を行うとすれば、明らかにペダルを放すまでの時間は自動車Aの方が短い。
このように、システムの性能によって同じ制御方法であってもシステムの出力が変化する、すなわちシステムによって最適な制御方法は異なるということである。システムにとって最適な制御方法を選択しなければ、制御はできても効率が悪い、もしくは制御の意味をなさないということになり、システムの安全な動作が保障できなくなる。よって、システムの解析は非常に重要なのである。
システムの表現方法
前項でシステムは数式で表現できることを示したが、その表現方法は主に二つある。
一つは、ラプラス変換という変換を用いて伝達関数という形で表現する方法で、もう一つは、状態変数という新たな変数を用いて状態方程式という形で表現する方法である。後者についてはまた別記事として書こうと考えているため、この記事では前者の表現方法について書く。
伝達関数による表現方法について書く前に、線形時不変なシステムについて下に書いておく。
線形時不変システム
システムの表現形式は、モデル化されているとはいえども非常に多くの種類の形式が存在し、一般のシステムに対する一定の解析方法は存在しない。
しかし、多くのシステムは線形時不変システムという形で表される、ないしは近似できることが知られている。線形時不変システムは下のような線形微分方程式で表される。
\sum_{i=0}^n a_i \frac{d^i x(t)}{dt^i} = \sum_{i=0}^m b_i \frac{d^i u(t)}{dt^i}
線形時不変システムの特徴は、線形性を持ちかつシステムの内部構造が時間変化に影響しないというものである。
なお、線形性を持つというのは、ある入力$u$に対する出力をシステム$f$を用いて$f(u)$と表すとすると、$\sum_{i=0}^n f(a_iu_i) = \sum_{i=0}^m a_i f(u_i)$が成り立つ、ということである。(入力や出力にn乗の項がないと思えばよい)
以下、システムの例として自動車を考える。自動車はエンジンやタイヤなどの多くの部品からなる非常に複雑な構造をもつが、ここでは非常に簡略化し、自動車の運動は下の微分方程式で表されるものとする。この方程式が線形時不変システムを表していることは容易にわかるであろう。
m\frac{dv(t)}{dt} + \mu v(t) = f(t)
この方程式を$A$とおく。
ただし、入力は力で$f(t)$、出力は速度で$v(t)$と表されるものとし、$m,\mu$はそれぞれ自動車の質量、走行する床面の動摩擦係数であり、正の定数である。この二つのパラメータにより、システムの性能が変化する。なお、このモデルで表現されるシステムには他に、例えば歯車の回転運動がある。
伝達関数によるシステムの表現
伝達関数とは、あるシステムへの入力がどのように変化して出力に現れるかを抽象的に表した関数である。一般に伝達関数は$G(s)$と表され、$s$は複素数である。
伝達関数は、ラプラス変換という手法により導かれる関数であり、ここでは関数$x(t)$のラプラス変換を$X(s)$と大文字で表す。
ラプラス変換がどのようなものについてかはここでは詳しくは触れないため、各自wikipediaなどで調べてもらいたい。
(参考 : ラプラス変換の基本的性質、変換表)
伝達関数を求める際には、ラプラス変換の基本的な性質と変換表が理解できれば大体は問題ないため、伝達関数を求めるだけならばラプラス変換の理論的な部分(定義や変換可能な条件など)はわからなくてもよい。
さて、方程式$A$の両辺をラプラス変換し、整理すると次のようになる。ただし初期値$v(0) = 0$とする。
V(s) = \frac{1}{ms + c} F(s) = G(s)F(s)
この方程式が、方程式$A$で表されるシステムの伝達関数を用いた表現である。
この形で表される伝達関数は一次遅れ系と呼ばれ、一般的にシステムの特性を把握しやすくするため次の形に変形される。この式を$B$とする。
G(s) = \frac{1/c}{(m/c)s + 1} = \frac{K}{Ts + 1}
Kは定常ゲインといい、十分に時間が経過したときのこのシステムの出力の値(定常値)に大きく関係している。
Tは時定数といい、出力が定常値の63.2%となる時間を表し、システムの出力がどのくらい早く出力が収束するかに大きく関係している。
また、分母が0になるような$s$をシステムの極といい、システムの出力が収束するか発散するかに大きく関係している。このシステムの場合、$s = -\frac{1}{T}$が極である。
ここで、入力を単位ステップ関数($0 \leq t$で$f(t) = 1$でそれ以外の$t$で$f(t) = 0$の関数)とした場合の出力は、方程式$B$の両辺をラプラス逆変換することで次のようになる。
v(t) = \frac{K}{T}(1 - e^{-\frac{1}{T}t})
上式と式Bを比較すると、一次遅れ系に関して例えば次のことがわかる。
- 速度の変化は指数関数的で、$T>0$から$v(t)$は必ず収束する(これを安定であるという)
- $t\to \infty$で$v(t)\to K/T$ すなわち十分時間が経過すると速度は$K/T$に収束する
- 極$s = -(1/T)$は、指数関数の指数部$t$の係数である
- $T$が大きくなると$t$の係数が小さくなるため、収束までの時間が短くなる
- さらに、$T$が大きくなると定常値は小さくなる
- Kが大きくなると定常値は大きくなる
これらのことから、伝達関数内に現れた定数$T,K$はそのままシステムの性能に対し影響を及ぼしていることがわかる。このことを用いれば、伝達関数さえわかれば、そのシステムの大まかな性能を予想することができシステムの解析に非常に有効な手法であることがわかる。
下に、$T,K$を変化させたときの$v(t)$のグラフを示す。上で箇条書きした内容が正しいことがよくわかるであろう。
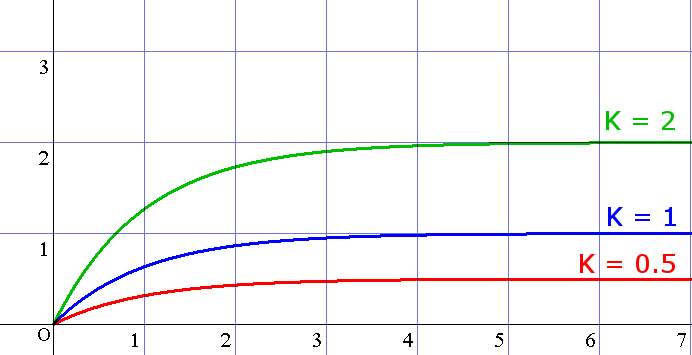
図2 $T=1$としたときのKの変化による$v(t)$のグラフ
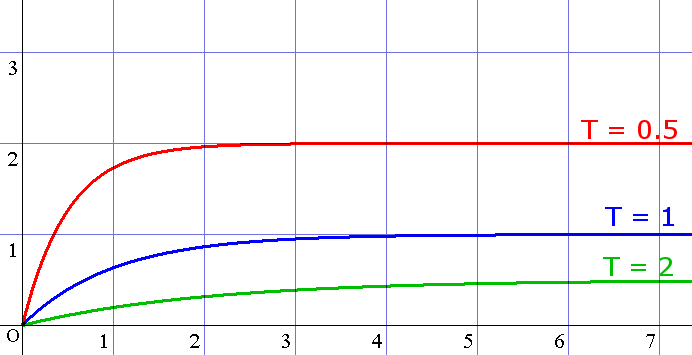
図2 $K=1$としたときのTの変化による$v(t)$のグラフ
まとめ
ここまででシステムとは何か、そしてその表現方法について書いてきた。個人的には、このシステムの制御はとても面白い分野であると思っている。どんなシステムでも、こちらでうまいこと制御を行えば思い通りの出力、つまり結果を出すことができるということである。この、思い通りの制御ができる、というのは僕にとっては非常に興味深く楽しいと思えるものである。今、この制御を用いて面白いゲームを作れないか、とも考えている。制御に関してはまだ素人であるがこれからの学習で自由にシステムの制御ができるようになるくらいにはなりたいと考えている。
この記事では、伝達関数を用いた実際の制御についてと状態方程式を用いたシステムの表現および制御については記述していない。これは、著者の理解がまだ至らない部分があるのと時間の都合で書くことができないからである。そのため、また別の記事でそれらについて書きたいと考えている。
参考文献
システム Wikipedia https://ja.wikipedia.org/wiki/%E3%82%B7%E3%82%B9%E3%83%86%E3%83%A0 2018年12月2日アクセス
佐藤和也、平元和彦、平田研二『はじめての制御工学』講談社,2010年
佐藤和也、下本陽一、熊澤典良『はじめての現代制御理論』講談社,2012年