オミータです。ツイッターで人工知能のことや他媒体の記事など を紹介していますので、人工知能のことをもっと知りたい方などは @omiita_atiimoをご覧ください!
他にも次のような記事を書いていますので興味があればぜひ!
Transformerに畳み込みを!新たに誕生した画像認識モデルCvTを解説!
本記事の流れ:
- 忙しい方へ
- CvTの説明
- CvTの実験結果
- まとめと所感
- 参考
原論文: "CvT: Introducing Convolutions to Vision Transformers", Wu, H., Xiao, B., Codella, N., Liu, M., Dai, X., Yuan, L., Zhang, L., (2021)
実装(非公式): PyTorch
(*) 論文内に記載されている公式実装は2021年5月4日現在でリンク切れになっています。
0. 忙しい方へ
- CvT(Convolutional vision Transformer)は、ViTに畳み込みを導入した画像認識モデルだよ
- CvTは、次の2箇所に畳み込みを導入したよ
- 最初の埋め込み層
- Self-Attentionの埋め込み層
- CvTは、他のViTモデルやResNetモデル(BiT)よりも少ないパラメータ数およびFLOPs数で、より高い分類精度(ImageNet)を叩き出したよ
- CvTは、ViTと異なり位置エンコーディングが必要ないよ
1. CvTの説明
ViT(Vision Transformer)は、畳み込みを一切用いずSelf-Attentionだけで画像を埋め込んでいくモデルでした。ViTでは、1枚の画像を16x16個の小さいパッチに分けることでSelf-Attentionを適用させていました。ViTの簡単な流れを示すと下のようになっています。(大枠の流れです。詳しくは拙著解説を参照してください。)
Patch -> Flatten -> Embed -> Trans -> Trans -> ... -> Trans -> Linear
ここでPatchが画像を16x16個のパッチに分けること、TransがTransformerブロックを示しています。最後のLinearは単なる識別器です。Transの中を少しだけ丁寧に書くと、下のようになります。
Norm -> MSA -> add -> Norm -> MLP -> add
ここで、MSAはMulti-head Self-Attentionのことです。MLPはMulti-Layer Perceptronです。
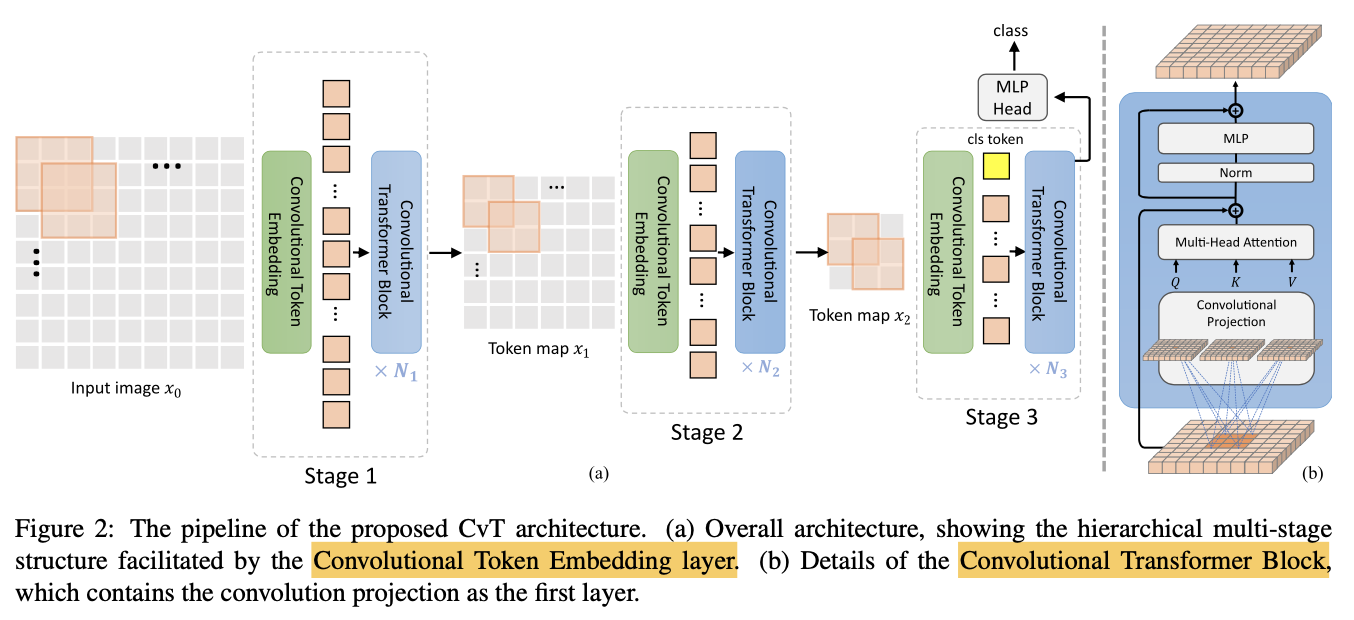
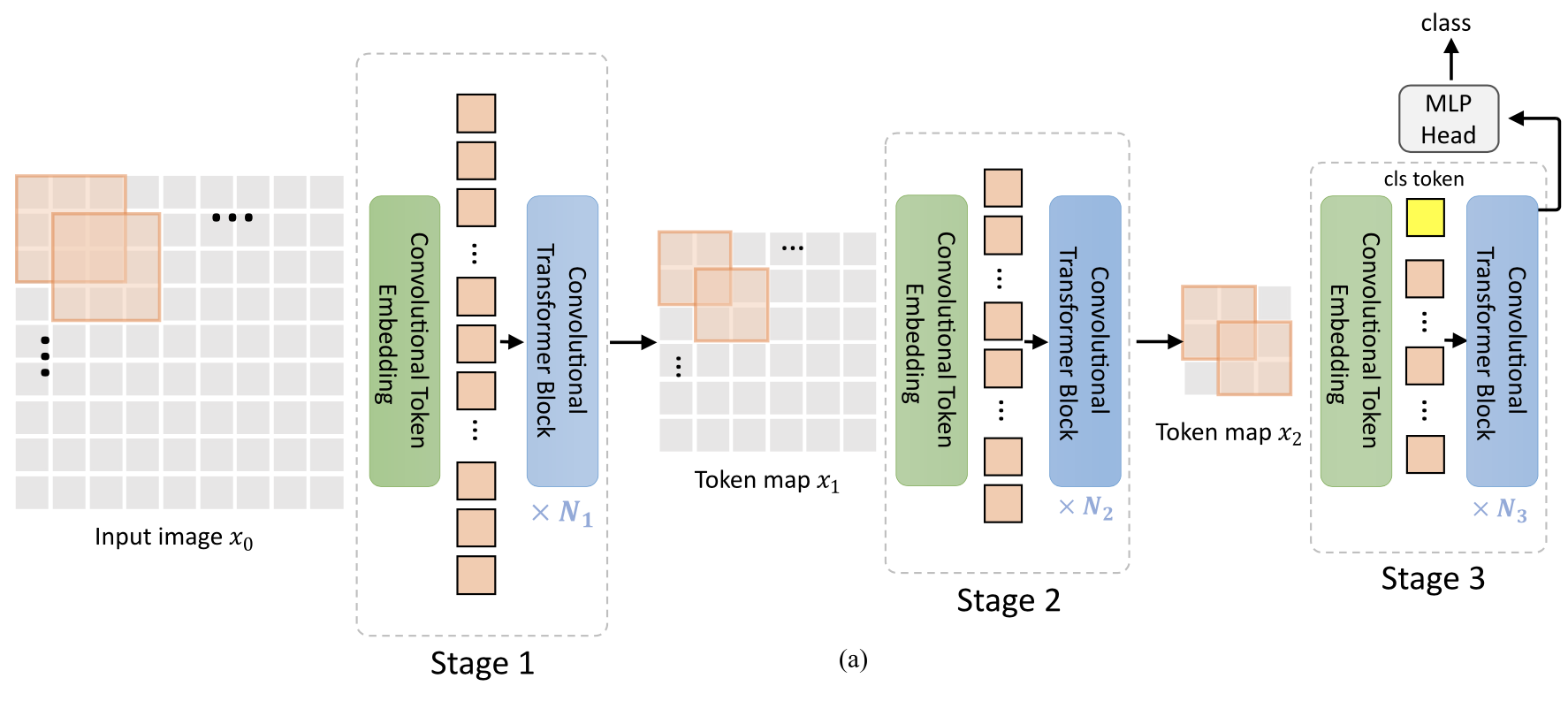
CvTでは、EmbedとMSAに畳み込みを導入しています。論文中ではこれらを新たにConvolutional Token EmbeddingとConvolutional Projectionと呼んでいます。それではCvTを理解するために次の3つの順番で説明していきます。
- Convolutional Token Embedding
- Convolutional Projection
- CvTのアーキテクチャ
1.1 Convolutional Token Embedding
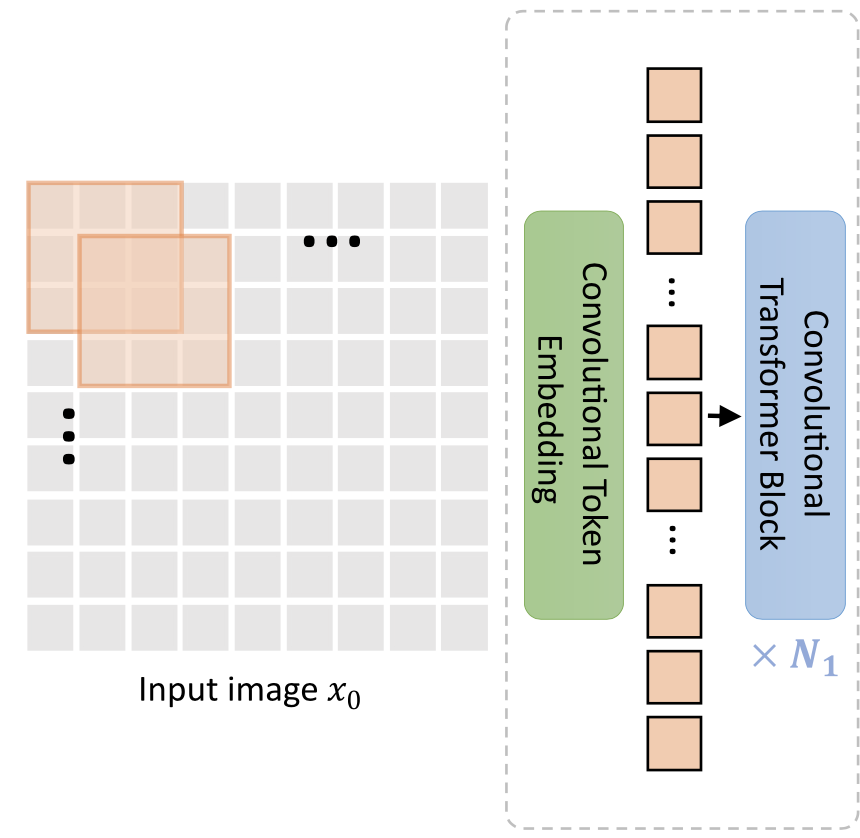
まず、最も単純なCvTは上図のようになっています。入力画像に対して、Convolutional Token Embedding(緑、以下Conv. Embed.)を行います。Conv. Embed.は、何も難しいものではなく、ただの畳み込み層のことです。厳密に言えば、「畳み込み層+Flatten層+LayerNorm」になります。畳み込んで一次元にFlattenしたらレイヤーノームするだけです。
あとは何層(上図中では$N_1$個)にも連なるConvolutional Transformer Block(青)に通すだけです。Convolutional Transformer Blockは単にConvolutional Projection(次節)を用いたTransformer Blockのことです。
CvTではこのConv. Embed.と一連のConv. Trans. Blockのかたまりをステージと定義しています。最終的にCvTは上図のように3ステージで構成されています。ここで特筆すべきはステージ3におけるCLSトークン(黄色)についてです。識別器(MLP)で用いられるCLSトークンはCvTでは最終ステージでのみ登場します。次節ではConv. Trans. Blockで用いられるConvolutional Projectionについて見ていきましょう。
1.2 Convolutional Projection
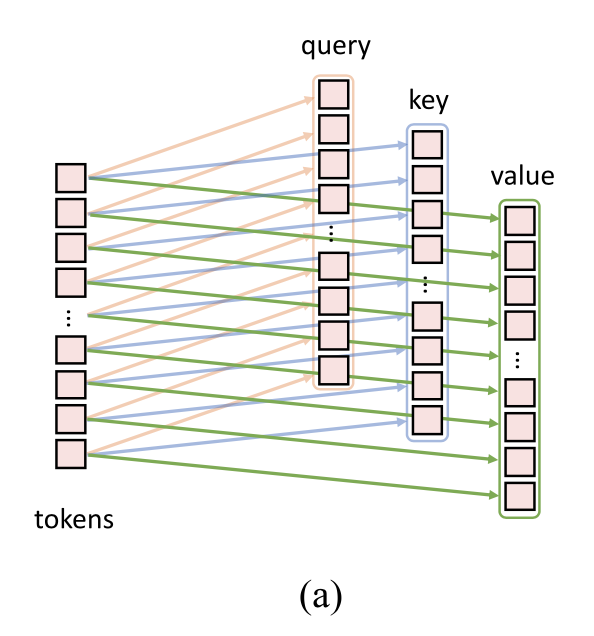
Convolutional Projectionとは、Self-Attentionにおける最初の線形変換を畳み込みで行うもののことです。Conv. Proj.の前に通常のSelf-Attentionにおける線形変換を復習しましょう。上図のように入力ベクトルに対して全結合層で線形変換を行なうことでquery、key、valueたちを手に入れます。線形変換では、ベクトルが入って、ベクトルが出て行ってますね。あとはこれらのquery、key、valueベクトルたちを用いることでSelf-Attentionを計算します。
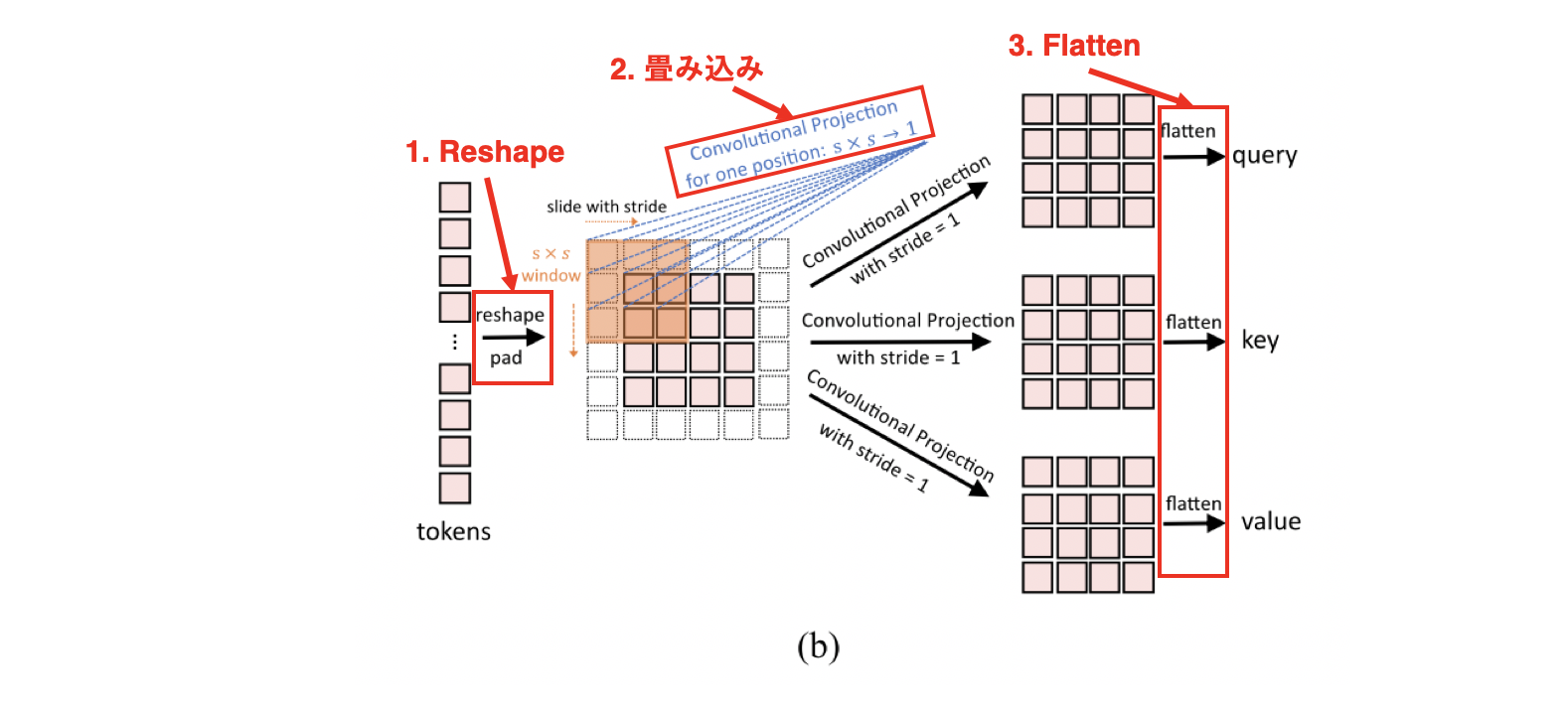
続いてConv. Proj.ですが、そもそもConv. Proj.の目的は畳み込みで線形変換したいというものです。Conv. Proj.ではこの目的を達成するために次の3つの操作を行われています。
- 二次元データへのreshape
- 畳み込み層による線形変換
- 一次元ベクトルへのflatten
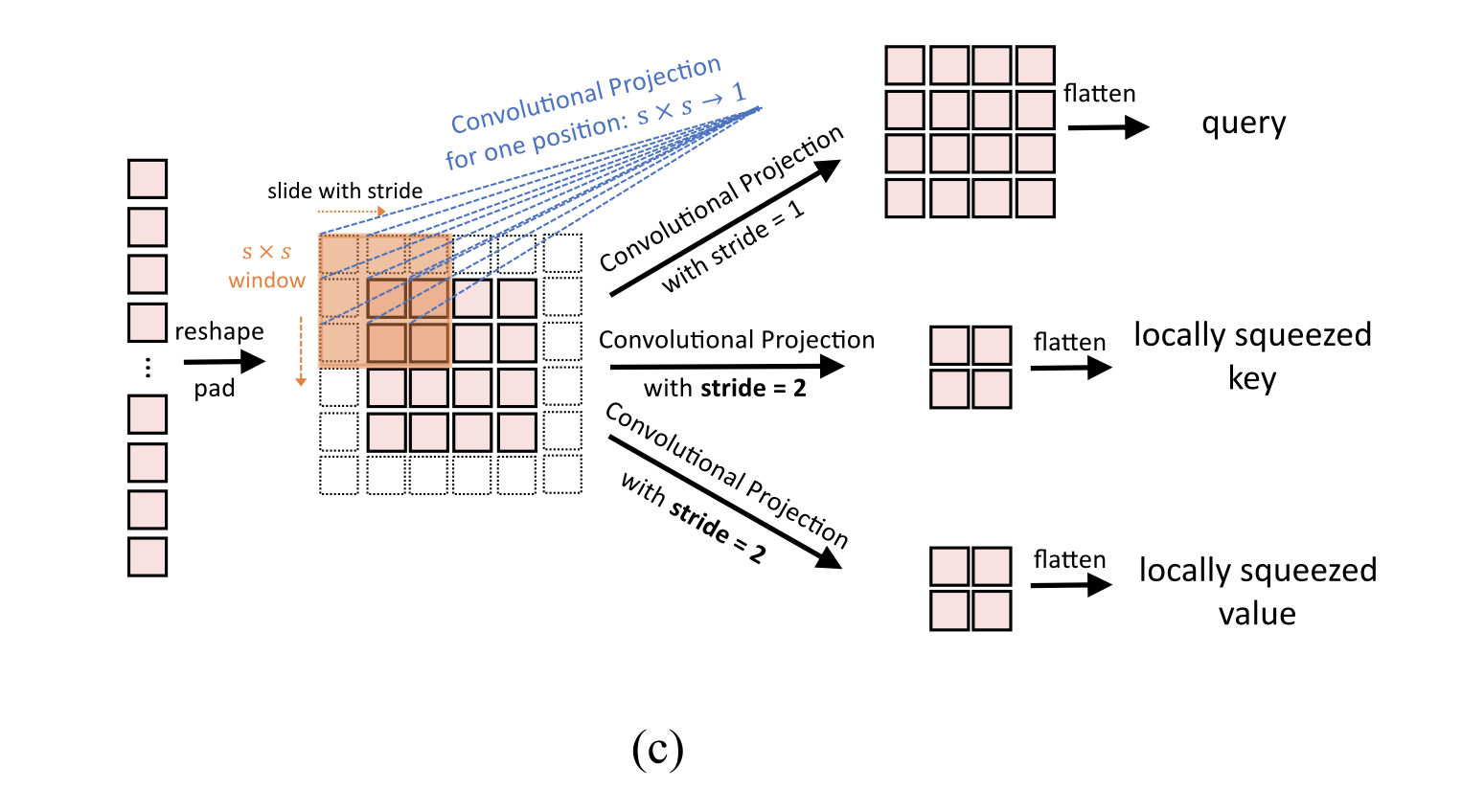
Conv. Proj.の流れを文章で表すと次のようになります。畳み込み層によって線形変換をしたいので、まずは入力ベクトルを二次元にreshapeして、畳み込み層を通したらそれ以降は元どおりのSelf-Attentionの計算ができるように一次元ベクトルへとflattenして戻してあげる。こうしてquery、key、valueを手に入れています。最初と最後だけを見てあげるとConv. Proj.でもベクトルで入ってベクトルで出て行ってくれていることがわかります。なのであとは通常通りSelf-Attentionを計算するだけになります。本論文ではさらにConv. Proj.の計算量を減らすためにkeyおよびvalueを計算する時の畳み込みのストライドを2としています。(畳み込み後の大きさが半分になる。)これをSqueezed Convolutional Projectionと呼び、CvTでは基本的にこれを用いています。図で表すと下のようになります。
1.3 CvTのアーキテクチャ
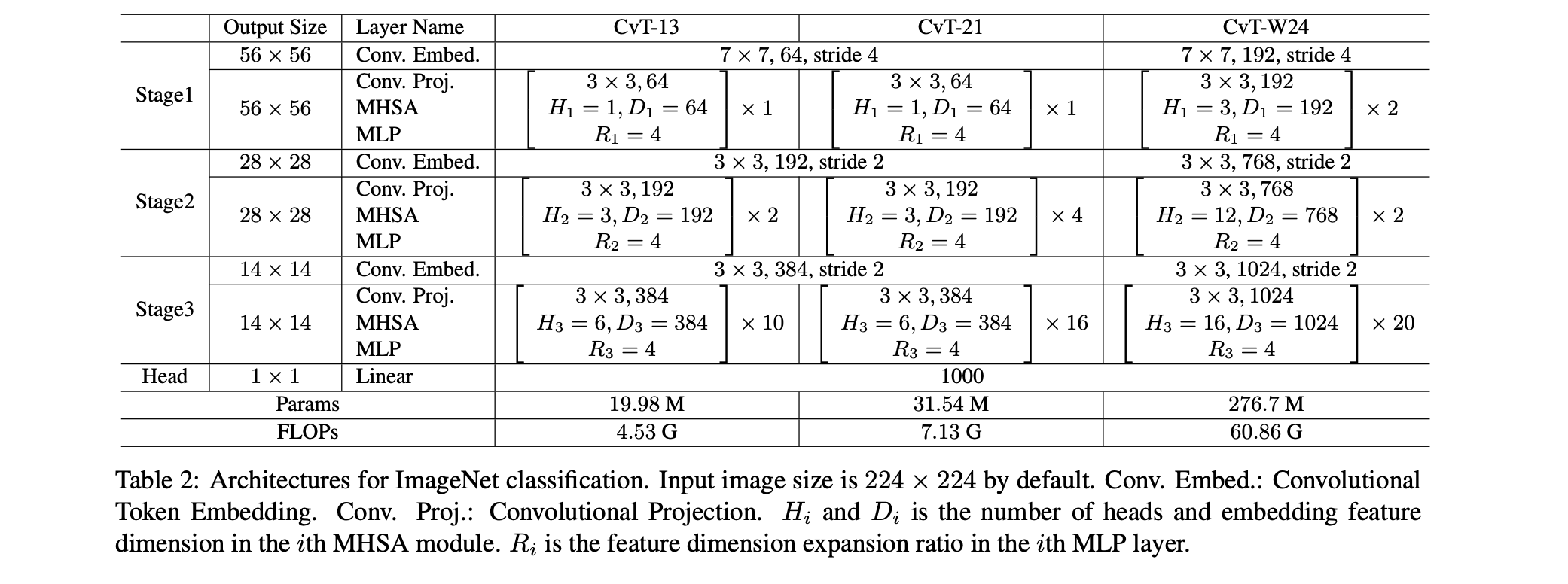
CvTのアーキテクチャは上表でまとめらています。本論文ではConv. Trans. Blockの数に合わせてCvT-13/-21/-W24の3つが提案されています。ここで、W24のWはWideのことを表しており、モデルの幅が広くなっています。実際にConv. Embed.やMHSAにおける次元数が大きくなっていることがわかります。
CvTについてより詳しく理解するためにここでは、CvT-13のステージ1におけるデータの次元の変化を見てみましょう。各ステージはConv. Embed. とConv. Trans. Block(=Conv. Proj. + MHSA + MLP)によって構成されています。入力データを$X\in\mathbb{R}^{B\times C\times H\times W}$とし、具体的な数字としてバッチサイズ$B=4$、チャネル数はカラーなので$C=3$、画像の高さおよび幅は上表に合わせて$(H,W)=(224, 224)$とします。バッチサイズが4なのは特に意味がありません。私の好みです。
まずConv. Embed. についてですが、これは単なる畳み込みです。上表を見ると、CvT-13においてカーネルサイズ$k=7$、出力チャネル数$64$、ストライド$s=4$となっています(パディング$p=2$です。)。出力の特徴マップの高さおよび幅は下の式によって計算でき、$(h,w)=(56, 56)$となります。つまり、この畳み込みによる出力の次元は$(4, 64, 56, 56)$となります。以降、特に断りがない限り、tensorの次元は同様に括弧で表します。
h=\frac{H-2p+k}{s}+1
あとはこの特徴マップを一次元ベクトルにreshapeするので、$(4, 56\cdot 56, 64)=(4, 3136, 64)$となります。(チャネルの位置が変わっていることに気をつけてください。各ピクセルが長さ64の長さのベクトルを持っていると考えるとわかりやすいと思います。)これにLayer Normを適用すればConv. Embed.は終わりです。
つづいてConv. Trans. Blockに入ります。ここの入力はもちろん$(4, 3136, 64)$です。Conv. Trans. Block.では、Conv. Proj.、MHSA(Multi-Head Self-Atention)、MLPの3つがあることがわかります。
Conv. Proj. では「2次元へのreshape、畳み込み、1次元へのflatten」の3つの操作を行うのでした。まず2次元へのreshapeで、$(4, 3136, 64)$を$(4, 64, 56, 56)$へと戻します。続いて畳み込みを行います。ここでの畳み込みは実はDepthwise Separable Conv.(以下、Sep. Conv.)という畳み込みで、パラメータ数の少ない畳み込みになっています。Sep. Conv.については拙著記事:MobileNet(v1,v2,v3)を簡単に解説してみた
をご覧ください。Sep. Conv.での出力チャネル数は$64$です。よってConv. Proj.の出力の次元は$(4, 64, 56, 56)$のまま変わりません。
MHSAでは、再び特徴マップを一次元ベクトルへとreshapeすることから始めます。ただし、ここでMulti-Headなので、ヘッドの数だけ分ける必要もあります。つまり、$(B, head, N, C/head)$の形へとreshapeしたいです。今回ヘッドの数は1なので$(4, 64, 56, 56)$を$(4, 1, 56\cdot 56, 64)=(4, 1, 3136, 64)$へとreshapeします。あとはSelf-Attentionをすると出力として$(4, 3136, 64)$が出てきます。
最後にMLPですが、これは2層の全結合層であり、$R_1=4$は隠れ層におけるベクトルの長さが入力の4倍になっているということです。論文中ではexpansion ratio(拡張率)と呼ばれています。入力、隠れ層、出力の形でデータの次元の流れを書くと、$(4, 3136, 64)\rightarrow(4, 3136, 64\cdot 4)\rightarrow(4, 3136, 64)$となっています。あとはこの$(4, 3136, 64)$を特徴マップに戻すと次のステージへと渡せるので$(4,64, 56,56)$にreshapeすれば終了です。あとはこれらの流れが繰り返されるだけです。それではCvTの実験結果を見ていきましょう。
2. CvTの実験結果
- SoTAとの比較
- 転移学習
- アブレーションスタディ
2.1 SoTAとの比較
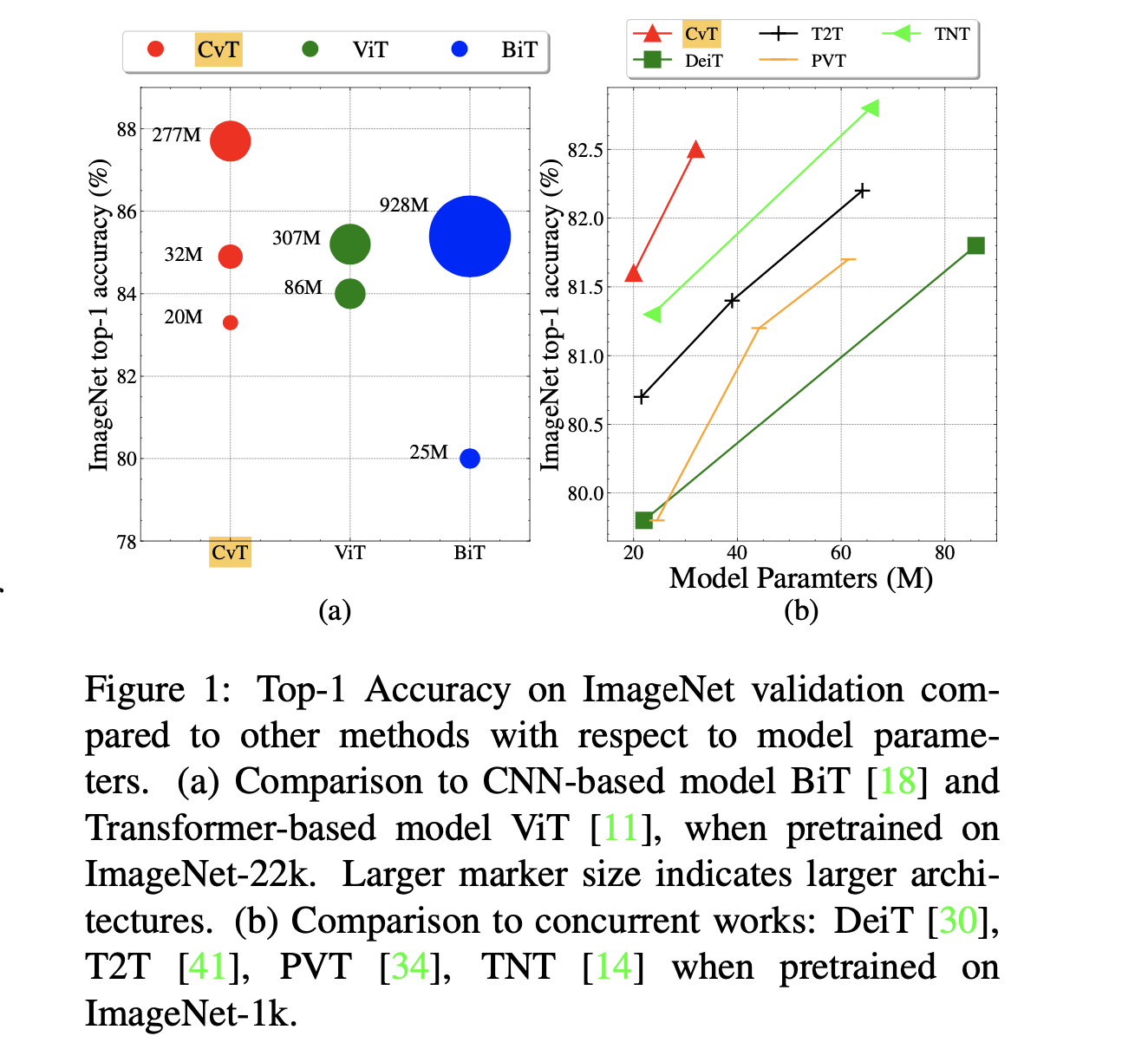
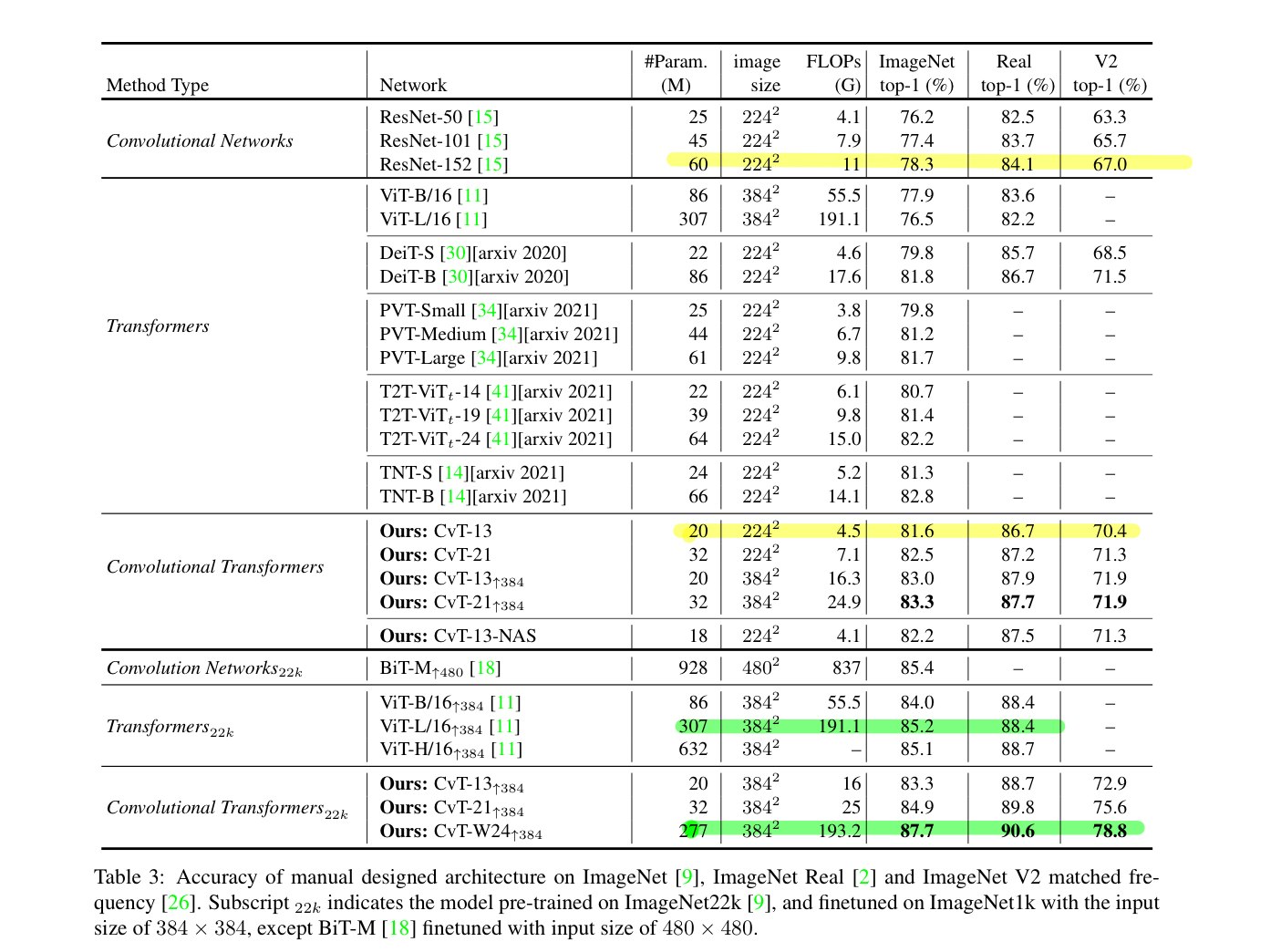
ImageNetを用いてCNNおよびTransformerたちとの比較を行っています。上表で下半分の22kとついてあるのはImageNet-ILSVRC2012よりも巨大な画像データセットであるImageNet-22kで事前学習を行った場合の結果になっています。性能評価はImageNetの評価用データセットだけでなく、より正しいラベル付けがされたReaL(詳細は拙著記事:画像認識の定番データセットImageNetはもう終わりかをご覧ください)やV2も用いられています。ここで特筆すべきなのは黄色と緑色のマーカーで引っ張った2箇所です。
黄色のマーカーではわずか20Mほどのパラメータ数のCvT-13がResNet-152を3.2%も上回っていることを示しています。緑色のマーカーではImageNet-22kで事前学習をしたモデルの比較ですが、CvT-W24が同程度のパラメータ数およびFLOPs数を有するViT-L/16を2.5%も上回っていることがわかります。
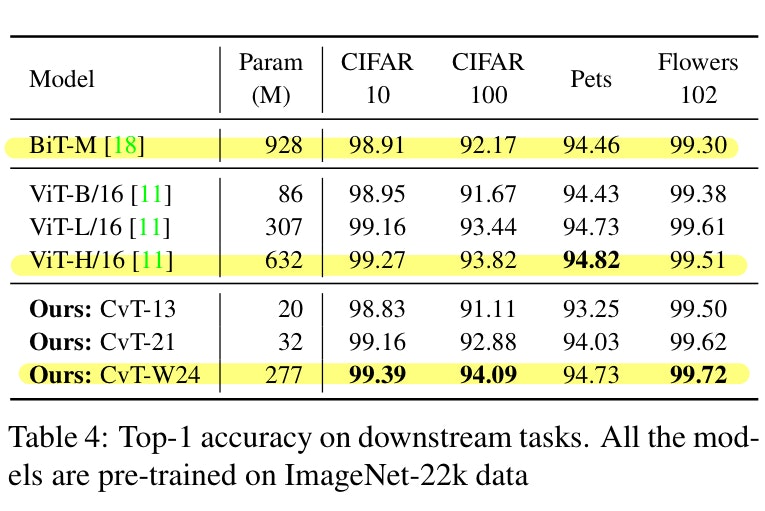
2.2 転移学習
ImageNet-22kで事前学習した場合の転移学習の結果を見ています。転移学習先のデータセットとしてCIFAR-10/CIFAR-100/Oxford-IIIT Pets/Oxford-IIIT Flowers-102の4つを用いています。CvT-W24がCNNのBiT-MやTransformerのViT-H/16を上回っていることがわかりますね。転移学習においてCvTがViTよりも高い性能を示すようなのでCvTの学習済み重みを使うことで私たちも恩恵に授かれそうです。
2.3 アブレーションスタディ
アブレーションスタディでは次の3つについて実験をしています。
- 位置エンコーディング
- Conv. Embed.
- Conv. Proj.
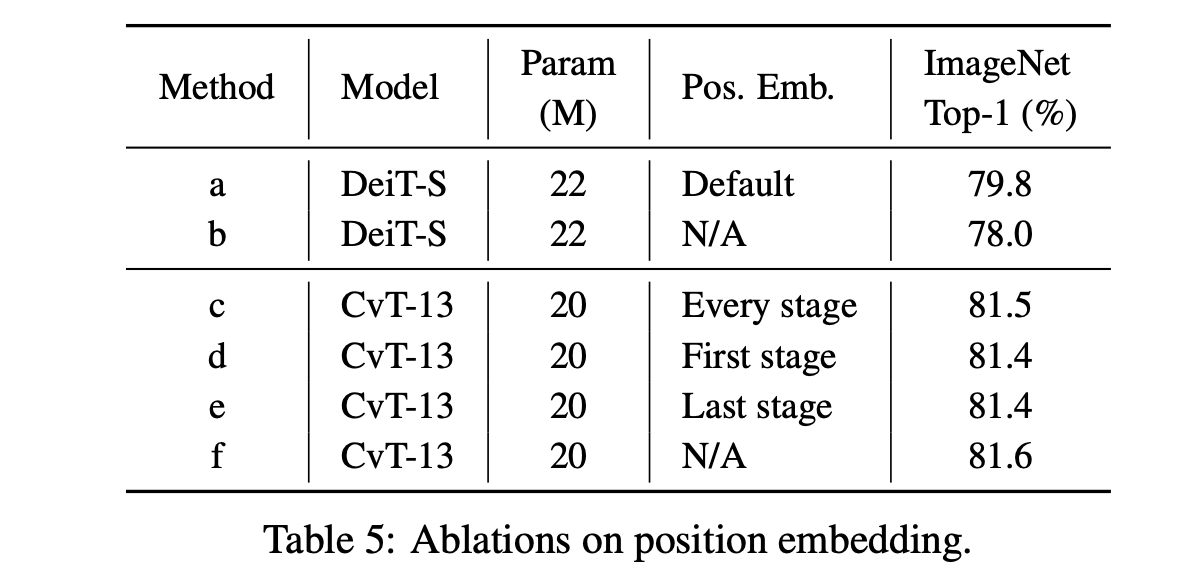
2.3.1 位置エンコーディングの実験
ここでは畳み込みを導入したことによって位置エンコーディングが必要なくなるということをImageNetを用いた実験を通して確認します。まずは通常のViT系(ここではDeiT-S)における位置エンコーディングの必要性を見てみます。上の表において位置エンコーディングがある場合(a)とない場合(b)を比較してみると、位置エンコーディングがなくなると1.8%も分類精度が落ちてしまっていることがわかります。一方でCvT-13を(c~f)を比較してみると、位置エンコーディングが有っても無くても同じ分類精度になっていることがわかります。このことからCvTでは位置エンコーディングが(最低でもImageNetにおいては)必要ないことがわかります。
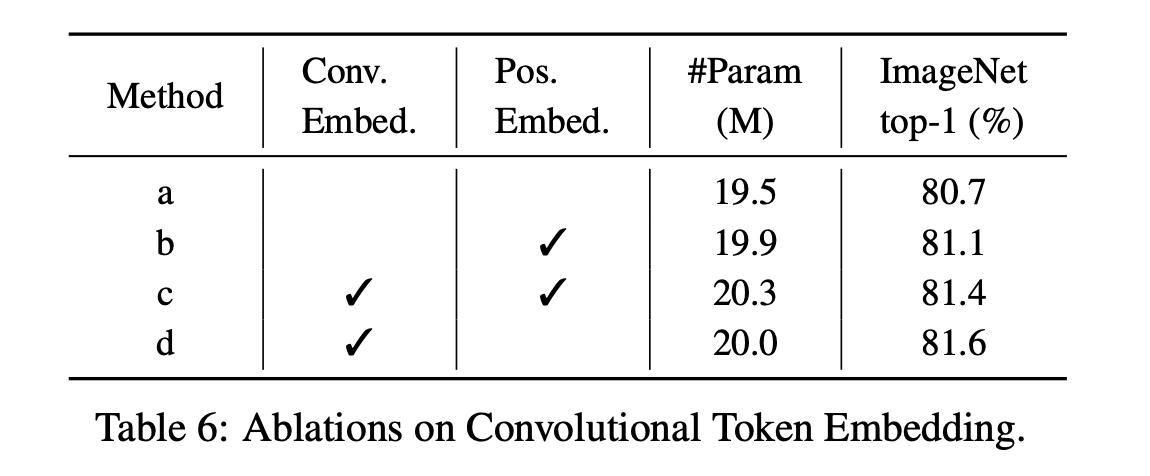
2.3.2 Conv. Embed.の実験
ここではConv. Embed.の重要性を見てみます。上表ではConv. Embed.とPos. Embed.を有無で4つのパターンに分けています。Methodのdを起点として見るとわかりやすいと思います。dはCvT-13のことです。一番重要なのはdとaの比較です。aはCvT-13からConv. Embed.を取り除き、ViTのように画像をパッチに分けて入力したモデルを表しています。CvT-13(d)からConv. Embed.を取り除いてしまうと0.9%もドロップが起きてしまっていることがわかります。このことからConv. Embed.がCvTには欠かせないことがわかります。ちなみにbとcを比較することで、Pos. Embed.があった場合(b)でもConv. Embed.を適用すること(c)で0.3%ほどゲインがあることがわかりますね。
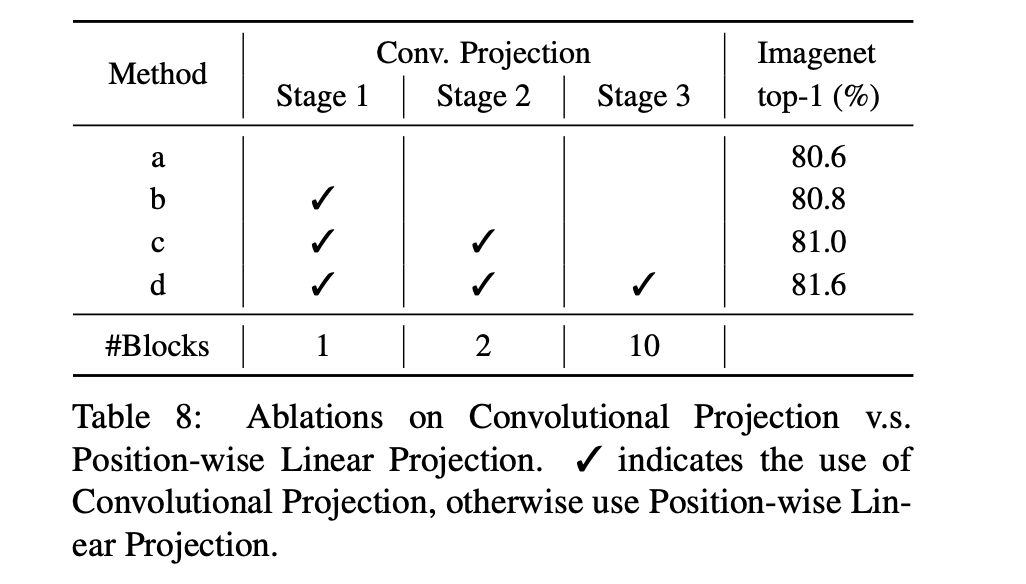
2.3.3 Conv. Proj.の実験
上表はConv. Proj.を適用したTransformerブロックを増やした時に精度がどのように変わるかを示しています。結論としては、Conv. Proj.を適用するステージを増やすと分類精度が上がることがわかります。最終的には全ステージをConv. Proj.にすること(d)で1.0%ものゲインが得られています。
3. まとめと所感
本記事ではViTに畳み込みをうまく組み込んだCvTについて解説しました。ViTが登場するまでは、CNNにどうやってSelf-Attentionを組み込むかという流れだったのに対し今ではTransformerにどうやって畳み込みを組み込むかという流れになっているのがとても面白いです。ViTが登場してというもの画像認識ではTransformerモデルが爆発的に増えています。今後もViTから目が離せませんね!
Twitterで人工知能のことや他媒体の記事などを紹介していますので@omiita_atiimoもご覧ください。
こちらもどうぞ: