はじめに
ベイズ最適化を用いて、最適なパラメータを導出する方法について解説致します。
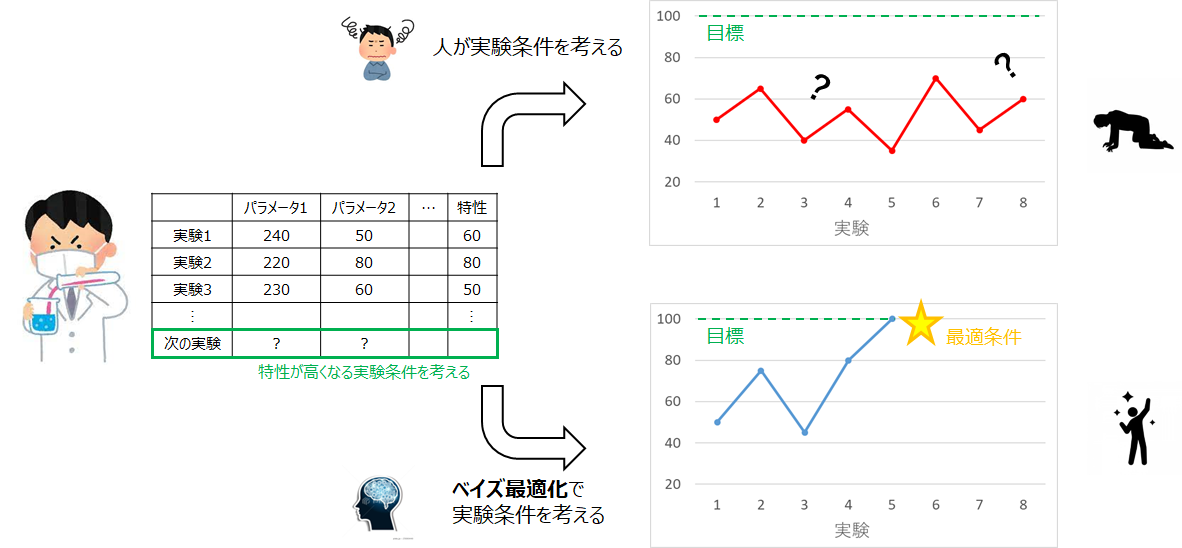
具体的には**「実験において、早く最適な条件に到達することを目的として、ベイズ最適化によって次の実験条件を提案」**してくれるプログラムについて説明します。ベイズ最適化を用いて最適条件を探索するという内容はよく見かけるのですが、既知の関数の最適化に焦点が当てられているものがほとんどだと思います。**でも、実際の実験って関数(起こっている物理現象)が分からないから、イマイチ参考にできないんだよね…と思っていました。この投稿ではそのような悩みを解消し、「実際の実験で使える」ベイズ最適化による条件探索について解説します。**ベイズ最適化の理論についてこちらにまとめました。
※機械学習やプログラミング関係の内容を他にも投稿していますので、よろしければこちらの一覧から他の投稿も見て頂けますと幸いです。
やりたいこと(想定シチュエーション)
- パラメータを調整しながら、所望の特性を得る実験
- パラメータの種類や範囲は固定されている(プロセス自体は決まっている)
- 何度か実験して、いくつか実験データが得られている(説明変数xと目的変数yのペアがいくつかある)
- 既知の実験データを用いて(参考にして)、次の実験条件を決定する
- ベイズ最適化を活用し、人よりも早く(少ない実験回数で)最適条件に到達したい
※「最適」条件と書いていますが、実際には目標値を満たす特性が得られるorより高い特性が得られる実験条件というイメージです
ベイズ最適化を用いた最適条件の導出
以下で紹介するサンプルデータを用いて、次に実験する条件を導出することを考えていきます。
今回取り扱うデータ
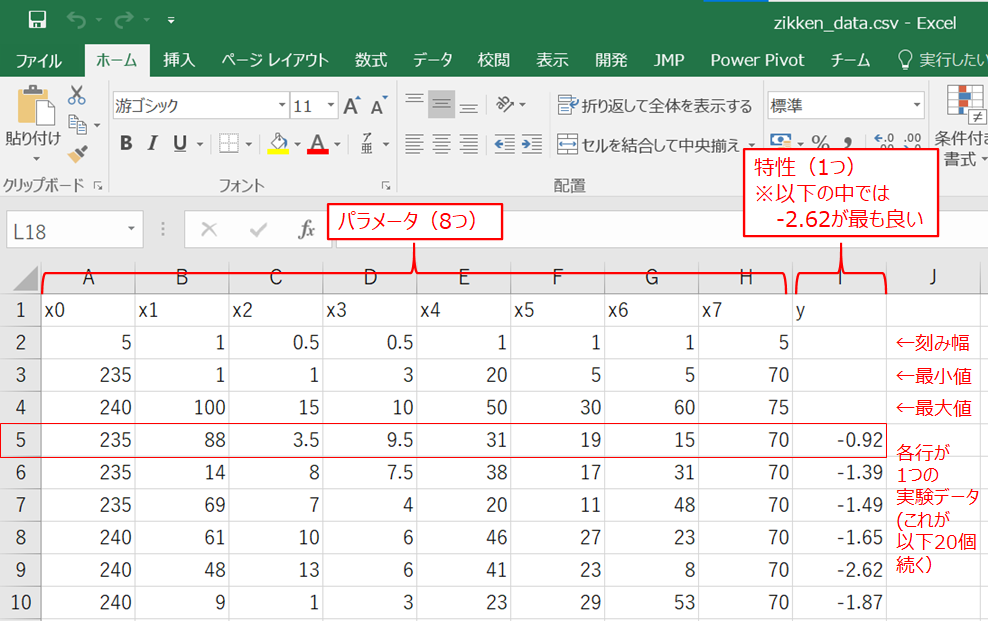
データはこちらのGitHubに保存したzikken_data.csvのデータを使っていきます。
- パラメータ(説明変数)はx0~x7の8つ
- csvの3行目に各パラメータの最小値が記載されている
- csvの4行目に各パラメータの最大値が記載されている
- csvの2行目に各パラメータの刻み幅が記載されている
- 特性(目的変数)はyの1つ
- yは望小特性で小さい方が良い(負の値で絶対値が大きい方が良い)とする
- 既知の実験データはcsvの5行目以下に計20個保存されている
※パラメータの刻み幅は装置の制約(例:整数でしかパラメータを入力できない)や
条件検討の粗さ(例:定義域が0~100までなら、まずは10刻みで検討)が反映されるイメージです
環境
- Python 3.6.6
- pandas 0.23.4
- numpy 1.19.4
- scikit-learn 0.23.2
- GPy 1.9.5
- GPyOpt 1.2.5
作成したコード
まずはインプットする既知の実験データを標準化します。
# ライブラリー類のインポート
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
# 既知の実験データを読み込み前処理(標準化)を実行
data = pd.read_csv("zikken_data.csv", encoding="shift_jis")
# 実験における変数の数を定義
num_x = len(data.columns)-1
# 各変数の刻み幅(step),最小値(min),最大値(max),標準化後の刻み幅(norm_step),標準化後の定義域(norm_range)を定義
for i in range(num_x):
exec("x"+str(i)+"_step = data.iloc[0,"+str(i)+"]")
exec("x"+str(i)+"_min = data.iloc[1,"+str(i)+"]")
exec("x"+str(i)+"_max = data.iloc[2,"+str(i)+"]")
exec("norm_x"+str(i)+"_step = ((x"+str(i)+"_step)/((x"+str(i)+"_max)-(x"+str(i)+"_min)))")
exec("norm_x"+str(i)+"_range = np.arange(0, (1+norm_x"+str(i)+"_step), norm_x"+str(i)+"_step)")
# MinMaxScalerを用いて標準化処理を実行(標準化前:data→標準化後:norm_dataにデータ名を変更)
# 読み込んだ既知の実験データに定義域外のデータ(最小値や最大値の範囲を超える設定値)がある場合はこの方法では上手くいかないので注意
# 読み込んだデータの3行目(最小値)以下のxの値のみを標準化を実行
data_before_norm = data.iloc[1:,:-1]
mmscaler = MinMaxScaler()
mmscaler.fit(data_before_norm)
norm_data_wo_y = mmscaler.transform(data_before_norm)
norm_data_wo_y_df = pd.DataFrame(norm_data_wo_y)
# norm_data_wo_y_dfの先頭2行(行番号0と1)は最小値と最大値なので取り除く
new_norm_data_wo_y = norm_data_wo_y_df.iloc[2:,:]
new_norm_data_wo_y_reset = new_norm_data_wo_y.reset_index(drop=True)
df_new_norm_data_wo_y_reset = pd.DataFrame(new_norm_data_wo_y_reset)
# 標準化処理したデータにもともとのyの値を結合していくためにyの値だけ格納されたデータフレームを作成していく
data_y = data.iloc[3:,-1]
# のちのデータフレームの結合を考えてindex番号をリセット
data_y_reset = data_y.reset_index(drop=True)
df_data_y_reset = pd.DataFrame(data_y_reset)
# 標準化したxのみのデータフレームとyのみのデータフレームを結合し、csvファイルに書き出し
norm_data = pd.concat([df_new_norm_data_wo_y_reset, df_data_y_reset], axis=1)
norm_data.columns = data.columns
norm_data.to_csv("norm_zikken_data.csv", index=False)
次に標準化したデータにベイズ最適化を適用します。
# 正規化後のデータに対してベイズ最適化を実行(yの値をなるべく小さくする条件探索)
import datetime
import GPy
import GPyOpt
# 開始時刻
start_time = datetime.datetime.today()
print ("開始時刻: " + start_time.strftime('%Y-%m-%d_%H-%M-%S'))
# 乱数初期化(設定は必須でない?)
np.random.seed(1234)
# 定義域(条件の探索範囲)の設定
# typeは'continuous':連続変数,'discrete':離散変数,'categorical':カテゴリで指定
bounds = [{'name': 'x0', 'type':'discrete', 'domain': norm_x0_range},
{'name': 'x1', 'type': 'discrete', 'domain': norm_x1_range},
{'name': 'x2', 'type': 'discrete', 'domain': norm_x2_range},
{'name': 'x3', 'type': 'discrete', 'domain': norm_x3_range},
{'name': 'x4', 'type': 'discrete', 'domain': norm_x4_range},
{'name': 'x5', 'type': 'discrete', 'domain': norm_x5_range},
{'name': 'x6', 'type': 'discrete', 'domain': norm_x6_range},
{'name': 'x7', 'type': 'discrete', 'domain': norm_x7_range}]
# 既知データをインプットしていく
# データ入力用の箱を作っておく
X_step=[]
Y_step=[]
# 標準化済みのcsvデータ(既知の実験データ)を読み込む
norm_data = pd.read_csv("norm_zikken_data.csv", encoding="shift_jis")
norm_data_x = norm_data.iloc[:,0:num_x] #全行のxを読み込む
norm_data_y = norm_data.iloc[:,num_x:num_x+1] #全行のyを読み込む
# xとyをリスト化する
X_step=np.asarray(norm_data_x)
Y_step=np.asarray(norm_data_y)
# グラフ描写用のリストを作っておく
i_list=[]
y_pre_list=[]
y_exp_list=[]
y_var_list=[]
# 以下のパラメータでベイズ最適化を実行する
params = {'acquisition_type':'LCB',#獲得関数としてLower Confidence Boundを指定
'acquisition_weight':1,#LCBのパラメータを設定.デフォルトは2
'kernel':GPy.kern.Matern52(input_dim=len(bounds), ARD=True), #GPに使うカーネルの設定 #boundsの次元でinputの次元を定義
'f':None, #最適化する関数の設定(実験結果は分からないので設定しない).
'domain':bounds, #パラメータの探索範囲の指定
'model_type':'GP', #標準的なガウシアンプロセスを指定.
'X':X_step, #既知データの説明変数(インプットするx)
'Y':Y_step, #既知データの目的変数(インプットするy)
'de_duplication':True, #重複したデータをサンプルしないように設定.
"normalize_Y":True, #defaltはTrue
"exact_feval":False #defaltはFalse
}
# ベイズ最適化のモデルの作成
bo_step = GPyOpt.methods.BayesianOptimization(**params)
# 次の候補点のx,y(予測値,分散)の計算
x_suggest = bo_step.suggest_next_locations(ignored_X=X_step)
y_predict = bo_step.model.model.predict(x_suggest) #y_predictは(予測平均,予測分散)がタプルで返ってくる
y_mean=y_predict[0]
y_variance=y_predict[1]
# 次の実験候補点のxについて標準化処理をしない状態のスケールで表示(もう少し上手いやり方があると思われる)
for j in range(num_x):
exec("next_x"+str(j)+"_0 = x"+str(j)+"_min+(x_suggest[0,"+str(j)+"])*((x"+str(j)+"_max)-(x"+str(j)+"_min))")
print("次の実験点のx0は "+ "{:.1f}".format(next_x0_0) +"です")
print("次の実験点のx1は "+ "{:.1f}".format(next_x1_0) +"です")
print("次の実験点のx2は "+ "{:.2f}".format(next_x2_0) +"です")
print("次の実験点のx3は "+ "{:.2f}".format(next_x3_0) +"です")
print("次の実験点のx4は "+ "{:.1f}".format(next_x4_0) +"です")
print("次の実験点のx5は "+ "{:.1f}".format(next_x5_0) +"です")
print("次の実験点のx6は "+ "{:.1f}".format(next_x6_0) +"です")
print("次の実験点のx7は "+ "{:.1f}".format(next_x7_0) +"す")
# y_meanとy_varianceはndarrayなのでfloatに変換
print("次の実験点でのmeanは "+ "{:.4f}".format(float(y_mean)) +"です")
print("次の実験点でのstdは "+ "{:.4f}".format(float(y_variance)) +"です")
end_time = datetime.datetime.today()
print ("終了時刻: " + end_time.strftime('%Y-%m-%d_%H-%M-%S'))
print ("所要時間: " + str(end_time - start_time))
開始時刻: 2021-**-**_**-**-**
The set cost function is ignored! LCB acquisition does not make sense with cost.
次の実験点のx0は 240.0です
次の実験点のx1は 38.0です
次の実験点のx2は 15.50です
次の実験点のx3は 5.00です
次の実験点のx4は 21.0です
次の実験点のx5は 26.0です
次の実験点のx6は 15.0です
次の実験点のx7は 70.0す
次の実験点でのmeanは -0.5090です
次の実験点でのstdは 0.8362です
終了時刻: 2021-**-**_**-**-**
所要時間: 0:00:00.416719
※「The set…」の表示ですが、計算コストを設定していないことが原因かと思いますがここでは無視して問題ないです (詳細はこちらなど参照下さい)
このように次の実験条件が出力されます。この条件で実験を行い、新たに特性yを取得します。(実際には試験や測定など行うイメージです)そして、このxとyのペアを既知の実験データに追加して新たなインプットとしてベイズ最適化を行い、次の実験条件を得ます。この繰り返しによって少ない実験回数で最適条件に到達することが期待されます。
コードの解説
インプットデータの標準化
各パラメータ間でオーダーが違うこともあり、今回は標準化しました。各パラメータの取り得る値の範囲は分かっていると仮定しているので、正規化ではなく標準化を行いました。また刻み幅を設定することで、提案された実験条件が妥当な値になるように工夫しました。
(ここで刻み幅を設定しないと実際には装置にインプットできない条件が導出されるなどの不都合が生じます)
ベイズ最適化のパラメータ
paramsで設定していますが、公式ドキュメントを参照すると以下の通りです。このハイパーパラメータの選定は最適化において非常に重要であると考えられます。獲得関数LCBのacquisition_weightについてはこちらで検討しましたので、参考にして下さい。
今回検討したパラメータ
| 引数名 | 引数の説明 | 引数の設定 |
|---|---|---|
| acquisition_type | 獲得関数の種類 | ‘EI’: expected improvement(defalt: ‘EI’) ‘EI_MCMC’: integrated expected improvement (requires GP_MCMC model) ‘MPI’: maximum probability of improvement ‘MPI_MCMC’: maximum probability of improvement (requires GP_MCMC model) ‘LCB’: GP-Lower confidence bound ‘LCB_MCMC’: D16integrated GP-Lower confidence bound (requires GP_MCMC model) |
| acquisition_weight | 獲得関数のパラメータ (活用と探索の割合) |
獲得関数がLCB時は"exploration_weight "とも言い、大きくすると探索重視になる(defalt: 2) 獲得関数がEIなどの場合は"jitter"で表されてexplorative(探索)の度合いを決める(defalt: 0.01) |
| kernel | カーネル関数 | Maternカーネル以外にはRBFカーネルなどがある ARD(Automatic Relevance Determination)をTrueにすることで出力に影響が大きい成分を自動的に決定 |
| f | 最適化する関数 | 既知の関数を最適化する場合は数式などの入力 (今回は未知なので"None"を指定) |
| domain | インプットする変数の説明 (定義域) |
辞書型のリストで指定(defalt: None) (今回は各パラメータが取れる値を"bounds"で指定) |
| model_type | 代理モデルのタイプ | ‘GP’: standard Gaussian process(defalt: ‘GP’) ‘GP_MCMC’: Gaussian process with prior in the hyper-parameters ‘sparseGP’: sparse Gaussian process ‘warperdGP’: warped Gaussian process ‘InputWarpedGP’: input warped Gaussian process ‘RF’: random forest (scikit-learn) |
| X | 初期のインプット | 2d numpy arrayで設定(今回は既知の実験データのx)(defalt: None) |
| Y | 初期のアウトプット | 2d numpy arrayで設定(今回は既知の実験データのy)(defalt: None) |
| de_duplication | 実験点の重複を認めるか否か | Trueにすると既にインプットされた条件は出力されない(defalt: False) (同一条件を実験しないという方針であればTrueがよい) |
| normalize_Y | 出力yを正規化するか否か | 実スケールに近づけたい場合はFalseがよい?(defalt: True) |
| exact_feval | 出力yを正しいとするか否か | 実験結果(得られたy)に誤差を認めるか否かのイメージ(defalt: False) ※"normalize_Y:False, exact_feval:True"にすると少ないサンプル数でも実スケールに近づく |
その他のパラメータ
| 引数名 | 引数の説明 | 引数の設定 |
|---|---|---|
| constraints | 問題の制約 | 辞書型のリストで指定(defalt: None) x0とx1の和が100以下という制約があれば、"x0+x1-100"のように記載 ※詳細はGPyOpt.core.space.Design_space classを参照 |
| cost_withGradients | 計算コスト | 指定する際はevaluation_timeなどをインプット(defalt: None) |
| initial_design_numdata | 初期点の数 | 関数fが既知の場合、何点を初期のインプットとしてモデルに投入するか(defalt: 5) |
| initial_design_type | 初期点の生成方法 | ‘random’: to collect points in random locations(defalt: ‘random’) ‘latin’,to collect points in a Latin hypercube (discrete variables are sampled randomly.) |
| acquisition_optimizer_type | ‘lbfgs’: L-BFGS(defalt: ‘lbfgs’) ‘DIRECT’: Dividing Rectangles ‘CMA’: covariance matrix adaptation |
|
| model_update_interval | モデル更新の間隔? | (defalt: 1) |
| evaluator_type | 予測したモデルの評価方法? | ‘sequential’: sequential evaluations ‘random’: synchronous batch that selects the first element as in a sequential policy and the rest randomly ‘local_penalization’: batch method proposed in (Gonzalez et al. 2016) ‘thompson_sampling’: batch method using Thompson sampling ※all methods are equivalent if the batch size is one |
| batch_size | バッチサイズ (出力される条件数) |
1回の実験でまとめて実験できる実験数を指定するとよい(defalt: 1) |
| num_cores | 評価時のコア数 | (defalt: 1) |
| verbosity | (defalt: False) | |
| verbosity_model | (defalt: False) | |
| maximize | 関数fを設定していなければ影響なし?(defalt: False) |
exec関数
プログラムの中で用いているexec関数について少し解説します。exec関数とはPythonの組み込み関数の一つです。引数で与えたPythonコードを動的に解釈、実行できます。例えば、for文を使うと以下のようなことが可能です。(これは基本ですね)
for i in range(5):
print(i)
0
1
2
3
4
for i in range(5):
print("x_" +str(i)+ "_step")
x_0_step
x_1_step
x_2_step
x_3_step
x_4_step
しかし、この要領でx_0_step=0, x_1_step=1,…と変数を作ることはできません。
for i in range(5):
"x_" + str(i) + "_step" = i
File "<ipython-input-3-46c8f51ac0a2>", line 2
"x_" + str(i) + "_step" = i
^
SyntaxError: can't assign to operator
そこで、この問題をexec関数を使って解決しました。
for i in range(5):
exec("x_"+str(i)+"_step = str(i)")
print(x_0_step)
print(x_1_step)
print(x_2_step)
print(x_3_step)
print(x_4_step)
0
1
2
3
4
ただ、こちらのサイトなどに書かれていますが、このように変数名を動的に変える場合にexecを用いるのはあまりオススメ方法ではないようです。
まとめ
実験において早く最適な条件に到達することを目的として、ベイズ最適化を用いた最適なパラメータの導出方法について解説しました。