LoginSignup
58
70

More than 1 year has passed since last update.

@Mopepe51(雪下)

ベイズ最適化でハイパーパラメータを調整する

Last updated at Posted at 2020-03-02

ベイズ最適化とは？

(雑な)A. なるべく実験をサボりつつ一番良いところを探す方法．

ある関数$f$を統計的に推定する方法「ガウス過程回帰」を用いて，なるべく良さそうなところだけ$y=f(x)$の値を観測して$f$の最適値を求める方法．

実際の活用例としてはこの記事がわかりやすいですね．
ベイズ最適化で最高のコークハイを作る - わたぼこり美味しそう

最近使う機会があったのでそのために調べたこと、予備実験としてやった計算をご紹介します。
数学的な詳しい議論は ボロが出るので PRMLの6章や、「ガウス過程と機械学習」の6章を読めばわかるので本記事ではイメージ的な話と実験結果をご紹介します。(実行コードは最後にGitHubのリンクを載せておきます)

※ 2022/09/26 グラフを修正

ガウス過程回帰とは？

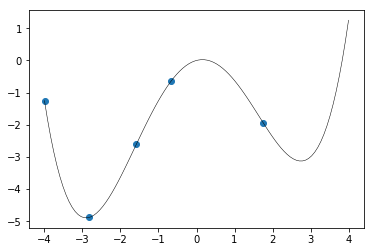
下図の黒線のような関数を予想したいとします。実際の関数は $y=\frac{1}{16}x^4-x^2+\frac{5}{16}x$ですがこの関数形を知ることはできません。
端から端まで全部確認するのは大変なので、適当に5個点を取って(青丸)ここから全体を予想してみましょう。

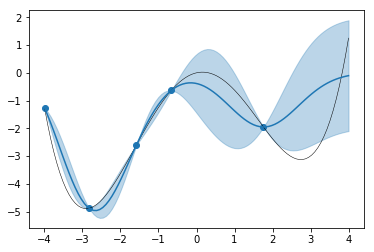
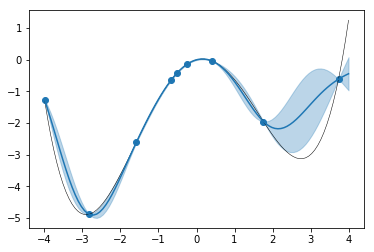
image.png

ここで「ガウス過程回帰」にこの点の情報を入力して予測してみると、なんやかんやあって1以下のようになります。

image.png

ガウス過程回帰では予測が「関数の確率分布」として出てきます。このあたりを通る確率がどのくらい、という情報です。図の青線がこの確率分布の平均値、薄い青で塗りつぶされた部分がその確率のバラツキ具合(ここでは標準偏差の2倍。$2\sigma$なのでこの範囲にある確率が95%となります。)を示しています。
実際の関数$y=\frac{1}{16}x^4-x^2+\frac{5}{16}x$がいい具合に誤差範囲に収まっていて、観測点の周りでは誤差範囲が小さく、点から離れると誤差範囲が大きくなっているのがわかります。

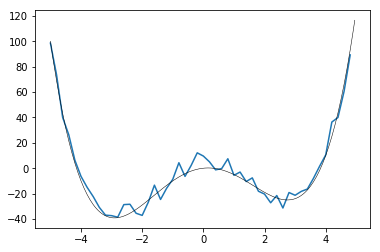
適当にもう少し点を増やしてみると、
image.png
のようになります。$x=-3～1$あたりの範囲ではかなり正確に予測できるようになりました。

※実際の観測にはノイズも含まれるためそれも織り込んで計算します。

「良さそうなところ」の決定方法

ここで「関数全部の形がわからなくても良いので最小値だけ求めたい」という問題を考えると
値が大きくなるとわかりきっているところ($x=-1～1$あたり)を何度も観測するのは無駄だなあという感じがします。値が小さそうなところを優先的に探索したいですよね。
また、まだあまり探索していなくて不確かさが大きいところ($x=3$あたり)はもう少し点を増やしておきたいです。

このように、「最適値がありそうなところ」と「まだ未確定なところ」をバランス良く得点化しようというのが「獲得関数」です。とはいえどちらを重視すべきかというのは場合によって変わってくるので戦略に応じて様々な獲得関数があります。

旧版
+ EI戦略 (期待改善度 expected improvement) 現在までに観測した点の最小値からどれだけ最小値を更新できるかの期待値 $$E[y_{\text{min}}-\hat{y}] =(y_{\text{min}} - \mu)\Phi\left(\frac{y_{\text{min}}-\mu}{\sigma}\right) + \sigma \phi\left(\frac{y_{\text{min}}-\mu}{\sigma}\right)$$ $\phi(x)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{x^2}{2})$はガウス関数、$\Phi(x)$はその累積密度関数。
  • LCB戦略 (信頼性下限関数 lowrer confidence bound)
    信頼区間の下限
    $$\mu-\sigma\times\kappa\sqrt{\frac{\log N}{N}}$$
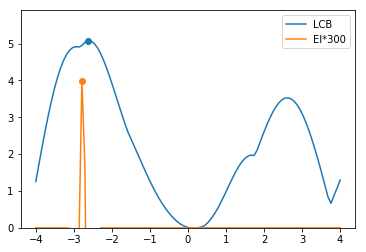
    $\kappa$は信頼区間を使う倍率。観測した点の数$N$に応じて適当に信頼区間の幅を変化させます。（なんだかEIの曲線がおかしなことになってるので間違っているかもしれません……）

etc...

image.png
それぞれプロットしてみるとこのような形になり、ともに$-2.7$あたりを次に観測すべき点と予測しています。

2022/09/26更新

  • EI戦略 (期待改善度 expected improvement)
    現在までに観測した点の最小値からどれだけ最小値を更新できるかの期待値が大きいところを探索する。
    $$E[ \max\{y_{\text{min}}-\hat{y}(x), 0\} ]
    =(y_{\text{min}} - \mu(x))\Phi\left(\frac{y_{\text{min}}-\mu(x)}{\sigma(x)}\right) + \sigma(x) \phi\left(\frac{y_{\text{min}}-\mu(x)}{\sigma(x)}\right)$$
    $\phi(x)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{x^2}{2})$はガウス関数、$\Phi(x)$はその累積密度関数。

  • LCB戦略 (信頼性下限関数 lowrer confidence bound)
    信頼区間の下限が小さいところを探索する。
    $$\mu(x)-\kappa\times\sigma(x)$$
    $\kappa$は信頼区間を使う倍率。
    データが少なく推定の幅が大きいところでは$\sigma$が大きくなるので推定値は大きくてもまだよくわかっていないところを探索するようになります。

他にもありますが割愛。

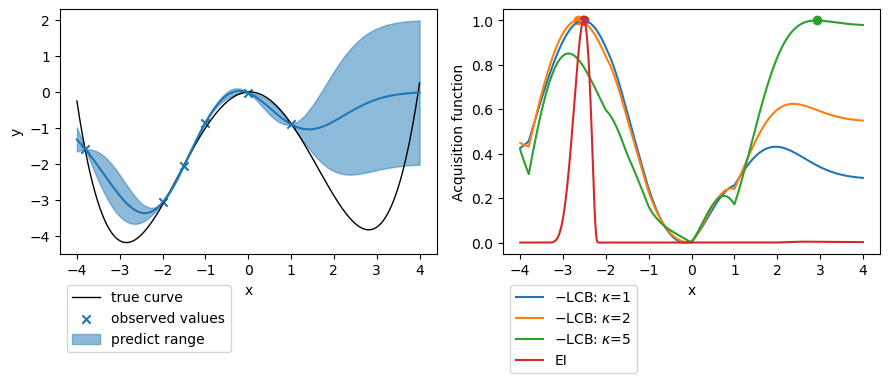
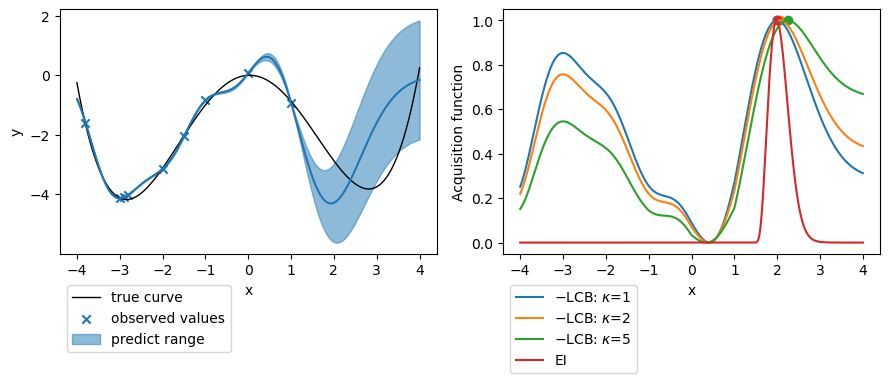
適当に観測値を6点で取ったとき、予測と獲得関数（LCBは符号を反転・0~1のレンジになるよう規格化している）は下図のようになります。
$\bullet$ で示したのが獲得関数が最適となる点です。
EIやLCBで$\kappa$が大きくない場合は予測値の小さい$x=-2.5$付近を提案しているのに対し、$\kappa=5$のときのLCBでは不確かさの大きい$x>2$のあたりを提案しています。

image.png

$x=-3$ 周辺にもっと観測点を増やしていき、不確かさが小さくなってくれば他の戦略でも不確かさの大きい領域を提案するようになります。

image.png

BayesianOptimization

毎度このような計算を書くのも面倒なので GPyOpt2というPythonパッケージのBayesianOptimizationを利用します。
ターゲットは上記と同じ形の $y=x^4-16x^2+5x$ 3 を使います。

image.png

ノイズを含んでいます。

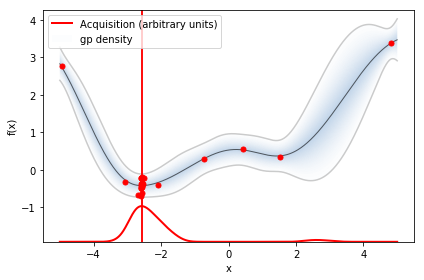
まず適当に3点とってガウス過程回帰を行うと予測と獲得関数(ここではEIを使いました)はこのようになります。赤の縦線のところを次観測すべきところと決定されました。
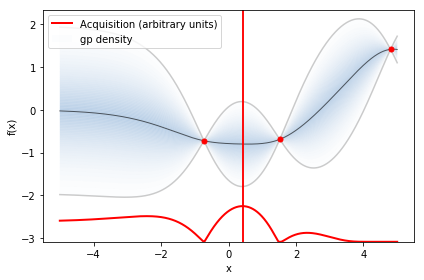
image.png

この提案された値（$x\fallingdotseq0.5$）を観測して点を加え、回帰をやり直すとこうなります。x=0の周辺の不確かさがかなり小さくなりました。
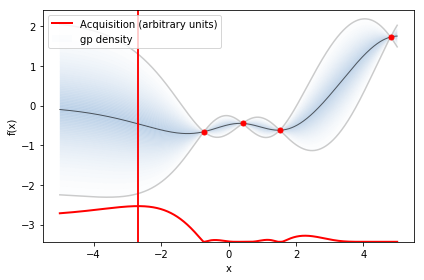
image.png

このサイクルを20回ほど繰り返すと以下のようになります。
image.png

最小値を取るxの値は -2.59469813と予測されました。真の解は-2.9035... なので結構ズレていますがノイズが大きいのである程度は仕方ないですね。

2次元の場合

一般により高次元の空間でも同様に最適化探索が行えます。
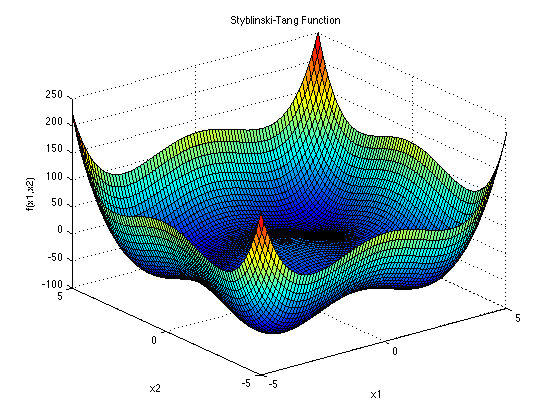
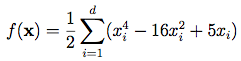image.png
image.png （STYBLINSKI-TANG FUNCTION より）

同じくこんな形の関数で最小化してみます。

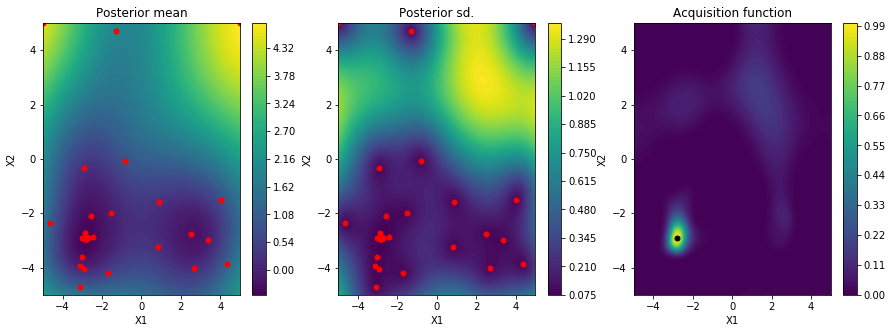
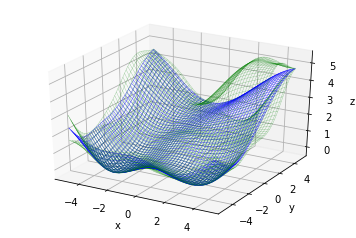
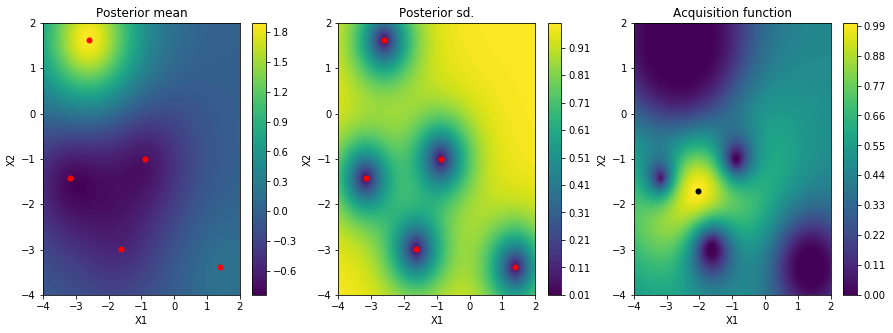
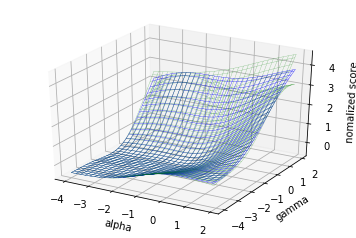
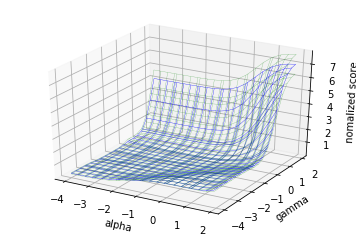
適当に5点とってガウス過程回帰を行った結果、平均値・標準偏差・獲得関数はこのようになります。
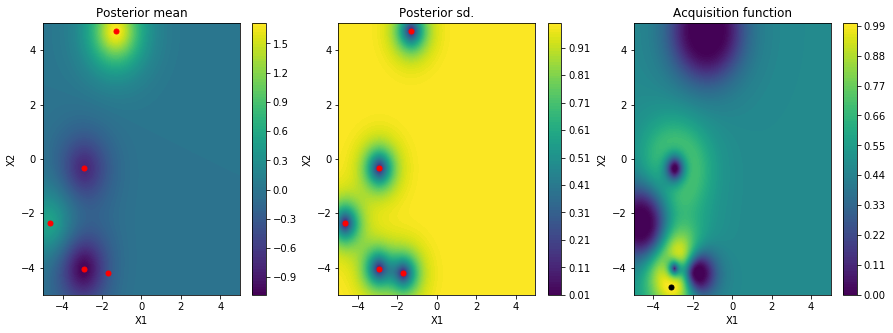
image.png
3Dプロットしてみるとこんな感じです。(青が平均、緑が標準偏差を±した値)
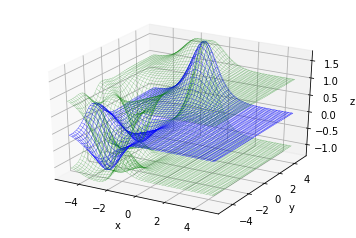
image.png
初期は観測点の周り以外では情報が無いのでデフォルトの仮定の$z=0$となっていることがわかります。

同様に観測を55サイクル行うと
image.png
image.png

かなり真の関数に近い形が得られています。
最小値を取るxの値は (-2.79793531, -2.91749935)と予測されました。先程より精度が良さそうです。
もしx, yをそれぞれ-5～5まで0.1刻みで探索したとすると10×10で100回の実験が必要になることを考えると、実験回数を節約できましたね。

ハイパーパラメータ―の最適化

ベイズ最適化は個々の値での観測のコストが大きく、探索空間の次元が大きめの時に威力を発揮します。
データ数が膨大になると一回一回の計算時間が大きくなる機械学習のパラメーター調整にこれを適用してみましょう。

※実用的には機械学習のためにチューニングされているOptunaなどのツールを使用したほうがより良い最適化が得られます。Optunaではベイズ最適化をより発展させたTPE（Tree-structured Parzen Estimator）というアルゴリズムを使用しているそうです。
やっていることの理解の一歩としても、ここでは簡単な例を扱ってみましょう。

KerneRidgeのハイパーパラメータ―

KernelRidge回帰という機械学習のモデルにはalphaとgammaという2つのハイパーパラメータ―(自動的に決定されず、データに応じて外部から与えてやる必要のあるパラメーター)があります4。alphaは正則化(過学習しないよう抑える働き)の強度、gammaは適用する関数の形を決めるパラメーターです。

sklearn.datasetsに含まれているbostonデータセットで住宅価格を予測するモデルの精度を最大化するパラメーターを求めてみましょう。

まずはデフォルトのパラメーター値での精度を確認してみます。

KernelRidge(kernel='rbf').fit(train_x, train_y).score(test_x, test_y)
#=> 0.4802674032751879

0.48となりました。

パラメーターの桁も大きく変わりうるのでそれぞれ対数にしてパラメーターサーチを行います。

def get_score_KR(x):
    alpha, gamma = x
    predictor = KernelRidge(kernel='rbf', alpha=alpha, gamma=gamma)
    return cross_val_score(predictor, train_x, train_y, cv=5).mean()
def get_score_KR_log(x):
    print(x)
    return get_score_KR((10**x[0][0], 10**x[0][1]))

このような関数でalpha、gammaに対するモデルの精度を検証し、実験としてフィードバックに使います。


import GPyOpt
bounds = [{'name': 'log alpha', 'type': 'continuous', 'domain': (-4,2)},
         {'name': 'log gamma', 'type': 'continuous', 'domain': (-4,2)}]
bo = GPyOpt.methods.bayesian_optimization.BayesianOptimization(
    f=get_score_KR_log, domain=bounds, model_type='GP', acquisition_type='EI', initial_design_numdata=5, maximize=True)
bo.run_optimization()
bo.plot_acquisition()

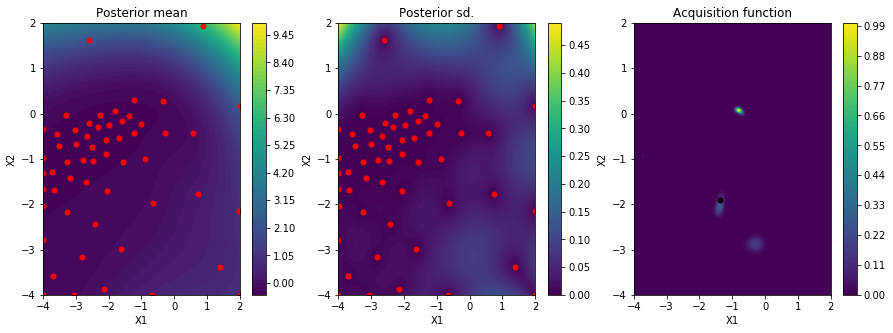
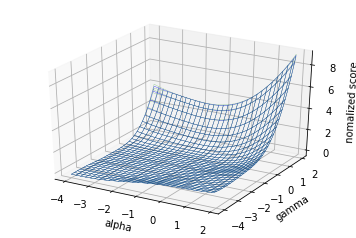
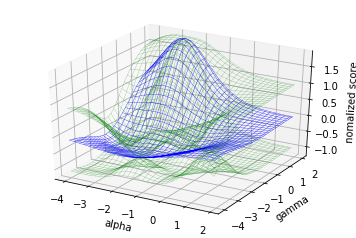
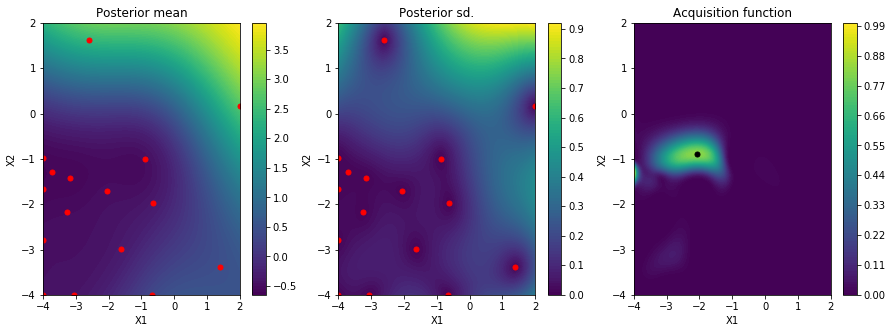
image.png
image.png
最初の5点ではこんな感じ。

image.png
image.png
11サイクル進めるとこんな感じになりました。

image.png
image.png
51サイクルでこんな感じ。5
xの最適値は[-1.97439296, -0.25720405]、つまりalpha=0.0106, gamma=0.553 という結果になりました。

predictor_opt = KernelRidge(kernel='rbf', alpha=10**bo.x_opt[0], gamma=10**bo.x_opt[1])
predictor_opt.fit(train_x, train_y)

predictor_opt.score(test_x ,test_y)
#=> 0.8114250068143878

この値を使って再び精度を確かめてみると、結果は精度0.81と、最適化前と比べてかなり向上しました。やったね。

グリッドサーチとの比較

一般的にハイパーパラメータ―調整には空間を一様に探索する「グリッドサーチ」を使うとするドキュメントが多いです6。
同じく$10^{-4}～10^2$のパラメーター空間を探索してみましょう。

from sklearn.model_selection import GridSearchCV
parameters = {'alpha':[i*10**j for j in [-4, -3, -2, -1, 0, 1] for i in [1, 2, 4, 8]], 
              'gamma':[i*10**j for j in [-4, -3, -2, -1, 0, 1] for i in [1, 2, 4, 8]]}
gcv = GridSearchCV(KernelRidge(kernel='rbf'), parameters, cv=5)
gcv.fit(train_x, train_y)

bes = gcv.best_estimator_
bes.fit(train_x, train_y)
bes.score(test_x, test_y)
#=> 0.8097198949264954

image.png

ガウス最適化での予測曲面と大体同じような形になりましたね。
このグリッドサーチではalphaとgammaをそれぞれ24点、合計576点で「実験」を行っているのでデータ数が大きく計算に時間がかかるような状況では大変です。

まとめ

というわけで無事ベイズ最適化でグリッドサーチの場合と同等の精度を発揮するパラメーターを計算量を約1/10の実験回数で見つけることができました！

なにか間違い・質問などありましたらコメントください。

それぞれの項の実行コード、途中経過などは以下に掲載しています。

ベイズ最適化とは？：BayesianOptimization_Explain
BayesianOptimization：BayesianOptimization_Benchmark
ハイパーパラメータ―の最適化：BayesianOptimization_HyperparameterSearch

参考文献

C.M.ビショップ, 元田浩 et al.監訳(2012)「パターン認識と機械学習 上・下 ベイス理論による統計的予測」丸善出版
持橋大地，大羽成征(2019)「ガウス過程と機械学習」講談社
Pythonでベイズ最適化を行うパッケージ GPyOpt
ベイズ最適化の数学
ベイズ最適化で最高のコークハイを作る
Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011.
GPyOpt

  1. この5点が観測として得られたとして、そうなるような関数はどのようなものか、ということをノイズがガウス分布に従うとか関数が一定の表現で得られる形であるというような仮定を置くことで確率分布を導出します。 ↩

  2. パッケージ名誤りのため 2022/09/26 修正 ↩

  3. この関数は一般の次元で複数極小を持つ関数として、よく最適化のベンチマークに使われるものです。 STYBLINSKI-TANG FUNCTION ↩

  4. 本当は理論的に適切なパラメーターを決定する方法はあるのですがここではそれは考えず無作為に探索することとします。 ↩

  5. alphaが小さい側に振り切れてしまっているようですがこれはデータ数が少ないからだと思われます。あまりalphaが小さすぎると正則化が効かず汎化性能が落ちてしまうのでこのへんまでの探索にとどめます。 ↩

  6. 例：Scikit-learn ドキュメント 3.2. Tuning the hyper-parameters of an estimator ではグリッドサーチとランダムパラメータ最適化が紹介されており、グリッドサーチが広く使われていると記述があります。 ↩

58
70
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
58
70