はじめに
ベイズ最適化の獲得関数について考察したので紹介します。具体的には**獲得関数をLCBに設定し、標準偏差にかける係数を変えた際の挙動の違いについて検討しました。**ベイズ最適化の理論についてはこちら、Pythonでの実装方法についてはこちらにまとめましたので参考にして頂けると幸いです。
※機械学習やプログラミング関係の内容を他にも投稿していますので、よろしければこちらの一覧から他の投稿も見て頂けますと幸いです。
獲得関数とは?
**獲得関数とは、ガウス過程法によって推定される期待値μと標準偏差σを用いて表現される関数です。**ベイズ最適化ではこの獲得関数を用いて次のサンプリング点(実験条件)を決定していきます。
獲得関数には"改善確立PI(Probability of Improvement)"や"期待改善度EI(Expected Improvement)"などがありますが、今回は表現がシンプルである"信頼性下限関数LCB(Lower Confidence Bound)"を用いて検討を進めます。
※今回は最小値を求める問題なので"信頼性上限関数UCB(Upper Confidence Bound)"は用いません
LCBとは?
LCBは推定される期待値μと標準偏差σを用いて以下の式で表されます。
$$ LCB=μ-β×σ $$
**今回はβの値を変えた際の最適条件探索の挙動の違いについて検討しました。**βは"exploration_weight"と呼ばれ、公式ドキュメントには以下のように説明されています。
exploration_weight – positive parameter to control exploration / exploitation
つまり、βは探索(exploration)と活用(exploitation)の割合をコントロールする係数です。
- 探索(exploration):未知の領域(データが少ない場所)を攻めていく
- 活用(exploitation):ある程度良さそうと分かっている場所を攻めていく
式をから読み取れるようにβの値は標準偏差にかかっており、標準偏差(不確かさ)どの程度見積もるかということを意味します。つまり、βを大きくすると不確かさをより大きく見積もるので探索重視という方向性になります。イメージとしては以下の図のような理解をしています。
活用に重きを置くと最適解に早くたどり着ける可能性が上がる一方で、局所解に陥るといったデメリットもあります。探索に重きを置くとデータが少ない領域などをサンプリングすることで今までの最適解よりも大幅に優れた解が得られる可能性がある一方で、あくまでその可能性はあまり高くなく、なかなか最適解にたどり着けないというデメリットもあります。実験の初期(サンプル点が少ない状況)では探索重視にして、ある程度でデータが揃ってきたら活用に重きを置くといった戦略もあり、サンプル点数に応じてβを設定するという手法も知られています。
検討した内容
具体的な検討方法に関して
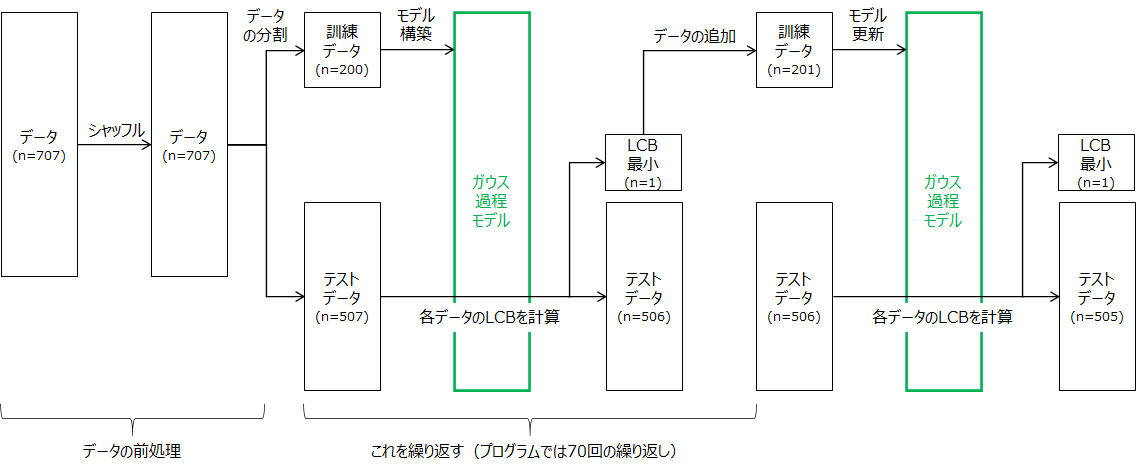
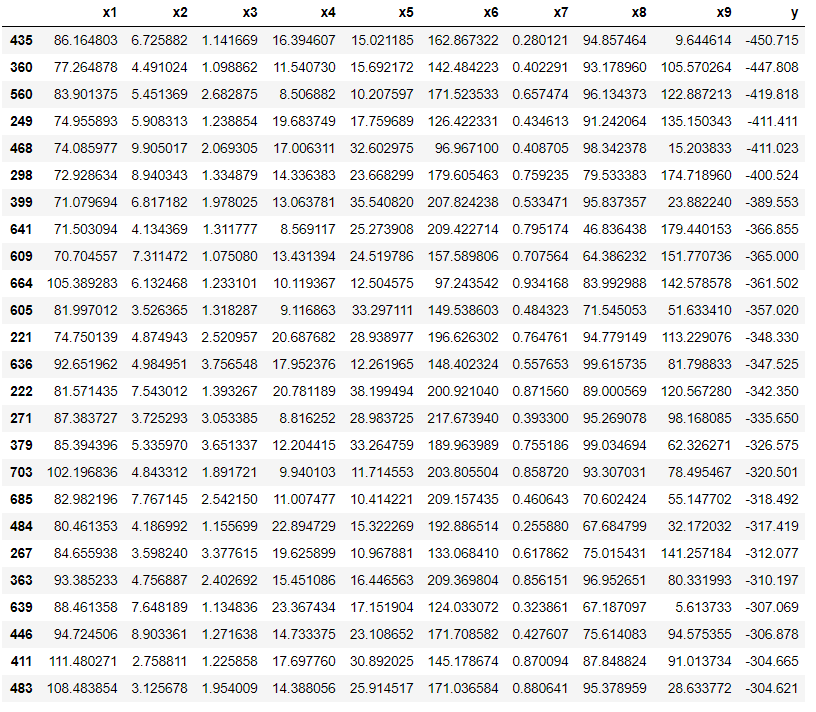
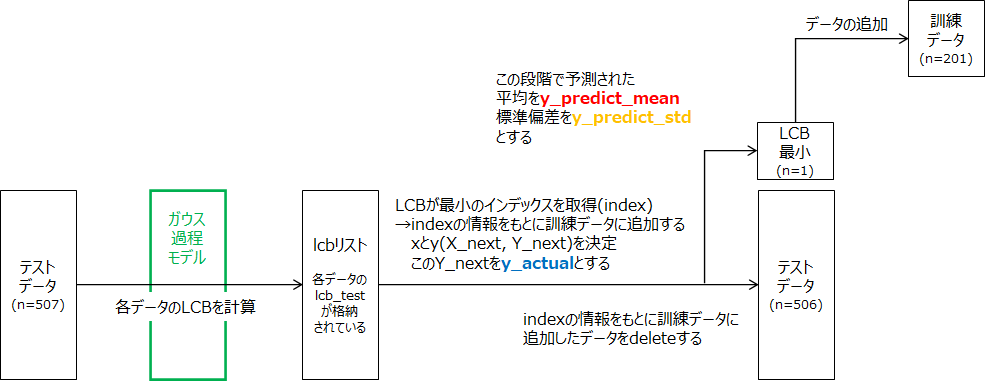
こちらのGitHubに保存しているデータ数707個のdf.csvのデータを用いて、以下の図に示すようなフローで最適条件(最小値を与える実験点)の探索を行いました。
<データの前処理>
①データをシャッフルする
②データを分割する(モデルを作る訓練データ200個とモデルに当てはめる507個に分割)
<ベイズ最適化の適用>
③訓練データからモデルを構築
④モデルをテストデータに当てはめて、各データのLCBを計算
⑤LCBが最小のデータを訓練データに追加
⑥③~⑤を繰り返し、LCBが最小と予測されたデータの挙動(最適解への到達の挙動)を検討する
今回はβが1,2,3の3条件で検討を行いました。
データの前処理
# データの読み込み
import pandas as pd
df = pd.read_csv("df.csv", encoding="shift_jis")
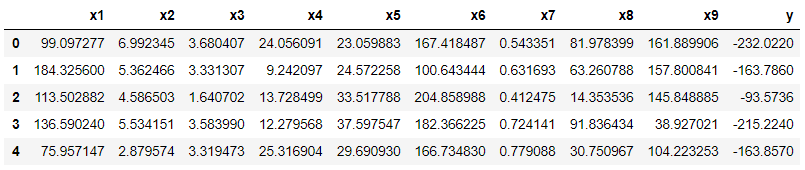
df.head()
最小値問題にするためにyに負号をつけておきます。
df["y"] = df["y"]*(-1)
df.head()
特にyの値が順番になっているわけではないですが、念のためデータの並びをシャッフルしておきます。
df_shuffled = df.sample(frac=1, random_state=0).reset_index(drop=True)
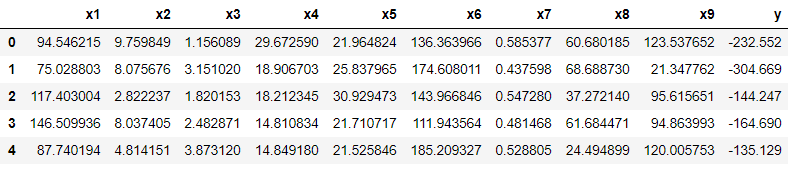
df_shuffled.head()
- データフレームにsample()メソッドを適用して引数frac=1とすることでデータフレーム全体をシャッフルすることができます。fracは割合を指定し、1を指定することでデータフレームの100%に作用します。
データを訓練データとテストデータに分割します。ここでは、シャッフル後のデータフレームの上位200件を訓練データとします。分割後、データの大きさを確認しておきます。
# 訓練データ(上から順番に200個)とテストデータ(残り507個)に分割
df_train = df_shuffled[:200]
df_test = df_shuffled[200:]
# 分割データの確認
print(df_shuffled.shape)
print(df_train.shape)
print(df_test.shape)
(707, 10)
(200, 10)
(507, 10)
訓練データのyの最小値およびその付近のデータを確認します。
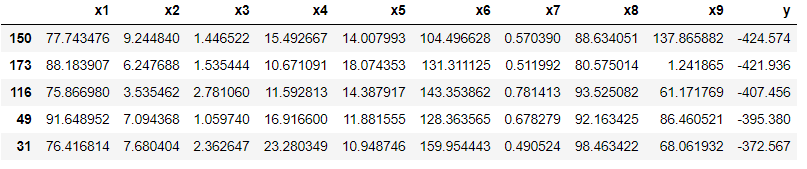
df_train.sort_values(by=["y"], ascending=True).head()
訓練データのyの最小値は-424であることが確認できました。次にテストデータのyの最小値およびその付近のデータを確認します。
df_test.sort_values(by=["y"], ascending=True).head(25)
テストデータのyの最小値は-450であることが分かりました。yの値が400以下のデータ数は6つであり、テストデータ全体の1%程度であることが読み取れます。また、テストデータの下位5%のyは-304以下であることも確認されます。以下のベイズ最適化ではいかに早くyが-450の条件をピックアップできるかが重要です。(実際の実験などを考えると早期に-400付近のデータが取得できれば十分かと思いますが…)
ベイズ最適化の実行(β=2の場合)
以下のコードでベイズ最適化を実行していきます。今回は繰り返し回数は70回としました。(もう少し少なくてもよかったかも…)
# ライブラリのインポート
import numpy as np
import os
import pandas as pd
import GPy
import GPyOpt
import datetime
# 訓練データ(スタート時200個)の読み込み
data = df_train
# 変数の個数を定義
num_x = len(data.columns)-1
# データ入力用のリストを作っておく
X_step=[]
Y_step=[]
# 訓練データをxとyに分割する
data_x=data.iloc[:,0:num_x]
data_y=data.iloc[:,num_x:num_x+1]
# DataFrame→numpy arrayに変更
X_step=np.asarray(data_x)
Y_step=np.asarray(data_y)
# テストデータ(スタート時507個)の読み込み
data_test = df_test
# テストデータをxとyに分割する
data_test_x = data_test.iloc[:,0:num_x]
data_test_y = data_test.iloc[:,num_x:num_x+1]
# DataFrame→numpy arrayに変更
X_test = np.asarray(data_test_x)
Y_test = np.asarray(data_test_y)
# グラフ描画用にリストを生成しておく
times = []
Y_mean = []
Y_std = []
Y_actual = []
# 最適化の開始時刻
start_time = datetime.datetime.today()
print ("開始時刻: " + start_time.strftime('%Y-%m-%d_%H-%M-%S'))
for j in range(70):
print("繰り返し"+ str(j+1) +"回目")
# 定義域の設定:'continuous':連続変数(一応設定したが、なくても良い?)
bounds = [{'name': 'x0', 'type':'continuous', 'domain': (70, 200)},
{'name': 'x1', 'type': 'continuous', 'domain': (2.5, 10)},
{'name': 'x2', 'type': 'continuous', 'domain': (1, 4)},
{'name': 'x3', 'type': 'continuous', 'domain': (7.5, 30)},
{'name': 'x4', 'type': 'continuous', 'domain': (10, 40)},
{'name': 'x5', 'type': 'continuous', 'domain': (95, 225)},
{'name': 'x6', 'type': 'continuous', 'domain': (0.2, 0.95)},
{'name': 'x7', 'type': 'continuous', 'domain': (10, 100)},
{'name': 'x8', 'type': 'continuous', 'domain': (0.1, 180)}]
#乱数初期化(必須ではない?)
np.random.seed(1234)
#最適化のパラメータの設定
params = {'acquisition_type':'LCB',#獲得関数としてLower Confidence Boundを指定
'acquisition_weight':2,#LCBのパラメータを設定
'kernel':GPy.kern.Matern52(input_dim=len(bounds), ARD=True),#GPに使うカーネルの設定 #boundsの次元でinputの次元を定義
'f':None,#最適化する関数の設定.通常は関数として定義できないので設定しない.
'domain':bounds,#パラメータの探索範囲の指定
'model_type':'GP',#標準的なガウシアンプロセスを指定.
'X':X_step,#既知データの説明変数
'Y':Y_step,#既知データの目的変数
'de_duplication':True, #重複したデータをサンプルしないように設定.
"normalize_Y":False, #予測を実スケールにするためにFalseを指定
"exact_feval":True #予測を実測に近づけるためにTrueを指定
}
#テストデータの各点に対して、(予測平均, 標準偏差)を算出していく
#ベイズ最適化のモデルの指定
bo_step = GPyOpt.methods.BayesianOptimization(**params)
#以下のコードを入れないとNotypeにはpredictできないとエラーがくる
x_suggest = bo_step.suggest_next_locations(ignored_X=X_step) #既にサンプリングした点を除くためにignored_Xで入力点を指定
y_predict = bo_step.model.model.predict(x_suggest)
#テストデータ(スタート時507個)に対してモデルをフィットして、予測平均と標準偏差を算出する
y_test_predict = bo_step.model.model.predict(X_test)
y_test_mean = y_test_predict[0]
y_test_std = y_test_predict[1]
#各テストデータの獲得関数(LCB)を計算していく
lcb = []
#LCBの計算
for i in range(len(X_test)):
# lcb( =mean - acq_weight*std )を計算していく
lcb_test = (y_test_mean[i]) - (params["acquisition_weight"]) * (y_test_std[i])
lcb.append(lcb_test)
#LCBが最小のインデックスを取り出す(重複がある場合を考えず、番号が若い方を優先)
index = lcb.index(min(lcb))
print(index)
#次に訓練データにインプットするxとyのペアを取得する
X_next = X_test[index]
Y_next = Y_test[index]
#次にインプットするデータと既にインプットしたデータを結合して次のインプット(訓練)データにする
X_step = np.vstack((X_step, X_next))
Y_step = np.vstack((Y_step, Y_next))
#探索点の予測平均、標準偏差、実際のyをリスト化しておく(グラフに描写のため)
#この操作はnp.delete前に実行しないと最下部のデータが次の候補点だった場合除外されてエラーが出る
times.append(j)
Y_mean.append(y_test_mean[index])
Y_std.append(y_test_std[index])
Y_actual.append(Y_test[index])
#訓練データに入力したデータをindex指定してテストデータから削除する
X_test = np.delete(X_test, index, 0)
Y_test = np.delete(Y_test, index, 0)
#lcbのリストも空にしておく(この段階でリセットをかける)
lcb.clear()
#stepの数が減って、testの数が増えているかprint文で確認しておく
print(X_step.shape)
print(X_test.shape)
# 最適化の終了時刻
end_time = datetime.datetime.today()
print ("終了時刻: " + end_time.strftime('%Y-%m-%d_%H-%M-%S'))
print ("所要時間: " + str(end_time - start_time))
開始時刻: 2021-**-**_**-**-**
繰り返し1回目
The set cost function is ignored! LCB acquisition does not make sense with cost.
444
(201, 9)
(506, 9)
繰り返し2回目
The set cost function is ignored! LCB acquisition does not make sense with cost.
93
(202, 9)
(505, 9)
︙
繰り返し70回目
The set cost function is ignored! LCB acquisition does not make sense with cost.
351
(270, 9)
(437, 9)
終了時刻: 2021-**-**_**-**-**
所要時間: 0:21:53.694803
1回目のLCBの計算ではindex番号444のデータがLCBの最小値として判断されたことが分かります。70回繰り返すことで、訓練データの数が200個から270個になり、テストデータの数が507個から437個に減っていることが読み取れます。プログラムとして狙い通りに動いてくれていそうです!
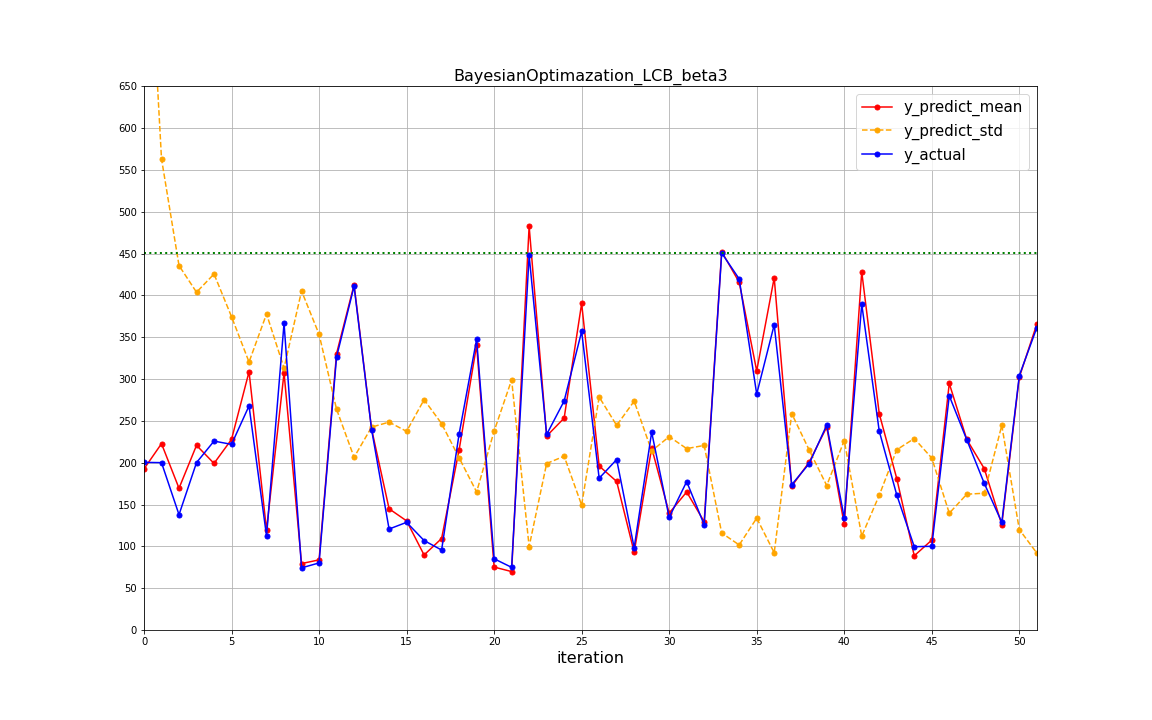
次にこのベイズ最適化の挙動を可視化します。直感的に理解しやすくするため、yは絶対値処理をしているので、以下ではyが大きいほうが良い(最大値を求める問題に変換された)と読み取ってください。
import matplotlib.pyplot as plt
# 最適条件の明示(yが最小の値)
y_450 = np.linspace(450.7, 450.7, 70)
plt.figure(figsize=(16, 10))
plt.plot(times, np.abs(Y_mean), label='y_predict_mean', marker="o", markersize=5, linestyle="solid", color="r")
plt.plot(times, Y_std, label='y_predict_std', marker="o", markersize=5, linestyle="dashed", color="orange")
plt.plot(times, np.abs(Y_actual), label='y_actual', marker="o", markersize=5, linestyle="solid", color="b")
plt.plot(times, y_450, color="green", linestyle=":", linewidth = 2.0)
# plt.xtickes(目盛り)でx軸を指定
plt.xticks(np.arange(0,71,5))
plt.yticks(np.arange(0,700,50))
plt.xlim([0,51])
plt.ylim([0,650])
plt.xlabel("iteration", fontsize=16)
plt.title("BayesianOptimazation_LCB_beta2", fontsize=16)
plt.grid()
plt.legend(fontsize=15)
plt.show()
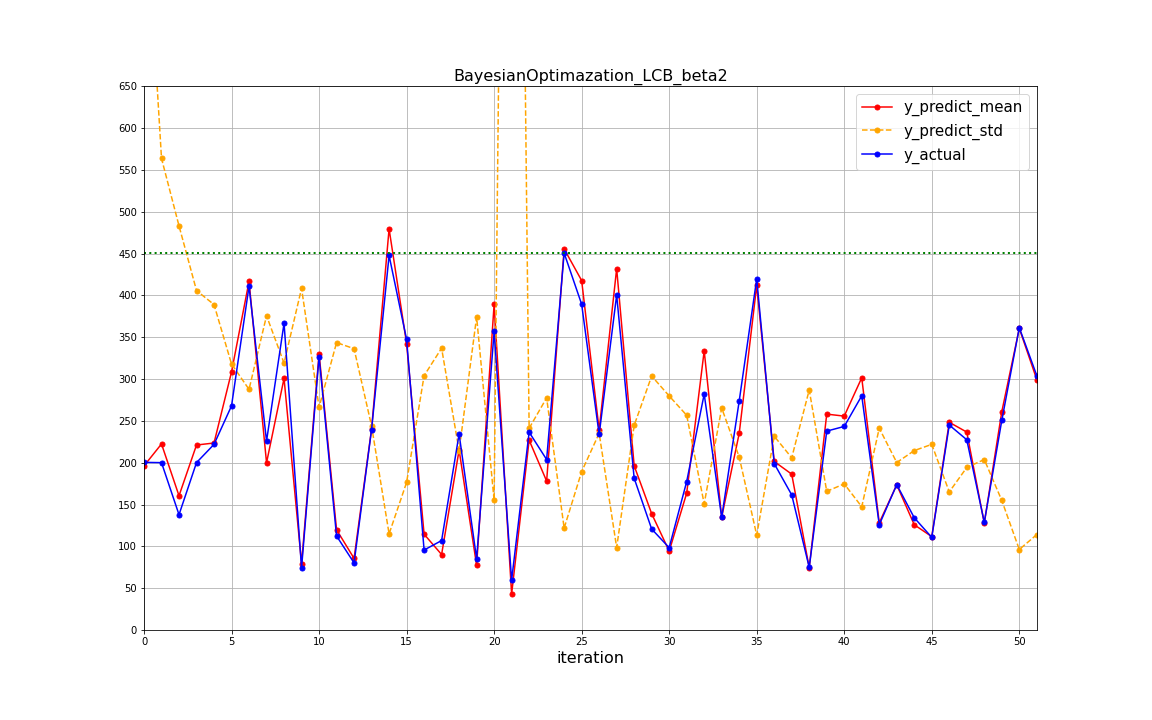
このグラフからは様々なことが読み取れます。
- β=2のベイズ最適化では繰り返し25回目で最適解に到達している(青色のプロットが緑のラインと被った回数)
- 7回目で400を超える特性が得られており、ランダムにピックアップするよりは十分に良い結果と考えられる
- 赤の予測と青の実際の値はほぼ同じ値で同じ挙動をしており、ベイズ最適化でyの値が精度よく予測されている
- オレンジ色の標準偏差は繰り返し回数を経るごとに小さくなってきており、不確実な領域が減っていると推測される
- 標準偏差(オレンジ)と予測平均(赤)は相反する挙動をしているが、標準偏差が大きく不確実な領域ではあまり良い特性が得られておらず(攻めに行ったがあまり良くなかったイメージ)、逆に標準偏差が小さい領域ではよい特性が得られており(ある程度自信を持って予測を行っているイメージ)ベイズ最適化のコンセプトが実現されているように思われる
コードについての解説
以下の図に示すような思想で"for j …"の繰り返し処理を行っています。ここは結構苦労しました…。
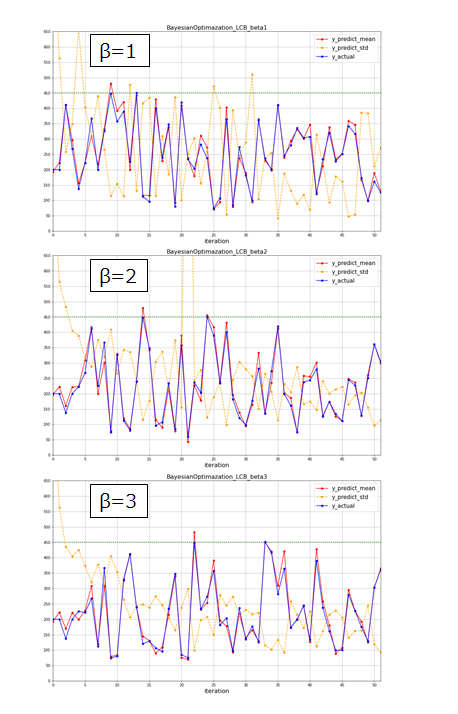
獲得関数に関する考察(β=1,2,3の比較検討)
上記のコードでacquisition_weightを変更した際の予測の挙動のグラフを示します。コードは割愛し、β=2の結果は再掲します。
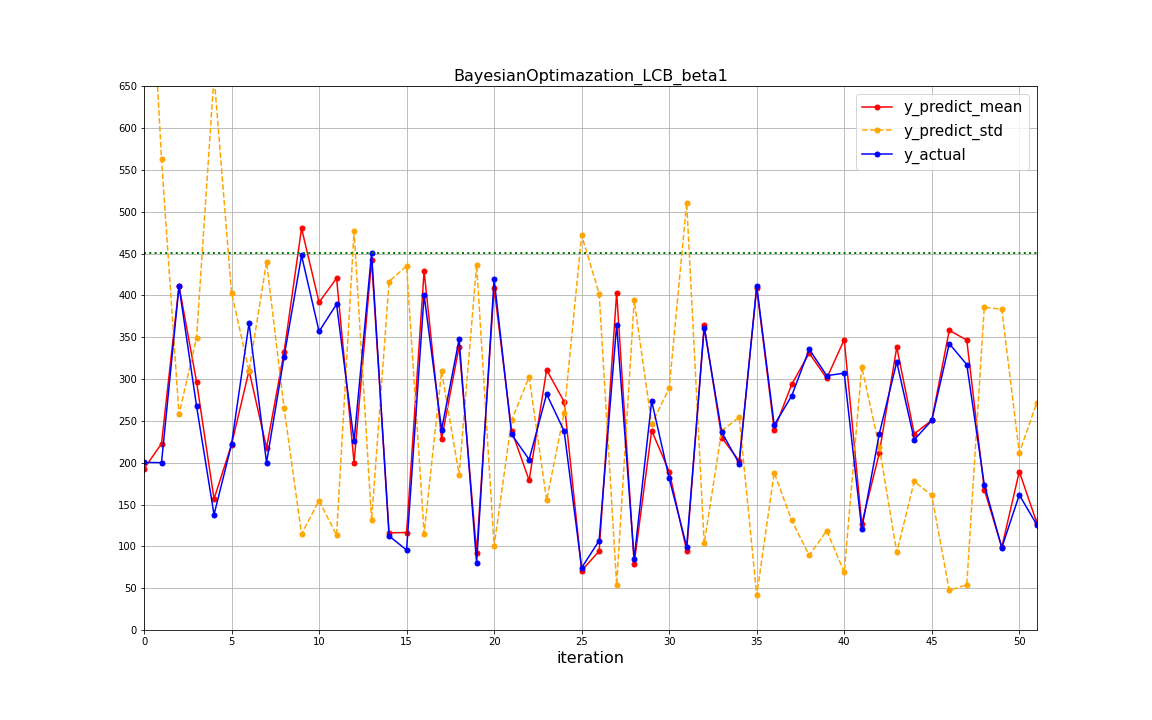
β=1の場合
β=2の場合
β=3の場合
並べて表示してみます
- 最適値への到達は、β=1で14回目、β=2で25回目、β=3で34回目であり、活用重視(βを小さくする)にした方が少ない回数で最適値に到達していることが分かります。(今回は起こりませんでしたが、その分局所解に陥りやすいという欠点もあります)このことから、ベータは探索と活用をコントロールするパラメータとして機能していることが読み取れます。
- β=1の条件は繰り返し回数を重ねても標準偏差が大きいデータが多いが、β=3では繰り返し回数を重ねると標準偏差は(β=1に比べると)小さく落ち着ている傾向が見られます。β=3では初期に不確実領域を探索していくことで、標準偏差が大きい領域をなくすことができていったのではないかと推測されます。
まとめ
ベイズ最適化の獲得関数について考察しました。LCBにおいては標準偏差にかける係数を大きくすることで探索重視になることが実データを用いた検証でも確認されました。