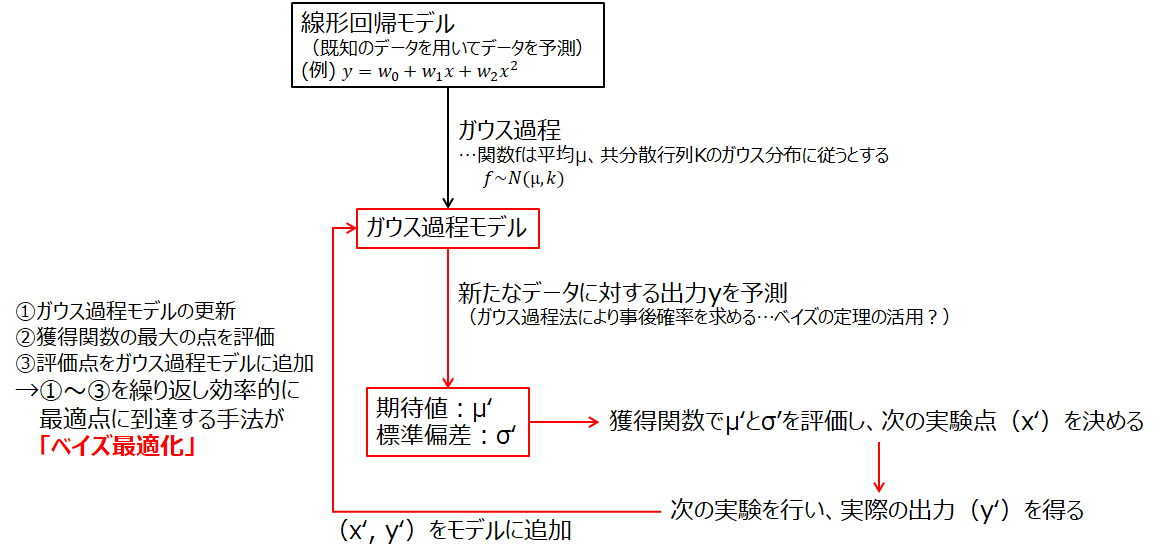
はじめに
**ベイズ最適化の理論についてまとめます。**Pythonでの実装方法についてはこちらの投稿を参考にして下さい。
この記事を書くにあたっては、「ガウス過程と機械学習」が非常に参考になりました。初見では結構難しかったですが、何周もすると理解が深まりました。（もう10周以上は読んだ気がします…）数式も交えてベイズ最適化を根本から理解されたい方はその文献か参考に挙げているサイトをご覧ください。
※機械学習やプログラミング関係の内容を他にも投稿していますので、よろしければこちらの一覧から他の投稿も見て頂けますと幸いです。
ベイズ最適化とは？
簡単に言えば、**「最適解が得られる確率が高い点を順番にサンプリングすることで早く最適解にたどり着く手法」**と理解しています。
具体例を用いた説明
以下の図の①～⑦に従って、ベイズ最適化が何をしようとしているのか説明します。①の図で0<x<9の範囲でy（グレーで示した関数）を最小にするxを求めることを考えます。
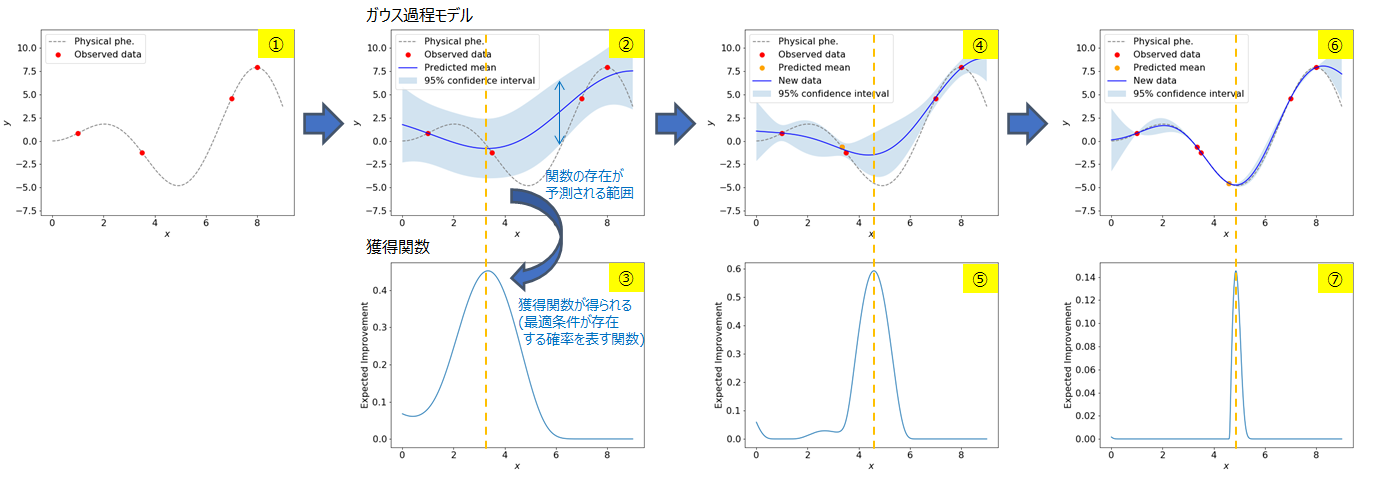
①まず初めに4点を実験（サンプリング）して、yを求めたとします。図中で赤色で示した4点が得られます。もちろんですが、この段階で関数がどのような形状をしているかは分からないのでグレーの点線は実際には分からないものとします。
②**この赤の4点にガウス過程モデルを適用することで、関数の予測（青色のライン）と関数が存在していそうな範囲（水色で示した幅のある領域）が求まります。**この関数の予測はのちで説明する期待値μ、関数が存在していそうな範囲は標準偏差σで表されます。（標準偏差σの説明は間違ってはいますが、イメージをつかむためにはとりあえずこの説明でよしとします）
③関数の予測と関数が存在していそうな範囲が求まると、それらから獲得関数という関数が計算されます。（厳密には違いますが）この獲得関数は最適条件が存在する確率を表す関数であると思ってください。獲得関数を見ると、x=3付近で最大値をとっていることが分かります。獲得関数が最大のx=3付近で最適条件が得られる確率が最も高いので、次はx=3付近を実験します。
④x=3付近を実験して、yを得たとします。この点はグラフ上ではオレンジ色でプロットされます。先ほどの赤の4点にこのオレンジの1点を加えることで、②と比較して関数の予測と関数が存在していそうな範囲が更新されていることが分かります。
⑤**関数の予測と関数が存在していそうな範囲が更新されたことを受けて、獲得関数も更新されます。**次はx=5付近で最適条件が得られる確率が最も高いということが分かります。ですので、次はx=5付近を実験します。
⑥x=5付近を実験して、yを得たとします。この点はグラフ上ではオレンジ色でプロットされます。先ほどの赤の5点（④でオレンジ色でプロットされた点は赤色になります）にこのオレンジの1点を加えることで、再び④と比較して関数の予測と関数が存在していそうな範囲が更新されていることが分かります。（関数が存在していそうな範囲に関してはx=0, x=9付近で大きくなっていますが、1<x<8の領域では比較的小さくなっていることが分かります。既にデータが取得できた領域では関数がある程度正確に予測され、不確実性が減っていることを意味します。②の段階では0<x<9の全体で関数が存在していそうな範囲が一様に大きく広がっており、どの領域も自信を持って予測ができていないと状態と言えます。）
⑦関数の予測と関数が存在していそうな範囲が更新されたことを受けて、再び獲得関数も更新されます。
この例では⑥の段階でほぼ最適解が得られていますが、このようにガウス過程モデルと獲得関数の更新を繰り返し、最適解を探索していく手法が「ベイズ最適化」です。
概念的な説明
- 予測したい関数やデータはガウス分布に従っていると仮定
- カーネル関数は変数間の関係を規定し、予測モデルに大きく影響する
- ガウス過程法による関数の推定結果は、事後確率の期待値と標準偏差で与えられる
- 事後確率の期待値と標準偏差によって獲得関数は定義される
- 獲得関数が最大の点を次のサンプリング点としてデータを取得する手法がベイズ最適化
図にすると以下のようになると理解しました。
用語の解説
ベイズ最適化を学習してる段階で出会った用語について解説します。
ガウス分布
正規分布とも呼ばれる。連続的な変数に関する確率分布の一つであり、データが平均値の付近に集積するような分布を表す。
共分散
変数間の相関を表し、共分散行列が対角行列である場合は変数間は互いに独立であるが、対角行列でない場合は変数間は独立でなく相関を持つ。1次元で言う分散に対応するワード。
次元の呪い
低次元では上手く処理できるが、高次元になると計算量が膨大になって対応できない問題を指す。
周辺化
モデルから積分消去すること。
カーネルトリック
特徴ベクトル（予測モデルを構築する関数）を明示的に表現することなく、カーネル関数の計算だけで特徴ベクトルをもとめること。
まとめ
ベイズ最適化の理論に関して理解したことをまとめました。
参考
理論系
- ベイズ最適化入門
- ベイズ最適化でハイパーパラメータを調整する
- ベイズ最適化の数学
- ベイズ最適化を用いた高次元ブラックボックス最適化手法の検証
- 『ガウス過程と機械学習』Pythonのnumpyだけで実装するガウス過程回帰
実装系