最近『ガウス過程と機械学習』を読んだので、Pythonで実装してみました。
内容としては、Chapter 3 の「3.4.2 ガウス過程回帰の計算」になります。

シカちゃんが目印。分かりやすくて結構おすすめです。
ガウス過程とはなんぞや?
まずはじめにガウス過程を一言で説明すると、
Y=f(X)において
「入力Xが似ていれば出力Yも似ている。」
という性質を数学的に表現するための道具です。
今回はこのガウス過程を用いた回帰分析である「ガウス過程回帰」を実装していきます!
ガウス過程回帰までの4ステップ
ここでは、以下のようなステップを踏んで解説していきます。
線形回帰
↓
リッジ回帰
↓
線形回帰, リッジ回帰をガウス分布(確率分布)で考える
↓
ガウス過程回帰
上記のステップを踏む理由は2点あります。
第一に、ガウス過程回帰はリッジ回帰を拡張した非線形モデルだからです。
ゆえにガウス過程回帰を理解する前提として、リッジ回帰の理解が必要となります。
またリッジ回帰の前提である線形回帰の理解も言わずもがな必要。そのため大前提の線形回帰から解説します。(「急がば回れ」的なことです。)
第二に、ガウス過程回帰はガウス分布(確率分布)からサンプリングによって予測値を得ていくからです。
詳しくは後々解説しますが、ガウス過程回帰がリッジ回帰(または線形回帰)と大きく異なるのは、サンプリングするガウス分布の分散が、ガウス過程にしたがって変化していくことです。
そのため、リッジ回帰(または線形回帰)でも同じようにガウス分布からのサンプリングによって予測するというステップを挟み、ガウス過程回帰がリッジ回帰(または線形回帰)の時とどう違うのかを理解できるようにしました。
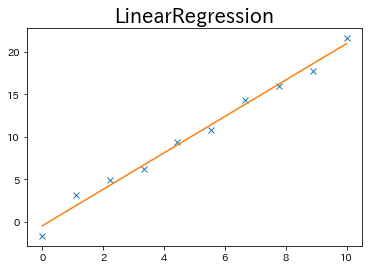
1. 線形回帰
ガウス過程回帰を理解する最初のステップとして、まずは線形回帰の復習から始めましょう。
線形回帰は入力行列をX, 係数ベクトルをw, 出力ベクトルをyとすると、
y=Xw \\
s.t. \min_{x}|Y-Xw|^2
という式で表すことができます。
s.t.は線形回帰の制約条件を示しており、
実測値Yと予測値(y=)Xwとの二乗誤差を最小にする。
という意味です。
特にこの制約条件をwで微分することにより、係数wの解を求めることができます。
w=(X^TX)^{-1}X^Ty
今回は一次関数で予測しましたが、入力Xが二乗, 三乗,…などの高次数の値でデータに追加されている場合、二次関数や三次関数など高次数の関数でも予測値を求めることもできます。
2. リッジ回帰
次にリッジ回帰です。リッジ回帰は線形回帰にさらなる制約が追加されたものです。
y=Xw \\
s.t. \min_{x} |Y-Xw|^2 + \alpha|w|^2
s.t.で表される制約条件に係数ベクトルwの二乗(の定数倍)項があります。
これは、
実測値Yと予測値(y=)Xwとの二乗誤差を最小にする。
尚且つ、係数wはできるだけ小さくする。
という意味です。
この追加制約によって2つの利点が得られます。
1.計算の安定化
線形回帰の係数wを求める際、実は以下の逆行列
(X^TX)^{-1}
が存在するという前提で計算が行われていました。
そのためこの逆行列が存在しない場合には、計算が不可能になるというデメリットがあります。
そこでリッジ回帰では制約条件に係数ベクトルwの二乗(の定数倍)項を追加することで、線形回帰の時と同様に制約条件をwで微分すると、
w=(X^TX + \alpha I)^{-1}X^Ty
となり、単位行列αIで意図的に逆行列を生み出しているため、計算が可能になるのです。
- 過学習を防ぐことができる。
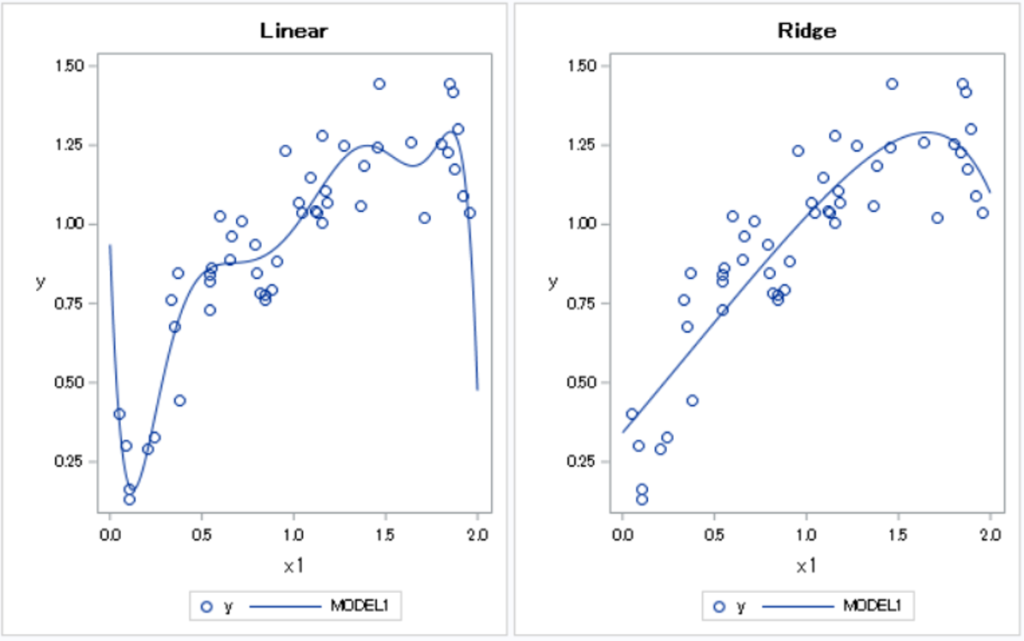
左の図が過学習してしまった線形回帰の結果, 右の図がリッジ回帰による結果です。
(線形回帰の過学習を抑えよう ~Ridge回帰とLasso回帰~よりグラフ引用)
先程、説明したように線形回帰は高次数の関数でも予測することができるため、回帰式が過度に複雑化してしまうことがあり、この現象を過学習と読んでいます。
そこでグラフが示すように、リッジ回帰ではあえて係数を小さく制限することで、予測値を算出する際の過学習を防ぐことができます。
3. ガウス分布と線形回帰, リッジ回帰
これまで説明してきた線形回帰とリッジ回帰を実際に使用した場合、予測値yと実測値Y
の間にはある程度の誤差が生じます。
つまり「予測誤差が生じる」ことを考慮して、あるxが与えられた予測値yはガウス分布
N(w^Tx, \sigma ^2)
に従ってサンプリングされると言えます。
ここで、線形回帰とリッジ回帰の係数wは既に求めているので、それぞれ変形すると、
線形回帰は
N \Bigl(\bigl((X^TX)^{-1}X^Ty \bigr)^Tx, \sigma ^2 \Bigr)
リッジ回帰は
N \Bigl(\bigl((X^TX + \alpha I)^{-1}X^Ty \bigr)^Tx, \sigma ^2 \Bigr)
からサンプリングすることによってそれぞれの予測値yが得られるということになります。
ここで特に押さえておいてほしいポイントは、
線形回帰とリッジ回帰ではガウス分布の平均が異なる。
しかし分散は変わらず、どちらも「等分散」を仮定している。
という点です。
4. ガウス過程回帰
それでは最後にガウス過程回帰を説明していきます!
ガウス過程回帰は、リッジ回帰に
「入力Xが似ていれば出力Yも似ている。」
というガウス過程の特徴を制約条件として加えたものです。
つまり、ガウス過程回帰の予測値yも先ほどの線形回帰やリッジ回帰のように、あるガウス分布からサンプリングして得られる値と考えた場合、
ガウス過程回帰が従うガウス分布は、
リッジ回帰のような「等分散」を仮定しておらず、
入力x, x'の距離(つまり似ているかどうか)に従って予測値y, y'の分散が変化する。
ということが言えます。
このことを前提としてガウス過程回帰が従うガウス分布を確認してみましょう。
N(k_*^TK^{-1}y, k_{**}-k_*^TK^{-1}k_*)
ここで見慣れないkやKが出てきました。
このkやKはカーネルといい、「2つの入力xから求められる値」です。
後に詳しく説明しますが、ここでは
K : 学習データ間の入力xから求められるカーネル
k* : 学習データの入力xとテストデータの入力xから求められるカーネル
k** : テストデータ間の入力xから求められるカーネル
として、ガウス過程回帰が従うガウス分布の平均と分散に上記のカーネルのどれかが含まれているため
様々な入力x同士の位置関係がガウス過程回帰が従うガウス分布の平均と分散の両方に影響を与える。
ということがわかります。
ガウス過程回帰の実装
データの作成
今回は以下のようなデータを準備します。
元データ: 人工的に作成したノイズ入り混合信号
学習データ: 元データから部分的に得たランダムなサンプル点
予測データ: 元のノイズ入り混合信号
import numpy as np
# 元データの作成
n=100
data_x = np.linspace(0, 4*np.pi, n)
data_y = 2*np.sin(data_x) + 3*np.cos(2*data_x) + 5*np.sin(2/3*data_x) + np.random.randn(len(data_x))
# 信号を欠損させて部分的なサンプル点を得る
missing_value_rate = 0.2
sample_index = np.sort(np.random.choice(np.arange(n), int(n*missing_value_rate), replace=False))
ここで、matplotlibのpyplotで確認してみましょう。
from matplotlib import pyplot as plt
%matplotlib inline
plt.figure(figsize=(12, 5))
plt.title('signal data', fontsize=20)
# 元の信号
plt.plot(data_x, data_y, 'x', color='green', label='correct signal')
# 部分的なサンプル点
plt.plot(data_x[sample_index], data_y[sample_index], 'o', color='red', label='sample dots')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=12)
plt.show()
結果は以下の通りです。
※ np.random.choice()でランダムなサンプル点を得ているので、グラフが変化することがあります。
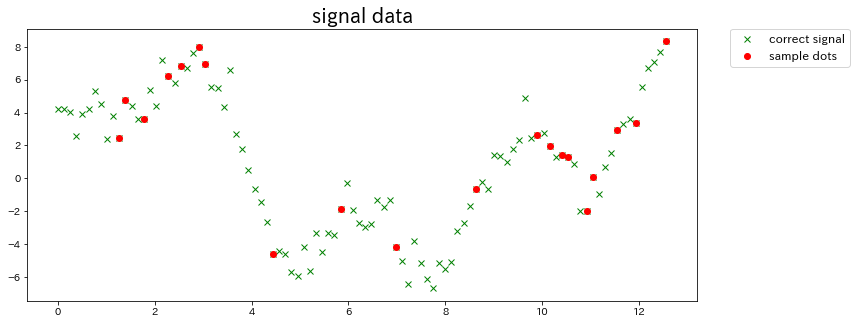
かなり複雑なデータですが、ガウス過程はどのように予測するのでしょうか…(ちょっと不安。)
カーネルの定義
1. カーネルについて
ここで突然出てきたカーネルですが、ざっくりと説明すると、
係数ベクトルwを計算せずにガウス過程回帰の共分散行列を求める
ツールのことです。
先程、ガウス過程は「予測値yに平均と分散を持つリッジ回帰」であると説明しました。
またこの平均と分散はガウス過程の特徴に従って、「入力Xが似ていれば出力Yも似ている」という関係性から計算されます。
例えば、入力Xが1次元データかつ-10から10まで1.0間隔とした場合、ガウス過程の予測値y(=xw)は入力Xの類似度つまり位置関係から導くので、yは21個求まり、係数ベクトルwは21次元になります。
ここで入力Xを2次元とすると、係数ベクトルは行列に代わり、その要素は441個に増加します。
更に3次元, 4次元, … と増やしていくと、係数行列の要素は指数関数増加し、通常では計算不可能な膨大な量になってしまいます。
また次元だけでなく、入力Xの範囲も更に拡大する可能性もあるため、これでは計算能力がいくらあっても足りません。
そこで登場するのがカーネルです。
カーネルを利用すると係数ベクトル(または行列)wを計算せずに、直接2つの入力x, x'間に相当する2つの出力y, y'の類似度を計算していき、ガウス過程回帰に必要な共分散行列を求めることができるのです!
2. カーネルの実装
カーネルにはいくつか種類がありますが、今回はガウス誤差を含んだガウスカーネル(RBFカーネル)を使用します。
ガウスカーネルには、
「入力x, x'の距離に応じて値がガウス分布のように指数的に減衰していく。」
といった特徴があります。
式は以下のように表されます。
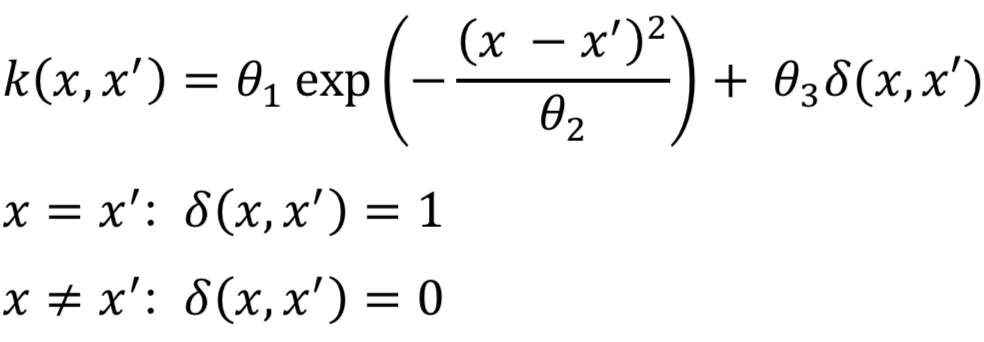
ここで、今回のパラメータ値は以下の3つとします。
θ1, θ2: ガウスカーネルのパラメータ
θ3: ガウス誤差の分散
また、ガウス誤差の関数δは、
2つの入力値xとx'が等しい: δ(x, x') = 1
それ以外: δ(x, x') = 0
のように条件分岐します。
それでは式を関数として実装します。
# ガウスカーネルを関数化
def kernel(x, x_prime, p, q, r):
if x == x_prime:
delta = 1
else:
delta = 0
return p*np.exp(-1 * (x - x_prime)**2 / q) + ( r * delta)
θ1, θ2, θ3 は p, q, r
x, x' は x, x_prime
となっています。
アルゴリズムの実装
ここからは、Chapter 3 の「図3.17 ガウス過程回帰の計算の基本アルゴリズム」に沿って進めていきます。
とりあえず本の表記に従い、先ほど作成した信号データを「学習データ」と「テストデータ」に分けて、わかりやすく再定義しておきます。
# データの定義
xtrain = np.copy(data_x[sample_index])
ytrain = np.copy(data_y[sample_index])
xtest = np.copy(data_x)
それでは実装に入っていきます。
ここでは、以前提示したガウス過程回帰が従うガウス分布
N(k_*^TK^{-1}y, k_{**}-k_*^TK^{-1}k_*)
における平均と分散の両方をガウスカーネルを用いて計算していきます。
# 平均
mu = []
# 分散
var = []
# 各パラメータ値
Theta_1 = 1.0
Theta_2 = 0.4
Theta_3 = 0.1
# 以下, ガウス過程回帰の計算の基本アルゴリズム
train_length = len(xtrain)
# トレーニングデータ同士のカーネル行列の下地を準備
K = np.zeros((train_length, train_length))
for x in range(train_length):
for x_prime in range(train_length):
K[x, x_prime] = kernel(xtrain[x], xtrain[x_prime], Theta_1, Theta_2, Theta_3)
# 内積はドットで計算
yy = np.dot(np.linalg.inv(K), ytrain)
test_length = len(xtest)
for x_test in range(test_length):
# テストデータとトレーニングデータ間のカーネル行列の下地を準備
k = np.zeros((train_length,))
for x in range(train_length):
k[x] = kernel(xtrain[x], xtest[x_test], Theta_1, Theta_2, Theta_3)
s = kernel(xtest[x_test], xtest[x_test], Theta_1, Theta_2, Theta_3)
# 内積はドットで計算して, 平均値の配列に追加
mu.append(np.dot(k, yy))
# 先に『k * K^-1』の部分を(内積なのでドットで)計算
kK_ = np.dot(k, np.linalg.inv(K))
# 後半部分との内積をドットで計算して, 分散の配列に追加
var.append(s - np.dot(kK_, k.T))
ちょっと長いので、順に解説していきますね。
まず今回求めるのは、信号の予測平均値および分散になります。
(予測値の間隔は元データと同じなので、100個の平均値と分散をリストに格納しています。)
またパラメータ値は先に指定しておきます。
アルゴリズムの中身は書籍と同じですが、Pythonで実装する場合は以下の変更が必要です。
・ K[x, x']を計算する前にカーネル行列Kの下地準備が必要。
(今回はゼロ行列で作成し、要素を書き換えていきました。)
・ 書籍の「*」は行列同士の内積を表すので、np.dot()に書き換える。
・ k[x]も計算前に下地準備が必要。
・分散の計算における3つの行列の内積は二段階に分けてnp.dot()に書き換える。
以上の点を抑えておけば、ガウス過程回帰はバッチリです!
最後に、matplotlibのpyplotで確認してみましょう。
plt.figure(figsize=(12, 5))
plt.title('signal prediction by Gaussian process', fontsize=20)
# 元の信号
plt.plot(data_x, data_y, 'x', color='green', label='correct signal')
# 部分的なサンプル点
plt.plot(data_x[sample_index], data_y[sample_index], 'o', color='red', label='sample dots')
# 分散を標準偏差に変換
std = np.sqrt(var)
# ガウス過程で求めた平均値を信号化
plt.plot(xtest, mu, color='blue', label='mean by Gaussian process')
# ガウス過程で求めた標準偏差を範囲化 *範囲に関してはコード末を参照
plt.fill_between(xtest, mu + 2*std, mu - 2*std, alpha=.2, color='blue', label= 'standard deviation by Gaussian process')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=12)
plt.show()
# 平均値±(標準偏差×2) … 95.4%の確率で範囲内に指定の数値が現れる
結果は以下の通りです。
※ 冒頭でも記載しましたが、ランダムに得たサンプル点の位置によってグラフは変化します。
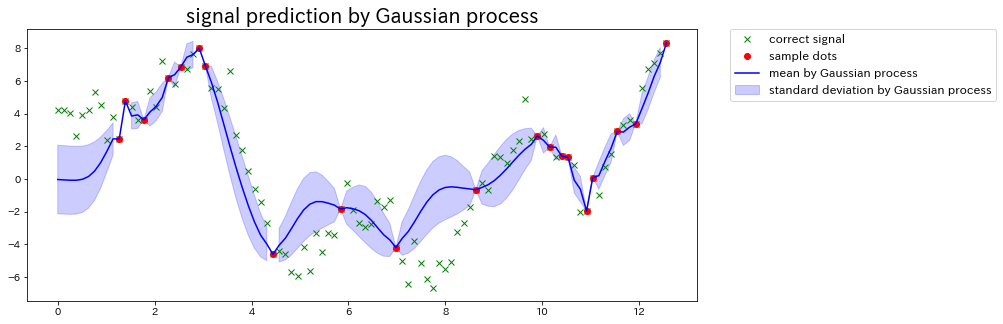
コードにも記載しましたが、今回は予測した分散を標準偏差に変換しています。
また標準偏差の2倍をガウス過程の予想範囲としました。
※ 範囲の決定方法に関しては、to-kei.net -全人類がわかる統計学- に記載されている以下の表を参照しました。
| 範囲 | 範囲内に指定の数値が現れる確率 |
|---|---|
| 平均値±標準偏差 | 68.3% |
| 平均値±(標準偏差×2) | 95.4% |
| 平均値±(標準偏差×3) | 99.7% |
ガウス過程のメリット
ガウス過程回帰には大きく分けて2つの利点があります。
1. 非線形モデルが簡単に求められる
線形回帰やリッジ回帰では非線形のモデルを作成する場合、n次関数を複数用意して学習することで対応していました。
そのため、**「何次の関数までを考慮すべきか」**という点がネックとなり、モデル構築にかなりの労力を費やさなければなりません。
しかしガウス過程回帰では、「カーネルを用いる」ことでn次関数を用意せずに非線形モデルを求めることができます。
よって学習の際の計算プロセスやアルゴリズムは複雑化しますが、少ない労力で複雑なモデル構築ができるのです。
2. 部分的な予測精度を確認できる
先ほどアルゴリズムを実装して求めたガウス過程回帰のグラフを観察すると、元データのおおよその特徴は掴んでいますが、ガウス過程の性質上、**サンプル点の間隔が大きい箇所(横軸:8付近など)**は予測がかなり外れています。
しかし、そのような予測の外れている箇所は他の箇所と比較して「分散」が広く、ガウス過程自体が予測に自信がないと自白しているようにも考えられます。
つまりガウス過程は部分的な予測精度を確認できるモデルであると言えます。
参考文献・参考リンク
『ガウス過程と機械学習』
線形回帰の過学習を抑えよう ~Ridge回帰とLasso回帰~
to-kei.net -全人類がわかる統計学-