ベイズ最適化シリーズ（1） ーベイズ最適化の可視化ー

ベイズ最適化とは

ベイズ最適化は、機械学習のハイパーパラメータ探索でよく使われます。その実行はGPyOptで簡単にできます。ベイズ最適化とGPyOptについて詳しく知りたい方は、以下のサイトを参考にしてください。
https://qiita.com/marshi/items/51b82a7b990d51bd98cd

ベイズ最適化は様々な場面で使えます。例えば、下記の用途が挙げられます。
・実験条件を最適化したい
・生産ラインの歩留まりが、最も良くなる設定値を見つけたい
・グラタンが美味しく焼けるオーブンの温度と加熱時間を求めたい

GPyOptでベイズ最適化

GPyOptを使って、ベイズ最適化の可視化を行います。
使う非線形関数のコードはこちら

Z = 0.1*(X**2+Y**2-16)**2 + 10*np.sin(3*X)

可視化すると以下のようになります。

import matplotlib.pyplot as plt
import numpy as np

#関数の定義
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)

X, Y = np.meshgrid(x, y)
Z = 0.1*(X**2+Y**2-16)**2 + 10*np.sin(3*X)#Zは山の高さ

#グラフのプロット
plt.figure()
cont = plt.contour(X, Y, Z, cmap="Greys")
cont.clabel(fmt='%1.1f', fontsize=14)
plt.xlabel("X")
plt.ylabel("Y")
plt.show()

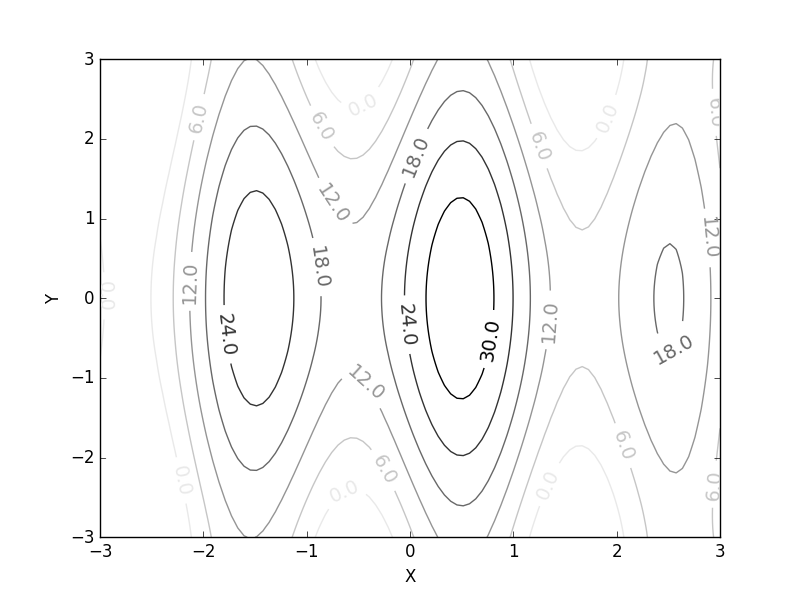
山が三つほどあり、中央の山(高さ35くらい)が最も高い地点です。今回は、ベイズ最適化で最も高い地点(中央の山の頂上)を見つけ出します。

通常、GPyOptは最低値を探索します。そのため、関数にマイナスをかけて最適化します。

import GPy
import GPyOpt
import numpy as np 

#最適化する関数
def f(x):
    xx,y = x[:,0],x[:,1]
    z = -(0.1*(xx**2+y**2-16)**2 + 10*np.sin(3*xx))#Zは山の高さ
    print(-z)
    return z

#状態変数の幅
bounds = [{'name': 'xx', 'type': 'continuous', 'domain': (-3,3)},
          {'name': 'y', 'type': 'continuous', 'domain': (-3,3)}]

#ベイズ最適化
myBopt = GPyOpt.methods.BayesianOptimization(f=f, domain=bounds)
myBopt.run_optimization(max_iter=30)

最適値の出力：(x,y)とz

print(myBopt.x_opt)
print(-myBopt.fx_opt)

探索履歴を保存します。

result_x = myBopt.X
result_z = -myBopt.Y

ベイズ最適化の可視化

探索履歴を可視化します。

plt.figure()
cont = plt.contour(X, Y, Z, cmap="Greys")
cont.clabel(fmt='%1.1f', fontsize=14)
plt.xlabel("X")
plt.ylabel("Y")
sc = plt.scatter(result_x[:,0], result_x[:,1],s=50,
 c=range(len(result_x)),cmap="autumn")
plt.colorbar(sc)
plt.plot(result_x[:,0], result_x[:,1], linestyle="dashed")
plt.show()

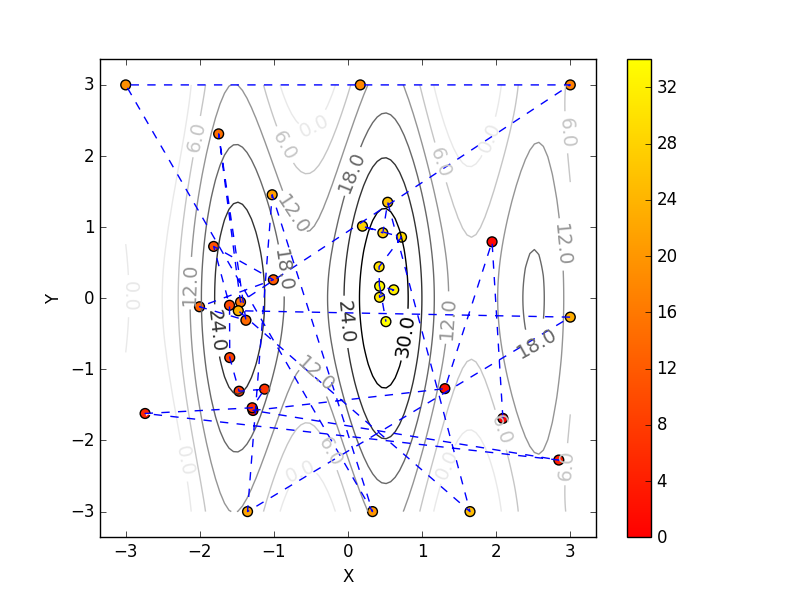
探索した順番で、点と点を繋いでみました。
・序盤は左の山を探索しています（赤い点）。
・中盤は隅っこを探索しています（オレンジの点）。
・終盤は中央の山を集中的に探索しています（黄色い点）。

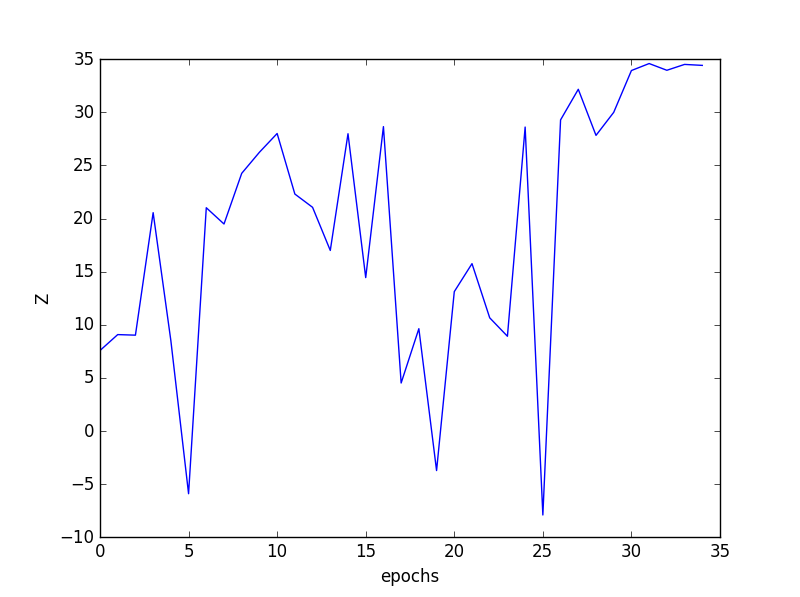
高さ（Z）の探索履歴を可視化します。最初はランダムに5個の地点を探索し、その後30回のベイズ最適化による探索をしているため、合計で35個のプロットが得られます。

plt.figure()
plt.plot(result_z)
plt.xlabel("epochs")
plt.ylabel("Z")
plt.show()

見事、最高点（高さ35付近）を見つけることができました！今回は二次元関数でしたが、n次元関数のときは、主成分分析などをして可視化すると直感的に分かりやすいかもしれません。

次回は、GPyOptを使ってXGBoostのハイパーパラメータを探索してみます。
次回は、GPyOptを使ってアンサンブル学習を最適化してみます。