- a=c×cos(θ)
- b=c×sin(θ)
- a=b×tan(θ)
今回の出発点は三角比(Trigonometric Ratio)とします。
一次元球面的分布(1D Spherical Distribution)における平均(Mean)と分散(Variance)
【数理考古学】ピタゴラスの定理あるいは三平方の定理からの出発 - Qiita

線分ab=線分ac=1の時、θ=角bacが0から直角(Right Angle)$\frac{π}{2}$に推移するとCos(θ)=線分adは1から0に、Sin(θ)=線分bdは0から1に推移する。これが三角比(Trigonometric Ratio)の世界。ここで座標直交(Orthogonal)時のCos($\frac{π}{2}$)=0を余弦定理(Cosine Theorem)$線分bc=\sqrt{線分ab^2+線分ac^2-2線分ab線分acCos(θ)}$に代入すると絶対値(Absolute ValueまたはModulus)=ユークリッド距離(Euclidean Distance)$R=\sqrt{Cos(θ)^2+Sin(θ)^2}$の公式が得られ平方対角線距離$\sqrt{2}$が求まる。これをさらに2乗した結果が分散(Variance)2。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出? - Qiita
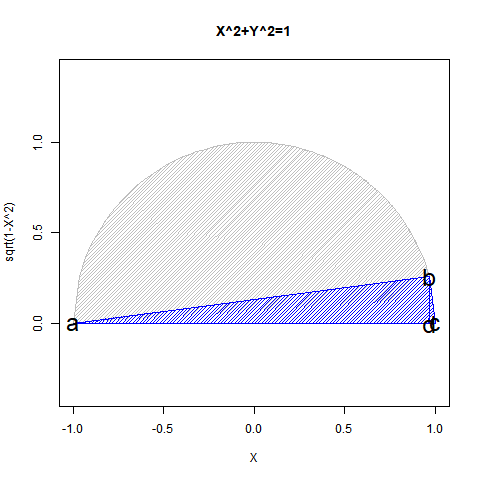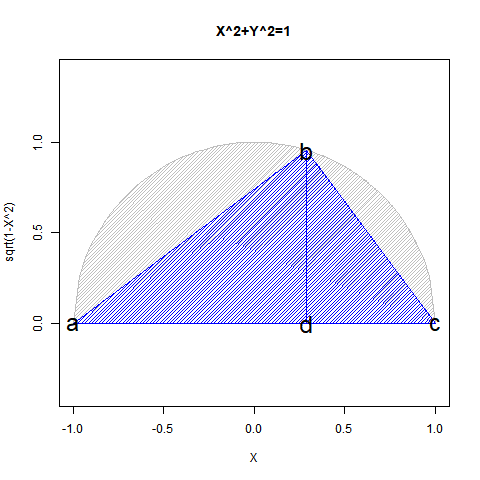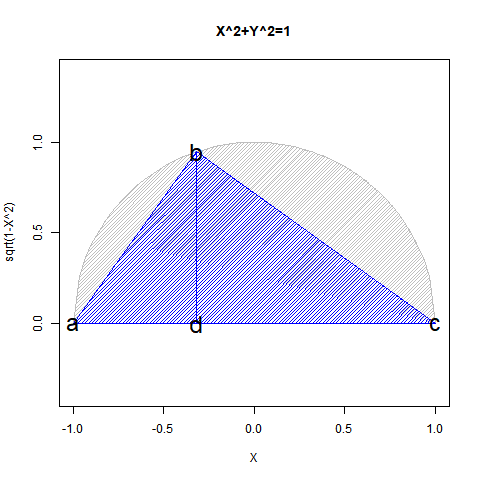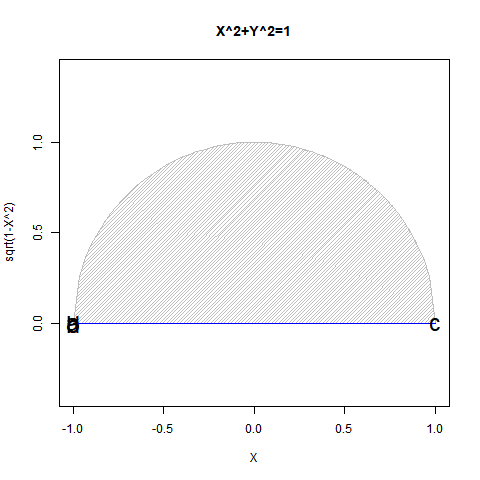
それでは「分散2」とはどういう状態なのか。あえて単純化して表現するなら「絶対値=半径=1の時の直径」である。θが0→$\frac{π}{2}$→πと推移するならCos(θ)は1→0→-1、Sin(θ)は0→1→0と推移する。
【初心者向け】「三角不等式(Triangle Inequality)」の体感方法? - Qiita

ここでCos(π)は三角不等式(Triangle Inequality)‖x+y‖≦‖x‖+‖y‖において‖x+y‖=‖x‖+‖y‖が成立する場合、すなわち‖x‖と‖y‖が同一直線上にあり三角形の面積は0に潰れてしまっている状態を指す(二次元空間から一次元空間への縮退)。この時x=yならz=2x=2yが成立。中心0=平均(Mean)$\frac{-1+1}{2}$,半径(絶対値)=1,直径(分散)=2が自ずと定まる訳である。この考え方が記述統計学(Descriptive Statistics)の出発点となる。
【Python演算処理】大源流における記述統計学との密接な関連性? - Qiita
【Pyrhon演算処理】記述統計との狭間 - Qiita
幾何学分野ではかかる「平均0,最小値-1,最大値+1,分散2」の線分範囲を一様分布(Uniform Distribution)前提で「1次元球面的分布(1D Spherical Distribution)」と見做し「2次元球面的分布(2D Spherical Distribution)=円弧(対数写像を取ると線形)」「3次元球面的分布(3D Spherical Distribution)=球表面(対数写像を1回取ると円面積、2回取ると長方形面積)」と拡張していく。
一様分布
線から円環への指数写像(Exponential Map)

円盤から球表面への指数写像(Exponential Map)

【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復 - Qiita
円筒座標系(Cylindrical Coordinate System)、球面座標系(Spherical Coordinate System)、円錐座標系(Conical Coordinate System)
ところで円描画関数$e^{θi}$(θ=0→2π,ここでいうiとは何かについては後述)に時間軸tの概念を1次元球面-1→0→+1ないしは+1→0→-1に従って与えると円筒座標系(Cylindrical Coordinate System)が現れる。この時水平方向からのx軸からの観測結果がCos(θ)波、y軸からの観測結果がSin(θ)波となるのは言うまでもない。
【Pyrhon演算処理】加法的同心集合とは? - Qiita


Cos(θ)波

Sin(θ)波

これをさらに球面座標系(Spherical Coordinate System)に拡張するには、さらにこの円筒座標系に時間軸tに沿って半弦描画関数$\sqrt{1-x^2}$を「(水平面における)半径の拡大縮小率」として与える。



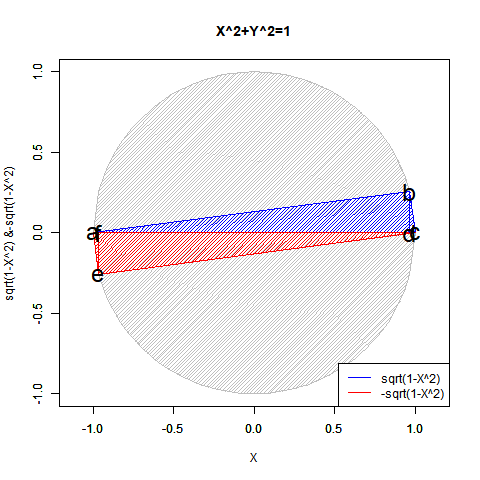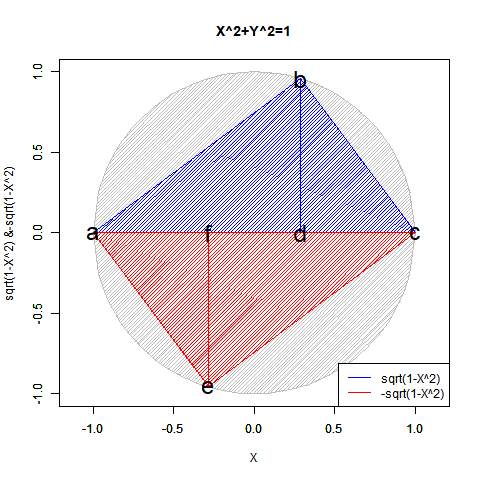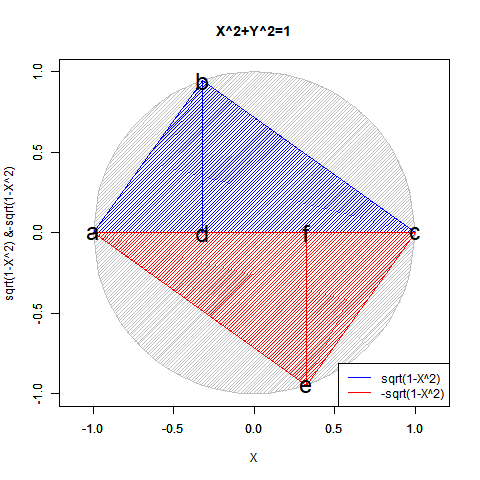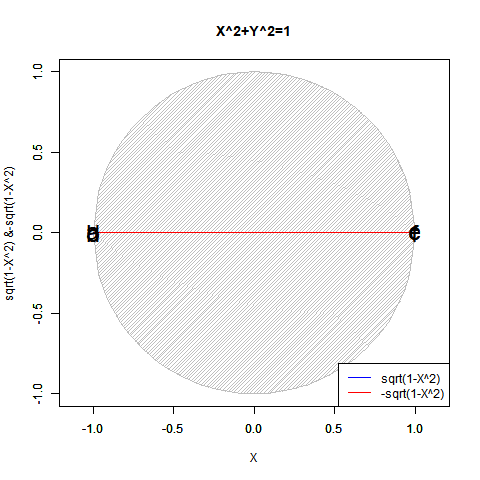
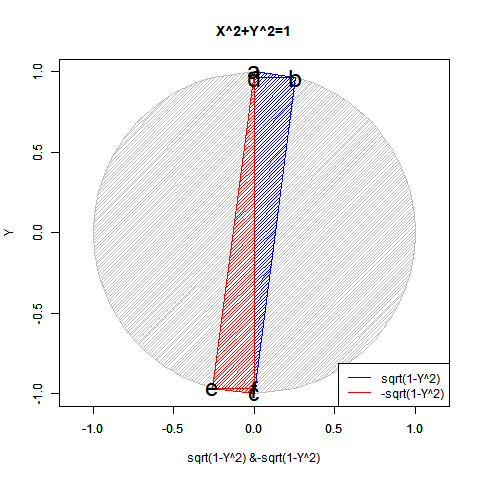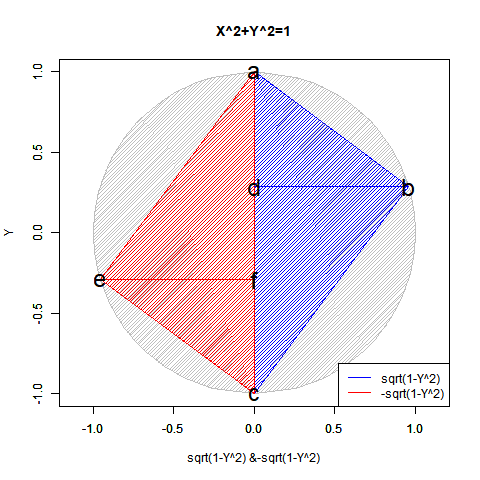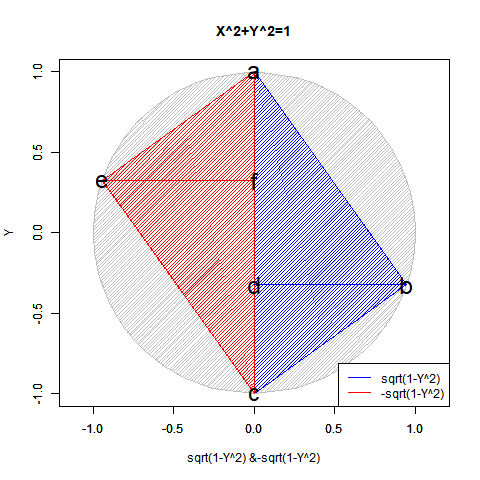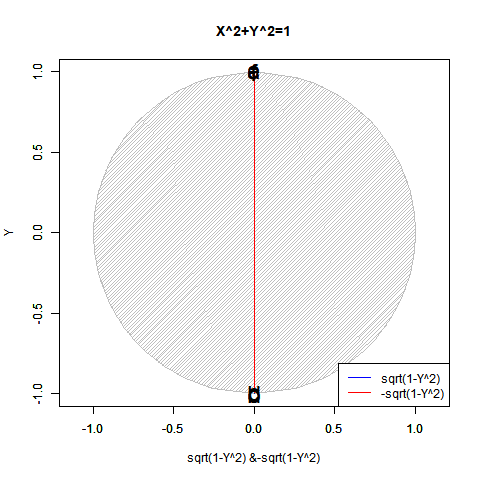
半弦描画関数$±\sqrt{1-x^2}$を用いても円描画は可能だが、この場合1次元球面(-1→0→+1)とその反転版(+1→0→-1)を組み合わせた往復分に半弦描画関数$\sqrt{1-x^2}$を「y軸への拡大縮小率」として与えた数学的構造となる。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出? - Qiita
これを三次元表示した座標系は円筒座標系ではなく円錐座標系(Conical Coordinate System)となる。1次元線形関数y=x(x=-1→0→+1ないしはx=+1→0→-1)を水平面における1周(0→2π)と対応付けたイメージ。それは絶対値関数y=|x|を半周(0→π)回転させた結果と重なる。
【連続極座標系】円筒形座標系による加法群と乗法群と商群の統合



複素平面(Complex Plane)概念とユニタリ変換(Unitary Transformation)概念の導入
ところでx座標とy座標の置換は「90度回転」を意味する。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出? - Qiita
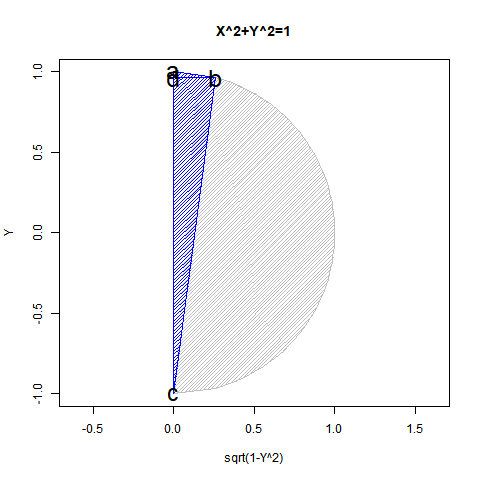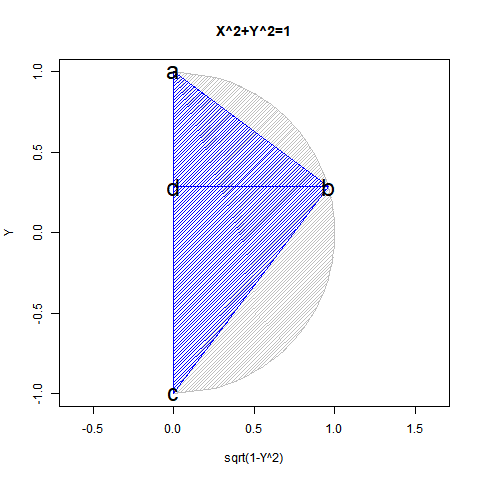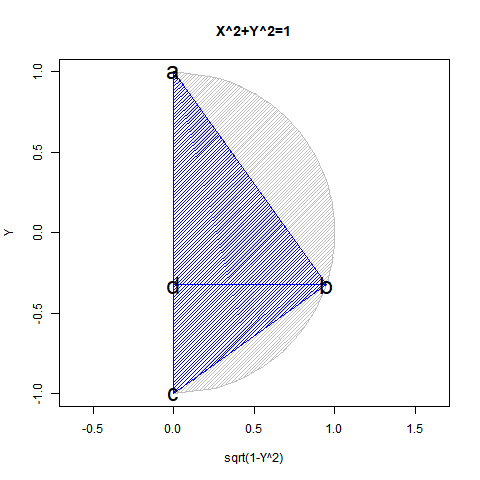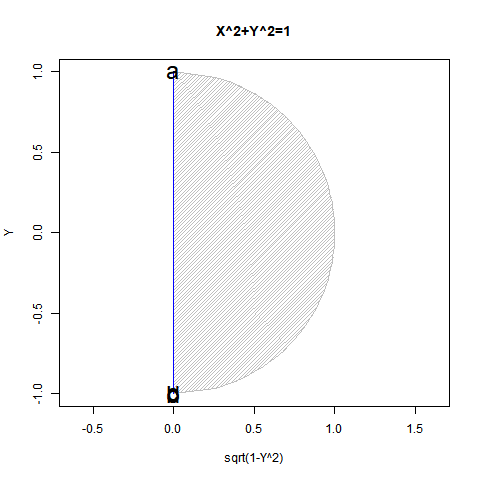
こうして第一象眼±90度(第一象眼$x^2=1$、第二、第三象眼$-x^2=-1$)までは扱う目処が立ちつが、第三象眼を扱うにはどうしても$x^2=-1$という考え方が必要となってくる。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出? - Qiita
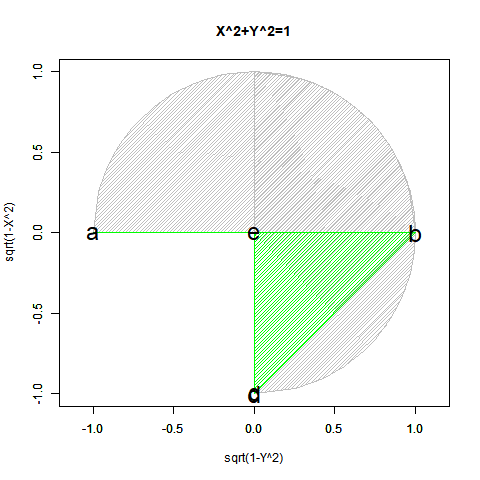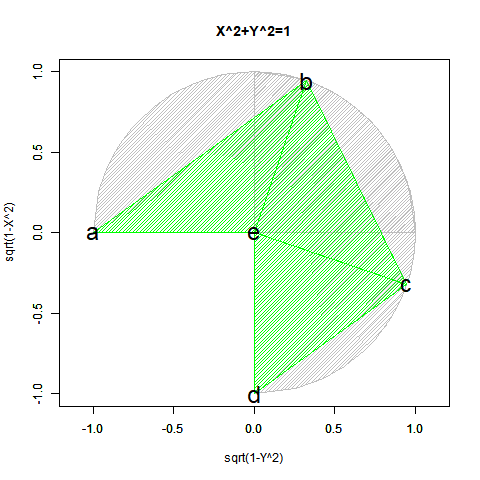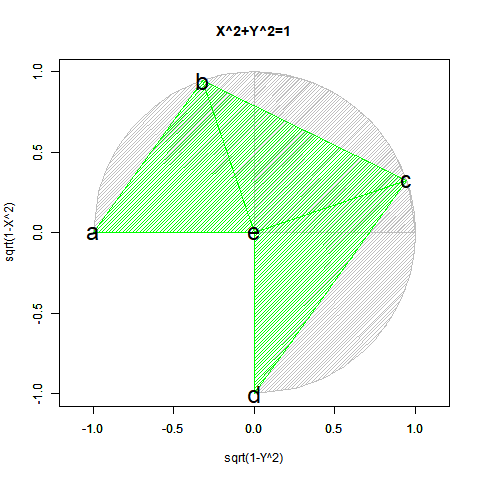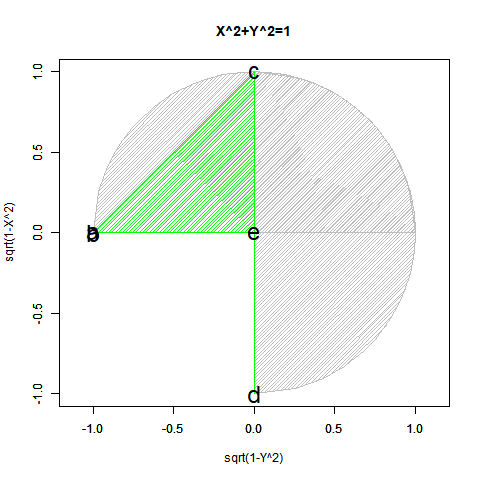
そこでいっその事、複素数(Imaginal)$i^2=-1$の概念を導入して第1象眼$-i^2=1+0i$、第2象眼0+1i、第3象眼$i^2=-1$、第4象眼0-1iと考えてしまった方が一貫性があって色々都合が良いというのが複素平面(Complex Plane)のコンセプトとなる。やっとこの考え方に到達したのが実に19世紀前半という…
【連続微小領域環】「地球平面説」から、いかに逃れるか? - Qiita

ちなみに線形代数では水平方向の回転は回転行列で済ませ、垂直方向の回転にこの考え方を導入する(いわゆるユニタリ変換)。
まずはざっとこの辺りをここでいう数学的思考法の出発点としたいと思います。
