はじめに

数理計画の凸最適化を中心に良記事と思われるURLを記載しました。
補足的な事項を記事として書いていこうと思います。

線形計画問題(LP)

線形計画は式1で記述される。

\begin{eqnarray}
\min &  &c^Tx \\
s.t. & &Ax=b\\
     & &x\geq 0
\end{eqnarray}
\tag{1}

参照

二次計画問題(QP)

二次計画は式2で記述される。

\begin{eqnarray}
\min &  &\dfrac{1}{2}x^TQx+c^Tx \\

s.t. & &Ax=b\\
     & &x\geq 0
\end{eqnarray}
\tag{2}

参照

半正定値計画(SDP)

半正定値計画は式3で記述される。

\begin{eqnarray}
\min &  & C \bullet X\\

s.t. &  & \ \ A_{i}\bullet X = b_{i} \ \ (i=1,2,...,m)\\
     &  & \ \ X\succeq 0
\end{eqnarray}
\tag{3}

参照

二次錐計画(SOCP)

参照

二次制約二次計画(QCQP)

確率計画

参照

確率計画法とその周辺の紹介

ロバスト最適化(RO)

参照

分布的ロバスト最適化(DRO)

分布的ロバスト最適化は、経験分布$\hat{\mathbb{P}}_N$の不確実性を集合で表し、その集合の中で最悪ケースの期待コストの最小化を目指す。

\inf_{\xi}\sup_{\mathbb{Q}\in\mathbb{B}_{\epsilon}(\hat{\mathbb{P}}_N)} 
\mathbb{E}^{\mathbb{Q}}[l(\xi)]

不確実性集合$\mathbb{B}_{\epsilon}(\hat{\mathbb{P}}_N)$は、下式で与えられる。

\mathbb{B}_{\epsilon}(\hat{\mathbb{P}}_N)
:=
\{\mathbb{Q}\in\mathcal{M}(\Xi):
d_{W}(\hat{\mathbb{P}}_N,\mathbb{Q})\leq\epsilon\}

経験分布$\hat{\mathbb{P}}_N$を中心とした半径$\epsilon$のWasserstein球とみることができる。

参照

リーマン多様体上の最適化

リーマン多様体$\mathcal{M}$としたとき、

\begin{eqnarray}
\min &  &f(x) \\

s.t. & & x\in \mathcal{M}

\end{eqnarray}
\tag{4}

参照

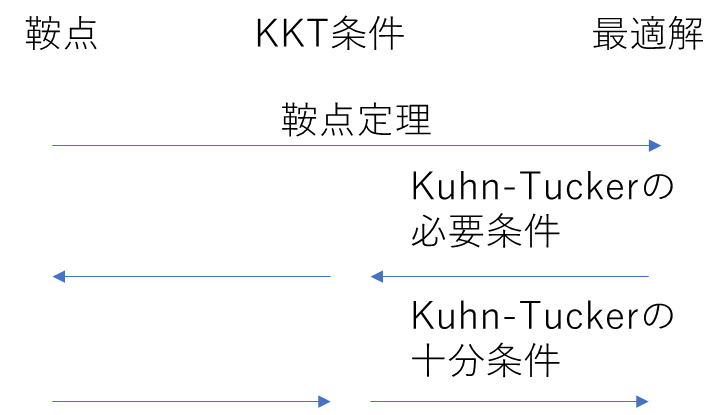
KKT条件

主問題を考える。

\begin{eqnarray}
\min &  &f(x) \\

\mathrm{s.t.} & &g(x)\leq 0\\
              & & x\in X
\end{eqnarray}

$\Phi(x,u)=f(x)+\langle u,g(x)\rangle, u\geq0$とおくとき、$\Phi(x_0,u_0)$の鞍点を下式で定義する。

\Phi(x_0,u)\leq\Phi(x_0,u_0)\leq\Phi(x,u_0)

このとき、凸最適化問題では、鞍点とKKT条件と主問題の最適解には以下の関係がある。

参照

数理計画法　～KKT条件～

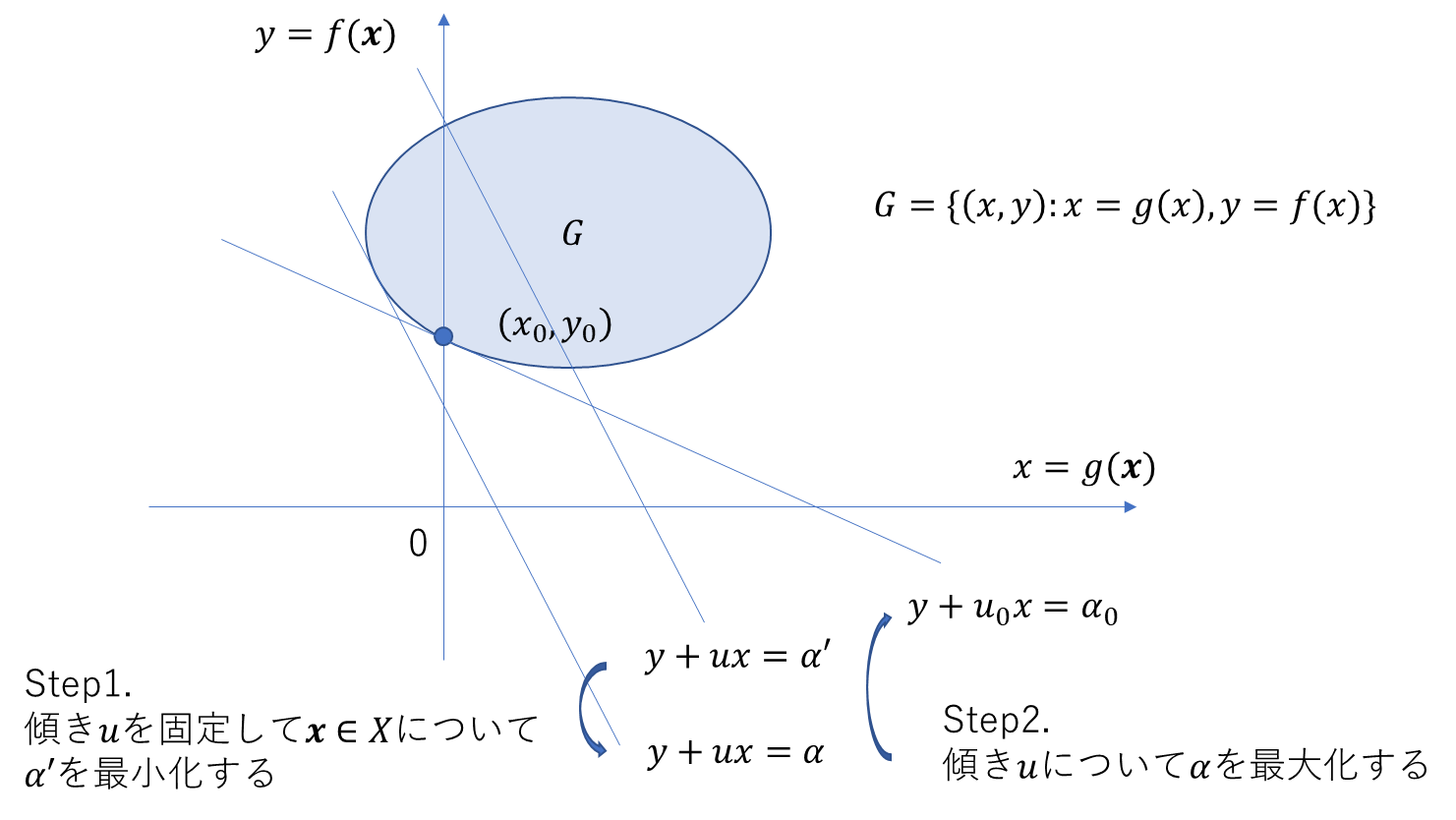
ラグランジュ双対問題

主問題を考える。

\begin{eqnarray}
\min &  &f(x) \\

\mathrm{s.t.} & &g(x)\leq 0\\
              & & x\in X
\end{eqnarray}

このときのラグランジュ双対問題は、$\theta(u):=\inf_{x\in X}\lbrace f(x)+u^Tg(x)\rbrace$とおけば、

\begin{eqnarray}
\max &  &\theta(u) \\

\mathrm{s.t.} & &u\geq 0\\
\end{eqnarray}

凸最適化問題について考えると、主問題とラグランジュ双対問題は下図の関係にある。
$(x_0,y_0)$は主問題の最適解である。凸最適化問題では、主問題とラグランジュ双対問題の最適解は一致する(強双対性)。ラグランジュ双対問題を考えるとき、傾き$u\geq0$の条件をつけないといけないことに注意する。

参照

不動点近似法

ADMMなどの近接分離最適化など凸最適化問題の収束について考えるときに用いる。

不動点理論と最適化

ADMM

\begin{array}{ll}
\mathrm{ min } & f(x) + g(z) \\
\mathrm{ s.t. } & Ax + Bz = c
\end{array}

SAM

SAMのわかりやすい記事

凸解析

最適性条件で出てくる凸解析の用語のイメージについて

代数幾何

参照

凸代数幾何と最適化理論

整数計画のモデリング

参照

数理計画 ～目次～