内点法による二次計画法

#二次計画問題
前回は内点法(カーマーカー法)を用いて線形計画問題を解くことをしました。今回は同様に内点法を用いて二次計画問題を解くことを行ってみます。
二次計画問題は目的関数が二次形式、制約条件が線形の形で表されており、以下のようなベクトル$x$を最小化する問題として表現されます。

\min \frac{1}{2} {\bf x}^T {\bf D} {\bf x} + {\bf c}^T {\bf x}\\
subject \ \ \ {\bf A}{\bf x} \ge {\bf b}

ここで${\bf x}$の次元を$n$、制約数を$m$とすると、${\bf x},{\bf c},{\bf b}$は$n$次元ベクトルで、${\bf A}$は$n \times m$の行列、${\bf D}$は$n \times n$の正値対象行列となります。

#二次計画問題における内点法
今回、二次計画問題を内点法で解く方法としてNumerical Optimizationの中で紹介されている予測子修正子法というものを今回実装してみました。線形計画問題に比べると複雑さは増しています。

#!/usr/bin/python
#coding:utf-8
import numpy as np

EPS_ZERO = 1.0e-9

def select_alpha(alphas):
    return 1.0 if alphas.size == 0 or np.min(alphas) > 1.0 else np.min(alphas)

def inv_vec(vec):
    inv = np.matrix(zeros((vec.shape[0], 1)))
    cond = np.where(np.abs(vec) > EPS_ZERO)
    inv[cond] = 1.0 / vec[cond]
    return inv

def less_zero(vec):
    return vec <= -EPS_ZERO

def quadratic_programming(x, gmat, c, amat, b,
                          tau=0.5, eps=1.0e-3, nloop=30):
    """
    内点法(Predictor-Collector)による2次計画問題の解法
    object  min z = 0.5 * x^T * G * x + cT * x
    subject Ax >= b
    """
    ndim  = gmat.shape[0] # 次元数
    ncnst = amat.shape[0] # 制約数
    x_idx, y_idx, l_idx = np.split(np.arange(0, ndim + 2 * ncnst),
                                   [ndim, ndim + ncnst])
    y_l_idx = np.r_[y_idx, l_idx]
    zeros_d_c = np.zeros((ndim, ncnst))
    zeros_c2 = np.zeros((ncnst, ncnst))
    eye_c = np.identity(ncnst)

    f = np.bmat([[-gmat * x - c],
                 [zeros((ncnst, 1))],
                 [amat * x - b]])
    exmat = np.bmat([[gmat, zeros_d_c, -amat.T],
                     [zeros_d_c.T, zeros_c2, eye_c],
                     [-amat, eye_c, zeros_c2]])
    delta_xyl0 = np.linalg.pinv(exmat) * f

    abs_yl0 = np.abs(delta_xyl0[y_l_idx])
    abs_yl0[abs_yl0 < 1.0] = 1.0
    y, lmd = np.vsplit(abs_yl0, 2)
    rd = gmat * x - amat.T * lmd + c
    rp = amat * x - y - b

    for n in range(nloop):
        err = np.linalg.norm(rd)**2 + np.linalg.norm(rp)**2 + np.asscalar(y.T * lmd)
        if err < eps:
            break
        # affine scaling step
        iy = inv_vec(y)
        f = np.bmat([[-rd],
                     [-lmd],
                     [rp]])
        exmat = np.bmat([[gmat, zeros_d_c, -amat.T],
                         [zeros_d_c.T, np.diag(np.multiply(lmd, iy).A1), eye_c],
                         [-amat, eye_c, zeros_c2]])
        d_xyl_aff = np.linalg.pinv(exmat) * f
        # alphaの計算
        y_l_cnb = np.bmat([[y],
                           [lmd]])
        cnd = less_zero(d_xyl_aff[y_l_idx])
        alpha_aff = select_alpha(-y_l_cnb[cnd] / d_xyl_aff[y_l_idx][cnd])
        # 中心パラメータ
        mu = np.asscalar(y.T * lmd / ncnst)
        mu_aff = np.asscalar((y + alpha_aff * d_xyl_aff[y_idx]).T * (lmd + alpha_aff * d_xyl_aff[l_idx]) / ncnst)
        sig = (mu_aff / mu)**3
        # corrector step
        dl_y_aff = np.multiply(np.multiply(d_xyl_aff[y_idx],
                                           d_xyl_aff[l_idx]),
                               iy)
        f = np.bmat([[-rd],
                     [-lmd - dl_y_aff + sig * mu * iy],
                     [rp]])
        d_xyl = np.linalg.pinv(exmat) * f
        # alpha_pri, alpha_dualの計算
        cnd = less_zero(d_xyl)
        alpha_pri = select_alpha(-tau * y[cnd[y_idx]] / d_xyl[y_idx][cnd[y_idx]])
        alpha_dual = select_alpha(-tau * lmd[cnd[l_idx]] / d_xyl[l_idx][cnd[l_idx]])
        alpha_hat = min([alpha_pri, alpha_dual])
        # x, y, lmdの更新
        x, y, lmd = np.vsplit(np.r_[x, y, lmd] + alpha_hat * d_xyl,
                              [ndim, ndim + ncnst])
        rp = (1.0 - alpha_pri) * rp
        rd = (1.0 - alpha_dual) * rd + (alpha_pri - alpha_dual) * gmat * d_xyl[x_idx]
    return x, y, lmd

if __name__ == "__main__":
    c = np.matrix([[-2.0],
                    [-4.0]])
    dmat = np.matrix([[2.0, 0.0],
                      [0.0, 2.0]])
    amat = np.matrix([[1.0, 1.0],
                      [1.0, -1.0],
                      [-3.0, 1.0]])
    b = np.matrix([[-0.5],
                   [1.0],
                   [-3.0]])
    # 描画
    from pylab import *

    ax = subplot(111, aspect='equal')
    x = np.arange(-3.0, 3.01, 0.15)
    y = np.arange(-3.0, 3.01, 0.15)
    X,Y = meshgrid(x, y)
    t = arange(-3.0, 3.01, 0.15)
    func = lambda x, y : 0.5 * (dmat[0, 0] * x**2 + dmat[1, 1] * y**2) + c[0, 0] * x + c[1, 0] * y
    const = [lambda x : -amat[i, 0] / amat[i, 1] * x + b[i, 0] / amat[i, 1] for i in range(amat.shape[0])]
    Z = func(X, Y)
    s = [const[i](t) for i in range(amat.shape[0])]
    pcolor(X, Y, Z)
    for i in range(amat.shape[0]):
        ax.plot(t, s[i], 'k')
    x, y, lmd = quadratic_programming(np.matrix([[0.0], [0.0]]),
                                      dmat, c, amat, b,
                                      tau=0.5, eps=1.0e-3, nloop=25)
    print x
    ax.plot([x[0, 0]], [x[1, 0]],'yo')
    axis([-3, 3, -3, 3])
    show()

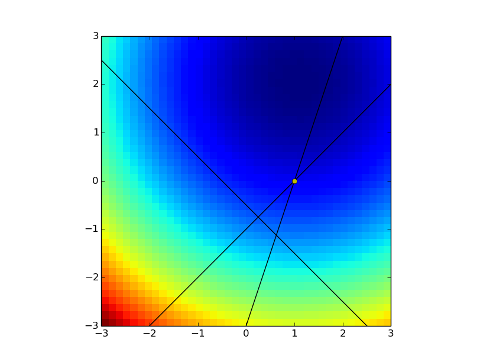
前回同様、2次元の問題で描画してみます。3本の線の中が制約を満たす解の領域で、青が濃くなる方向が最適値です。
グラフの中で黄色の点が最終的な最適解を示しており、初期値を制約の外から与えても適切な解を出せていることが分かります。

今回作成したコードはPythonなので、計算速度的には遅いですが、アルゴリズムの理解は多少しやすいのかなと思いました。
今回のコードではステップを求める際に擬似逆行列を用いたのですが、共役勾配法を用いたり、exmatの疎性を利用することで高速化できるようです。