特異値分解をリーマン多様体上の最適化で実装してみた。

はじめに

Euclid空間における最適化問題の１つとして古典的な制約付き最適化がある。この制約式を多様体上の空間で取り扱うことで、リーマン多様体上の最適化は、制約付き最適化を無制約最適化問題として扱えるようにしている。無制約最適化問題というくらいなので、最急降下法、共役勾配法およびニュートン法が活躍する。

リーマン多様体上の最適化の初歩的な解説は下の記事が参考になる。

リーマン多様体上の最適化は、特異値分解、主成分分析、独立成分分析、ロバスト主成分分析、低ランク行列分解などに定式化できることが知られている。

文献1では特異値分解をリーマン多様体上の最適化に定式化して解いている。文献1では、最急降下法、共役勾配法およびニュートン法に定式化している。本記事で、PythonとPymanoptでそれぞれ実装したものをおいたので遊んでみてほしい。

特異値分解を例としたリーマン多様体上の最適化のざっくりとした説明は下にある。

特異値分解とは

特異値分解（Singular Value Decomposition, SVD）は、式(1)のように行列分解することである。

$$
A=U\Sigma V^T \tag{1}
$$

$$
U\in O(m), \ \ V\in O(n),\ \ \Sigma=
\left(
\begin{array}{c}
\Sigma_1 \
0
\end{array}
\right)
$$

ただし、$U$は$m\times m$の直交行列、$V$は$n\times n$の直交行列、$\Sigma_1=\mathrm{diag}(\sigma_1,\cdots,\sigma_n), \sigma_1\geq\cdots\geq\sigma_n\geq 0$である。

リーマン多様体上の最適化による定式化

特異値分解は式(2)の最適化問題に帰着できる。

$$
\mathrm{minimize}\ \ \ \ \ - \mathrm{tr}(U^TAVN) \tag{2}
$$

$$
\mathrm{subject \ \ to}\ \ (U,V)\in \mathrm{St}(p,m)\times \mathrm{St}(p,n)
$$

ただし、$N=
\left(
\begin{array}{c}
N_1 \
0
\end{array}
\right),N_1=diag(\mu_1,\cdots,\mu_n), \mu_1>\cdots>\mu_n> 0$である。$\mathrm{St}(p,m)$はシュティーフェル多様体と呼ばれるものであり、

\mathrm{St}(p,m)=\left\{Y\in\mathbb{R}^{n\times p}|Y^TY=I_p\right\}

と定義される。

リーマン多様体上での最急降下法

Euclid空間における最急降下法と同じではある。しかし、曲がった空間での最適化であることに注意する必要がある。曲がった空間で最適化を行うので、$x_k+t_kd_k$は曲がった空間からはみ出してしまうので、レトラクション$R$をすることで元の曲がった空間に戻す必要がある。

1. 初期化: $x_0\in \mathcal{M},\ k\leftarrow 0$
2. 停止条件が満たされるなら，$x_k$ を出力
3. 探索方向 $d_k\leftarrow -{\mathop{\mathrm{grad}}}f(x_k)\in T_{x_k}\mathcal{M}$
4. 直線探索によるステップ幅 $t_k\geq0$ を計算
5. $x_{k+1}\leftarrow {R_{x_k}}(t_k d_k)$ で更新
6. $k \leftarrow k+1$ として，ステップ 1 へ

リーマン多様体上の最適化の無制約最適化問題のうち最急降下法について解説した下記の記事が参考になる。

リーマン多様体上での共役勾配法

Euclid空間における非線形共役勾配法と同じではある。しかし、曲がった空間での最適化であることに注意する必要がある。曲がった空間で最適化を行うので、$x_k+t_kd_k$は曲がった空間からはみ出してしまうので、レトラクション$R$をすることで元の曲がった空間に戻す必要がある。また、$d_k$の$x_k$における接空間と$\mathrm{grad}f(x_{k+1})$の$x_{k+1}$における接空間は異なるので、ベクトル輸送${\mathcal T}$をすることで、$x_k$における接空間を$x_{k+1}$における接空間に移動する必要がある。

1. $x_0$ を初期化する．
2. $d_0=−{\mathop{\mathrm{grad}}} f(x_0)$ で探索方向を初期化する．
3. for $k=0,1,\ldots$ do

• 3.1 Wolfe条件を満たすステップ幅 $t_k$ を計算する．
• 3.2 $x_{k+1}={R_{x_k}}\left(t_kd_k\right)$ で更新する．
• 3.3 $\beta_k$を計算する．
• 3.4 $d_{k+1}=−\mathop{\mathrm{grad}} f(x_{k+1})+\beta_k{\mathcal T_{t_kd_k}}(d_k)$ で探索方向を更新する．

1. end for

リーマン多様体上の最適化の無制約最適化問題のうち共役勾配法について解説した下記の記事が参考になる。

Pythonでの実装

特異値分解の最急降下法、共役勾配法、ハイブリッド法(共役勾配法とニュートン法の組み合わせ)の実装をGitHubに置いた。文献1をもとに実装している。Wolfe条件を満足するステップ幅を探索する直線探索は文献2のNumerical Optimizationを参考に実装した。

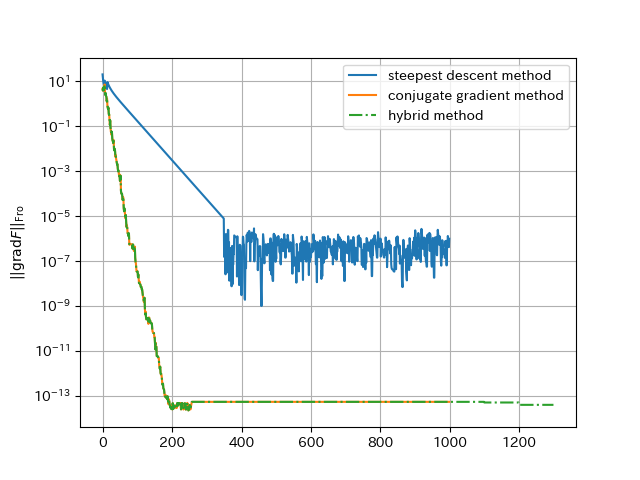
イテレーションに対する最急降下法、共役勾配法、ハイブリッド法の勾配のノルムを下図に示す。最急降下法が共役勾配法とハイブリッド法より勾配のノルムの収束が悪いことがわかる。

Pymanoptでの実装

Pymanoptでは、Wolfe条件を満足するステップ幅を探索する直線探索は実装されておらず、Armijo条件を満足するステップ幅を探索する直線探索が実装されている。そのため、文献1の共役勾配法を厳密に実装したものではないのでご注意ください。

import pymanopt
import autograd.numpy as np
from pymanopt.manifolds.stiefel import Stiefel
from pymanopt.manifolds.product import Product
from pymanopt.optimizers import ConjugateGradient

m, n, rank = 100, 100, 100
matrix = np.random.normal(size=(m, n))

st1 = Stiefel(n=m,p=rank,k=1)
st2 = Stiefel(n=n,p=rank,k=1)
manifold = Product([st1,st2])

N = [i+1 for i in range(rank)]
N.reverse()
N = np.diag(N)

@pymanopt.function.autograd(manifold)
def cost(U,V):
  return -np.trace(U.T@matrix@V@N)

problem = pymanopt.Problem(manifold,cost)
optimizer = ConjugateGradient(verbosity=2 , beta_rule="PolakRibiere")
U,V = optimizer.run(problem).point

おわりに

連続最適化の夏季学校でリーマン多様体上の最適化を知り、幾何学が最適化でも使われるなんて面白いなと思いました。まだよく理解してないので間違いがあるかもしれないです。気づいた方はやさしく教えて頂けると嬉しいです。

参照

[1]Riemannian Optimization Algorithms and Their Applications to Numerical Linear
Algebra, Sato, Hiroyuki, 2013
[2]Numerical Optimization, Jorge Nocedal, Stephen J. Wright, 2006
[3]Optimization Algorithms on Matrix Manifolds