凸最適化の概要と主双対内点法のアルゴリズムの解説

はじめに

凸最適化問題に使われている主双対内点法の解説を目標に、凸最適化の概要を説明します。二次計画がメインターゲットです。

この記事は

• ソルバーは使ったことあるけど、もう少しアルゴリズムの中身が知りたい
• 凸最適を学びたいけど、最適化の章までの道のりが長すぎてつらい

な方が対象です。いまどき1から凸最適アルゴリズム実装しようなんて物好きは稀だと思いますが、この記事の目的は主双対内点法を実装するための知識を全体的にふわっと理解することです。

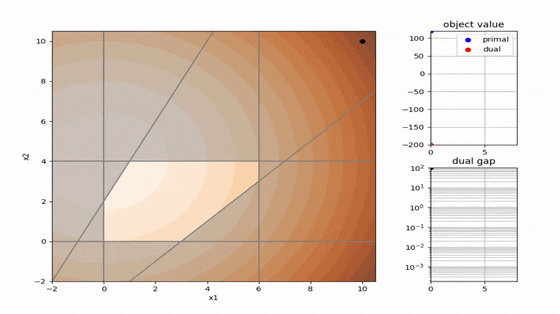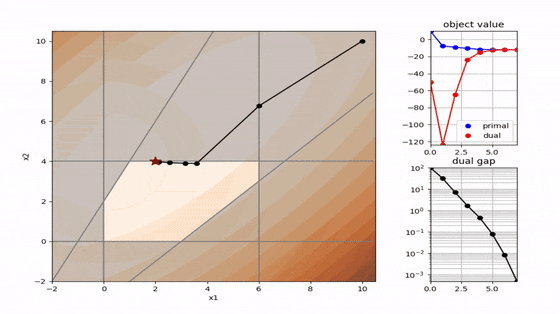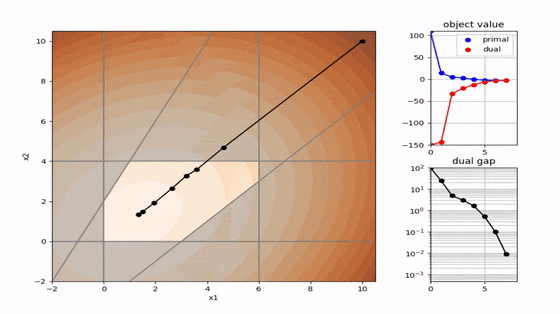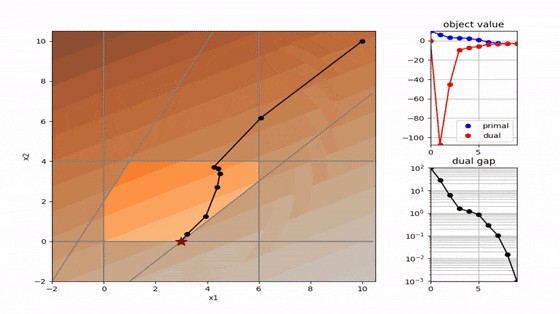
二次計画でよく使われる 主双対内点法 と 有効制約法 を以下に可視化しました。解の求め方が全く異なることが分かります。コードはpythonです。

主双対内点法（primal dual interpoint）

• 内点法の系譜（有効領域の内部を進む）
• 徐々に相補性残差を減少させて最適解を得る
• 線形計画、二次計画、非線形計画まで幅広く対応可能
• 高次元の問題が得意

有効制約法（active set）

• 単体法の系譜（有効領域の壁に沿って進む）
• 二次計画専用
• 等式制約が成立する拘束条件を探索して最適解を得る
• 拘束条件の数が少ない場合は高速

※ 初学者向けの記事ですので、厳密性は欠きます。ご容赦ください。

なぜ凸最適化問題は複雑なのか

凸最適は実用性が高いツールであり、matlabやpythonなどの言語を使えば数行で凸最適を実行できます。そのため「まず使ってみる」から入る人が多数だと思います。

そこから、もう少し複雑な問題が解きたい！と勉強し始めると、双対定理、制約想定、実行可能解、スラック変数、ラグランジアン、などなど知らない単語がたくさん出てきます。アルゴリズムを知るために理解しないといけないことが多すぎます（もちろん重要なのですが）。

凸最適の理論を複雑にしている原因の１つが、「不等式制約」の存在です。

具体的な説明に入る前に、以下の3つケースについて解法をざっと比較してみます。

1. 等式制約なし
2. 等式制約付き
3. 不等式制約付き

※ 簡単のために、この章は関数は全部1次元としてます。式は厳密ではないのでご注意を。

1. 制約なしのケース

まずは 制約なし凸最適化問題 です。

\min \ f(x) \tag{1}

この解は勾配が0になる点、つまり $\nabla f(x)=0$ を満たす$x$を探すことによって最適解を得ます。これはただの方程式なので、ニュートン法などを使えば簡単に解けます。

2. 等式制約付きのケース

等式制約付きの問題設定は以下の形。

\min \ f(x),\quad {\rm s.t.}\ \ g(x) = 0. \tag{2}

これはラグランジュの未定乗数法 と呼ばれるテクニックを用いて、

\begin{aligned}
\nabla f(x)+ \lambda \nabla g(x) &= 0,\\
\ g(x)&=0.
\end{aligned}

を満たす $x, \lambda$ を計算すれば最適解が求まります。少し式が複雑になりましたが、これも結局ただの連立方程式なので、ニュートン法で解けます。低次元であれば手計算も可能で、大学の定期テストでも出てきます。ちなみに、ラグランジュの未定乗数法は18世紀（一説では1788年）には完成していました。

3. 不等式制約付きのケース

これは最も一般的な最適化の形で、問題設定は以下。

\min \ f(x),\quad {\rm s.t.}\ \ h(x) \leq 0. \tag{3}

先の(2)と(3)の違いは等式制約「=」が不等式制約「<=」に変わっただけです。このケースは以下で表されるKKT条件を満たす解を計算することによって求めます。

\begin{aligned}
  \nabla f(x) + \lambda \nabla g(x) +  \mu \nabla h(x)=0,\\[6pt]
  g(x) = 0,\quad \quad h(x) \leq 0,\\[6pt]
  \mu \geq 0,\quad \quad \mu h(x) = 0.
\end{aligned}

一気に式が複雑になりました。まず、このKKT条件は不等式が入っているので、これまで有効だったニュートン法が（直接は）使えません。また、このKKT条件の論文が公開されたのは1951年であり、ラグランジュの未定乗数法の発見から200年近くも経っています。等式を不等式に変えただけで200年かかるのです。このKKT条件の導出には双対などの複雑な概念が取り入れられています。また、凸最適問題のほとんどがこの不等式付きのケースであるため、凸最適化全体が難しく見えてしまっているわけです。

つまり、凸最適化の理論は研究者たち長年かけて作り上げてきたものなので、そりゃ難しいよね、という結論です。

（※無理やり近似して解く方法はもっと前から知られていたらしいですが。）

ですが、目的もよくわからない概念を勉強していたら1日が終わっていた、なんてことは避けたいので、ここからは完璧な理解よりアルゴリズムの実装に重点を置いて凸最適の概要をまとめます。

今はとりあえず、不等式ってそんなめんどくさかったんだ、程度に思っていただければ大丈夫です。

もっと詳しく知りたいなーと思った方は、コチラをどうぞ。

凸最適化とは

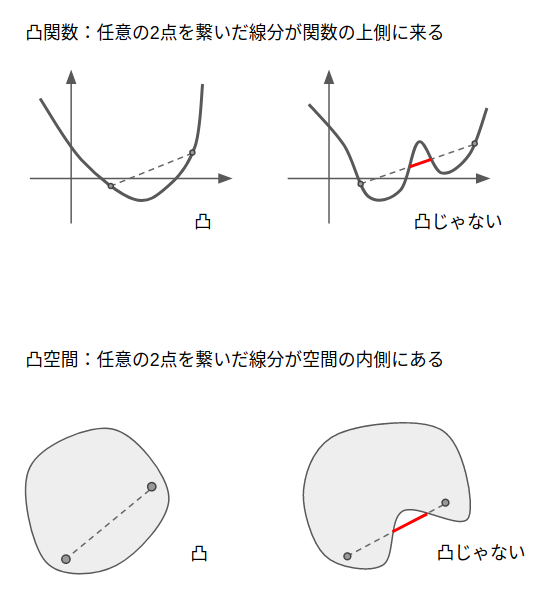
凸最適化問題とは、凸空間で凸関数を最小化する問題です。「凸」がここまで注目される理由は、とにかく数学的に扱いやすいからです。

凸関数
定義：関数上の任意の二点を結んだ直線が必ずもとの関数の上に存在する。
特徴：極値が1つしかない
つまり：極小値が必ず最小値になる。

凸空間
定義：空間上の任意の二点を結んだ直線が必ずもとの空間の内部に存在する。
特徴：直線で任意の空間上を移動できる。
つまり：直線で移動できない領域は考えなくて良い。

これらの特徴のおかげで、勾配方向に直線探索をしながら極小値を求めれば、それが最適解であることが保証されます。

逆に凸関数ではない場合は、たとえ極小値であっても最小値と確定することはできません。
また凸空間ではない場合は、直線探索で境界にぶつかった際に、その境界を回り込んだ裏の空間の存在も考えければなりません。

とりあえず定式化と標準形

凸最適化は一般的に凸関数 $f(x),\ h(x)$ を用いて以下の形で書かれます。

\min \ f(x),\ \ {\rm s.t.}\ h(x) \leq 0.

ここで、$h(x)\leq 0$ は凸空間を表しています（ $h(x)\leq 0$ が凸空間を表す...？ってなった方はこちら）。

これを凸最適の標準形に変形します。

ここで、下のような一次関数を考えます（凸最適ではアフィン関数という名前でよく出てきます）。

g(x)=Ax+b

この一次関数は定義上は凸関数であり、符号を逆転した $-g(x)$ も凸関数であるという特徴があります。これを利用して、

g(x) \leq 0,\ \ -g(x) \leq 0

と制約を作ることによって、実質 $g(x)=0$ という等式制約条件を凸最適化の中に入れ込むことができます。

これを利用して、凸最適化問題は凸関数 $f(x)$, $h(x)$ および一次関数 $g(x)$ を用いて以下のように標準化されます。

\begin{aligned}
\min \ &f(x),\\
{\rm s.t.}\ \ &g(x) = 0,\\
&h(x) \leq 0.
\end{aligned} \tag{4}

標準形というよりは、一次関数という特殊ケースに対応した特殊形のように思えるのですが、等式制約というのが非常に有用なので、この形式を標準形として議論を進めることが多いです。

標準形をもっと簡単な形にしたい（スラック変数による変形）

標準形(4)では $h(x)\leq 0$ という不等式制約がありますが、はじめにも述べたとおり、基本的に最適化問題において「不等式」制約は非常に厄介な代物で、「等式」制約のほうが遥かに簡単に取り扱えます。

そこで、なんとかしてこの不等式制約 $h(x)\leq 0$ を等式制約に変形します。このとき使われる変数はスラック変数と呼ばれ、変数 $s$ で表されることが多いです。

スラック変数の効果を確認します。まず、

\ h(x) \leq 0 

この不等式は、

\ h(x)+s=0,\quad s\geq 0 

と同じ意味であることを確認してください。"スラック" は日本語で "緩み" や "余裕" みたいな意味なので、 不等式を直接扱うのではなく、等式からの "余裕" に対して不等式制約を付けるイメージです。この要領で、最適化問題の標準形は、スラック変数を用いて

\begin{aligned}
\min_{x,\ s}\ &f(x),\\
\ {\rm s.t.}\ \ &g(x)=0,\ h(x)+s=0,\\[5pt]
& s \geq 0
\end{aligned}

と書くことができます。

これの何が嬉しいかと言うと、最適化問題において最も厄介な不等式制約が、$s\geq 0$ という非常に簡単な形で書き下せることです。

ただ、今の状態では変数 $x$ とスラック変数 $s$ の2つが変数として存在し、そのうちスラック変数のみに不等式制約がついています。これではすこし使いづらいので、もう少し工夫をします。変数$x$を

x=x^+-x^-,\ \ x^+\geq 0,\ x^- \geq 0

と分解してやると、最適化問題を

\begin{aligned}
\min_{x^+,x^-,s}\ &f(x),\\
\ {\rm s.t.}\ \ &g(x)=0,\ h(x)+s=0,\\[5pt]
&  x^+\geq 0,\ x^- \geq 0,\ s \geq 0
\end{aligned}

と書き換えることができます。不等式制約を見ると、最適化変数として使用されている$(x^+,x^-,s)$の全てに対して不等式制約がついています。これをまとめて $x=[x^+,x^-,s]^T$ と再定義して、等式制約もすべてまとめて $g(x)$と定義しなおせば、最終的に最適化問題は

\begin{aligned}
\min_{x}\ &f(x),\\
\ {\rm s.t.}\ \ &g(x)=0,\\[5pt]
&  x \geq 0
\end{aligned} \tag{5}

と書くことができます。変数の次元が2倍以上になりましたが、それでも厄介な不等式制約を $x\geq 0$といった単純な形にできるのは大きなメリットがあります。

(4)式、(5)式のどちらも標準形としてよく出てくる形ですが、一般論を議論するときは(4)、アルゴリズムの説明では(5)を用いることが多いです。

凸最適化で用いる用語の説明

凸最適化には双対性など色々と小難しい用語が出てきますが、計算を回すだけであれば、凸性の特徴とKKT条件の形だけ知っていればなんとかなります。

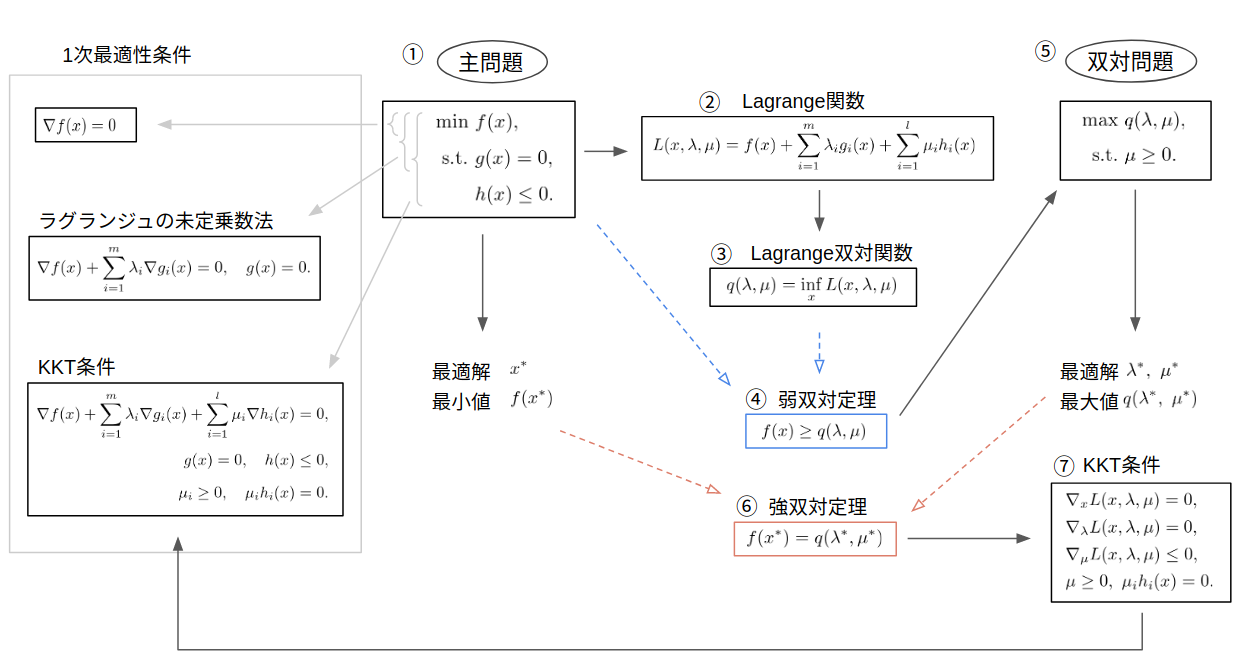
この記事でも、双対みたいな難しい用語はなるべく使いたくないのですが、このあたりの流れを知らないと、凸最適（というより最適化問題）で一番重要なKKT条件が完全にブラックボックス化してしまいます。そして論文やドキュメントの多くでは、これは双対変数の〜と言った書き方をされるので、ある程度用語を知らないと理解が進みません。なので、かなり雑ではありますが、全体の用語のつながりを説明します。（一つ一つの詳細は省きます。）

※ 表記や可解性のような厳密さは無視するのでご容赦ください

忙しい人へ

• KKT条件
  不等式制約付き最適化問題の最適解が満たすべき必要条件。凸最適化問題ではほとんどのケースで必要十分条件となる。式に出てくる$\lambda$や$\mu$は、導出の仮定で双対問題の変数になったり、ラグランジュ関数の係数になったりするので、双対変数とかラグランジュ乗数とか呼ばれる。

• 双対問題
  与えられた問題（主問題）に対応するラグランジュ関数を最大化する問題。この問題自体が重要と言うよりは、双対定理と組み合わせて初めて意味がある。

• 双対定理
  KKT条件の元になった定理で、最適解において双対問題と主問題の目的関数が一致するという定理。

• 相補性条件
  KKT条件に出てくる式の一つで、解釈が重要なので名前がついている。最適解においては、不等式制約の関数か、そのラグランジュ乗数のどちらかが0である、という式。

• 双対ギャップ
  主問題と双対問題の目的関数の差。双対定理から、最適解であれば差は0であるため、どれだけ最適解から離れているかの指標として使われる。

これらの単語の関係性をまとめたものが下図。以下はこの図をベースに説明します。

１次最適性条件

図の左側で四角く囲まれている部分です。ここだけ先にまとめてバッと説明します。

１次最適性条件とは、最適解において1階導関数が満たすべき必要条件です。「制約なし」最適化問題では

\nabla f(x)=0

となり、見慣れた形になります。

ちなみに、2次最適性条件というのもあり、制約なし最適化問題の2次最適性条件は $\nabla^2 f(x)>0$ となります。凸関数は定義から常に2次最適性条件を満たすため、凸最適に限っては特に意識しません。

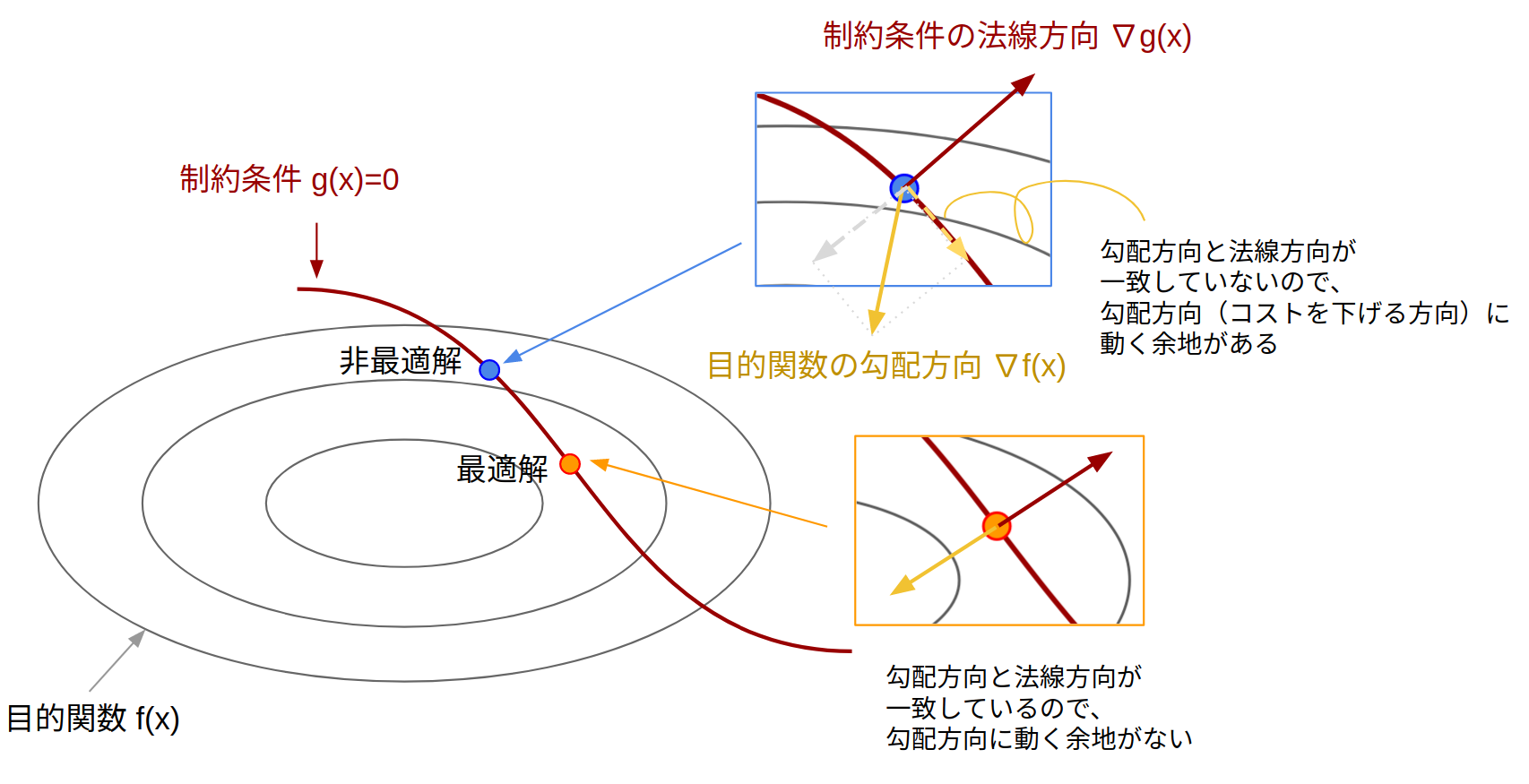
ラグランジュの未定乗数法

「 "等式" 制約付き最適化問題における1次の最適性条件」を導出する方法がラグランジュの未定乗数法であり、以下の式で表されます。

\begin{aligned}
  \nabla f(x) + \sum_i \lambda_i \nabla g_i(x) =0,\quad g(x) = 0
\end{aligned}

これは大学で習った人も多いと思います。ラグランジュ未定乗数法から得られる以下の式：

-\nabla f(x)=\sum_i \lambda_i\nabla g_i(x)

これは「（左辺）コストを下げる方向が（右辺）制約条件の法線方向と同じ向きである」ということを意味しています。逆に向きが同じでない場合は、「制約を満たしながら移動可能な方向にコストを下げる方向成分がある」ことを意味し、その点は最適解ではないことになります。以下はよく出てくる幾何的解釈の図。

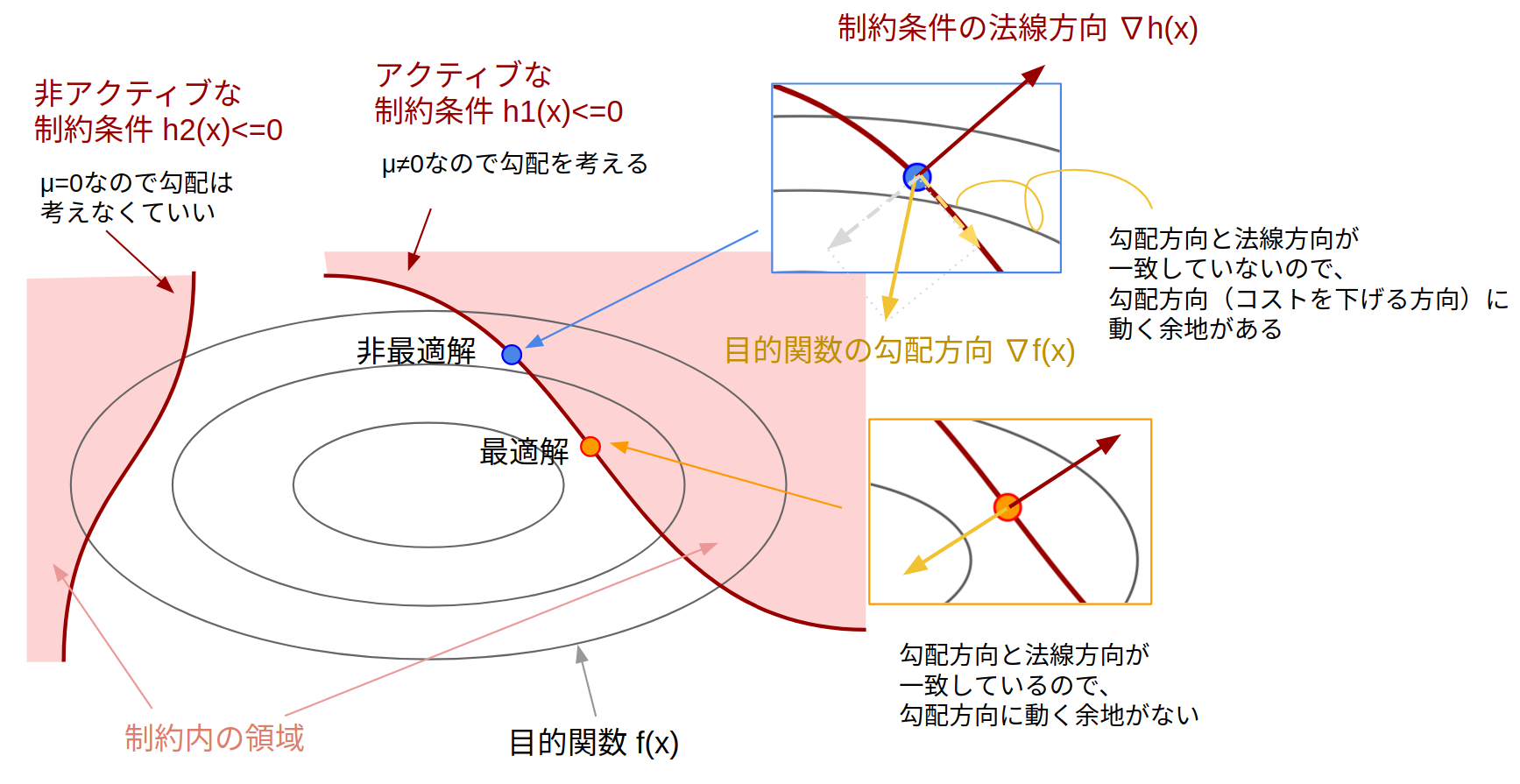
KKT条件

「"不等式" 制約付き最適化問題における1次の最適性条件」を KKT条件（Karush-Kuhn-Tucker condition） と言い、以下で表されます。

\begin{aligned}
  \nabla f(x) + \sum_i \lambda_i \nabla g_i(x) +  \sum_i \mu_i \nabla h_i(x)=0,\\[6pt]
  g(x) = 0,\quad \quad h(x) \leq 0,\\[6pt]
  \mu \geq 0,\quad \quad \mu_i h_i(x) = 0.
\end{aligned}

式の形はラグランジュの未定乗数法に似ていますが、その他にも条件がいくつか追加されています。また、このKKT条件は常に成り立つわけではないのですが、問題が凸であればほとんどのケースで成立するので、特に考えなくてokです（制約想定について）。

KKT条件の1つ目の式：

-\nabla f(x)=\sum_i \lambda_i\nabla g_i(x) + \sum_i \mu_i \nabla h_i(x)

これもラグランジュの未定乗数法と同じように幾何的な解釈が可能です。厄介なのが不等式制約の $h(x)$ なのですが、これはKKT条件の5番目の式（相補性条件）：

\mu_i h(x)_i=0

から、$h(x)\neq 0$ （制約が非アクティブ） のときは $\mu=0$ であるため、実際に勾配を考えるのは $h(x)= 0$ の場合だけとなります。なので結局ラグランジュの未定乗数法とイメージは同じになります。

KKT条件の導出仮定（凸最適問題の流れ）

ここからKKT条件の導出仮定を大雑把にまとめます。上の図で番号を降ったので、その順番で解説していきます。

①主問題

解きたい凸最適化問題です。後に示す双対問題と比較して、主問題と呼ばれます（Pは主：Primalの意味）。

(P)\ \ \min \ f(x),\ \ {\rm s.t.}\ \ g(x)=0,\ h(x) \leq 0.

②ラグランジュ関数

主問題が与えられましたが、いきなりこれを解くのは大変です。とりあえず制約条件が厄介なので、目的関数 $f(x)$ と制約条件 $g(x)$, $h(x)$ に重みを付けて足し合わせたら、何か分からないかな？なノリで、与えられた主問題に対して、ラグランジュ変数と呼ばれる変数 $\lambda,\ \mu$ を導入してラグランジュ関数を作ります。

L(x, \lambda, \mu) = f(x)+\sum_{i=1}^m\lambda_ig_i(x)+\sum_{i=1}^l\mu_ih_i(x)

難しいことはしていません。ただそれぞれの関数に変数を掛けて足しただけです。

③ラグランジュ双対関数

②で作ったラグランジュ関数は、凸関数の和なので凸関数になります。拘束条件がないので最小化しやすそうです。なのでとりあえず最小化しましょう。
ラグランジュ関数に対して、$x$ で最小化したものをラグランジュ双対関数といいます。

q(\lambda, \mu) = \inf_x \ L(x, \lambda, \mu)

ここでもまだ難しいことはしていません。ただ最小化した値を$q$と定義しただけです。

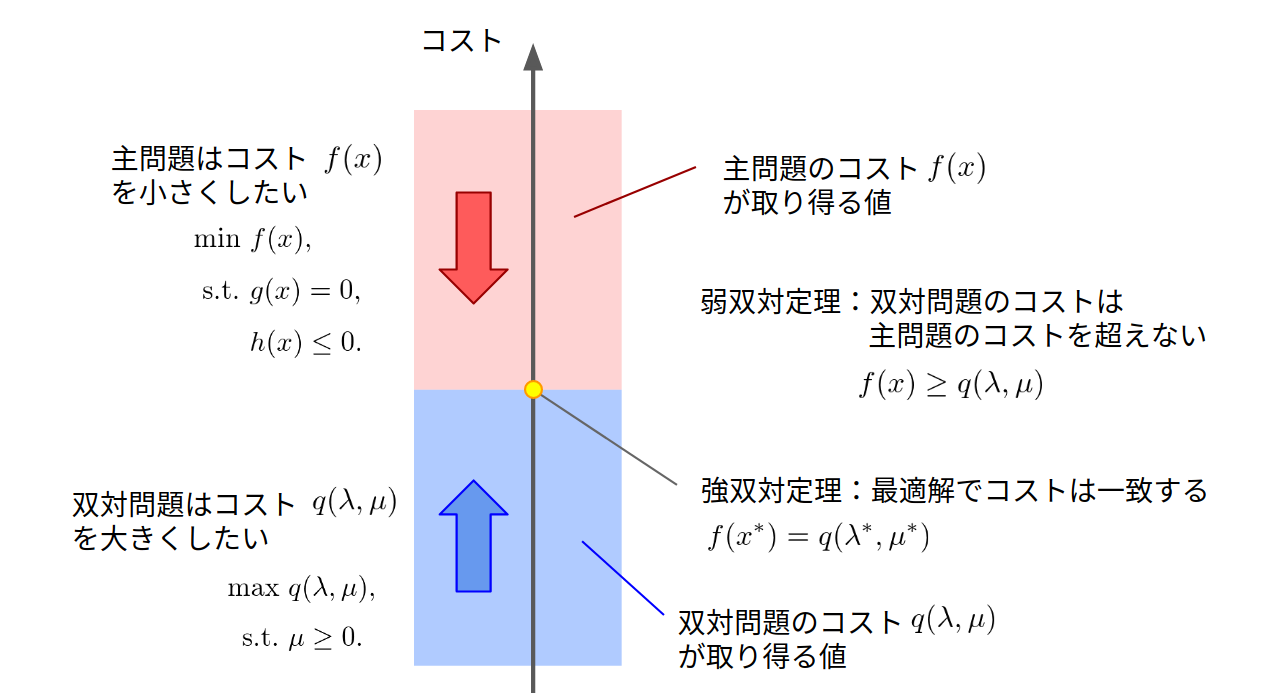
このラグランジュ双対関数の値$q$と主問題の目的関数 $f(x)$の値を比較することによって、次の弱双対定理が得られます。

④弱双対定理

弱双対定理は 「$\mu\geq 0$のとき、ラグランジュ双対関数の値 $q(\lambda, \mu)$ は、主問題の目的関数の値 $f(x)$ を超えない」 というものです。数式で書くと、こう。

\forall \lambda \in \mathbb{R}^m,\ \forall \mu \in \mathbb{R}^l_{+},\ \ \  f(x)\geq q(\lambda, \mu)

これは簡単に証明ができます。（制約条件から $g(x)=0,\ \mu h(x)\leq 0$ であることを考えれば、すぐ導出できます。）

この定理の何が嬉しいのかというと、不等式制約のせいで解くのが難しい主問題に対して、制約条件を取り除いたラグランジュ双対関数を最適化すれば、少なくとも主問題の下界が計算できるようになります（下界：最小値以下のなんらかの値）。ラグランジュ双対関数の最適化問題は制約なし凸最適化のため、非常に簡単に実行可能です。

しかし、あくまで求まるのは下界であり、下界が10だとしても、実際の最小値は100かも1000かもしれません。

ちなみに、この下界と、実際の最小値の差 $f(x)- q(\lambda, \mu)$ を双対ギャップと呼びます。

こうなると、この下界をどこまで実際の最小値に近づけることができるのか（ラグランジュ双対関数の値はどこまで大きくできるのか？）という問題を考えたくなります。これが双対問題です。

⑤双対問題

ラグランジュ双対関数は変数として $\lambda$ と $\mu$ を持っています。なので、この変数を変化させれば、より正確に下界を見積もることができるはずです。このように、ラグランジュ双対関数の最大値を求める問題を双対問題といいます。

この問題のニーズは上の弱双対定理から来ているので、弱双対定理の前提である $\mu \geq 0$ が制約条件に入っています（Dは双対：Dualの意味）。

(D) \ \ \max \ q(\lambda, \mu),\ \ {\rm s.t.}\ \ \mu \geq 0.

⑥強双対定理

主問題の最適解を $x^{\ast}$ 、双対問題の最適解を $\lambda^{\ast}, \mu^{\ast}$ とします。

強双対定理とは 「主問題の最小値 $f(x^{\ast})$ と双対問題の最大値 $q(\lambda^{\ast}, \mu^{\ast})$ は一致する」 というものです。つまり、弱双対定理のときに考えた「この下界をどこまで実際の最小値に近づけることができるのか」に対する答えは、「完全に一致できる」となります。

f(x^{\ast}) = q(\lambda^{\ast}, \mu^{\ast})

主問題と双対関数の目的関数の差は双対ギャップと呼ばれるので、強双対定理は 「最適解では双対ギャップは0である」 と言い換えることもできます。

今まで何となくラグランジュ関数を作って、ゴニョゴニョしてきたのも、全てはこの強双対定理を導くためです。感覚的には、こいつがラスボスです。

この定理の何がすごいかというと、

• 双対問題を解けば、主問題の最適値も求まる
• 双対ギャップを計算するだけで、その解が最適かどうか分かる

という点です。

そもそも不等式制約がついた最適化問題は解析が難しいので、この定理が無いと、最適解かどうかを見極めるだけで一苦労です。それがこの定理のおかげで（双対問題という謎の問題を１つ余分に解かなくてはいけませんが）2つの目的関数の差を計算するだけで最適解かどうかを判定することができます。

このように、今まで何となくラグランジュ関数やら双対問題やらを定義してきましたが、この定理でそれら全てが関連付けられます。

なお、この定理は常に成り立つわけではなく、主問題が制約想定（constraint qualification）と呼ばれる条件を満たしている必要が有ります。強双対定理を使うときは、主問題がこの制約想定が満たされているか確認する必要があるのですが、凸最適化問題の場合は大抵のケースで満たされているため、ここでは深く言及しません。

⑦KKT条件

強双対定理をベースに、主問題の1次最適性条件を書き出したのがKKT条件です。

\begin{aligned}
  \nabla f(x) + \sum_{i=1}^m \lambda_i \nabla g_i(x) + \sum_{i=1}^l \mu_i \nabla h_i(x)=0,\\
  g(x) = 0,\\
  h(x) \leq 0,\\
  \mu_i \geq 0,\\
  \mu_i h_i(x) = 0.
\end{aligned} \tag{6}

2~4本目の式は、主問題と双対問題の拘束条件から持ってきたもので、1と5本目の式は強双対定理を解析すると出てきます。

基本的にすべてのアルゴリズムは、この条件を満たす解を求めるのが目標なので、最低限このKKT条件の式の形だけ知っていればなんとかなります。

⑦-2 相補性条件

KKT条件の中で5本目の式は特に解釈が重要で、 「相補性条件」 と名前がついています。これは不等式制約の関数 $h(x)$ もしくは、その制約に対応する双対変数 $\mu$ のどちらかが0でなければならない、ということを意味しており、有効制約法の有効制約の判定などに用いられます。

後ほど説明する主双対内点法では、この相補性の右辺を大きな値から徐々に0に近づけて行くことによって最適解を見つけます。

アルゴリズム

用語の説明が終わったところで、実際の最適化アルゴリズムの説明に入ります。

主双対内点法の説明がメインですが、すべての内点法は「実行可能領域の内部で解を徐々に変化させて最適解を求める」という方針のため、極論その解の変化方向と変化量をどう決めるかという問題に帰着します。その違いを確認するためにも、ここでは 主内点法 の一種であるバリア法と、主双対内点法 の一種であるパス追従法について説明します。

バリア関数法（主内点法）

バリア関数法のほうが理解しやすいため、先に説明してしまいます。

バリア法は内点法の一種で、不等式制約をlog関数で近似して、ニュートン法でゴリ押しで解く方法です。非常に直感的で、ここに双対とかラグランジュといったワードは出てきません。（現在は主双対内点法が主流なのであまり使われていないようです。）

ここではまず、凸最適化問題の標準形(5)

\min_x f(x),\quad {\rm s.t.}\ g(x)=0,\ \ x \geq 0

を、以下の形

\min_x f(x) - \nu \sum_{i=1}^l\log (x_i),\quad {\rm s.t.}\ g(x)=0.

に近似します。等価な変形でないことに注意してください。変化点は、不等式制約が消えたことと、目的関数に以下の関数が追加されたこと。

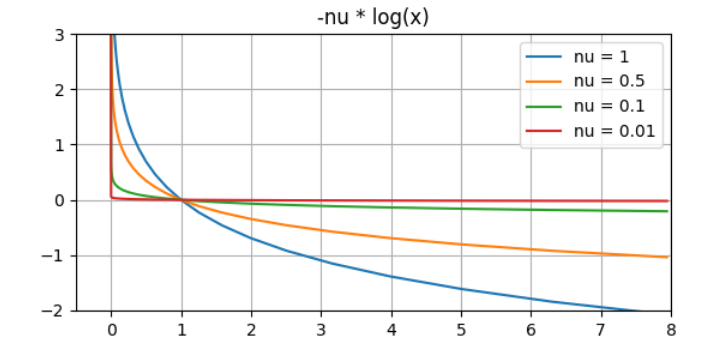
- \nu \sum_{i=1}^l\log (x_i)

これはバリア関数と呼ばれ、$x_i$ が正の方向から0に近づくに従って無限大に発散する関数で、$x_i\geq 0$ の制約の代わりとして近似的に使うことができます。

下の図がバリア関数ですが、$\nu$ が小さくなるに従って、壁が急になり、かつ $x>0$ の部分の値はほぼ$0$であることが分かります。 なので、 $\nu$ が小さい値であれば、殆どの領域でコスト関数に影響を及ぼさず、かつ $x>0$ の制約を取り込むことが可能です。

この時点で、問題から不等式制約が消えているので、ニュートン法を適用したら解くことができます。そして $\nu$ が十分小さい値であれば近似精度も良いはずです。ただし、問題が1つ。急すぎるバリア関数は $x=0$ に近づくと勾配がほぼ無限大になってしまうため、ニュートン法のような微分を使う計算がうまく回りません。

そこで、とりあえず大きな $\nu$ の値をとって、ニュートン法で解きます。その解を初期点として、$\nu$ を少し小さくした問題に対して、またニュートン法で解きます。このように徐々に $\nu$ を小さくして行きながら、本当の解に近づけていきます。こうすると、たとえ勾配が非常に大きな値でも、目標点が初期値のすぐ近くにあるため、計算が発散することはありません。

双対のような概念も現れず、直感的に分かりやすい方法ですが、バリアパラメータ $\nu$ のイテレーションとニュートン法のイテレーションの2種類の反復計算が行われるため、あまり効率の良い方法ではありません。

主双対内点法

主双対内点法は、主問題と双対問題をまとめて解くことによって、主問題の最適解を求める方法の総称です。

そもそも、本来求めたい解を得るためには双対問題は不要であり、無駄に次元を増やしているだけに感じますが、KKT条件を使って主問題と双対問題をまとめて解いたほうが高速と言うことが知られてから頻繁に使われるようになりました。なぜ主双対内点法が高速なのかについて（個人的な）考察は後ほど。

先程で述べた主内点法では $x_{k+1}=x_k+dx_k$ のように徐々に主問題の変数 $x$ を変化させて最適値を探しました。
一方で主双対内点法は、主問題の変数 $x$ と双対問題の変数 $\lambda,\ \mu$ の3変数を同時に変化させて最適値を探す方法です。

\begin{aligned}
x_{k+1}&=x_k+dx_k\\
\lambda_{k+1}&=\lambda_k+d\lambda_k\\
\mu_{k+1}&=\mu_k+d\mu_k
\end{aligned}

特徴としては、

• 変数、拘束条件の次元が大きい場合に有利
• 非線形最適化にも適用可能

が挙げられます。

主双対内点法にも勾配計算の違いによって、アフィンスケーリング法、パス追従法、ポテンシャル法などの種類がありますが、基本方針はどれも 「KKT条件を満たす解をニュートン法で求める」 です。

1つ理解してしまえば後は似た感じです。ここではイメージしやすい パス追従法 を取り上げて説明します。

例として、二次計画問題で確認してみます。二次計画問題の標準形は以下のようになります。

\min \ \frac{1}{2}x^TQx+c^Tx,\quad Ax=b,\ x\geq 0.

この問題に対するKKT条件(6)は

\begin{aligned}
&Ax = b,\ \  x \geq 0,\\
&A^T \lambda+ \mu=Qx+c,\ \  \mu \geq 0,\\
&x_i  \mu_i=0
\end{aligned}

となります。この式が $(x, \lambda, \mu)$ について解ければ万事解決なのですが、厄介な箇所が二点。

• $x\geq 0,\ \mu \geq 0$ の不等式制約の存在
• 相補性条件が非線形項 $x_i \mu_i$ を含む

この2点がクリアされれば、このKKT条件はただの線形連立方程式になるので解析的に解くことができます。

まず、1点目の不等式制約はとりあえず無視します（あとで対応する）。2点目の双線形は、適当な解の近傍で線形近似する、といった方針で進めます。

まずは不等式制約を無視しましょう。また、相補性条件 $x_i\mu_i$ も添字 $i$ がややこしいので、行列 $X$ を導入してベクトルで形式記述しておきます。 すると、解きたい方程式はこうなります。

\begin{aligned}
&Ax = b,\\
&A^T \lambda+ \mu=Qx+c,\\
&X  \mu=0.\\[6pt]
& {\rm where}\ \ X={\rm diag}(x_1, \cdots, x_n)
\end{aligned} \tag{7}

次に線形近似について考えます。KKT条件の変数 $(x, \lambda, \mu)$ に対して、適当に初期値 $(x_0, \lambda_0, \mu_0)$ を取ってやります。ちなみにこの初期値は $e$ を単位ベクトルとして $x_0=10^5e,\ \lambda=0,\ \mu_0=10^5e$ のような値を選ぶことが多いそうです。

このとき、初期値 $(x_0, \lambda_0, \mu_0)$ を、

\begin{aligned}
x_{k+1} \leftarrow x_k + dx\\
\lambda_{k+1} \leftarrow \lambda_k + d\lambda \\
\mu_{k+1} \leftarrow \mu_k + d\mu
\end{aligned} \tag{8}

と動かして(7)式を満たす解を求めることを考えます。記述が面倒なので、変数 $z=(x, \lambda, \mu)$ を導入して、この式を下のように書いておきます。

z_{k+1}\leftarrow z_k+dz

移動後の解 $z_k+dz$ には方程式(7)を満たしていてほしいので、$z=z_k+dz$ を(7)に代入すると、

\begin{aligned}
&A(x_k+dx) = b,\\
&A^T( \lambda+d \lambda)+( \mu_k+d \mu)=Q(x_k+dx)+c,\\
&(X_k+dX)( \mu_k+d \mu)=0
\end{aligned} \tag{9}

となります。ここで$dz$が微小であるとして2次の変分量 $dXd\mu \simeq0$ と線形近似を施してやります。すると、(9)の3本目の相補性条件の式は

\begin{aligned}
&(X_k+dX)( \mu_k+d \mu) \\[6pt] & \simeq  X_{k} \mu_{k} + X_{k}d \mu +  \mu_{k}dX = 0
\end{aligned}

と近似されます。ここまでをまとめると、解くべき式は

\begin{aligned}
&A(x_k+dx) = b,\\
&A^T( \lambda+d \lambda)+( \mu_k+d \mu)=Q(x_k+dx)+c,\\
&X_{k} \mu_{k} + X_{k}d \mu +  \mu_{k}dX = 0
\end{aligned}

となります。ここまででやっているのは、線形近似して変化量を求めるという、通常のニュートン法の考え方です。正直これをいきなり解いても良いのですが、この式をいきなり $dz$ について解くと、目的値が適当に取った初期値から離れすぎてしまい、線形近似で用いた $dz$ が微小という仮定が破綻してします。そのためパス追従法では「現在の相補性条件の左辺値 $(x_i\mu_i)$ を大きく変化させない範囲で $z$ を動かす」という方針を取ります。

今の解 $z_k$ におけるの $X_i\mu_i$ の平均値 $\nu_k$ を計算しましょう。（とりあえずここでは 相補性残差 と呼びます）

\nu_k= \frac{1}{N}\sum_i^N \left( x_i\mu_i \right)_k

この現在の相補性残差に近い値として、スケールを掛けた相補性残差 $\sigma \nu_k,\ \sigma \in [0, 1)$ を用いて計算を行います。なので結局、KKT条件はこんな感じで近似されます。

\begin{aligned}
&A(x_k+dx) = b,\\
&A^T( \lambda+d \lambda)+( \mu_k+d \mu)=Q(x_k+dx)+c,\\
&X_{k} \mu_{k} + X_{k}d \mu +  \mu_{k}dX=\sigma \nu_k
\end{aligned} \tag{10}

これを行列形式で書いたものがこちら。

\begin{aligned}
  &\begin{bmatrix}
  A & 0 & 0 \\
  -Q & A^T & I\\
  M_k & 0 & X_k
  \end{bmatrix}
  \begin{bmatrix}
  dx \\ d \lambda \\ d \mu
  \end{bmatrix}
  =
\begin{bmatrix}
  b-Ax_k \\
  Qx_k+c-A^T \lambda_k- \mu_k\\
  \sigma\nu_k e - X_k \mu_k
\end{bmatrix},\\[9pt]
&X_k={\rm diag}(x_{k1}, \cdots, x_{kn}),\\
&M_k={\rm diag}(\mu_{k1},\cdots,\mu_{kl}),\quad e=[1,\cdots,1]^T.
\end{aligned} \tag{11}

この式の左辺はKKT行列などとも呼ばれます。この式はただの $(dx, d\lambda, d\mu)$ の一次連立方程式なので、数値計算で容易に解けます。この解 $dz$ をもとに本来求めたい解 $z$ を更新していきます。（実用上 $\sigma$ は0.1や0.01といった値が用いられるそうです。）

この更新のタイミングで、一番最初に無視した不等式条件を考慮します。

ここで、式(8)から求めた変化量を $dz_k$としましょう。このときの解の更新における方針は、スカラ係数 $\alpha$ を使って、不等式制約を壊さないように $\alpha$ の値を調節しながら、

z_{k+1} \leftarrow z_k + \alpha dz_k

のように解の値を更新するというものです。そして、これは簡単な計算から、 $\alpha$ が以下の式を満たしていれば、更新によって不等式制約 $x\geq0,\ \mu\geq 0$ が破られることがないことが分かります。

\alpha = \min \left\{ \min_{dx_i<0} \left(-\frac{x_i}{dx_i}\right),\ \min_{d\mu_i<0} \left( -\frac{\mu_i}{d\mu_i}\right) ,1\right\}

この更新によって求められた解を新たな初期値として、(11)式を解いて徐々に双対ギャップを下げていき、ある一定値以下になったところで計算をストップし、最適解を得ます。

解の収束性などの議論はすっ飛ばしましたが、これが大まかな主双対内点法の概要になります。

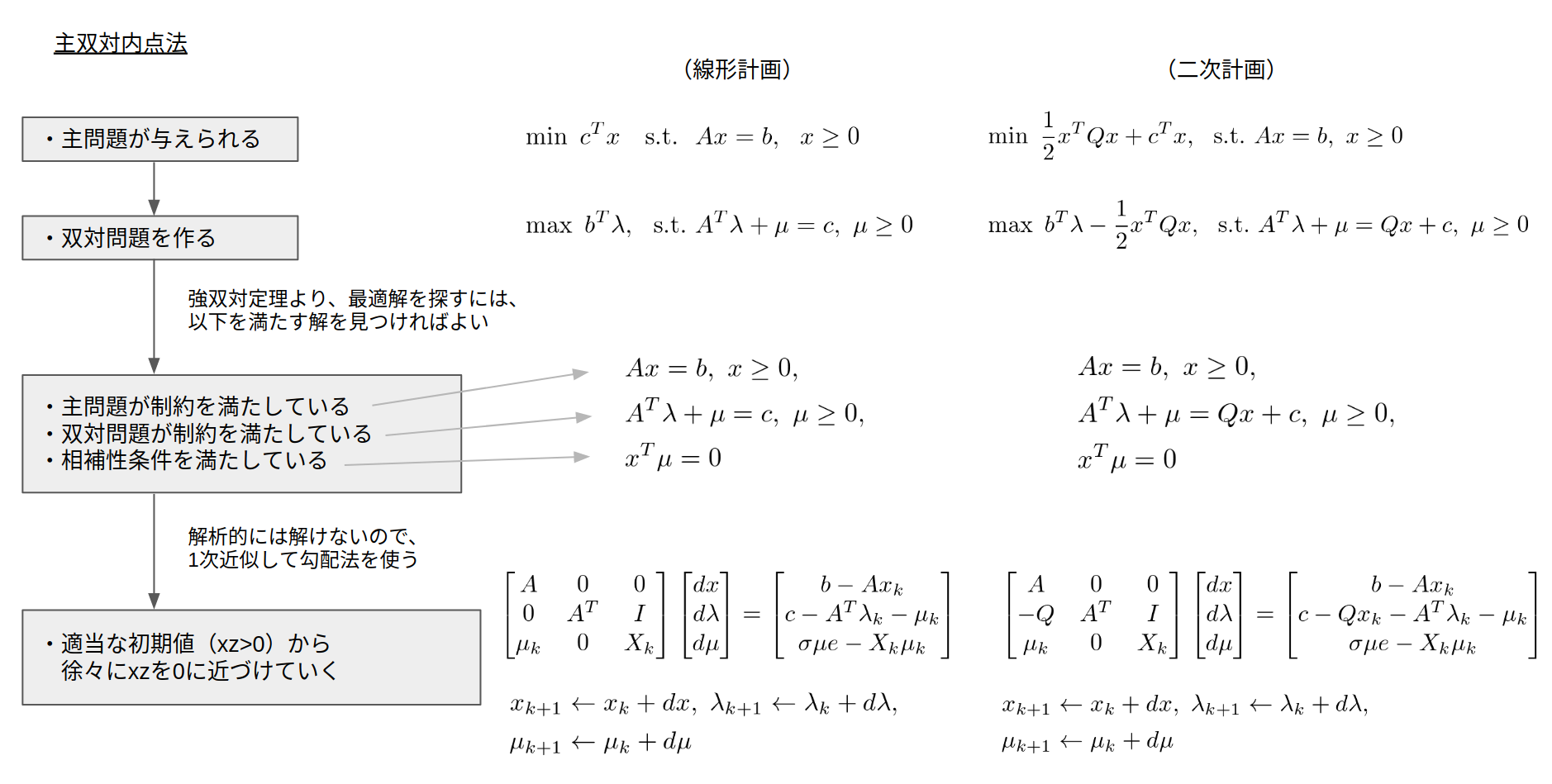
線形計画、二次計画に適用した場合は以下のような方針になります。

参考記事：

• 内点法 - wikipedia
• 主双対内点法 - 線形計画におけるパス追跡法
• ２次計画問題と内点法 - 東京工業大学 講義資料
• Primal-Dual Interior-Point Methods - CMU Lecture Notes

実装例：IPOPT

バリア法と主双対内点法の共通点（なぜ主双対内点法は高速なのか）

ここを読むと、主双対内点法がなぜ高速計算可能なのかのイメージが（少し）湧きます。（若干発展的な話なので読まなくても良いです。）

バリア関数法を二次計画問題に適用します。二次計画の標準形はこの形。

\min \ \frac{1}{2}x^TQx+c^Tx,\ \ {\rm s.t.}\ \ Ax=b,\ \ x \geq 0.

これに対してバリア関数の近似を入れたのが、こんな形。

\min \ \frac{1}{2}x^TQx+c^Tx - \sum_{i}\nu_i \log(x_i) \,\ \ {\rm s.t.}\ \ Ax=b.

この式は等式制約条件つきの最適化問題なので、ラグランジュの未定乗数法が適用できます。すると、以下の式が得られます。

\begin{aligned}
&Ax=b,\\
&\nabla \left( \frac{1}{2} x^TQx+c^Tx - \sum_{i}\nu_i \log(x_i) \right) + \nabla\lambda^T (b-Ax)=0
\end{aligned}

実際に勾配の計算をすると、こうなります。

\begin{aligned}
&Ax=b,\\
&Qx+c- \frac{\nu}{x}-A^T\lambda=0, \quad \frac{\nu}{x}=\left[\frac{\nu_1}{x_1}, \cdots, \frac{\nu_n}{x_n} \right]
\end{aligned} \tag{12}

ラグランジュの未定乗数法から出てきた式なので、これを満たす $x, \lambda$ が見つかれば、それは最適解になっています。

ここで、$\nu/x$ の部分が見にくいので、新たな変数 $\mu$ を用いて
以下の式でまとめます。

\frac{\nu}{x}=\mu  \quad \quad (\ \Leftrightarrow \ x_i\mu_i=\nu_i)

すると(12)式は

\begin{aligned}
&Ax=b,\\
&Qx+c- \mu-A^T\lambda=0,\\
&x_i\mu_i=\nu_i
\end{aligned}

となります。変数が増えましたが、これを満たす $x, \lambda, \mu$ が見つかれば、それは最適解です。

よく見るとこの式は、主双対内点法の各ステップで解いていた方程式(10)と全く同じものになっています。つまり、主双対内点法で求めていた解は、バリア関数法の解と等価であり、相補性残差 $X\mu$ を徐々に小さくしながら解を求めていたのは、バリア関数の係数を徐々に小さくしていきながら最適化問題を解いていたのと同じことだったということです。

バリア関数法は「バリアパラメータ $\nu$のイテレーションとニュートン法のイテレーションの2種類の反復計算が行われるため、あまり効率の良い方法ではない」がデメリットでした。また、$\nu$ の更新の仕方によっては、勾配が急すぎて計算できない or 勾配が小さすぎて解が更新されない、といった問題も起こります。

一方で主双対内点法では「バリアパラメータなどの複数の変数を、相補性残差を0に近づけるという1つの方針に従って同時に最適化する」ことによって高速な計算を可能にしています。

（※ あくまで、ざっくりした個人的考察です。厳密に何で早いかという話は内点法の幾何学とかの論文を読めば書いてあるのかな？詳しい人がいたら教えていただけると嬉しいです。）

有効制約法

ここからは申し訳ない程度に、他のアルゴリズムを載せておきます。

有効制約法は線形計画における単体法を改良して、二次計画に適用したものです（QPの解法として普及した最初のアルゴリズムだそうです）。

手法の大雑把な説明としては、複数の制約条件の中から数個のみを取り出して、その制約条件が有効な場合の解をラグランジュの未定乗数法を用いて求める。相補性条件により、有効制約のラグランジュ定数が全て非負であれば、その解は最適解となる。すべて非負でない場合は、いい感じに制約を追加したり取り除いたりして、全て非負になるまで繰り返す。

という感じです。（言葉で書くより、この記事の冒頭に載せたgifを見ていただいたほうが分かりやすそうです。）

参考記事：

• 講義資料 - 有効制約法
• Algorithms for Quadratic Programming
• 大規模最適化問題へのアプローチ - 有効制約法、内点法、外点法
• 2次計画法 Pythonと機械学習 - Hatena Blog

実装例:qpOASES

交互方向乗数法(ADMM)

特殊な構造を持つ凸最適化問題に対して高速で問題を解くことができる手法です。

最近Oxford大学が公開したOSQPというQPソルバーがADMMをベースにしており、非常に高速だと巷で有名です。このアルゴリズムの解説もしたかったのですが、肝心の何で高速なの？が論文読んでもいまいちつかめなかったので、時間がある時にまとめようと思います。

実装例:OSQP

その他備考

凸関数で凸空間を表す

教授「凸空間は凸関数 $h(x)$ を用いて $h(x)\leq 0$ で表せるよ」と言われた時に、一瞬理解できなかった経験があるのでメモ。

凸関数を平面でカットしたときの下側の空間は凸空間になります。

例えば

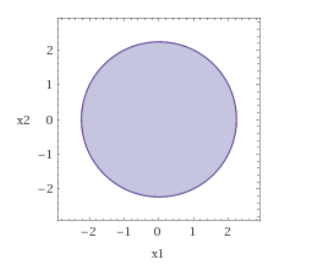
・凸関数：$x^2+y^2-5$ を0でカットした下側の空間 $x^2+y^2\leq 5$ は円であり、これは凸空間です。

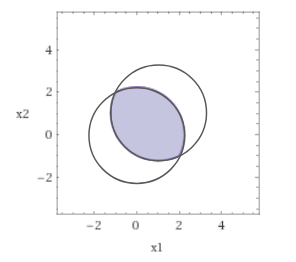
・2つの凸関数：$x^2+y^2-5$, $(x-1)^2+(y-1)^2-5$ を0でカットした下側の空間 $x^2+y^2\leq 5 \cap (x-1)^2+(y-1)^2\leq 5$ は凸空間です。

・1つの凸関数：$x^2+y^2-5$ と 1つの非凸関数 $-(x-1)^2-(y-1)^2+5$ を0でカットした下側の空間 $x^2+y^2\leq 5 \cap (x-1)^2+(y-1)^2\geq 5$ は凸空間ではありません。

制約想定

強双対性が成り立つための十分条件。（KKT条件も強双対性から来てるので、KKT条件が成り立つための条件でもある。）

なので、KKT条件を使う場合は、最適化問題がこの制約想定を満たしているか確認する必要がある。

制約想定の中にも、1次独立条件やSlater条件などの種類があり、どれか1つでも満たしていればok。

ちなみに凸最適で頻出の Slater条件 は、以下で表される「凸最適化問題」において、

\min \ f(x),\ \ {\rm s.t.}  \ \ g(x)=0,\ \ h(x)\leq 0

制約の内点に実行可能解を持つ、つまり

g(x)=0,\ \ h(x)< 0

を満たす $x$ が1点でも存在する、という条件です。（※ $h(x)$ の制約から等号が消えていることに注意してください。）

KKT条件を線形計画問題で確認する

KKT条件を線形計画問題で確認します。

まず、線形計画法の標準形は下の形式で与えられます。

(P)\ \ \min_x c^T x, \quad {\rm s.t}. \  Ax=b,\ \ x \geq 0

よって、ラグランジュ関数は

L(x, \lambda, \mu) = c^Tx + \lambda^T (b - Ax) + \mu^T (-x)

となり、ラグランジュ双対関数は

\begin{aligned}
q(\lambda, \mu) &= \inf_x \left[ c^Tx + \lambda^T (b - Ax) - \mu^T x \right] \\[5pt]
&= \inf_x \left[ (c^T - \lambda^TA - \mu^T) x + \lambda^T b  \right]\\[5pt]
&=
\begin{cases}
-\infty \quad (c - A^T\lambda - \mu \neq 0)\\[3pt]
\lambda^T b \quad \  (c - A^T\lambda - \mu = 0)
\end{cases}
\end{aligned}

となります。 （$\infty$が出てきたのは線形計画だけのレアケースです。）

ここで、$q=-\infty$ の場合は双対問題に実行可能解が存在しない、という意味になります。上の説明では省きましたが、双対定理が成り立つためには実行可能解が存在することが条件として必要であるため、意味があるのは2つ目の $\lambda^Tb$ になります。よって、実行可能解が存在するための拘束条件を追加して双対問題を以下のように設定します。

(D) \ \ \max \ \lambda^Tb, \ \ {\rm s.t.}\ \ c - A^T\lambda - \mu = 0,\ \mu \geq 0.

これに対して、双対定理を確認してみます。双対ギャップ（主問題と双対問題の目的関数の差）は、

c^Tx - \lambda~b

です。この値を(P)と(D)の拘束条件を用いて変換すると、

\begin{aligned}
c^Tx - \lambda^Tb &= c^Tx - b^T \lambda \\
&= c^Tx - (Ax)^T \lambda \\
&= c^Tx - x^TA^T\lambda \\
& = c^Tx - x^T (c - \mu) \\
&= x^T\mu
\end{aligned}

となります。拘束条件から $x \geq0,\ \mu \geq 0$ なので、$x^T \mu \geq 0 $ が成り立ちます。よって

c^Tx \geq b^T\lambda

が示せます。これは弱双対定理そのものですね。

対して強双対定理は、最適解において

c^Tx=b^T\lambda\ \  \Leftrightarrow \ \ x^T \mu =0

が成り立つことです。これも先程の式変形から

x^T \mu =0

と等価であることが分かります。これは相補性条件の式そのものを表しています。

最後に、この例題に対してKKT条件を書き下してみます。

\begin{aligned}
\nabla  f(x) + \sum_{i=1}^m \lambda_i &\nabla g_i(x) + \sum_{i=1}^l \mu_i \nabla h_i(x) \\
  = \nabla(c^Tx) +  \nabla &(b - Ax)^T \lambda + \nabla (-x)^T \mu \\
 = c - \lambda^TA -\mu &= 0,\\[7pt]
Ax&=b,\\
 -x &\leq 0, \\
\mu &\geq 0,\\
 x^T\mu&=0
\end{aligned}

5つの式がありますが、1つ目は双対問題の可解性を満たすために導入した条件、2~4つ目は主・双対問題の拘束条件なので無条件で満たしています。5つ目は強双対定理から得られる式となっていて、 $(x,\ \mu)$ が最適解であればこの条件が満たされます。

したがって、主・双対問題の最適解においてKKT条件が満たされていること（KKT条件が最適解の必要条件であること）が分かります。

参考

• Convex Optimization – Boyd and Vandenberghe：凸最適で最も有名な本。著者曰く初心者向けらしいですが、基本的な情報は網羅されてる。書籍、講義ノートともに無料PDF公開されてる。
• Lecture 1 | Convex Optimization I (Stanford)：上の本の著者によるスタンフォード大の講義シリーズ。
• CMU Lecture Note：CMUの講義ノート。これもたぶんBoydの本がベース。
• Wisconsin Univercity - NEOS guide：実際の最適化アルゴリズムについて良くまとまってる
• NTTデータ - Numerical Optimizerアルゴリズム解説：日本語の万能記事
• KKT conditions and Duality：KKT条件の分かりやすいスライド