はじめに
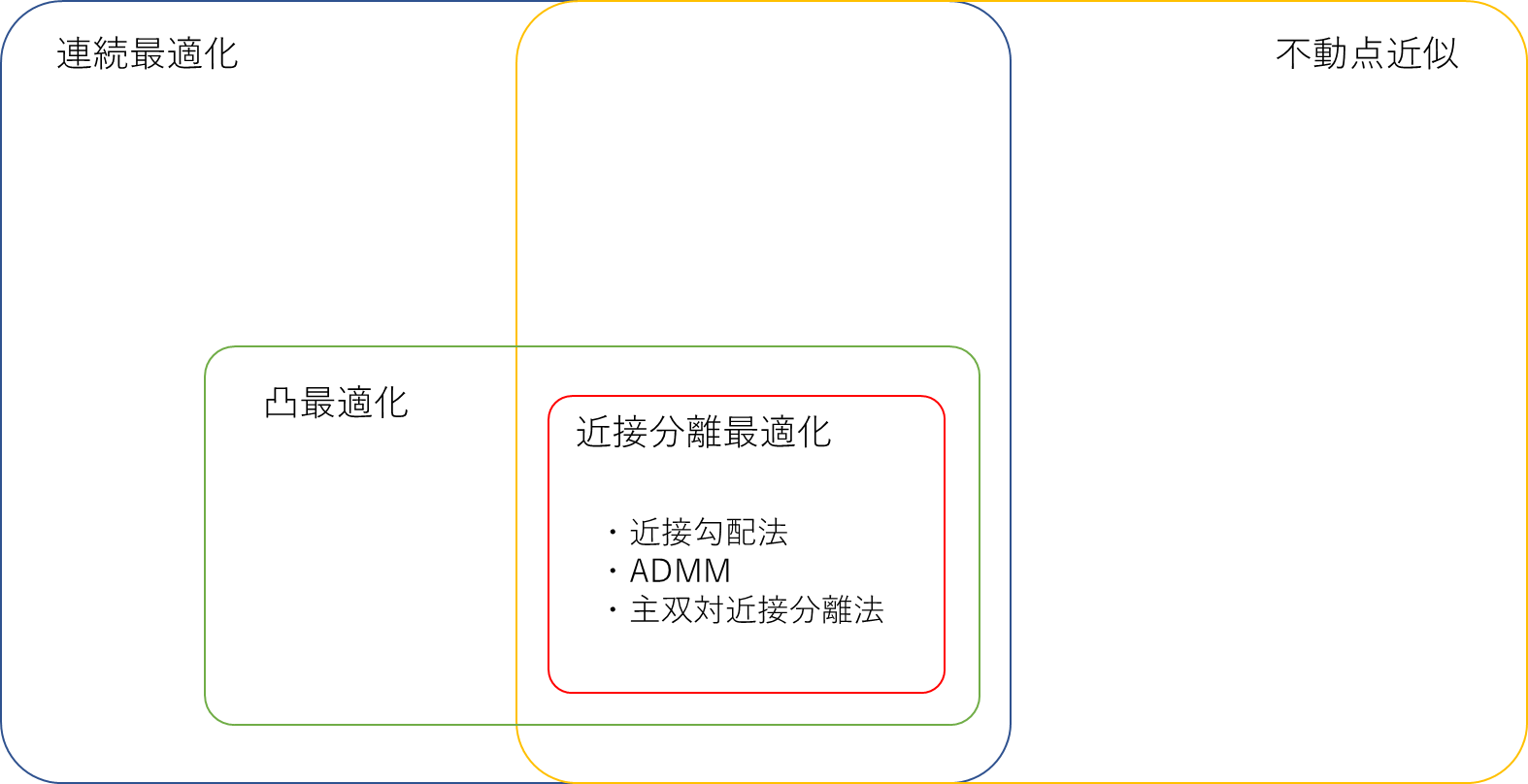
近年、近接分離最適化は、計測・制御・情報で注目されている凸最適化である。近接分離最適化の中でも交互乗数法(Alternating Direction Method of Multipliers:ADMM)はスパースモデリングでよく用いられる。本記事では、浅学非才の身ではあるが、なぜADMMが最適解に収束するの?という素朴な疑問にこたえるためのあらすじを記したい。
交互乗数法(ADMM)てなに?
一般的な最適化問題を考える。
\begin{array}{ll}
\mathrm{ min } & f(x) + g(Mx)
\end{array}
この最適化問題の主問題は以下の式で表される。
\begin{array}{ll}
\mathrm{ min } & f(x) + g(w) \\
\mathrm{ s.t. } & Mx = w
\end{array}
この問題の拡張ラグランジュ関数は
L_\lambda (x, w, p) = f(x) + g(w) + \langle p,Mx-w\rangle + \frac{\lambda}{2} \|Mx-w \|_2^2
である。ここで、ADMM は罰金項の係数 $\lambda$ を動かすことなく、次のように $x, w, p$ を更新していく。
\begin{array}{rcl}
x^{k+1} &:=& \mathrm{argmin}_x ~ L_\lambda (x, w^k, p^k) \\
w^{k+1} &:=& \mathrm{argmin}_w ~ L_\lambda (x^{k+1}, w, p^k) \\
p^{k+1} &:=& p^k + \lambda(Mx^{k+1} - w^{k+1})
\end{array}
なんでADMMは最適解に収束するの?
基本的な考え方は?
$f(x)$を凸関数とする。最適化問題$\min f(x)$を考えると、$0\in\partial f(\hat{x})$のとき、$\hat{x}$は最適解である。つまり、零点集合$(\partial f)^{-1}0$について、$\hat{x}\in(\partial f)^{-1}0$となる。
$$
(\partial f)^{-1}0=\lbrace x:0\in\partial f(x)\rbrace
$$

$\partial f(x)$は単調作用素であるという事実に着目する。点列が単調作用素の零点集合の元に収束するものが見つかるのであれば、凸関数の劣勾配が0になる点に点列が収束するといえる。劣勾配が0である点は最適化問題は最適値になるので、点列が最適解に収束することがわかる。
つまり、点列が単調作用素の零点集合の元に収束するものが見つかるのであれば、点列が最適解に収束することがわかる。
もうちょっと抽象化して考えてみると?
このことから、点列が単調作用素$T$の零点集合$T^{-1}0$の元に収束する点列の更新方法が定理としてあるとする。
$$
T^{-1}0=\lbrace x\in\mathcal{H}:0\in T(x)\rbrace
$$
この定理を用いて凸最適化問題を解くアルゴリズムの点列の更新方法が本当に凸最適化問題の最適解に点列が収束するのかを証明できると予想できる。
つまり、不動点近似の理論を道具として利用することで、ある凸最適化問題のアルゴリズムが最適解に収束するのかを解析することが出来るのである!(かっこいい!)
ADMMに適用してみると?
単調作用素(monotone operator)$T$の零点集合$T^{-1}0$の元を見つける手法としてProximal point algorithmがある。Proximal point algorithmの特殊なケースとして、Douglas-Rachford splitting methodがある。Douglas-Rachford splitting methodは、単調作用素$T$を2つの単調作用素の和$T=A+B$に分けて、その和の零点集合$T^{-1}0$の元を見つける手法である。ADMMにおける凸最適化問題の点列の更新方法が本当に最適解に点列が収束するかは、Douglas-Rachford splitting methodにより証明を与えることが出来る。
ADMMにDouglas-Rachford splitting methodを適用してみよう。最適化問題のFenchel双対問題は以下の式で与えられるのであった。
\begin{array}{ll}
\mathrm{ max } & -\left( f^\ast(-M^Tp) + g^\ast(p) \right)\\
\end{array}
極大単調作用素$A=\partial f^\ast\circ(-M^T)$と$B=\partial g^\ast$とおけば、Douglas-Rachford splitting methodから、点列は極大単調作用素$T=A+B$の零点集合の元に収束することがわかる。よって、ADMMの更新される点列は最適解に収束することがわかる。論文では$x^k$、$w^k$および$p^k$が最適解$x^\ast$、$w^\ast$および$p^\ast$に収束することを解析的に証明している。
なぜ、Douglas-Rachford splitting methodが単調作用素$T$をわざわざ2つの単調作用素$A$と$B$に分けるのか?という疑問を読者は持ったと思う。実は、Proximal point algorithmは、零点集合の元を見つけるとき、単調作用素$T$のリゾルベント$(I+\lambda T)^{-1}$を評価することを求めるのだが、それが困難な時がある。そういう時は困難は分割せよではないが、単調作用素$T$を2つの単調作用素の和$T=A+B$に別けて、単調作用素$A$のリゾルベント$(I+\lambda A)^{-1}$、単調作用素$B$のリゾルベント$(I+\lambda B)^{-1}$について評価することで、単調作用素$T=A+B$の零点集合の元を見つける問題を簡単にするのである。このような方法をSplitting methodというが、主に4つのクラスに分類することが出来る。
- forward-backward
- double-backward
- Peaceman-Rachford
- Douglas-Rachford
文献ではDouglas-Rachfordに焦点をあてて、Proximal point algorithm、Douglas-Rachford splitting methodおよびADMMについて述べている。詳細な内容は、文献を読んでみてください。わかりやすい論理展開で説明されているのでワクワクしながら読めます。おすすめの論文です!
On the Douglas-Rachford splitting method and proximal point algorithm for maximal monotone operators
おわりに
連続最適化の夏季学校を開催してくださった田中未来先生、成島康史先生および檀寛成先生と、夏季学校で不動点理論と最適化を講演してくださった飯塚秀明先生のおかけでADMMについて理解を深めることができました。勝手ながらこの場にて感謝申し上げます。
この記事に間違いがあれば私にありますのでご容赦ください。