はじめに
数理最適化 Advent Calendar 2020 イロモノ枠。
Riemann多様体上の連続最適化は、Euclid空間上の制約付き最適化問題を、Riemann多様体上の無制約最適化問題に落とし込む手法である。
Riemann多様体上の連続最適化は汎用的な手法だが、近頃の若いもんが興味を持ちそうな範囲で言えば、双曲空間での機械学習などに応用がある。基本的な部分では固有値分解、特異値分解、主成分分析、独立成分分析、角度データのモデリングなどに用いられうる。
この分野のバイブルは Absil らの『Optimization Algorithms on Matrix Manifold』であり、レトラクションを用いた効率的な手法が導入された。PDFも公開されている。本記事の内容もその書籍に基づく。
日本語の資料はほとんどないが、数学が得意な人は佐藤寛之氏らの『リーマン多様体上の共役勾配法およびその特異値分解問題への応用 (最適化手法の理論と応用の繋がり)』を読むとよい。また『機械学習のための連続最適化』の最後のほうにも記載がある。
本記事では具体例として低ランク行列分解をRiemann多様体上の連続最適化で解く方法を通して、Riemann多様体上の連続最適化の一般的な枠組みを簡単に紹介する。
本記事で使用するコードは Google Colaboratory で公開してある。各自自由に利用してよい。
質問、指摘、感想、特異値分解について夜通し語り合いたい、その他なにかあれば、コメントまたはTwitter: @wsuzumeまで。
低ランク行列分解
本記事では例として低ランク行列分解をRiemann多様体上の勾配法で解く方法を紹介する。低ランク行列分解は、レコメンデーションのための協調フィルタリングなどで用いられるアルゴリズムである。
低ランク行列分解は、与えられた行列$A \in \mathbb{R} ^ {m \times n}$を、係数行列$W \in \mathbb{R} ^ {m \times p}$と基底行列$X \in \mathbb{R} ^ {n \times p}$の積
$$
A = W X ^ \mathrm{T}
$$
の形に分解する問題である。ただし$p \leq \operatorname{min}(m,n)$である。
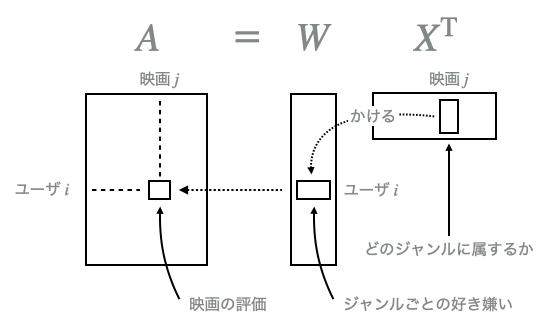
具体的なユースケースとしては、たとえば$A$の各行はユーザ、各列は映画に対応しているとして、$A$の$i$行$j$列目にはユーザ$i$が映画$j$を5段階評価のうち星いくつつけたかが格納されている状況などがある(Netflix Prize dataなど)。
このとき、$W$の各行にはユーザがどのジャンルが好きか、$X ^ \mathrm{T}$の各列には映画がどのジャンルに属するかの情報が抽出される。$m$がユーザ数、$n$が映画数、$p$がジャンル数ということになる。
たとえばジャンル1の映画が2くらい好きなユーザが、ジャンル1の映画に属する度合いが2の映画を見れば、星4(=2x2)くらいの評価をする、というわけである。
この問題は、最適化問題
$$
\underset{W \in \mathbb{R} ^ {m \times p}, , X \in \mathbb{R} ^ {n \times p}}{\operatorname{arg} \operatorname{min}} f(W, X) = \underset{W \in \mathbb{R} ^ {m \times p}, , X \in \mathbb{R} ^ {n \times p}}{\operatorname{arg} \operatorname{min}} \| A - W X ^ \mathrm{T} \| _ F ^ 2 \tag{1}
$$
を解くこととして定式化される。ただし$\| \cdot \| _ F$は行列のFrobeniusノルムである。$X$が既知であればこの問題は最小二乗法による多重線形回帰の問題
$$
\underset{W \in \mathbb{R} ^ {m \times p}}{\operatorname{arg} \operatorname{min}} ,,\| Y - W X ^ \mathrm{T} \| _ F ^ 2
$$
と一致するが、$X$も未知であることが低ランク行列分解の問題を複雑にする。
オマケ: 非負値行列分解
$A$の要素がすべて非負である場合(映画のレーティングは0〜5とかなので)、$W, X$の要素もすべて非負に制約して解く非負値行列分解(NMF: non-negative matrix factorization)という手法もある。これは要素の値が更新中に負にならないようにうまく調整した勾配法(multiplicative update)か、負になった値を$0$に戻すような操作が追加された射影勾配法という手法で解くことができる。
非負値に制約すると「どうでもいい〜とても好き」の情報を表現できることになり、非負制約をつけなければマイナスの値を取りうる、つまり「嫌い」という情報を表現できることになる。
問題が複雑になる理由
$W \in \mathbb{R} ^ {m \times p}, X \in \mathbb{R} ^ {n \times p}$という条件下では解の自由度が大きすぎてアルゴリズムが発散することがある。いま$W ^ \ast, X ^ \ast$がこの問題の最適解であるとき、
$$
A = W ^ \ast (X ^ \ast) ^ \mathrm{T}
$$
が成り立つ。ここで任意の正則行列$B \in \mathbb{R} ^ {p \times p}$を用意すると、
$$
A = W ^ \ast B ^ {-1} B (X ^ \ast) ^ \mathrm{T}
$$
が成り立つので、$W' = W ^ \ast B ^ {-1}, ,X' = X ^ \ast B ^ \mathrm{T}$もこの問題の解である。たとえば$c$を任意のスカラーとして、$W' = \frac{1}{c} W ^ \ast, X' = c X ^ \ast$も解になっているので、どんな最適解にも$c \to + \infty$の極限でコンピュータ上で表現することが不可能になりうる自由度が存在する(最適解のノルムが不定である)。
これを防ぐには大きく分けて二つの方法が存在する。
1. 目的関数に正則化項を加える方法
分解後の行列$W, X$のノルムが常識的な範囲に収まるように、これらのノルムも正則化項として付加し、最小化の対象とする。具体的には
$$
\underset{W \in \mathbb{R} ^ {m \times p}, , X \in \mathbb{R} ^ {n \times p}}{\operatorname{arg} \operatorname{min}} f(W, X) = \underset{W \in \mathbb{R} ^ {m \times p}, , X \in \mathbb{R} ^ {n \times p}}{\operatorname{arg} \operatorname{min}} \| A - W X ^ \mathrm{T} \| _ F ^ 2 + \lambda _ 1 \| W \| _ F ^ 2 + \lambda _ 2 \| X \| _ F ^ 2
$$
を解けばよい。線形回帰やカーネル回帰などでリッジ回帰の正則化項を付け加えたときと同様である。
これはPMF(Probabilistic Matrix Factorization)を最尤推定で解く場合に一致する。
正則化項の係数$\lambda _ 1, \lambda _ 2$の影響を受けて解の質やオプティマイザの挙動が変動するという欠点はあるが、Euclid空間上での勾配法で容易に解くことができる。
2. Xにノルム制約を課し、制約付き最適化問題として解く方法
行列$W, X$のどちらか一方について、各列ベクトルのノルムを$1$に制約する。すなわち、$X'$の$i$列目のベクトルのノルムを$c _ i$とおけば、各列ベクトルのノルムが$1$である行列$X$を用いて
$$
X' = X \left(
\begin{matrix}
c _ 1 & 0 & \cdots & 0 \\
0 & c _ 2 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & c _ p
\end{matrix}
\right) = X C
$$
と表せるので、
$$
W (X') ^ \mathrm{T} = WCX ^ \mathrm{T} = (WC) X ^ \mathrm{T} = W' X ^ \mathrm{T}
$$
によって$W' = WC$の側にノルムの自由度を押し付けることができる。制約付き最適化問題なので解くのが若干難しくなる(Lagrangeの未定乗数法などで解けるかどうかは各自試してみてほしい、解けたらコメントで報告していただけると大変嬉しい)が、$X$のノルムが固定されているので、必然的に$W'$のノルムが発散することもない。
Riemann多様体上の連続最適化を用いるモチベーション
Euclid空間上で見る限りは「ノルムが$1$に制約されたベクトルを用いよ」という制約付き最適化問題に見えるが、では、はじめからノルムが$1$のベクトルだけを集めた集合上で最適化が行えるとしたらどうだろう?
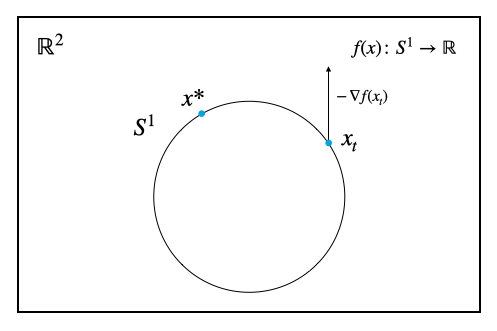
ノルムが$1$のベクトルだけを集めた集合とは、2次元で見れば円周、3次元で見れば球面である。
円周上や球面上で最適化を行う限り、「ノルムが$1$に制約されたベクトルを用いよ」という制約は自動的に満たされ続けるから、これは無制約最適化問題となる。
無制約の連続最適化問題であれば、勾配法のカテゴリに属する手法で解くことができる。また、「$X$の各列が直交している」といった、通常では保証するのが難しいような条件も厳密に保証したまま最適化することができる。
円周や球面のような、曲がってはいるが、折れたり千切れたりしていないような滑らかな空間はRiemann多様体に一般化される。Euclid空間はたまたま曲がっていない特殊なRiemann多様体であり、Euclid空間上で定義された勾配法を一般のRiemann多様体上に拡張するときは、その曲がり具合を補正するいくつかの手順が追加される。
Riemann多様体上の最急降下法
ここではもっともわかりやすい例として、円周上での最急降下法を例に取りながら解説する。
復習: Euclid空間上での最急降下法
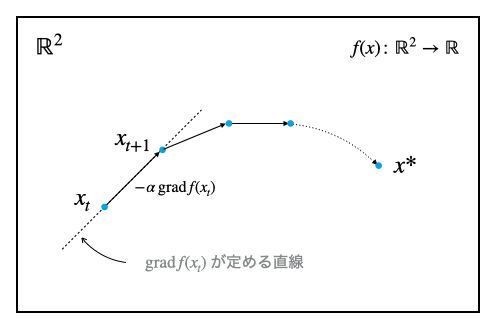
Euclid空間$\mathbb{R} ^ 2$上の最急降下法では、各点$x \in \mathrm{R} ^ 2$に対して目的関数$f(x) \colon \mathbb{R} ^ 2 \to \mathbb{R}$が定義されているものとする。
最適化をはじめる点$x _ 0$はランダムで、$t$ステップ目の点$x _ t$から、点$x _ t$における勾配$\operatorname{grad}f(x _ t)$の逆方向(最急降下方向、勾配に$-1$をかけた方向)へ、微小な正の値$\alpha$をかけた分だけ移動することで$t + 1$ステップ目の点を得る。
これを繰り返すことで、$t$を十分に大きく取れば、$x _ t$は最適解$x ^ \ast$(条件が悪い場合は局所解)へと好きなだけ近づくことができる。
正の値$\alpha$はステップサイズ、または学習率(learning ratio)とも呼ばれ、厳密にはArmijo規準やWolfe規準といった条件を満たす$\alpha$を探す必要があるが、ハイパーパラメータとして人間が設定してしまうことも多い。
1. Riemann多様体をEuclid空間に埋め込む
『Optimization Algorithms on Matrix Manifold』で紹介されている手法を用いるには、最適化を行いたいRiemann多様体はEuclid空間へ埋め込み可能でなければならない。埋め込み(embedding)というのは比喩ではなく、れっきとした数学用語である。ここでは直感的に座標変換と思っておけばよい。
たとえば円周$S^1$は2次元のEuclid空間$\mathbb{R}^2$へ埋め込み可能である。円周は動径が決め打ちされていて偏角$\theta$の情報だけで円周上の1点を示すことが可能だから、円周は本来1次元のRiemann多様体だが、あえて冗長に円周上の点を
$$
x _ t = \left(
\begin{matrix}
x _ t ^ 1 \\
x _ t ^ 2
\end{matrix}
\right)
$$
と2次元Euclid空間上の点で表現する。目的関数は$S^1$上で定義されていれば十分である。
2. Euclid空間上での勾配を計算する
ここから先、Euclid空間上での勾配とRiemann多様体上での勾配が出てきてややこしい。幸い、Euclid空間上での勾配はベクトル微分演算子$\nabla$を$f(x)$に適用した結果に一致するので、この記事では
- Euclid空間上での勾配 ... $\nabla f(x)$
- Riemann多様体上での勾配 ... $\operatorname{grad} f(x)$
と書いて区別する(本記事以外ではどの勾配を指しているのか都度確認されたし)。
Riemann多様体上での勾配$\operatorname{grad} f(x)$はEuclid空間上での勾配$\nabla f(x)$を用いて計算するので、とりあえずは通常の勾配法のように、埋め込んだ先でのEuclid空間上での勾配をまずは普通に計算する。
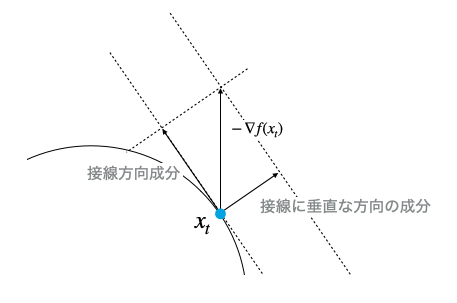
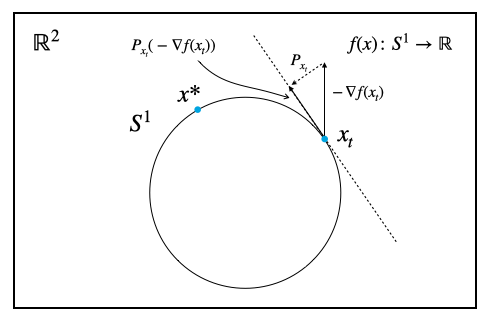
3. Euclid空間上で計算した勾配を多様体の接空間に射影する
Euclid空間上で計算した勾配は、接線方向成分(多様体に沿って移動する方向の成分)と、それに垂直な方向の成分(多様体からはみ出ようとする成分)に分解できる。
Riemann多様体上の連続最適化では、接線に垂直な方向の成分を無視する操作を追加する。解析力学のアナロジーでは、目的関数の次元がエネルギー[$kg \cdot m ^ 2 / s ^ 2$]であれば、勾配の次元は力[$kg \cdot m / s ^ 2$]になり、水平な地表を走る車の運動を考えるときに地球の中心に向けて落下する方向の力を考慮しなくていい(必ずそれにつり合う垂直抗力が地面から与えられる)ことに相当する。
円周における接線の概念は、球面においては接平面、それよりも複雑な多様体では接空間(tangent space)に一般化される。
Euclid空間上の勾配から多様体の接空間に沿った方向の成分を取り出す操作を直交射影(orthogonal projection)という。直交射影$P _x (v)$は、多様体上の点$x$において、点$x$を足とするベクトル$v$に対する操作である。Riemann多様体上での勾配$\operatorname{grad} f(x)$は、この直交射影を用いて、
$$
\operatorname{grad}f(x) = P _ x \left( \nabla f(x) \right)
$$
と定義される。
単位円周上の最適化であれば接線に垂直な方向の成分は$(v \cdot x)x$で求まるから、
$$
P _x (v) = v - (v \cdot x)x
$$
である(上式はより一般に、単位超球面$S ^ n$上でも用いることができる)。ただし $\cdot$ はベクトルの内積である。
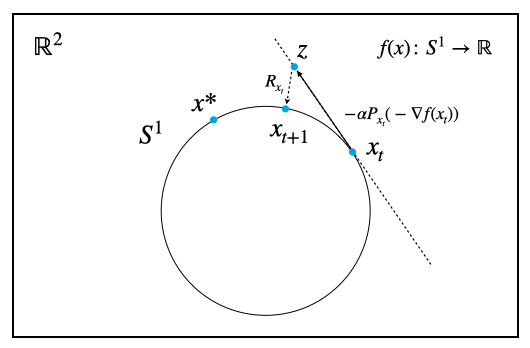
4. 勾配方向に移動してはみ出た点を多様体上に引っ張り戻す
Riemann多様体上での勾配法では、先ほど求めたRiemann多様体上の勾配の方向にステップサイズ$\alpha$の分だけ移動する。
しかし円周はずっと曲がり続けていて平坦な部分がないので、直線に沿って移動する限り、いくら接線方向に沿って移動したとしても、仮にステップサイズが非常に小さかったとしても、円周上からはほんのちょっとはみ出てしまう。
こうしてちょっとだけはみ出てしまった点を多様体上に引っ張り戻す操作がレトラクション(retraction)である。レトラクション$R _ x (z)$は、多様体上の点$x$において、接空間上にはみ出た点$z$を再び多様体上に戻す操作である。
単位円周上の最適化であれば、単に移動後のベクトルのノルムを$1$にするよう正規化すればよい。
$$
R _ x (z) = \frac{ x + z}{\| x + z \|}
$$
上式はより一般に、単位超球面$S ^ n$上でも用いることができる。
ちなみに、レトラクションは指数写像の一次近似なので、近似の仕方によって複数通り定義できることがあるが、レトラクションとしての条件を満たす限りはどれを用いてもよい。
また、レトラクションを訳すときに「引き戻す」という言葉を使ってはいけない。埋め込みと同様で、引き戻しは "pull back" という数学用語の訳語として当てられている。レトラクションは引き戻しとは何の関係もない。
レトラクションにはまだ日本語訳が当てられていない。しかし訳すとしたら re(再び)-tract(引く) = (引き戻す) なので、この記事では苦し紛れに「引っ張り戻す」として区別した。
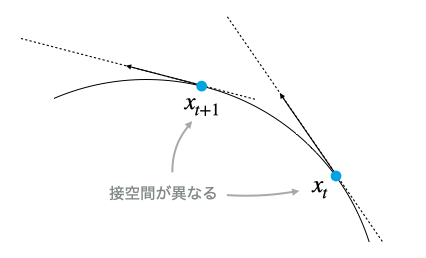
5. オマケ: 異なる点で計算した勾配はベクトル輸送する
最急降下法では考える必要がないことなのでここは読み飛ばしてもよいが、より複雑な共役勾配法、L-BFGS法など、他の地点で計算した勾配を用いる手法ではもう一段階修正が必要になる。
『2. Euclid空間上での勾配を計算する』で説明したように、Riemann多様体上の勾配法では勾配の接空間に沿った成分しか意味を持たないのだが、接空間は多様体上の点ごとに異なるのである。
ある接空間上の勾配を別の接空間上に運ぶには、厳密には測地線(多様体に沿って移動したときに最短距離となる曲線)に沿った平行移動を考えなければならない。しかし測地線に沿った平行移動は計算量的に最適化に用いるのは困難(測地線を求めること自体も最適化問題になる)なので、代わりにベクトル輸送(vector transport)を用いる。
ベクトル輸送は平行移動よりも若干条件が緩い。レトラクション同様、複数通り考えることができ、平行移動は必ずベクトル輸送の条件を満たす。
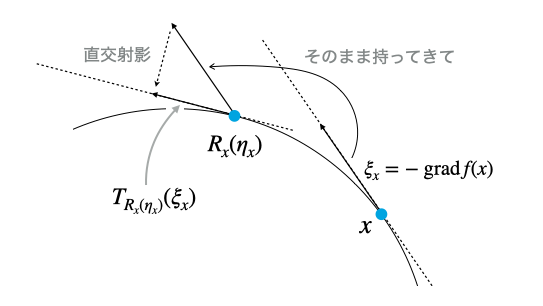
Riemann多様体$\mathcal{M}$がレトラクション$R$を持ち、かつユークリッド空間の部分多様体であれば、以下で定義される$\mathcal{T}$はベクトル輸送になる。
$$
\mathcal{T} _ {\eta _ x} (\xi _ x) := P _ {R _ x(\eta _ x)}(\xi _ x)
$$
ただし$\eta _x , \xi _x \in T _ x \mathcal{M}$で、$P$は直交射影である。
$T _ x \mathcal{M}$は多様体$\mathcal{M}$上の点$x$における接ベクトル空間を指す(円周で言えば接線)。Riemann多様体上の勾配は接ベクトル空間の元になっているので、勾配の定数倍や線形和は$\eta _ x, \xi _ x$に代入してもよい。
上で定義したベクトル輸送のイメージを掴むには、$\eta _ x = - \alpha \operatorname{grad}f(x), \xi _ x = - \operatorname{grad} f (x)$を代入してみればよい。このとき$R _ x (\eta _ x)$は勾配法で更新した後の点である。
共役勾配法などでは$t$ステップ目で計算した勾配と、$t - 1$ステップ目で計算した勾配で内積を取ることがあるが、この場合はRiemann多様体の接空間上での内積なので、本来ならばRiemann計量を考慮する必要がある。しかし本記事で紹介したようにRiemann多様体がEuclid空間$\mathcal{E}$に埋め込まれていれば、Euclid空間からの誘導内積を用いることができるので、普通にEuclid空間と同じように内積を取ればよい。
$$
\left< \xi, \eta \right> _ {T _ x \mathcal{M}} := \left< \xi, \eta \right> _ \mathcal{E}
$$
各々の多様体に適したより「真っ当な」内積は canonical inner product と呼ばれるので、もし必要なら各自調べてほしい。
本記事で使用するコード
今回はサンプルなので議論を簡略化する。
$$
A = W X ^ \mathrm{T}
$$
と行列分解したいとき、$X$が直交行列(広義の。各列が直交する単位ベクトル)であれば、上式に右から$X$をかけて
$$
W = AX
$$
となり、$X$が決まれば$W$は自動的に定まるから、$X$に関してのみ最適化を行えばよい($X$を更新するたびに上式で$W$も更新する、交互最適化を行う)。
直交する$p$本の$n$次元単位ベクトルをひとつの元として、すべて集めた集合はStiefel多様体と呼ばれるRiemann多様体で$\mathrm{St}(p, n)$と表記される。その元$X \in \mathrm{St}(p,n)$は$n \times p$行列の各列に単位ベクトルを格納した形で、Euclid空間$\mathbb{R} ^ {n \times p}$に埋め込むことができる。
新しい多様体が出てきたが、Riemann多様体上の連続最適化では
- Euclid空間上での勾配
- 直交射影
- レトラクション
の3つがわかっていれば実装可能で、共役勾配法など複雑な手法の場合は追加で
- ベクトル輸送(直交射影とレトラクションから構成可能)
- Riemann計量
の2つをチェックすればよい。それでは実装してみよう。
1. Euclid空間上での勾配
$W$を固定しているとみなせるので、多重線形回帰の最小二乗法とまったく同じになる。
$$
\nabla f(X) = -2 (A - WX ^ \mathrm{T}) ^ \mathrm{T} W
$$
2. Riemann多様体上での勾配
Stiefel多様体における直交射影は以下で定義される。
$$
P _ X (Z) = Z - X \operatorname{sym}(X ^ \mathrm{T} Z)
$$
ただし$\operatorname{sym}$は対称行列を作る操作で、
$$
\operatorname{sym}(A) = \frac{1}{2}(A + A ^ \mathrm{T})
$$
である。$X \operatorname{sym}(X ^ \mathrm{T} Z)$が接空間からはみ出る成分で、Euclid空間上の勾配からこれを引く必要がある。
この直交射影を用いて、Stiefel多様体上の勾配は
$$
\operatorname{grad} f(X) = P _ X (\nabla f(X))
$$
となる。
3. レトラクション
Stiefel多様体に付随するレトラクションは行列の極分解(polar decomposition)に基づいたものと、QR分解(QR factorization)に基づいたものが提案されているが、QR分解に基づいたもののほうが効率的である。
$$
R _ X (Z) = \operatorname{qf}(X+Z)
$$
ただし$\operatorname{qf}(A)$は行列$A$をQR分解した結果の、Qのほうの行列(q-factor of QR factorization)である。
以上、本記事で説明した内容をコードに落とし込むと、以下のようになる。
import numpy as np
np.random.seed(0)
def dataset(m, n, p, proba=0.8):
W = np.random.normal(0, 100, (m, p))
X = np.linalg.qr(np.random.normal(0, 100, (n, p)))[0]
A = W.dot(X.T)
# 欠損値補完のときに使う、欠損値を表すマスク
mask = np.random.binomial(1, proba, A.shape)
return A, W, X, mask
def gradient_descent(A, p, alpha=1e-6, maxiter=300):
n = A.shape[1]
X = np.linalg.qr(np.random.normal(0, 100, (n, p)))[0]
W = A.dot(X)
# 対称行列を作る補助関数
def sym(A):
return (A + A.T) / 2
# 点 X はEuclid空間に埋め込まれた多様体 M 上の点
# 点 X におけるEuclid空間上での勾配
def gradient(A, W, X):
return -2 * W.T.dot(A - W.dot(X.T))
# Z はEuclid空間上の点 X における勾配
# 直交射影(orthogonal projecition)はEuclid空間上での勾配を多様体 M の点 X における接空間に射影する
def orthogonal_projection(Z, X):
return Z - X.dot(sym(X.T.dot(Z)))
# 更新によって多様体からはみ出た点を多様体上へ「引っ張り戻す」
def retraction(X, xi):
return np.linalg.qr(X + xi)[0]
_errors = []
for t in range(maxiter):
# 1. Euclid空間上で普通に勾配を計算する
grad_X = gradient(A, W, X)
# 2. Euclid空間上の勾配を多様体の接空間に射影する
grad_X = orthogonal_projection(grad_X.T, X)
# 3. 更新によってはみ出た点を多様体上に引っ張り戻す
new_X = retraction(X, -alpha * grad_X)
# 本来はここで Armijo 条件を満たすかチェックしつつ学習率を調整するが、
# 簡易的に無条件で新しい点を採用している
X = new_X
W = A.dot(X)
_errors.append(np.linalg.norm(A - W.dot(X.T)))
return W, X, _errors
# データセットを生成
# A ... 低ランク行列分解の対象となる行列
# W ... 係数行列の ground truth
# X ... 基底行列の ground truth
# mask ... 欠損値をシミュレートしたい場合、欠損値のある場所が 0 になっているマスク
A, W, X, mask = dataset(50, 20, 10)
# 低ランク行列分解
# W_hat ... 推定した係数行列
# X_hat ... 推定した基底行列
# errors ... 目的関数の平方根(RMSE)
W_hat, X_hat, errors = gradient_descent(A, p=10)
# 推定した係数・基底行列から再構成する
A_hat = W_hat.dot(X_hat.T)
上のコードは Google Colaboratory でも公開してあるので、リンク先からすぐに実行することができる。
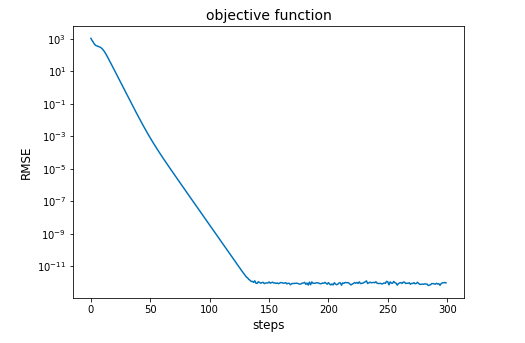
最適化が進行して目的関数が減少する過程は
from matplotlib import pyplot as plt
plt.plot(errors)
plt.yscale('log')
で確認できる。出力例は以下。
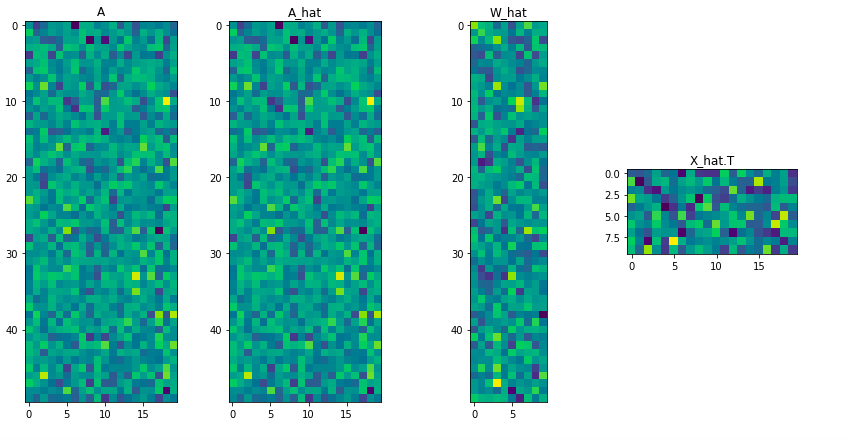
下図は行列を可視化したもので、左から順に
- A_true ... 行列$A$の真の値(ground truth)
- A_hat ... 推測された行列$A$の値$(\hat{A} = \hat{W} \hat{X} ^ \mathrm{T})$
- W_hat ... 推測された行列$W$の値
- X_hat ... 推測された行列$X$の値
である。
オマケ: 低ランク行列補完
ここまで触れてこなかったが、実応用上、行列分解したい行列がすべて埋まっているとは限らない。たとえば映画のレーティングではすべてのユーザがすべての映画についてレーティングをつけている状況はまずありえない。
ここまで解説してきた方法は、議論を簡略化しているので、欠損値がある場合に対応していない。それでは困る人もいようから、欠損値がある場合についても簡単に解説しておこう。
まず冒頭で示した目的関数$(1)$を変形する。
$$
\begin{align}
f(W, X) &= \| A - W X ^ \mathrm{T} \| _ F ^ 2 \\
&= \sum _ {k = 1} ^ m \sum _ {l = 1} ^ n \Bigl( a _ {kl} - \sum _ {r = 1} ^ p w _ {kr} x _ {lr} \Bigr) ^ 2
\end{align}
$$
ただし$a _ {ij}$は行列$A$の$i$行$j$列目を表しており、$w, x$に関してもこれにならう。上の目的関数は、$A$のうちで観測された要素に関する誤差の和の形になっている。いまは$A$の要素がすべて観測された状況を考えているが、もしも観測されていない要素がある場合、観測された要素のみの再構成誤差を最小化すればよい。
すなわち、$A$のうちで観測されたインデックスの集合を$D$として、
$$
f(W,X) = \sum _ {(k,l) \in D} \Bigl( a _ {kl} - \sum _ {r = 1} ^ p w _ {kr} x _ {lr} \Bigr) ^ 2
$$
を新たな目的関数とする。行列分解は連立方程式を解くことと等価なので、$p$が小さく変数の数が十分に少ない状況であれば、多少の欠損があっても(連立する式の数が減っても)解けるだろう、という期待に基づく。伝統的な方法では欠損値を$0$や平均値で埋めたりもするが、そのアプローチは連立方程式に誤った式を追加することになるのでうまくいかない。
この辺りの話をきちんと論文になっている方法で解きたいという人は
- 『Low-Rank Matrix Completion by Riemannian Optimization』
- 『Low-rank matrix completion via preconditioned optimization on the Grassmann manifold』
あたりを読んでくれればよい。
おわりに
残念ながら日本におけるRiemann多様体上の連続最適化の競技人口は少なく、私の把握する限り、研究室単位で取り組んでいそうなのは京都大学、東京大学、電気通信大学くらいなものであった。つまり競技人口は日本でも年に数人〜十数人単位でしか増えないドマイナーな分野である。
未だに日本語の資料は少ないので「もっともわかりやすいRiemann多様体上の連続最適化入門」を目標に本記事を書いた。Riemann多様体上の連続最適化に興味を持った人たちの一助となれば幸いである。
質問、指摘、感想、その他なにかあれば、コメントまたはTwitter: @wsuzumeまでお気軽にどうぞ。