はじめに
数理最適化の入門書を読み、ではデータが与えられた状態でどのように最適化問題を構築すれば良いかと疑問に思われた方を対象に、古典的な手法から近年注目されているモデリング手法について紹介します。
基となる最適化問題を大幅に単純化するために以下では主に
$$
\begin{align}
\min_x\quad & c^{\top}x \
\mbox{s.t.}\quad & Ax\leq b,\
& x \in \mathbb{R}^n,
\end{align}
$$
の形式の線形計画問題を取り扱いますが、多くは凸最適化問題、整数最適化問題に拡張することができます。
1. 確率計画法 (Stochastic Programming)
確率的に振る舞うパラメータが存在し、その分布が判明しているかデータが十分に存在する場合を取り扱います。
1.1. 目的関数の不確定性
目的関数の係数である$c$が確率的に振る舞う場合を考えます。乱数を$\omega$と置き、$c(\omega)$を目的関数に代入して解きたいのですが、$\omega$が不確定であるために最適化問題として不適切となってしまいます。そこで、$\omega$をどう取り扱うか以下で考えます。
1.1.1. 期待値最小化
目的関数の期待値を取り、それを最小化する問題を考えます。
$$
\begin{align}
\min_x\quad & \mathbb{E}\left[c(\omega)^{\top}x\right] \
\mbox{s.t.}\quad & Ax\leq b, \
& x \in \mathbb{R}^n.
\end{align}
$$
しかし、ここでも問題が生じます。$c(\omega)$が連続的に変化する場合、期待値は積分で表現されるので計算が容易でなくなります。そこで標本平均近似(Sample Average Approximation)が使われます。$\omega$が従う分布$p(\omega)$から$N$個のサンプルを抽出し、その集合を$\Omega$とします。これで期待値を標本平均で置き換えるわけです。つまり、最適化問題は
$$
\begin{align}
\min_x\quad & \frac{1}{N}\sum_{\omega\in\Omega}c(\omega)^{\top}x \
\mbox{s.t.}\quad & Ax\leq b, \
& x \in \mathbb{R}^n,
\end{align}
$$
となり、線形計画問題で使われたアルゴリズムでも解ける標準形で表されるようになります。$N$が大きくなる極限で近似解が期待値最適化問題の解と一致することが知られています。
実際の応用面では分布$p(\omega)$が知られていることよりも過去の$\omega$のデータが得られているケースが多く、データの数が多い場合は以上の近似解で十分なことが多いです。
1.1.2. バリューアットリスク (Value at Risk) 最小化
目的関数のValue at Risk (VaR)とは例えば$x$が与えられた状態で目的関数$c(\omega)^{\top}x$を$\omega$に応じて最小から最大まで順に並べた時に、最小値から数えて(例えば)95%の値を指します。$c(\omega)$の分散が大きいとき、期待値を最小化する場合に運が悪いとパフォーマンスがとても悪くなってしまいます。(※ここでのパフォーマンスとは与えられた$\omega$と解$x$のもとでの目的関数の値のこと)そこで、95%の確率でパフォーマンスを保証したいケースに意義が生まれます。ここで$\beta=0.95$とし最適化問題は次のように表されます。
$$
\begin{align}
\min_x\quad & \mbox{VaR}_{\beta}\left[c(\omega)^{\top}x\right] \
\mbox{s.t.}\quad & Ax\leq b, \
& x \in \mathbb{R}^n.
\end{align}
$$
しかし、残念なことにこの問題の目的関数は$x$について凸ではなく、容易には解けません。そのため、VaRの上限である Conditional Value at Risk (CVaR)が使われます。CVaRはVaR以上の値の平均値を取った物で、標本平均近似を用いて次のように問題が書き換えられます。
$$
\begin{align}
\min_{x,y,\alpha}\quad & \alpha + \frac{1}{N(1-\beta)}\sum_{\omega\in\Omega}y(\omega) \
\mbox{s.t.}\quad & y(\omega)\geq c(\omega)^{\top}x - \alpha,\ \forall \omega\in\Omega,\
& y(\omega) \geq 0,\ \forall \omega\in\Omega,\
& Ax\leq b, \
& x \in \mathbb{R}^n,\ \alpha \in \mathbb{R}.
\end{align}
$$
ここで、$\alpha$がこの問題の解におけるVaRの値となります。しかし、CVaRについて最適化しているのでVaRを最適化した場合の値とは異なります。
1.2. 制約条件の不確定性
制約条件のパラメータ$(A,b)$が不確定な場合を考えます。この場合、制約条件が確率$\beta$で満たされれば良いといった考え方の確率制約条件を使ったモデルの手法があります。つまり、
$$
\begin{align}
\min_x\quad & c^{\top}x \
\mbox{s.t.}\quad & \mbox{Pr}\left[a(\omega)^{\top}x\leq b(\omega)\right]\geq\beta,\
& x \in \mathbb{R}^n,
\end{align}
$$
という問題です。ここでは簡単のため制約条件が1次元だけの場合を考えます。
これは、前出のVaRを使って以下のように書くことができます。
$$
\begin{align}
\min_x\quad & c^{\top}x \
\mbox{s.t.}\quad & \mbox{VaR}_{\beta}\left[a(\omega)^{\top}x-b(\omega)\right]\leq0,\
& x \in \mathbb{R}^n.
\end{align}
$$
しかし、先程と同じようにVaRが$x$の凸関数ではないために解くのが非常に困難です。同様に、標本平均近似とCVaRを使って問題を緩和することができます。
$$
\begin{align}
\min_{x,y,\alpha}\quad & c^{\top}x \
\mbox{s.t.}\quad & \alpha + \frac{1}{N(1-\beta)}\sum_{\omega\in\Omega}y(\omega)\leq 0\
& y(\omega)\geq a(\omega)^{\top}x-b(\omega)-\alpha,\ \forall \omega\in\Omega\
& y(\omega) \geq 0,\ \forall \omega\in\Omega,\
& x \in \mathbb{R}^n,\ \alpha \in \mathbb{R}.
\end{align}
$$
一方で、二値変数を使った整数最適化問題を取り扱うことで標本平均近似を用いたうえでの厳密解を得るアプローチもあります。ここでは$\mathcal{X}\subset\mathbb{R}^n$は有界とします。
$$
\begin{align}
\min_{x,z}\quad & c^{\top}x \
\mbox{s.t.}\quad & a(\omega)^{\top}x-Mz(\omega)\leq b(\omega),\ \forall \omega\in\Omega\
& \frac{1}{N}\sum_{\omega\in\Omega}z(\omega)\leq 1-\beta,\
& x \in \mathcal{X},\
& z(\omega)\in\{0,1\},\ \forall \omega\in\Omega.
\end{align}
$$
ここで、$z(\omega)$は事象$\omega$において制約条件が違反されることを示す二値変数で、$M$は$M\geq\max_{x\in\mathcal{X},\omega\in\Omega}a(\omega)^{\top}x-b(\omega)$を満たす実数です。この問題は分岐限定法などを使って解かれますが、収束性を向上させるにはできるだけ下限値に近い$M$を選ぶ必要があります。
1.3. 2段階確率計画法 (Two-stage Stochastic Programming)
乱数の値が判明する前に決定する変数と後に決定する変数の二種類が存在する場合について考えます。前者を$x$、後者を$y$とし、次のように書くことができます。
$$
\begin{align}
\min_x\quad & c^{\top}x + \mathbb{E}\left[Q(x,\omega)\right] \
\mbox{s.t.}\quad & Ax\leq b, \
& x \in \mathbb{R}^n,
\end{align}
$$
$$
\begin{align}
Q(x,\omega)=\min_{y}\quad & q(\omega)^{\top}y \
\mbox{s.t.}\quad & W(\omega)y\leq h(\omega)-T(\omega)x, \
& y \in \mathbb{R}^m.
\end{align}
$$
ここで、$Q(x,\omega)$は1段階目の決定変数$x$と乱数$\omega$が判明したあとで解かれる問題の最適値となっています。ここでも期待値を標本平均近似で置き換え、1段階目と2段階目を統合して大規模な最適化問題
$$
\begin{align}
\min_x\quad & c^{\top}x + \frac{1}{N}\sum_{\omega\in\Omega}q(\omega)^{\top}y(\omega) \
\mbox{s.t.}\quad & Ax\leq b, \
& x \in \mathbb{R}^n,\
& W(\omega)y(\omega)+T(\omega)x\leq h(\omega), \forall \omega \in \Omega,\
& y(\omega) \in \mathbb{R}^m, \forall \omega \in \Omega,
\end{align}
$$
を解くことができますが、行列の疎性を活かしてL型分解法などのアルゴリズムを構築することができます。(多くの数理計画ソフトは内部で行列の構造を検出してこれを実行していると言われています。)一方で、このアルゴリズムは2段回目の問題の双対を利用するので整数条件が存在する問題を取り扱うのは難しく、特殊な構造を利用して分解法を構築する必要があります。あえてここではアルゴリズムの解説をせず問題の紹介に留めます。
2. ロバスト最適化 (Robust Optimization)
パラメータが従う確率分布が不明であるものの、その値が取りうる領域がわかっている場合に使われます。
2.1. 目的関数の不確定性
例えば目的関数の係数$c$がある領域$\Xi$の中の値をとることが知られているとします。$c$が最悪のケースだった場合を最適化すれば少なくともそれ以外のケースではより良いパフォーマンスが得られるというアイデアのもと、以下のモデルが考えられます。
$$
\begin{align}
\min_x\quad & \max_{c\in\Xi}c^{\top}x \
\mbox{s.t.}\quad & Ax\leq b,\
& x \in \mathbb{R}^n.
\end{align}
$$
以下、領域$\Xi$は凸集合であると仮定しますが、最も簡単なケースである超多面体(polytope)であるケースを考えます。
$$
\Xi=\left\{c\in\mathbb{R}^n\ :\ c^{\top}E\leq d^{\top}\right\}
$$
としましょう。すると、内側の最大化問題は次のようになります。
$$
\begin{align}
\max_{c}\quad & c^{\top}x \
\mbox{s.t.}\quad & c^{\top}E\leq d^{\top},\
& c \in \mathbb{R}^n.
\end{align}
$$
制約条件を$m$次元とすればこの双対問題は
$$
\begin{align}
\min_y\quad & d^{\top}y \
\mbox{s.t.}\quad & Ey = x,\
& y \in \mathbb{R}^m_+,
\end{align}
$$
と表すことができるので、元に戻してあげると
$$
\begin{align}
\min_{x,y}\quad & d^{\top}y \
\mbox{s.t.}\quad & Ax\leq b,\
& x-Ey=0,\
& x \in \mathbb{R}^n,\
& y \in \mathbb{R}^m_+,
\end{align}
$$
と線形計画問題で書き表すことができます。この問題の最適解$x^{\star}$は$c$が$\Xi$のいかなる値を取ったとしてもこの問題の最適値よりも同じかより良いパフォーマンスが得られます。また、$x^{\star}$は$c$の値に応じたパフォーマンスの変動が少なく、最適でない解$x'$は一部の$c$では$x^{\star}$よりパフォーマンスが良くとも他の$c$の値では$x^{\star}$よりパフォーマンスが悪くなると言えます。
2.2. 制約条件の不確定性
同様に制約条件についてもロバスト性を議論できます。ここでは例として$A$の各行$a_i^{\top}$に関して楕円体の不確定領域が付随している場合を考えます。
中心が$a_i^c$の場合、正定値行列$P_i$を用いて楕円体不確定領域を次のように表すことができます。
$$
\Xi_i=\left\{a_i\in\mathbb{R}^n\ :\ (a_i - a_i^c)^{\top} P_i^{-1} (a_i - a_i^c)\leq 1\right\}.
$$
これは次の形式に書くことができます:
$$
\Xi_i=\left\{a_i^c + P_i^{1/2}u\ :\ ||u||_2\leq 1\right\}\subseteq\mathbb{R}^n.
$$
これを用いてロバスト最適化問題を以下のように表します。
$$
\begin{align}
\min_x\quad & c^{\top}x \
\mbox{s.t.}\quad & a_i^{\top}x\leq b_i,\ \forall a_i\in\Xi_i,\ \forall i\
& x \in \mathbb{R}^n.
\end{align}
$$
これは「$\Xi_i$に存在する全ての$a_i$について制約条件を満たす」といった条件となっております。さらにこれは
$$
\begin{align}
\min_x\quad & c^{\top}x \
\mbox{s.t.}\quad & \max_{a_i\in\Xi_i}a_i^{\top}x\leq b_i,\ \forall i\
& x \in \mathbb{R}^n
\end{align}
$$
と書くことができ、コーシー・シュワルツの式を使うことで
$$
\begin{align}
\max_{a_i\in\Xi_i}a_i^{\top}x&=a^{c\top}_ix+\max_{||u||_2\leq 1}u^{\top}P^{1/2}{}^{\top}_ix\
&=a^{c\top}_ix+\Bigl|\Bigl|P^{1/2}_i{}^{\top}x\Bigr|\Bigr|_2
\end{align}
$$
とすることができます。
なのでロバスト最適化問題は
$$
\begin{align}
\min_x\quad & c^{\top}x \
\mbox{s.t.}\quad & \Bigl|\Bigl|P^{1/2}_i{}^{\top}x\Bigr|\Bigr|_2\leq -a_i^{c\top}x+b_i,\ \forall i\
& x \in \mathbb{R}^n.
\end{align}
$$
と二次錐計画問題(用語second-order cone programmingについては文献[5]を参照)で表すことができます。
3. 分布的ロバスト最適化 (Distributionally Robust Optimization)
ロバスト最適化はしばしば極端に保守的な解を出してしまうという問題があります。さらに、データが存在する場合にその情報がうまく活用されません。また、確率計画法では十分なサンプル数がない場合に標本平均近似の精度が悪いという問題があります。分布的ロバスト最適化は両者の一般化と言うことができ、これらの課題を部分的に解決することができます。
分布的ロバスト最適化では$\omega$に関する確率分布$F$の不確定領域$\mathcal{D}$を考慮し、最悪ケースの確率分布によって計算される期待値について最小化します。
ここでこれまでのルールをちょっと破り区分線形凸(piecewise-linear convex)計画問題
$$
\begin{align}
\min_x\quad & \max_{k=1,\ldots,K}c_k^{\top}x \
\mbox{s.t.}\quad & Ax\leq b,\
& x \in \mathbb{R}^n,
\end{align}
$$
を考えます。(一応、線形計画問題に変換することができます。)
目的関数が不確定な場合、次のように表すことができます。
$$
\begin{align}
\min_x\quad & \max_{F\in\mathcal{D}}\mathbb{E}_F\left[\max_{k=1,\ldots,K}c_k(\omega)^{\top}x\right] \
\mbox{s.t.}\quad & Ax\leq b, \
& x \in \mathbb{R}^n.
\end{align}
$$
(お気づきの方もいらっしゃるかもしれませんが、単純な線形計画問題の場合は目的関数が$\mathbb{E}_F\left[c(\omega)\right]^{\top}x$とすることができてしまうので単に期待値集合に関するロバスト計画問題となってしまいあまり面白くなくなってしまいます。)
この不確定領域$\mathcal{D}$はサンプルデータから構築することができます。以下にいくつか例を紹介します。
3.1. モーメント
$\omega=\left(\omega_1^{\top},\ldots,\omega_K^{\top}\right)^{\top}$とし、簡単のため$c_k(\omega)=\omega_k$と仮定します。$\omega$を$N$個サンプルしたとき、$\omega$の標本平均と標本分散をそれぞれ$\hat{\mu}$と$\hat{\Sigma}$とし、$\omega$が取りうる値の領域$\Phi$は有界で凸とします。$\gamma_1$、$\gamma_2$を$N$とある微小確率$\delta$の関数とすれば(詳細は文献[3]を参照)、確率$1-\delta$より高い確率で真の分布$F$は
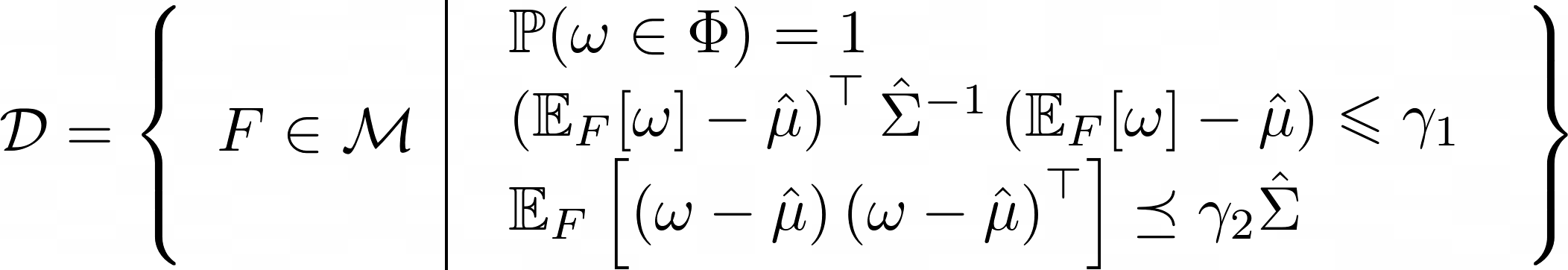
に含まれます。($\mathcal{M}$は$m$次元測度空間)
第一式は$\omega$の値が必ず領域$\Phi$の中の値を取ることを意味し、第二式は真の期待値が標本平均と標本分散で表される楕円体の中に含まれることを意味します。
最後の不等式は(右辺)$-$(左辺)の行列が半正定値行列であるという条件です。
内側の最大化問題を書くと、
$$
\begin{align}
\max_{F}\quad &\int_{\Phi}\left(\max_{k=1,\ldots,K}\omega_k^{\top}x\right)F(\omega)d\omega\
\mbox{s.t.}\quad&\int_{\Phi}F(\omega)d\omega=1,\
&\int_{\Phi}
\begin{bmatrix}
\hat{\Sigma} & (\omega-\hat{\mu})\
(\omega-\hat{\mu})^{\top} & \gamma_1
\end{bmatrix}
F(\omega)d\omega\succeq 0,\
&\int_{\Phi}(\omega-\hat{\mu})(\omega-\hat{\mu})^{\top}F(\omega)d\omega\preceq\gamma_2\hat{\Sigma},\
&F\in\mathcal{M},
\end{align}
$$
と表せます。第二の制約条件はシューア補元(Schur complement)により元の条件から変形されています。変数は$F(\omega)$と無限個存在しますが、ここでは厳密性を無視してロバスト最適化と同じ要領でその双対である最小化問題に変換します。すると最終的に、最初のminmax問題は
$$
\begin{align}
\min_{x,Q,q,r,t}\quad & r+t\
\mbox{s.t.}\quad & r\geq \omega_k^{\top}x-\omega^{\top}Q\omega+\omega^{\top}q,\ \forall \omega\in\Phi,\ k=1,\ldots,K,\
& t\geq \left(\gamma_2\hat{\Sigma}+\hat{\mu}\hat{\mu}^{\top}\right)\bullet Q+\hat{\mu}^{\top}q+\sqrt{\gamma_1}\Bigl|\Bigl|\hat{\Sigma}^{1/2}(q+2Q\hat{\mu})\Bigr|\Bigr|_2,\
& Q \succeq 0,\
& Ax\leq b, \
& x \in \mathbb{R}^n.
\end{align}
$$
のように半正定値計画問題(用語semidefinite programmingについては文献[5]を参照)で書けます。($\bullet$は行列のフロベニウス積)
ここで、1番目の制約条件は$\omega\in\Phi$全てについての制約なので数が無限個あります。
これについては一度制約条件を無視して徐々に制約条件を加えていくという手法を取ります。与えられた解$( x^{\star},Q^{\star},q^{\star},r^{\star} )$を使って次の問題を全ての$k$について解きます。
$$
\begin{align}
\max_{\omega}\quad& s_k\
\mbox{s.t.}\quad& s_k\leq \omega_k^{\top}x^{\star}-\omega^{\top}Q^{\star}\omega+\omega^{\top}q^{\star},\
&\omega\in\Phi.
\end{align}
$$
もしこの解$(s_k^{\star},\omega^{\star})$が$s_k^{\star}>r^{\star}$を満たすとき、先程の1番目の制約条件は満たされないことになりますので新たに制約条件
$$
r\geq \omega_k^{\star} {}^{\top}x-\omega^{\star\top}Q\omega^{\star}+\omega^{\star\top}q
$$
を元の問題に加えます。これを繰り返すと最適値に収束します。
3.2. Wasserstein距離
前節と同様に$\omega=\left(\omega_1^{\top},\ldots,\omega_K^{\top}\right)^{\top}$とし、簡単のため$c_k(\omega)=\omega_k$と仮定します。また、$\omega$の取りうる値の領域$\Phi$は超多面体
$$
\Phi=\left\{\omega\in\mathbb{R}^m\ :\ \omega^{\top}E\leq d^{\top}\right\}
$$
とします。$N$個のサンプルが与えられたとし、標本分布を$\hat{F}_N$とすると$N$が大きくなるにつれて標本分布が真の分布に近づくことが期待できますが、この距離をWasserstein距離で測ります。確率分布$P$と$Q$の間の1-Wasserstein距離は
$$
\begin{align}
W(P,Q) = \inf_{\Pi}\quad& \int_{\Phi^2}||\omega_1-\omega_2||\Pi(d\omega_1,d\omega_2)\
\mbox{s.t}\quad &\mbox{$\Pi$は周辺分布を$P$,$Q$とする同時確率分布}.
\end{align}
$$
で定義されます。これは、確率分布$P$の$\omega_1$にある確率密度を$\omega_2$に移動させて確率分布$Q$を再現することを考えた時に、移動させる労力を$||\omega_1-\omega_2||$とした時にかかる最小の労力量と解釈することができます。
確率$1-\delta$より大きい確率で真の分布と標本分布のWasserstein距離が$\epsilon_N$以下であると仮定します(詳細は文献[4]を参照)。すると、真の分布$F$は
$$
\begin{align}
\mathcal{D} = \left\{F\in\mathcal{M}\ :\ W(F,\hat{F}_M)\leq \epsilon_N\right\}
\end{align}
$$
で表されるWasserstein球体の中に存在する可能性が高いと言えます。
さて、$\hat{\omega}^i$をサンプルされた$\omega$の値とし、同じように内部の最大化問題の双対をとると、最終的に最適化問題は
$$
\begin{align}
\min_{x,\lambda,s,\nu}\quad&\lambda \epsilon_N + \frac{1}{N}\sum_{i=1}^N s_i\
\mbox{s.t.}\quad & \hat{\omega}_k^i {}^{\top}x+(d^{\top}-\hat{\omega}^i {}^{\top} E)\nu_{ik}\leq s_i,\ \forall i=1,\ldots, N,\ k=1,\ldots, K,\
& ||E\nu_{ik}-I_k x||_{*}\leq \lambda,\ \forall i=1,\ldots, N,\ k=1,\ldots, K,\
& \nu_{ik}\geq 0,\ \forall i=1,\ldots, N,\ k=1,\ldots, K,\
& Ax\leq b\
& x\in\mathbb{R}^n
\end{align}
$$
となります。($||\ ||_{*}$は双対ノルム、(用語dual normについては文献[5]を参照))ここで$I_k$は$k$番目のブロックが単位行列でそれ以外が零行列となっている$\mathbb{R}^{nK\times n}$の行列です。
このWasserstein距離を利用した確率分布の不確定領域は、$\epsilon_N=0$の時には真の分布が標本分布と一致するので確率計画問題、$\epsilon_N\rightarrow\infty$の極限では距離に関する制約が無くなって$\Phi$だけが残り、ロバスト計画問題とすることができるので分布的ロバスト計画問題は両者の一般化であることがわかります。
似たようなアプローチでKLダイバージェンスやその一般形である$f$-ダイバージェンスに関する分布的ロバスト最適化問題も考えることができます。
4. まとめ
確率計画問題は線形計画問題で最も有名なアルゴリズムの一つである単体法が開発されて以降、活発に研究されてきました。特に近年ではデータ量の増加によりますます重要度が高まってきており、機械学習を使って大規模な確率計画問題の特徴をとらえて効率良く解く研究も進んでいます。
一方で比較的少ないデータを元に決定を下さなければならない場面についてロバストや分布的ロバストなアプローチの有効性が示されています。機械学習でもデータが少ない領域での学習に課題があり、今後は両方の研究分野が統合していくと期待されています。
この記事では最も単純な線形計画問題(と区分線形凸計画問題)を取り上げましたが、最初に述べたとおり多くは凸計画問題でも同様の議論が行えます。しかし、その際に多項式時間で解けていた問題がNP困難となるケースも存在するので注意が必要です。また、2段階ロバストや2段解分布的ロバスト計画問題を定式化することも可能です。2段階をより一般化した多段階確率計画法や、分布的ロバストな確率制約条件も存在します。この記事では全てを紹介することはできませんでしたが、興味のある方は以下の文献を起点に論文を探してみてください。
5. 参考文献
[1] Shapiro, A., Dentcheva, D., & Ruszczyński, A. (2014). Lectures on stochastic programming: modeling and theory. Society for Industrial and Applied Mathematics.
[2] Ben-Tal, A., El Ghaoui, L., & Nemirovski, A. (2009). Robust optimization (Vol. 28). Princeton University Press.
[3] Delage, E., & Ye, Y. (2010). Distributionally robust optimization under moment uncertainty with application to data-driven problems. Operations research, 58(3), 595-612.
[4] Esfahani, P. M., & Kuhn, D. (2018). Data-driven distributionally robust optimization using the Wasserstein metric: Performance guarantees and tractable reformulations. Mathematical Programming, 171(1-2), 115-166.
[5] Boyd, S. P., & Vandenberghe, L. (2004). Convex optimization. Cambridge university press.