カーブフィッティング手法 scipy.optimize.curve_fit の使い方を理解する では、様々な曲線に近似する方法を学びました。それでは、次のように、y が0か1しかない場合にはどんな曲線に近似すれば良いでしょうか?
X1 = [4.7, 4.5, 4.9, 4.0, 4.6, 4.5, 4.7, 3.3, 4.6, 3.9,
3.5, 4.2, 4.0, 4.7, 3.6, 4.4, 4.5, 4.1, 4.5, 3.9,
4.8, 4.0, 4.9, 4.7, 4.3, 4.4, 4.8, 5.0, 4.5, 3.5,
3.8, 3.7, 3.9, 5.1, 4.5, 4.5, 4.7, 4.4, 4.1, 4.0,
4.4, 4.6, 4.0, 3.3, 4.2, 4.2, 4.2, 4.3, 3.0, 4.1,
6.0, 5.1, 5.9, 5.6, 5.8, 6.6, 4.5, 6.3, 5.8, 6.1,
5.1, 5.3, 5.5, 5.0, 5.1, 5.3, 5.5, 6.7, 6.9, 5.0,
5.7, 4.9, 6.7, 4.9, 5.7, 6.0, 4.8, 4.9, 5.6, 5.8,
6.1, 6.4, 5.6, 5.1, 5.6, 6.1, 5.6, 5.5, 4.8, 5.4,
5.6, 5.1, 5.1, 5.9, 5.7, 5.2, 5.0, 5.2, 5.4, 5.1]
Y = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
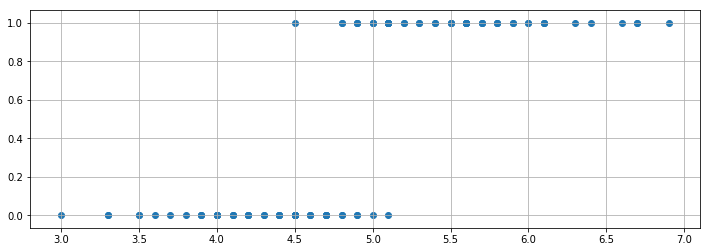
とりあえずデータを図示してみましょう。
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(12,4))
plt.scatter(X1, Y)
plt.grid()
plt.show()
このような関係を近似するときに、シグモイド曲線に近似する「ロジスティック回帰」を使います。scipy.optimize.curve_fit で実装してみましょう。
# Python の List を Numpy の Array に変換しておきましょう。
import numpy as np
X1 = np.array(X1)
Y = np.array(Y)
説明変数が1つのシグモイド曲線に近似する
説明変数が1つのシグモイド曲線 func1 を定義します。a と b を最適化することになります。
import numpy as np
def func1(X, a, b): # シグモイド曲線
f = a + b * X
return 1. / (1. + np.exp(-f))
func1 の使用例はこんな感じ。
func1(X1, 1, 1)
array([0.99666519, 0.99592986, 0.99726804, 0.99330715, 0.99631576,
0.99592986, 0.99666519, 0.98661308, 0.99631576, 0.99260846,
0.98901306, 0.9945137 , 0.99330715, 0.99666519, 0.9900482 ,
0.99550373, 0.99592986, 0.9939402 , 0.99592986, 0.99260846,
0.99698158, 0.99330715, 0.99726804, 0.99666519, 0.9950332 ,
0.99550373, 0.99698158, 0.99752738, 0.99592986, 0.98901306,
0.99183743, 0.9909867 , 0.99260846, 0.99776215, 0.99592986,
0.99592986, 0.99666519, 0.99550373, 0.9939402 , 0.99330715,
0.99550373, 0.99631576, 0.99330715, 0.98661308, 0.9945137 ,
0.9945137 , 0.9945137 , 0.9950332 , 0.98201379, 0.9939402 ,
0.99908895, 0.99776215, 0.99899323, 0.99864148, 0.99888746,
0.9994998 , 0.99592986, 0.99932492, 0.99888746, 0.99917558,
0.99776215, 0.99816706, 0.99849882, 0.99752738, 0.99776215,
0.99816706, 0.99849882, 0.99954738, 0.99962939, 0.99752738,
0.9987706 , 0.99726804, 0.99954738, 0.99726804, 0.9987706 ,
0.99908895, 0.99698158, 0.99726804, 0.99864148, 0.99888746,
0.99917558, 0.99938912, 0.99864148, 0.99776215, 0.99864148,
0.99917558, 0.99864148, 0.99849882, 0.99698158, 0.9983412 ,
0.99864148, 0.99776215, 0.99776215, 0.99899323, 0.9987706 ,
0.99797468, 0.99752738, 0.99797468, 0.9983412 , 0.99776215])
scipy.optimize.curve_fit を使って、a と b の最適解を得ます。scipy.optimize.curve_fit の詳細は カーブフィッティング手法 scipy.optimize.curve_fit の使い方を理解する をご参考に。
from scipy.optimize import curve_fit
popt, pcov = curve_fit(func1,X1,Y) # poptは最適推定値、pcovは共分散
popt
array([-47.16056308, 9.69474387])
これが a と b の最適解になります。この最適解を用いて X1 をシグモイド曲線に回帰すると
func1(X1, -47.16056308, 9.69474387)
array([1.68644172e-01, 2.83542138e-02, 5.85084618e-01, 2.28993573e-04,
7.14423738e-02, 2.83542138e-02, 1.68644172e-01, 2.58619345e-07,
7.14423738e-02, 8.68655657e-05, 1.79777399e-06, 1.58966852e-03,
2.28993573e-04, 1.68644172e-01, 4.73992195e-06, 1.09469179e-02,
2.83542138e-02, 6.03528723e-04, 2.83542138e-02, 8.68655657e-05,
3.48465186e-01, 2.28993573e-04, 5.85084618e-01, 1.68644172e-01,
4.18037811e-03, 1.09469179e-02, 3.48465186e-01, 7.88040835e-01,
2.83542138e-02, 1.79777399e-06, 3.29483517e-05, 1.24969836e-05,
8.68655657e-05, 9.07428265e-01, 2.83542138e-02, 2.83542138e-02,
1.68644172e-01, 1.09469179e-02, 6.03528723e-04, 2.28993573e-04,
1.09469179e-02, 7.14423738e-02, 2.28993573e-04, 2.58619345e-07,
1.58966852e-03, 1.58966852e-03, 1.58966852e-03, 4.18037811e-03,
1.41107138e-08, 6.03528723e-04, 9.99983430e-01, 9.07428265e-01,
9.99956313e-01, 9.99199923e-01, 9.99884826e-01, 9.99999951e-01,
2.83542138e-02, 9.99999096e-01, 9.99884826e-01, 9.99993715e-01,
9.07428265e-01, 9.85536807e-01, 9.97893310e-01, 7.88040835e-01,
9.07428265e-01, 9.85536807e-01, 9.97893310e-01, 9.99999981e-01,
9.99999997e-01, 7.88040835e-01, 9.99696394e-01, 5.85084618e-01,
9.99999981e-01, 5.85084618e-01, 9.99696394e-01, 9.99983430e-01,
3.48465186e-01, 5.85084618e-01, 9.99199923e-01, 9.99884826e-01,
9.99993715e-01, 9.99999657e-01, 9.99199923e-01, 9.07428265e-01,
9.99199923e-01, 9.99993715e-01, 9.99199923e-01, 9.97893310e-01,
3.48465186e-01, 9.94464672e-01, 9.99199923e-01, 9.07428265e-01,
9.07428265e-01, 9.99956313e-01, 9.99696394e-01, 9.62748681e-01,
7.88040835e-01, 9.62748681e-01, 9.94464672e-01, 9.07428265e-01])
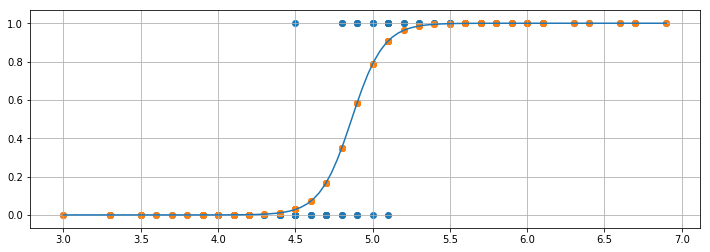
回帰曲線と確率分布の図示
図示してみましょう。青いドットが元データ、曲線が回帰曲線、オレンジのドットが回帰後のデータになります。この縦軸は、「0か1のどちらに分類されるか予測するとき、1への分類が正しいとされる確率」と解釈できます。
x_latent1 = np.linspace(min(X1), max(X1), 100)
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(12,4))
plt.scatter(X1, Y)
plt.plot(x_latent1, func1(x_latent1, -47.16056308, 9.69474387))
plt.scatter(X1, func1(X1, -47.16056308, 9.69474387))
plt.grid()
plt.show()
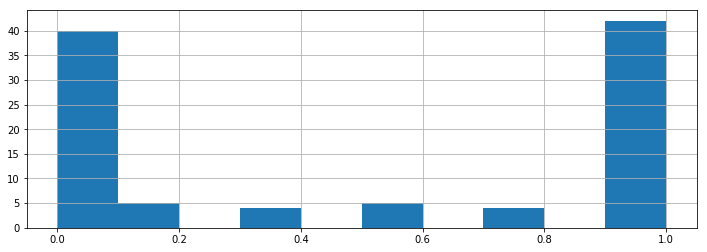
その確率の分布を見てみましょう。
plt.figure(figsize=(12,4))
plt.hist(func1(X1, -47.16056308, 9.69474387))
plt.grid()
plt.show()
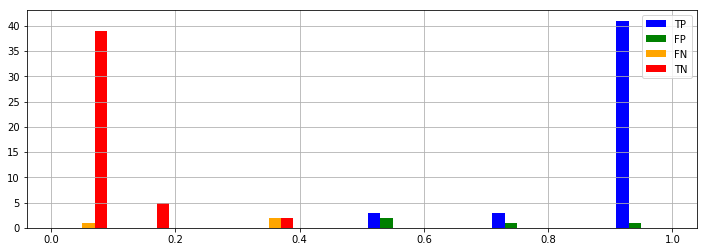
予測精度の見積もり
実際の分類(0か1か)は Y という変数に入っています。回帰して得られた値が 0.5 以上のときは1、0.5 未満の時は0に分類するとした場合、それがどのくらい正確かを計算できます。ここで、
- TP (True Positives, 真の陽性):1と予想したものが本当に1だった
- FP (False Positives, 偽陽性):1と予想したものが実は0だった
- FN (False Negatives, 偽陰性):0と予想したものが実は1だった
- TN (True Negatives, 真の陰性):0と予想したものが本当に0だった
とします。評価指標はいろいろありますが、ここでは最も単純な
Accuracy (正答率) = (TP + TN) / (TP + FP + FN + TN) を計算しましょう。
def confusion_table(y_pred, y_true):
true_positives = [] # TP
false_positives = [] # FP
false_negatives = [] # FN
true_negatives = [] # TN
for y1, y2 in zip(y_pred, y_true):
if y1 >= 0.5:
if y2 >= 0.5:
true_positives.append(y1)
else:
false_positives.append(y1)
else:
if y2 >= 0.5:
false_negatives.append(y1)
else:
true_negatives.append(y1)
return (true_positives, false_positives, false_negatives, true_negatives)
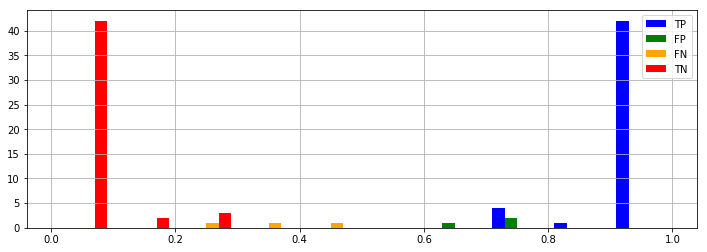
def show_result(TP, FP, FN, TN):
print("Accuracy: ", len(TP + TN) / len(TP + FP + FN + TN))
plt.figure(figsize=(12,4))
plt.hist([TP, FP, FN, TN], label=['TP', 'FP', 'FN', 'TN'], color=['blue', 'green', 'orange', 'red'])
plt.legend()
plt.grid()
plt.show()
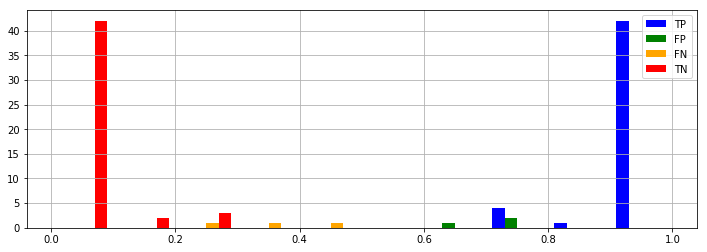
TP, FP, FN, TN = confusion_table(func1(X1, -47.16056308, 9.69474387), Y)
show_result(TP, FP, FN, TN)
Accuracy: 0.93
説明変数が2つのシグモイド曲線に近似する
説明変数が2つの場合を試してみましょう。
X2 = [1.4, 1.5, 1.5, 1.3, 1.5, 1.3, 1.6, 1.0, 1.3, 1.4,
1.0, 1.5, 1.0, 1.4, 1.3, 1.4, 1.5, 1.0, 1.5, 1.1,
1.8, 1.3, 1.5, 1.2, 1.3, 1.4, 1.4, 1.7, 1.5, 1.0,
1.1, 1.0, 1.2, 1.6, 1.5, 1.6, 1.5, 1.3, 1.3, 1.3,
1.2, 1.4, 1.2, 1.0, 1.3, 1.2, 1.3, 1.3, 1.1, 1.3,
2.5, 1.9, 2.1, 1.8, 2.2, 2.1, 1.7, 1.8, 1.8, 2.5,
2.0, 1.9, 2.1, 2.0, 2.4, 2.3, 1.8, 2.2, 2.3, 1.5,
2.3, 2.0, 2.0, 1.8, 2.1, 1.8, 1.8, 1.8, 2.1, 1.6,
1.9, 2.0, 2.2, 1.5, 1.4, 2.3, 2.4, 1.8, 1.8, 2.1,
2.4, 2.3, 1.9, 2.3, 2.5, 2.3, 1.9, 2.0, 2.3, 1.8]
X = np.array([X1, X2])
X
説明変数が2つのシグモイド曲線 func2 を定義します。a と b と c を最適化することになります。
import numpy as np
def func2(X, a, b, c): # シグモイド近似
f = a + b * X[0] + c * X[1]
return 1. / (1. + np.exp(-f))
scipy.optimize.curve_fit を使って、a と b と c の最適解を得ます。scipy.optimize.curve_fit の詳細は カーブフィッティング手法 scipy.optimize.curve_fit の使い方を理解する をご参考に。
from scipy.optimize import curve_fit
popt, pcov = curve_fit(func2,X,Y) # poptは最適推定値、pcovは共分散
popt
array([-34.73855674, 4.53539756, 7.68378862])
これが a と b と c の最適解になります。この最適解を用いて X をシグモイド曲線に回帰すると
func2(X, -34.73855674, 4.53539756, 7.68378862)
array([6.50775384e-02, 5.71307677e-02, 2.71025515e-01, 1.34765416e-03,
8.70621930e-02, 1.28644139e-02, 2.44507030e-01, 5.62684424e-06,
2.00985810e-02, 1.84541829e-03, 1.39380145e-05, 1.53042211e-02,
1.34585285e-04, 6.50775384e-02, 2.19881845e-04, 1.75412448e-02,
5.71307677e-02, 2.11803849e-04, 5.71307677e-02, 1.84377888e-04,
7.03114052e-01, 1.34765416e-03, 2.71025515e-01, 1.47501521e-02,
5.23352988e-03, 1.75412448e-02, 9.87363752e-02, 7.31229933e-01,
5.71307677e-02, 1.39380145e-05, 1.17156994e-04, 3.45248338e-05,
3.97483365e-04, 6.65083780e-01, 5.71307677e-02, 1.15555797e-01,
1.30504519e-01, 8.21224927e-03, 2.11939802e-03, 1.34765416e-03,
3.82539381e-03, 4.23536522e-02, 6.25445853e-04, 5.62684424e-06,
3.33161217e-03, 1.54784801e-03, 3.33161217e-03, 5.23352988e-03,
3.11214086e-06, 2.11939802e-03, 9.99991567e-01, 9.52173582e-01,
9.99713144e-01, 9.88909228e-01, 9.99790606e-01, 9.99988005e-01,
2.19800890e-01, 9.99531388e-01, 9.95492831e-01, 9.99994642e-01,
9.77236005e-01, 9.80125609e-01, 9.98242469e-01, 9.64634357e-01,
9.98923608e-01, 9.99062882e-01, 9.82654924e-01, 9.99996466e-01,
9.99999338e-01, 3.69145119e-01, 9.99847153e-01, 9.45446145e-01,
9.99983567e-01, 7.88467214e-01, 9.99289738e-01, 9.98175546e-01,
7.03114052e-01, 7.88467214e-01, 9.98882592e-01, 9.79383083e-01,
9.99461706e-01, 9.99935936e-01, 9.99481475e-01, 4.79425062e-01,
8.04863544e-01, 9.99975087e-01, 9.99888432e-01, 9.82654924e-01,
7.03114052e-01, 9.97236655e-01, 9.99888432e-01, 9.97681895e-01,
9.52173582e-01, 9.99938290e-01, 9.99967122e-01, 9.98525888e-01,
9.26738041e-01, 9.85415267e-01, 9.99404375e-01, 9.02277503e-01])
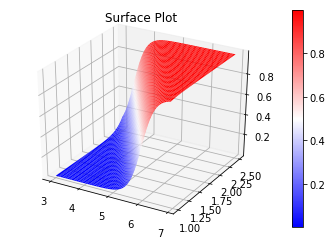
回帰曲面と確率分布の図示
説明変数が2つありますので、回帰「曲線」ではなく回帰「曲面」になります。matplotlibで3Dプロット を参考に図示してみましょう。
N = 1000
x1_axis = np.linspace(min(X[0]), max(X[0]), N)
x2_axis = np.linspace(min(X[1]), max(X[1]), N)
x1_grid, x2_grid = np.meshgrid(x1_axis, x2_axis)
x_mesh = np.c_[np.ravel(x1_grid), np.ravel(x2_grid)]
y_plot = func2(x_mesh.T, -34.73855674, 4.53539756, 7.68378862).reshape(x1_grid.shape)
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(x1_grid, x2_grid, y_plot, cmap='bwr', linewidth=0)
fig.colorbar(surf)
ax.set_title("Surface Plot")
fig.show()
ここで大事なことは、シグモイド曲線(あるいは曲面)に回帰していますが、分類問題として考えると、分類境界は「直線」(あるいは平面)であるということです。
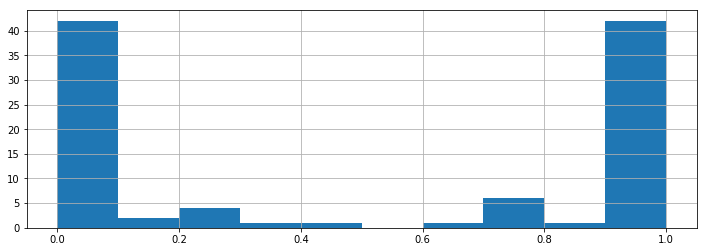
その確率の分布と見てみましょう。
plt.figure(figsize=(12,4))
plt.hist(func2(X, -34.73855674, 4.53539756, 7.68378862))
plt.grid()
plt.show()
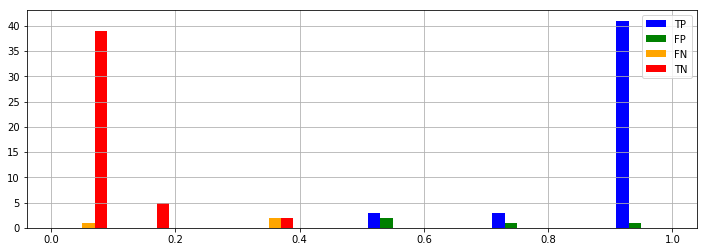
予測精度の見積もり
TP, FP, FN, TN = confusion_table(func2(X, -34.73855674, 4.53539756, 7.68378862), Y)
show_result(TP, FP, FN, TN)
Accuracy: 0.94
1変数のみを用いた時より少しだけ精度が向上しました。
多変数のシグモイド曲線に近似する
より多くの説明変数に対応できるように改良しましょう。
X3 = [7.0, 6.4, 6.9, 5.5, 6.5, 5.7, 6.3, 4.9, 6.6, 5.2,
5.0, 5.9, 6.0, 6.1, 5.6, 6.7, 5.6, 5.8, 6.2, 5.6,
5.9, 6.1, 6.3, 6.1, 6.4, 6.6, 6.8, 6.7, 6.0, 5.7,
5.5, 5.5, 5.8, 6.0, 5.4, 6.0, 6.7, 6.3, 5.6, 5.5,
5.5, 6.1, 5.8, 5.0, 5.6, 5.7, 5.7, 6.2, 5.1, 5.7,
6.3, 5.8, 7.1, 6.3, 6.5, 7.6, 4.9, 7.3, 6.7, 7.2,
6.5, 6.4, 6.8, 5.7, 5.8, 6.4, 6.5, 7.7, 7.7, 6.0,
6.9, 5.6, 7.7, 6.3, 6.7, 7.2, 6.2, 6.1, 6.4, 7.2,
7.4, 7.9, 6.4, 6.3, 6.1, 7.7, 6.3, 6.4, 6.0, 6.9,
6.7, 6.9, 5.8, 6.8, 6.7, 6.7, 6.3, 6.5, 6.2, 5.9]
X4 = [3.2, 3.2, 3.1, 2.3, 2.8, 2.8, 3.3, 2.4, 2.9, 2.7,
2.0, 3.0, 2.2, 2.9, 2.9, 3.1, 3.0, 2.7, 2.2, 2.5,
3.2, 2.8, 2.5, 2.8, 2.9, 3.0, 2.8, 3.0, 2.9, 2.6,
2.4, 2.4, 2.7, 2.7, 3.0, 3.4, 3.1, 2.3, 3.0, 2.5,
2.6, 3.0, 2.6, 2.3, 2.7, 3.0, 2.9, 2.9, 2.5, 2.8,
3.3, 2.7, 3.0, 2.9, 3.0, 3.0, 2.5, 2.9, 2.5, 3.6,
3.2, 2.7, 3.0, 2.5, 2.8, 3.2, 3.0, 3.8, 2.6, 2.2,
3.2, 2.8, 2.8, 2.7, 3.3, 3.2, 2.8, 3.0, 2.8, 3.0,
2.8, 3.8, 2.8, 2.8, 2.6, 3.0, 3.4, 3.1, 3.0, 3.1,
3.1, 3.1, 2.7, 3.2, 3.3, 3.0, 2.5, 3.0, 3.4, 3.0]
X = np.array([X1, X2, X3, X4])
任意の数の説明変数に対応できるよう関数を改良します。scipy.optimize.curve_fit の詳細は カーブフィッティング手法 scipy.optimize.curve_fit の使い方を理解する をご参考に。
import numpy as np
def func(X, *params):
f = np.zeros_like(X[0])
for i, param in enumerate(params):
if i == 0:
f = f + param
else:
f = f + np.array(param * X[i - 1])
return 1. / (1. + np.exp(-f))
最初の1変数だけ使った予測
from scipy.optimize import curve_fit
popt, pcov = curve_fit(func,X,Y, p0=[0, 0]) # poptは最適推定値、pcovは共分散
popt
array([-47.16139101, 9.6949171 ])
TP, FP, FN, TN = confusion_table(func(X, -47.16139101, 9.6949171), Y)
show_result(TP, FP, FN, TN)
Accuracy: 0.93
最初の2変数だけ使った予測
from scipy.optimize import curve_fit
popt, pcov = curve_fit(func,X,Y, p0=[0, 0, 0]) # poptは最適推定値、pcovは共分散
popt
array([-34.73582353, 4.53510012, 7.68301933])
TP, FP, FN, TN = confusion_table(func(X, -34.73582353, 4.53510012, 7.68301933), Y)
show_result(TP, FP, FN, TN)
Accuracy: 0.94
最初の3変数だけ使った予測
from scipy.optimize import curve_fit
popt, pcov = curve_fit(func,X,Y, p0=[0, 0, 0, 0]) # poptは最適推定値、pcovは共分散
popt
array([-483.42867713, 157.66806522, 129.22275895, -79.90984995])
TP, FP, FN, TN = confusion_table(func(X, -483.42867713, 157.66806522, 129.22275895, -79.90984995), Y)
show_result(TP, FP, FN, TN)
Accuracy: 0.98
4変数全てを使った予測
from scipy.optimize import curve_fit
popt, pcov = curve_fit(func,X,Y, p0=[0, 0, 0, 0, 0]) # poptは最適推定値、pcovは共分散
popt
array([-1331.681895 , 338.23424537, 356.96064159, -79.18057166,
-149.46135291])
TP, FP, FN, TN = confusion_table(func(X, -1331.681895 , 338.23424537, 356.96064159, -79.18057166,
-149.46135291), Y)
show_result(TP, FP, FN, TN)
Accuracy: 0.99
説明変数を増やすと精度が向上したことを確認しました。
ロジスティック回帰
以上のような計算を「ロジスティック回帰」と呼びます。ロジスティック回帰は、機械学習における「分類」手法の1つとして使われます。ロジスティック回帰の理解を深めるには、ロジスティック回帰をExcelで理解する をご参照されると良いかもしれません。
また、今回はロジスティック回帰の理解と scipy.optimize.curve_fit の使用方法の理解を目的としましたが、実用的には scikit-learn という機械学習ライブラリを用いた計算が便利です。詳細は 機械学習で二値分類 をご参照ください。
今回のデータの正体
もうお気付きの方もいらっしゃるかもしれませんが、今回のデータの正体は、機械学習の勉強でよく用いられる「あやめのデータ」です。「あやめのデータ」に関する説明は 実習用データ を、「あやめのデータ」の可視化例は 総合実験(1日目)Jupyter Notebook を使った基本統計量の計算と可視化 をご参照ください。