あやめのデータ(2品種)を例に説明します
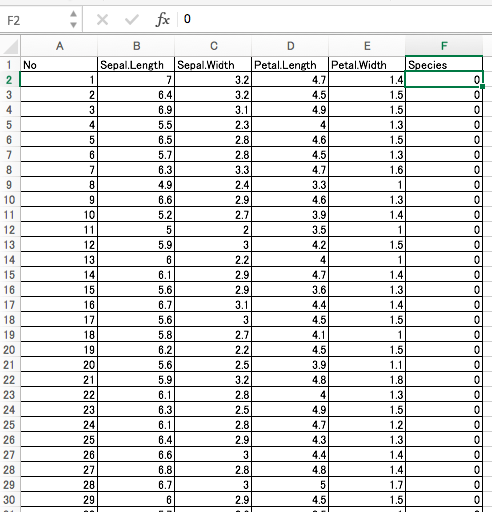
あやめのデータ(2品種) のエクセルファイルをダウンロードしてください。
あやめのデータは機械学習の勉強でよく使われるデータで、花片や萼の長さ・太さから品種を当てる(予測する)という問題がよく解かれます。本来は3品種150サンプルのデータなのですが、ここでは2品種100サンプルだけにしてあります。
B-E列が説明変数X、F列が目的変数Yと思ってください。普通の「回帰」では目的変数Yは連続値ですが、ロジスティック回帰では目的変数Yは0か1かの2値(2クラス)のうち1の発生確率を予測するため、ロジスティック回帰という名前にも関わらず「回帰」ではなく「分類」の一種として使われることがあります。
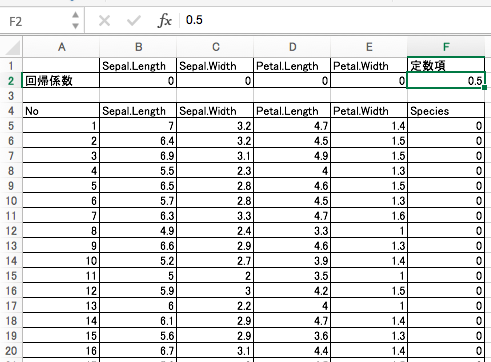
1. 回帰係数と定数項
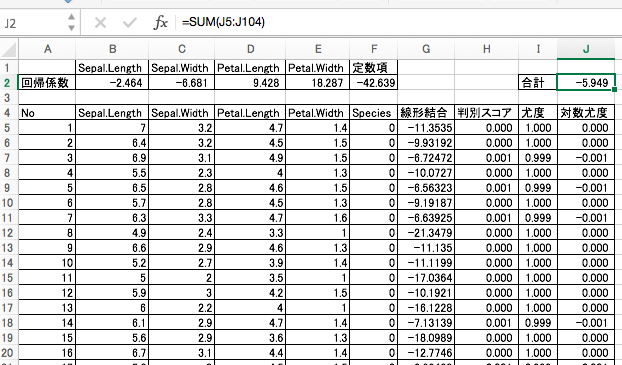
下記を参考にセルを配置して、テキトーな初期値を入れてください。
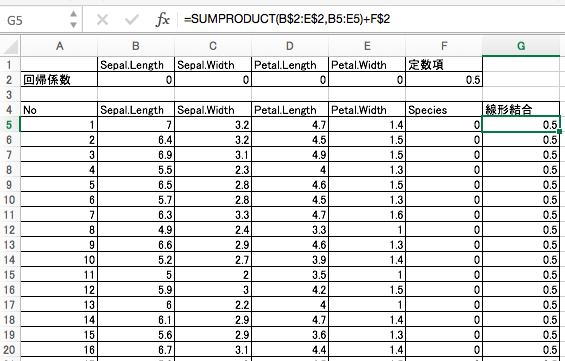
2. 線形結合(一次結合)
下記を参考に、各サンプルごとに線形結合を計算してください。線形結合って何?って思ったらググってね!
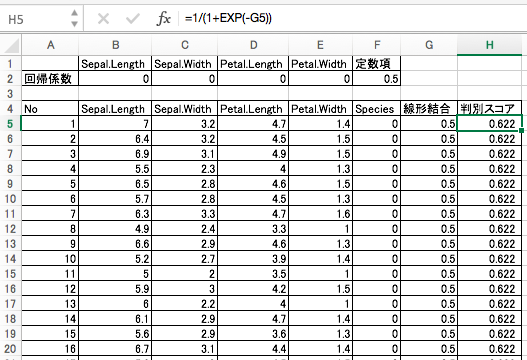
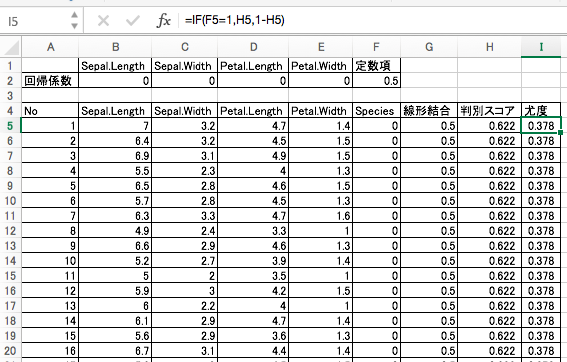
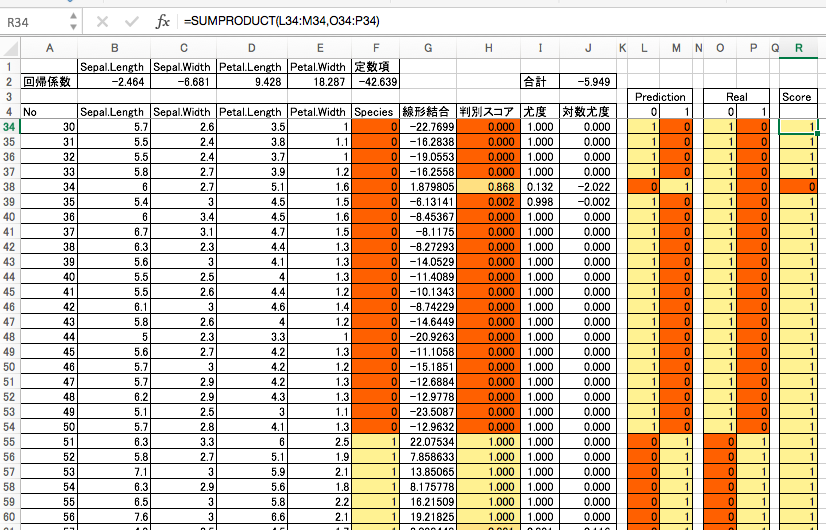
3. 判別スコア
判別スコアが、ロジスティック回帰によって予測された「クラス1に属する確率」なります。通常は、その値が0.5未満であればクラス0であるとみなされ(予測され)、0.5以上であればクラス1であるとみなされる(予測される)ことになります。現段階では、テキトーな判別スコアしか算出されていません。
判別スコアは、線形結合の値をシグモイド関数に渡した値です。シグモイド関数って何?と思ったらググってね!
4. 尤度
尤度は、もしクラス1なら判別スコアと等しく、もしクラス0なら1-判別スコアと等しくなるようにした値です。
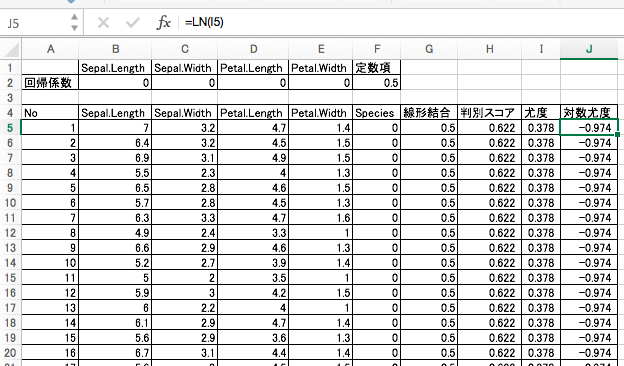
5. 対数尤度
尤度の自然対数が対数尤度です。
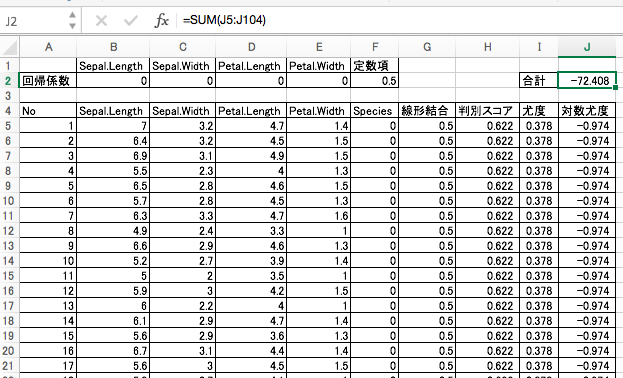
6. 対数尤度の合計
対数尤度の合計値を求めます。この対数尤度の合計を最大にするような回帰係数と定数項を求めるのです!
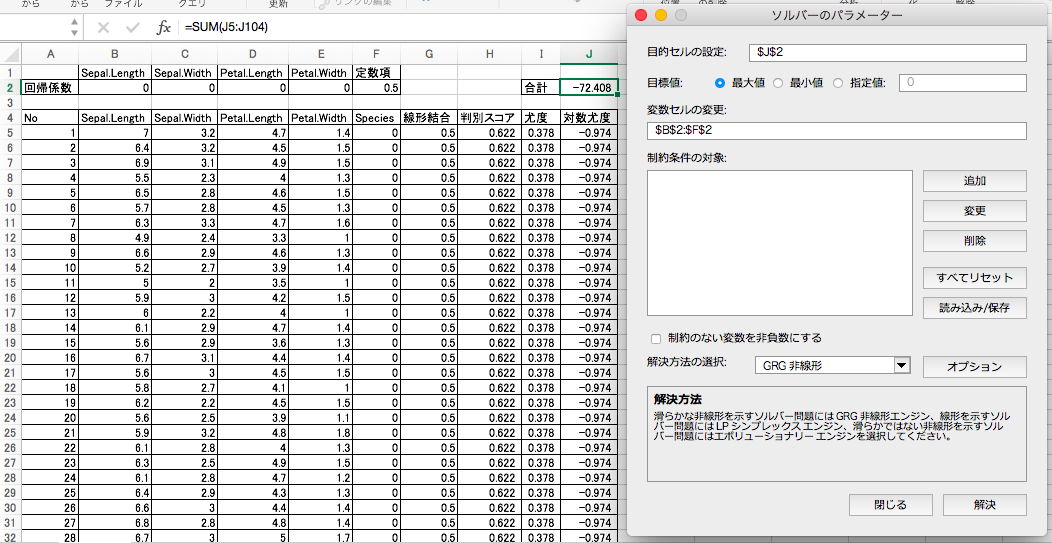
7. ソルバーを用いた最適化
まず「データ」タブに「ソルバー」というボタンがあるかどうか確認します。ない場合は、ソルバーのアドインを追加します。(アドイン追加方法についてわからなかったらググってね!)
「ソルバー」ボタンを押して出てきたウインドウに、「目的セル」「変数セル」に正しく入力し、目標値を「最大値」にし、「制約のない変数を非負数にする」のチェックを外し、「解決」ボタンをクリック。
ソルバーが解決してくれました!
8. 結果の解釈
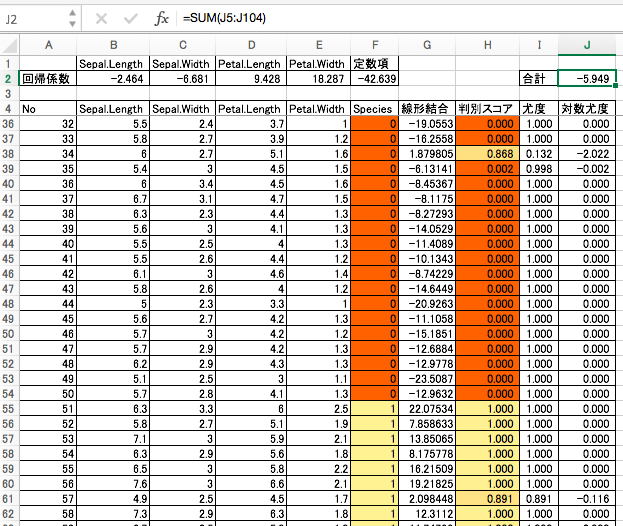
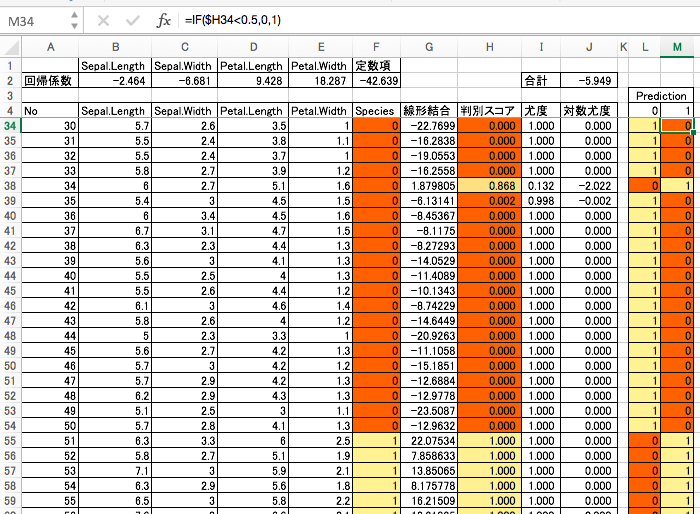
各サンプルに対する予測
各サンプルに対する予測が当たったかどうかは、「形式」→「条件付き書式...」を使って2色スケールの彩色を行なうと見やすいよ!
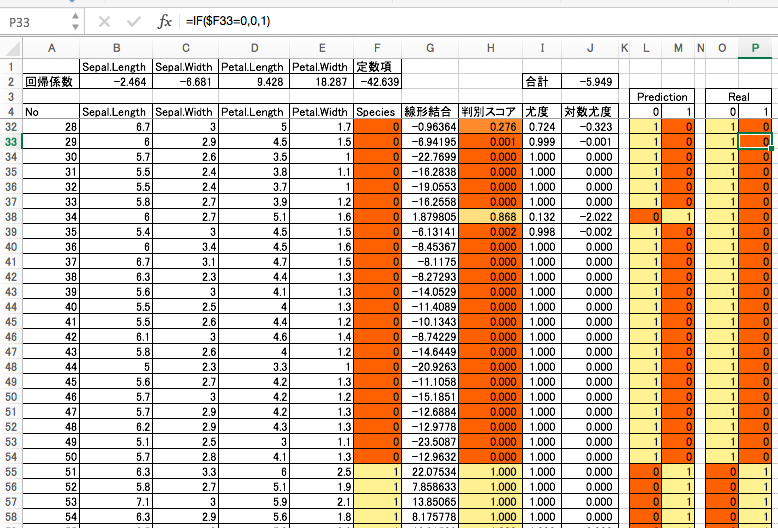
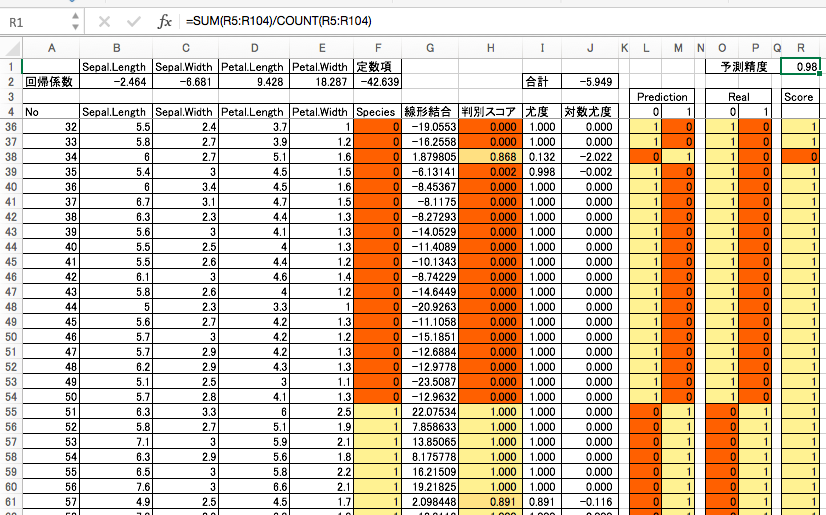
答え合わせ
予測精度を算出するにはいくつか方法がありますが、ここでは SUMPRODUCT 関数を用いた方法を紹介します。
精度は 98% と出ました。
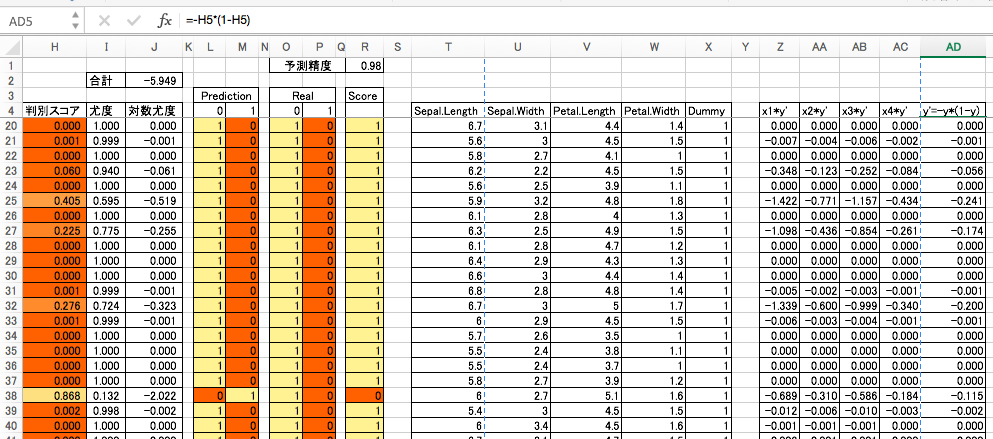
各成分の有意性
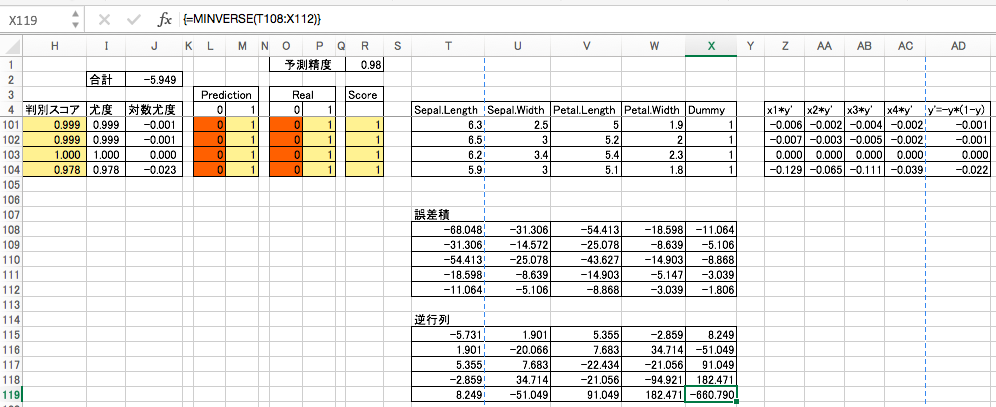
各成分ごとに標準誤差を算出するために以下の計算をします。
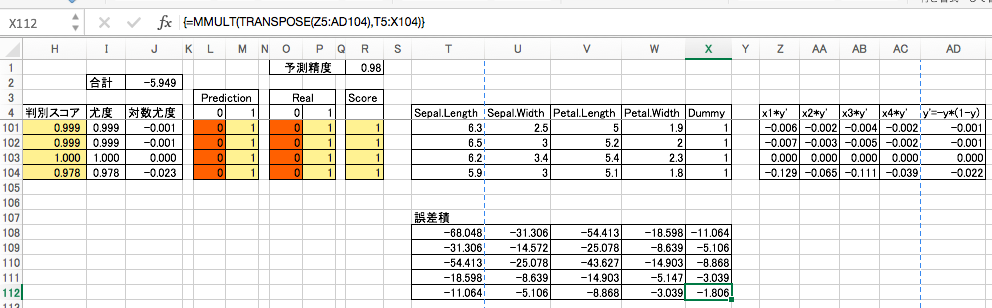
誤差積
(行列演算の出力時は、出力範囲を選択して[shift]+[ctrl]+[return]します。)
逆行列
(行列演算の出力時は、出力範囲を選択して[shift]+[ctrl]+[return]します。)
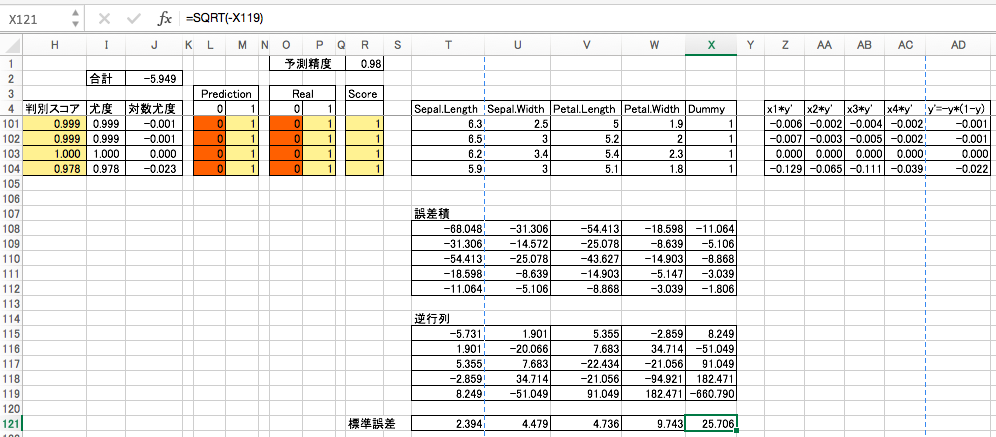
標準誤差
得られた逆行列の対角成分の絶対値の平方根を標準誤差とします。
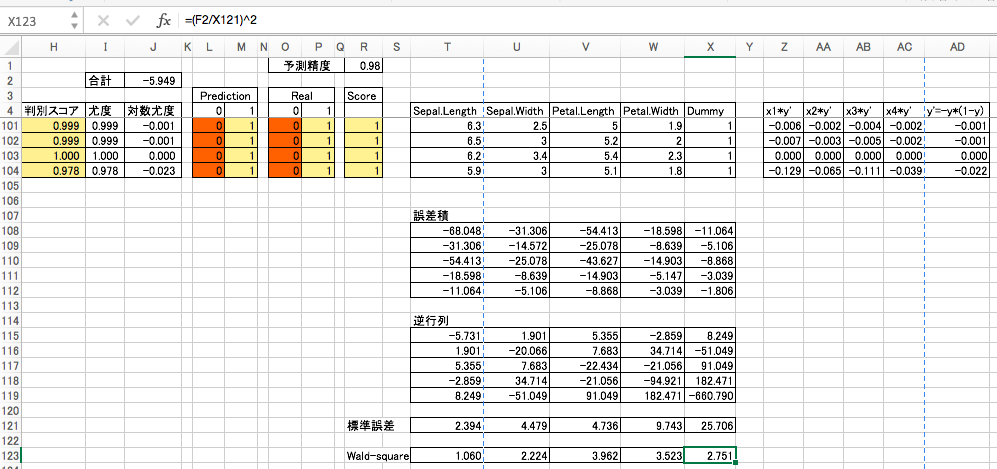
Wald 検定
回帰係数を標準誤差で割った値を2乗したものを Wald-squareといいます。
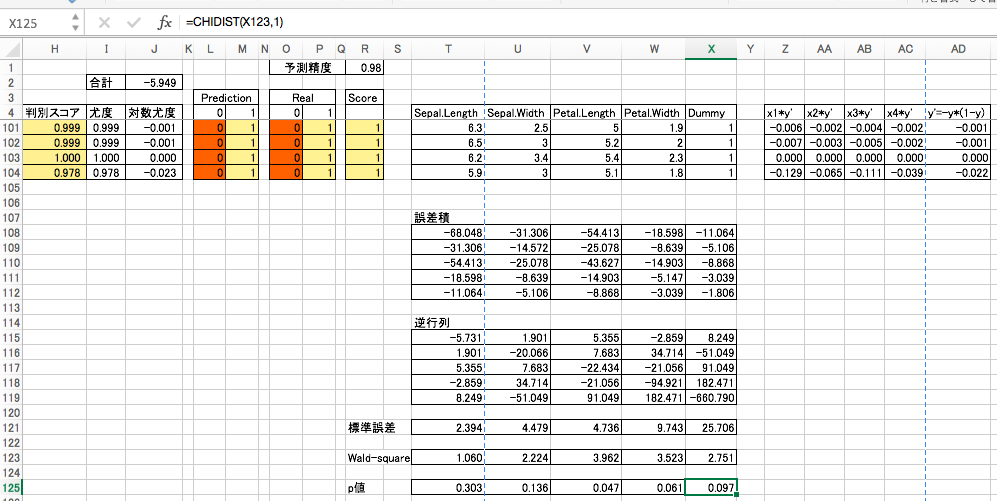
Wald-squareは自由度1のカイ2乗分布に従うとされるので、「回帰係数はゼロである」を帰無仮説としたカイ2乗を行なってp値を計算します。
p値が0.05未満なら、有意水準5%で帰無仮説を棄却できます。
課題
この例では4変数を使ってロジスティック回帰を行いました。今回の課題では、この中から最もp値の小さい2変数を選んで、その2変数でロジスティック回帰を行なってください。
次に、その2変数を使って2品種100サンプルのアヤメを色分けして散布図を描いてください。(Excelでのプロットの描き方が分からなかったらググってね!)
さらにそのプロットに、回帰係数と定数項を用いてアフィン超平面を描き入れてください。(実際には、2次元なので超平面ではなく直線になります。直線の描き方が分からなかったらググってね!)
以上の計算により得られた結果を踏まえて、ロジスティック回帰が何を行なっているのか考察してください。
最後に、演習用データから「ピマ・インディアンの糖尿病診断」を取得し、糖尿病の人と糖尿病ではない人を区別するためのロジスティック回帰モデルを作成し、そのモデルを評価してください。
課題の解答例(一部)
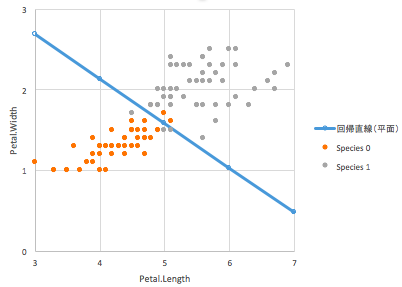
最もp値の小さい2変数は、ロジスティック回帰で2種を分類するのに最も寄与した2変数と言えます。その2変数でプロットし、回帰超平面(2変数なので直線になります)を描き入れると、下図のようになります。普通の線形回帰で求めるものは、データを最もよく表現する直線(または平面・超平面)になりますが、ロジスティック回帰で求めるものは、2種類のデータを最もよく分離する直線(または平面・超平面)だということです。ぜひ、実際に計算してみてください。