こんにちは、大学 1 年生になったばかりの E869120 です。
私は競技プログラミングが趣味で、AtCoder や日本情報オリンピックなどに出場しています。ちなみに、2021 年 4 月 7 日現在、AtCoder では赤(レッドコーダー)です。
本記事では、アルゴリズムの学習や競技プログラミングで使える数学的な部分を総整理し、それらについて解説したいと思います。前編・中編では数学的知識、後編(2021/4/26 公開予定)では数学的考察の側面から書いていきます。
【シリーズ】
- アルゴリズム・AtCoder のための数学【前編:数学的知識編①】 ← 本記事
- アルゴリズム・AtCoder のための数学【中編:数学的知識編②】
- アルゴリズム・AtCoder のための数学【後編:数学的考察編】
1. はじめに
21 世紀も中盤に入り、情報化社会(いわゆる「IT 化」)が急激に進行していく中、プログラミング的思考やアルゴリズムの知識、そしてアルゴリズムを用いた問題解決力が日々重要になってきています。2020 年にプログラミング教育が小学校で必修化され、2025 年から大学入試共通テストに「情報」という新科目の追加が検討されたことが、重要性に拍車をかけています。
しかし残念ながら、単にプログラミング関連の知識をそのまま学ぶだけでは、そのような能力はあまり身につかないと考えています。例えば、
- アルゴリズムを学んでいく
- それに関連する競技プログラミングの実力を上達させ、問題解決力を高める
といったことを行うためには、数学的な面が重要になりつつあるのです。
アルゴリズムの裏には様々な数学が潜んでいる
実際、ソートアルゴリズム・二分探索・最短経路問題などの基本的なアルゴリズムですら、裏には様々な数学的知識・数学的考察が潜んでいます。分かりやすい例として、以下のようなものが挙げられます。
- 有名なアルゴリズムの 1 つである二分探索は時間計算量 $O(\log N)$ で処理を行うことができるが、対数関数が何かを理解できていなければ、例えば $O(\log N)$ の高速さを実感することもできない
- 最短経路問題はダイクストラ法というアルゴリズムを使うと高速に解くことができるが、その裏には大学で初めて習う離散数学の一分野である「グラフ理論」が潜んでいる
- 「クイックソートの計算量は $O(N \log N)$ である」という事実だけでも、対数関数・数列・極限・確率分布と統計的な推測などの数学的知識が出現する
競プロでも数学的知識や考察が重要
また、競技プログラミングの多くの問題では、解法を思いつくために数学的知識や数学的考察が要求されることがあります。詳しくは 2 章で述べますが、場合によっては問題文や解説の理解にすら、高校数学以上の知識が必要となることもあるのです。
それだけでなく、
などアルゴリズム・競プロに関連する書籍の多くは、「高校数学までの履修は前提」として話を進めているため、前提となる数学の知識がなければ、競技プログラミングの実力アップにも影響を与えてしまう可能性があります。
だが全部が重要ということではない
しかし、大学数学までのすべての知識がアルゴリズム・競技プログラミングの能力向上にとって重要という訳ではありません。例えば、以下のような知識はほぼ登場しません。
\int_{0}^{1} \frac{1}{1+x^2} dx = \int_{0}^{\frac{\pi}{4}} \frac{1}{1+\tan^2 \theta} \cdot \frac{dx}{d\theta} \cdot d\theta \\
= \int_{0}^{\frac{\pi}{4}} \frac{1}{1+\tan^2 \theta} \cdot \frac{1}{\cos^2 \theta} d\theta\\
= \int_{0}^{\frac{\pi}{4}} \cos^2 \theta \cdot \frac{1}{\cos^2 \theta} d\theta = \int_{0}^{\frac{\pi}{4}} d\theta = \frac{\pi}{4}
本当に世界トップレベルになろうとすれば話は別ですが、例えば黄色コーダー(上位約 3 %)になるために要求される知識はそれほど多くないのです。
本記事のゴール
そこで、本記事では、アルゴリズムや競プロと関連が深い数学的事柄を中心に、特に AtCoder Beginner Contest (ABC) に出題されるようなアルゴリズムに絞ってまとめたいと思います。最終的には、
- 高校数学/大学数学未履修の中高生や、数学を学び直したい人に対して、アルゴリズム・競プロの学習に役立ててもらうこと
- 全読者の皆さんに、アルゴリズムと数学の密接な繋がりに気づいてもらうこと
この 2 つを最大の目標にします!!!!!

(https://readingmonkey.blog.fc2.com/blog-entry-627.html?sp)
目次
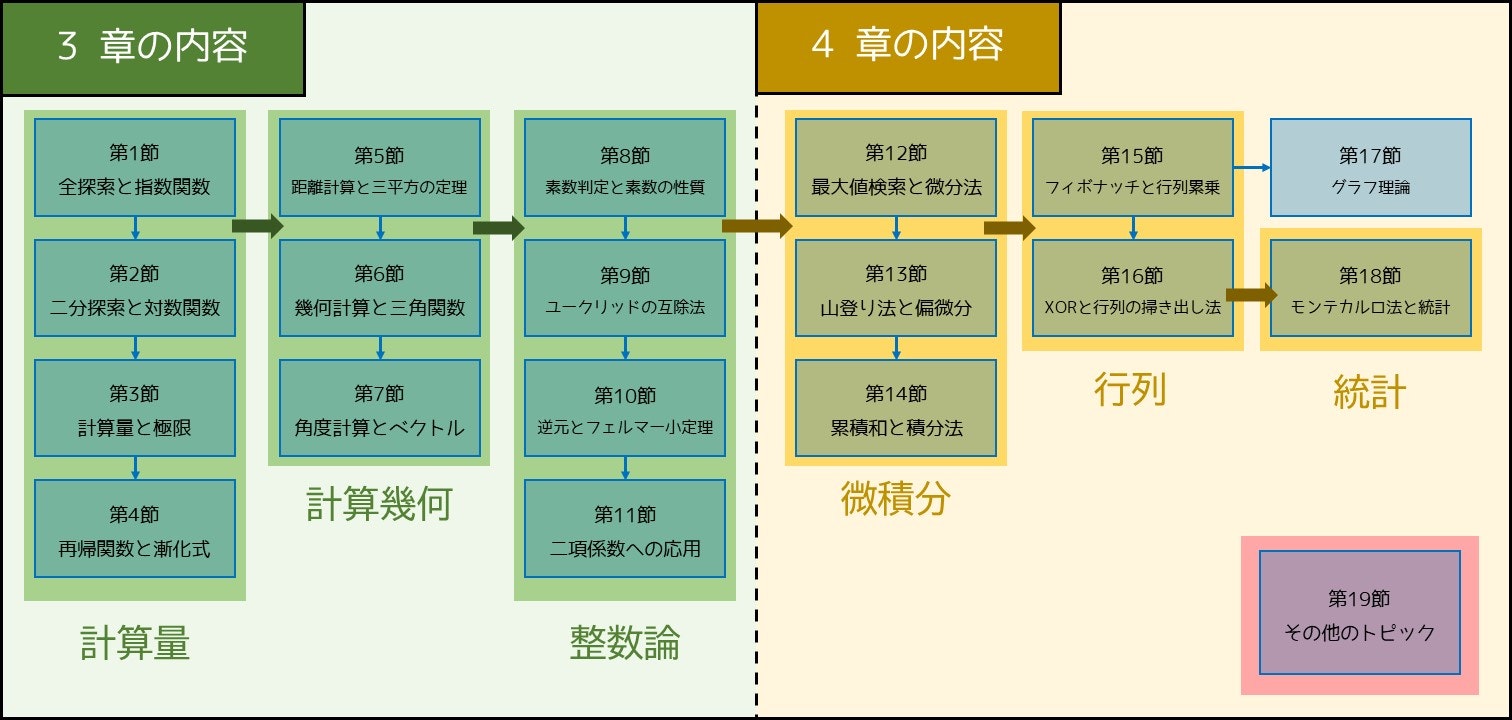
前編
| 章 | タイトル | 備考 |
|---|---|---|
| 1. | はじめに | |
| 2. | これが分からないと問題が理解できない! ~最重要ポイント 12 選~ | ここからサポートします |
| 3. | アルゴリズムと密接に関わる数学<初級編> | 本記事のメインです(1 ~ 11 個目のトピックを扱います) |
中編
| 章 | タイトル | 備考 |
|---|---|---|
| 4. | アルゴリズムと密接に関わる数学<中級編> | 本記事のメインです(12 ~ 19 個目のトピックを扱います) |
| 5. | これだけ解けば理解が深まる! ~演習問題 32 問~ | 2 章から 4 章の内容をサポートします |
後編
| 章 | タイトル | 備考 |
|---|---|---|
| 6. | なぜ数学的考察が重要か? | 後編では数学的考察を扱います |
| 7. | 競プロで頻出! ~汎用的な数学的考察 7 選~ | |
| 8. | 問題特有の数学的考察テクニック 14 選 | 後編のメインです |
| 9. | おわりに | |
| 10. | 参考文献 |
2. これが分からないと問題が理解できない! ~最重要ポイント 12 選~
本記事の最初に、次の問題を読んでください。
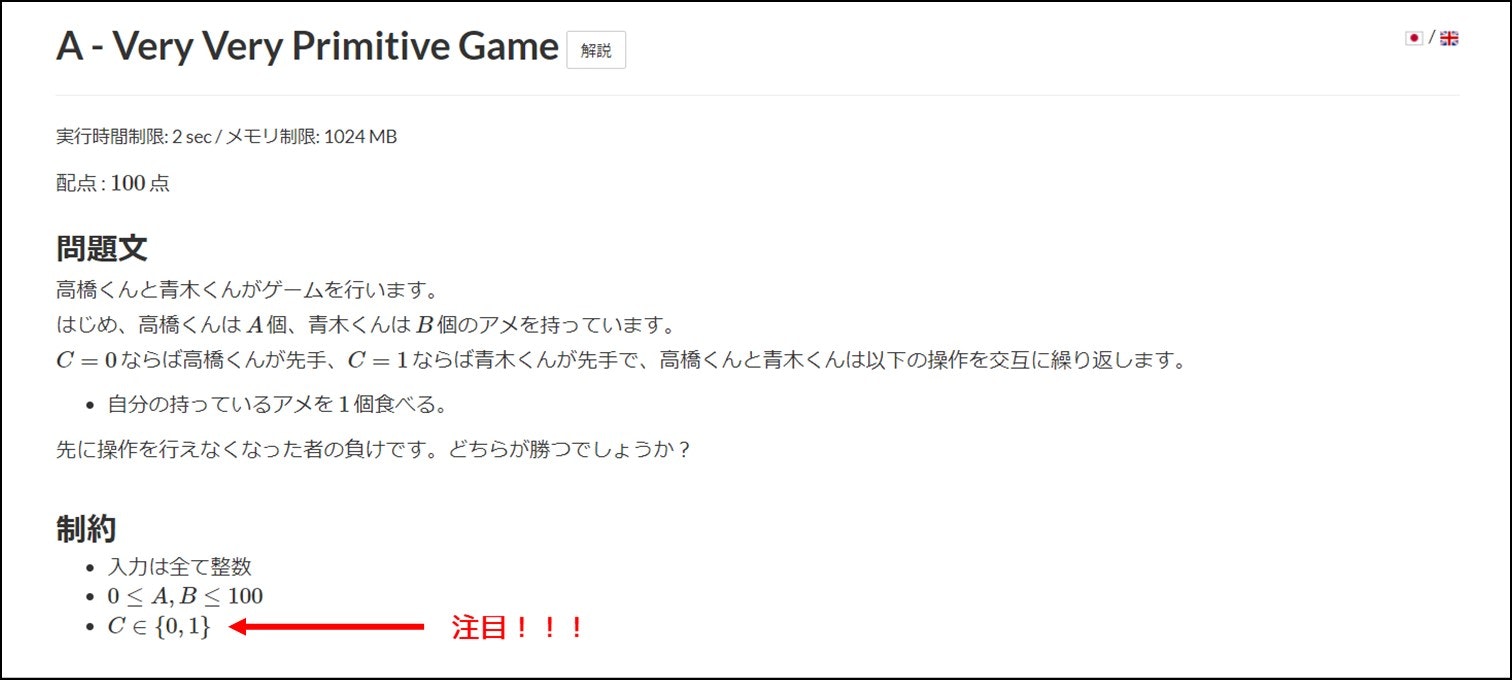
これは AtCoder Beginner Contest (ABC) 190 の A 問題です。AtCoder の中で最も初心者向けのコンテストである ABC の、しかも一番最初の A 問題、つまり最も簡単な問題です。
それにも関わらず、「$\in$」という記号が使われていることが分かるでしょう。これは中学数学では一切習わず、高校 1 年になってようやく「数学 I|集合と命題」という単元で初めて学習する記号です。しかし、この記号が分からなければ問題文の意図がつかめません。つまり、高校数学未履修の中学生や、高校数学を忘れてしまった人は、プログラミング以前の問題で挫折してしまうのです。そこで私は、
これはやばい!
数学的な部分を何とかできないか!
と思いました。これが本記事の執筆に至ったきっかけです。
2 章で紹介する内容
そこで本章では、最初に**「競プロの基本や問題文の意図を理解するために必要な数学的知識」**を 12 個の最重要ポイントに分けて紹介したいと思います。構成は次表の通りです。
| 分野 | 紹介する節 |
|---|---|
| 中 1 レベルまでの本当に基礎的な知識 | 2-1. 節 |
| プログラム実装に必要な知識 | 2-2. 節 |
| 計算量オーダーの理解に必要な知識 | 2-3. 節 |
| 2 進数とビット演算 | 2-4. 節、2-5. 節 |
| 問題文に出てくる整数論の知識 | 2-6. 節 |
| 問題文に出てくる数列関連の知識 | 2-7. 節、2-8. 節、2-9. 節 |
| 問題文に出てくる集合関連の知識 | 2-10. 節、2-11. 節 |
| その他、競プロで頻出の数式等 | 2-12. 節 |
2-1. 中学 1 年レベルまでの基本的用語・数式の整理
本章の最初に、競技プログラミングの問題文などを読むにあたって絶対必要な、中学 1 年生レベルまでの知識をまとめることにします。読者の多くは知っていると思うので、読み飛ばしていただいても構いませんが、本記事ではこの段階からサポートします。
整数・自然数・非負整数
-8, -4, 3, 9, 100 のような、小数点以下がないような数のことを整数といいます。整数の中にもさらに「自然数」「非負整数」などといった分類があります。
| 用語 | 説明 |
|---|---|
| 自然数 | 1 以上の整数。1, 2, 3, 4, ... など。1 |
| 正の整数 | 1 以上の整数。1, 2, 3, 4, ... など。(自然数と同じ) |
| 非負整数 | 0 以上の整数。0, 1, 2, 3, 4, ... など。 |
| 負の整数 | -1 以下の整数。-1, -2, -3, -4, ... など。 |
倍数・約数・素数
「〇は△の倍数」とは、〇が△で割り切れることを指します。
「〇は△の約数」とは、△が〇で割り切れることを指します。
例えば 100 は 5 の倍数、12 は 84 の約数です。
また、素数とは 1 と自分自身以外で割り切れない 2 以上の整数のことです。例えば 13 は素数です。
剰余(mod)
$a \bmod b$ とは、$a$ を $b$ で割った余りを指します。
例えば $8691 \bmod 100 = 91$ です。C++ では a % b といった形で計算できます。
また、競プロでは「$\bmod 1000000007$ で求めよ」といった形式の問題文がよく出てきますが、これは「答えを $1000000007$ で割った余りを求めよ」という意味です。
文字式
$A, B$ などの文字を使って表された式です。プログラミングの文脈において、$A, B$ などの文字は変数として入力されることが多く、例えばこんな感じの問題文になることがあります。
整数 $A, B$ が与えられます。$A+B$ の値を出力してください。
感覚的には $A$ の値と $B$ の値を入力された数字に書き換えれば分かりやすいと思います。(例えば $A = 5, B = 10$ のとき $15$ と出力すれば良いです)
文字式の積
文字式に使われる数値 $A, B$ に対して、$A \times B$ の値を $AB$ と表すことがあります。したがって、例えば次の問題で $A$ に $6$ が、$B$ に $9$ が入力された場合、$69$ ではなく $6 \times 9 = 54$ が正解となります。
整数 $A, B$ が与えられます。$AB$ の値を出力してください。
階乗
$N! = 1 \times 2 \times 3 \times ... \times N$ です。
例えば $3! = 6$、$4! = 24$、$10! = 3628800$ です。
べき乗
$a$ を $b$ 回掛け合わせた数を $a^b$($a$ の $b$ 乗)と書きます。例えば、
- $2^3 = 2 \times 2 \times 2 = 8$
- $10^2 = 10 \times 10 = 100$
- $3^7 = 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 = 2 \ 187$
といった感じになります!!!
平方根
$a \times a = N$ となるような数 $a$ を「$N$ の平方根」といいます。例えば $9$ の平方根は $3$ と $-3$ です。
この中で正の数であるものを**「ルート $N$」**といい、$\sqrt{N}$ と表します。例えば $\sqrt{9}=3, \sqrt{25}=5, \sqrt{2}=1.41421356...$ です。
ここまで、本当に基礎的な内容について紹介しましたが、本章の最初に述べた通り、プログラミングコンテストで最も簡単な問題でも、高校数学の知識が要求される場合があります。2-2. 節以降では、競プロ参加者なら絶対に押さえておきたい数学的知識を紹介します。
2-2. 関数とは何か? ~プログラム実装で重要~
まず、以下のプログラムを読んでみてください。
# include <iostream>
using namespace std;
double f(double a) {
return 2.0 * a * a + a;
}
int main() {
double a;
cin >> a;
cout << f(a) << endl;
return 0;
}
そこで、例えば引数 $a$ に $7$ を入力すると $2 \times 7 \times 7 + 7 = 105$ が出力されるのは直感的に分かると思いますが、$f(a)$ とは一体何なのでしょうか。これが関数です。関数とは $f(x)$ のような形で表され、$x$ の値が決まると $f(x)$ の値が $1$ つに決まるもののことを指します。例えば $f(a) = 2a^2 + a$ の場合、
- $f(0.6) = 1.32$
- $f(7) = 105$
- $f(1001) = 2005003$
となります。C++ などでは関数でとる値を返り値と呼ぶこともあり、例えば $f(5)$ の返り値は $55$ です。また、以下のように $y=f(x)$ のグラフで表される場合も多いです。これは現在の学習指導要領では中学 1 年で習う範囲であり、読者の多くは知っていると思います。
注意すべき点
しかし、注意しておかなければならない点があります。これは以下の 4 点です。
- $y=x^2$ のように連続した値を取るとは限らず、引数や返り値がとびとびの値なこともある
- 関数は $f(N, M)$ のように関係する値(引数)が $2$ つ以上となる場合もある
- 関数の引数・返り値は整数や実数などの値とは限らず、
string型のように文字列の場合、pair型のように $2$ つの整数の場合なども考えられる -
void型のように、何も値を返さない関数も存在する
以下のソースコードの例を考えてみると、分かりやすいと思います。
- $func1(N)$ は $N = 0, 1, 2, 3, 4, 5$ の場合にのみ定義され、とびとびの値を取っている
- 例えば
func1(1.5)の値は定義されていない - 例えば
func1(6)の値も定義されていない
- 例えば
- $func2(a, b) = \sqrt{a^2 + b^2}$ は複数の値が引数となっているが、これも関数である
- 特に、2 つの引数をもつ関数は「2 変数関数」という
- $func3(S)$ は値ではなく文字列が引数となっているが、これも関数である
- 文字列 $S$ を逆から読んだものを出力する関数になっている
- $func4(N)$ は何も返さないものとなっているが、これも関数である
-
aを $N$ 個繋げたものを出力する関数 - 高校数学では見ないが、C++ における
void型のようなものも関数として扱われる
-
int func1(int N) {
if (N == 0) return 3;
if (N == 1) return 1;
if (N == 2) return 4;
if (N == 3) return 1;
if (N == 4) return 5;
if (N == 5) return 9;
}
double func2(int a, int b) {
return sqrt(1.0 * a * a + 1.0 * b * b);
}
string func3(string S) {
string T = "";
for (int i = (int)S.size() - 1; i >= 0; i--) {
T += S[i];
}
return T;
}
void func4(int N) {
for (int i = 1; i <= N; i++) {
cout << "a";
}
cout << endl;
}
なお、その他にも C++ などでは「再帰関数(3-4. 節で紹介)」というものがあります。数学ではあまり見ないかもしれないですが、以下のように「自分自身を呼び出す関数」のことを指します。
int func(int N) {
if (N == 1) return 1;
if (N == 2) return 1;
return func(N - 1) + func(N - 2);
}
詳しくは以下の記事をお読みください。
2-3. 対数とは何か? ~O(N log N) の本当の意味~
アルゴリズムを学んでいくと、「二分探索の計算量は $O(\log N)$ である」「クイックソートの計算量は $O(N \log N)$ である」という事実を知る人が多いと思うのですが、果たして $\log$ はどれくらい速いのでしょうか。まず、$\log_{a} b$ の値は以下のように定義されます。
$a^x = b$ のとき、$\log_{a} b = x$ である。
$a$ を底といい、$b$ を真数という。$a > 0, a \neq 1, b > 0$ の範囲で定義される。
例えば、以下の式が成り立ちます。
- $12^2 = 144$ であるため、$\log_{12} 144 = 2$
- $2^{10} = 1024$ であるため、$\log_{2} 1024 = 10$
- $4^{2.5} = 32$ であるため、$\log_{4} 32 = 2.5$
そこで、$N$ と $\log N$を比較してみましょう。ただし log の底は 2 であるものとします。2
| N | 10 | 100 | 1000 | 10000 | 100000 | 1000000 |
|---|---|---|---|---|---|---|
| $N$ 回の場合の計算回数 | 10 | 100 | 1000 | 10000 | 100000 | 1000000 |
| $\log N$ 回の場合の計算回数 | 約 3.32 | 約 6.64 | 約 9.97 | 約 13.29 | 約 16.61 | 約 19.93 |
計算量 $O(\log N)$ はとてつもなく高速であることが分かります。このように、対数(log)を知っておくと、アルゴリズム効率化の素晴らしさがより深く実感できるのです。「計算回数 $\log N$」に関する詳しい話は 3-2. 節で述べますので、是非ご覧ください。
2-4. 2 進数とは何か?
人間は 10 進数を扱いますが、実はコンピューターの各メモリは on と off の 2 通りしか値を持てないので、2 進数を用いて計算しているのです。(例えば、int 型が $-2^{31}$ 以上 $2^{31}$ 未満の値しか持てないことにも、そういった背景があります。)
では、2 進数とはどのようなものでしょうか。次の通りです。
2 進数で「$c_{N-1}c_{N-2}...c_{1}c_{0}$」と表される数は、10 進数では $\left( 2^{N-1} \times c_{N-1} \right) + \left( 2^{N-2} \times c_{N-2} \right) + ... + \left( 2^{1} \times c_{1} \right) + \left( 2^{0} \times c_{0} \right)$ である。
数式だけだとあまり良く分からないかもしれないので、図を用いて説明すると、以下のようになります。$10$ 進数を $2$ 進数に直す方法とその逆が紹介されています。
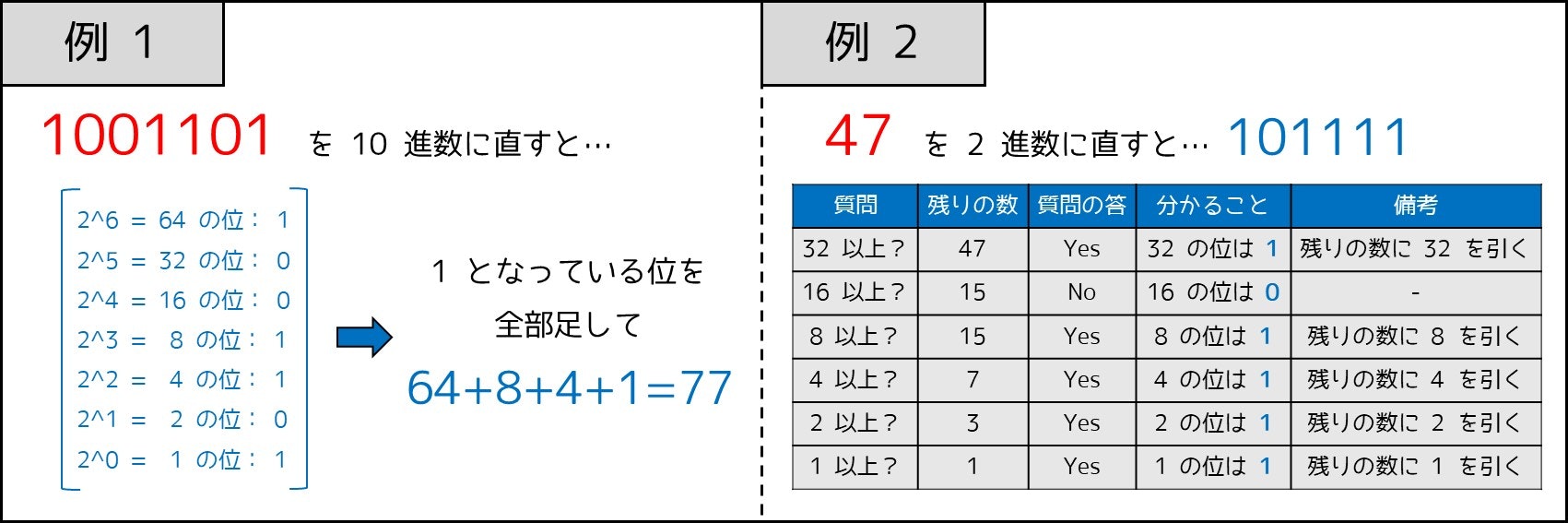
2-5. 論理演算とは何か? ~AND・OR・XOR~
競プロでは、ABC197C・ABC147D など、問題文中に AND・OR・XOR といったビット演算が登場することが増えています。これは一体どのようなものなのでしょうか。元々の意味としては、以下の表のように TRUE(1) と FALSE(0) に対する演算となっています。
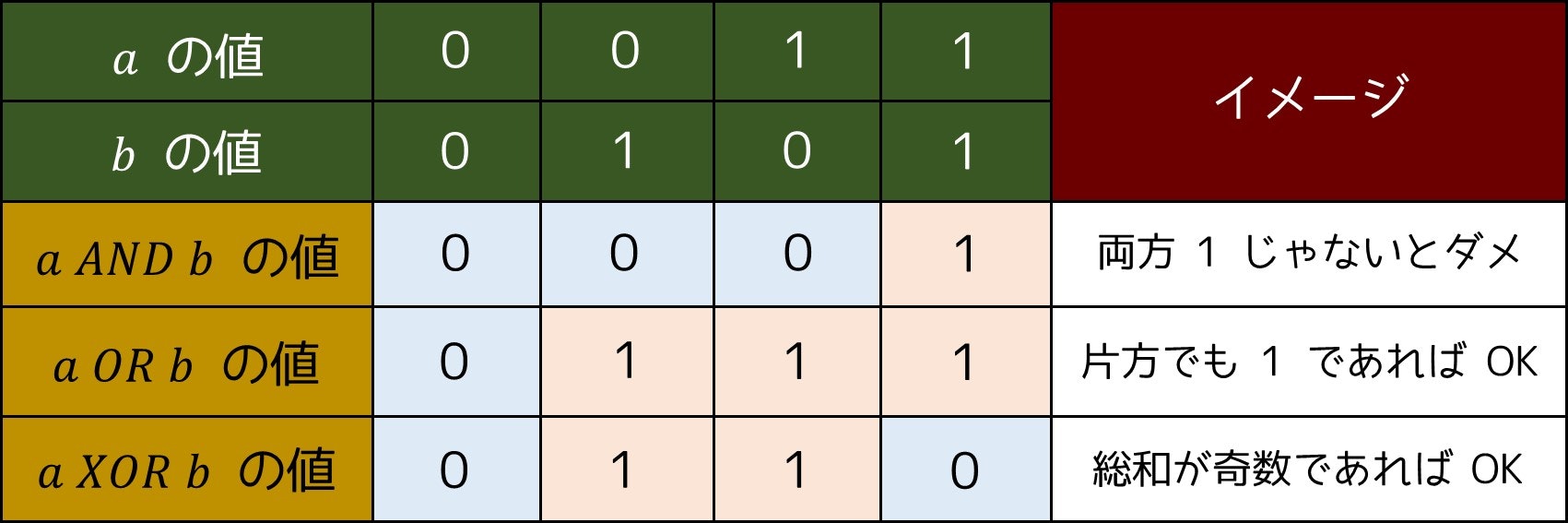
しかし、この論理演算は以下の図のように、a と b を両方 2 進数に変換した上で桁ごとに考えることで、整数同士の演算に拡張することができるのです。
また、3 つ以上の数の論理演算(AND・OR・XOR)も行うことができ、同じ種類の演算では計算順序によって答えが変わりません3。例えば 22 xor 13 = 27、5 or 9 or 17 = 5 or (9 or 17) = 5 or 25 = 29 が成り立ちます。アルゴリズムや競プロの文脈では、このように拡張した AND・OR・XOR が扱われることが多いです。

なお、論理演算やビット演算についてより詳しく知りたい方は、
をお読みください。
2-6. 互いに素とは何か? ~GCD と LCM~
まず、競プロで頻出の GCD・LCM は以下のようなものです。
-
LCM(a, b):$a$ と $b$ の最小公倍数。$a, b$ 両方の倍数であるような正整数のうち最小のもの。 -
GCD(a, b):$a$ と $b$ の最大公約数。$a, b$ 両方の約数であるような正整数のうち最大のもの。
例えば、GCD(9, 6) = 3、LCM(9, 6) = 18 です。また、GCD と LCM は 3 つ以上の整数に対して定義される場合もあり、例えば GCD(8, 12, 16) = 4、LCM(8, 12, 16) = 48 です。次に、「$a$ と $b$ が互いに素」とは何でしょうか。
などの問題文に出ているキーワードですが、最大公約数が $1$ である、つまり GCD(a, b) = 1 であることを指します。例えば $7$ と $5$ は互いに素ですが、$10$ と $8$ は互いに素ではありません。これについて、詳しくは 3-9. 節で述べますので、是非ご覧ください。
2-7. 数列とは何か?
競プロでは、例えば以下のような問題文に遭遇することがあります。これは AtCoder Beginner Contest で 2 番目に簡単である B 問題ですが、「数列」というキーワードが出現しており、これを理解していなければプログラミング以前の問題で止まってしまいます。
長さ $X$ の整数列 $A$ と整数 $X$ が与えられる。$A$ から $X$ と等しい要素を全て取り除き、残った要素をそのままの順序で並べた数列 $A'$ を出力せよ。(出典:ABC191B - Remove It)
そこで、「数列」とは何でしょう。皆さんは以下のようなものを想像すると思います。
| 数列 | 法則性 |
|---|---|
| (1, 2, 3, 4, 5, 6, 7, ...) | 整数を並べただけ |
| (1, 4, 9, 16, 25, 36, 49, ...) | 整数の 2 乗を並べただけ |
| (1, 1, 2, 3, 5, 8, 13, ...) | フィボナッチ数列 |
このように、数列は値が順番に並んだものであり、数列 $A$ の $i$ 番目の要素(第 $i$ 項)を $A_i$ と書きます。例えば数列 $C = (1, 4, 9, 16, 25, ...)$ では $C_4=16$ です。**特に、整数のみからなる数列を整数列といいます。**よくある誤解として、
- 数列はフィボナッチ数列のように無限に続かなければならないのか?
- 最初に紹介した 3 つの数列のように規則性がなければならないのか?
という疑問が挙げられますが、全部違います。例えば $A = (8, 6, 9, 1, 2, 0)$ といった法則性のない有限なものも数列であり、競プロの文脈では以下のように有限数列を扱う方が多いです。
長さ $N$ の数列 $A = (A_1, A_2, ..., A_N)$ が与えられます
単に数が $N$ 個並んでいる列である、と捉えておくと分かりやすいと思います。
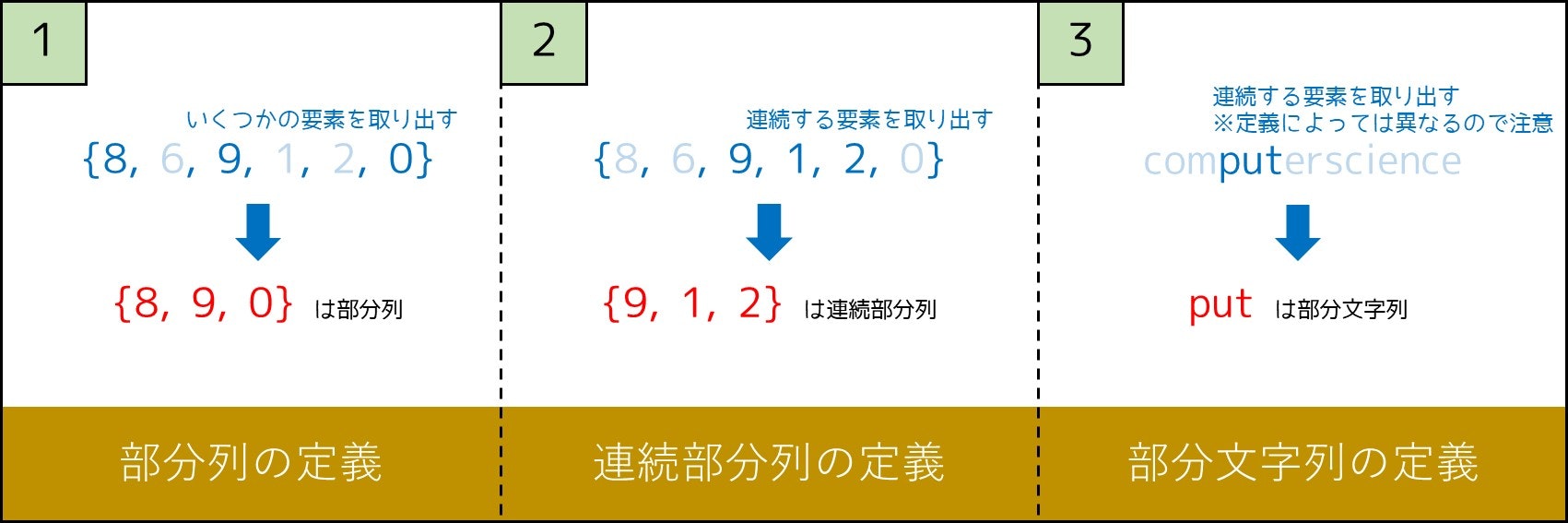
2-8. 部分列とは何か?
これも競技プログラミングで頻出の用語であり、部分列の定義は以下の通りです。
もとの数列から一部の項を取ってきた数列を部分列と言います。部分列を作るときには、取ってきた項の順序を入れ替えてはいけません。(引用元)
例えば、数列 $A = (8, 6, 9, 1, 2, 0)$ から、左から数えて $1, 3, 6$ 番目の要素のみを取り出した $(8, 9, 0)$ という数列は、$A$ の部分列です。
また、連続部分列は、数列の中のある連続する区間のみを取り出し、順番を保ってできたものです。例えば、$A = (8, 6, 9, 1, 2, 0)$ から、左から数えて $3, 4, 5$ 番目の要素のみを取り出した $(9, 1, 2)$ という数列は $A$ の連続部分列ですが、前述の $(8, 9, 0)$ は連続部分列ではないです。
そして、連続部分列と同じような概念は文字列にも適用でき、これを部分文字列といいます。例えば $3, 4, 5$ 文字目のみを取り出した put は computerscience の部分文字列ですが、$1, 2, 11, 13$ 文字目のみを取り出した coin は部分文字列ではありません。**ただし、問題によっては部分列と同じ定義をする場合もあるので要注意。**まとめると下図のようになります。
2-9. シグマ記号とは何か?
これも競プロの問題文において頻出の記号で、例えば ABC147D、ABC194C、ARC107A などで見受けられます。一体どのようなものでしょうか。まず、シグマ記号は以下のように表記されます。
\left( A_L + A_{L+1} + ... + A_{R} \right)= \sum_{i=L}^{R} A_i
シグマ記号の下の値から上の値まで、全部足すイメージです。例えば、以下が成り立ちます。
\sum_{i=3}^{5} i = \left( 3 + 4 + 5 \right) = 12, \ \sum_{i=4}^{6} i^2 = \left( 16 + 25 + 36 \right) = 77
また、問題によっては「二重シグマ」が出てくることがあります。高校数学ではあまり扱わない表記ですが単純で、for 文を二重に書くようなイメージです!!!
\left( A_{L1, L2} + A_{L1, L2 + 1} + A_{L1, L2 + 2} + ... + A_{R1, R2} \right) = \sum_{i=L1}^{R1} \sum_{j=L2}^{R2} A_{i,j} \\
example1: \sum_{i=1}^{2} \sum_{j=1}^{3} ij = \left(\left(1 + 2 + 3\right) + \left(2 + 4 + 6\right)\right) = 18 \\
example2: \sum_{i=1}^{4} \sum_{j=1}^{i} j = \left(\left(1\right) + \left(1 + 2\right) + \left(1 + 2 + 3\right) + \left(1 + 2 + 3 + 4\right)\right) = 20
サンプルコードで書くと次のような感じになり、変数 sum の値が求める二重シグマの値になります。三重シグマ以降も同様に考えることができます。
// L1, R1, L2, R2, A[i][j] は入力済みとする
int sum = 0;
for (int i = L1; i <= R1; i++) {
for (int j = L2; j <= R2; j++) {
sum += A[i][j];
}
}
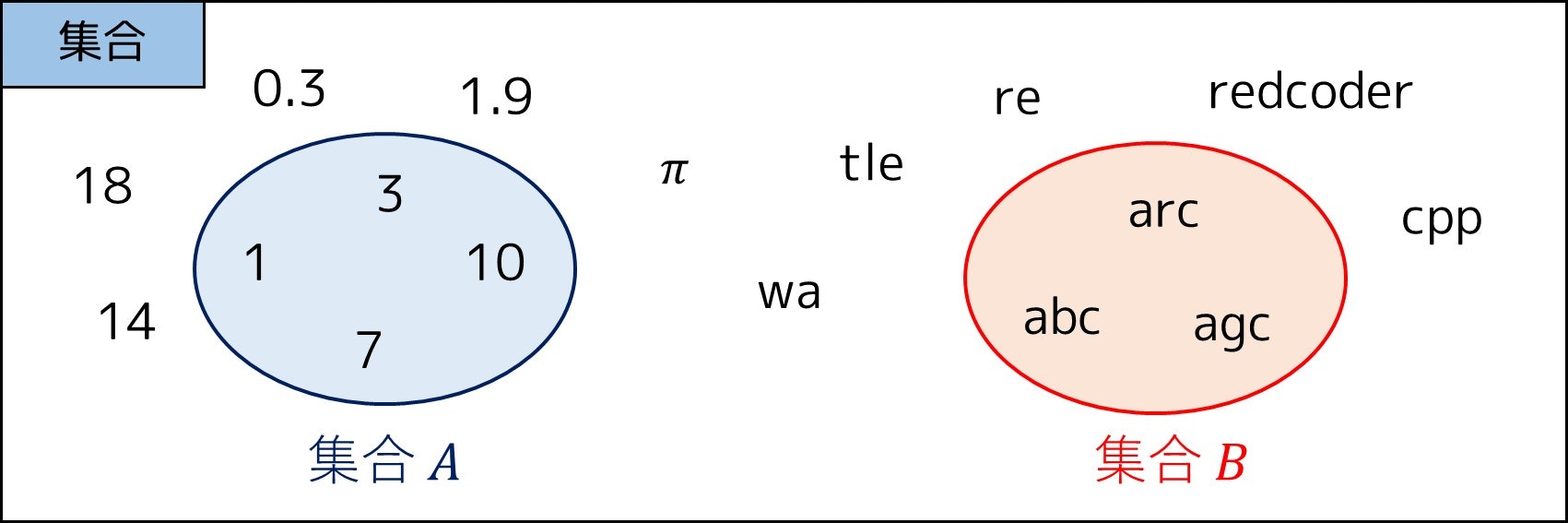
2-10. 集合とは何か?
まず、用語を整理するところから始めましょう。
-
集合とは値・文字列など、何らかの条件によってグループ分けできる「もの」の集まりです。例えば「1 以上 5 以下の整数」「20 以下の素数」「整数全体」「
aから始まる 3 文字の文字列」などが挙げられます。 - 要素(または元)とは集合を構成している一つ一つのものを指します。例えば、「1 以上 5 以下の整数」の要素は 1, 2, 3, 4, 5 であり、11 は「20 以下の素数」という集合の要素のひとつです。
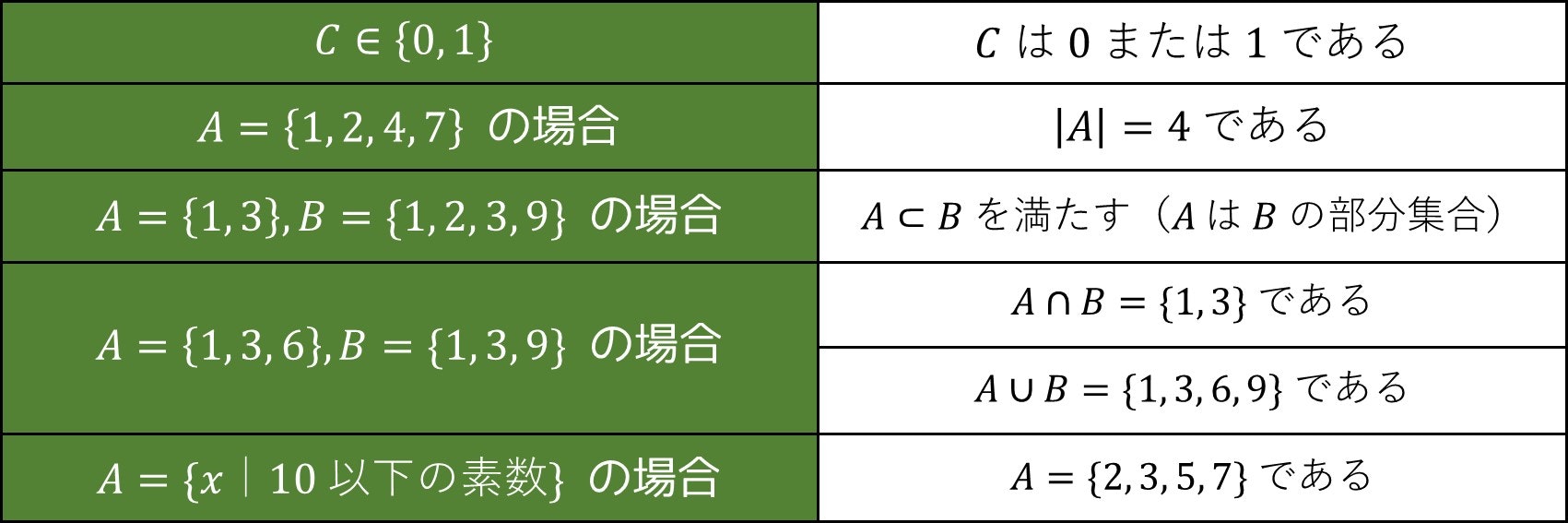
例えば、集合 $A$ を「以下の図の中にある 1 以上 10 以下の整数」、集合 $B$ を「以下の図の中にある a から始まる文字列」とすると、集合 $A$ と $B$ の要素は以下のようになります。
- $A$ の要素:$1, 3, 7, 10$
- $B$ の要素:
abc、arc、agc
そこで、慣例的には、集合は「$A = \{$ 集合の要素 $\}$」という形で表記します。
例えば「$A = \{1, 3, 7, 10\}$」「$B = \{$abc$,$arc$,$agc$\}$」といった感じになります。
2-11. 頻出の集合の表記・用語たち
アルゴリズムや競プロの文脈において頻出の表記・用語を、次表にまとめておきます。
| 用語 | 用語に関する表記 | 説明 |
|---|---|---|
| - | $x \in A$ | $x$ は集合 $A$ の要素のひとつである |
| 集合のサイズ | $\lvert A \rvert$ | 集合の要素の数 |
| 部分集合 | $A \subset B$ | 集合 $A$ は集合 $B$ のうちいくつかの要素を選んで取り出したものである($A$ は $B$ の部分集合) |
| 共通部分 | $A \cap B$ | 集合 $A$ と $B$ の両方に含まれる要素の集まり |
| 和集合 | $A \cup B$ | 集合 $A$ と $B$ の少なくとも一方に含まれる要素の集まり |
| 条件 | $A = \{x \ \lvert$ 条件 $T\}$ | 条件 $T$ を満たす要素の集まりが集合 $A$ である4 |
図で分かりやすく説明すると、次のようになります。

また、表記を使った例は次の通りになります。(Qiita だと表記が崩れるので、図を貼り付けておきます)
2-12. その他の競プロで頻出の表記たち
最後に、本節では 2-11. 節までに挙がらなかった、競技プログラミングで頻出の表記について紹介します。是非覚えておきましょう。
端数切り捨て(floor)
$\lfloor x \rfloor$ は、負でない実数 $x$ の小数点以下を切り捨てた値です。
例えば、$\lfloor 8.4 \rfloor = 8$、$\lfloor 9 \rfloor = 9$、$\lfloor 6.99 \rfloor = 6$ です。
などに登場しています!
端数切り上げ(ceil)
$\lceil x \rceil$ は、負でない実数 $x$ の小数点以下を切り上げた値です。
例えば、$\lceil 8.4 \rceil = 9$、$\lceil 15 \rceil = 15$、$\lceil 12.01 \rceil = 13$ です。
ガウス記号
$[x]$ は、$x$ を超えない最大の整数のことを指します。
例えば、$[6.99] = 6$、$[77] = 77$、$[7.4] = 7$ です。前述の floor と同じです。
掛け算のシグマ記号
$\prod_{i=L}^{R} A_i$ は、$A_L \times A_{L+1} \times A_{L+2} \times ... \times A_R$ のことを指します。
シグマ記号は総和でしたが、この記号は総積といった感じです。
例えば、$\prod_{i=1}^{4} i = 24$、$\prod_{i=1}^{n} i = n!$ が成り立ちます。
閉区間・半開区間
$[l, r]$ は、$l$ 以上 $r$ 以下の区間のことを指し、閉区間といいます。
$[l, r)$ は、$l$ 以上 $r$ 未満の区間のことを指し、半開区間といいます。
特に整数から成る場合、区間 $[l, r]$ は $l, l+1, l+2, ..., r$ のことを、区間 $[l, r)$ は $l, l+1, ..., r-1$ のことを指します。
二項係数
$n$ 個のものの中から $r$ 個選ぶ方法の数は、基本的に以下のように表記されます。例えば ${}_8C_3 = 56$ です。
$$
{}_nC_r = \frac{n!}{r!(n-r)!}
$$
しかしながら、別の書き方で表すこともあります。
\begin{pmatrix}
n \\
r
\end{pmatrix}
= \frac{n!}{r!(n-r)!}
AtCoder Regular Contest 110 D - Binomial Coefficient is Fun などに登場しています!
行列
「行列とは何か」だけ簡単に説明すると、$H \times W$ のマス目に書かれている整数の情報を表したみたいな感じです。以下のように表記されます。($H = 3, W = 5$ の場合の例です)
\begin{pmatrix}
3 & 1 & 4 & 1 & 5 \\
9 & 2 & 6 & 5 & 3 \\
5 & 8 & 9 & 7 & 9
\end{pmatrix}
行列の $i$ 行目 $j$ 列目の成分を $(i, j)$ 成分ということがあります。例えば上の例の場合、$(2, 4)$ 成分は $5$ です。「行列」というキーワードは、
などに登場しています!
2-13. 2 章のまとめ
2 章では、以下の数学的知識を扱ってきました。
| 節 | 紹介した内容 | 何に使われるか |
|---|---|---|
| 2-2. | 関数 | プログラムの実装 |
| 2-3. | 対数(log) | 計算量の理解 |
| 2-4. | 2 進数 | コンピューターの仕組み・ビット演算の理解 |
| 2-5. | 論理演算 | ビット演算(AND・OR・XOR)の実装 |
| 2-6. | 最大公約数・互いに素 | 競プロの問題文で頻出 |
| 2-7./2-8. | 数列・部分列・部分文字列 | 競プロの問題文で頻出 |
| 2-9. | シグマ記号 | 競プロの問題文で頻出 |
| 2-10./2-11. | 集合 |
std::set、競プロの問題文や解説など |
| 2-12. | ガウス記号など | 競プロの問題文や解説など |
ここまでの内容は、主にプログラムの実装を行うにあたって、あるいは競技プログラミングの問題文を理解するために、重要なものを中心にまとめました。3 章では少しだけレベルを上げ、様々なアルゴリズムと密接に結びついている数学的知識について紹介します。
3. アルゴリズムと密接に関わる数学<初級編>
2 章ではプログラミングコンテストに参加するにあたって重要な最低限の知識を 12 個のポイントに絞ってまとめました。しかし、競プロに出題されるようなアルゴリズムだけを考えても、数学と結びつく場面はまだまだたくさんあります。例えば、
などの点が挙げられます。そこで 3・4 章では主に 19 個のポイントに分けて、アルゴリズムを数学的側面から捉えてみたいと思います。皆さんにアルゴリズムと数学が如何に密接に関わっているかを体感してもらうことが最大の目標です。
3-1. 全探索に学ぶ、指数関数(レベル: 1)
1)
まず、次の問題を考えてみましょう。部分和問題といわれる有名問題です。
$N$ 個の整数 $A_1, A_2, ..., A_N$ からいくつかを選ぶことで、選んだ整数の合計が $S$ となるような方法は存在するか、判定してください。($1 \leq A_i, S \leq 10^{18}$)
最初に思いつくアルゴリズムは**「考えられる選び方を全通り探索すること」**だと思います5。この方法を使った場合、何通りのケースを探索せねばならないでしょうか。
例えば N=3 では、「1 個目の整数が選ばれているか」「2 個目の整数が選ばれているか」「3 個目の整数が選ばれているか」がそれぞれ Yes/No の 2 通りずつなので、2×2×2=8通りを探索していることが分かります。
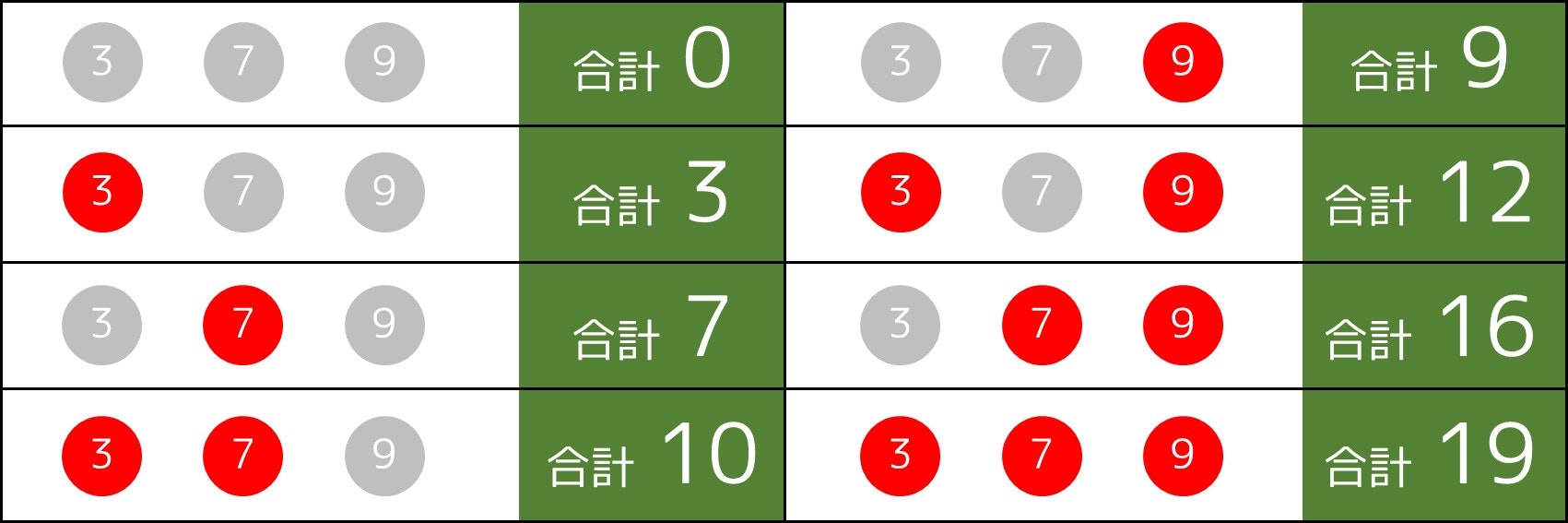
一般に、$a$ を $b$ 個掛け算した値を $a^b$ と表すため、$N=3$ のときに探索すべき通り数は $2^3$ 通りであることが分かります。また、関数については 2-2. 節で解説済みですが、特に $f(x) = a^x$ の形で表される関数は指数関数といいます。
そこで、$N$ に対する探索パターン数を関数 $f(N)$ で表すとき、$f(N) = 2^N$ と指数関数になっているのです。これはどの程度恐ろしいものなのでしょうか。
- N=10 のとき f(10) = 1 024 通り
- N=20 のとき f(20) = 1 048 576 通り
- N=30 のとき f(30) = 1 073 741 824 通り
- N=100 のとき f(100) = 1 267 650 600 228 229 401 496 703 205 376 通り
を探索していることになります。家庭用コンピューターが 1 秒に 10 億回程度しか計算できないことを考慮すると、N=100 の時点で実行時間が宇宙の年齢を超えてしまうのです。また、下のプログラムを実行してみると、N=20 では 1 秒以内で終わる一方、N=40 では 1 時間経過しても答えが出ないのが分かると思います。
入力の大きさ $N$ に対して指数関数的な計算回数($2^N$ 回・$3^N$ 回など)を要するプログラム設計のことを指数時間アルゴリズムというのですが、指数関数とは何かを知っておくと、このような指数時間アルゴリズムの恐ろしさが実感できると思います!!!
# include <iostream>
using namespace std;
long long N, S;
long long A[200];
int main() {
// 入力
cin >> N >> S;
for (int i = 0; i < N; i++) cin >> A[i];
// 全通り探索
for (long long i = 0; i < (1LL << N); i++) {
long long sum = 0;
for (int j = 0; j < N; j++) {
if ((i & (1LL << j)) != 0LL) sum += A[j];
}
if (sum == S) { cout << "Yes" << endl; return 0; }
}
cout << "No" << endl;
return 0;
}
3-2. 二分探索に学ぶ、対数関数(レベル: 2)
2)
2-3. 節では対数について紹介しましたが、実際にアルゴリズムと対数(log)はどのような点で密接に関わっているのでしょうか。以下の問題を考えてみましょう。
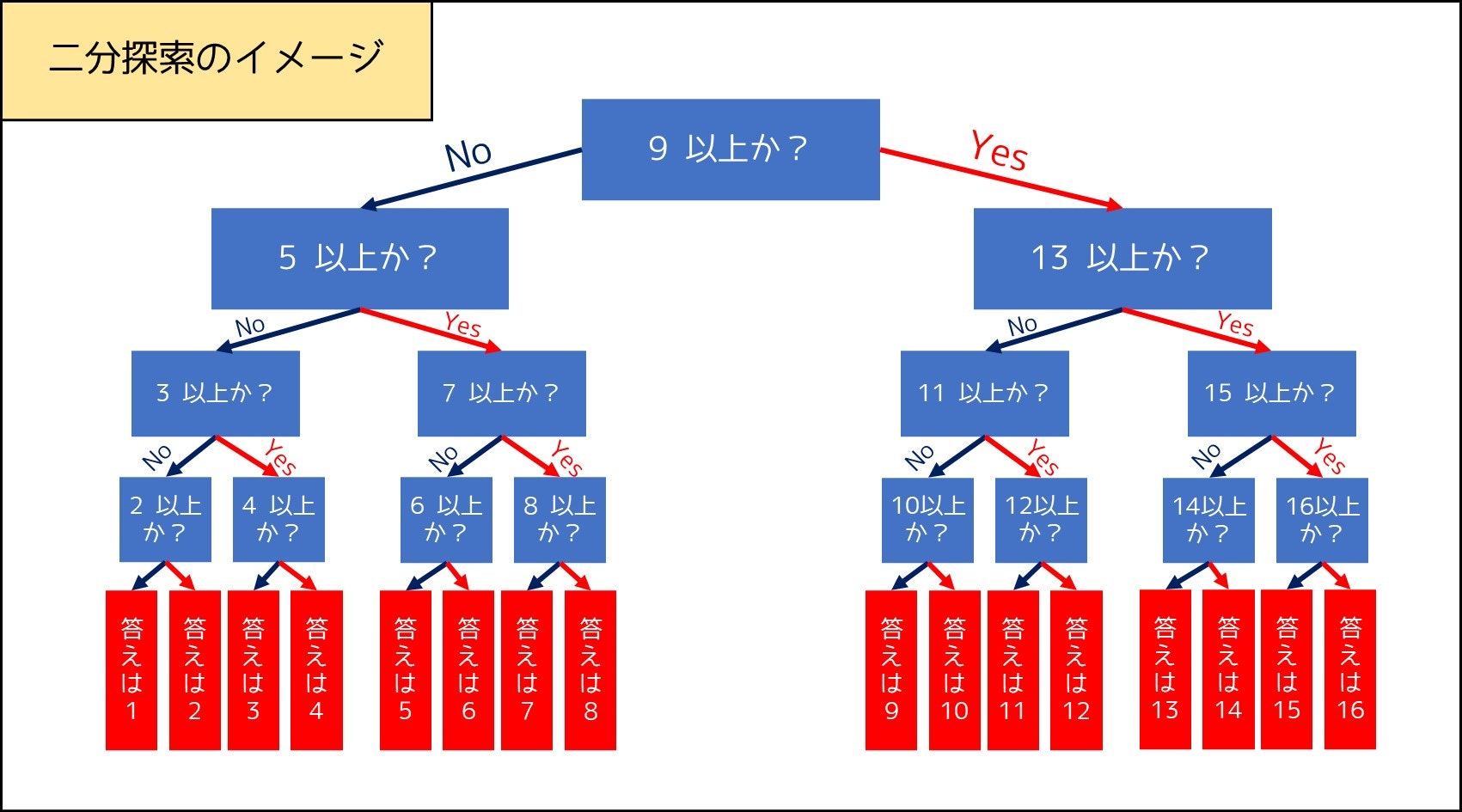
Qiita 君はとある整数を頭に思い浮かべています。この整数は $1$ 以上 $16$ 以下であることが最初から分かっています。あなたは「整数は〇〇以上ですか?」という形式の質問を行うことができます。$4$ 回以内の質問で彼が思い浮かべている整数を当ててください。
この問題は、二分探索という手法により解くことができます。有名なアルゴリズムです。
次に、「$1$ 以上 $16$ 以下」ではなく「$1$ 以上 $N$ 以下」の場合について考えてみましょう。なお、このように、ある実例での特性を一般的な概念や主張として定式化することを一般化といいます。($N=16$ では $4$ 回の質問で答えが分かるという主張を、一般の $N$ の場合に拡張したということです)
二分探索アルゴリズムでは、$1$ 回の質問につき探索範囲が $\frac{1}{2}$ 倍になるので、最初の質問で $N$ 通りだった探索範囲が高々 $\lceil \frac{N}{2} \rceil$ 通りに絞れます。例えば、$N=16$ のとき、元々区間 $[1,16]$ が探索範囲だったのが、
- 「$9$ 以上か?」という質問に対して Yes の場合は $[9, 16]$ に
- 「$9$ 以上か?」という質問に対して No の場合は $[1, 8]$ に
絞りこむことができます。($\lceil x \rceil$ や $[1, 16]$ のような表記については 2-11. 節参照)
$2$ 回目以降の質問も同様に考えることができます。
- $2$ 回目の質問では探索範囲が $\lceil \frac{N}{4} \rceil$ 通りになる
- $3$ 回目の質問では探索範囲が $\lceil \frac{N}{8} \rceil$ 通りになる
- $4$ 回目の質問では探索範囲が $\lceil \frac{N}{16} \rceil$ 通りになる
- $\vdots$
- $a$ 回目の質問では探索範囲が $\lceil \frac{N}{2^a} \rceil$ 通りになる
そこで、探索範囲が $1$ 通りになったら答えが分かるので、$N \leq 2^a$ となるような回数だけ質問しなければなりません。2-3. 節で述べた対数の定義より $a \geq \log_{2} N$ と式変形することができるため、$\lceil \log_{2} N \rceil$ 回の質問で Qiita 君が思い浮かべている整数を当てることができるのです。
そこで、$N$ に対する質問回数を関数 $g(N)$ として表すと、$g(x) = \lceil \log_{2} x \rceil$ となります。このような関数を対数関数というのですが、$N$ が大きくても $g(N)$ が小さいままであることが分かるでしょう。例えば、g(1000) = 10、g(1000000000) = 30 です。
二分探索の他にも、マージソートやセグメントツリーなどの計算回数に $\log$ が出てきます。このように、対数関数とは何かを知っておくと、このような対数時間アルゴリズムの便利さが実感できると思います!!!
3-3. 計算量オーダーに学ぶ、極限(レベル: 3)
3)
アルゴリズムや競プロに触れていると、以下のような文章を見ることも多いと思います。
単純に全通り探索すると計算量 $O(N^2)$ となり実行時間超過(TLE)となってしまいますが、アルゴリズムの工夫により、計算量は $O(N \log N)$ まで削減できます。
さて、$O(N^2)$ とは一体何なのでしょうか。簡単に書くと「おおよそ $N^2$ 回の計算回数が必要」ということを意味します。しかし、厳密に議論するためには**極限(lim)**を知っておく必要があります。
極限の定義
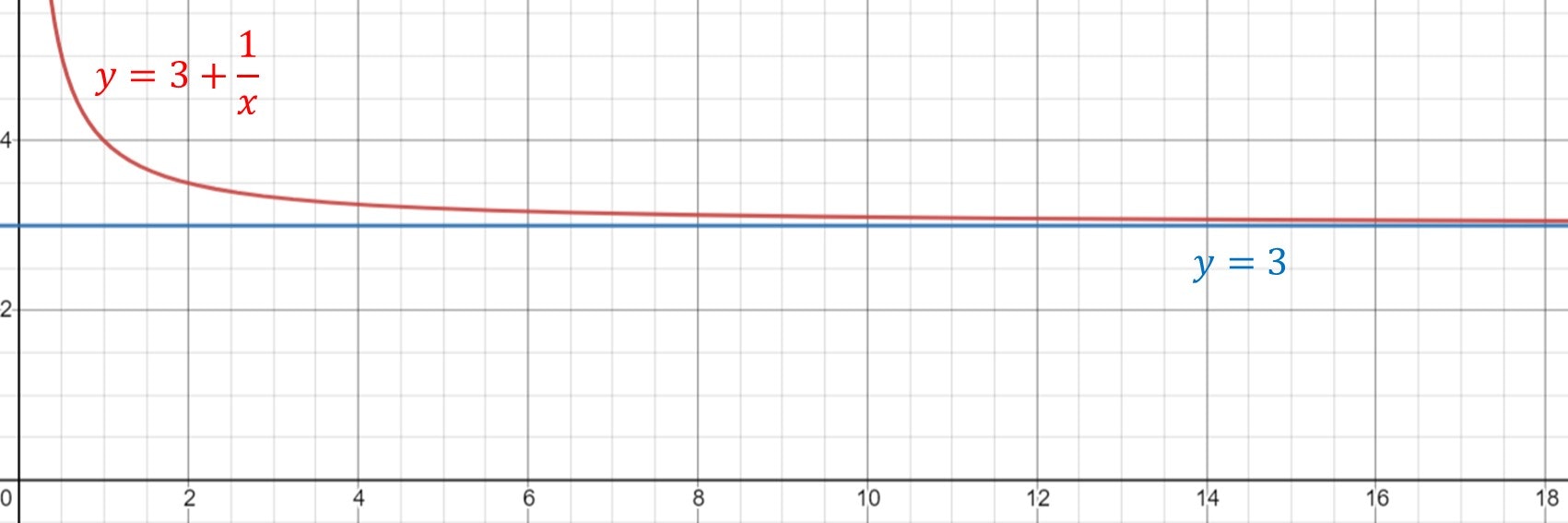
関数 $f(N)$ に対して、極限は以下のように定義されます。これは、$N$ の値が $a$ に限りなく近づいたとき、$f(N)$ の値がどうなるかということを意味します。6
\lim_{N \to a} f(N) = [極限の値]
例えば、$f(N) = 3 + \frac{1}{N}$ の場合、$f(10) = 3.1$、$f(100) = 3.01$、$f(1000) = 3.001$、といった感じで $3$ に近づくので、次式が成り立ちます。
\lim_{N \to \infty} \left( 3 + \frac{1}{N} \right) = 3
計算量オーダーの定義
では、計算量オーダーはどのように定義されるのでしょうか。簡潔に説明すると、$N$ に対するプログラムの計算回数を関数 $f(N)$ とするとき、以下が成り立てば「計算量は $O(g(N))$ である」といえます。
どのような $N$ に対しても、$a \leq \frac{f(N)}{g(N)} \leq b$ を満たすような定数 $a, b$ が存在する。
特に、$E = \lim_{N \to \infty} \frac{f(N)}{g(N)}$ が存在するとき、この値が無限大になってはならない。
特に、$a>0$ で成り立つとき「計算量が $\Theta (g(N))$ である」といえます。
例は次表の通りになります。
| 計算回数 | 説明 |
|---|---|
| $2N+3$ 回、$O$ 記法 | $O(N)$ であり、$O(N^2)$ である |
| $2N+3$ 回、$\Theta$ 記法 | $\Theta (N)$ であるが、$\Theta (N^2)$ ではない |
また、$E$ の値の大小によって、プログラムの定数倍の評価がなされることがあります7。例えば、計算に $0.1N^2 + 100N$ 回かかるプログラムの場合、
| 計算量の見積もり | 定数倍の見積もり |
|---|---|
| $\Theta(N^2)$ | $E = 0.1$(比較的定数倍が軽い) |
となります。このように、極限(lim)を知っておくと、計算量オーダーに関するより厳密な理解、そして定数倍に関する議論ができます!!!
なお、計算量オーダーに関するさらに詳しい話は、
をご覧ください。
3-4. 再帰関数に学ぶ、数列の漸化式(レベル: 3)
3)
まず、以下の問題を考えてみましょう。
- $a_1 = 1, a_2 = 1$
- $a_{N} = a_{N-1} + a_{N-2}$ $(N \geq 3)$
とします。そのとき、$T$ が与えられるので $a_T$ を求めてください。
つまり、フィボナッチ数の第 $T$ 項を求めてください。
この問題は、再帰関数を使うことで簡単に解くことができます。fibonacci(T) を呼び出したときの返り値が、求める答えです。
int fibonacci(int T) {
if (T == 1) return 1;
if (T == 2) return 1;
return fibonacci(T - 1) + fibonacci(T - 2);
}
ですが、このプログラムはどの程度実行に時間がかかるのでしょうか。$T=45$ の時点で、相当な時間がかかっていることが分かります。
| T | 30 | 35 | 40 | 45 |
|---|---|---|---|---|
| 実行時間 | 0.008 秒 | 0.036 秒 | 0.209 秒 | 2.147 秒 |
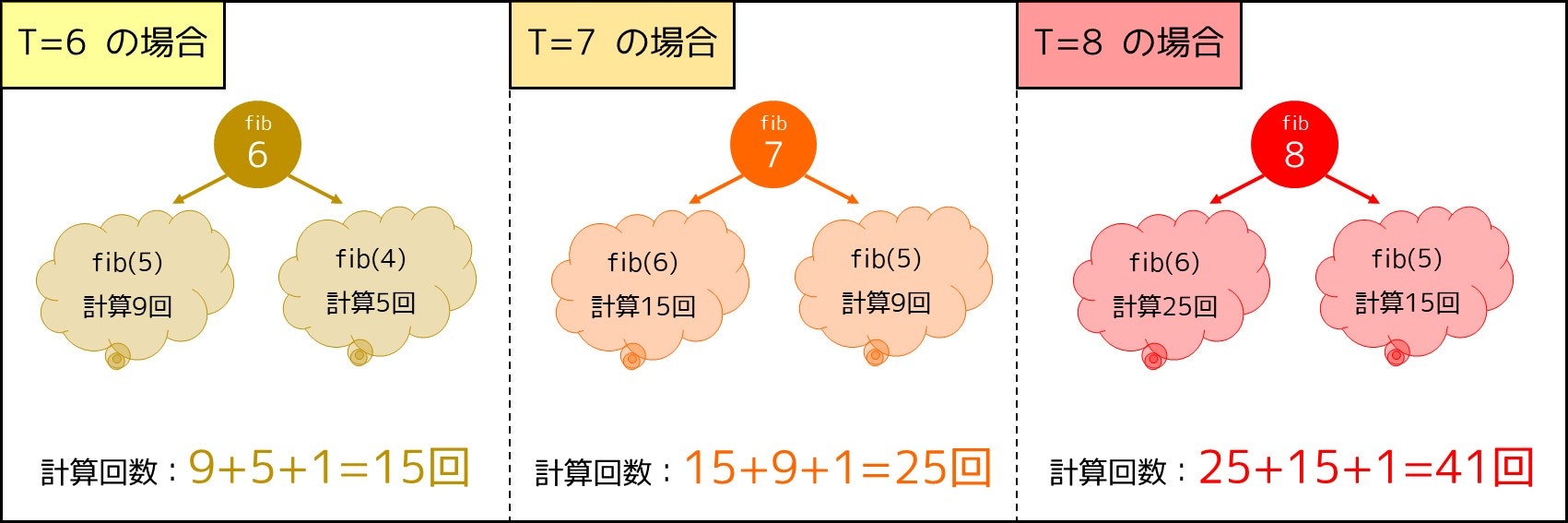
理由は簡単で、次図のように枝分かれ上に再帰関数を呼び出しているからです。では、実際の計算量はいくつなのでしょうか。そもそも多項式時間アルゴリズム8なのでしょうか。(fib(6) を呼び出した場合の例です)

計算量を見積もってみよう
基本的に、計算回数は再帰の呼び出し回数に比例すると考えることができます。そこで、fib(T) を呼び出したときの計算回数を $b_T$ 回とするとき、その値は以下の式で表されます。
- $T = 1$ のとき:
fib(1)からの再帰呼び出しはないので、$b_T = 1$ - $T = 2$ のとき:
fib(2)からの再帰呼び出しはないので、$b_T = 1$ - $T \geq 3$ のとき:
fib(T)からfib(T-1)とfib(T-2)を呼び出しているため、$b_T = b_{T-1} + b_{T-2} + 1$ である。内訳は次の通りである:-
fib(T-1)の計算に $b_{T-1}$ 回 -
fib(T-2)の計算に $b_{T-2}$ 回 -
fib(T-1)+fib(T-2)の計算に $1$ 回
-
イメージとしては次図のような感じです。
そこで、少し難しいですが、漸化式は以下のように解くことができます。(漸化式とは、数列の各項をその前の頃から順にただ 1 通りに定める規則を表す式のことです。)
\begin{align}
& \ b_{T} = b_{T-1} + b_{T-2} + 1 \\
\Leftrightarrow & \ b_{T} + \frac{\sqrt{5}-1}{2}b_{T-1} + \frac{\sqrt{5}+1}{2} = \frac{\sqrt{5}+1}{2} \left( b_{T-1} + \frac{\sqrt{5}-1}{2}b_{T-2} + \frac{\sqrt{5}+1}{2} \right) \\
\Leftrightarrow & \ b_{T} - \frac{\sqrt{5}+1}{2}b_{T-1} - \frac{\sqrt{5}-1}{2} = - \frac{\sqrt{5}-1}{2} \left( b_{T-1} - \frac{\sqrt{5}+1}{2}b_{T-2} - \frac{\sqrt{5}-1}{2} \right) \\
\end{align}
そこで、
c_T = b_{T} + \frac{\sqrt{5}-1}{2}b_{T-1} + \frac{\sqrt{5}+1}{2} \\
d_T = b_{T} - \frac{\sqrt{5}+1}{2}b_{T-1} - \frac{\sqrt{5}-1}{2}
とおくと、
c_2 = 1 + \sqrt{5}, \ c_T = c_2 \left(\frac{\sqrt{5}+1}{2}\right)^{T-2} = 2 \left(\frac{\sqrt{5} + 1}{2}\right)^{T-1} \\
d_2 = 1 - \sqrt{5}, \ d_T = d_2 \left(\frac{1-\sqrt{5}}{2}\right)^{T-2} = 2 \left(\frac{1 - \sqrt{5}}{2}\right)^{T-1} \\
b_T = \frac{3 + \sqrt{5}}{5 + \sqrt{5}} c_T + \frac{2}{5 + \sqrt{5}} d_T - 1
となるため、求める $b_T$ の値は、
b_T = \frac{6+2\sqrt{5}}{5+\sqrt{5}} \times \left(\frac{\sqrt{5}+1}{2}\right)^{T-1} + \frac{4}{5+\sqrt{5}} \times \left(\frac{1-\sqrt{5}}{2}\right)^{T-1} - 1
となります。したがって、計算量は $\Theta \left(\frac{\sqrt{5}+1}{2}^{T}\right)$ であることが分かりました。このように、数列の漸化式を知っておくと、再帰関数などを用いたプログラムの計算量を見積もることができます!!!
3-5. 距離計算に学ぶ、三平方の定理(レベル: 1)
1)
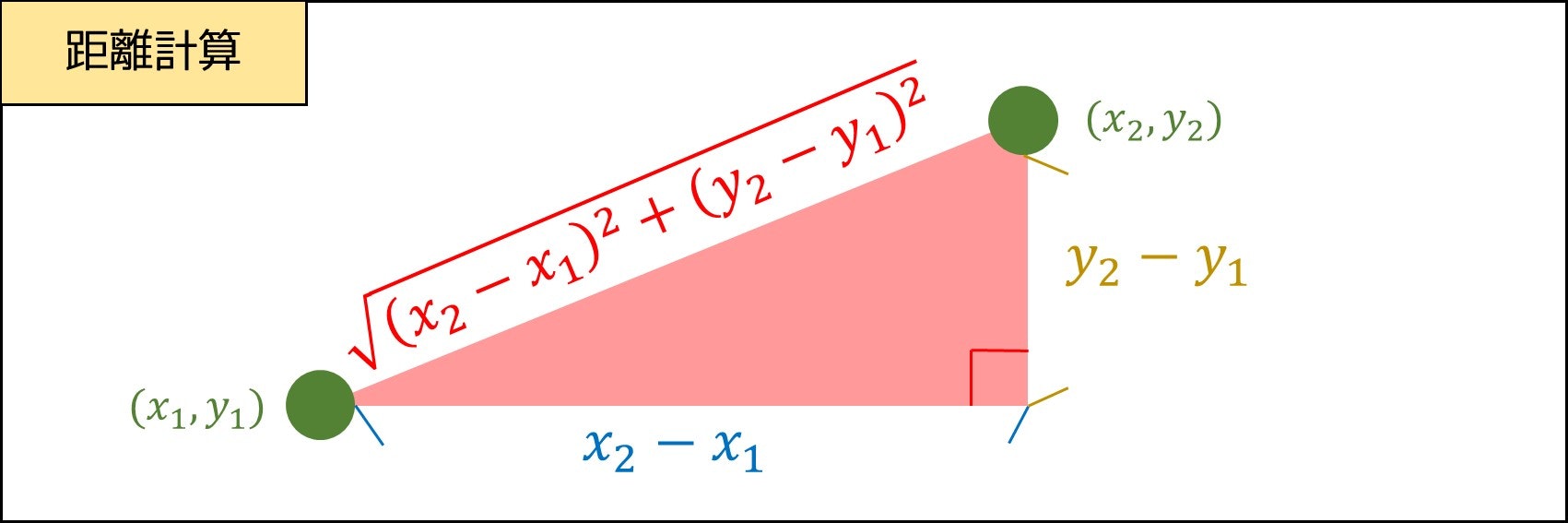
ここから 3-7. 節までは計算幾何に関する話題になります。競技プログラミングやアルゴリズムの問題で、$2$ 点間の距離を計算する場面は多いですが、どうやって計算するのでしょうか。
これは三平方の定理を使うことで、座標 $(x_1, y_1)$ と座標 $(x_2, y_2)$ の間の距離が $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$ であることが分かります。例えば $(0, 3)$ と $(4, 6)$ の間の距離は $\sqrt{(4-0)^2+(6-3)^2}=5$ です。
C++ では、std::sqrt 関数を使うことで以下のように実装することができます。
他にも、距離の計算を使うことで解ける問題は以下のようにたくさんあります。
double getDistance(double x1, double y1, double x2, double y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
3-6. 幾何計算に学ぶ、三角関数(レベル: 2)
2)
まず、以下の問題を考えてみましょう。
時針と分針の長さがそれぞれ $A$ センチメートル、$B$ センチメートルであるアナログ時計を考えます。$H$ 時 $M$ 分になったとき、時針の先端と分針の先端(固定されていない方の端点)は何センチメートル離れているでしょうか。(出典:AtCoder Beginner Contest 168 C - Colon)
これは、時計の中心座標を $(0, 0)$ としたときの時針・分針の端点の座標が分かれば、3-5. 節に書かれている通り、2 点間距離を計算するだけで解けます。では座標はどうやって求めるのでしょうか。**ここで出現するのが三角関数です。**まず、定義から確認していきましょう。
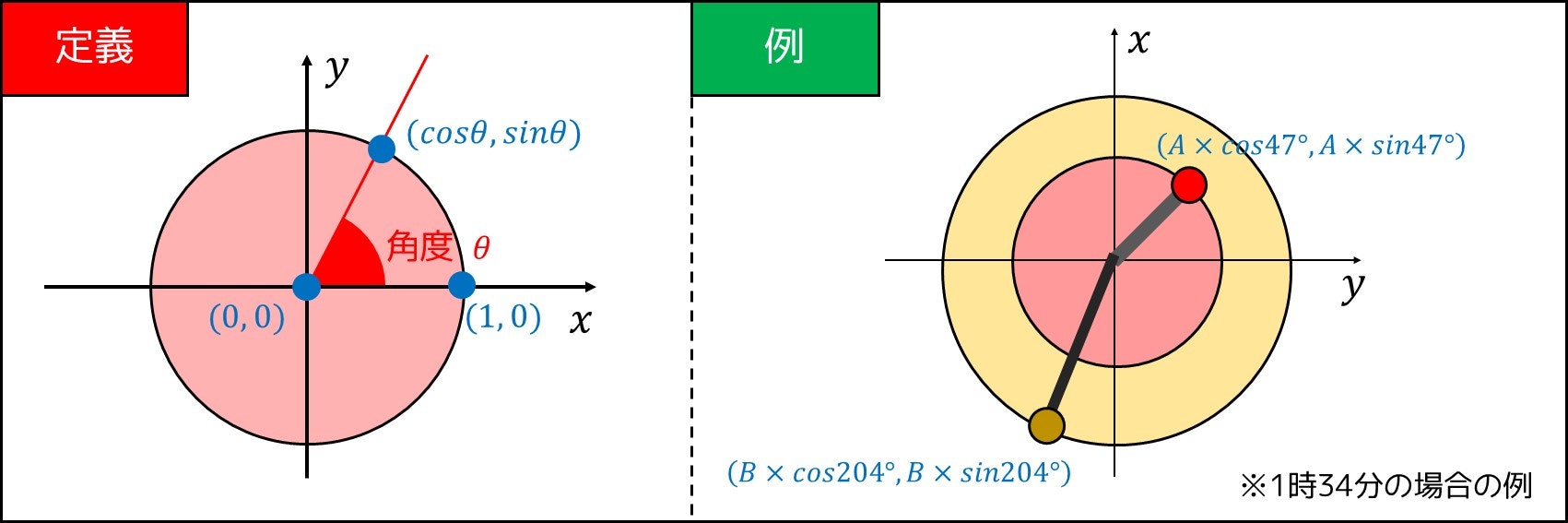
三角関数の定義
- $x$ 軸の正の部分を原点中心に $\theta$ 度反時計回りに回転させたような半直線
- 単位円(原点、つまり座標 $(0, 0)$ を中心とする半径 $1$ の円)
の交点の座標が $(\cos \theta, \sin \theta)$ であると定義されます。詳しくは下図をご覧ください。では、どうやって三角関数を使って問題を解くのでしょうか。
分針の座標を求める
まず、分針の向きは $12$ 時の方向から $6M$ 度時計回りに回転させた方向です。
分針の端点は原点を中心とする半径 $B$ の円上にあるので、前述した定義より、求める座標は $(B \times \cos6M°, B \times \sin6M°)$ であると分かります。例えば $1$ 時 $34$ 分の場合、求める座標は $(B \times \cos204°, B \times \sin204°)$ です。
時針の座標を求める
まず、時針の向きは $12$ 時の方向から $30H + 0.5M$ 度時計回りに回転させた方向です。
時針の端点は原点を中心とする半径 $A$ の円上にあるので、前述した定義より、求める座標は $(A \times \cos(30H + 0.5M)°, A \times \sin(30H + 0.5M)°)$ であると分かります。例えば $1$ 時 $34$ 分の場合、求める座標は $(A \times \cos47°, A \times \sin47°)$ です。
三角関数はどのような問題で使えるか?
このように、「点 $A$ が距離 $L$ 離れていて角度 $\theta$ 度の方向にあるとき、点 $A$ の座標を求めよ」といった形式など、円や角度などが出てくる問題の多くでは三角関数が使えます。例えば以下の問題が挙げられます。
なお、C++ では std::sin(x) や std::cos(x) を使うことで実装できますが、x が度数法ではなくラジアンであるため、sin(x) の値は $\sin x°$ とは異なることにご注意ください。
例えば、$\sin 45°$ の値は sin(45.0 * 3.1415926535 / 180.0) で計算できます。なお、三角関数だけでなく、3-7. 節で登場する逆三角関数も頻出です。三角関数関連のより発展的な内容については、
を是非ご覧ください。
int main() {
int A, B, H, M;
cin >> A >> B >> H >> M;
double x1 = 1.0 * A * cos((30.0 * H + 0.5 * M) * 3.14159265358979 / 180.0);
double y1 = 1.0 * A * sin((30.0 * H + 0.5 * M) * 3.14159265358979 / 180.0);
double x2 = 1.0 * B * cos((6.0 * M) * 3.14159265358979 / 180.0);
double y2 = 1.0 * B * sin((6.0 * M) * 3.14159265358979 / 180.0);
double Answer = getDistance(x1, y1, x2, y2);
printf("%.12lf\n", Answer);
return 0;
}
3-7. 角度計算に学ぶ、ベクトルの内積と逆三角関数(レベル: 3)
3)
まず、以下の問題を考えてみましょう。
点 $A, B, C$ の座標 $(xa, ya), (xb, yb), (xc, yc)$ が与えられる。
角 $BAC$ の大きさを求めてください。
しかし、単純に三角関数を使うだけだと難しいので、ベクトルという概念を導入しましょう。
ベクトルとは何か
ベクトルとは、向きと大きさを持つ量のことを指します。点 $A$ から点 $B$ に進む矢印のような感じで表現され、表記等は次図のようになっています。

ベクトルの内積
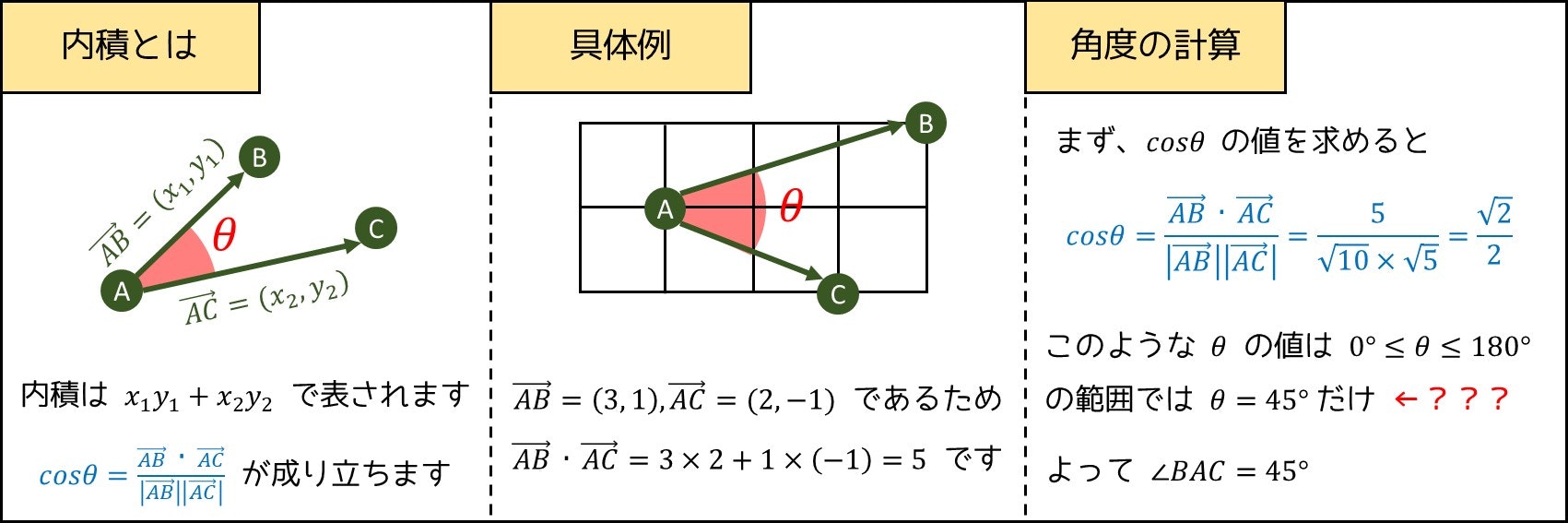
では、この問題を解くにあたって重要な概念を一つ紹介しましょう。内積です。点 $A, B, C$ が二次元平面上にある場合、次のように定義されます。
$\vec{AB}=(x_1, y_1), \vec{AC}=(x_2, y_2)$ であるとき、内積 $\vec{AB} \cdot \vec{AC} = x_1x_2 + y_1y_2$ である。
そこで、角 $BAC$ の大きさを $\theta$ とするとき、以下の重要な性質が成り立つのです。
$$
\cos \theta = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}||\vec{AC}|}
$$
次図の例のように計算すれば、内積を使うことで簡単に $\cos \theta$ の値が求められます。では、どうやって $\cos \theta$ から角 $\theta$ の大きさを出すことができるのでしょうか。
逆三角関数の導入
そこで、三角関数の逆を求めることができる逆三角関数を紹介します。C++ で代表的なものは次表の通りです。ただし、pi = 3.1415926535... です。
| 逆三角関数の種類 | 説明 |
t の範囲 |
|---|---|---|
acos(x) |
cos(t) = x となるとき、acos(x) = t
|
0 <= t <= pi |
asin(x) |
sin(t) = x となるとき、asin(x) = t
|
-pi/2 <= t <= pi/2 |
atan(x) |
tan(t) = x となるとき、atan(x) = t
|
-pi/2 <= t <= pi/2 |
atan2(y, x) |
座標 (x, y) の偏角
|
-pi <= t <= pi |
したがって、$T = \cos \theta$ とするとき、acos(T) の値が求まれば角 $BAC$ の角度が計算できます。なお、逆三角関数の返り値はラジアンであることにご注意ください。例えば acos(0) = 90 ではなく acos(0) = 1.570796... です。度数法での値は acos(x) * 180 / 3.1415926... であり、プログラム実装例は次の通りになります。9
double getAngle(double xa, double ya, double xb, double yb, double xc, double yc) {
double VectorAB = sqrt((xb - xa) * (xb - xa) + (yb - ya) * (yb - ya));
double VectorAC = sqrt((xc - xa) * (xc - xa) + (yc - ya) * (yc - ya));
double Naiseki = (xb - xa) * (xc - xa) + (yb - ya) * (yc - ya);
double cosTheta = Naiseki / (VectorAB * VectorAC);
return acos(cosTheta) * 180.0 / 3.14159265358979;
}
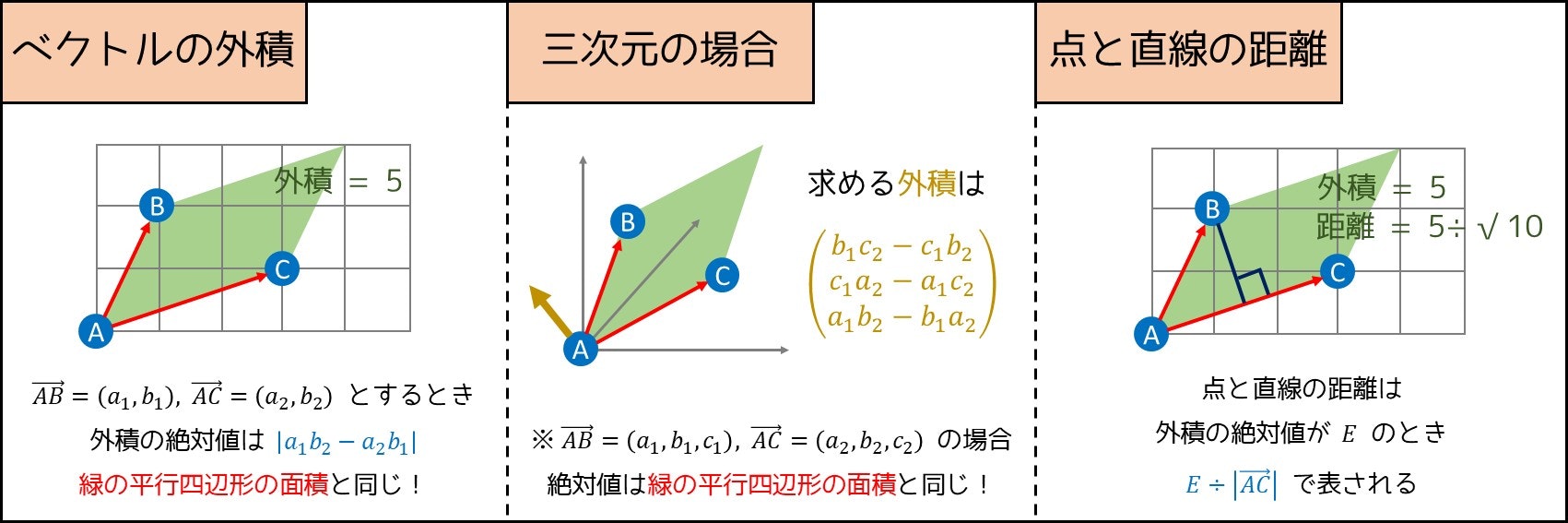
補足説明として、幾何計算ではベクトルの外積の絶対値(大きさ)が使われることもあります。特に二次元座標では、$\vec{AB} = (a_1, b_1), \vec{AC} = (a_2, b_2)$ とするとき、外積の絶対値は $|a_1b_2 - a_2b_1|$ となります。$AB, AC$ を $2$ 辺とする平行四辺形の面積と等しいことから、以下の図の通り点と直線の距離などを求めるのに使われます。
このような知識を使うことで、例えば
- AtCoder Beginner Contest 144 D - Water Bottle
- AtCoder Beginner Contest 033 D - 三角形の分類
- JOI 2021 春合宿 Aerobatics
- AIZU ONLINE JUDGE CGL-2-B Intersection
- AIZU ONLINE JUDGE CGL-2-D Distance
- AIZU ONLINE JUDGE CGL-4-A Convex Hull
などを解くことができます!!!(上から 3 つは外積を使わなくても解けます)
3-8. 素数判定法に学ぶ、素数の性質と背理法(レベル: 1)
1)
ここからは整数論に関する話題になります。
皆さん「素数」という言葉を聞いたことがあるでしょうか? 2-1. 節に書かれている通り、
- $2, 3, 5, 7, 11, 13, ...$ のような、$1$ と $N$ 以外で割り切れない 2 以上の整数 $N$
のことを指します。では、どうやって「整数 $N$ が素数か」判定すればよいのでしょうか。
最も単純なアルゴリズム
多くの読者にとっては、次のアルゴリズムが最初に思いつくのではないかと思います。
- $N$ は $2$ で割り切れますか? → 割り切れたら合成数(
false) - $N$ は $3$ で割り切れますか? → 割り切れたら合成数(
false) - :
- $N$ は $N-1$ で割り切れますか? → 割り切れたら合成数(
false) - いずれでも割り切れなければ素数(
true)
C++ でのプログラム実装例は次の通りです。
bool prime_check(int N) {
for (int i = 2; i <= N - 1; i++) {
if (N % i == 0) return false;
}
return true;
}
しかし、このプログラムは計算量 $O(N)$ と非効率的であり、例えば prime_check(1000000007) を呼び出すと、答えを出すまでに 3.049 秒かかってしまいます10。果たして良いアルゴリズムはないのでしょうか。そこで、ある数学的性質を使います。
約数に関する重要な性質とその証明
実は、$2, 3, ..., \lfloor \sqrt{N} \rfloor$ で割り切れなければ素数であることが背理法によって証明できるのです。なお、背理法とは次のような手法のことを指します。
あることがら P を示すのに、「P が成り立たないと仮定し,そうすると矛盾が起こることを導く」ことにより、P が成り立つことを証明する手法(引用元)
では証明してみましょう。次の通りです。
- $N$ が $2, 3, ..., \lfloor \sqrt{N} \rfloor$ のいずれにも割り切れないが、ある整数 $a$ $(\sqrt{N} < a < N)$ で割り切れる場合を考えます。
- そのとき、$a \times b = N$ となる整数 $b$ $(2 \leq b \leq N - 1)$ が必ず存在します。
- また、1. の仮定より $a, b > \sqrt{N}$ となります。
- そうすると、$a \times b > \sqrt{N} \times \sqrt{N} = N$ となり、青色部分に矛盾します。
- したがって、$N$ が素数ではない場合、必ず $2$ 以上 $\lfloor \sqrt{N} \rfloor$ 以下の整数で割り切れます。
より高速なアルゴリズム
したがって、$\lfloor \sqrt{N} \rfloor$ まで調べ上げた上で $1$ つも割り切れなければ、素数である(true)と判定すればよいです。計算量は $O(\sqrt{N})$ と高速で、例えば prime_check(1000000007) を呼び出した場合でも僅か 0.000113 秒で答えを出すことができました。
bool prime_check(int N) {
int B = min(N - 1, (int)(sqrt(1.0 * N)));
for (int i = 2; i <= B; i++) {
if (N % i == 0) return false;
}
return true;
}
3-9. 最大公約数に学ぶ、ユークリッドの互除法(レベル: 2)
2)
次は 2-6. 節で紹介した最大公約数(GCD)について考えていきたいと思います。
整数 $a, b$ の最大公約数を求めてください
という問題はどれほど高速に解けるのでしょうか。
「ユークリッドの互除法」の紹介
以下のようなアルゴリズムを考えてみましょう。ユークリッドの互除法といわれる有名なものであり、高校数学で習った方も多いと思います。
- $a$ と $b$ のうち片方が $0$ になるまで次の操作を行う。
- $a < b$ の場合、$b$ の値を $b \bmod a$ に書き換える。
- $a \geq b$ の場合、$a$ の値を $a \bmod b$ に書き換える。
- 操作が終わった時点で $a, b$ のうち $0$ ではない方が、求める最大公約数である。
なお、これで最大公約数が求められることの証明はこちらをご覧ください。
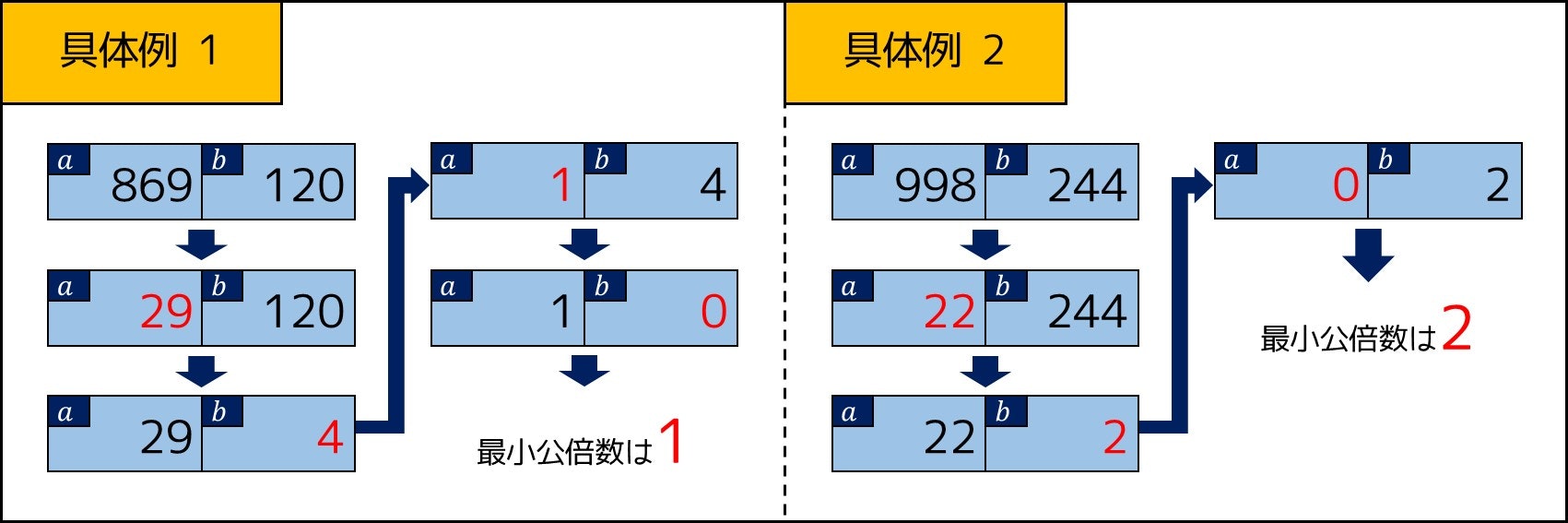
「ユークリッドの互除法」はどれくらい速いのか?
結論から述べると、このアルゴリズムは $O(\log (a+b))$ で動作します。これは、以下のように $2$ 段階で証明することができます。
段階 1: 1 回の操作で a+b の値が 3 分の 2 以下になっていることを証明する
- $a \geq b$ の場合のみを考えます。なお、$a < b$ の場合は $a$ と $b$ を逆にして考えれば良いので、$a \geq b$ を仮定しても一般性を失いません。
- まず、$a \div b \geq 2$ の場合:
- 操作後の $a$ の値を $a'$ とするとき、明らかに $a' < b$ です。
- 操作前の $a+b$ の値は $a \geq 2b$ より $3b$ 以上です。
- 操作後の $a+b$ の値は $a' < b$ より $2b$ 未満であり、3 分の 2 以下になっています。
- 次に、$1 \leq a \div b < 2$ の場合:
- 操作後の $a$ の値を $a'$ とするとき、$a' = a - b$ です。
- そこで、操作前の $a+b$ の値を $S_1$、操作後の $a+b$ の値を $S_2$ とします。
- そのとき、$\frac{S_2}{S_1} = \frac{a' + b}{a + b} = \frac{a}{a + b} = 1 - \frac{1}{a \div b + 1} \leq \frac{2}{3}$ となっています。
- したがって、どのような場合でも操作後の $a+b$ の値は 3 分の 2 以下になります。
段階 2: 計算量が O(log (a+b)) であることを証明する
$1$ 回の操作で $a+b$ の値が $\frac{2}{3}$ 倍以下になるため、$N$ 回の操作を行うと $a+b$ の値は $\left( \frac{2}{3} \right)^N$ 倍以下になります。よって、$N$ 回後の操作における $a+b$ の値を $E_N$ とするとき、
$$
E_N \leq \left(a + b \right) \times \left( \frac{2}{3} \right)^N
$$
が成り立ちます。そこで、$E_N = 0$ の場合は、既に最大公約数(GCD)の値が求まっており操作が終了しているので、$N$ 回目の時点で操作がまだ続いているためには $E_N \geq 1$ を満たす必要があります。よって、2-3. 節で紹介した対数関数への変換を使うと、
$$
1 \leq \left(a + b \right) \times \left( \frac{2}{3} \right)^N \ (\Leftrightarrow) \ N \leq \log_{\frac{3}{2}} (a+b)
$$
が成立し、最大でも $\log_{1.5} (a+b) = O(\log (a + b))$ 回しか操作が行われないことが証明できました。このように、ユークリッドの互除法を知っておくと、$a, b = 10^{18}$ 程度の大きい値でも十分高速に最大公約数をで求めることができるのです。
なお、$a$ と $b$ の最小公倍数(LCM)も、次の式を使えば簡単に実装できます。
$$
lcm(a, b) = a \times b \div gcd(a, b)
$$
// 再帰関数を使わない実装
long long gcd(long long a, long long b) {
while (a >= 1LL && b >= 1LL) {
if (a >= b) a = a % b;
else b = b % a;
}
if (a >= 1LL) return a;
return b;
}
3-10. 逆元に学ぶ、フェルマーの小定理(レベル: 3)
3)
まず、次の問題を読んでください。
$2 \div 3$ の値を $\bmod 1000000007$ で求めてください。
読者の多くはこの問題を読んで、「?????」と感じると思います。分数の mod を計算するのは正直意味が分からないと思うのですが、実は mod を割り算にも拡張することができるのです。
mod の拡張「逆元」
では、$2 \div 3 \pmod{11}$ の値は一体何なのでしょうか。普通の整数の世界では $2 \div 3$ は割り切れないのですが、**mod 11 という特殊な条件下では、なんと、割り切れてしまうのです。**先に答えを書いてしまうと、
- $2 \div 3 = 8 \pmod{11}$
となるのです。なぜなら、$3 \times 8 = 24 \equiv 2 \pmod{11}$ が成り立つからです。一応その他の例もいくつか載せておきます。
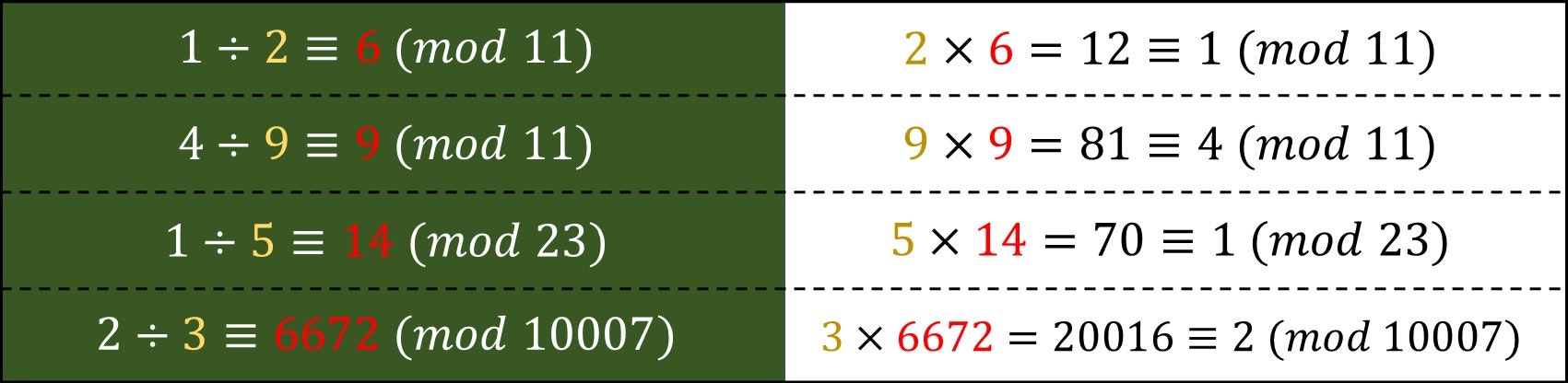
一般に $p$ が素数の場合、$bx \equiv a \pmod{p}$ が成り立つとき $a \div b = x \pmod{p}$ となるのです11。でも、なぜこのように定義されるのか。直感的には「$b$ で割って $b$ で掛けると元の整数に戻るから」、つまり
$$
\left( a \div b \right) \times b = x \times b \equiv a \pmod{p}
$$
となって便利だから、と考えると理解しやすいかと思います。
「フェルマーの小定理」の登場
では $bx \equiv a \pmod{p}$ となるような整数 $x$ の値はどのように求めるのでしょうか。そこで
$$
b^{p-1} \equiv 1 \pmod{p}
$$
というフェルマーの小定理を使うことを考えます。左辺を式変形すると、
$$
b \times b^{p-2} \equiv 1 \pmod{p} \ ( \Leftrightarrow ) \ b \times \left(a \times b^{p-2} \right) \equiv a \pmod{p}
$$
となるため、$\left( a \times b^{p-2} \right) \equiv x \pmod{p}$ となる値 $x$ が答えになるのです。これは以下のような「繰り返し二乗法」と呼ばれる手法で、$O(\log p)$ で答えを出すことができます。
- $b^2 = b^1 \times b^1 \pmod{p}$ と計算できる
- $b^4 = b^2 \times b^2 \pmod{p}$ と計算できる
- $b^8 = b^4 \times b^4 \pmod{p}$ と計算できる
-
- ~ 3. と同じ要領で、$b^{16}, b^{32}, b^{64}, ...$ を計算できる
- $x$ を $2$ 進数表記することで $b^x$ を $b^1, b^2, b^4, b^8, ...$ の積で表すことができるので、それを掛け算する(例:$b^{27} = b^{16} \times b^{8} \times b^{2} \times b^{1}$)
例えば、次のような実装が考えられます。
long long modpow(long long a, long long b, long long mod) {
long long p = 1, q = a;
for (int i = 0; i < 31; i++) {
if ((b & (1 << i)) != 0) { p *= q; p %= mod; }
q *= q; q %= mod;
}
return p;
}
long long Div(long long a, long long b, long long mod) {
return (a * modpow(b, mod - 2, mod)) % mod;
}
3-11. 二項係数への応用(レベル: 3)
3)
前編の最後に、3-10. 節で紹介した逆元がどのような場面で役に立つのかを紹介して終わりたいと思います。一つの例として、二項係数が挙げられます。
$$
{}_nC_r = \frac{n!}{r!(n-r)!}
$$
では、$p$ が素数のとき、${}_nC_r \pmod{p}$ の値はどのようにして求められるのでしょうか。
- $n!$ の値と $r! (n-r)!$ の値は単純に掛け算をすることによって $O(n)$ で計算できる
- $\frac{a}{b}$ の値は $O(\log p)$ で高速に計算できるので、$a = n! \ mod \ p$、$b = (r!(n-r)!) \ mod \ p$ と代入することによって、$O(\log p)$ で計算できる
といったアルゴリズムが使えるのです。
二項係数は応用範囲が広く、例えば競プロでは以下の問題に応用することができます。
あなたは以下の行動のうちいずれかを $H+W$ 回繰り返すことで、座標 $(0, 0)$ から $(H, W)$ まで行きたい。移動方法は何通りあるか。$1000000007$ で割った余りを求めよ。
- $x$ 座標の正の方向に $1$ 進む
- $y$ 座標の正の方向に $1$ 進む
この問題は「$H+W$ 回の移動のうち $H$ 回が $x$ 座標正方向に進むものである」という発想を使うと、求める通り数が ${}_{H+W}C_H$ であることが分かり、二項係数を求めるアルゴリズムによって簡単に解くことができるのです。
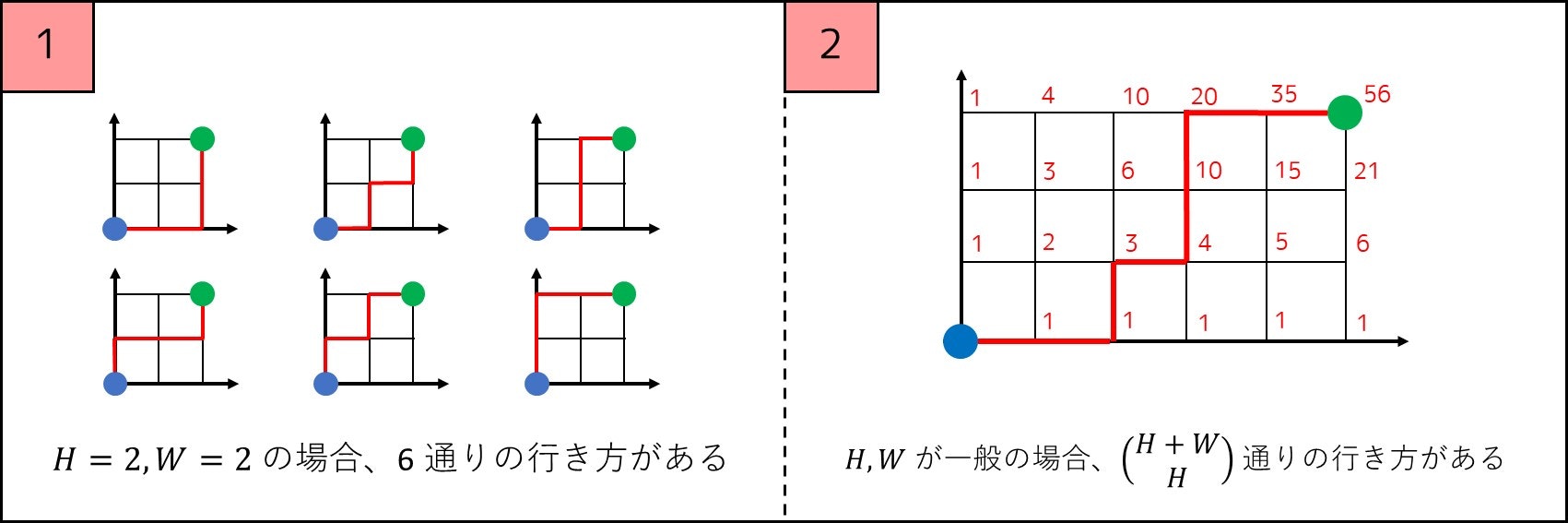
その他にも、例えば以下の問題で二項係数を使うことができます。
- AtCoder Beginner Contest 034 C - 経路
- AtCoder Beginner Contest 185 C - Duodecim Ferra
- AtCoder Beginner Contest 167 E - Colorful Blocks
- AtCoder Regular Contest 116 C - Multiple Sequences
3-XX. 本記事を終えた次は?
本記事の内容をマスターできれば、水色コーダーになるまでに問われる数学的知識はほとんどカバーできたと言って良いと思います。しかし、
- さらにアルゴリズムを勉強したい!
- アルゴリズムと数学の関連性をもっと感じたい!
- もう少し数学的知識を付けて、数学力で戦えるようにしたい!
という考えを持つのは良いことです。**また、後編では数学的知識だけでなく、多様なレベル層に合わせた「数学的な考察パターン」についても扱います。**興味があれば是非、中編・後編もお読みください。
中編
後編
-1. つづく
次は、中編に続きます。
-
文献によっては稀に $0$ 以上の場合もありますが、競技プログラミングの場合ではまず $1$ 以上だと思って良いと思います。 ↩
-
一般に競プロやアルゴリズムの文脈では $\log$ の底が $2$ の場合が多く、仮に「計算回数 $\log N$ 回」のように底が書かれていない表記をしていても、暗黙的に底が $2$ となっていることも多いです。なお、$\log$ の底は $2$ でなくても $O(\log N)$ といったオーダー表記をすることがあります。なぜなら $a>1$ のとき、$\log_{2} N$ と $\log_{a} N$ は高々定数倍しか変わらないからです。例えば底の変換公式より、$\log_{2} N = 3.32... \times \log_{10} N$ が成り立ちます。(ここでは $\log_{2} 10 = 3.32...$ です) ↩
-
5 or 9 or 17 = (5 or 9) or 17 = 5 or (9 or 17) = 29が成り立ちます。同様に、(3 xor 5) xor 6 = (3 xor 6) xor 5 = (5 xor 3) xor 6 = (5 xor 6) xor 3 = (6 xor 3) xor 5 = (6 xor 5) xor 3が成り立ちます。 ↩ -
厳密に述べると、全体集合 $U$ という概念が存在して、$A$ の要素は「$U$ の中に入っておりかつ条件 $T$ を満たす」という感じです。例えば $U$ が整数全体として、$A = \{x | 1 \leq x \leq 4\}$ の場合、$A = \{1, 2, 3, 4\}$ となります。 ↩
-
もう少し厳密な定義もありますが、厳密に極限を定義するためには ε-δ 論法などの難しい証明方法を導入する必要があるため、ここでは割愛させていただきます。 ↩
-
プログラムを書く時は計算量オーダーも重要ですが、定数倍も重要であり、例えば「同じ $O(N \log N)$ でも、定数倍が軽いプログラムは通るが、定数倍が重いプログラムは落ちる」といった場合もよくあります。日本情報オリンピックの過去問などで多く見られます。 ↩
-
$O(N^2)$ や $O(N^{869120})$ など、計算量オーダーが $N$ の多項式($N^a$ のような形)で表されるアルゴリズム設計のことを多項式時間アルゴリズムといいます。また、$O(2^N)$ など、計算量オーダーが指数関数で表されるようなアルゴリズム設計のことを指数時間アルゴリズムといいます。(厳密には、$O(N^2)$ のような多項式時間も指数時間アルゴリズム(クラス EXP)に含まれていますが、競プロの文脈ではほとんどの場合、$N$ の指数関数となる場合を指します) ↩
-
ベクトルの内積を使う方法だけでなく、
atan2を使ってゴリ押す方針もあります。 ↩ -
AtCoder コードテストで実験した時の値です。 ↩