金融の分野では予測というとなにか魔術的なイメージがあります。しかし、物理や化学、工学の分野では高い精度の予測を可能としています。代表的なたとえが、ニュートンの法則による惑星の動きです。また、日常的には、耐震強度とか、製品寿命のような形で、ものの性質の予測が行われ、積極的に活用されています。同じような形で経済、金融の分野でも予測が用いられています。たとえば価格が需要と供給の間が平衡状態にあるとして
$$ p_t=\mu_1+p_{t-1}+\alpha d_{t-1} \
d_t=\mu_2-\beta p_{t-1}-\gamma d_{t-1} \ $$
というような形式でモデル化されます。$p$と$d$は、商品の価格と需要を表します。データの数が少ないとたくさんの$\alpha$、$\beta$,$\gamma$,$\mu$の組み合わせが可能ですが、安定した価格の関係を与えてくれるものは限られています。そのような係数が得られるとそのような状態には固有値が存在するといいます。そして、それを確率過程の関係で表すと、
$$
x_t=\mu + A x_{t-1} + \eta_t
$$
と書ことができます。(Python3ではじめるシステムトレード: 予測につい(訳) 参照)しかし、このようなモデルで予測をしても便利とは言えません。なぜなら将来の価格が一期前の価格の関数ということは、一期前の価格が動けば、将来の価格も影響を受け、不安定になります。システムトレードの世界で予測を活用する場合にはもう少し、単純な形になってほしいものです。最も理想的な形は
$$
x_t=\alpha + \beta t + \eta_t
$$
という形式です。これを時間トレンドといいます。将来の価格が時間の線形の関数になっています。また、これを確定的なモデルとも呼びます。もっと簡単に表現すると、トレンドに合わせて直線を引いているのです。
予測の理論には古い歴史があり、それは、WienerとKolmogorovが定常過程という概念と最小二乗法という方法を導入して発展させました。また、最近ではカルマンフィルター、状態空間方程式という方法や考え方が注目を浴びています。長い間、経済や金融の分野では、予測の対象となるデータの差分を求めたり、変化率を求めたりして、安定した状態、定常性を得る方法が主流となってきました。一方で、フィルタリングという方法を用いてデータの特徴を分解していく方法に着目しているグループもいました。カルマンフィルター、または状態空間方程式などはこちらに分類されます。こちらはデータを遂次的に与え、パラメータを最適化、更新していくという方法です。
冒頭で、物理、工学の分野の予測は確定的といいましたし、経済・金融の分野の予測は魔術のようだといいました。この点を明確にする必要があります。第一点として経済・金融分野のデータの予測は惑星の軌道のようにはいきません。まず、安定とか均衡とか、定常という状態があるかどうかが問題で、経済・金融の分野では状態はいつでも別の状態にジャンプしやすと考えたほうがいいのです。2番目の問題として、経済、金融の要素はちゃんと測定できるのかという点です。これも物理、工学の分野のようにはいきません。しかし、どのような分野でも同じような問題を抱えています。ですからアポロ計画では衛星の位置を得るためにカルマンフィルターを必要としたのです。ということで、同じ方法を金融の価格データに応用してみましょう。
ローカルレベルモデル
$$
y_t=x_t+\varepsilon_t
$$
を観測方程式といいます。$y_t$は観測値で、$x_t$が本来あるべき値です。$\varepsilon_t$を観測ノイズといいます。観測の際に発生するノイズです。
$$
x_{t+1}=x_{t}+\eta_t
$$
を状態方程式とか、システム方程式と呼びます。こちらは本来あるべき姿を現しています。この場合には価格はランダムウォークにしたがうとしています。価格の差は乱数$\eta_t$で表現されています。観測方程式の$\epsilon_t$がなければ、普通のランダムウォークのモデルです。この単純な構成のモデルをローカルレベルモデルといいます。それはランダムウォークにしたがう価格のローカル(局所的な)なレベルを表現しているからです。確率方程式では将来の予測は分布として与えられます。しかし、ローカルレベルモデルではレベルで表現してくれます。ローカルレベルモデルの基本はランダムウォークですから、ランダムにトレンドが発生します。やってみましょう。
%matplotlib inline
import matplotlib.pyplot as plt #描画ライブラリ
import numpy as np
P=[1]
for i in range(1,1440):
w=np.random.normal(0,1)
P.append(P[i-1]+0.0002*w)
plt.plot(P)
P2=[1]
for i in range(1,1440):
w=np.random.normal(0,1)
P2.append(P2[i-1]+0.0002*w)
plt.plot(P2)
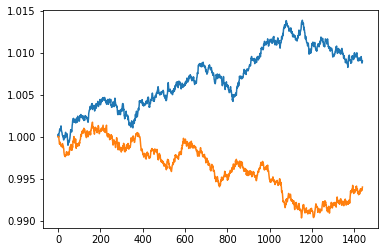
2本の価格時系列を発生させています。なんどかプログラムを実行してみると価格のトレンドが出てきます。片一方が上昇トレンド、もう片一方が下落トレンドを作るなどというものも出てきます。この回数は確率的に計算できます。
カルマンフィルターを使うと、この価格に予測値が追随してくれます。
ローカル線形トレンドモデル
つぎに私たちが欲しいのは確率的なトレンドではなく確定的なトレンド、すなわち確実なトレンドです。時間トレンドがまさしくそれです。そこでローカルレベルモデルに時間トレンド加えることにしましょう。これがローカル線形トレンドモデルです。それは
$$
y_t=x_t+\mu_t
$$
を観測方程式として、状態方程式を
$$
x_{t+1}=x_{t}+z_{t-1}+\eta_t \
z_{t}=z_{t-1}+\lambda_t
$$
と書きます。2番目の状態方程式がトレンドを表しています。このトレンドはランダムウォークの形をしているので、確率的に変化していきます。ですので、時間トレンドではありません。しかし、$\lambda$をゼロと置くことで時間トレンドにすることができます。このローカル線形トレンドモデルは、ローカルレベルモデルの上に成り立っているので、レベルの中にトレンドが含まれています。トレンドがランダムウォークのように変化しているなんて、実際の経験にマッチしませんか?
自己回帰モデル
2番目に登場した式ですが、
$$
x_t=\mu + A x_{t-1} + \eta_t
$$
は自己回帰モデルと呼びます。$A=1$にするとランダムウォークになります。さらに重要なことはこのモデルのベースは畳み込みを用いているということです。
実装
初期化
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.stats.api as sms
import matplotlib.pyplot as plt
import pandas_datareader.data as web
from statsmodels.compat import lzip
QQQのダウンロード
tsd = web.DataReader("QQQ",'yahoo','2019/5/6').dropna()
tsd=tsd.loc[:,['Open','High','Low','Adj Close']]
tsd.columns=['open','high','low','close']
print(tsd.tail(1))
状態空間方程式
ローカルレベルモデル
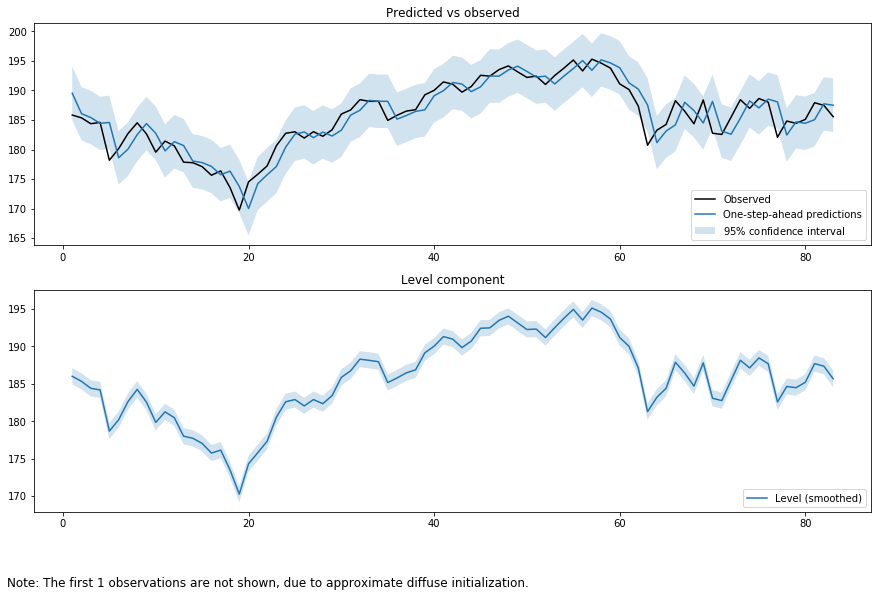
output_mod = sm.tsa.UnobservedComponents(tsd['close'], "llevel")
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));
Unobserved Components Results
==============================================================================
Dep. Variable: close No. Observations: 84
Model: local level Log Likelihood -186.971
Date: Tue, 03 Sep 2019 AIC 377.941
Time: 23:09:29 BIC 382.779
Sample: 0 HQIC 379.885
- 84
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 0.3453 0.581 0.594 0.552 -0.793 1.484
sigma2.level 4.6638 1.197 3.897 0.000 2.318 7.010
===================================================================================
Ljung-Box (Q): 39.05 Jarque-Bera (JB): 7.97
Prob(Q): 0.51 Prob(JB): 0.02
Heteroskedasticity (H): 1.33 Skew: -0.69
Prob(H) (two-sided): 0.46 Kurtosis: 3.62
===================================================================================
ここでローカルレベルモデルについて少し詳しく見てみましょう。そうすることでカルマンフィルターの仕組みが良くわかります。
$y_t=x_t+\varepsilon_t$
$x_{t+1}=x_{t}+\eta_t$
この際に$\varepsilon_t \sim N(0,\sigma_{\varepsilon}^2)$と$\eta_t \sim N(0,\sigma_{\eta}^2)$はハイパーパラメータで事前に与えます。実際には得られた観測値から推定します。一般には最尤推定が用いられます。
まずステップバイステップで見ていきます。
$E_0(\hat{x_0})=\hat{x_{0|0}}=y_0$
$var_0(\hat{x_0})=\hat{\Sigma_{0|0}}$
と書きます。
つぎに、つぎの期の期待値を今のあるデータを用いて算出します。$t=1$のときの期待値を$t=0$の情報から計算します。
$\hat{x_{1|0}}=\hat{x_{0|0}}=y_0$
$\hat{\Sigma_{1|0}}=\hat{\Sigma_{0|0}}+\sigma_{\eta}^2$
$\hat{Y_{1|0}}=\hat{x_{1|0}}$
と予測します。すると
$\hat{Y_{1|0}}=y_0$
となります。カルマンゲイン$K_1$は
$K_1=\frac{\hat{\Sigma_{1|0}}}{\hat{\Sigma_{1|0}}+\sigma_{\varepsilon}^2}$
です。
極端な場合を想定します。まず、$K_1=1$となってほしいので、
- $\sigma_{\varepsilon}^2=0$のとき、
$K_1=\frac{\hat{\Sigma_{1|0}}}{\hat{\Sigma_{1|0}}+\sigma_{\varepsilon}^2}=1$
フィルタリング------------
$\hat{x_{1|1}}=\hat{x_{1|0}}+K_1(y_1-\hat{Y_{1|0}})=y_0+y_1-y_0=y_1$
$\hat{\Sigma_{1|1}}=(1-K_1)\hat{\Sigma_{1|0}}=0$
1期差予測------------
$\hat{x_{2|1}}=\hat{x_{1|1}}=y_1$
$\hat{\Sigma_{2|1}}=\hat{\Sigma_{1|1}}+\sigma_{\eta}^2=\sigma_{\eta}^2$
$\hat{Y_{2|1}}=\hat{x_{2|1}}=y_1$
$K_2=\frac{\hat{\Sigma_{2|1}}}{\hat{\Sigma_{2|1}}+\sigma_{\varepsilon}^2}=1$
この場合には$y$の予測値は観測値の実現値の系列と同じになります。観測誤差がないということは状態モデルが観測値をモデル化できていることを示しています。
ローカル線形トレンドモデル
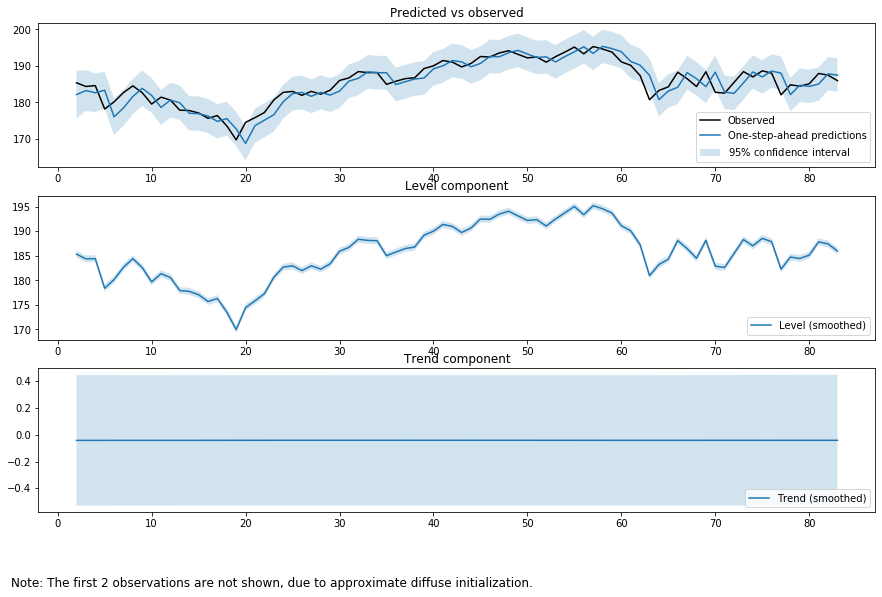
output_mod = sm.tsa.UnobservedComponents(tsd['close'], "lltrend")
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));
Unobserved Components Results
==============================================================================
Dep. Variable: close No. Observations: 84
Model: local linear trend Log Likelihood -187.377
Date: Wed, 04 Sep 2019 AIC 380.755
Time: 01:30:20 BIC 387.975
Sample: 0 HQIC 383.654
- 84
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 0.1367 0.557 0.246 0.806 -0.955 1.228
sigma2.level 5.1170 1.433 3.570 0.000 2.308 7.926
sigma2.trend 1.822e-05 0.023 0.001 0.999 -0.045 0.045
===================================================================================
Ljung-Box (Q): 35.68 Jarque-Bera (JB): 5.96
Prob(Q): 0.67 Prob(JB): 0.05
Heteroskedasticity (H): 1.34 Skew: -0.57
Prob(H) (two-sided): 0.46 Kurtosis: 3.65
===================================================================================
最も重要な点
ここまで読んでこられた方で、カルマンフィルターを用いる際に最も重要な要素は何だと思いますか?状態方程式の形でしょうか?季節性を含むとか、ビジネスサイクルを含むということでしょうか?たぶん違うと思います。もっとも重要な要素は、ハイパーパラメータを決めるデータの数です。この部分をカルマンフィルターはやってくれません。これは自分で行うしかありません。もし疑問に思う方は、標本データの数を増やしたり減らしたりして、ローカルレベルモデルやローカル線形トレンドモデルを動かしてみてください。パイパーパラメータの推定値は動くはずです。
2019/11/13 16:43に加筆しました。
実際にやってみましょう。データの取得期間を長くします。
tsd = web.DataReader("QQQ",'yahoo','2000/1/1').dropna()
tsd=tsd.loc[:,['Open','High','Low','Adj Close']]
tsd.columns=['open','high','low','close']
print(tsd.tail(1))
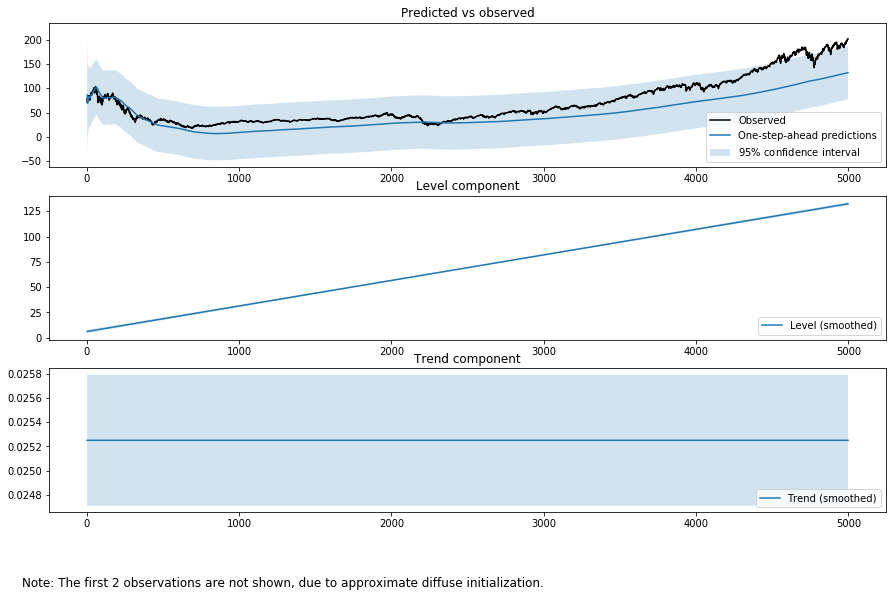
つぎにローカルレベルモデルを使います。
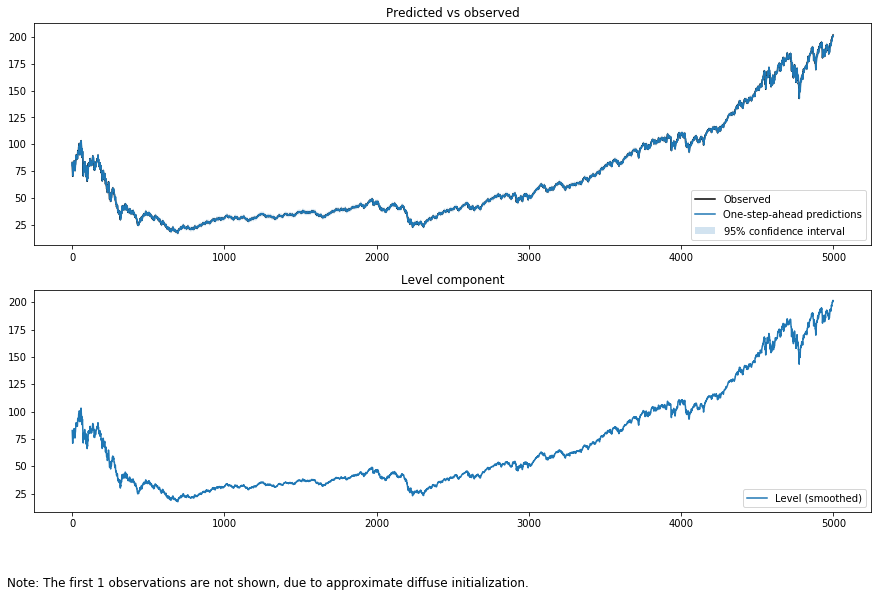
output_mod = sm.tsa.UnobservedComponents(tsd['close'], "llevel")
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));
結果は異なります。観測ノイズとシステムノイズを見てください。一般的には期間が長くなると観測ノイズが小さくなます。
Unobserved Components Results
==============================================================================
Dep. Variable: close No. Observations: 4999
Model: local level Log Likelihood -7713.769
Date: Wed, 13 Nov 2019 AIC 15431.538
Time: 16:14:39 BIC 15444.572
Sample: 0 HQIC 15436.106
- 4999
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 0.0703 0.009 8.185 0.000 0.053 0.087
sigma2.level 1.1478 0.021 55.255 0.000 1.107 1.189
===================================================================================
Ljung-Box (Q): 192.11 Jarque-Bera (JB): 17770.28
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 1.26 Skew: -0.32
Prob(H) (two-sided): 0.00 Kurtosis: 12.22
===================================================================================
同じようにローカル線形トレンドモデルを使ってみましょう。
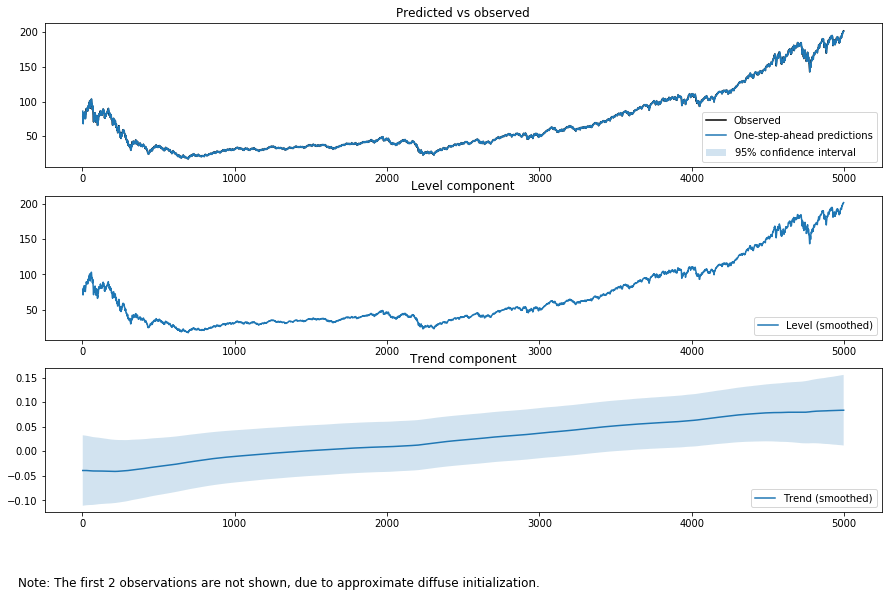
output_mod = sm.tsa.UnobservedComponents(tsd['close'], "lltrend")
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));
結果は再び異なります。システムノイズ、観測ノイズ、トレンドノイズを見てください。ランダムウォークの割合が増えています。観測ノイズとトレンドノイズが小さくなり、システムノイズの割合が増えています。しかし、同時にジャックベラの結果も見てください。帰無仮説の正規分布を否定しています。誤差は正規分からファットテイルをもつようになったということです。
ここでフィルターの意味を復習しておきましょう。「フィルターとは時系列データから誤差を落として信号だけを取り出すための装置や手続きをいう。」(入門ベイズ統計 松原望 p.118)
Unobserved Components Results
==============================================================================
Dep. Variable: close No. Observations: 4999
Model: local linear trend Log Likelihood -7713.151
Date: Wed, 13 Nov 2019 AIC 15432.301
Time: 16:15:14 BIC 15451.851
Sample: 0 HQIC 15439.153
- 4999
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 0.0742 0.009 8.512 0.000 0.057 0.091
sigma2.level 1.1366 0.021 54.808 0.000 1.096 1.177
sigma2.trend 1.588e-06 2.61e-06 0.609 0.543 -3.52e-06 6.7e-06
===================================================================================
Ljung-Box (Q): 193.25 Jarque-Bera (JB): 20444.86
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 1.26 Skew: -0.32
Prob(H) (two-sided): 0.00 Kurtosis: 12.89
===================================================================================
statsmodelsは観測ノイズ、2つのシステムノイズを推定してくれるので、これらがパイパーパラメータだろうかと迷うことがあるかもしれません。しかし、データの期間を選択した時点で、分析者がパイパーパラメータを決めていたのです。
Blackさんのいう金融理論では効率的価格の意味が間違っているを検証
ブラック-ショールズモデルの生みの親は独特の考え方をもっていたことで有名です。主流派の経済学者からは無視されていました。その1つが効率的価格の意味です。ブラックさんは市場で取引されている価格は間違っていて、その半分でも2倍でもおかしくないといっていました。それを見てみましょう。モデルをfixed slopeを選びます。確定的トレンドがシステムモデルになります。そしてこう解釈するのです。確定的トレンドが正しい効率的な価格で、観測される価格はノイズである。やってみましょう。
output_mod = sm.tsa.UnobservedComponents(tsd['close'], "fixed slope")
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));
システムモデルをランダムウォークにすると見えなかった観測ノイズがバカでかくなりました。
Unobserved Components Results
==============================================================================
Dep. Variable: close No. Observations: 4999
Model: fixed slope Log Likelihood -23776.090
Date: Wed, 13 Nov 2019 AIC 47554.179
Time: 16:17:31 BIC 47560.696
Sample: 0 HQIC 47556.463
- 4999
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 789.9347 16.160 48.883 0.000 758.262 821.607
===================================================================================
Ljung-Box (Q): 184632.99 Jarque-Bera (JB): 545.32
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 8.33 Skew: 0.76
Prob(H) (two-sided): 0.00 Kurtosis: 3.56
===================================================================================
ブラックさんの主張そのものですね。観測ノイズがバカでかい。
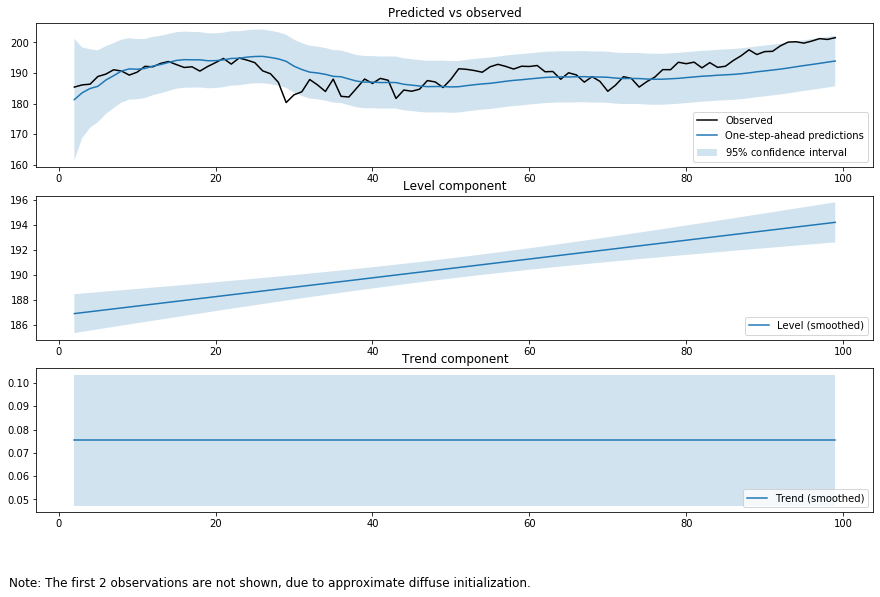
つぎに、データの期間を短くしてみましょう。
output_mod = sm.tsa.UnobservedComponents(tsd['close'].iloc[-100:], "fixed slope")
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));
結果は100日分のデータを使っているのでもっともらしいです。
Unobserved Components Results
==============================================================================
Dep. Variable: close No. Observations: 100
Model: fixed slope Log Likelihood -286.140
Date: Wed, 13 Nov 2019 AIC 574.281
Time: 16:18:15 BIC 576.866
Sample: 0 HQIC 575.326
- 100
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 17.1007 2.478 6.902 0.000 12.245 21.957
===================================================================================
Ljung-Box (Q): 428.31 Jarque-Bera (JB): 2.86
Prob(Q): 0.00 Prob(JB): 0.24
Heteroskedasticity (H): 1.78 Skew: -0.39
Prob(H) (two-sided): 0.10 Kurtosis: 3.31
===================================================================================
グラフにしてみるとさらにもっともらしいです。
deterministic trendにしても結果は一緒です。
長期のトレンドのとらえ方
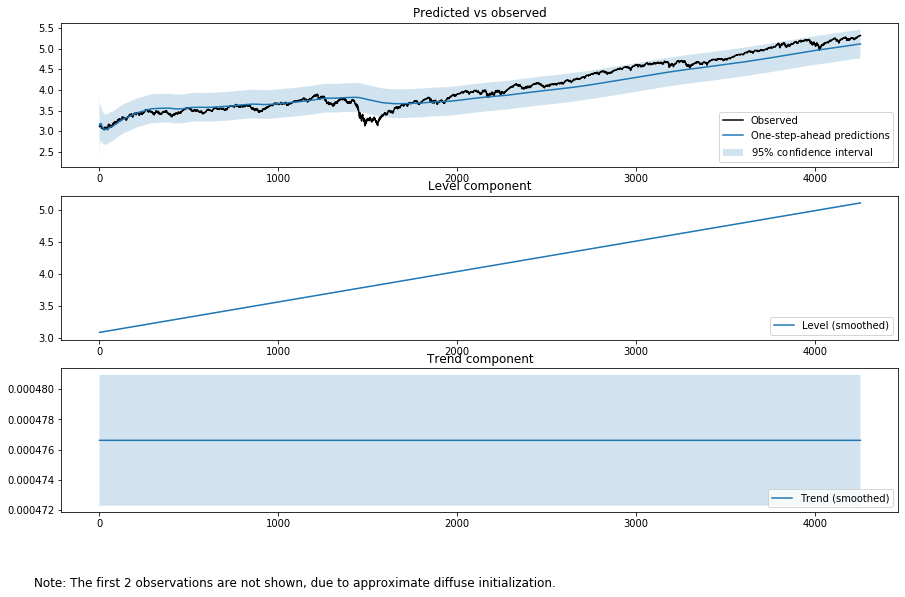
2003年からQQQは強い上昇トレンドをもちます。それを"deterministic trend"を使うとどのようになるかを見てみましょう。長期の時系列なので、価格の対数を取ります。
tsd = web.DataReader("QQQ",'yahoo','2003/1/1').dropna()
tsd=tsd.loc[:,['Open','High','Low','Adj Close']]
tsd.columns=['open','high','low','close']
print(tsd.tail(1))
output_mod = sm.tsa.UnobservedComponents(np.log(tsd['close']), "dtrend")
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));
Unobserved Components Results
===============================================================================
Dep. Variable: close No. Observations: 4253
Model: deterministic trend Log Likelihood 1317.309
Date: Thu, 21 Nov 2019 AIC -2632.618
Time: 01:04:18 BIC -2626.263
Sample: 0 HQIC -2630.372
- 4253
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 0.0313 0.001 44.996 0.000 0.030 0.033
===================================================================================
Ljung-Box (Q): 154678.60 Jarque-Bera (JB): 1429.33
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 8.25 Skew: -1.10
Prob(H) (two-sided): 0.00 Kurtosis: 4.80
===================================================================================
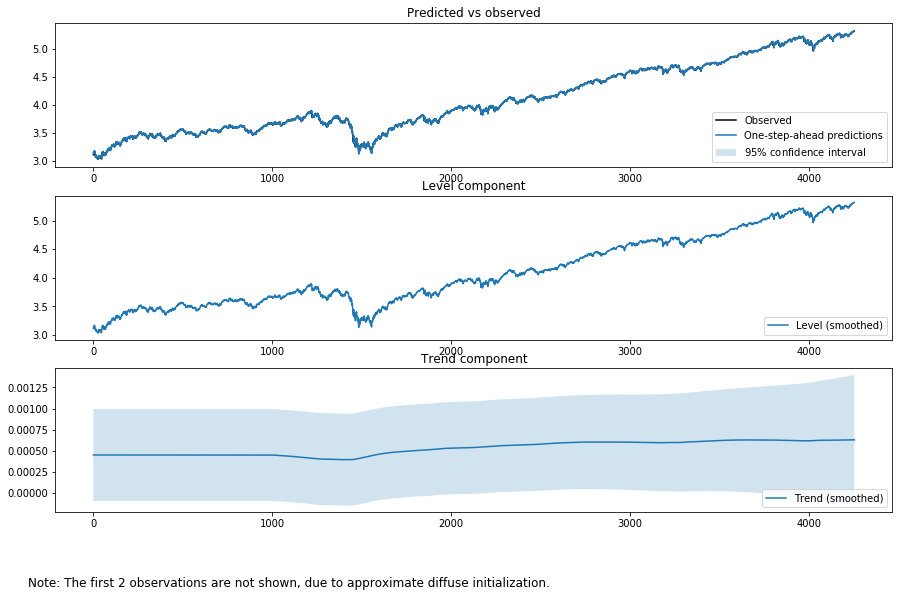
ランだぬウォークの要素が入ったほうがいいのではという意見もあると思います。そこで
output_mod = sm.tsa.UnobservedComponents(np.log(tsd['close']), "lldtrend")
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));```
Unobserved Components Results
============================================================================================
Dep. Variable: close No. Observations: 4253
Model: local linear deterministic trend Log Likelihood 12520.832
Date: Thu, 21 Nov 2019 AIC -25037.664
Time: 01:10:16 BIC -25024.954
Sample: 0 HQIC -25033.173
- 4253
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 4.231e-06 1.56e-06 2.710 0.007 1.17e-06 7.29e-06
sigma2.level 0.0002 3.58e-06 42.687 0.000 0.000 0.000
===================================================================================
Ljung-Box (Q): 80.63 Jarque-Bera (JB): 6804.26
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 0.78 Skew: -0.16
Prob(H) (two-sided): 0.00 Kurtosis: 9.19
===================================================================================
どちらがいいとは言えませんが、ランダムウォークの要素を入れたとしても残差が正規分布になるわけではありません。
トレンドの構成要素もよりダイナミックに動くようになるのではないかと思われますが、リーマンショック等のボラティリティーの極端なクラスタリングを経験しながらもトレンドの要素はほぼ一定です。
トレンド以外の成分
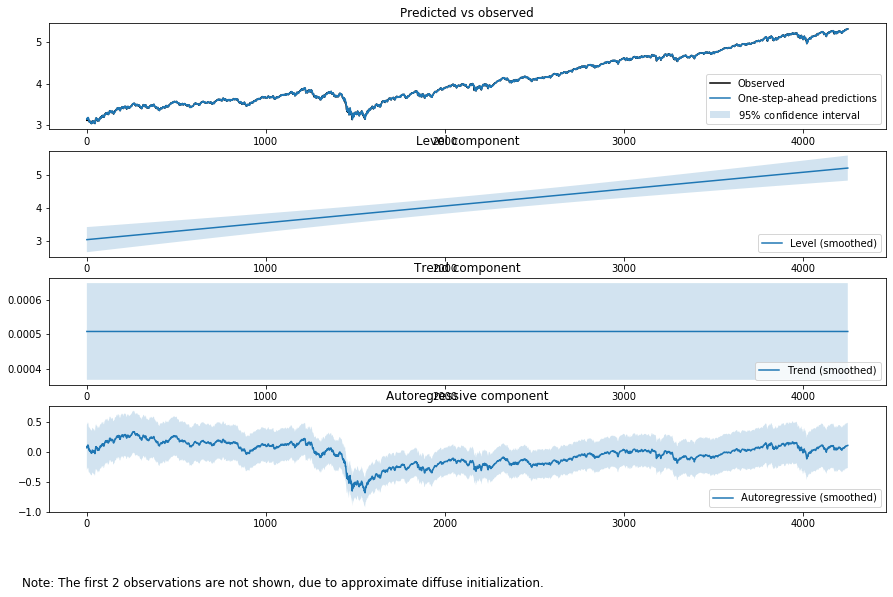
さらに季節性、サイクルを加えることもできます。まずは季節性の役割をするARの要素を入れてみましょう。
$y_t=\mu_t+\eta_t$
$\mu_{t+1}=\mu_{t-1}+\eta_{t+1} $
$\phi(L)\eta_t=\nu_t$
output_mod = sm.tsa.UnobservedComponents(np.log(tsd['close']), "dtrend",autoregressive=4)
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));
Unobserved Components Results
===============================================================================
Dep. Variable: close No. Observations: 4253
Model: deterministic trend Log Likelihood 12526.430
+ AR(4) AIC -25040.861
Date: Thu, 21 Nov 2019 BIC -25002.731
Time: 01:17:35 HQIC -25027.386
Sample: 0
- 4253
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 2.371e-05 1.16e-05 2.050 0.040 1.04e-06 4.64e-05
sigma2.ar 0.0001 2.74e-05 4.044 0.000 5.7e-05 0.000
ar.L1 1.1581 0.150 7.697 0.000 0.863 1.453
ar.L2 -0.2431 0.212 -1.148 0.251 -0.658 0.172
ar.L3 0.1186 0.091 1.307 0.191 -0.059 0.296
ar.L4 -0.0348 0.030 -1.147 0.251 -0.094 0.025
===================================================================================
Ljung-Box (Q): 64.83 Jarque-Bera (JB): 6317.17
Prob(Q): 0.01 Prob(JB): 0.00
Heteroskedasticity (H): 0.77 Skew: -0.22
Prob(H) (two-sided): 0.00 Kurtosis: 8.96
===================================================================================
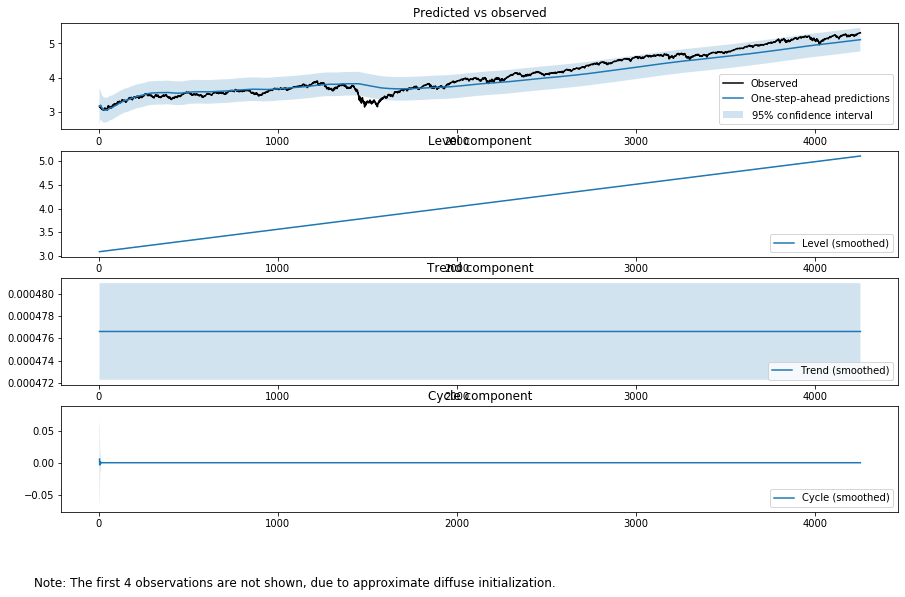
次の例はfrequency cycleを加えたものです。
$$
y_t=\mu_t+\eta_t
$$
$\mu_{t+1}=\mu_{t-1}+\epsilon_{t+1} $
$\eta_{t+1}=(\eta_t cos \lambda_\eta t +\eta_t^* sin \lambda_\eta) + \tilde{\omega_t}$
$\eta_{t+1}^*=\rho_c (-\bar{c_t}cos \lambda_c t +\bar{c_t}^* sin \lambda_c) + \hat{\omega_t}^*$
output_mod = sm.tsa.UnobservedComponents(np.log(tsd['close']), "dtrend",cycle=True,stochastic_cycle=True, damped_cycle=True)
output_res = output_mod.fit(method='powell', disp=False)
print(output_res.summary())
fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9))
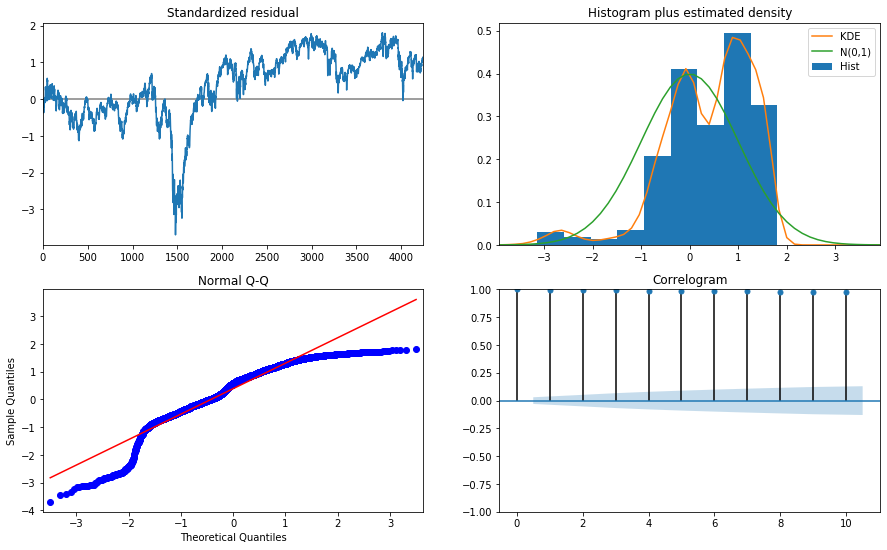
fig = output_res.plot_diagnostics( figsize=(15, 9))
Unobserved Components Results
=====================================================================================
Dep. Variable: close No. Observations: 4253
Model: deterministic trend Log Likelihood 1316.946
+ damped stochastic cycle AIC -2625.892
Date: Thu, 21 Nov 2019 BIC -2600.474
Time: 02:48:41 HQIC -2616.909
Sample: 0
- 4253
Covariance Type: opg
====================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 0.0313 0.001 41.522 0.000 0.030 0.033
sigma2.cycle 2.579e-17 0.001 4.31e-14 1.000 -0.001 0.001
frequency.cycle 2.3597 3.002 0.786 0.432 -3.525 8.244
damping.cycle 0.7063 3.896 0.181 0.856 -6.930 8.343
===================================================================================
Ljung-Box (Q): 154620.24 Jarque-Bera (JB): 1433.89
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 8.26 Skew: -1.10
Prob(H) (two-sided): 0.00 Kurtosis: 4.80
===================================================================================
------------------------------------------------------------------------------------
sigma2.irregular 2.433e-05 1.16e-05 2.106 0.035 1.69e-06 4.7e-05
sigma2.ar 0.0001 2.74e-05 4.034 0.000 5.68e-05 0.000
frequency.cycle 2.5011 0.000 7360.027 0.000 2.500 2.502
ar.L1 1.1601 0.151 7.676 0.000 0.864 1.456
ar.L2 -0.2461 0.213 -1.155 0.248 -0.664 0.172
ar.L3 0.1200 0.092 1.309 0.191 -0.060 0.300
ar.L4 -0.0351 0.031 -1.149 0.251 -0.095 0.025
===================================================================================
Ljung-Box (Q): 65.83 Jarque-Bera (JB): 6125.21
Prob(Q): 0.01 Prob(JB): 0.00
Heteroskedasticity (H): 0.77 Skew: -0.20
Prob(H) (two-sided): 0.00 Kurtosis: 8.87
===================================================================================
観測データが徐々に分解されていく様子が分かると思います。ただしここで行っていることは長期のデータを使ってシステムを同定しているだけで、長期の予測をしているわけではありません。あくまでの予測は1期先のみです。また、残差の分析も行っています。きれいであるとはいえません。これはデータの長さが長すぎるからです。
直感的意味
カルマンフィルター
$\hat{\mu_{t|t}}=\hat{\mu_{t|t-1}}+K_t (y_t-\hat{\mu}_{t|t-1})$
$K_t$は近似的に観測誤差とシステム誤差(local level model)の比
つまり状態が変化すれば変化するハイパーパラメータの比
指数平滑
$\hat{\mu_{t|t}}=\hat{\mu_{t|t-1}}+w (y_t-\hat{\mu}_{t|t-1})$
平均
$\hat{\mu_{t|t}}=\hat{\mu_{t|t-1}}+\frac{1}{n} (y_t-\hat{\mu}_{t|t-1})$
参考:
特にシステムトレードに興味のある方
Yahoo Finance USから株価をダウンロードしてみた
人工知能関連
誰でもわかるニューラルネットワーク:アプリのように動かす人工知能ーテンソルフロープレイグラウンド
誰でもわかるニューラルネットワーク:正則化をテンソルフロープレイグラウンドで試してみた
参考文献
「Python3ではじめるシステムトレード」(パンローリング)