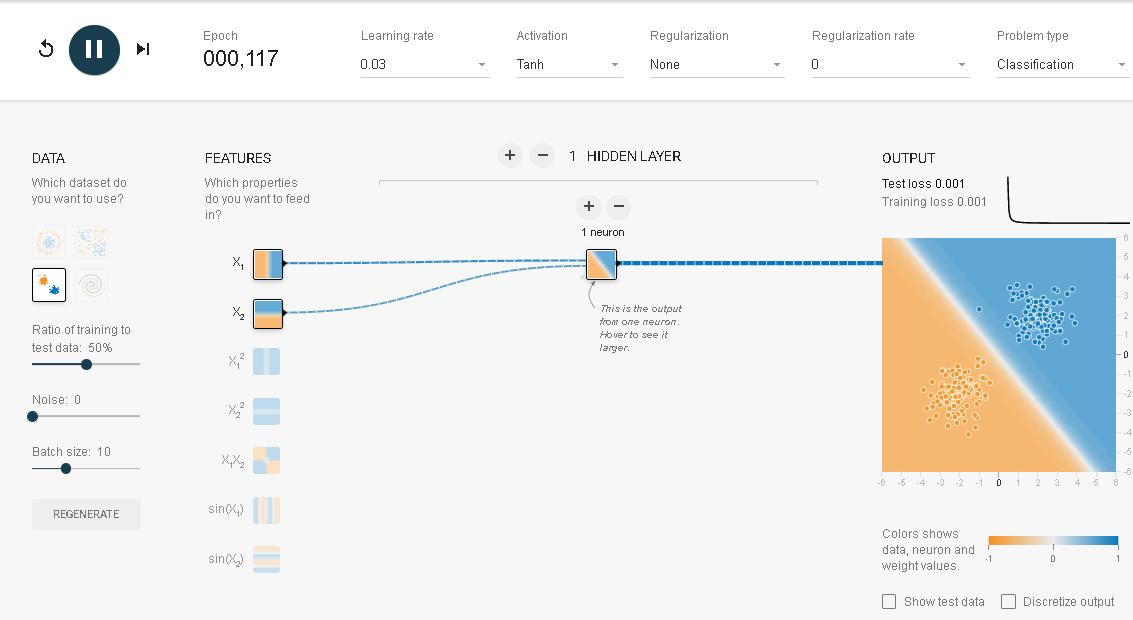
直感的にニューラルネットワークの仕組みを理解してみましょう。
深層学習とかニューラルネットワークとか、人工知能という言葉が世間で飛び交っています。いったい、これらがどのようなものなのかを理解したいと思っている人は多いのではないでしょうか?でもプログラミングの知識もなければ、ITの知識もないという人には高いハードルのように感じられます。そのような人のために、テンソルフロープレイグラウンドというツール、アプリが用意されているのをご存知ですか。
ブラウザーを開いてつぎのURLを開いてみてください。
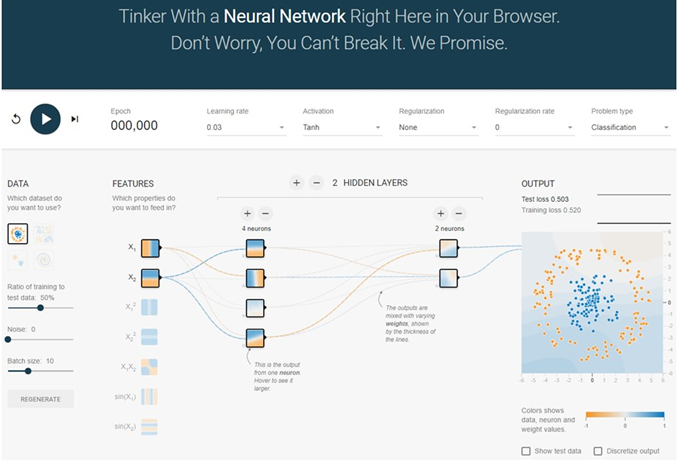
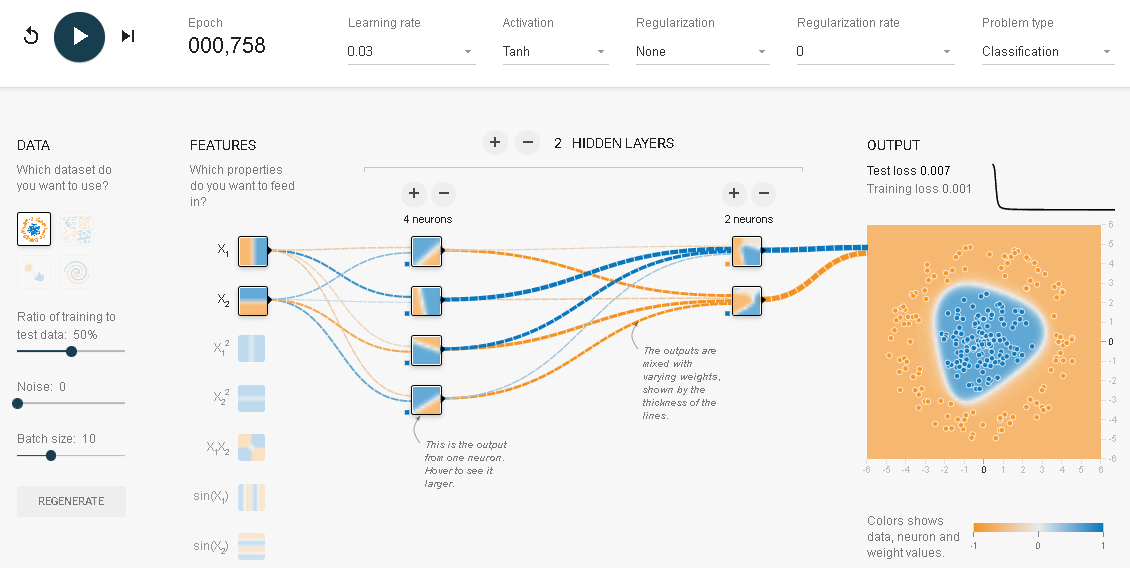
つぎのような画面が現れます。
これはニューラルネットワークを学ぶための学習ツールです。ニューラルネットワーク・シミュレーターとでも呼んだらいいのでしょうか?
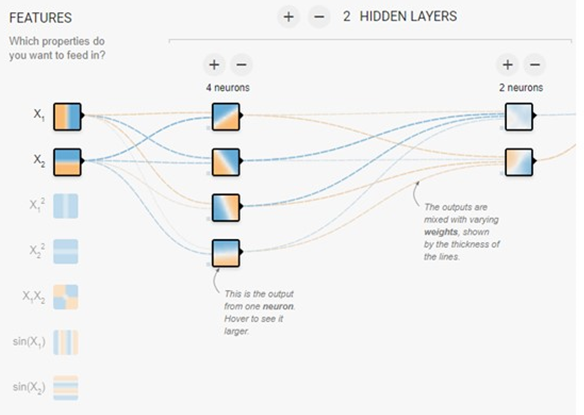
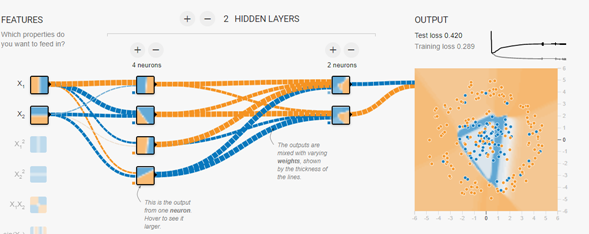
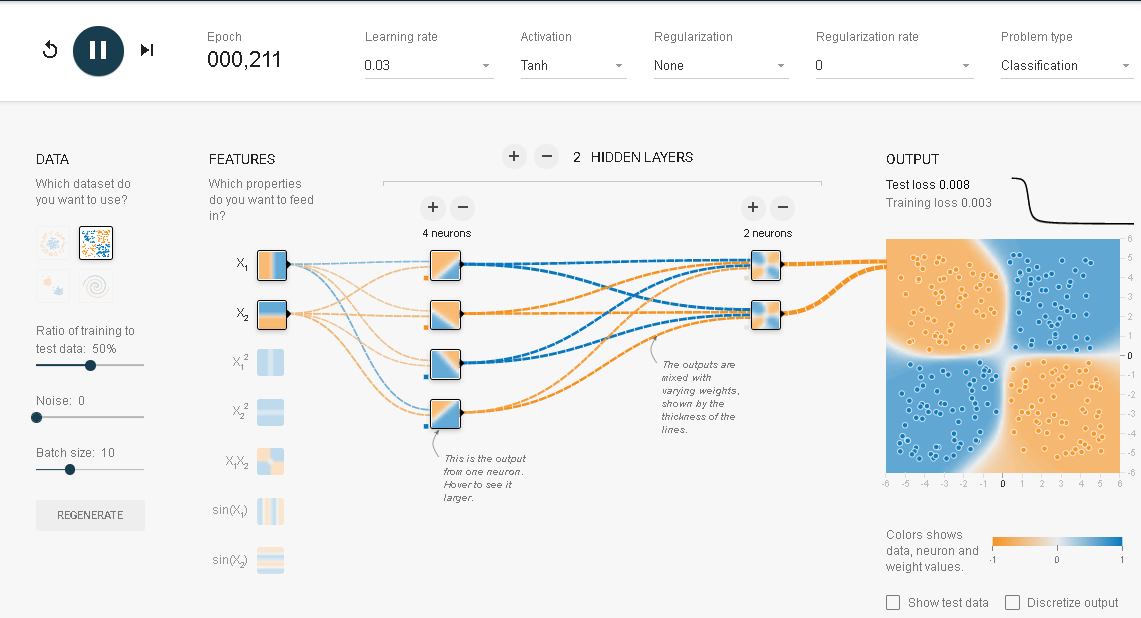
この場合には、入力データは$X_1$と$X_2$が選ばれています。また出力はサークルが描かれています。青い点が円形に、赤い点がそれを取り巻く輪として配置されています。このニューラルネットワークでは隠れ層(Hidden layers)が2つでそれぞれに4つのニューロンと2つのニューロンが配置されています。ニューロンって何だろうと思ってしまいます。でも何か聞いたこともありそうです。そうです。たぶん聞いたことがあるはずです。脳を構成する神経細胞のことです。
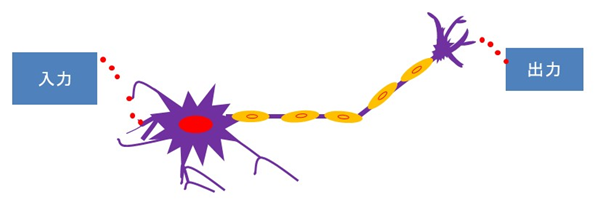
大きく頭の部分としっぽの部分、そしてそれをつなぐ筒のような胴体の3つの部分で構成されています。この神経細胞(ニューロン)の機能は数学的にモデル化されています。数学的にモデル化されたと聞くとこれからたくさん数式が出てきて厄介だと思われる方もいるかもしれません。心配いりません。極力、直感を頼りに理解できるように説明して行きます。
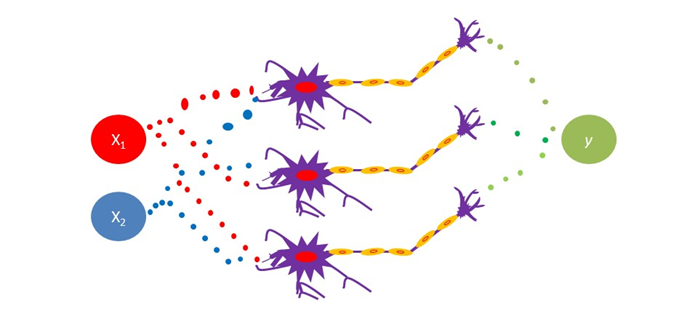
実際のニューロンは複数の電気信号を入力として受けとり、それを加工してつぎのニューロンに電気信号として出力しています。簡単な図で示すとつぎにようになります。
実は人間の脳では入力も出力も電気パルスという電気信号であったり、化学物質の1つであるシナプスであったりと、いろいろな媒介をとおして情報のやり取りをしています。上図の赤い点はこのシナプスをイメージしています。つぎの図を見てください。$X_1$, $X_2$が入力でyが出力です。
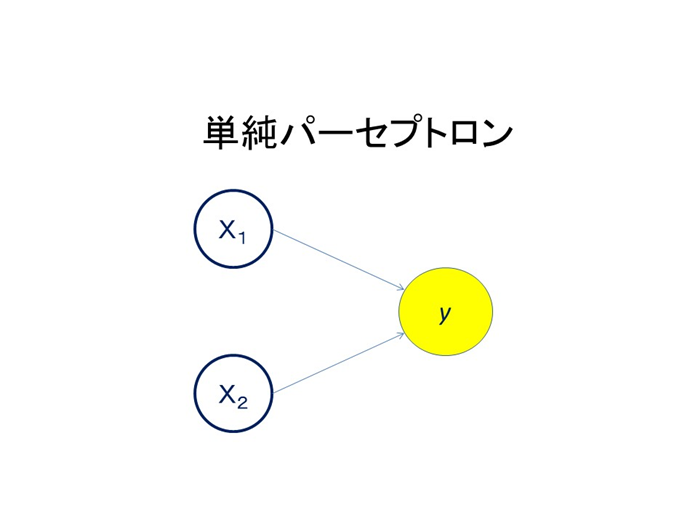
ニューロンを大まかに表現すると多数決素子といえます。入力を受け取るとその総和を計算します。興奮した情報をたくさん受け取ると、その情報は強まり、抑制性の情報を受け取るとその分差し引かれます。さらに簡単に書き表してみましょう。〇と→のついた直線で書き表してみました。矢印は情報の流れを表しています。電気パルスもシナプスという難しい仕組みは忘れてもっと単純化しましょう。
このモデルを単純パーセプトロンと呼びます。
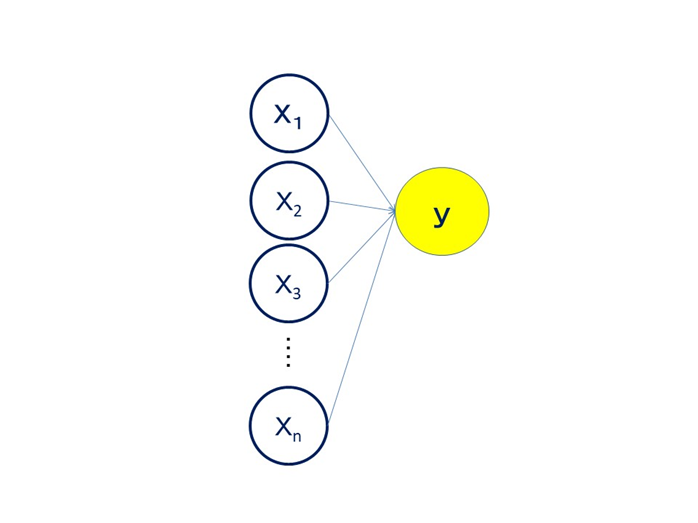
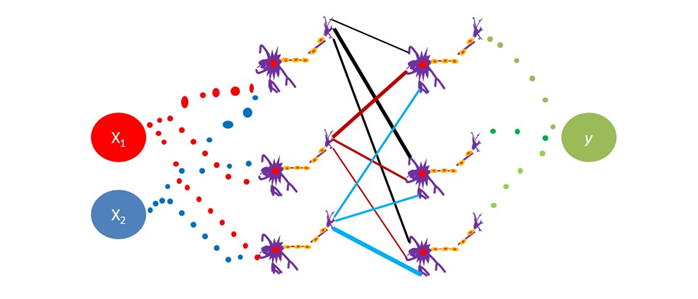
ニューロンの頭には木の枝のようなものがたくさん付いていました。ここで他のニューロンからの情報を受け取っています。数が多ければその分多くの情報を受け取れます。多数決の判断も多い分正確になる可能性があります。実際のニューロンも数千、数万の情報を受け取っています。実際の脳では1000億個のニューロンが網目構造を作っています。この網目構造ですが、19世紀の後半の脳の研究では、この構造に議論が巻き起こりました。ニューロンの先端がつながっているのか、離れているのかが問題となったのです。結局、両方の説の主張者にノーベル賞が授与されました。真実は先端がつながっていないニューロン説でした。

ニューロンの頭には木の枝のようなものがたくさん付いていました。ここで他のニューロンからの情報を受け取っています。数が多ければその分多くの情報を受け取れます。
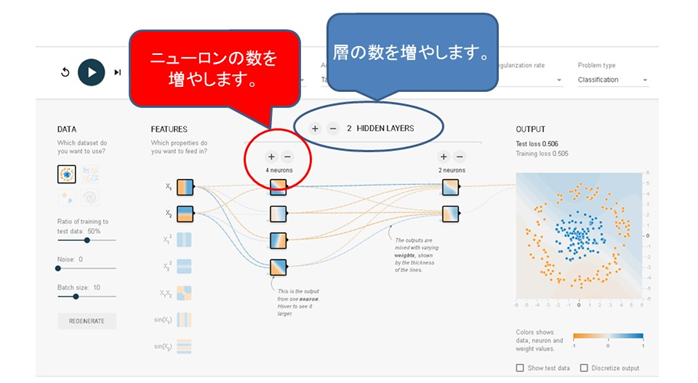
複雑な問題を解く場合に、ニューロンの数が足らなければ増やすことができます。3個に増やしてみましょう。
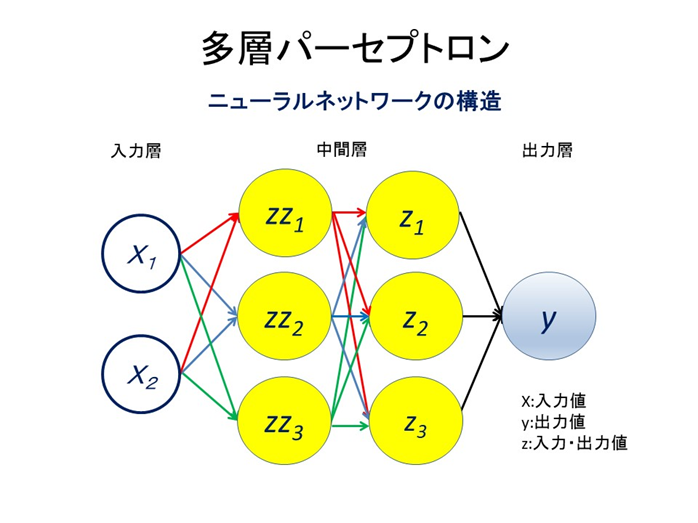
ニューロンの数だけではなく、層の数も増やせます。
書き直すと
となります。まとめると
このイメージにヒントを得て作られたのがニューラルネットワークです。ニューラルネットワークは分類問題を解くことを得意としているので、テンソルフロープレイグラウンドではディフォルトとして分類問題を解くように設定されています。つまり私たちの目の前にあるのはニューラルネットワーク(NN) なのです。これをいじってNNを理解していこうというのです。まず最初に左上の黒い丸の中に三角形が白抜きされている実行ボタンを押してみてください。
結果はつぎのようになるはずです。
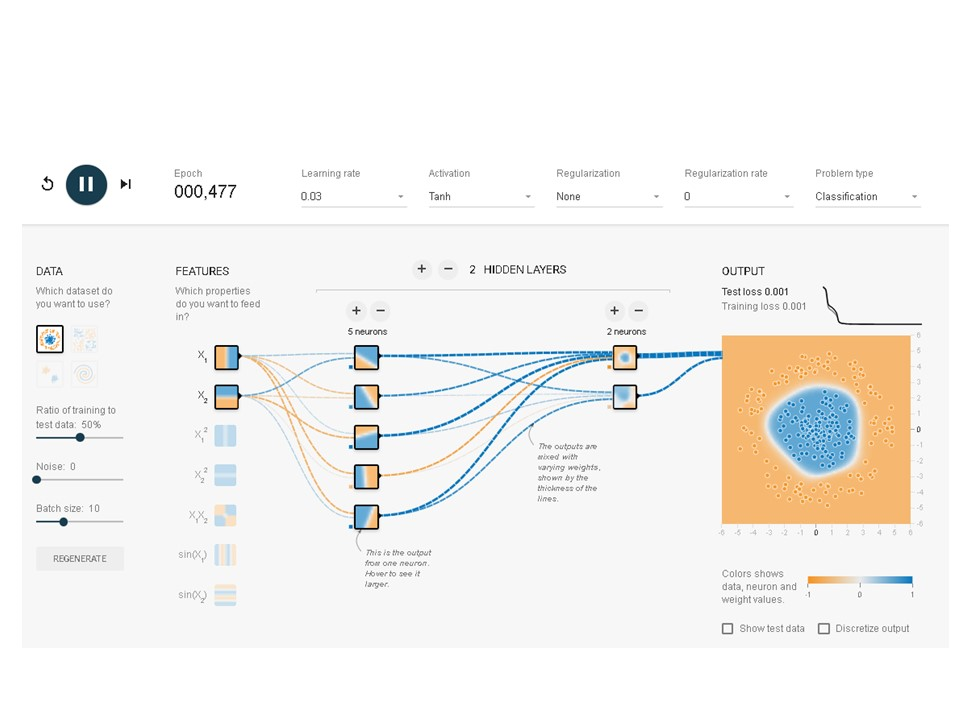
背景の色と点の色が同じで何か境界線で2つの色の点が分離されていれば分類は成功したといえます。きれいなマルとはいえないまでも何となく分類されています。
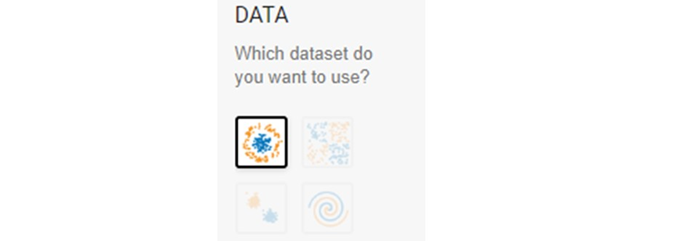
DATA(データ):4つの模様(出力)から1つ選びます。
FEATURES(入力特徴量)とHIDDEN LAYERS(隠れ層)はニューラルネットワークの骨格の部分です。
DATA(データ)
まずはDATAです。ここから先ほどの画像に加えてあと3枚の画像を選ぶことが出来ます。ここで選んでいるのはOUTPUTのタイプです。出力される赤と青の点の模様を選んでいると考えてください。
左上はサークル、その右はXOR、左下は正規分布、その右はらせんと名前が付けられています。
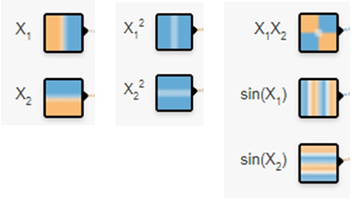
入力データの選択
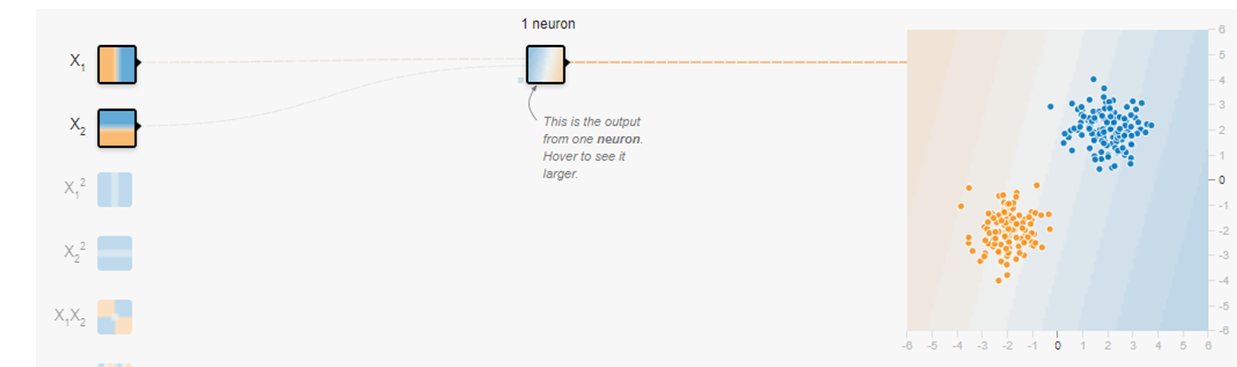
7つの画像をクリックすることで最大7つの入力データを選択することができます。それぞれのボックスには名前がついています。最初は$X_1$、つぎは$X_2$です。
HIDDEN LAYERS(隠れ層)
HIDDEN LAYERSは隠れ層、中間層のことです。ここには+と-のボタンが付いています。+を押すと隠れ層の数を増やすことができます。-を押すと隠れ層の数を減らすことができます。とりあえず隠れ層を1つとします。
Nuerons(ニューロン、ユニット)
NueronsもHIDDEN LAYERSと同じように+と-のボタンからなりたっています。このボタンはそれぞれの隠れ層についています。特定の隠れ層の+/-のボタンを押せばその層のニューロンの数を増減できます。このニューロンはユニットと呼ばれることもあります。
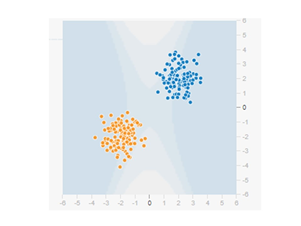
正規分布データの分類
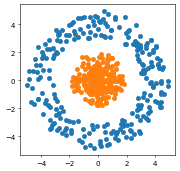
つぎの出力データ(模様)を正規分布と呼びます。それぞれ2つの赤と青のデータのグループが正規分布から作られているのでこのように呼ばれています。
入力データは7つありますが、選択するべきは$X_1$、$X_2$のどちらか1つ、または両方の2つに限ります(少しずつ使うデータの数を増やしていきます)。$X_1$と$X_2$の両方の入力データを選択してみます。
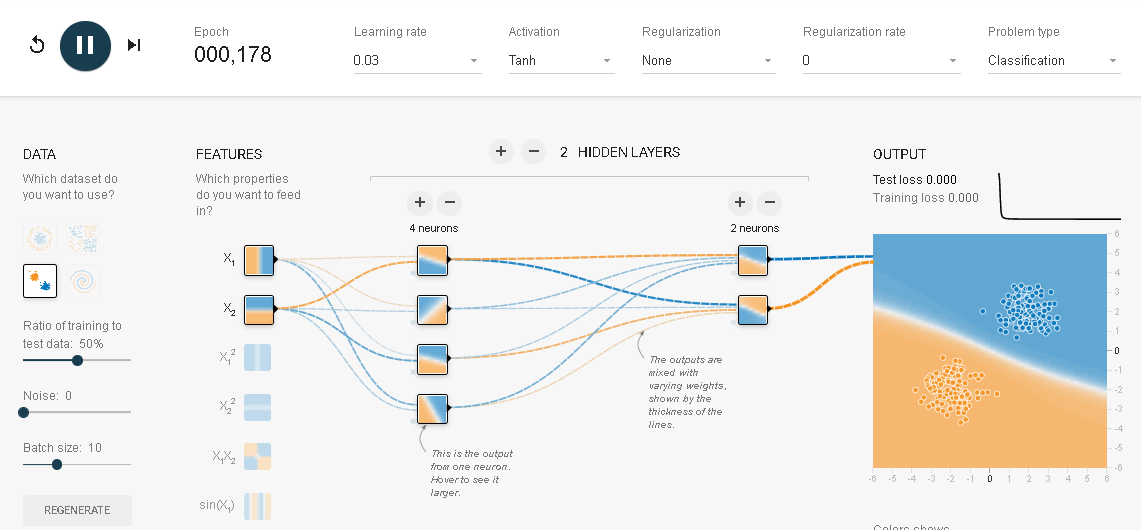
そして、実行ボタンを押してみてください。一瞬のうちにつぎのような結果になるはずです。
2つがきれいに分離されています。
サークル
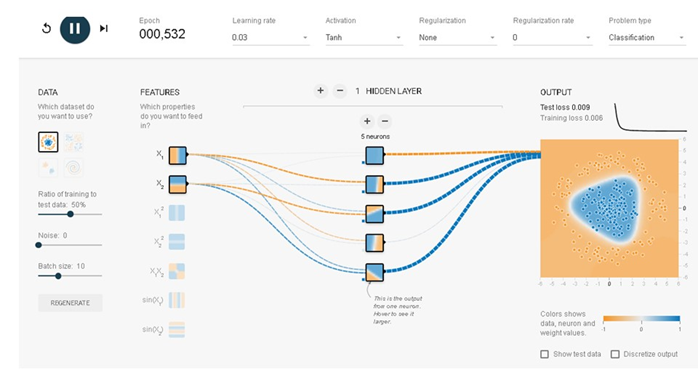
つぎに入力データを変えることなくサークルを分類してみましょう。
隠れ層の数を増やすか、またはニューロンの数を増やすかしてニューラルネットワークを変更していきます。
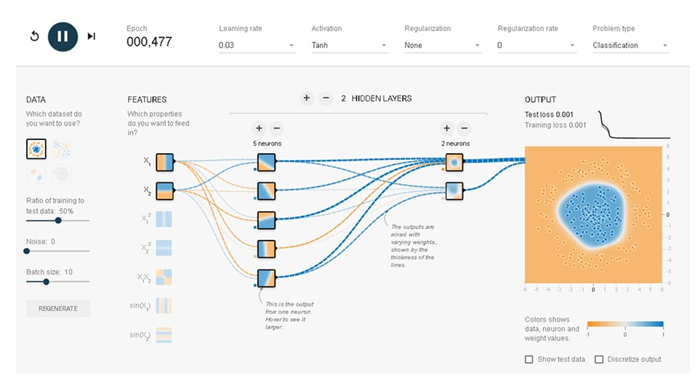
結果はマルではなく3角形に近くなりました。それでも分類するという作業は達成されています。乱数により生成されているので形は若干変わります。隠れ層を2層にしてみましょう。
分離曲線は円形に近くなってきました。ニューロンを増やしたり、隠れ層の数をさらに増やしたりして試してみてください。隠れ層の1層目は線形の分析をしています。2層目からは非線形の分析をしているといわれています。
どちらの結果も2つのデータを分離しているので正解です。ですが、理想的なニューラルネットワークであるかどうかはわかりません。
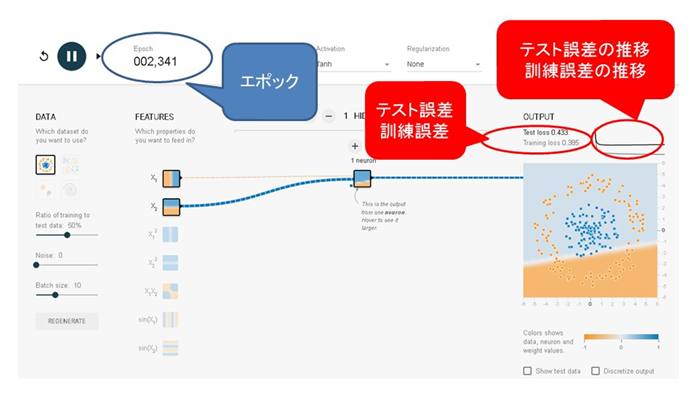
右側の出力(OUTPUT)の右上の端のところにグラフが表示されています。またその左横には テスト誤差(test loss)と訓練誤差(training loss)が表示されています。誤差は学習の結果として得られた予測値と実際の値との差を示しています。
グラフは訓練誤差とテスト誤差を可視化したものです。時間の経過とともにどのように変化しているのかが分かります。数値は小さければ小さいほど良い結果です。実際の値が青で予測値も青であれば、予測誤差はゼロになります。また、実効ボタンの横にエポック(epoch)の数が示されています。今回は500個のデータが用いられているので、1エポックは500個のデータになります。(正確には訓練データの総数を1エポックとします。)2エポックでは500×2=1000個のデータになります。
ノイズを加えてみよう
つぎにノイズを加えてみてください。
まずはディフォルトの状態に戻してください。そしてプレイグラウンドの左の中央のnoiseと書かれているスライドをいじります。これのボッチを右にずらすとノイズを加えることができます。50%までめいっぱい増やして実行ボタンを押します。
今度はきれいに分離ができません。これはニューラルネットワークがノイズに影響されて与えられたデータをきちっと学習できていない証拠です。ニューラルネットワークは自由度が高く、いろいろな問題に対処できるのですが、自由度が高い分、ノイズには弱いのです。ではノイズに強いNNを作るにはどうしたらよいのでしょうか?それは背後にある状況を正確に把握してニューラルネットワークの構造を作ることです。ではやってみましょう。
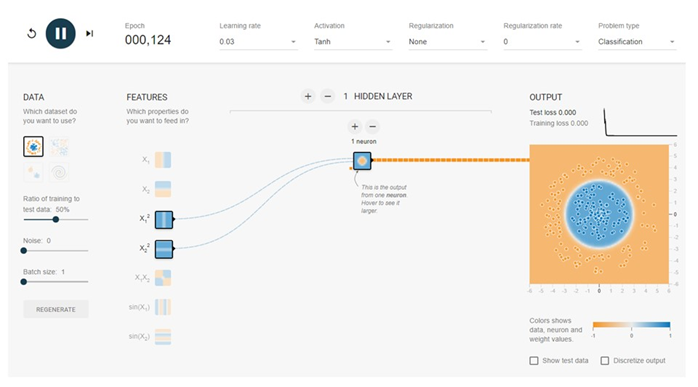
サークルの答え
なんとあっという間に分類ができてしまいました。うまくいった原因を考えてみましょう。それは入力データの選択にあります。中学で習った数学を思い出してください。円を描くには$X_1^2+X_2^2=1$とすればよいことを学びました。ニューラルネットワークでも同じことです。
つぎにノイズを加えてみてください。

なんとさきほどよりもずっと原型をとどめてくれます。これはNNの構造が入力データの選択、隠れ層の数、ニューロンの数と出力に対して適切だからです。もちろん他にもいろいろな方法でノイズに強いNNを作ることができますが、まずは構造が重要です。左下のGENERATEボタンを押すと乱数をリセットでき、いろいろなノイズを試すことができます。やってみましょう。
誰でもわかるニューラルネットワーク:貧困の撲滅
AIの使い道が急激に広がっています。多くの人がそれを実感しているのではないでしょうか。いたるところでAIと接する機会が増えました。しかし、ここでは一般とはちょっと違う別の用途を紹介します。
貧困の撲滅
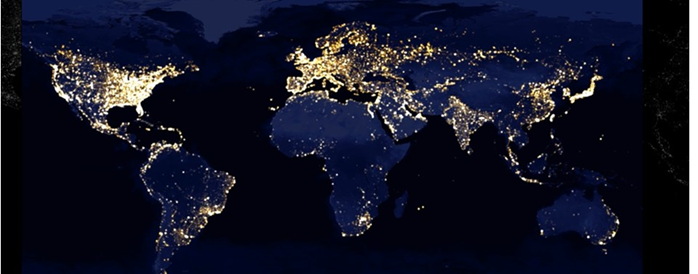
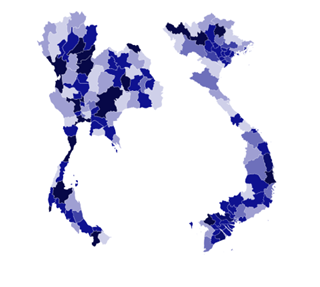
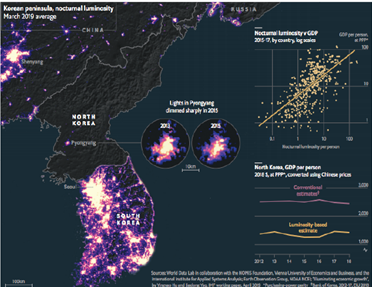
AIが活躍するのは先進国だけではありません。開発途上の国々では先進国以上にAIに注目が集まっています。特に災害時の緊急対応、農業、医療、教育の分野で注目されています。過疎の地域では、教育、医療の問題は深刻です。今まで何の解決策も見いだされなかった分野に光が灯ろうとしています。また、貧困の撲滅にもAIは一役買っています。衛星からの高密度精細画像を分析することで貧困地域を発掘し解決策を見出そうとしているのです。昼夜の衛星写真から経済の活動度を推定し、貧困の撲滅に活かそうとする試みがあります。つぎの図はそのような活動に使われる夜間の衛星写真です。
出所:http://sustain.stanford.edu/predicting-poverty
AIは開発途上の国々の子供たちに教育の機会を与えることを可能とします。それが貧困の連鎖を断ち切り貧困の撲滅につながるのです。
出所:「シミュレーターでまなぶニューラルネットワーク」(アマゾンkindle出版)
(https://www.amazon.co.jp/gp/product/B07MJ9R2T8?pf_rd_p=7b903293-68b0-4a33-9b7c-65c76866a371&pf_rd_r=4JRRRHRRE1FHXSY1EP5G)

2015年のネパール、カトマンズの大地震ではドローンが被害状況の把握と地図の作成に利用され、救助活動の加速化を可能としました。
出所:「シミュレーターでまなぶニューラルネットワーク」(アマゾンkindle出版)
(https://www.amazon.co.jp/gp/product/B07MJ9R2T8?pf_rd_p=7b903293-68b0-4a33-9b7c-65c76866a371&pf_rd_r=4JRRRHRRE1FHXSY1EP5G)
また、AIは地震、森林火災、洪水、台風、ハリケーンの予測などに活かされようとしています。
世界の貧困は多くの人たちの努力により減っています。しかし、サハラ以南のアフリカは別です。
過去30年で世界の貧困層の割合は確実に減っていますが、グラフにあるように減り方が頭打ちになりつつあります。根深い貧困の原因があるからです。
アジアは極貧状態を克服できましたが、サハラ以南の地域では増えています。
全体では減っているが、新しい局面に到達!
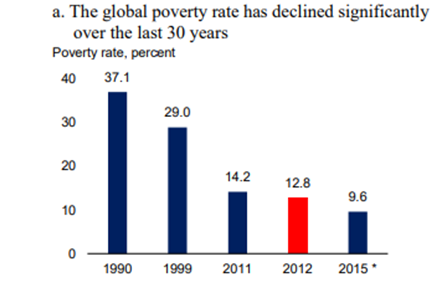
出所:Ending Extreme Poverty and sharing prosperity:Progress and Policies, World Bank Group
http://pubdocs.worldbank.org/en/109701443800596288/PRN03Oct2015TwinGoals.pdf
サハラ以南の極貧状態に注目!
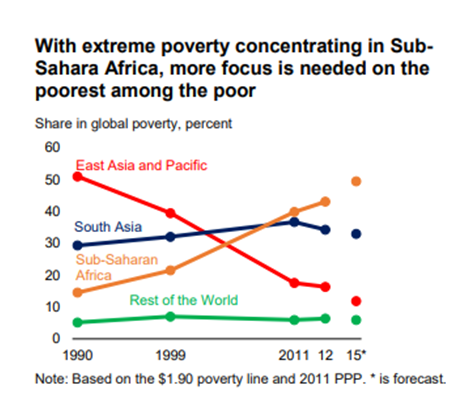
出所:Ending Extreme Poverty and sharing prosperity:Progress and Policies, World Bank Group
今ある富の分配に問題が!
青いバーは人口全体の収入の増加率を示しています。
橙のバーは収入の低い40%の人達の収入の増加率を示しています。
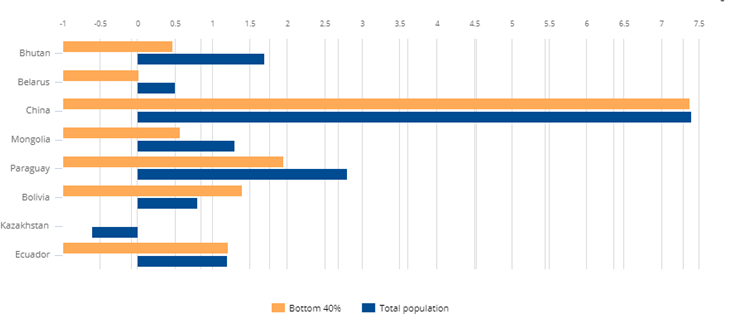
出所:Poverty & Equity Data Portal, World Bank Group
http://povertydata.worldbank.org/poverty/home/
今気になるWEBサイト
gapminder
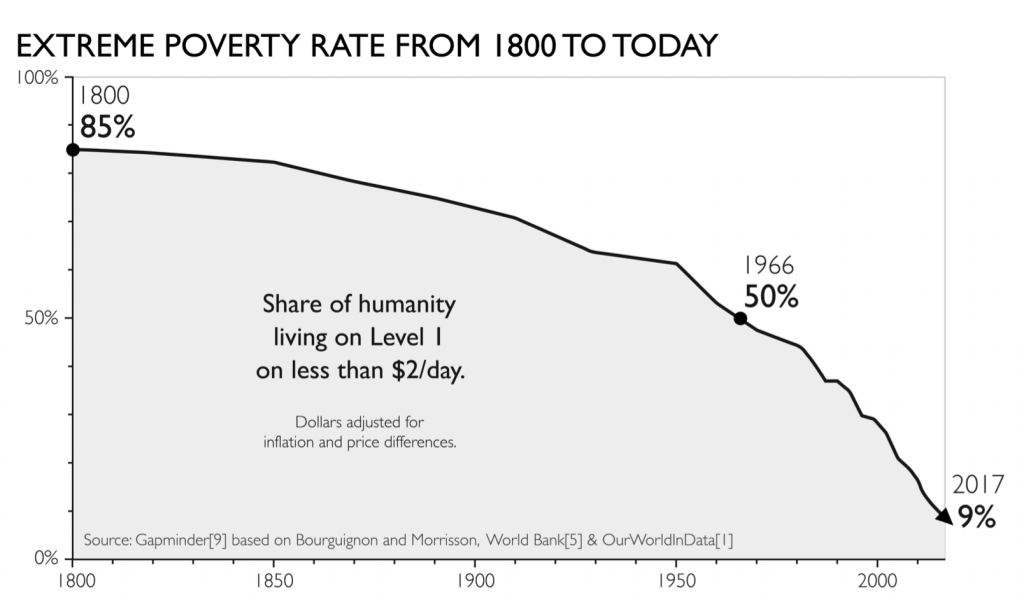
貧困の傾向 extreme poverty
世界の貧困率は改善している。しかし、...
平均寿命
本のついこの間まで、世界の平均寿命は短かった。
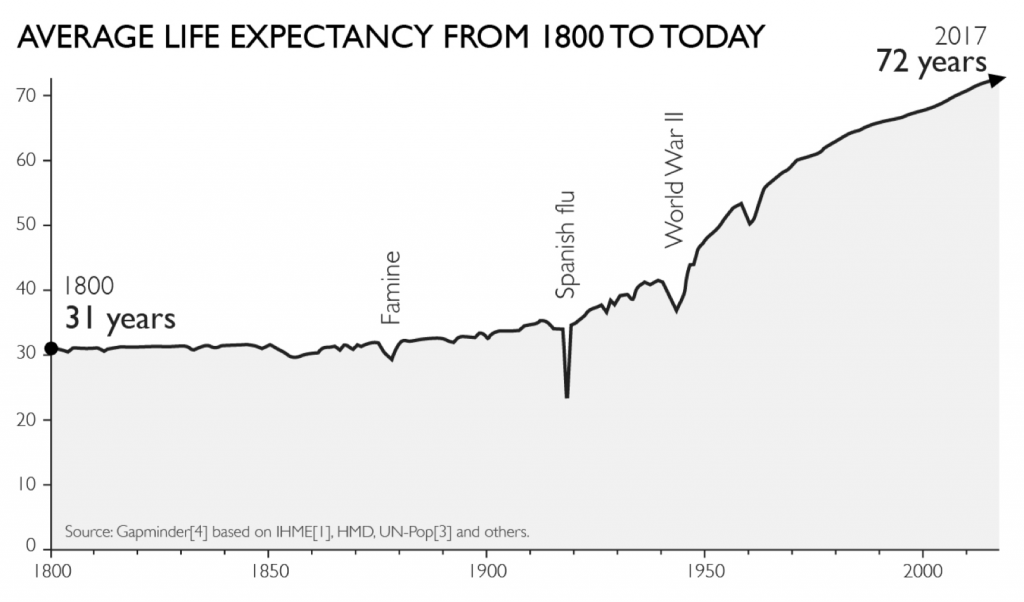
https://www.gapminder.org/topics/life-expectancy/
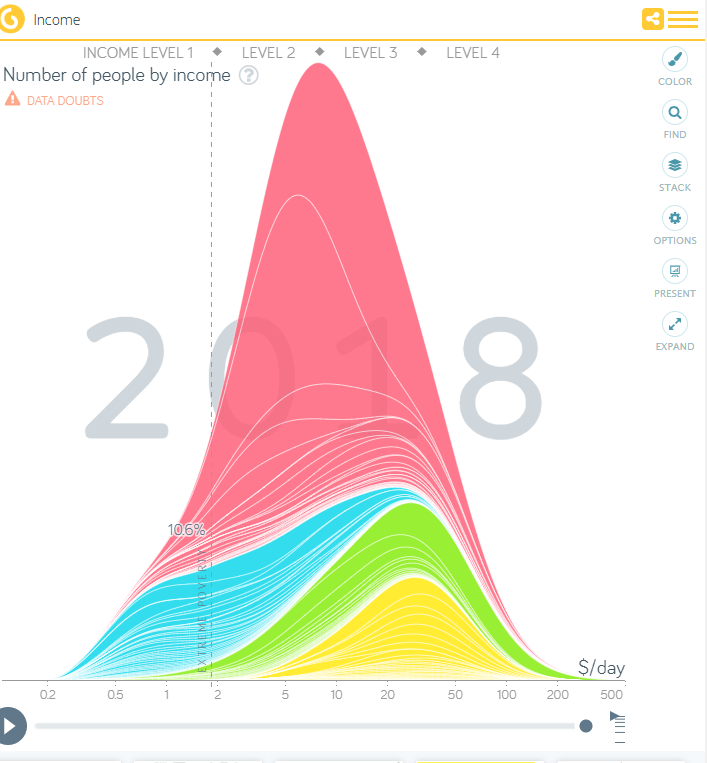
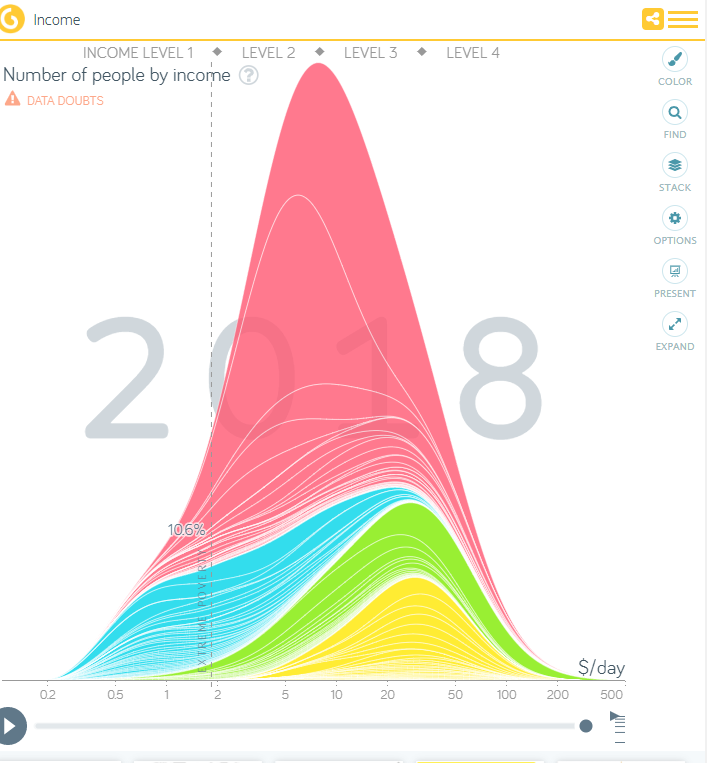
地域別収入
Global Poverty|WorldDataLab
北朝鮮の貧困状態を衛星写真から人工知能で把握。全く光がない。
3D プリンター
貧困とテクノロジー:AIが貧困者を予測し、3Dプリンタが格安住宅を建てる
つぎのURLをクリックすると3つの記事が出てきます。
AI IMPROVES FARMING WITH GOOGLE’S TENSORFLOW
A LOOK AT THE POSITIVE SIDE OF AI AND DRONES
ARTIFICIAL INTELLIGENCE, GLOBAL POVERTY, HEALTH, TECHNOLOGY ON ARTIFICIAL INTELLIGENCE AND POVERTY
参考文献
sustainability and artificial intelligence lab
http://sustain.stanford.edu/predicting-poverty
Kerasでテンソルフロープレイグラウンドを理解する
しかし、より詳細にその内容を理解するためには同じものを別のプログラミング言語で作ってみるのも一つの手です。本記事ではこれをkerasを用いて行います。
サークル
上述の画像はテンソルフロープレイグラウンドの初期画面です。出力データにサークルが選択され、入力データにX1とX2が選ばれています。実行してみます。
これが何を行っているかを正確に理解するために、同じ動きをKerasで実現してみるのも一つの手です。そこでつぎのようなプログラムを作ってみました。
# 初期化
%matplotlib inline
import pandas_datareader.data as web
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime
import keras
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
from keras import models
from keras import layers
from keras import regularizers
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
データの構築
n=250
theta=np.random.uniform(0, 360, n)
x1=np.sin(theta)*np.random.uniform(3,5, n)
x2=np.cos(theta)*np.random.uniform(3,5, n)
y=np.ones(n)
plt.figure(figsize=(4, 4), dpi=50)
plt.scatter(x1,x2)
theta=np.random.uniform(0, 360, n)
x11=np.sin(theta)*np.random.uniform(-0, 2, n)
x22=np.cos(theta)*np.random.uniform(-0,2, n)
yy=np.zeros(n)
plt.scatter(x11,x22)
# 訓練データ、テストデータの作成
x1=np.concatenate([x1,x11],axis=0)
x2=np.concatenate([x2,x22],axis=0)
y=np.concatenate([y,yy],axis=0)
X=np.stack([x1,x2],1)#.reshape(-1,2)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.5, random_state=42)
ネットワークの構築と最適化
model = models.Sequential()
model.add(layers.Dense(8, activation='tanh', input_shape=(2,)))
model.add(layers.Dense(8, activation='tanh'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(
X_train,
y_train,
batch_size=10,
epochs=500,
verbose=0)
# 結果の評価
results = model.evaluate(X_train, y_train)
results
# 8/8 [==============================] - 0s 1ms/step - loss: 3.0139e-05 - accuracy: 1.0000
# [3.0139368391246535e-05, 1.0]
results = model.evaluate(X_test, y_test)
results
# 8/8 [==============================] - 0s 2ms/step - loss: 1.6788e-04 - accuracy: 1.0000
# [0.0001678814151091501, 1.0]
どちらの結果も誤差はゼロです。全問正解でした。
さらに理解を深めるために入力データを変更してみます。

単純パーセプトロンでデータをきれいに分類できました。これをKerasで行ってみましょう。
X2=np.stack([x1**2,x2**2],1)#.reshape(-1,2)
X2_train, X2_test, y_train, y_test = train_test_split(
X2, y, test_size=0.33, random_state=42)
model = models.Sequential()
model.add(layers.Dense(1, activation='tanh', input_shape=(2,)))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(
X2_train,
y_train,
batch_size=10,
epochs=500,
verbose=0)
結果はつぎに様になりました。
results = model.evaluate(X2_train, y_train)
results
# 11/11 [==============================] - 0s 3ms/step - loss: 8.3843e-08 - accuracy: 1.0000
# [8.38432754335372e-08, 1.0]
results = model.evaluate(X2_test, y_test)
results
# 6/6 [==============================] - 0s 2ms/step - loss: 8.3747e-08 - accuracy: 1.0000
# [8.374658477805497e-08, 1.0]
どちらも正解率100%で誤差はゼロです。
正規分布
つぎは正規分布です。
まずはデータを構築します。
n=250
x1=np.random.normal(2,0.5, n)
x2=np.random.normal(2,0.5, n)
y=np.ones(n)
plt.figure(figsize=(4, 4), dpi=50)
plt.scatter(x1,x2)
x11=np.random.normal(-2,0.5, n)
x22=np.random.normal(-2,0.5, n)
yy=np.zeros(n)
plt.scatter(x11,x22)
x1=np.concatenate([x1,x11],axis=0)
x2=np.concatenate([x2,x22],axis=0)
y=np.concatenate([y,yy],axis=0)
X=np.stack([x1,x2],1)#.reshape(-1,2)
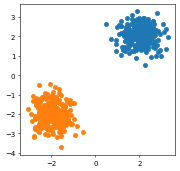
ニューラルネットワークはサークルのときと同じものを使います。その結果は
results = model.evaluate(X_train, y_train)
results
# 8/8 [==============================] - 0s 1ms/step - loss: 3.0139e-05 - accuracy: 1.0000
# [3.0139368391246535e-05, 1.0]
ふたたび誤差ゼロの正解率100%となりました。
XOR
n=125
x1=np.random.uniform(0,5, n)
x2=np.random.uniform(0,5, n)
y=np.ones(n)
x11=np.random.uniform(-5,0, n)
x22=np.random.uniform(-5,0, n)
yy=np.ones(n)
x1=np.concatenate([x1,x11],axis=0)
x2=np.concatenate([x2,x22],axis=0)
y=np.concatenate([y,yy],axis=0)
plt.figure(figsize=(4, 4), dpi=50)
plt.scatter(x1,x2)
x11=np.random.uniform(0,5, n)
x22=np.random.uniform(0,-5, n)
yy=np.zeros(n)
x111=np.random.uniform(-5,0, n)
x222=np.random.uniform(0,5, n)
yyy=np.zeros(n)
x11=np.concatenate([x11,x111],axis=0)
x22=np.concatenate([x22,x222],axis=0)
yy=np.concatenate([yy,yyy],axis=0)
plt.scatter(x11,x22)
len(x1),len(x2)
# (250, 250)
250個のデータができたのが分かります。
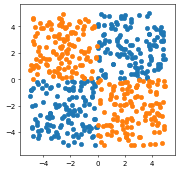
訓練データとテストデータにシャッフルをして分割します。
x1=np.concatenate([x1,x11],axis=0)
x2=np.concatenate([x2,x22],axis=0)
y=np.concatenate([y,yy],axis=0)
X=np.stack([x1,x2],1)#.reshape(-1,2)
len(y)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.5, random_state=42)
このデータを2層(第一層4ユニット,第二層2ユニット)のNNで分類を試みます。結果は
results = model.evaluate(X_train, y_train)
results
# 8/8 [==============================] - 0s 2ms/step - loss: 0.0818 - accuracy: 0.9640
# [0.08181502670049667, 0.9639999866485596]
results = model.evaluate(X_test, y_test)
results
# 8/8 [==============================] - 0s 2ms/step - loss: 0.1269 - accuracy: 0.9520
# [0.1269153356552124, 0.9520000219345093]
誤差はほぼゼロで、正解率も9割を超えています。
X_train, X_test, y_train, y_test = train_test_split(
x1*x2, y, test_size=0.33, random_state=42)
model = models.Sequential()
model.add(layers.Dense(1, activation='tanh', input_shape=(1,)))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(
X_train,
y_train,
batch_size=10,
epochs=500,
verbose=0)
結果はつぎのようになりました。
results = model.evaluate(X_train, y_train)
results
# 11/11 [==============================] - 0s 1ms/step - loss: 5.6793e-04 - accuracy: 1.0000
# [0.0005679333116859198, 1.0]
results = model.evaluate(X_test, y_test)
results
# 6/6 [==============================] - 0s 3ms/step - loss: 0.0070 - accuracy: 0.9939
# [0.007003221195191145, 0.9939393997192383]
誤差はほぼゼロで、正解率もほぼ100%になりました。
誰でもわかるニューラルネットワーク:正則化をテンソルフロープレイグラウンドで試してみた
参考:
「シミュレーターでまなぶニューラルネットワーク」(アマゾンkindle出版)
((https://www.amazon.co.jp/gp/product/B07MJ9R2T8?pf_rd_p=7b903293-68b0-4a33-9b7c-65c76866a371&pf_rd_r=4JRRRHRRE1FHXSY1EP5G))

「脳・心・人工知能 数理で脳を解き明かす」(ブルーバックス)
「圧縮センシングにもとづくスパースモデリングへのアプローチ」