プレイグラウンド入門
ニューラルネットワークの学習は初めて学ぶ人にとってはハードルがかなり高いばかりではなく、進歩のスピードもけた違いなのでひたすら圧倒されて終わってしまいます。本を開いても、ネットを検索しても難しい専門用語で満ち溢れています。かつ、プログラミングの経験のないものにとってはなおさらです。ニューラルネットワークを少し理解し始めて自分の考えや理解を試してみたくてもプログラムができなければ、どうすることもできません。これはIT以外の専門家が自分の専門分野の問題をニューラルネットワークで試してみたいなどというときにも起こります。そんなときに初学者が自分の理解を簡単に試せるアプリがあります。それがテンソルフロープレイグラウンドです。すでにたくさんの解説がネット上で公開されています。
誰でもわかるニューラルネットワーク:テンソルフロープレイグラウンド
などがあります。
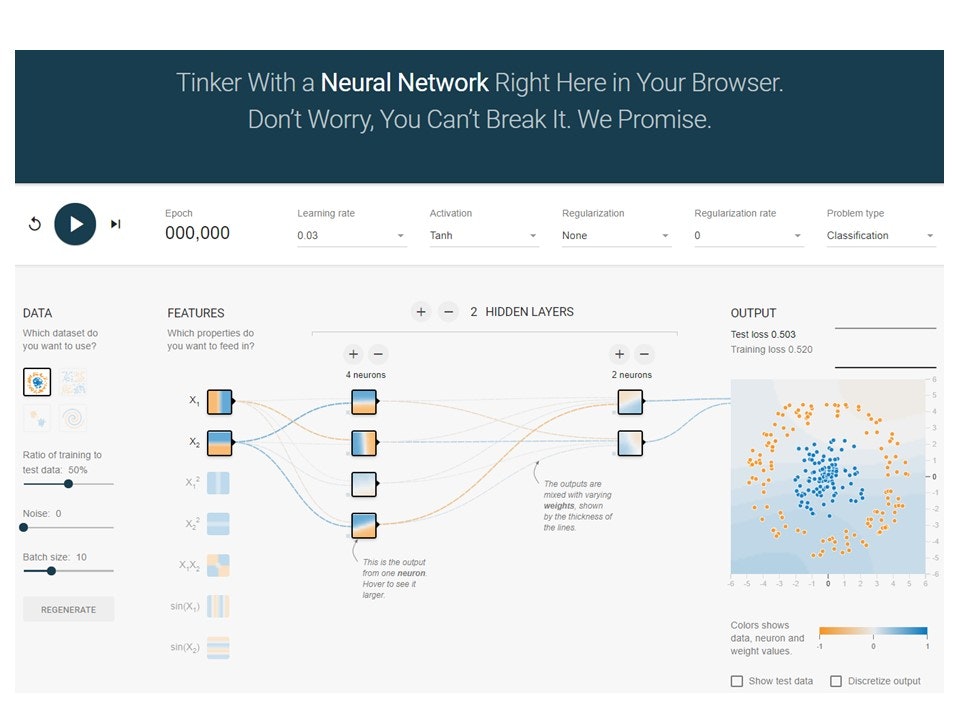
まず、テンソルフロープレイグラウンドをクリックするとA Neural Network Playgroundが立ち上がります。
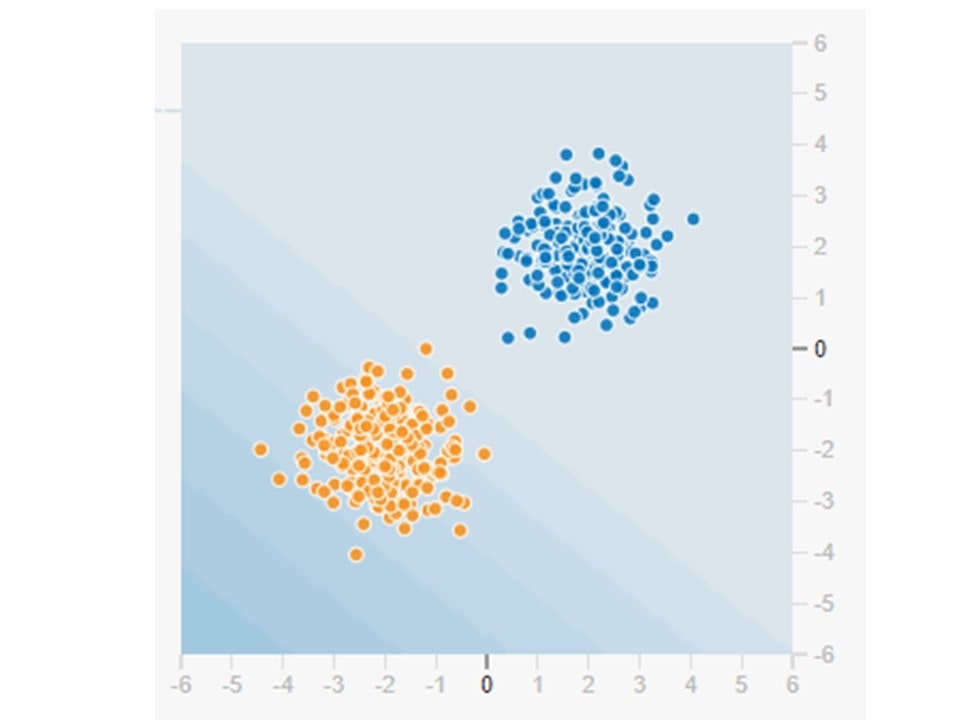
左端の4つのボックスから出力の画像を選びます。今回は正規分布といわれる青の点が第一象限に赤の点が第三象限にあるものを選びます。
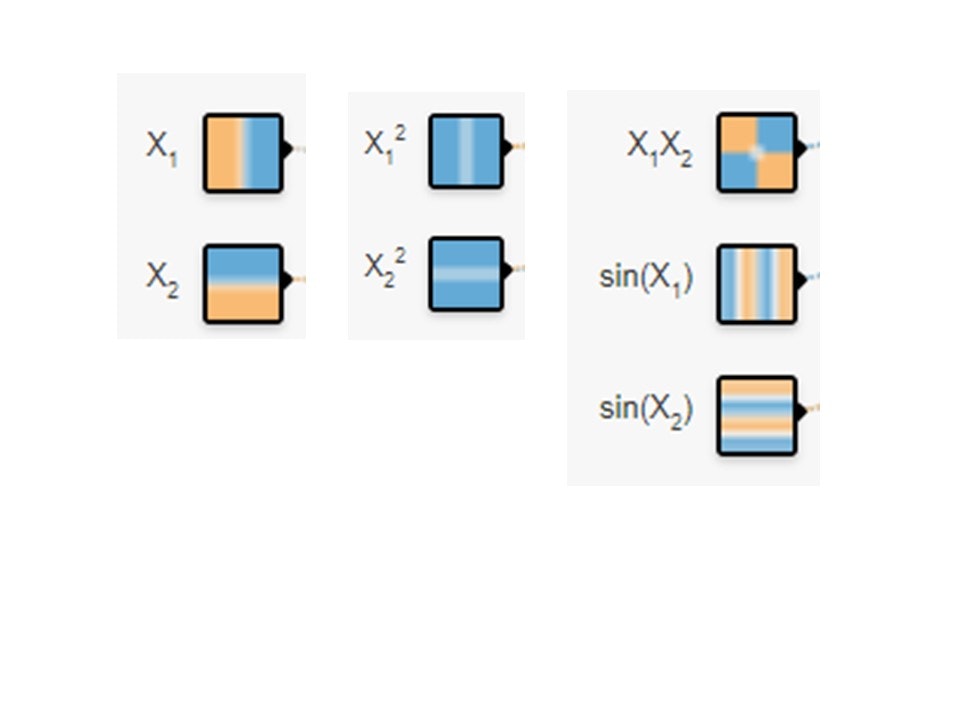
この赤と青を分離するためには単純パーセプトロンで十分です。単純パーセプトロンは一般には入力が2つで隠れ層の数が1つ、ユニットの数も1つです。したがって入力には
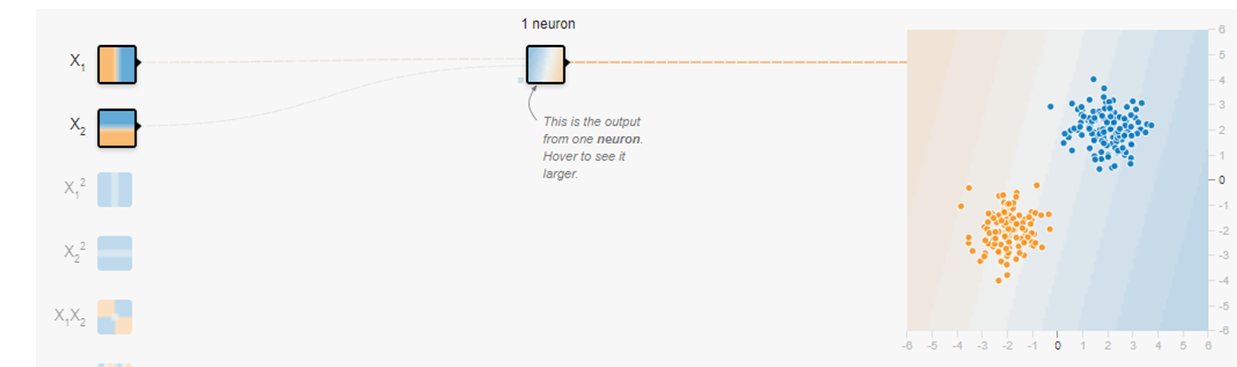
の中から$X_1$と$X_2$を選びます。そうしてつぎのようなニューラルネットワークを作ります。
実行ボタンを押して少し経つと画面が動いて、2つの赤と青の点が分離されます。
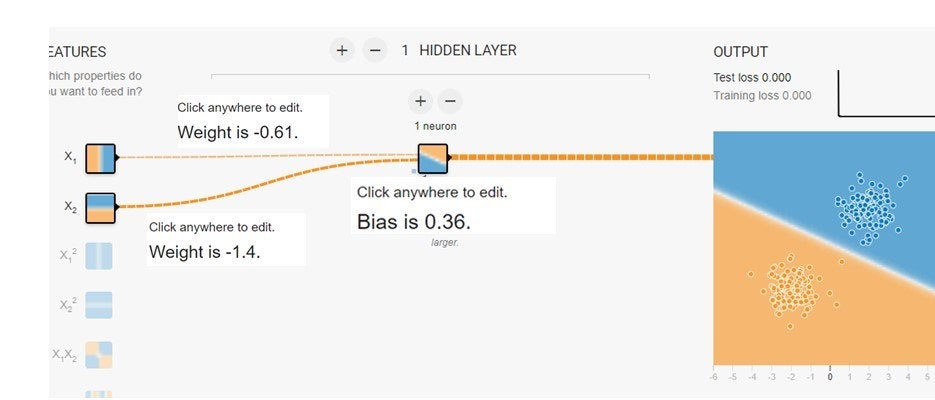
カーソルをニューロンを結ぶ線の上に持って行ってみてください。重みが現れます。ニューロンの左下の黒いボッチに持って行ってみてください。バイアスが現れます。これらの重みとバイアスは青と赤の点を分離する境界線を表現します。式で表してみましょう。
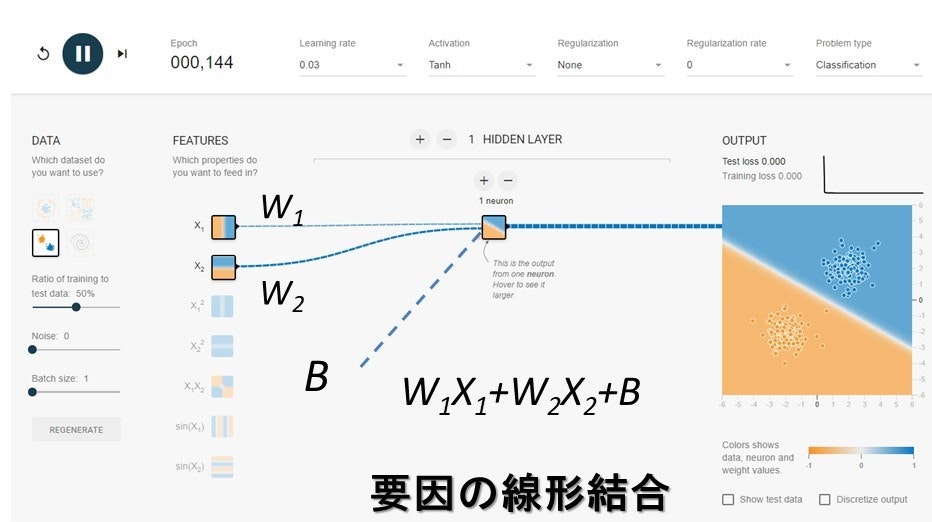
正則化を試す
ディープラーニングでは層を増やしたり、ユニットの数を増やしたりして、複雑なパターンに対応できるモデルを構築します。そのために、自由度が高くなりすぎて、過学習が起きやすくなります。したがって、この過学習を抑制する技術が必要です。
過学習に陥る原因として
- パラメータの数が多すぎる
- 訓練データの数が十分ではない
- データにノイズが含まれている
の3つが主に考えられます。これらの過学習を抑える方法として正則化という方法が考えられています。これはある特定の重みが大きくなることで起きてしまう過学習を防ごうという考え方です。重みの最適化では損失関数の値を最小にします。そこで、重みが大きくなりすぎることを避けるために、損失関数の中に重みの関数を加えて、重みが大きくなることを防ぐのです。その方法には2つあり、
L1正則化:
ペナルティーとして損失関数に
$\sum ||w_i||$
を加える。
L2正則化(荷重減衰):
ペナルティーとして損失関数に
$\sum ||w_i||^2$
を加える。
つぎに入力にすべての入力データを選択し、隠れ層もニューロンもめいっぱい増やしましょう。
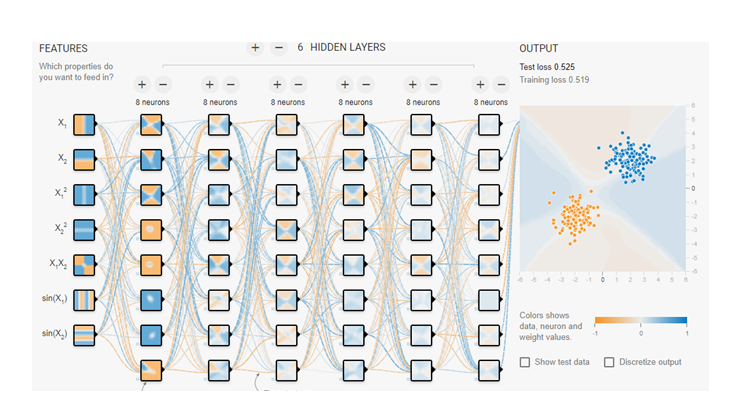
これを実行するととりあえずはうまく分離ができますが、すこしひん曲がってしまいます。
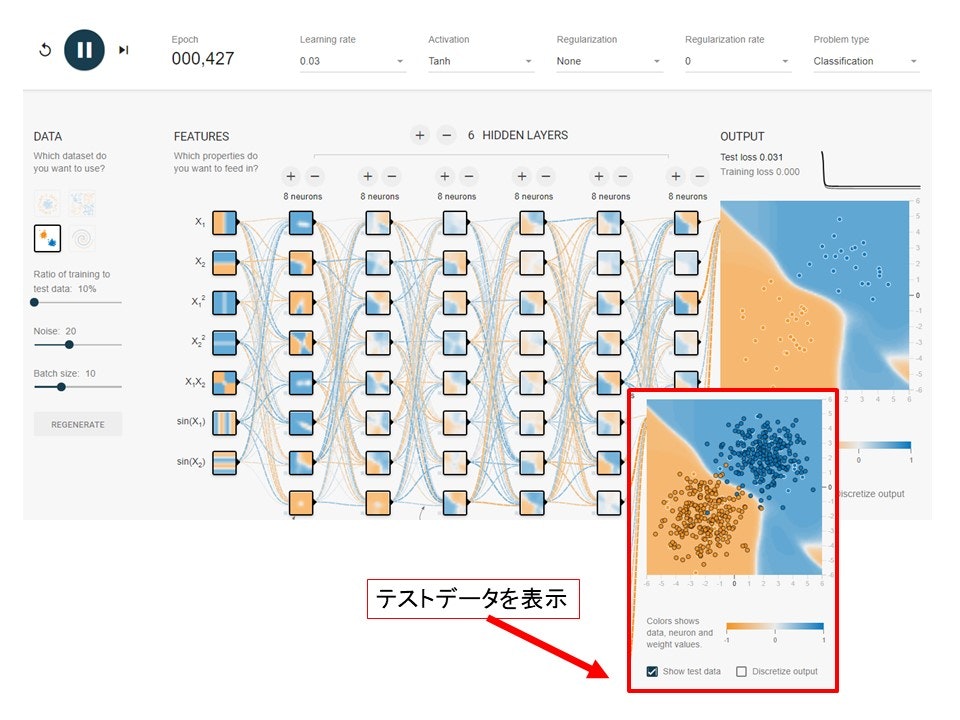
どうでしょうか?これにもっとノイズを加えてください。分離はぐちゃぐちゃになってしまいます。それぞれのニューロンとニューロンをつなぐ線を見てみるとばらばらに配分されていることが分かります。
そこで活躍するのが正則化の技術です。まずはRegularizationをL1に変更し、rateを0.03にします。結果は以下の通りです。
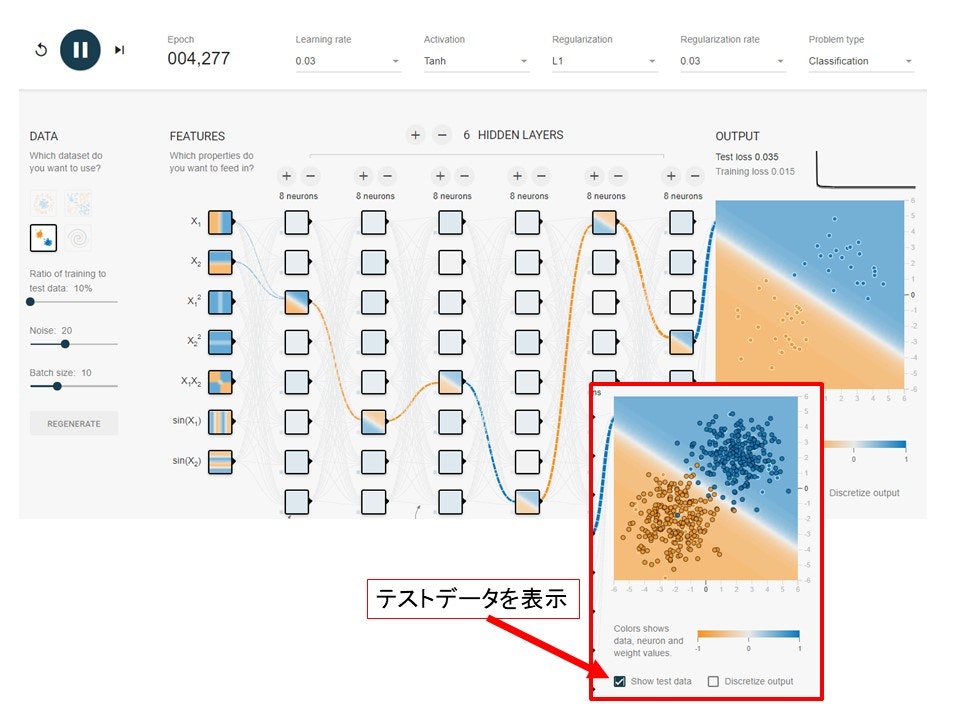
なんと入力のデータが$X_1$と$X_2$に限定されました。そして隠れそうですが、ニューロンの数が1つに限定され、ボックスのなかの模様を見るとどれも同じような直線になっているので、機能を限定しているのが分かります。
つぎにL2正則化を使ってみましょう。RegularizationをL2に変更し、rateを同じく0.03に設定します。
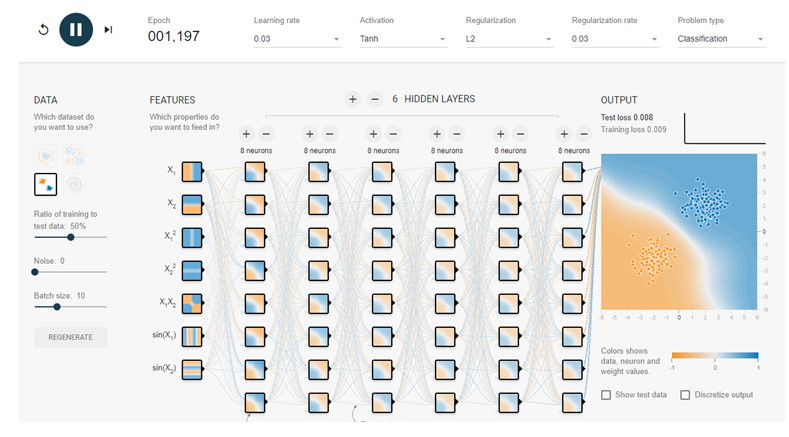
L1ほどではないにしても効果はありそうです。それぞれのニューロンを結ぶ線とボックスの中の模様を見てみてください。L1正則化とは全く違う形で機能しているのが分かります。
一般にL1正則化は重要なものを選択する機能があって、L2正則化は均等に配分する性質があることが分かります。同じ正則化でも用途によって使い分けをしないと、うまく機能しないことがこんな簡単なテストからわかります。
熱ゆらぎと量子ゆらぎ
ニューラルネットワークの重みを更新する際にノイズを加える方法があります。焼きなまし法と呼ばれます。この方法は勾配法に熱ゆらぎを加えていることになります。また、正則化はこの点からするの量子ゆらぎを加えていることになります。量子コンピュータが人工知能を加速する。参照
参考:
「脳・心・人工知能 数理で脳を解き明かす」(ブルーバックス)
「圧縮センシングにもとづくスパースモデリングへのアプローチ」