More than 1 year has passed since last update.

Python3ではじめるシステムトレード: システムトレードにおける対数の役割

Last updated at 2023-05-03Posted at 2019-01-31

システムトレードという言葉は和製英語で正式にはsystematic tradingといいます。予め定められた規則に従って株式、債券、為替などの流動性の高い(取引の活発な)金融商品を売買する方法だと考えればよいと思います。長い間、金融商品の価格を科学的に分析するといっても、十分なデータが得られずに来ました。そのために、イデオロギーや概念、語り継がれている売買手法が注目を浴びてきました。しかし、システマティック・トレーディングの世界ではデータを重視して、売買の方法を探していきます。したがって、本書がもっとも大事にしているのが

データ
モデル
売買の規則
一貫性
です。

データを客観的に分析するために、価格の動きのメカニズムを説明するモデルを考えます。また、投資目的を達成するために売買の方法を作り上げていきます。設計した売買が実現可能かどうかを判断するためには、金融市場の売買のメカニズムを知っている必要があります。そして、出来上がった取引手法の作り出す成果、またはその効果を客観的に判断するために、統計的手法を用います。

利回り、収益率、変化率

投資によりどれだけの収益が得られたかを表す用語として、利回りとか、収益率とか、変化率とか、金融の世界では混乱を招く表現が数多くあります。利回りとは、投資期間中に得られた収益を、その投資額で割った比率です。この収益には投資期間中に得られた利子、配当、資産価格の変化が含まれます。

利回り

たとえば銀行に100万円預金したときに、利子率が5%で5年間投資すると、利子25万円が得られます。そうするとそのときに収益は25万円になります。年間収益は(25/5)万円=5万円になります。これを投資金額の100万円で割ると5%になります。これを利回りと呼び、このような利回りは単利といいます。

つぎに途中で支払われる利子にも利子が支払われる場合があります。このような性質をもつ利子は、単利ではなく複利といいます。

1年後の元利合計　100x(1+0.05)=105　　

2年後の元利合計　105x(1+0.05)=110.25　　

3年後の元利合計　110.25x(1+0.05)=115.7625　　

4年後の元利合計　115.7625x(1+0.05)=121.55　　

5年後の元利合計　121.55x(1+0.05)=127.63　　

になります。将来の受取額は

預金元本ｘ(1+利子率）^年数

になります。単利と複利で受取額が異なるので注意してください。また、年何回の利子を得るかでも計算は違ってきます。

つぎに利子が支払われない割引債の投資を考えてみましょう。

単利では　(償還価格－買付価格)/買付価格x365/未経過日数(1年未満)x100

複利では (償還価格/買付価格)^(1/残存年数)x100

になります。このような計算は、日本、米国、ヨーロッパで方式が異なるので注意しましょう。

つぎにこの複利の考え方を連続複利の考え方へと拡張します。
連続複利にするということは

r^n=(償還価格/買付価格)

として、ｎを無限にするということです。
これは実際に対数を用いて計算することになります。

r^n=(償還価格/買付価格)=1.03

r-1=log(償還価格/買付価格)=log(1.03)=0.02955880224154443

検算してみます。

(1+(r-1)/100000)^100000=1.0299999955093537

大体1.03になりました。

株価の対数をとるということは、買付価格＝１として償還価格＝株価としていることになります。
連続複利とした場合の変化率を計算していることになります。これは瞬間的変化率を計算していることになります。

リターン

さて、投資、金融工学の文献にはリターンという用語がよくでてきます。xを価格、価格の変化をdxとし、変化率を(dx)/xと定義すると、多くの場合、リターンは変化率という意味で使われています。たとえば、株式の売買で価格の変化により得た利益は、利息とか、配当とかは関係ありません。つまり、価格の変化の度合いだけによって、利益が確定しています。したがって、リターンは

売付価格/買付価格―1

で表現されます。これを年率に換算したい場合があります。その際には、

(売付価格/買付価格)^(252/投資営業日数)-1

が用いられる場合があります。営業日をもとに考える場合、1年間の長さは国によって異なり、大体250－260の間の数字が使われるようです。

対数リターン・対数収益率

長期の投資では対数リターンが用いられる場合もあります。対数リターンは

ln(S(t))-ln(S(t-1))

で計算されます。対数リターンの平均は

E(X)=(X1+X2+,....,+Xn)/n

で求められます。ここでX1=ln(X(t))-ln(X(t-1))です。X(t)はｔ時の価格です。

これを年率換算するには

exp(E(X))^252

となります。E(X)は幾何平均で近似可能です。

ボラティリティの計算

金融市場でのボラティリティとは、年率換算した価格の変動性を示します。一般には日々の対数リターンの標準偏差を年率換算します。対数リターンは

ln(S(t))-ln(S(t-1))

で計算されます。分散はそれぞれの確率変数(X1,X2,...,Xn)が独立であれば

V(X1,X2,...,Xn)=V(X1)+V(X2),...,V(Xn)

が成り立つので、年率換算した分散は日足の対数リターンから求めた分散を252倍、V(X)x252すれば求められます。

したがって、その標準偏差は日足の対数リターンの標準偏差に252の平方根を掛ければ、得られます。

対数リターンの代わりに幾何平均を用いて近似が可能です。

実際にデータを取得してグラフに描いてみましょう

%matplotlib inline 
import matplotlib.pyplot as plt #描画ライブラリ
import pandas_datareader.data as web #データのダウンロードライブラリ
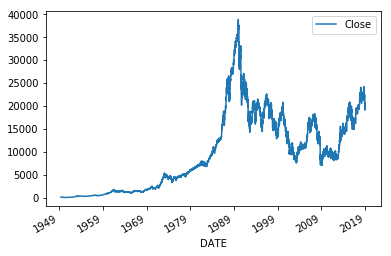
ts = web.DataReader("NIKKEI225","fred","1945/1/1").dropna()#jpy
ts.columns=['Close']
ts.plot()

まさしくどこかこ金融当局のおえらさんが言っているように最近は金融市場のボラティリティが高くてけしからんという話になります。
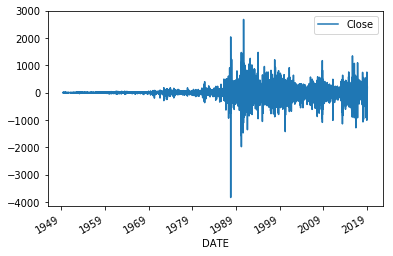
どれくらい価格の変動が激しいかは価格の差を取ってグラフにしてみると大抵のことは簡単にわかります。

ts.diff().plot()

確かにバブル崩壊後は価格変動が激しくてけしからん。高頻度取引(HFT)のせいだということになります。

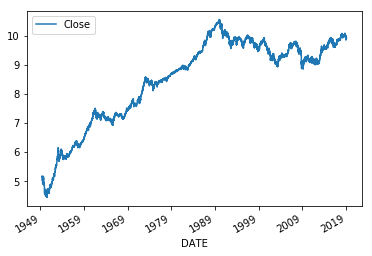
そこで価格の対数を取ってみましょう。まずは対数リターンのグラフです。

np.log(ts).plot()

なんと全然違うグラフになりました。金融市場では人の感情に特別な思いを描かせるのは非常に簡単なことなのです。つぎに価格の変動制について見てみましょう。

lnts=np.log(ts).dropna()
lnts.diff().plot()

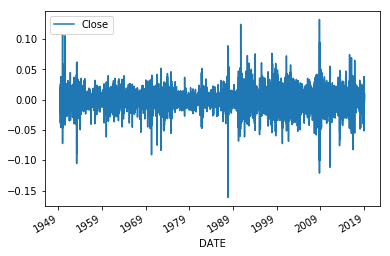
価格の対数を取るとなんと全然違う価格の動きになります。投資をするときにはこちらの動きのほうが大事です。金融工学ではすべて価格の対数を取るのはこのためです。

価格の対数をとるのはなぜですか？

価格の桁の調整

価格は上昇し続けると価格の桁が変わってしまいます。そのような価格上昇をグラフに描くと右肩上がりの指数関数的な上昇になります。そのようなグラフでは、直近の価格の動きは把握しやすいのですが、価格の水準の低いときの価格の動きはすべてつぶれてしまいます。そのようなグラフでは直感的に価格の動きをつかめません。

たとえば、価格が1,10,100,1000,10000,100000,1000000と動くとき、ｘ軸に時間、y軸に価格をとると、時間の経過とともに、指数関数的に上昇するグラフになります。

この価格を10の0,1,2,3,4,5,6乗と表現することができます。この整数の部分をy軸にプロットすると直線のグラフになり、見やすくなります。

このような計算には対数を用います。対数には常用対数と自然対数があります。常用対数ではx=a^pをlog_a(x)=pのようにあらわします。aを底と呼びます。自然対数ではa=e(ネイピア数)とします。x=e^pをln(x)=pと書きます。ここで気をつけなければいけないのは、本書のプログラムの中ではnupmyのlogを用いています。しかし、このlogはlnの意味です。間違えないようにしましょう。さらにnumpyで常用対数を使いたいときには、log10を用います。