今回は最大公約数について特集します!
最大公約数は、初等整数論の醍醐味をたっぷりと味わえる題材です。競プロをやっている方だけでなく、大学受験を志す方にも有益なものが満載です。
(なお、最近の Qiita スマホ表示の不具合により、スマホでは数式がうまく表示されない可能性があります)
0. はじめに
今回は AtCoder の整数問題の中でも特に多い最大公約数に関する知見をまとめます。今回も前回と同様、登場するアルゴリズム自体はたった 1 個です。
Euclid の互除法とは、二つの整数 $a, b$ の最大公約数を求めるアルゴリズムです。たったそれだけなのですが、最大公約数については考えることがものすごく沢山あります。前回の素因数分解と同様、最大公約数も
単にアルゴリズムを覚えるだけでなく、最大公約数という概念について深く理解すること
がとても重要だと思います。最大公約数が登場するような問題は、問題文だけからはそのことが読み取れず、editorial で突然登場するものと思われがちです。しばしば「地頭ゲー」などとよばれてしまいます。しかし、最大公約数が登場するのには明確な背景や理由があります!!
本記事では、最大公約数が登場するシチュエーションを徹底的に特集します!前半は 300 点問題相当の易しい話題ですが、後半は 500〜600 点問題相当の話題に及びます。前半の話題が簡単過ぎると感じた場合には、「5 章: 「互いに素」の性質」の辺りから読み始めていただけたらと思います。
前半 (易しめ)
後半 (難しめ)
ラスト
本記事の目標の一つは、整数 $a, m$ が与えられたときに、
$0, a, 2a, 3a, 4a, \dots$
を $m$ で割ったあまりの分布について、明快なイメージを得ることです。まずはその前に Euclid の互除法そのものについて確認しましょう。
1. Euclid の互除法とは
まずは本記事全体を通して用いる Euclid の互除法を紹介します。
1-1. Euclid の互除法
Euclid の互除法は、以下のようなフローチャートにしたがって二つの整数 $a, b$ の最大公約数を求めるアルゴリズムです。
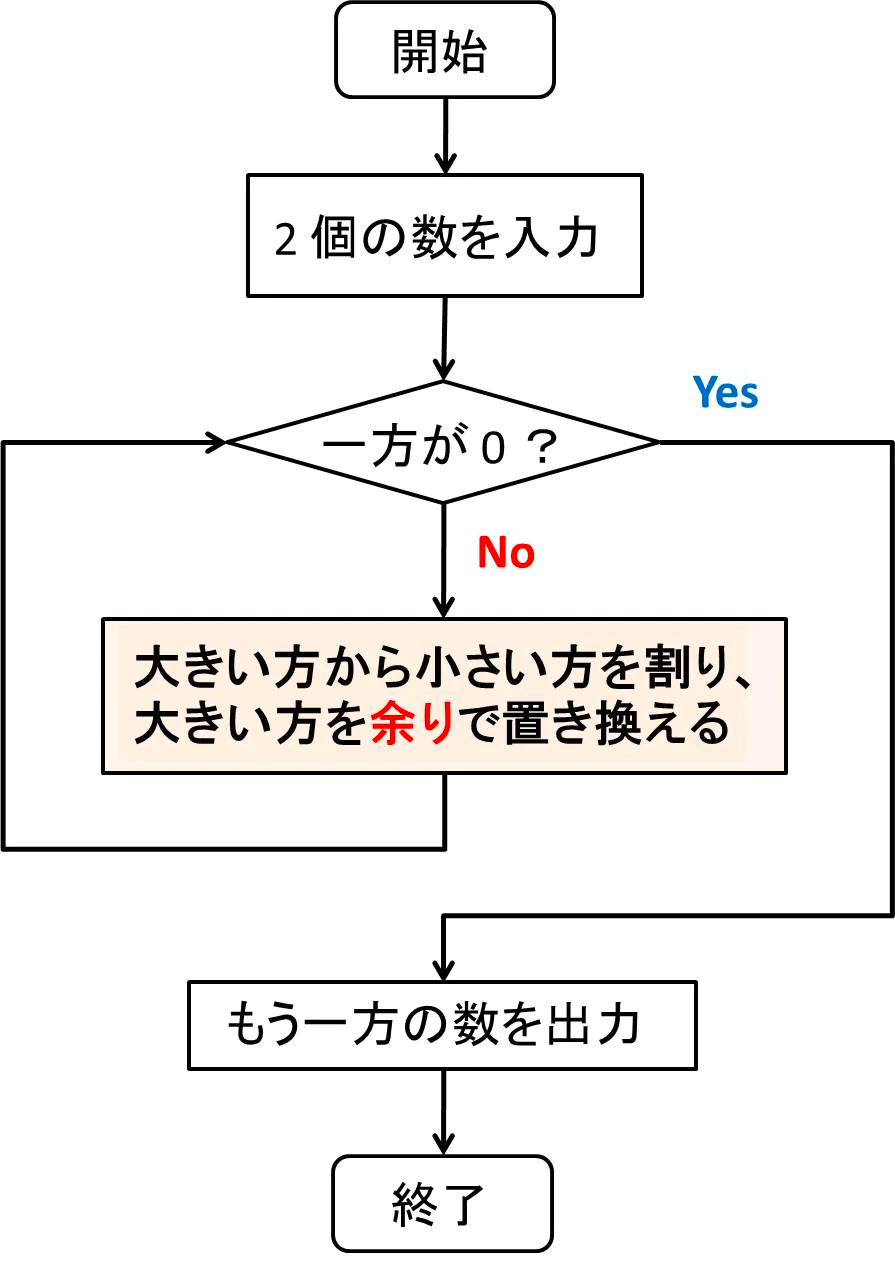
たとえば、$81$ と $30$ の最大公約数は次のように求められます。
- $81$ を $30$ で割る: $81 ÷ 30 = 2$ あまり $21$
- $30$ を $21$ で割る: $30 ÷ 21 = 1$ あまり $9$
- $21$ を $9$ で割る: $21 ÷ 9 = 2$ あまり $3$
- $9$ を $3$ で割る: $9 ÷ 3 = 3$ あまり $0$
- 割り切れたらおしまい。最後に残った数は $3$ と $0$ で、答えは $3$
という風になります。最大公約数は $3$ です。さて、以上の手続きは、再帰関数を用いると明快に実装することができます。また、本記事ではこれ以降、$a, b$ の最大公約数を ${\rm GCD}(a, b)$ と表すことにします。
// a と b の最大公約数を返す関数
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
1-2. Euclid の互除法のイメージ
Euclid の互除法の大まかなイメージを掴むことを試みます。まず二つの整数 $a, b$ の最大公約数とは、次のように解釈できます。
- 縦の長さが $a$、横の長さが $b$ であるような長方形がある
- それを、なるべく一辺の大きな正方形で敷き詰めたい
- 正方形の一辺の長さの最大値が、$a, b$ の最大公約数である
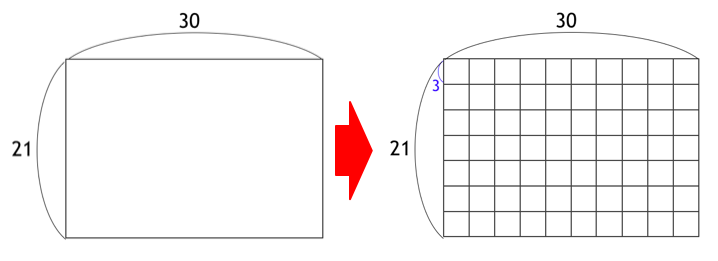
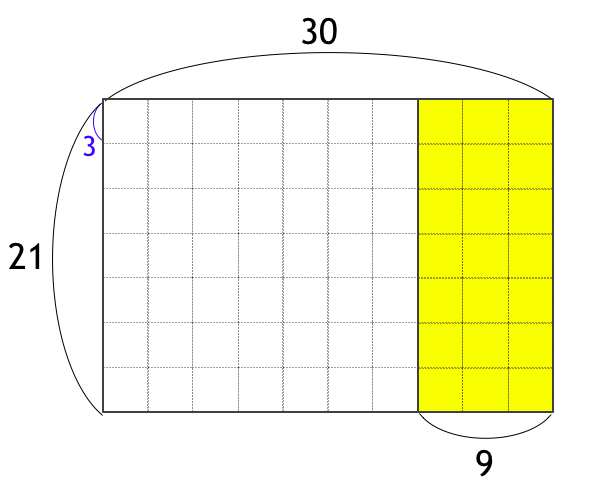
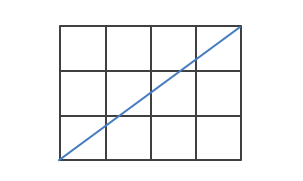
$a = 21, b = 30$ の場合は、下図のように 3 x 3 の正方形で敷き詰めることができます。これ以上大きな正方形で敷き詰めることはできないです。
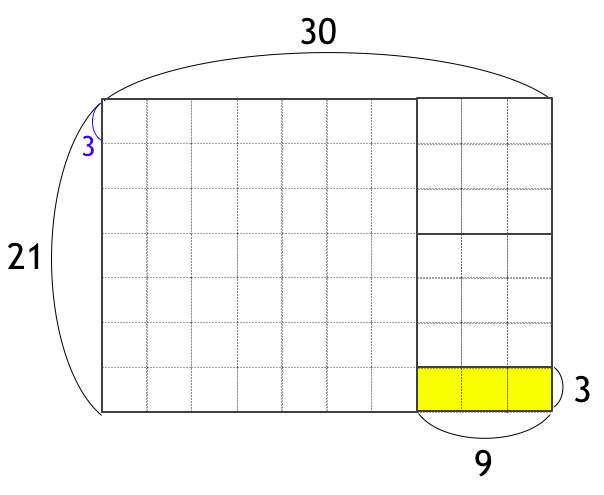
Euclid の互除法は、下図のように、「長方形から正方形を切り取る」のを繰り返す処理に対応しています。まず、21 x 30 から正方形を切り取ると、9 x 21 が残ります。
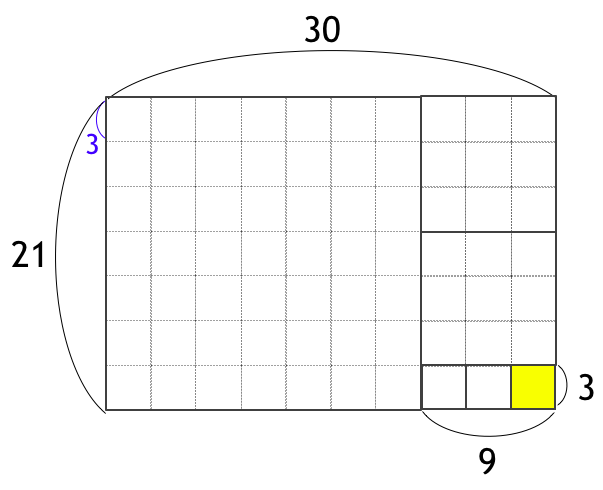
次に、9 x 21 の長方形から、正方形を 2 個切り取ると、3 x 9 が残ります。
最後に、3 x 9 は、「3 x 3」の正方形 3 個で構成されることになります。こうして最後に残った正方形は 3 x 3 なので、最大公約数は 3 だとわかりました。直感的には、一連の操作の過程で、常に「点線」に沿って切っていくことになるので、最後に残るのは点線の正方形の最小単位になりそうです。
Euclid の互除法によって正しく最大公約数が求められることの正式な証明は、あとで行いましょう。まずは簡単な問題を通して、最大公約数の考え方に慣れることを目指します。
1-3. Euclid の互除法の計算量
二つの整数 $A, B$ の最大公約数を求めるのに要する計算量は、$A < B$ とすると、$O(\log A)$ となります。対数オーダーということで、非常に高速です!!!
対数オーダーになる理由については、以下の記事に詳しく記したので、参考にしていただけたらと思います。
2. 単純に「最大の公約数」を求める
まずは文字通り、単純に「最大の公約数を求めたい」というタイプの問題を考えます。「最小公倍数」についても見ていきます。
2-1. 単純な最大公約数ゲー
次の問題を考えてみましょう。
問題 1: ABC 109 C - Skip (300 点)
$N$ 個の都市が一直線上に並んでおり、それぞれの座標は $x_1, x_2, \dots, x_N$ である。座標 $X$ から出発して、最終的にすべての都市に訪れたい。
ここである正の整数 $D$ を設定する。その後、座標 $X$ から出発して、$D$ ずつの移動しかできない (座標 $x$ から移動できる地点は、$x + D$ と $x - D$ のみ)。すべての都市を訪れることが可能であるような $D$ の設定のうち、最大値を求めよ。
- $1 \le N \le 10^5$
- $1 \le X, x_i \le 10^9$
(数値例)
・$N = 3$
・$X = 3$
・$x = (1, 7, 11)$
答え: 2
座標 3 から出発して、3 → 1 → 3 → 5 → 7 → 9 → 11 という移動で全都市を回ることができます。
条件を整理すると、次のようになります。
- $|X - x_1|$ が $D$ で割り切れる
- $|X - x_2|$ が $D$ で割り切れる
- ...
- $|X - x_N|$ が $D$ で割り切れる
この条件を満たしていれば、たとえば、$X$ から $x_1$ へ行って、一旦 $X$ へと戻って、また $x_2$ へと行って、一旦 $X$ へ戻って... と繰り返すことで、全都市を回ることができます。
この条件は、
- $D$ が $N$ 個の整数 $|X - x_1|, |X - x_2|, \dots, |X - x_N|$ の公約数である
と言い換えることができます。そのうちの最大のものを求めたいのですから、答えはこれらの最大公約数です。
なお、3 個以上の値の最大公約数を求めるためには、
-
res = 0と初期化 - 各 i に対して
res = GCD(res, x[i])と更新する
という風にして求めることができます。
# include <iostream>
using namespace std;
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
int main() {
int N; cin >> N;
long long X; cin >> X;
long long res = 0;
for (int i = 0; i < N; ++i) {
long long x; cin >> x;
res = GCD(res, abs(x - X));
}
cout << res << endl;
}
2-2. 単純な最小公倍数ゲー
続いて最小公倍数についても見ていきましょう。
問題 2: ABC 148 C - Snack (300 点)
パーティ来場者のためにお菓子を配りたい。パーティ参加人数は $A$ 人である可能性と、$B$ 人である可能性とがある。どちらの場合においても各参加者に配るお菓子の個数が均等になるようにしたい。
そのようなことが可能となるようなお菓子の個数の最小値を求めよ。
- $1 \le A, B \le 10^5$
(数値例)
・$A = 2, B = 3$
答え: 6
6 個のお菓子があれば、2 人の場合は 3 個ずつ、3 人の場合は 2 個ずつ配ることができます。
これはもう本当に単純に「$A$ と $B$ の最小公倍数を求めてください」という問題ですね!!!
最小公倍数は最大公約数を用いて求めることができます。$A, B$ の最大公約数を $G$ とおくと、$A, B$ の最小公倍数を $L$ として、
$G \times L = A \times B$
が成り立ちます。よって、$L$ は
L = A / GCD(A, B) * B
と求めることができます。ここで注意点として、A * B / GCD(A, B) としてもよいのですが、A * B の部分でオーバーフローしてしまうリスクを少しでも軽減するために、上のようにするのをしばしば見かけます。
# include <iostream>
using namespace std;
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
int main() {
long long A, B;
cin >> A >> B;
cout << A / GCD(A, B) * B << endl;
}
3. Euclid の互除法っぽい「操作」
ここまでの問題は、問題文を読めば最大公約数・最小公倍数を求めたいということが明らかなタイプの問題でした。ここから先は、慣れてないと見抜きにくい問題になります。
3-1. Euclid の互除法の原理
まず、Euclid の互除法の原理をおさらいします。以下では、合同式を用いているので、それに馴染みのない方は定義を確認してもらえたらと思います。
【Euclid の互除法の原理】
$a \equiv b \pmod m$ であるとき、
{\rm GCD}(a, m) = {\rm GCD}(b, m)
が成立する。
アルゴリズムとしての Euclid の互除法は、上の原理における $b$ に対して「$a$ を $m$ で割ったあまり」を代入したものを、再帰的に適用するものでした。しかしここで注意したいことは、$b$ は必ずしも「$a$ を $m$ で割ったあまり」ではなくてもよいということです。$a \equiv b \pmod m$ でありさえすればよいのです。たとえば $a \equiv a - m \pmod m$ ですから、
- ${\rm GCD}(a, m) = {\rm GCD}(a-m, m)$
が成立します。このことを利用して次の問題を解いてみましょう。
問題 3: ABC 118 C - Monsters Battle Royale (300 点)
$N$ 匹のモンスターがいて、それぞれ体力は $A_1, A_2, \dots, A_N$ となっている。モンスターは互いに互いを攻撃し合う。
- 体力が $a$ のモンスターが体力 $b$ のモンスターを攻撃したとき、
- 体力 $b$ のモンスターの体力は $b-a$ となる
- 体力が $0$ 以下となったモンスターは消える
最後まで残ったモンスターの体力として考えられる最小値を求めよ。
(制約条件)
- $2 \le N \le 10^5$
- $1 \le A_i \le 10^9$
(数値例)
・$N = 4$
・$A = (2, 8, 10, 12)$
答え: 2
先頭のモンスターが他のモンスターを攻撃し続けたとき、最後に残るモンスターの体力は $2$ になります。
二匹のモンスターの体力 $(a, b)$ が $(a, b-a)$ になるというのが、いかにも Euclid の互除法っぽいですね。この時点で、答えが最大公約数になりそうな予感がしてきます。僕はコンテスト本番では正直、この時点で GCD を実装し始めていました。
しかし一応きちんと証明してみましょう。まず、$g = {\rm GCD}(a_1, a_2, \dots, a_N)$ としたとき、答えを $g$ より小さくすることは絶対にできません。なぜなら、どんなに操作を繰り返しても、
「どのモンスターの体力も $g$ の倍数である」
という状態は一生変わらないためです。このように、どのように操作を施しても変わらないものを不変量とよびます。適切な不変量を見つけることは、AtCoder の問題に挑むときにしばしば重要です。
よって、答えはどんなに小さくても $g$ 以上であることがわかりました。逆に $g$ を達成できることは、Euclid の互除法からわかります。Euclid の互除法の動きをシミュレートすればよいだけです。
以上をまとめると、答えは $g = {\rm GCD}(a_1, a_2, \dots, a_N)$ となります。
# include <iostream>
using namespace std;
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
int main() {
long long N;
cin >> N;
long long g = 0;
for (int i = 0; i < N; ++i) {
long long a; cin >> a;
g = GCD(g, a);
}
cout << g << endl;
}
3-2. Euclid の互除法の原理の証明
最後に、Euclid の互除法の原理を示してみましょう。$a \equiv b \pmod m$ のとき、${\rm GCD}(a, m) = {\rm GCD}(b, m)$ が成立することを示します。以下の二つを示せばよいです。
- ${\rm GCD}(b, m)$ が ${\rm GCD}(a, m)$ で割り切れること
- ${\rm GCD}(a, m)$ が ${\rm GCD}(b, m)$ で割り切れること
お互いがお互いを割り切るので、結局「両者は等しい」ということになります。対称性から前者のみ示せば十分です。
$g = {\rm GCD}(a, m)$ とおきます。このとき
- $a$ は $g$ の倍数
- $m$ は $g$ の倍数
となっていることに注意しておきましょう。さて、$a \equiv b \pmod m$ であることより、整数 $q$ を用いて
b = a + mq
と表すことができます。ここで $a, m$ がともに $g$ の倍数であることを思い出すと、$b$ も $g$ の倍数であることがわかります。よって、逆に
- $g$ は $b$ の約数
ということになります。また $g$ は元々 $m$ の約数でもありました。したがって、$g$ は $b, m$ の公約数です。これは、$g$ が ${\rm GCD}(b, m)$ の約数であることを意味します。以上より、示されました。
(証明終わり)
4. 「互いに素」への帰着
最大公約数を考える理由のかなり多くは「互いに素な場合に帰着したいから」です!!!
二つの整数 $a, b$ が互いに素であるとは、以下の条件を満たすような整数 $d$ が存在しないことをいいます:
- $d > 1$
- $a$ は $d$ で割り切れる
- $b$ は $d$ で割り切れる
つまり、言い換えれば「${\rm GCD}(a, b) = 1$」ということです。
4-1. 「互いに素」への帰着方法
二つの整数 $a, b$ が与えられたとき、その最大公約数を $g$ とすると、
- $a = ga'$
- $b = gb'$
とおくことができて、$a', b'$ は互いに素となります。たとえば $a = 12, b = 20$ のとき、最大公約数である $4$ で割ると、$a' = 3, b' = 5$ となって、これらは確かに互いに素となっています。
「互いに素」という性質は、整数論によって極めて強力で重要なものです。まずは簡単な例題を通して、互いに素への帰着という考え方を体験しましょう。蟻本の例題にもなっている有名問題です。
問題 4: 線分上の格子点の個数
平面上の二つの格子点 $(a_x, a_y), (b_x, b_y)$ が与えられる。
この二点を結ぶ線分上に何個の格子点があるか求めよ (両端を含まない)。
- $-10^{9} \le a_x, a_y, b_x, b_y \le 10^{9}$
(数値例)
・$(1, 1), (5, 5)$
答え: 3
$(2, 2), (3, 3), (4, 4)$ の 3 個の格子点があります。
二つの格子点の位置関係だけが重要なので、
- $x = |a_x - b_x|$
- $y = |a_y - b_y|$
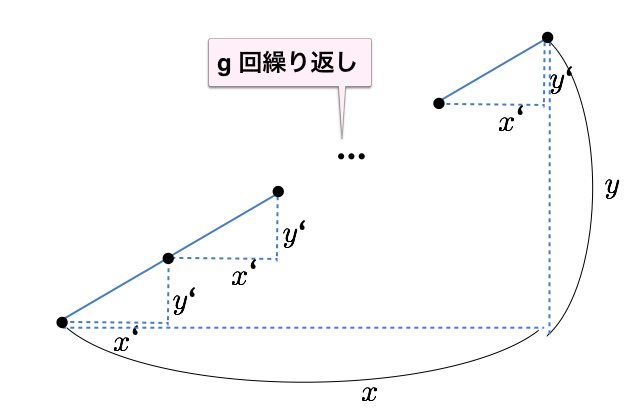
として、線分 $(0, 0), (x, y)$ について考えましょう。実は、仮に $x, y$ が互いに素であれば簡単です。下図は $x = 4, y = 3$ の場合を示しています。$x, y$ が互いに素である場合には、線分が格子点を通ることはないです (格子点を通ると仮定すると、「傾き」を表す $\frac{y}{x}$ が既約分数ではないということになります。それは $x, y$ が互いに素であることに矛盾します)。
$x, y$ が互いに素である場合には簡単に答えが出ることがわかったので、その場合に帰着させましょう。$g = {\rm GCD}(x, y)$ とします。
- $x = gx'$
- $y = gy'$
とすると、$x', y'$ は互いに素となります。そして元の線分は、$(x', y')$ の差分移動を $g$ 回繰り返したものになることがわかります。よって答えは、$g-1$ 個です。
# include <iostream>
using namespace std;
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
int main() {
long long ax, ay, bx, by;
cin >> ax >> ay >> bx >> by;
cout << GCD(abs(ax-bx), abs(ay-by)) - 1 << endl;
}
4-2. もう一例
もう一つ例を見てみましょう。競プロよりむしろ大学入試でよく見るタイプの「式の扱い」かもしれません。
問題 5: yukicoder No.442 和と積
2つの正整数 $A, B$ が与えられるので、和 $A + B$ と積 $AB$ の最大公約数を求めてください。
- $1 \le A, B \le 10^{18}$
(数値例)
・$A = 2, B = 4$
答え: 2
${\rm GCD}(2 + 4, 2 \times 4) = {\rm GCD}(6, 8) = 2$ です。
$A \le 10^{18}, B \le 10^{18}$ より、$AB \le 10^{36}$ となるので、まともに $AB$ という値を用いると、64-bit 整数の範囲内で扱うことができず、多倍長整数が必要となります。ここでは、64-bit 整数の範囲内で解くことを考えましょう。
まずは $A, B$ が互いに素である場合を考えます。突然ですが、$A, B$ が互いに素ならば、$A + B, AB$ も互いに素です!!!
このことは慣れてくればすぐに見えるのですが、順を追ってみていきましょう。まず、$A, B$ が互いに素であるとき、$A + B, A$ も互いに素です。それは Euclid の互除法より、
{\rm GCD}(A + B, A) = {\rm GCD}(B, A) = 1
となるからです。同様に、$A + B, B$ も互いに素です。ここで、一般に $m, a$ が互いに素で、$m, b$ も互いに素であるとき、$m, ab$ は互いに素となることに注意しましよう (素因数分解を考えれば納得できます)。以上から $A + B, AB$ が互いに素であることがわかりました。
改めて、$A, B$ が互いに素とは限らない一般の場合を考えましょう。$g = {\rm GCD}(A, B)$ として、
- $A = gA'$
- $B = gB'$
とします。先ほどの $A' + B'$ と $A'B'$ が互いに素であるという知見を用いると、
\begin{align}
{\rm GCD}(A + B, AB) &= {\rm GCD}(g(A' + B'), g^2A'B') \\
&= g{\rm GCD}(A' + B', gA'B') \\
&= g{\rm GCD}(A' + B', g)
\end{align}
という風に計算できます。ここで、${\rm GCD}(A' + B', gA'B') = {\rm GCD}(A' + B', g)$ の部分について補足します。一般に $a$ と $b$ が互いに素であるときに ${\rm GCD}(a, bc) = {\rm GCD}(a, c)$ が成立します。今回は、$A' + B'$ と $A'B'$ が互いに素であることから、${\rm GCD}(A' + B', gA'B') = {\rm GCD}(A' + B', g)$ が成立します。
ここまで来れば、${\rm GCD}(A' + B', g)$ の値は 64-bit 整数の範囲内で扱うことができます。
# include <iostream>
using namespace std;
long long GCD(long long x, long long y) {
if (y == 0) return x;
else return GCD(y, x % y);
}
int main() {
long long A, B;
cin >> A >> B;
long long g = GCD(A, B);
A /= g, B /= g;
cout << g * GCD(A + B, g) << endl;
}
5. 「互いに素」の性質たち
いよいよ本記事の核心部に入っていきます。
「互いに素」はとても強力な性質です。これから挙げる性質たちは、実は全部ほとんど同じことを言っていて、「同じ構造」を別の側面から眺めたものになっています。これらの性質と触れ合うことで、整数の整除の構造に対する手触りを強く感じ取ることを目指します。
性質(1): ax + by
整数 $a, b$ が互いに素であるとき、
ax + by = 1
を満たす整数 $x, y$ が存在する。
大学受験では超お馴染みで、競プロでもよく見かける性質ですね。たとえば $a = 7, b = 9$ のとき、$x = 4, y = -3$ とすると、$ax + by = 28 - 27 = 1$ となって条件を満たします。
このような整数 $x, y$ は、拡張 Euclid の互除法とよばれるアルゴリズムによって具体的に構成することができます (お馴染みの modint の割り算でも活躍するアルゴリズムですね!)。その詳細は
に書きましたが、簡単に振り返ってみます。$b$ を $a$ で割った商を $q$、あまりを $r$ とすると、
b = aq + r
と書くことができます。これを元の式に代入すると、
ax + (aq + r)y = 1 \\
\Leftrightarrow ry + a(x + qy) = 1
と変形できます。これを見ると、係数 $(a, b)$ に関する問題が、係数 $(r, a)$ に関する問題へと帰着できたことがわかります。そして、$rx' + ay' = 1$ を満たす $(x', y')$ を再帰的に求めてあげて、
y = x' \\
x + qy = y'
という関係式によって $(x, y)$ を定めてあげればよいです。具体的には
x = y' - qx' \\
y = x'
と求まります。次のように実装することができます。下の実装では、より一般に、
ax + by = {\rm GCD}(a, b)
を満たす整数 $(x, y)$ を求めていて、$d = {\rm GCD}(a, b)$ を戻り値として返す関数を実装しています。
// ax + by = gcd(a, b) となるような (x, y) を求める
// 多くの場合 a と b は互いに素として ax + by = 1 となる (x, y) を求める
long long extGCD(long long a, long long b, long long &x, long long &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
// 再帰的に解く (x, y を入れ替えておく)
long long d = extGCD(b, a % b, y, x);
y -= a / b * x;
return d;
}
性質 (2): 特に大切な性質
整数 $a, b$ が互いに素であるとする。
このとき、$bc$ が $a$ で割り切れるならば、$c$ が $a$ で割り切れる。
「互いに素」の最重要性質といっても過言ではない性質です。実は、性質 (1) から簡単に示すことができます1。
$a, b$ が互いに素なので
ax + by = 1
を満たす整数 $x, y$ が存在します。このとき、
c = c(ax + by) = acx + bcy
となります。$acx$ は当然 $a$ の倍数であり、$bc$ も $a$ の倍数なので、$c = acx + bcy$ は $a$ の倍数となります。
性質 (3): 合同式の割り算
整数 $a, m$ が互いに素であるとする。
ax \equiv ay \pmod m
であるとき、
x \equiv y \pmod m
が成立する
これは、競プロでもよく登場しますね (ABC 158 E - Divisible Substring など)。性質 (2) からすぐに示すことができます。
$ax \equiv ay \pmod m$ は、$a(x - y)$ が $m$ の倍数であることを意味します。$a$ と $m$ が互いに素なので、$x - y$ が $m$ の倍数となります。よって
x \equiv y \pmod m
が成立します。
性質 (4): 倍数の周期性
整数 $a, m$ が互いに素であるとする。
0, a, 2a, \dots, (m-1)a
を $m$ で割ったあまりを並び替えると、
0, 1, 2, \dots, m-1
に一致する。
初等整数論であまりにもよく登場する定理ですね。特に、$m$ を素数とした場合を考察することで、有名な Fermat の小定理を導くこともできます。その話題については以下の記事にまとめました。
早速示してみましょう。まず、$0, a, 2a, \dots, (m-1)a$ を $m$ で割ったあまりが互いに相異なることを示します。$0 \le i < j \le m-1$ である $i, j$ であって、$ai \equiv aj \pmod m$ となるものが存在すると仮定して矛盾を導きます。性質 (3) より、$i \equiv j \pmod m$ となります。しかし $0 \le i < j \le m-1$ であって、$i \equiv j \pmod m$ となることは不可能なので矛盾です。
以上より、$0, a, 2a, \dots, (m-1)a$ を $m$ で割ったあまりに重複がないことが言えました。さらに、$0, a, 2a, \dots, (m-1)a$ を $m$ で割ったあまりをすべて列挙したとき、$0, 1, 2, \dots, m-1$ の中に登場しないものが存在すると仮定して矛盾を導きます。この仮定の下では、$0, a, 2a, \dots, (m-1)a$ を $m$ で割ったあまりは $m$ 個あるにもかかわらず、$m-1$ 種類以下のあまりしか登場しないことになります。よって鳩ノ巣原理から、$0, a, 2a, \dots, (m-1)a$ を $m$ で割ったあまりに重複が生じることになって矛盾です。
以上から、$0, a, 2a, \dots, (m-1)a$ を $m$ で割ったあまりは、$0, 1, 2, \dots, m-1$ がちょうど 1 回ずつ登場することが示されました。
性質 (5): 逆元と合同方程式
整数 $a, m$ が互いに素であるとする。任意の整数 $b$ に対して、
ax \equiv b \pmod m
を満たす $x$ が $m$ を法としてただ一つ存在する。特に $b = 1$ の場合の解を逆元とよぶ。
これは性質 (4) を言い換えただけです。しかしながら、「逆元」という重要な概念を抽出することができました。 modint の中心となる概念です。
性質 (6): Euler 関数は乗法的
$\varphi(n)$ を Euler 関数 (前回記事参照) とする。$a, b$ が互いに素であるとき
\varphi(ab) = \varphi(a) \varphi(b)
が成立する。なお、一般に互いに素な整数 $a, b$ に対して $f(ab) = f(a) f(b)$ が成立するような整数論的関数 $f$ を乗法的関数という。
この性質の証明は、中国剰余定理を認めればすぐですが、本記事では省略します。
ここではこの性質を用いて、Euler 関数の表式を導出してみましょう。$N$ を素因数分解して
N = p_1^{e_1} p_2^{e_2} \dots p_K^{e_K}
とすると
\varphi(N) = \varphi(p_1^{e_1}) \varphi(p_2^{e_2}) \dots \varphi(p_K^{e_K})
という風に式変形することができます。よって、一般に素数 $p$ に対して $\varphi(p^e)$ を計算できればよいです。$p^e$ と互いに素であるというのは、$p$ の倍数ではないということと同値です。$1, 2, \dots, p^e$ のうち、$p$ の倍数は $\frac{p^e}{p} = p^{e-1}$ 個であるから、
\varphi(p^e) = p^e - p^{e-1} = p^e(1 - \frac{1}{p})
となります。以上から、以下のように求められます。
\begin{align}
\varphi(N) &= \varphi(p_1^{e_1}) \varphi(p_2^{e_2)} \dots \varphi(p_K^{e_K}) \\
&= p_1^{e_1} p_2^{e_2} \dots p_K^{e_K} (1 - \frac{1}{p_1})(1 - \frac{1}{p_2}) \dots (1 - \frac{1}{p_K}) \\
&= N(1 - \frac{1}{p_1})(1 - \frac{1}{p_2}) \dots (1 - \frac{1}{p_K})
\end{align}
性質 (7): Euler の定理
整数 $a, m$ を互いに素であるとき
a^{\varphi(m)} \equiv 1 \pmod m
が成立する。
最後に、Euler の定理を紹介します。これは Fermat の小定理を一般化したものとみなせます。実際、$m$ を素数とすると、
\varphi(m) = m-1
ですので、Fermat の小定理に一致します。証明は本記事では省略します。
6. 問題例
ここまでに挙げた「互いに素の性質」を活用して、色々な問題を解いていきましょう!!!
6-1. ベズーの等式
5 章の性質(1) について、$a, b$ が互いに素でない場合に拡張すると、次のようになります。通常ベズーの等式と言われている性質であり、競プロでもたびたび登場します!
整数 $N$ が整数 $x, y$ を用いて $ax + by$ の形に表せる必要十分条件は、$N$ が ${\rm GCD}(a, b)$ の倍数であることである
$g = {\rm GCD}(a, b)$ として、$a = ga', b = gb'$ とおくと、
ax + by = g(a'x + b'y)
となります。よって、$ax + by$ の形で表せる整数は $g$ の倍数でなければなりません。一方 $a'x + b'y$ は任意の整数を表せることから、$ax + by = g(a'x + b'y)$ は任意の $g$ の倍数を表すことができます。
問題 6: ABC 060 B - Choose Integers (改題!元は 200 点)
正の整数であって $A$ の倍数であるような整数を何個か持ってきて総和をとる。同じ値を何個持ってきてもよい。
この総和を $B$ で割って $C$ あまるようにすることが可能かどうか判定せよ。
- $1 \le A, B \le 10^9$
- $0 \le C < B$
(数値例)
・$A = 7$
・$B = 5$
・$C = 1$
答え: YES
7 の倍数として 21 を選ぶと、21 を 5 で割ったあまりは 1 です。
まず、$A$ の倍数は何個足しても $A$ の倍数なので、作ることのできる整数は結局「$A$ の倍数全体」となります。よってこの問題は、$A$ の倍数が、$B$ で割って $C$ あまることがありうるかどうかを判定する問題に帰着されます。
実は元の問題では、制約が $1 \le A, B \le 100$ でした。それであれば、$A, 2A, 3A, \dots, BA$ をすべて試すだけでよいです。ここでは問題を難しくして、$A, B \le 10^9$ という制約で考えてみましょう。
この問題は言い換えれば、
Ax = By + C \\
\Leftrightarrow Ax - By = C
となるような整数 $x, y (x \ge 1, y \ge 0$) が存在するかどうかを問う問題となっています。上の式の左辺が「$A$ の倍数」を表し、右辺が「$B$ で割って $C$ あまる整数」を表しています。
ここで、先ほどの定理を使うと、$C$ が $g = {\rm GCD}(A, B)$ の倍数でなければダメであることがわかります。逆に $C$ が $g$ の倍数であれば OK です ($x \ge 1, y \ge 0$ という制約が気になりますが、仮にそれを満たしていなくても、満たすようになるまで $x += B, y += A$ を繰り返していけばよいです)。
# include <iostream>
using namespace std;
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
int main() {
long long A, B, C;
cin >> A >> B >> C;
if (C % GCD(A, B) == 0) cout << "YES" << endl;
else cout << "NO" << endl;
}
6-2. 「互いに素」の整除
互いに素であれば、合同式の掛け算・割り算が同値変形できることを活用していきましょう。
問題 7: AOJ 2610 Fast Division
$0$ 以上の整数 $N$ が与えられる。$N$ に対して、$2^{2^{\dots ^{2}}}$ ($2$ が $N$ 個) より大きい最小の素数を $p$ とおく。$111 \dots 1$ ($1$ が $p-1$ 個) を $p$ で割ったあまりを求めよ。
- $0 \le N < 1000$
- $N = 0$ のとき、$p = 2$
- $N = 1$ のとき、$p = 3$
- $N = 2$ のとき、$p = 5$
- $N = 3$ のとき、$p = 17$
- $\dots$
となります。$N \ge 4$ ともなると、$p$ は急速に大きくなります。大きな $p$ に対しては答えが自動的に決まるのではないかという予感がしてきます。一方、$111 \dots 1$ は
\frac{10^{p-1} - 1}{9}
と表すことができます。$p \neq 2, 5$ のときは、$10$ は $p$ の倍数でないので、Fermat の小定理より、
10^{p-1} - 1 \equiv 0 \pmod p
となります。さらに $p \neq 3$ のときは、$p$ と $9$ が互いに素なので、
\frac{10^{p-1} - 1}{9} \equiv 0 \pmod p
が成立します。以上から、$N \ge 3$ のときは答えが $0$ になることがわかりました。$N = 0, 1, 2$ の場合は個別に計算してあげます。
# include <iostream>
using namespace std;
int main() {
int n; cin >> n;
if (n == 0) cout << 1 << endl;
else if (n == 1) cout << 2 << endl;
else if (n == 2) cout << 1 << endl;
else cout << 0 << endl;
}
6-3. 倍数の周期性
次に 5 章の性質(4) を一般化した問題を考えてみましょう。
問題 8: TopCoder SRM 490 DIV1 Easy Starport
正の整数 $N, M$ が与えられる。
$0, M, 2M, \dots, (N-1)M$ を $N$ で割ったあまりの平均値を求めよ。
- $1 \le N, M \le 10^9$
(数値例)
・$N = 4$
・$M = 2$
答え: 1.0
0, 2, 4, 6 を 4 で割ったあまりは 0, 2, 0, 2 となります。これらの平均値は 1 となります。
$N, M$ が互いに素である場合に帰着させるため、$g = {\rm GCD}(N, M)$ として
- $N = gN'$
- $M = gM'$
とおきましょう。このとき、
0, M', 2M', \dots, (N'-1)M'
を $N'$ で割ったあまりは $0, 1, 2, \dots, N'-1$ の並び替えとなります。ここで、一般に $a$ を $b$ で割ったあまりが $c$ であるとき、$ag$ を $bg$ で割ったあまりは $cg$ になることに注意しましょう。よって、
0, M, 2M, \dots, (N-1)M \\
(= 0, gM', 2gM', \dots, (N-1)gM')
を $N (= gN')$ で割ったあまりは「$0, g, 2g, \dots, (N'-1)g$ の並び替えたもの」を $g$ 回繰り返したものになることがわかります。以上より、平均値は
\frac{N'-1}{2}g
となります。
# include <iostream>
using namespace std;
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
class Starport {
public:
double getExpectedTime(long long N, long long M) {
long long g = GCD(N, M);
N /= g; M /= g;
return (double)(N-1)*g/2;
}
};
6-4. Euler 関数を使う問題
次に Euler 関数に関連した問題を解いてみましょう。
問題 9: Educational Codeforces Round 81 D. Same GCDs
正の整数 $a, m$ が与えられる。
{\rm GCD}(a, m) = {\rm GCD}(a + x, m)
を満たす整数 $x$ ($0 \le x < m$) の個数を求めよ。
- $1 \le a < m \le 10^{10}$
例によって、$g = {\rm GCD}(a, m)$ として、
- $a = ga'$
- $m = gm'$
とします。このとき、まず ${\rm GCD}(a + x, m) = g$ となるためには、$x$ が $g$ の倍数であることが必要となります。よって、$x = gx'$ とおくと、問題の条件は
{\rm GCD}(a' + x', m') = 1
と表せます。これを満たす $x$' ($0 \le x' < m'$) の個数は、結局、${\rm GCD}(x', m') = 1$ を満たす $x'$ ($0 \le x' < m'$) の個数に等しくなります。ゆえに答えは $\varphi(m')$ となります。
# include <iostream>
# include <vector>
using namespace std;
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
vector<pair<long long, long long> > prime_factorize(long long N) {
vector<pair<long long, long long> > res;
for (long long a = 2; a * a <= N; ++a) {
if (N % a != 0) continue;
long long ex = 0;
while (N % a == 0) {
++ex;
N /= a;
}
res.push_back({a, ex});
}
if (N != 1) res.push_back({N, 1});
return res;
}
int main() {
int T; cin >> T;
for (int _ = 0; _ < T; ++_) {
long long a, m;
cin >> a >> m;
long long g = GCD(a, m);
m /= g;
const auto &pf = prime_factorize(m);
long long res = m;
for (auto p : pf) res = res / p.first * (p.first-1);
cout << res << endl;
}
}
7. 素因数分解で考えるテクニック
最後に、最小公倍数・最大公約数について考える上で、もう一つ大きな武器となる見方を紹介します。それは、たとえば $126$ という整数を、(素数 2 に対応する指数, 素数 3 に対応する指数, ...) という無限次元のベクトルに対応させて
(1, 2, 0, 1, 0, 0, 0, ...)
という風に考えることです。このように考えたとき、最大公約数を求める演算は、ベクトルを各要素ごとに min をとる演算に対応します。
この見方はこの記事でも紹介されているような、約数系包除原理や、GCD による畳み込み演算について考えるときにも有効です。ここでは一例として次の問題を考えてみましょう。
問題 10: DISCO presents ディスカバリーチャンネル コードコンテスト2017 本戦 B - GCDロボット (500 点)
$N$ 個の正の整数 $a_1, a_2, \dots, a_N$ が与えられる。
二つの正の整数 $X, Y$ が似ているとは、すべての $i$ に対して
{\rm GCD}(X, a_i) = {\rm GCD}(Y, a_i)
が成立していることをいう。正の整数 $Z$ が与えられるので、$Z$ と似ている整数のうち、最小のものを求めよ。
- $1 \le N \le 10^5$
- $1 \le Z, a_i \le 10^{18}$
上記のような、各素因数ごとの指数で考えることのポイントとして、「各素因数ごとに独立に考えることができる」というケースがとても多いです。今回も、$Z$ の最小値を求めるのに、各素因数ごとに指数を最小化すれば良いようになっています。
素因数 $p$ について、求める整数の指数を $x$、$Z$ の指数を $z$、$a_i$ の指数を $e_i$ とすると、条件は
\min(x, e_i) = \min(z, e_i)
という風に記述できます。これを満たす $x$ の最小値を考えます。個別の $i$ に対しては、
- $z \ge e_i$ のとき、$x = e_i$ が最小
- $z \le e_i$ のとき、$x = z$ が最小
となることから、まとめると $x = \min(z, e_i)$ が最小となります。これが任意の $i$ に対して満たす必要があるので、結局求める $x$ の最小値は
x = \max(\min(z, e_1), \min(z, e_2), \dots, \min(z, e_N))
となります。これが任意の素因数 $p$ に対して成り立つことから、求める $X$ の最小値は
X = {\rm LCM}({\rm GCD}(Z, a_1), {\rm GCD}(Z, a_2), \dots, {\rm GCD}(z, a_N))
と表せます。結局、考察の過程で素因数分解を用いたものの、最終的に得られたアルゴリズムでは、素因数分解そのものを実施する必要はないことがわかります。
# include <iostream>
using namespace std;
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
long long LCM(long long a, long long b) {
return a / GCD(a, b) * b;
}
int main() {
int N;
long long Z;
cin >> N >> Z;
long long res = 1;
for (int i = 0; i < N; ++i) {
long long a;
cin >> a;
long long g = GCD(Z, a);
res = LCM(res, g);
}
cout << res << endl;
}
8. おわりに
今回は初等整数論のうち、最大公約数に関連する部分を特集しました。
理論としても大変面白く、問題例も豊富なテーマです。この分野の問題は特に地頭系と言われやすいものですが、最大公約数に関する嗅覚を養うことで対応していけると思います!
9. 問題集
いい感じの問題たちを並べます。最大公約数ネタは発想力を問いやすいためか、AGC に多く見られます。
9-1. 単純な最大公約数・最小公倍数
- AtCoder ABC 070 C - Multiple Clocks (300 点)
- AtCoder ABC 125 C - GCD on Blackboard (300 点)
- AtCoder AGC 028 A - Two Abbreviations (300 点)
- AOJ 0211 みんなでジョギング
- AtCoder ABC 152 E - Flatten (500 点) (少し難しいです)
9-2. Euclid の互除法っぽい操作
- AtCoder AGC 018 A - Getting Difference (300 点)
- CODE THANKS FESTIVAL 2017 D - Bus Tour (300 点)
- Codeforces Round #201 (Div. 1) A. Alice and Bob
- AtCoder AGC 001 B - Mysterious Light (500 点) (少し難しいです)
- 九州大学プログラミングコンテスト 2018 I - Buffalo (難しいです)
9-3. 「互いに素」の性質
- AtCoder ABC 100 C - *3 or /2 (300 点) (2 と 3 は互いに素なので...)
- CODE FESTIVAL 2016 Relay E - 方眼紙と線分
- AtCoder ABC 158 E - Divisible Substring (500 点)
- TopCoder SRM 535 DIV1 Easy FoxAndGCDLCM (面白いです)
- CODE FESTIVAL 2014 決勝 F - 誤情報 (推定黄色難度で、だいぶ難しいです)
- AtCoder ARC 046 D - うさぎとマス目 (推定赤色難度で、非常に難しいです)
- Tenka1 Programmer Contest F - ModularPowerEquation!! (1400 点) (ラスボスの香りがあります)
9-4. ax + by
-
この性質は、素因数分解を考えれば当たり前だと思えるかもしれません。しかし整数論の理論では、むしろこの性質を使って素因数分解の一意性を示します。そのため、素因数分解の一意性を援用してこの性質を示すのは、やや循環論法気味です。 ↩