はじめに
NTT データ数理システムでアルゴリズムの探求をしている大槻 (通称、けんちょん) です。最近のマイブームなアルゴリズムは NTT (Number-Theoretic Transform) です。
NTT は FFT (高速フーリエ変換) の亜種です。日本語では高速剰余変換と呼ばれることが多いです。FFT ではどうしても登場しがちな「計算途中での丸め誤差」を回避するテクニックとして有効です。NTT を実運用する際には以下のような楽しい初等整数論的トピックたちを使用することになってすごく面白いです。
- ${\rm mod}. p$ の原始根 ($p$ は素数)
- 中国剰余定理 (Chinese Remainder Theorem)
今回はこのうちの中国剰余定理 (中国人剰余定理や中国式剰余定理や中国風剰余定理とも) について特集します。中国剰余定理もそれ自体、整数論的アルゴリズムや組合せ論的アルゴリズムにおいて非常に重要な定理であり、暗号をはじめとした様々な場面で活用されています。ユークリッドの互除法との関係も深いです。
本記事では以下のような応用例・問題例を紹介します:
応用例
- 巨大な数の数え上げ (数え上げお姉さん問題など)
- RSA 公開鍵暗号の高速化
- 多項式の Lagrange 補間
- NTT (Number-Theoretic Transform) への展望
問題例
- 中国剰余定理ライブラリ verify に
- yukicoder 0186 中華風 (Easy)
- yukicoder 0187 中華風 (Hard) (Garner のアルゴリズム)
- 応用問題
- 法が素数でない場合の数え上げ
- yukicoder 0695 square1001 and Permutation 4
- [HackerRank Ad Infinitum 10 C - Cheese and Random Toppings](Cheese and Random Toppings)
- mod. p での数え上げだが、指数が mod. p-1 (Fermat の小定理)
- SRM 449 DIV1 Hard StairsColoring (カタラン数)
1. 中国剰余定理とは
中学受験や高校受験において
「3 で割ったあまりが 2 で、5 で割ったあまりが 3 になるような 1 以上 100 以下の整数をすべて求めよ」
のような問題はお馴染みだったと思います。
上の図で見るように、「3 で割って 2 あまる数を表す赤線」と「5 で割って 3 あまる数を表す赤線」の模様具合が周期的に登場しているのがわかります。その周期は 3 と 5 の最小公倍数である 15 です。
さらによく見ると 3 で割って 2 あまり、5 で割って 3 あまる数の具体例として 8 があり、0 以上 15 以下の範囲内には 8 しかありません。したがって
- 「3 で割ったあまりが 2」かつ「5 で割ったあまりが 3」
という条件は、
- 「15 で割ったあまりが 8」
という条件と同値になります。「〜で割ったあまりが〜である」という複数の条件が、単一の条件にまとめ上げられたことになります。中国剰余定理はこの一般の場合を主張するものです。
1-1. 中国剰余定理
二元の場合について以下に記します。$n$ 元の場合も同様です。
$m_1$ と $m_2$ を互いに素な正の整数とする。
$x ≡ b_1$ $({\rm mod}. m_1)$
$x ≡ b_2$ $({\rm mod}. m_2)$
を満たす整数 $x$ が $0$ 以上 $m_1 m_2$ 未満にただ 1 つ存在する。特にそれを $r$ とすると
$x ≡ b_1$ $({\rm mod}. m_1)$, $x ≡ b_2$ $({\rm mod}. m_2)$
⇔ $x ≡ r$ $({\rm mod}. m_1 m_2)$
が成立する。
1-2. 中国剰余定理の証明
「解の一意性」と「解の存在性」の両方を証明します。
解の一意性
$x ≡ b_1$ $({\rm mod}. m_1)$, $x ≡ b_2$ $({\rm mod}. m_2)$ を満たす整数 $x$ が $0$ 以上 $m_1 m_2$ 未満に存在しても一意であることを示します。一意性の方が簡単です。
もし解が 2 つ存在して $x, y$ とおくと、
$x ≡ b_1$ $({\rm mod}. m_1)$, $y ≡ b_1$ $({\rm mod}. m_1)$ より
$x ≡ y$ $({\rm mod}. m_1)$
が成立し、同様に $x ≡ y$ $({\rm mod}. m_2)$ が成立するので合わせて
$x ≡ y$ $({\rm mod}. m_1 m_2)$
が成立します。$0 \le x, y < m_1 m_2$ であったことから $x = y$ となる他ないです。
解の存在性
証明方法は大きく 2 つあります:
- 構成的証明方法
- 「解の一意性」から間接的に示す方法
ここでは「拡張 Euclid の互除法」による構成的証明方法を示します。すなわち、拡張 Euclid の互除法をベースにして、具体的に解を求めるアルゴリズムを与えます。
- $x ≡ b_1$ $({\rm mod}. m_1)$
- $x ≡ b_2$ $({\rm mod}. m_2)$
を満たす $x$ を具体的に求めたいわけですが、まず拡張 Euclid の互除法から、
$m_1 p + m_2 q = 1$
を満たす整数 $(p, q)$ が構成できます ($m_1$ と $m_2$ は互いに素であるため)。このとき
- $m_2 q ≡ 1$ $({\rm mod}. m_1)$
- $m_1 p ≡ 1$ $({\rm mod}. m_2)$
が成り立つことに注意します。よって
$x = b_2 m_1 p + b_1 m_2 q$
とおくと、
- $x ≡ b_1 m_2 q ≡ b_1$ $({\rm mod}. m_1)$
- $x ≡ b_2 m_1 p ≡ b_2$ $({\rm mod}. m_2)$
が成立しているので、$b_2 m_1 p + b_1 m_2 q$ を $m_1 m_2$ で割ったあまりが答えとなります。
1-3. 法が互いに素でない場合への拡張
法が互いに素でないときは、解が存在しないこともあります。たとえば
- $x ≡ 4$ $({\rm mod}. 6)$
- $x ≡ 1$ $({\rm mod}. 8)$
を満たす $x$ は存在しないです。なぜなら $x ≡ 4$ $({\rm mod}. 6)$ であることから $x$ は偶数でなければならないですが、$x ≡ 1$ $({\rm mod}. 8)$ は $x$ が奇数であることを表しています。
一般に以下のことが言えます:
$x ≡ b_1$ $({\rm mod}. m_1)$
$x ≡ b_2$ $({\rm mod}. m_2)$
を満たす $x$ が存在する必要十分条件は $b_1 ≡ b_2$ $({\rm mod}. {\rm gcd}(m_1, m_2))$ が成立することである。またこれが成立しているとき、これを満たす $x$ が $0$ 以上 ${\rm lcm}(m_1, m_2)$ 未満の範囲にただ 1 つ存在する。
特にそれを $r$ とおくと
$x ≡ b_1$ $({\rm mod}. m_1)$, $x ≡ b_2$ $({\rm mod}. m_2)$
⇔ $x ≡ r$ $({\rm mod}. {\rm lcm}(m_1, m_2))$
が成立する。
証明の流れは先ほどとほぼ同様です。まず、解が存在するためには $b_1 ≡ b_2$ $({\rm mod}. {\rm gcd}(m_1, m_2))$ でなければならないことを示してみます。
解が存在するとき、$m_1$ は ${\rm gcd}(m_1, m_2)$ の倍数なので $x ≡ b_1$ $({\rm mod}. m_1)$ より
$x ≡ b_1$ $({\rm mod}. {\rm gcd}(m_1, m_2))$
が成立します。同様にして
$x ≡ b_2$ $({\rm mod}. {\rm gcd}(m_1, m_2))$
が成立するので、これらより
$b_1 ≡ b_2$ $({\rm mod}. {\rm gcd}(m_1, m_2))$
が成立します。
具体的な x の構成方法
アルゴリズム的観点からは具体的な $x$ の構成方法が気になります。やはり拡張 Euclid の互除法を用います。まず拡張 Euclid の互除法を適用することにより、$d = {\rm gcd}(m_1, m_2)$ とおいて
$m_1 p + m_2 q = d$
を満たす整数 $(p, q)$ が構成できます。$b_1 ≡ b_2$ $({\rm mod}. d)$ であることから、$b_2 - b_1$ は $d$ で割り切れます。そこで $s = \frac{b_2 - b_1}{d}$ とおくと
$s m_1 p + s m_2 q = b_2 - b_1$
となります。ここで
$x = b_1 + s m_1 p (= b_2 - s m_2 q)$
とおくと、
- $x ≡ b_1$ $({\rm mod}. m_1)$
- $x ≡ b_2$ $({\rm mod}. m_2)$
が成り立っていることがわかります。この構成方法に基づいた具体的なアルゴリズムの実装は 2-1 で示します。
2. 中国剰余定理のアルゴリズム
2-1. 拡張 Euclid の互除法を用いた方法
$x ≡ b_1$ $({\rm mod}. m_1)$
$x ≡ b_2$ $({\rm mod}. m_2)$
…
$x ≡ b_K$ $({\rm mod}. m_K)$
を満たす $x ≡ r$ $({\rm mod}. {\rm lcm}(m_1, m_2, \dots, m_K))$ を具体的に求めるアルゴリズムを与えます。解なしの場合はその旨を報告するようにします。
二元の場合
まずは簡単な
$x ≡ b_1$ $({\rm mod}. m_1)$
$x ≡ b_2$ $({\rm mod}. m_2)$
の場合を解きます。1-3 で見たとおり、$d = {\rm gcd}(m_1, m_2)$ として、拡張 Euclid の互除法によって
$m_1 p + m_2 q = d$
を満たす整数 $(p, q)$ を求め、
$x = b_1 + m_1 (\frac{b2-b1}{d}) p$
とすればよいです。以下に具体的な実装を載せます。「拡張 Euclid の互除法」の実装についてはこのページを見ていただけたらと思います。
// 負の数にも対応した mod
// 例えば -17 を 5 で割った余りは本当は 3 (-17 ≡ 3 (mod. 5))
// しかし単に -17 % 5 では -2 になってしまう
inline long long mod(long long a, long long m) {
return (a % m + m) % m;
}
// 拡張 Euclid の互除法
// ap + bq = gcd(a, b) となる (p, q) を求め、d = gcd(a, b) をリターンします
long long extGcd(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGcd(b, a%b, q, p);
q -= a/b * p;
return d;
}
// 中国剰余定理
// リターン値を (r, m) とすると解は x ≡ r (mod. m)
// 解なしの場合は (0, -1) をリターン
pair<long long, long long> ChineseRem(long long b1, long long m1, long long b2, long long m2) {
long long p, q;
long long d = extGcd(m1, m2, p, q); // p is inv of m1/d (mod. m2/d)
if ((b2 - b1) % d != 0) return make_pair(0, -1);
long long m = m1 * (m2/d); // lcm of (m1, m2)
long long tmp = (b2 - b1) / d * p % (m2/d);
long long r = mod(b1 + m1 * tmp, m);
return make_pair(r, m);
}
具体例として、冒頭の
$x ≡ 2$ $({\rm mod}. 3)$
$x ≡ 3$ $({\rm mod}. 5)$
が
$x ≡ 8$ $({\rm mod}. 15)$
であることを確かめてみます。
# include <iostream>
# include <vector>
using namespace std;
// 中国剰余定理の実装は略
int main() {
pair<long long, long long> res = ChineseRem(2, 3, 3, 5);
cout << "x ≡ " << res.first << " (mod. " << res.second << ")" << endl;
}
出力は以下のようになりました:
x ≡ 8 (mod. 15)
n 元の場合
二元の場合とほとんど同様です。初期値を
$x ≡ 0$ $({\rm mod}. 1)$ (任意の整数)
としておきます。この初期値からスタートして、各 $i$ に対する
$x ≡ b_i$ $({\rm mod}. m_i)$
とマージしていく感じです。二元の場合の実装を流用して以下のように実装できます:
inline long long mod(long long a, long long m) {
return (a % m + m) % m;
}
long long extGcd(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGcd(b, a%b, q, p);
q -= a/b * p;
return d;
}
// 中国剰余定理
// リターン値を (r, m) とすると解は x ≡ r (mod. m)
// 解なしの場合は (0, -1) をリターン
pair<long long, long long> ChineseRem(const vector<long long> &b, const vector<long long> &m) {
long long r = 0, M = 1;
for (int i = 0; i < (int)b.size(); ++i) {
long long p, q;
long long d = extGcd(M, m[i], p, q); // p is inv of M/d (mod. m[i]/d)
if ((b[i] - r) % d != 0) return make_pair(0, -1);
long long tmp = (b[i] - r) / d * p % (m[i]/d);
r += M * tmp;
M *= m[i]/d;
}
return make_pair(mod(r, M), M);
}
2-2. Garner のアルゴリズム
前節の拡張 Euclid の互除法による方法をより洗練させます。
$x ≡ b_1$ $({\rm mod}. m_1)$
$x ≡ b_2$ $({\rm mod}. m_2)$
…
$x ≡ b_K$ $({\rm mod}. m_K)$
簡単のため、$m_1, m_2, \dots, m_K$ はどの 2 つも互いに素であるとします。実用上そうでないケースを扱うことはまずないと言ってよいでしょう。仮に $m$ たちが互いに素でなかったとしても、後述する yukicoder 0187 中華風 (Hard) の解説で示す方法によって $m$ たちが互いに素になるように前処理することができます。さて、これを満たす $x$ を見つけたいのですが、基本的なアイディアとしては
$x = t_1 + t_2 m_1 + t_3 m_1 m_2 + \dots + t_{K} m_1 m_2 \dots m_{K-1}$
の形で条件を満たすものを探します。以下に見るように各 $k$ に対して $0 \le t_k < m_k$ を満たすように $t_1, t_2, \dots, t_K$ を定めることができます。このとき上の式で定義された $x$ は $0 \le x < m_1 m_2 \dots m_K$ を満たします (数学的帰納法で示せます)。このことは特に $x ≡ b_1$ $({\rm mod}. m_1)$, $x ≡ b_2$ $({\rm mod}. m_2)$, ..., $x ≡ b_K$ $({\rm mod}. m_K)$ を満たす最小の $0$ 以上の整数 $x$ を求めることができることを意味しています。
さて、記法として $m_j$ を法としたときの $m_i$ の逆元を $m_{i,j}^{-1}$ と表すことにします。まず $x ≡ b_1$ $({\rm mod}. m_1)$ より
$t_1 ≡ b_1$ $({\rm mod}. m_1)$
が成り立ちます。これを満たす $t_1$ として例えば $b_1$ を $m_1$ で割ったあまりをとればよいです。次に $x ≡ b_2$ $({\rm mod}. m_2)$ より、
$t_1 + t_2 m_1 ≡ b_2$ $({\rm mod}. m_2)$
⇔ $t_2 ≡ (b_2 - t_1)m_{1,2}^{-1}$ $({\rm mod}. m_2)$
が成り立ります。これを満たす $t_2$ として $0$ 以上 $m_2$ 未満の整数をとることができます。同様にして $x ≡ b_3$ $({\rm mod}. m_3)$
$t_1 + t_2 m_1 + t_3 m_1 m_2 ≡ b_3$ $({\rm mod}. m_3)$
⇔ $t_3 ≡ m_{1,3}^{-1}m_{2,3}^{-1}(b_3 - t_1 - t_2m_1)$ $({\rm mod}. m_3)$
⇔ $t_3 ≡ ((b_3 - t_1)m_{1,3}^{-1} - t_2)m_{2,3}^{-1}$ $({\rm mod}. m_3)$
が成り立ちます。さらに $t_1, t_2, \dots, t_{k-1}$ が求まっているとき $x ≡ b_k$ $({\rm mod}. m_k)$ より、
$t_k ≡ ((\dots((b_k - t_1)m_{1,k}^{-1} - t_2)m_{2,k}^{-1} - \dots)m_{k-2,k}^{-1} - t_{k-1})m_{k-1,k}^{-1}$ $({\rm mod}. m_3)$
となります。こうして得られた $t_1, t_2, \dots, t_K$ を用いて
$x = t_1 + t_2 m_1 + t_3 m_1 m_2 + \dots + t_{K} m_1 m_2 \dots m_{K-1}$
$= t_1 + (t_2 + (t_3 + \dots + (t_{K-1} + t_K m_{K-1}) m_{K-2}) \dots)m_2)m_1$
と解を陽に書き下すことができます。なお実際に Garner のアルゴリズムを実装するときには、以下に示すように、
$t_1 + t_2 m_1 + t_3 m_1 m_2 + \dots (t_k m_1 m_2 \dots m_{k-1}) ≡ b_k$ $({\rm mod}. m_k)$
といった合同方程式を毎回解く形にするのが楽です。
Garner のアルゴリズムの使いどころ 1
3-1 で後述するように、超巨大な場合の数を数え上げるような問題においては、直接多倍長整数を用いて数え上げるよりも、一旦数えたい値をいくつかの素数 $p_1, p_2, \dots, p_K$ で割った余りで求めてあげて、最後に Garner のアルゴリズムを用いて復元する手法が大変有効です。アルゴリズム全体の計算時間を $O(K^2)$ で済ませることができます。
超巨大な場合の数を数え上げるときに、直接多倍長整数を扱うよりも Garner のアルゴリズムを用いて復元する方が効率的であることについて、kirica_comp さんの記事「Garner のアルゴリズムと多倍長整数演算」でよく議論されています。
Garner のアルゴリズムの使いどころ 2
Garner のアルゴリズムは $x ≡ b_1$ $({\rm mod}. m_1)$, $x ≡ b_2$ $({\rm mod}. m_2)$, ..., $x ≡ b_K$ $({\rm mod}. m_K)$ を満たす最小の $0$ 以上の整数 $x$ を陽に求めることができます。したがって、ある整数 $M$ に対して
$x$ ${\rm mod}. M$
といった値も計算することができます。後述する yukicoder 0187 中華風 (Hard) などはこのことを利用して解くことができますし、NTT (Number-Theoretic Transform) による畳み込み計算を実施する際にもこの性質を利用します。
$x$ ${\rm mod}. M$ を求めるアルゴリズムを以下に示します。math314 さんの「任意modでの畳み込み演算をO(n log(n))で」を参考にしました。$b$ や $m$ が 0-indexed になっていることに注意です。
// 負の数にも対応した mod (a = -11 とかでも OK)
inline long long mod(long long a, long long m) {
long long res = a % m;
if (res < 0) res += m;
return res;
}
// 拡張 Euclid の互除法
long long extGCD(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGCD(b, a%b, q, p);
q -= a/b * p;
return d;
}
// 逆元計算 (ここでは a と m が互いに素であることが必要)
long long modinv(long long a, long long m) {
long long x, y;
extGCD(a, m, x, y);
return mod(x, m); // 気持ち的には x % m だが、x が負かもしれないので
}
// Garner のアルゴリズム, x%MOD, LCM%MOD を求める (m は互いに素でなければならない)
// for each step, we solve "coeffs[k] * t[k] + constants[k] = b[k] (mod. m[k])"
// coeffs[k] = m[0]m[1]...m[k-1]
// constants[k] = t[0] + t[1]m[0] + ... + t[k-1]m[0]m[1]...m[k-2]
long long Garner(vector<long long> b, vector<long long> m, long long MOD) {
m.push_back(MOD); // banpei
vector<long long> coeffs((int)m.size(), 1);
vector<long long> constants((int)m.size(), 0);
for (int k = 0; k < (int)b.size(); ++k) {
long long t = mod((b[k] - constants[k]) * modinv(coeffs[k], m[k]), m[k]);
for (int i = k+1; i < (int)m.size(); ++i) {
(constants[i] += t * coeffs[i]) %= m[i];
(coeffs[i] *= m[k]) %= m[i];
}
}
return constants.back();
}
3. 中国剰余定理の応用例
中国剰余定理の応用例をいくつか示します。
3-1. 巨大な数の数え上げ
唐突ですが、中国剰余定理の名前の由来は、中国の算術書『孫子算経』に
「3で割ると2余り、5で割ると3余り、7で割ると2余る数は何か」
と書かれていたことから来ています。そのお気持ちとしては、100 近くいる人数をカウントするのはとても大変なため、
- 3 人ずつグループに分けさせて何人あまるか
- 5 人ずつグループに分けさせて何人あまるか
- 7 人ずつグループに分けさせて何人あまるか
を測定し、それをもとに人数を 105 で割ったあまりを計上していたと言われています。この話は「巨大な数を扱うときには、いくつかの小さな素数で割ったあまりで管理すると扱いやすい」という好例になっています。
現代の計算機科学の世界においても、超巨大な整数を扱う場面では中国剰余定理が盛んに用いられます。有名な例として「数え上げお姉さん問題」があります。
数え上げお姉さん問題
巨大な数の数え上げ問題として「数え上げお姉さん問題」はとても馴染みが深い人も多いと思います。以下の資料に問題の概要がまとまっています:
- 「フカシギの数え方」 - 組合せ爆発に立ち向かう最先端アルゴリズム技術 (湊 ERATO プロジェクト講演資料)
- YouTube: 『フカシギの数え方』 おねえさんといっしょ! みんなで数えてみよう! (湊 ERATO プロジェクト作成動画)
このような巨大な数を数え上げるにあたって中国剰余定理を活用したことが以下の資料で報告されています:
- フカシギおねえさん問題の高速計算アルゴリズム (岩下 洋哲)
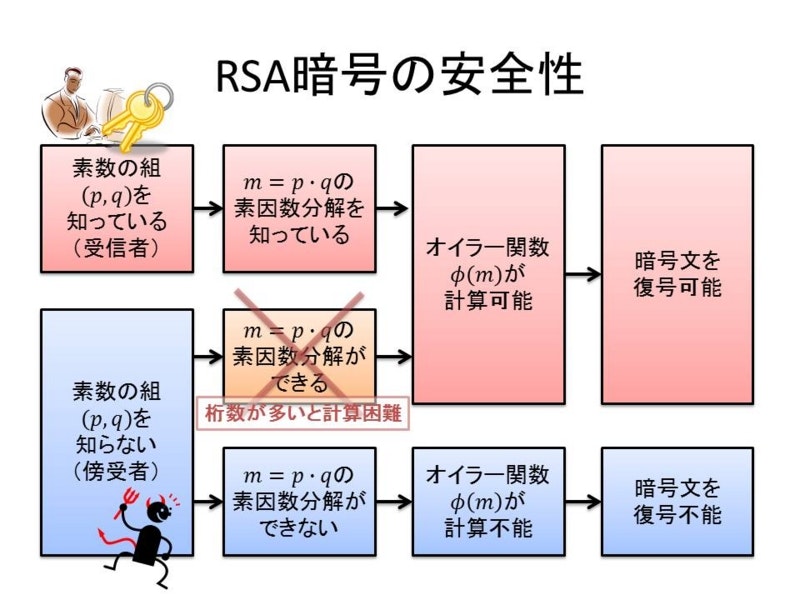
3-2. RSA 公開鍵暗号の高速化
RSA 公開鍵暗号方式において、復号の計算を「中国剰余定理」を用いて高速化することができます。英語版 wikipedia にの記述よると、この高速化テクニックは OpenSSL, Java, .NET などで盛んに用いられているようです。
3-2-1. RSA 公開鍵暗号とは
RSA 公開鍵暗号がどのようなものかについては、tsujimotter さんの記事「RSA 暗号がようやく分かった気がしたのでまとめてみる」が大変わかりやすいです。
暗号化したい元の文章を「平文」、暗号化したものを「暗号文」と呼びます。平文を暗号文にすることを暗号化、暗号文を平文にすることを復号と呼びます。RSA をはじめとした公開鍵暗号というものは
- 暗号化については、万人が公開鍵を用いて行えるようにしたい (文書を暗号化して秘密鍵の持ち主に送れるように)
- 復号については、秘密鍵の持ち主だけが行えるようにしたい
というモチベーションがあります。暗号化に必要な鍵は公開鍵と呼ばれ、万人が使用できるものです。数学的詳細をきちんと述べます。平文を $P$、暗号文を $C$ とします。以下の記述で $k$ の選び方が天下りに思えるかもしれませんが、Fermat の小定理を思い浮かべると自然だと思います。
- ランダムに大きな素数 $p$, $q$ を選ぶ (100 桁程度)
- $n = pq$ として $n$ を計算する (200 桁程度)
- $(p-1)(q-1)$ と互いに素な整数 $k$ を選び、$(n, k)$ のペアを公開鍵として公表する。暗号化の方法としては、平文 $P$ を $k$ 乗して $C ≡ P^k$ $({\rm mod}. n)$ によって暗号文 $C$ を得ることができる。
- $(p-1)(q-1)$ を法とした $k$ の逆元を $u$ として、$(n, u)$ のペアを秘密鍵として秘密にしておく。実はこのとき、$C^u ≡ P$ $({\rm mod}. n)$ が成立するので、暗号文 $C$ を $u$ 乗することで、暗号文を復号することができる。
$C^u ≡ P$ $({\rm mod}. n)$ が成立することを証明しておきます。
【証明】
$u$ が $(p-1)(q-1)$ を法として $k$ の逆元であることから、ある整数 $a$ を用いて
$ku = a(p-1)(q-1) + 1$
と表せる。Fermat の小定理より
$C^u = P^{ku} = (P^{p-1})^{a(q-1)} P ≡ P$ $({\rm mod}. p)$
$C^u = P^{ku} = (P^{q-1})^{a(p-1)} P ≡ P$ $({\rm mod}. q)$
であるから、$n = pq$ より、
$C^u ≡ P$ $({\rm mod}. n)$ が成立する。
(証明終)
この RSA 公開鍵暗号において重要なことは、
- 公開鍵 $(n, k)$ から秘密鍵 $(n, u)$ がバレることはない
ということです。なぜなら、$k$ から $u$ を計算するためには、
- $n = pq$ と素因数分解して (無理)
- $(p-1)(q-1)$ を法として $k$ の逆元を $u$ とする
ことが必要だからです。$n = pq$ と素因数分解することが極めて困難であることによって、RSA 公開鍵暗号の安全性が支えられています。
3-2-2. 復号計算の高速化
ここからようやく本題ですが、復号 $C^u$ の計算を中国剰余定理を用いて高速化することができます。この高速化テクニックは OpenSSL, Java, .NET などで盛んに用いられているようです。
$u ≡ u_1$ $({\rm mod}. p-1)$
$u ≡ u_2$ $({\rm mod}. q-1)$
とすると、$u_1$, $u_2$ は $u$ よりもずっと小さな整数となります。ここで求めたい値を $x ≡ C^u$ $({\rm mod}. n)$ とおくと、Fermat の小定理によって
- $x ≡ C^{u_1}$ $({\rm mod}. p)$
- $x ≡ C^{u_2}$ $({\rm mod}. q)$
となるので、これを満たす $x$ を中国剰余定理によって求めることができます。この方法によって、直接 $C^u$ $({\rm mod}. n)$ を計算するよりも高速に復号計算を実行できます。
3-3. 多項式の Lagrange 補間
中国剰余定理は抽象数学の言葉で記述すると $m_1, m_2, \dots, m_K$ をどの 2 つも互いに素な整数として
$ℤ / m_1ℤ × \dots × ℤ / m_nℤ ≅ ℤ / mℤ$
ということになります。両辺が環として同型であることを述べています。これは整数環 $ℤ$ についての定理ですが、一般の環においても成立します:
$R$ を環、$I_1, I_2, \dots, I_K$ をどの 2 つも互いに素な環 $R$ のイデアルとします ($i \neq j$ に対して $I_i + I_j = R$)。このとき、$I = \cap_{k=1}^{K} I_k$ とおくと
$R / I_1 × R / I_2 × \dots × R / I_K ≅ R / I$
が成立する。
イデアルというのは合同式の概念を一般化したようなものだと思うと掴みやすいかもしれません。このような抽象化は計算機科学の観点からはあまり意味をなさない場合も多いかもしれませんが、環として特に「体上の多項式」を選ぶと、Lagrange 補間などの重要な多項式補間アルゴリズムが生まれます。詳しくは anta さんの記事「中華風剰余定理」を参考にしていただけたらと思います。
3-4. NTT への展望
FFT (高速フーリエ変換) や NTT (高速剰余変換) については後日改めて記事を書きたいと思います。ここでは簡単に中国剰余定理がどのように使われるかの紹介のみにとどめます。
FFT とは、2 つの数列 $(a_0, a_1, \dots, a_n)$, $(b_0, b_1, \dots, b_n)$ が与えられた時に、以下で定義される数列 $(c_0, c_1, \dots, c_{2n})$ を高速に計算できるアルゴリズムです:
$c_k = \sum_{i+j=k} a_i b_j$
愚直に計算しようと思うと $O(n^2)$ の計算時間がかかりますが、FFT を用いると $O(n\log{n})$ で計算できます。しかし FFT の問題点の 1 つとして、桁が大きくなると計算の途中で「丸め誤差」が生じてしまうことが挙げられます。そこで、$a$ や $b$ が整数値の場合には、代表的な素数 $p_1, p_2, \dots$ を法として $c_k$ を計算しておいて、中国剰余定理によって復元する方法が大変有力です。ある種の素数 $p$ を法とすると FFT と同等の処理が実現できることが知られており、NTT と呼ばれています。
NTT の実装に関心のある方は
- NTT (整数環FFT) (satanic0258)
- 任意modでの畳み込み演算をO(n log(n))で (math314)
を参考にしていただけたらと思います。
4. 問題例
ここから先は中国剰余定理を実際に用いて解くことのできるプログラミングコンテストなどの問題たちを紹介していきます。
4-1. 中国剰余定理ライブラリの verify に使える問題たち
まずは中国剰余定理を最初に実装して挙動を確かめるのによい問題たちです。
問題 1: yukicoder 0186 中華風 (Easy)
【問題概要】
3 個の整数の組 $(X_1, Y_1), (X_2, Y_2), (X_3, Y_3)$ が与えられる。
$x ≡ X_1$ $({\rm mod}. Y_1)$
$x ≡ X_2$ $({\rm mod}. Y_2)$
$x ≡ X_3$ $({\rm mod}. Y_3)$
をすべて満たす最小の正の整数 $x$ を求めよ。存在しない場合には $-1$ をリターンせよ。
【制約】
- $0 \le X_i < Y_i \le 10^6$
【解法】
素直に 2-1 で紹介した、拡張 Euclid の互除法による実装で通すことができます。
注意点として、$X_1, X_2, X_3$ がすべて $0$ のときは $x = 0$ ではなく $x = {\rm lcm}(Y_1, Y_2, Y_3)$ を答える必要があります。
# include <iostream>
# include <vector>
using namespace std;
inline long long mod(long long a, long long m) {
return (a % m + m) % m;
}
// 拡張 Euclid の互除法
long long extGCD(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGCD(b, a%b, q, p);
q -= a/b * p;
return d;
}
// 答えを x ≡ r (mod. M) として、{r, M} をリターン, 存在しない場合は {0, -1} をリターン
pair<long long, long long> ChineseRem(const vector<long long> &b, const vector<long long> &m) {
long long r = 0, M = 1;
for (int i = 0; i < (int)b.size(); ++i) {
long long p, q;
long long d = extGCD(M, m[i], p, q); // p is inv of M/d (mod. m[i]/d)
if ((b[i] - r) % d != 0) return make_pair(0, -1);
long long tmp = (b[i] - r) / d * p % (m[i]/d);
r += M * tmp;
M *= m[i]/d;
}
return make_pair(mod(r, M), M);
}
int main() {
vector<long long> b(3), m(3);
bool exist_non_zero = false;
for (int i = 0; i < 3; ++i) {
cin >> b[i] >> m[i];
if (b[i]) exist_non_zero = true;
}
pair<long long, long long> res = ChineseRem(b, m);
if (res.second == -1) cout << -1 << endl;
else if (exist_non_zero) cout << res.first << endl;
else cout << res.second << endl;
}
問題 2: yukicoder 0187 中華風 (Hard)
【問題概要】
$N$ 個の合同式
$x ≡ X_i$ $({\rm mod}. Y_i)$
を満たす最小の正の整数 $x$ を $1,000,000,007$ で割った余りを求めよ。存在しない場合には -1 をリターンせよ。
【制約】
- $1 \le N\le 1000$
- $0 \le X_i < Y_i \le 10^9$
【解法】
前問とほとんど同じに見えるのですが、制約が異なります。
前問では解 $x ≡ r$ $({\rm mod}. M)$ の $r$ や $M$ が最大でも $10^{18}$ 以下になる設定でした ($Y_1, Y_2, Y_3 \le 10^6$ より、すべて互いに素でも $10^{18}$ 以下です)。今回は普通に拡張 Euclid の互除法で求めようと思うと、多倍長整数が必要になってしまいます。2-2 で示した Garner のアルゴリズムであれば多倍長整数を用いずに $x$ ${\rm mod}. 1000000007$ の値を計算することができます。
ただし Garner のアルゴリズムを適用するためには、法 $Y_1, Y_2, \dots, Y_K$ がどの 2 つも互いに素でなければなりません。そこで互いに素になるように以下のような前処理を行います:
各 $i < j$ に対して、$x ≡ X_i$ $({\rm mod}. Y_i)$, $x ≡ X_j$ $({\rm mod}. Y_j)$ をうまく処理して $Y_i, Y_j$ が互いに素になるようにします。簡単のため
$x ≡ a$ $({\rm mod}. s)$
$x ≡ b$ $({\rm mod}. t)$
とします。まずはこれらの条件が矛盾していないかどうかは 1-3 で述べた通り、$a - b$ が ${\rm gcd}(s, t)$ で割り切れるかどうかで判定できます。以下、条件が矛盾していないものとします。イメージ的には $s, t$ をそれぞれ素因数分解して、素因子が共通しているところは $p$ で表して
$s = p_1^{k_1} p_2^{k_2} \dots q_1^{l_1} q_2^{l_2} \dots$
$t = p_1^{m_1} p_2^{m_2} \dots r_1^{n_1} r_2^{n_2} \dots$
となったすると、$x ≡ a$ $({\rm mod}. s)$, $x ≡ b$ $({\rm mod}. t)$ は
$x ≡ a$ $({\rm mod}. p_1^{k_1})$
$\dots$
$x ≡ b$ $({\rm mod}. p_1^{m_1})$
$\dots$
$x ≡ a$ $({\rm mod}. q_1^{l_1})$
$\dots$
$x ≡ b$ $({\rm mod}. r_1^{n_1})$
$\dots$
と分解されるのですが、これをうまく再分配する感じです。
まず ${\rm mod}. p_1^{m_1}$ と ${\rm mod}. r_1^{n_1}$ の部分は独立しているのでそのままにしておきます。各 $p = p_i$ に対して
$x ≡ a$ $({\rm mod}. p^k)$
$x ≡ b$ $({\rm mod}. p^m)$
の部分の扱いを考えます。まず前者と後者とが矛盾していないことを前提にすれば、
- $k \ge m$ のとき、前者の方がより多くの情報を持っているはずなので、後者を消しても同値です
- $k \le m$ のとき、後者の方がより多くの情報を持っているはずなので、前者を消しても同値です
こうすれば最終的には
$x ≡ (どちらか)$ $({\rm mod}. p_1^{\max(k_1, m_1)})$
$\dots$
$x ≡ a$ $({\rm mod}. q_1^{l_1})$
$\dots$
$x ≡ b$ $({\rm mod}. r_1^{n_1})$
$\dots$
という風になります。これらを再び $a$ 側と $b$ 側とに振り分けます。$q$ と $r$ についてはそのまんま $a$ 側と $b$ 側に戻します。$p$ についてはそれぞれ「指数が大きかった側」に戻していきます。そうすると
$x ≡ a$ $({\rm mod}. s')$
$x ≡ b$ $({\rm mod}. t')$
が再構成されて、しかも
- $s'$ と $t'$ は互いに素
- $s't' = p_1^{\max(k_1, m_1)} \dots q_1^{l_1} \dots r_1^{n_1} \dots$ $= {\rm lcm}(s, t)$
を満たします。以上の処理を任意のペアについて実施することで、どの 2 つの法も互いに素な連立合同式に帰着することができます。
なお、以上のことを実装するときには陽に素因数分解はせず、「最大公約数」を上手く活用していきます。下の実装例を見るとわかると思います。
# include <iostream>
# include <vector>
# include <bitset>
using namespace std;
const long long MOD = 1000000007;
// 最大公約数
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
// Garner のアルゴリズムの前処理
long long PreGarner(vector<long long> &b, vector<long long> &m, long long MOD) {
long long res = 1;
for (int i = 0; i < (int)b.size(); ++i) {
for (int j = 0; j < i; ++j) {
long long g = GCD(m[i], m[j]);
// これを満たさなければ解はない
if ((b[i] - b[j]) % g != 0) return -1;
// s = m[i], t = m[j] を仮想的に素因数分解して s = p^k ... q^l ..., t = q^m ... r^n ... となったときに
m[i] /= g; // p については i の方が大きかったものについての j との差分、と q
m[j] /= g; // p については j の方が大きかったものについての i との差分、と r
/*
残る g を i と j に振り分ける (i の方が指数大きかった素因子 p の分は最終的に gi に、j の方が指数大きかった素因子 p の分は最終的に gj に)
*/
// ひとまず j 側にある p については gj のみに行くようにする
long long gi = GCD(m[i], g), gj = g/gi;
// 本来 i 側に行くべき p で gj 側にあるものを gi 側に寄せていく
do {
g = GCD(gi, gj);
gi *= g, gj /= g;
} while (g != 1);
// i 側と j 側に戻していく
m[i] *= gi, m[j] *= gj;
// m[i] と m[j] が元より小さくなったのに合わせて余りも計算し直しておく
b[i] %= m[i], b[j] %= m[j];
}
}
for (int i = 0; i < (int)b.size(); ++i) (res *= m[i]) %= MOD;
return res;
}
// 負の数にも対応した mod (a = -11 とかでも OK)
inline long long mod(long long a, long long m) {
long long res = a % m;
if (res < 0) res += m;
return res;
}
// 拡張 Euclid の互除法
long long extGCD(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGCD(b, a%b, q, p);
q -= a/b * p;
return d;
}
// 逆元計算 (ここでは a と m が互いに素であることが必要)
long long modinv(long long a, long long m) {
long long x, y;
extGCD(a, m, x, y);
return mod(x, m); // 気持ち的には x % m だが、x が負かもしれないので
}
// Garner のアルゴリズム, x%MOD, LCM%MOD を求める (m は互いに素でなければならない)
long long Garner(vector<long long> b, vector<long long> m, long long MOD) {
m.push_back(MOD); // banpei
vector<long long> coeffs((int)m.size(), 1);
vector<long long> constants((int)m.size(), 0);
for (int k = 0; k < (int)b.size(); ++k) {
long long t = mod((b[k] - constants[k]) * modinv(coeffs[k], m[k]), m[k]);
for (int i = k+1; i < (int)m.size(); ++i) {
(constants[i] += t * coeffs[i]) %= m[i];
(coeffs[i] *= m[k]) %= m[i];
}
}
return constants.back();
}
int main() {
int N; cin >> N;
vector<long long> b(N), m(N);
bool exist_non_zero = false;
for (int i = 0; i < N; ++i) {
cin >> b[i] >> m[i];
if (b[i]) exist_non_zero = true;
}
long long lcm = PreGarner(b, m, MOD);
if (!exist_non_zero) cout << lcm << endl;
else if (lcm == -1) cout << -1 << endl;
else cout << Garner(b, m, MOD) << endl;
}
4-2. 中国剰余定理を用いる応用問題たち
少し考え甲斐のある楽しい問題たちです。
問題 3: Codeforces 460 DIV2 E - Congruence Equation
【問題概要】
整数 $a, b, p, x$ が与えられる。
$Na^N ≡ b$ $({\rm mod}. p)$
が成立するような $1$ 以上 $x$ 以下の整数 $N$ を数え上げよ。
【制約】
- $2 \le p \le 10^{6}+3$
- $p$ は素数
- $1 \le a, b < p$
- $1 \le x \le 10^{12}$
【解法】
Fermat の小定理から以下のことが言えます:
- $N$ は $({\rm mod}. p$) において周期 $p$ である
- $a^{N}$ は $({\rm mod}. p$) において周期 $p-1$ である
したがって、$p$ と $p-1$ は互いに素だから、$Na^{N}$ ${\rm mod}. p$ は全体として周期 $p(p-1)$ となることがわかります。
ここで、$a^{N}$ の方を固定して集計することを考えます。すなわち、$N ≡ k$ $({\rm mod}. p-1)$ の場合について数えて条件を満たす $N$ の個数を数え上げて、それを $k = 0, 1, \dots, p-2$ について合算します。
$Na^{k} ≡ b$ $({\rm mod}. p$)
⇔ $N ≡ a^{-k}b$ $({\rm mod}. p$)
となることから、すなわち
- $N ≡ k$ $({\rm mod}. p-1$)
- $N ≡ a^{-k}b$ $({\rm mod}. p$)
を満たす $N$ を数え上げることになります。中国剰余定理により、
$N ≡ r$ $({\rm mod}. p(p-1)$)
を満たすような $r$ が求められるので、それを用いて $x$ 以下の整数を数え上げます。
# include <iostream>
# include <vector>
# include <cmath>
using namespace std;
inline long long mod(long long a, long long m) {
return (a % m + m) % m;
}
// 拡張 Euclid の互除法
long long extGCD(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGCD(b, a%b, q, p);
q -= a/b * p;
return d;
}
// 逆元
long long modinv(long long a, long long m) {
long long x, y;
extGCD(a, m, x, y);
return mod(x, m); // 気持ち的には x % m だが、x が負かもしれないので
}
// 中国剰余定理
pair<long long, long long> ChineseRem(long long b1, long long m1, long long b2, long long m2) {
long long p, q;
long long d = extGCD(m1, m2, p, q); // p is inv of m1/d (mod. m2/d)
if ((b2 - b1) % d != 0) return make_pair(0, -1);
long long m = m1 * (m2/d);
long long tmp = (b2 - b1) / d * p % (m2/d);
long long r = mod(b1 + m1 * tmp, m);
return make_pair(r, m);
}
long long a, b, p, x;
int main() {
cin >> a >> b >> p >> x;
long long res = 0;
long long pow = 1;
for (long long k = 0; k < p-1; ++k) {
// ≡ k(mod. p-1), ≡ a^{-k}b (mod. p)
long long b2 = modinv(pow, p) * b % p;
pair<long long, long long> c = ChineseRem(k, p-1, b2, p);
long long tmp = (x + (c.second - c.first) % c.second) / c.second;
res += tmp;
pow = pow * a % p;
}
cout << res << endl;
}
問題 4: Codeforces 196 Div1 D - GCD Table
【問題概要】
整数 $N$, $M$ と、$K$ 個の要素からなる数列 $A_0, A_1, \dots, A_{K-1}$ が与えられる。以下の条件を満たすような整数 $i$, $j$ ($1 \le i \le N$, $1 \le j \le M - K + 1$) が存在するかどうかを判定せよ。
- ${\rm gcd}(i, j) = A_0$
- ${\rm gcd}(i, j+1) = A_1$
- ${\rm gcd}(i, j+2) = A_2$
- $\dots$
- ${\rm gcd}(i, j+k-1) = A_{k-1}$
【制約】
- $1 \le N, M, A_i \le 10^{12}$
- $1 \le K \le 10^{4}$
【解法】
$i$ は $A_0, A_1, \dots, A_{K-1}$ の倍数であること、すなわち ${\rm lcm}(A_0, A_1, \dots, A_{K-1})$ の倍数であることが必要です。一方、$i$ が ${\rm lcm}(A_0, A_1, \dots, A_{K-1})$ の倍数でありさえすれば、${\rm gcd}(i, j) = A_0$ といった条件たちに特に影響はないです。したがって、$i$ はできるだけ小さくしたいので
$i = {\rm lcm}(A_0, A_1, \dots, A_{K-1})$
であるとしてよいです。これが $N$ 以下でなければその時点でダメです。さて、このとき
- ${\rm gcd}(i, j) = A_0$ であるためには「$j$ が $A_0$ の倍数であること」が必要
- ${\rm gcd}(i, j+1) = A_1$ であるためには「$j+1$ が $A_1$ の倍数であること」が必要
- $\dots$
- ${\rm gcd}(i, j+K-1) = A_{K-1}$ であるためには「$j+K-1$ が $A_{K-1}$ の倍数であること」が必要
になります。すなわち、
- $j ≡ 0$ $({\rm mod}. A_0)$
- $j ≡ -1$ $({\rm mod}. A_1)$
- $\dots$
- $j ≡ -(K-1)$ $({\rm mod}. A_{K-1})$
であることが必要になります。これを満たす $j$ を中国剰余定理によって求めます。そのような $j$ は複数考えられるのですが、${\rm lcm}(A_0, A_1, \dots, A_{K-1})$ を法として特に条件は変わらないです。したがって最小の $j$ を求めて
- $j \le M-K+1$ を満たすかどうか
- 実際に各 $k$ に対して ${\rm gcd}(i, j+k) = A_k$ を満たすかどうか (${\rm gcd}(i, j+k)$ が $A_k$ の倍数であることは保証されますが $A_k$ より大きくなってしまう可能性はあります)
を確認すればよいです。実装上は $A_k \le 10^{12}$ という制約があるために不用意に計算すると long long 型でもオーバーフローしてしまうため、「mod の値が大きいときの mod 演算」に示した方法によって実装しています。
# include <iostream>
# include <vector>
using namespace std;
// 最大公約数、最小公倍数
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
inline long long mod(long long a, long long m) {
return (a % m + m) % m;
}
// オーバーフロー対策
long long modmul(long long a, long long b, long long m) {
a = mod(a, m); b = mod(b, m);
if (b == 0) return 0;
long long res = modmul(mod(a + a, m), b>>1, m);
if (b & 1) res = mod(res + a, m);
return res;
}
long long modinv(long long a, long long m) {
long long b = m, u = 1, v = 0;
while (b) {
long long t = a/b;
a = mod(a - modmul(t, b, m), m); swap(a, b);
u = mod(u - modmul(t, v, m), m); swap(u, v);
}
return mod(u, m);
}
pair<long long, long long> ChineseRem(const vector<long long> &b, const vector<long long> &m, long long lcm) {
long long r = 0, M = 1;
for (int i = 0; i < (int)b.size(); ++i) {
long long d = GCD(M, m[i]);
if ((b[i] - r) % d != 0) return make_pair(0, -1);
long long p = modinv(M/d, m[i]/d);
long long tmp = modmul((b[i]-r)/d, p, m[i]/d);
r += modmul(M, tmp, lcm);
M *= m[i]/d;
}
return make_pair(mod(r, M), M);
}
// メイン
bool solve(long long N, long long M, long long K, vector<long long> A) {
// i を最小公倍数にできるか
long long lcm = 1;
for (int i = 0; i < K; ++i) {
long long g = GCD(lcm, A[i]);
lcm *= (A[i]/g);
if (lcm > N || lcm < 0) return false;
}
// 中国剰余定理
vector<long long> b(K), m(K);
for (int i = 0; i < K; ++i) b[i] = mod(-i, A[i]), m[i] = A[i];
pair<long long, long long> res = ChineseRem(b, m, lcm);
if (res.second == -1) return false; // 解がなかったらダメ
if (res.first == 0) res.first = lcm;
if (res.first > M-K+1) return false; // 最小の解が M-K+1 超えたらダメ
for (int k = 0; k < K; ++k) {
if (GCD(lcm, res.first + k) != A[k]) return false;
}
return true;
}
int main() {
long long N, M, K; cin >> N >> M >> K;
vector<long long> A(K); for (int i = 0; i < K; ++i) cin >> A[i];
if (solve(N, M, K, A)) cout << "YES" << endl;
else cout << "NO" << endl;
}
4-3. 法が素数でない場合の数え上げ
数え上げ問題は 1,000,000,007 といった素数で割った余りを求めさせる問題が多いですが、時々余りを求めるための法が素数でない問題も出題されます。そんなときは中国剰余定理の出番です。
問題 5: yukicoder 0695 square1001 and Permutation 4
【問題概要】
$m$ 個の整数 $x_i, x_2, \dots x_m$ が与えられる。
これらの中から整数を選んで合算することで合計値を $n-1$ にする方法が何通りあるかを $100 000 000 000 000 007$ で割ったあまりを求めよ。同じ整数を何個選んでもよい。
【制約】
- $2 \le n \le 2×10^7$
- $1 \le m \le 5$
- $1 \le x_i \le n-1$
【解法】
メモリ制限が特になければ $O(mn)$ な DP で求めることができます。基本的には
${\rm dp}[i]$ := $i$ を作る方法の数
として
${\rm dp}[0] = 0$
${\rm dp}[i] = \sum_{x[j] \le i} {\rm dp}[i - x[j]]$
の形の DP を考えればよいです。${\rm dp}[n-1]$ が答えです。今回はメモリ制限を満たすために以下の 2 つの工夫を盛り込む必要があります:
- $10^{17}+7 = 168647939 × 592951213$ より、$168647939$ と $592951213$ で割ったあまりをそれぞれ求めて中国剰余定理を適用する (これにより dp 配列を long long 型から int 型にできる)
- ${\rm dp}[n/2]$ まで求め、それを利用して ${\rm dp}[n-1]$ を算出する (これにより配列サイズを半分にできる)
2 については詳しくは公式解説を参照していただけたらと思います。
# include <iostream>
# include <vector>
using namespace std;
inline long long mod(long long a, long long m) {
return (a % m + m) % m;
}
// 拡張 Euclid の互除法
long long extGCD(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGCD(b, a%b, q, p);
q -= a/b * p;
return d;
}
// 逆元
long long modinv(long long a, long long m) {
long long x, y;
extGCD(a, m, x, y);
return mod(x, m); // 気持ち的には x % m だが、x が負かもしれないので
}
// 中国剰余定理
pair<long long, long long> ChineseRem(long long b1, long long m1, long long b2, long long m2) {
long long p, q;
long long d = extGCD(m1, m2, p, q); // p is inv of m1/d (mod. m2/d)
if ((b2 - b1) % d != 0) return make_pair(0, -1);
long long m = m1 * (m2/d);
long long tmp = (b2 - b1) / d * p % (m2/d);
long long r = mod(b1 + m1 * tmp, m);
return make_pair(r, m);
}
int n, m;
const int MOD[2] = {168647939, 592951213};
long long b[2];
vector<int> x;
int dp[10000010];
int main() {
cin >> n >> m; --n;
x.resize(m); for (int i = 0; i < m; ++i) cin >> x[i];
for (int iter = 0; iter < 2; ++iter) {
int p = MOD[iter];
dp[0] = 1;
for (int i = 1; i <= (n+1)/2; ++i) {
long long tmp = 0;
for (auto xv : x) if (i >= xv) (tmp += dp[i - xv]) %= p;
dp[i] = (int)tmp;
}
b[iter] = 0;
for (int i = 0; i <= (n+1)/2; ++i) for (auto xv : x) {
if (i + xv > (n+1)/2 && i + xv <= n) {
(b[iter] += (long long)(dp[i]) * dp[n - (i + xv)]) %= p;
}
}
}
pair<long long, long long> res = ChineseRem(b[0], MOD[0], b[1], MOD[1]);
cout << res.first << endl;
}
問題 6: [HackerRank Ad Infinitum 10 C - Cheese and Random Toppings](Cheese and Random Toppings)
【問題概要】
$T$ 個のテストケースが与えられる。
それぞれのテストケースで整数 $N, R, M$ を受け取って、$\binom{N}{R}$ $({\rm mod}. M$) を求めよ。
【制約】
- $1 \le T \le 200$
- $1 \le R \le N \le 10^9$
- $1 \le M \le 10^9$
- $M$ を素因数分解したとき、各素因子は $50$ 以下で、指数は $1$ である
【解法】
いわゆる「二項係数 mod. m」ですが、mod が素数でないため複雑なことになります。
幸いにも $M$ を素因数分解したときに
- 各素因子 $p$ は小さい ($50$ 以下)
- 各素因子 $p$ の指数は $1$
という特殊な状況にあるので、それを活かします。まず各素因子 $p$ に対する剰余を求めて、最後に中国剰余定理でまとめる流れです。
$\binom{n}{r}$ の $n$, $r$ について
- $n$ も $r$ も $10^7$ 以下であれば、二項係数 mod. p の冒頭のやり方が有力
- $n$ は大きいが $r$ が $10^7$ 以下であれば、同記事の二番目のやり方が有力
ですが、今回は $n$ も $r$ も最悪 $10^9$ と大きいので少し苦しいです。しかし $p$ が小さいので、そういうときは「リュカの定理」が有力です。詳しくはプログラミングコンテストチャレンジブックの P.262〜263 を読んでいただけたらと思います。
# include <iostream>
# include <vector>
using namespace std;
const int MAX_P = 100; // > 50
long long Fact[MAX_P];
long long mod(long long a, long long m) {
return (a % m + m) % m;
}
long long modinv(long long a, long long m) {
a = mod(a, m);
if (a == 1) return 1;
else return mod((1 - m * modinv(m % a, a)) / a, m);
}
// build n! table
void make_table(long long p) {
Fact[0] = 1;
for (int i = 1; i < p; ++i) {
Fact[i] = (Fact[i-1] * i) % p;
}
}
// find the value of "a" (n! = a p^e)
long long true_fact(long long n, long long p, long long& e) {
e = 0;
if (n == 0) return 1;
long long res = true_fact(n/p, p, e);
e += n/p;
if ( (n/p) % 2 != 0 ) return res * (p - Fact[n%p]) % p;
return res * Fact[n%p] % p;
}
// nCr mod.p
long long calc_com(long long n, long long r, long long p) {
if (n < 0 || r < 0 || n < r) return 0;
long long e1, e2, e3;
long long a1 = true_fact(n, p, e1), a2 = true_fact(r, p, e2), a3 = true_fact(n-r, p, e3);
if (e1 > e2 + e3) return 0;
return a1 * modinv(a2 * a3 % p, p) % p;
}
// 中国剰余定理
long long extGCD(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGCD(b, a%b, q, p);
q -= a/b * p;
return d;
}
pair<long long, long long> ChineseRem(const vector<long long> &b, const vector<long long> &m) {
long long r = 0, M = 1;
for (int i = 0; i < (int)b.size(); ++i) {
long long p, q;
long long d = extGCD(M, m[i], p, q); // p is inv of M/d (mod. m[i]/d)
if ((b[i] - r) % d != 0) return make_pair(0, -1);
long long tmp = (b[i] - r) / d * p % (m[i]/d);
r += M * tmp;
M *= m[i]/d;
}
return make_pair(mod(r, M), M);
}
// 素因数分解
vector<long long> prime_factor(long long n) {
vector<long long> res;
for (long long i = 2; i*i <= n; ++i) {
while (n%i == 0) {
res.push_back(i);
n /= i;
}
}
if (n != 1) res.push_back(n);
return res;
}
int main() {
int T; cin >> T;
for (int CASE = 0; CASE < T; ++CASE) {
long long N, R, M; cin >> N >> R >> M;
vector<long long> prs = prime_factor(M);
vector<long long> b, m;
for (auto p : prs) {
// 初期化
make_table(p);
long long r = calc_com(N, R, p);
b.push_back(r);
m.push_back(p);
}
pair<long long, long long> res = ChineseRem(b, m);
cout << res.first << endl;
}
}
4-4. mod. p での数え上げだが、指数が mod. p-1 (Fermat の小定理)
最後に時々見るパターンとして、問題全体としては mod. (素数) での数え上げの形をしているが、$a^{f(n)}$ $({\rm mod}. p)$ を求めることとなり、Fermat の小定理から $f(n)$ $({\rm mod}. p-1)$ を求める問題に帰着させるケースがあります。$p-1$ は通常素数とはならないので、中国剰余定理の出番です。
問題 7: SRM 449 DIV1 Hard StairsColoring
【問題概要】
$n$ 番目のカタラン数は $C(n) = \binom{2n}{n} - \binom{2n}{n-1}$ で与えられる。
整数 $k$ が与えられて、$k^{C(n)}$ を $1000000123$ で割ったあまりを求めよ。
【制約】
- $1 \le n, k \le 10^9$
【解法】
Fermat の小定理から、$C(n) = \binom{2n}{n} - \binom{2n}{n-1}$ を $1000000122 = 2×3×11×2089×7253$ で割ったあまりを求める問題に帰着します。各素数 $p$ について二項係数 $\binom{2n}{n}$ などを割った余りが求められたらいいのですが、$n$ の制約が大きくて大変なので、$p$ が小さいことを活かします。前問と同じく「リュカの定理」を用います。
# include <iostream>
# include <vector>
using namespace std;
long long MOD = 1000000123;
const int MAX_P = 10000;
long long Fact[MAX_P];
long long mod(long long a, long long m) {
return (a % m + m) % m;
}
long long pow(long long a, long long n, long long m) {
if (n == 0) return 1 % m;
long long t = pow(a, n/2, m);
t = mod(t * t, m);
if (n & 1) t = mod(t * a, m);
return t;
}
long long modinv(long long a, long long m) {
a = mod(a, m);
if (a == 1) return 1;
else return mod((1 - m * modinv(m % a, a)) / a, m);
}
// build n! table
void make_table(long long p) {
Fact[0] = 1;
for (int i = 1; i < p; ++i) {
Fact[i] = (Fact[i-1] * i) % p;
}
}
// find the value of "a" (n! = a p^e)
long long true_fact(long long n, long long p, long long& e) {
e = 0;
if (n == 0) return 1;
long long res = true_fact(n/p, p, e);
e += n/p;
if ( (n/p) % 2 != 0 ) return res * (p - Fact[n%p]) % p;
return res * Fact[n%p] % p;
}
// nCr mod.p
long long calc_com(long long n, long long r, long long p) {
if (n < 0 || r < 0 || n < r) return 0;
long long e1, e2, e3;
long long a1 = true_fact(n, p, e1), a2 = true_fact(r, p, e2), a3 = true_fact(n-r, p, e3);
if (e1 > e2 + e3) return 0;
return a1 * modinv(a2 * a3 % p, p) % p;
}
// 中国剰余定理
long long extGCD(long long a, long long b, long long &p, long long &q) {
if (b == 0) { p = 1; q = 0; return a; }
long long d = extGCD(b, a%b, q, p);
q -= a/b * p;
return d;
}
pair<long long, long long> ChineseRem(const vector<long long> &b, const vector<long long> &m) {
long long r = 0, M = 1;
for (int i = 0; i < (int)b.size(); ++i) {
long long p, q;
long long d = extGCD(M, m[i], p, q); // p is inv of M/d (mod. m[i]/d)
if ((b[i] - r) % d != 0) return make_pair(0, -1);
long long tmp = (b[i] - r) / d * p % (m[i]/d);
r += M * tmp;
M *= m[i]/d;
}
return make_pair(mod(r, M), M);
}
class StairsColoring {
public:
int coloringCount(long long N, long long K) {
vector<long long> fact;
fact.push_back(2); fact.push_back(3); fact.push_back(11); fact.push_back(2089); fact.push_back(7253);
int n = (int)fact.size();
vector<long long> vb(n);
for (int i = 0; i < n; ++i) {
long long p = fact[i];
make_table(p);
vb[i] = mod(calc_com(N*2, N, p) - calc_com(N*2, N-1, p), p);
}
pair<long long, long long> e = ChineseRem(vb, fact);
return (int)pow(K, e.first, MOD);
}
};
5. 参考資料
[1] アルゴリズムイントロダクションの第 33 章 (T. Cormen ら著, 浅野 哲夫ら訳)
[2] プログラミングコンテストチャレンジブックの第 4.1 節 (秋葉 拓哉ら)
[3] Algorithms for Computer Algebra (S. J. Lomonaco , Jr.)
[4] Chinese Remainder Theorem (CP-Algorithms)
[5] 任意modでの畳み込み演算をO(n log(n))で (math314)
[6] Garner のアルゴリズムと多倍長整数演算 (kirika_comp)
[7] フカシギおねえさん問題の高速計算アルゴリズム (岩下 洋哲)
[8] RSA 暗号がようやく分かった気がしたのでまとめてみる (tsujimotter)
[9] 中華風剰余定理 (anta)
[10] NTT (整数環FFT) (satanic0258)