お久しぶりです!
アルゴリズムと整数好きのけんちょんです!
今回は俗に「数学ゲー」と呼ばれるタイプの問題のうち、整数について語ります。
【他シリーズ】
- AtCoder 版!マスター・オブ・整数 (最大公約数編)
- エラトステネスの篩の活用法を総特集! 〜 高速素因数分解・メビウスの反転公式 〜
- フェルマーの小定理の証明と使い方
- 拡張ユークリッドの互除法 〜 一次不定方程式 ax + by = c の解き方 〜

(書籍画像は amazon ページ より)
追記:整数問題を練習できるオンライン教材
本記事に準拠した、整数アルゴリズムを学べるオンライン教材を作ってみました。素数判定から始めて、段階的に学べる教材としました。
1 問 1 問は下図のような構成になっています。各問題に対して、ユーザが実装したプログラムを提出すると、その場でサーバー上で実行し、正しく挙動したかどうかをジャッジするものです。ぜひ併せて活用してみてください。
1. 整数問題の分類
AtCoder の整数問題は、500 点以下であれば「素因数分解」と「最大公約数」と「エラトステネスの篩」と「合同式」に関する考察・アルゴリズムを自在に操れば、ほとんど解けるようになっています1。
- 素因数分解
- 最大公約数
- エラトステネスの篩
- 合同式
本記事ではこのうちの「素因数分解」に焦点を当てます。
ところで、どんな題材でもそうなのですが、それを学ぶということは「その題材に関するアルゴリズム自体を使いこなせるようになること」と「その題材を用いることで考察の助けとすること」の 2 つの側面があります。単に素因数分解アルゴリズムを覚えて使いこなせるようになるだけでなく
「与えられた整数を素因数分解してみる」というのを考察過程の一つの武器として使いこなせるようになること
が重要です2。さて、本記事では以下の順序で見ていきます。
一見多く見えますが、登場するアルゴリズムは実質 1 つだけです。「素数判定」のアルゴリズムは、ちょっと変形するだけで素因数分解もできますし、約数の列挙も、約数の個数も、約数の総和も、オイラー関数値も求められます!!!!!
2. 素数判定
まずは整数論的アルゴリズムの中で、最初に学ぶ印象が強い「素数判定」です!
2-1. 素数とは
念のために素数とは何かを確認しておきましょう。素数とは
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, \dots
といったように、「1 と自分自身以外では割り切れない整数」のことです3。$57$ は
$57 ÷ 3 = 19$
という風に、$1$ と $57$以外の整数である $3$ で割り切れるので素数ではないです。このような整数は合成数とよばれます。また注意点として、$1$ や $0$ は素数ではないものと考えます。
2-2. 素数判定
素数判定とは次のような問題です。
問題 1: 素数判定
正の整数 $N$ が与えられます。
$N$ が素数であるならば "Yes" を出力し、素数でないならば "No" を出力してください。
- $1 \le N \le 10^{12}$
このように素数判定を行う場面は、整数ゲーで極めて頻繁に発生します。まずは「素数」の定義を思い出して愚直な解法を考えてみましょう。素数とは「1 と自分自身以外では割り切れない整数」のことでした。そのことを愚直に確かめればよいでしょう。
たとえば $N = 7$ について考えます。
- $7 ÷ 1 = 7$
- $7 ÷ 2$ は割り切れない
- $7 ÷ 3$ は割り切れない
- $7 ÷ 4$ は割り切れない
- $7 ÷ 5$ は割り切れない
- $7 ÷ 6$ は割り切れない
- $7 ÷ 7 = 1$
- ...
という風になっています。$7$ より大きい整数ではどのみち割れることはないため、$2, 3, \dots, N-1$ について試し割りすれば十分です。$7$ は、$2, 3, 4, 5, 6$ で割れないので素数であるといえます。
これで $N-2$ 回の割り算でこの問題が解けることがわかりました。すなわち $O(N)$ の計算量で解くことができます。しかし今回は制約が $N \le 10^{12}$ となっていますので、このままでは TLE してしまいます。なんとか工夫して計算量を減らすことはできないでしょうか。
実は、$2, 3, \dots$ と試し割りしていくときに、$N-1$ までやる必要はなく $\sqrt{N}$ までやれば十分なのです。その理由を考えてみましょう。ここで先ほどの $57$ の例を振り返ってみます。
$57 ÷ 3 = 19$
という式は、ひっくり返せば
$57 ÷ 19 = 3$
となります。つまり $57$ は $3$ で割り切れると同時に、$19$ でも割り切れるということです。このことをよく観察すると、次の結論が導けます。
【素数判定のアイディア】
正の整数 $N$ が、$2$ 以上 $\sqrt{N}$ 以下の整数で割り切れないならば、$\sqrt{N}$ 以上 $N-1$ 以下の整数で割り切れることもない
初めて見るとショッキングな言明かもしれません。たとえば $113$ という整数が素数かどうかを試すとき、$\sqrt{113} = 10.63$ ですから、$2, 3, 4, 5, 6, 7, 8, 9, 10$ で割り切れなかったら、その時点で素数であることが確定するということです。下図のように、$2 〜 112$ を調べるのに比べて、随分と探索範囲を狭めることができます!
(余談ですが、さらに言えば、実際には $4, 6, 8, 9, 10$ も試す必要はありません。なぜなら、例えばもし $6$ で割れるようであれば、その約数である $2$ や $3$ でも割れるということですから。つまり合成数を試す必要はないのです。よって、$113$ が素数かどうかを確かめるには、$2, 3, 5, 7$ で割るだけでよいです。この程度なら一瞬でしょう。$113$ は素数です。)
さて、上記の性質を簡単に証明しておきましょう。$N$ が $\sqrt{N}$ 以上 $N-1$ 以下の整数 $a$ で割り切れると仮定して矛盾を導きます。割った結果を $b$ とおくと
- $N ÷ a = b$
となります。このとき $N$ は $b$ でも割り切れることに注意します。一方 $a \ge \sqrt{N}$ より、
$b = \frac{N}{a} \le \sqrt{N}$
となることから、$N$ が $\sqrt{N}$ 以下の整数 $b$ で割り切れることになって矛盾です。
要するに、大きい整数で割れるなら、その相方は小さな整数になるので、元々小さい整数でも割れていたはずだ、ということですね。その大きい・小さいの境界が $\sqrt{N}$ というわけです。以上から、$N$ が素数かどうかを判定するためには、$i = 2, 3, \dots, \sqrt{N}$ について試し割りすればよいことがわかりました。計算量は $O(\sqrt{N})$ となって間に合います。なお実装上は
for (long long i = 2; i * i <= N; ++i)
という風に簡潔に書くことができます。i * i <= N という部分が、$\sqrt{N}$ 以下の整数まで試すことを表しています。こうすれば、double 型変数を持ち出すことなく、整数型だけで処理できます。整数だけで済むなら整数で...数値誤差は怖いです4。
# include <iostream>
using namespace std;
bool is_prime(long long N) {
if (N == 1) return false;
for (long long i = 2; i * i <= N; ++i) {
if (N % i == 0) return false;
}
return true;
}
int main() {
long long N;
cin >> N;
if (is_prime(N)) cout << "Yes" << endl;
else cout << "No" << endl;
}
3. 約数列挙
次にステップアップして「約数をすべて列挙する」という問題を見ます。$N$ の約数とは、$N$ を割り切ることのできる整数のことです。たとえば $12$ の約数は $1, 2, 3, 4, 6, 12$ の $6$ 個になります。$5$ は、$12 ÷ 5$ が割り切れないので、$12$ の約数ではありません。
3-1. 約数列挙
次の問題を解いてみましょう。
これは「素数判定」を本質的に含む問題です。なぜなら、$N$ の約数を列挙したとき、それが $1$ と $N$ のみであるかどうかによって $N$ が素数かどうかを判定できるからです。
しかし約数列挙も、素数判定のロジックをほんの少し改変するだけで解くことができます。計算量も同じく $O(\sqrt{N})$ です。
問題 2: 約数列挙
正の整数 $N$ が与えられます。
$N$ の約数を小さい順にすべて出力してください。
- $1 \le N \le 10^{12}$
(数値例)
・$N = 12$
答え: 1 2 3 4 6 12
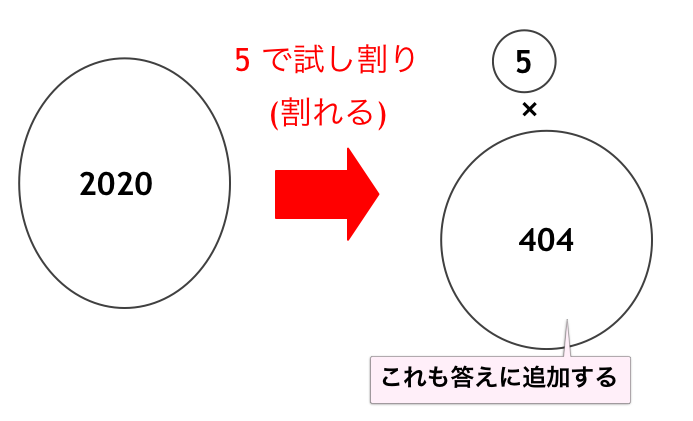
実は先ほどと全く同じように、$a = 1, 2, \dots, \sqrt{N}$ まで試し割りすればよいです。$\sqrt{N}$ より大きい約数については、次のようにして求めることができます:
$N$ が $a$ で割り切れるとき、$\frac{N}{a}$ も答えに追加する
注意点として $N$ が平方数の場合、$a$ と $\frac{N}{a}$ がちょうどピッタリ一致することがあります ($N = 25, a = 5$ など)。この種のケースで重複して答えに push しないように気をつけましょう。
# include <iostream>
# include <vector>
# include <algorithm>
using namespace std;
vector<long long> enum_divisors(long long N) {
vector<long long> res;
for (long long i = 1; i * i <= N; ++i) {
if (N % i == 0) {
res.push_back(i);
// 重複しないならば i の相方である N/i も push
if (N/i != i) res.push_back(N/i);
}
}
// 小さい順に並び替える
sort(res.begin(), res.end());
return res;
}
int main() {
long long N;
cin >> N;
const auto &res = enum_divisors(N);
for (int i = 0; i < res.size(); ++i) cout << res[i] << " ";
cout << endl;
}
3-2. 約数列挙の例題
実践的な問題として、AtCoder ABC の過去問を解いてみましょう。
問題 3: ABC 057 C - Digits in Multiplication (300 点)
正の整数 $N$ が与えられる。
$N = A \times B$ を満たす正の整数 $A, B$ の組をすべて考えたときの、「$A$ の桁数と $B$ の桁数のうちの大きい方の値」の最小値を求めよ。
- $1 \le N \le 10^{10}$
(数値例)
・$N = 10000$
答え: $3$ ($A = 100, B = 100$ のとき)
約数をすべて調べ尽くす全探索によって解くことができます。先ほどと同じように
- $A = 1, 2, \dots, \sqrt{N}$ まで試す
という風にすればよいです。$A > B$ であるような場合は、特に考えなくてもよいことに注意しましょう ($A = 3, B = 15$ のケースと、$A = 15, B = 3$ のケースは答えが全く一緒です)。
なお、「与えられた整数の桁数」の求め方については
を参考にしてもらえたらと思います。
# include <iostream>
using namespace std;
int calc_digit(long long N) {
int res = 0;
while (N) {
++res;
N /= 10;
}
return res;
}
int main() {
long long N;
cin >> N;
int res = (1<<29); // 十分大きい値で初期化
for (long long A = 1; A * A <= N; ++A) {
if (N % A == 0) {
long long B = N / A;
int F = max(calc_digit(A), calc_digit(B));
res = min(res, F);
}
}
cout << res << endl;
}
4. 素因数分解
次はいよいよ、整数ゲーを解くための超強力な道具である素因数分解です。素因数分解とは、
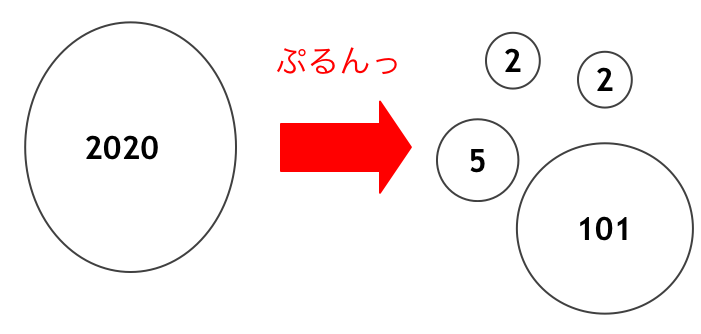
$2020 = 2 \times 2 \times 5 \times 101$
といったように、整数を「素数の積」で表すことです。素数とは「もうこれ以上分解できない数」というイメージです。なんだか分子みたいなものですね。物体を細かく分解していくと、いつかは「これ以上分解できないもの」になります。それが分子であり、素数です。
素数はそれ自体が素因数分解になっています ($113$ の素因数分解は $113$)。$N$ を割り切る素数は $N$ の素因数であるといいます。$2020$ の素因数は $2, 5, 101$ の $3$ 個です。また、素因数分解の結果を表現する方法ですが、多くの場合
$2020 = 2^2 \times 5^1 \times 101^1$
といったように、(素因数, 指数) でまとめると良いです。実装上は C++ では vector<pair<long long, long long> > 型で表すことにします。$2020$ の例では
{{2, 2}, {5, 1}, {101, 1}}
です。素因数分解も最初の「素数判定」とほとんど同じ方法でできます。計算量もはやり $O(\sqrt{N})$ です。この問題は
で verify することができます。
問題 4: 素因数分解
$2$ 以上の正の整数 $N$ が与えられる。
$N$ を素因数分解した結果を出力せよ。
- $2 \le N \le 10^{9}$
(数値例)
・$N = 2020$
答え: 2020: 2 2 5 101
素数判定と同じく、$a = 2, 3, \dots, \sqrt{N}$ で試し割りすればよいのですが、最初は少し難しく感じるかもしれません。最初にコードを載せてしまいます!計算量は $O(\sqrt{N})$ です。
# include <iostream>
# include <vector>
using namespace std;
vector<pair<long long, long long> > prime_factorize(long long N) {
vector<pair<long long, long long> > res;
for (long long a = 2; a * a <= N; ++a) {
if (N % a != 0) continue;
long long ex = 0; // 指数
// 割れる限り割り続ける
while (N % a == 0) {
++ex;
N /= a;
}
// その結果を push
res.push_back({a, ex});
}
// 最後に残った数について
if (N != 1) res.push_back({N, 1});
return res;
}
int main() {
long long N;
cin >> N;
const auto &res = prime_factorize(N);
cout << N << ":";
for (auto p : res) {
for (int i = 0; i < p.second; ++i) cout << " " << p.first;
}
cout << endl;
}
さて、素数判定や約数列挙と同じく、$a = 2, 3, \dots, \sqrt{N}$ で試し割りすればよいのですが、少し工夫します。
- $N$ が $a$ で割り切れるとわかったときは、割れる限り、割り続ける
という風にします。$N$ の値が変化することに注意しましょう。上の素因数分解コードのうち、以下の部分が相当します。
vector<pair<long long, long long> > res;
for (long long a = 2; a * a <= N; ++a) {
if (N % a != 0) continue;
long long ex = 0; // 指数
// 割れる限り割り続ける
while (N % a == 0) {
++ex;
N /= a;
}
// その結果を push
res.push_back({a, ex});
}
これによって、$N$ の素因数分解において、$a$ の指数 ($a$ で何回割れるか) がわかります。ここでちょっとイヤなのは $a$ 自身が合成数である場合には、$a$ をさらに分解しなければならないように感じてしまうことです。しかしなんと、少しビックリするかもしれませんが
- $N$ が $a$ で割れるとき、$a$ はかならず素数になっている
のです!!!!!!!なぜでしょう???
それは $a$ で試し割りする前に、$a$ を構成する各素因数 $p$ について $N$ が割れるだけ割られているからです。
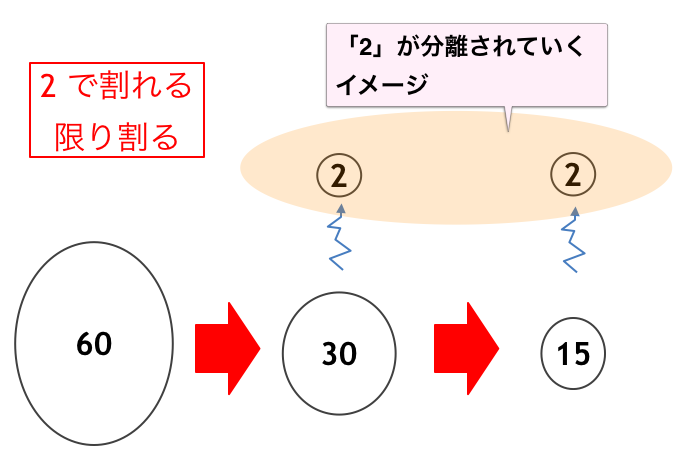
たとえば $N = 60$ のとき、これは $a = 6$ で割り切れます。しかしその前の $a = 2$ の段階で、
60 \rightarrow 30 \rightarrow 15
という具合に、$N$ は $2$ では割れない姿に変わり果てています。よって $a = 6$ の番が回ってきたときには、$N$ を割り切ることはできないのです。
最後に、以下のような処理をしています。これは何をしているのでしょうか?
// 最後に残った数について
if (N != 1) res.push_back({N, 1});
まず、$a \le \sqrt{N}$ まで割り終えたとき、$N$ がどうなっているかについて、以下の 2 つの場合が考えられます。
- $N = 1$ になっている
- $N > 1$ になっている
前者についてはもう素因数分解は完全に完了しています。それまでに得られた解を出力すればよいでしょう。
後者については、残った整数は素数です。なぜなら、それがもし合成数であれば、それを構成する素因数のうちの 1 つは $\sqrt{N}$ 以下になるはずだからです ($\sqrt{N}$ より大きい値を 2 回以上かけたら $N$ を超えることに注意)。最後の $N$ には、もう、そんな小さな素因数は残っているはずがありません。よって最後の $N$ は素数なので、それを答えに加えて終了します。
ここの議論は慣れていないと少し難しいかもしれません。これも当面は「残った数は $1$ か素数にしかならない」というのは、そういうものだと受け入れて、先に進んでもよいと思います。
5. 素因数分解の利用
素因数分解を活用すると、整数の様々な量を計算することができるようになります。ここでは
- 約数の個数
- 約数の総和
- オイラー関数
について考えてみます。いずれも競プロ・大学受験ともに頻出の話題ですね。これらについては、特にライブラリ化する必要はないと思っています。むしろ素因数分解から導出する過程を堪能することが重要だと思います。
5-1. 約数の個数 (問題 5)
約数の個数を求める問題を考えます。ただ単に約数の個数を求めるだけなら、すでに「約数の列挙」を行うアルゴリズムを紹介しているので、それで事足りるのですが、ここでは素因数分解の結果から約数の個数を求めることを考えます (約数の個数に関する問題例は ABC 052 C - Factors of Factorial など)。
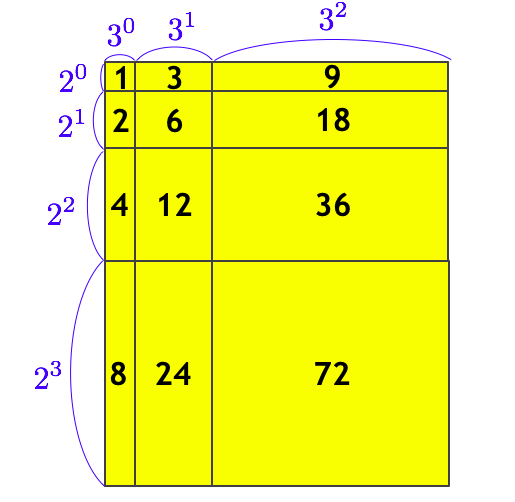
たとえば $72 = 2^3 \times 3^2$ の約数の個数を考えてみましょう。並べてみるとこうなります。以下の $12$ 個です。
- $1 = 2^0 \times 3^0$
- $2 = 2^1 \times 3^0$
- $3 = 2^0 \times 3^1$
- $4 = 2^2 \times 3^0$
- $6 = 2^1 \times 3^1$
- $8 = 2^3 \times 3^0$
- $9 = 2^0 \times 3^2$
- $12 = 2^2 \times 3^1$
- $18 = 2^1 \times 3^2$
- $24 = 2^3 \times 3^1$
- $36 = 2^2 \times 3^2$
- $72 = 2^3 \times 3^2$
これらは表にすると、以下のグリッドの各マスに対応しています。よって、$4 \times 3 = 12$ 個と計算することもできます。

今回は素因数が 2 個 (2 と 3 のみ) の場合だったので見やすい状態でしたが、素因数が 3 個以上になっても同様です。一般に
N = p_{1}^{e_{1}} p_{2}^{e_{2}} \dots p_{K}^{e_{K}}
と素因数分解できるとき、約数の個数は
(e_{1} + 1)(e_{2} + 1) \dots (e_{K} + 1) 個
となります。ところで、約数の個数を求めるだけなら素因数分解はオーバーキルで、約数列挙で十分です。しかし、素因数分解で考えることには大きなメリットがあります。それは「約数に関する考察をしやすい」ということです。そのような実例については、6 章で見ていきます。
また、素因数分解を $p_{1}^{e_{1}} p_{2}^{e_{2}} \dots p_{K}^{e_{K}}$ といった抽象的な数式で表すことにも慣れていきましょう。$K$ は素因数分解に登場する素因数の個数を表していて、$N$ の値によって変わります。
# include <iostream>
# include <vector>
using namespace std;
vector<pair<long long, long long> > prime_factorize(long long N) {
vector<pair<long long, long long> > res;
for (long long a = 2; a * a <= N; ++a) {
if (N % a != 0) continue;
long long ex = 0;
while (N % a == 0) {
++ex;
N /= a;
}
res.push_back({a, ex});
}
if (N != 1) res.push_back({N, 1});
return res;
}
int main() {
long long N;
cin >> N;
const auto &pf = prime_factorize(N);
long long res = 1;
for (auto p : pf) res *= p.second + 1;
cout << res << endl;
}
5-2. 約数の総和
次は $N$ の約数の総和を求める問題を考えてみましょう。たとえば $N = 12$ であれば、$1 + 2 + 3 + 4 + 6 + 12 = 28$ です。これも約数を列挙して足せばよいのですが、せっかくなので素因数分解を利用して求めてみましょう (約数の総和に関する問題例は ARC 026 B - 完全数 など)。
実は、「約数の個数」を求めたときの考え方をほんの少し改変するだけで求めることができます。ズバリ!!!下図の長方形全体の面積です!!!
$6$ や $18$ といった数値は、小さい区域の面積となっていて、それらが合算されると長方形全体の面積になります。この長方形全体の縦の長さは $2^0 + 2^1 + 2^2 + 2^3 = 15$ で、横の長さは $3^0 + 3^1 + 3^2 = 13$ です。よって求める総和は、
(2^0 + 2^1 + 2^2 + 2^3)(3^0 + 3^1 + 3^2) = 15 \times 13 = 195
となります。一般に
N = p_{1}^{e_{1}} p_{2}^{e_{2}} \dots p_{K}^{e_{K}}
と素因数分解できるとき、約数の総和は
(p_{1}^0 + p_{1}^1 + \dots + p_{1}^{e_{1}})(p_{2}^0 + p_{2}^1 + \dots + p_{2}^{e_{2}}) \dots (p_{K}^0 + p_{K}^1 + \dots + p_{K}^{e_{K}})
となります。実装上は、単に約数の総和を求めるだけならば、普通に約数列挙した方が楽でしょう。
5-3. オイラー関数
この辺りから聞いたことないという方も増えてくると思います。マスター・オブ・整数の 1-5 節で登場する話題です。
正の整数 $N$ が与えられたとき、$1, 2, \dots, N$ のうち $N$ と互いに素であるものの個数を $\varphi(N)$ と表します。これをオイラー関数とよびます。ここで「互いに素」という言葉が出てきました。「互いに素」という概念については、次回記事で深く掘り下げます。ここでは定義を簡単に確認しておきます。
【互いに素】
2 つの整数 $a, b$ が互いに素であるとは、以下の条件を満たすような整数 $d$ が存在しないことをいう:
- $d > 1$
- $a$ は $d$ で割り切れる
- $b$ は $d$ で割り切れる
具体例で考えてみましょう。
- $a = 6, b = 8$ のとき、$a$ も $b$ も $2$ で割り切れるので、$a, b$ は互いに素ではありません
- $a = 6, b = 11$ のとき、これらをともに割り切る正の整数は $1$ しかないので、$a, b$ は互いに素です
言い換えれば、$a$ と $b$ の「最大公約数が $1$」ということです。それではオイラー関数を求める問題を解きましょう。これは以下のページで verify できます。
問題 6: オイラー関数
正の整数 $N$ が与えられる。
$1, 2, \dots, N$ のうち、$N$ と互いに素であるものの個数を求めよ。
- $1 \le N \le 10^{12}$
(数値例)
・$N = 12$
答え: 4
$1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12$ のうち、$12$ と互いに素であるものは、$1, 5, 7, 11$ の $4$ 個です。
ちょっと難しいかもしれません。難しいと感じた場合には、一旦飛ばしてもらえたらと思います。結論から言うと、
N = p_{1}^{e_{1}} p_{2}^{e_{2}} \dots p_{K}^{e_{K}}
と素因数分解できるとき、オイラー関数値は
\varphi(N) = N(1 - \frac{1}{p_{1}})(1 - \frac{1}{p_{2}}) \dots (1 - \frac{1}{p_{K}})
となります。確かめてみましょう。$N = 12$ のとき、$12 = 2^2 \times 3$ ですから、確かに
\varphi(12) = 12 \times (1 - \frac{1}{2}) \times (1 - \frac{1}{3}) = 4
となります。このことの証明はちょっと難しいですが、直感的にはすぐにわかります。「$12$ と互いに素」という条件は、次の 2 つの条件をともに満たすことと同値です。
- $2$ と互いに素である
- $3$ と互いに素である
まず一個目の条件を考慮してみましょう。$1$ から $12$ までの整数のうち、$2$ の倍数を除外しましょう。
1 2 3 4 5 6 7 8 9 10 11 12
o x o x o x o x o x o x
$1〜12$ のうち、$2$ の倍数の割合は $\frac{1}{2}$ ですから、それを除外した個数は
12 \times (1 - \frac{1}{2} ) = 6
となります。次に $3$ の倍数を除外します。
1 2 3 4 5 6 7 8 9 10 11 12
o x x x o x o x x x o x
このとき、$3$ の倍数の割合は $\frac{1}{3}$ ですから、それを除外した個数は
12 \times (1 - \frac{1}{2} ) \times (1 - \frac{1}{3}) = 4
となります。オイラー関数を求める計算量は、素因数分解がボトルネックで $O(\sqrt{N})$ となります。
# include <iostream>
# include <vector>
using namespace std;
vector<pair<long long, long long> > prime_factorize(long long N) {
vector<pair<long long, long long> > res;
for (long long a = 2; a * a <= N; ++a) {
if (N % a != 0) continue;
long long ex = 0;
while (N % a == 0) {
++ex;
N /= a;
}
res.push_back({a, ex});
}
if (N != 1) res.push_back({N, 1});
return res;
}
int main() {
long long N;
cin >> N;
const auto &pf = prime_factorize(N);
long long res = N;
for (auto p : pf) {
res *= (p.first - 1);
res /= p.first;
}
cout << res << endl;
}
6. 素因数分解を活用した考察
最後に、素因数分解を単なるアルゴリズムの知識として覚えるだけでなく、考察の道具として積極的に使えるようになることを目指しましょう!!!
そもそも人類にとって、素因数分解をすると何が嬉しいのでしょうか???
ザッと以下のような点が嬉しいと思います。
- 最大公約数に関する考察がやりやすくなる
- ひねった状況でも「約数の個数」がわかる
- 素数を分け合う
- 「約数の構造」を知る
- $p$ で何回割れるのかに着目
6-1. 最大公約数に関する考察がやりやすくなる
最大公約数に関する話は、次の記事で改めて掘り下げようと思いますが、ここでは素因数分解に関連する部分を考えます。「最大公約数」とは、二つの整数 $a, b$ に関するものです。
【公約数と最大公約数】
整数 $d$ が二つの整数 $a, b$ の公約数であるとは、$d$ が $a$ の約数でもあって、$b$ の約数でもあることを言います。
$a, b$ の公約数のうち、最大のものを最大公約数とよびます。
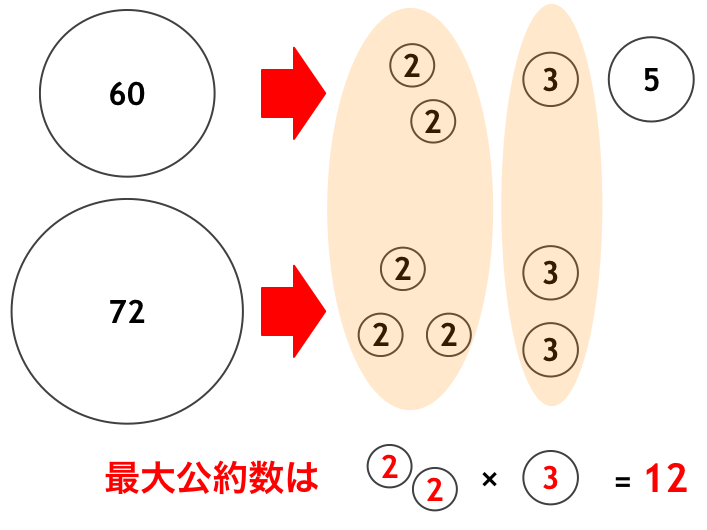
たとえば、$60$ と $72$ の公約数について考えてみましょう。これらを素因数分解すると
- $60 = 2^2 \times 3^1 \times 5^1$
- $72 = 2^3 \times 3^2$
となります。これらの公約数は、以下の 6 個です。
- $1 = 2^0 \times 3^0$
- $2 = 2^1 \times 3^0$
- $3 = 2^0 \times 3^1$
- $4 = 2^2 \times 3^0$
- $6 = 2^1 \times 3^1$
- $12 = 2^2 \times 3^1$
そして最大公約数は $12$ になります。最大公約数は、各素因数についての指数が、$60$ と $72$ のうちの指数が小さい方に合わせたものになっていることがわかります。
なお注意点として、$a, b$ の最大公約数をアルゴリズム的に求めるだけならば、次回記事でやる Euclid の互除法を使った方がよいです。しかし考察の道具として素因数分解を持ち出すのは有効です。
さて、公約数を眺めていると、さらに次のこともわかります5。
【公約数と最大公約数】
二つの整数 $a, b$ の公約数は、$a, b$ の最大公約数の約数である。
実際、$60$ と $72$ の公約数である $1, 2, 3, 4, 6, 12$ はすべて、最大公約数である $12$ の約数になっています。
6-2. ひねった状況でも「約数の個数」がわかる
百聞は一見にしかずで、次の問題を考えてみましょう。
問題 7: ABC 052 C - Factors of Factorial (300 点)
正の整数 $N$ が与えられる。
$N!$ の正の約数の個数を $1000000007$ で割ったあまりを求めよ。
- $1 \le N \le 1000$
(数値例)
・$N = 3$
答え: 4
$3! = 6$ の約数は、$1, 2, 3, 6$ の $4$ 個です。
いきなり、約数列挙で解ける!!!と思ってしまうと辛いことになります。$N!$ はとてつもなく大きな整数になり得るので、$N!$ を求めてから約数列挙をするのは無理です。
ここで、素因数分解を活用した約数の個数の求め方を思い出しましょう。一般に、正の整数 $M$ が
M = p_{1}^{e_{1}} p_{2}^{e_{2}} \dots p_{K}^{e_{K}}
と素因数分解できるとき、$M$ の約数の個数は
(e_{1} + 1)(e_{2} + 1) \dots (e_{K} + 1) 個
と求められるのでした。よって、なんらかの方法によって、$N!$ を計算しなくても $N!$ の素因数分解が求められればよいということになります。実はそれは簡単です。たとえば $N = 6$ のとき、
- $2 = 2^1$
- $3 = 3^1$
- $4 = 2^2$
- $5 = 5^1$
- $6 = 2^1 \times 3^1$
であることから、
\begin{align}
6! &= 1 \times 2 \times 3 \times 4 \times 5 \times 6 \\
&= (2^1) \times (3^1) \times (2^2) \times (5^1) \times (2^1) \times (3^1) \\
&= 2^4 \times 3^2 \times 5^1
\end{align}
と求められます。つまり、$2, 3, \dots, N$ をそれぞれ素因数分解して、その結果をマージすることで、$N!$ の素因数分解ができるのです。実装上は
- ex[ p ] := N! を素因数分解したときの、素因数 p の指数
という配列を用意してあげると楽だと思います。制約が $N \le 1000$ なので、登場する素因数 $p$ も $1000$ 以下なので、連想配列にする必要はなく、贅沢にメモリを使って大丈夫です。計算量は $O(N\sqrt{N})$ になります。
# include <iostream>
# include <vector>
using namespace std;
vector<pair<long long, long long> > prime_factorize(long long N) {
vector<pair<long long, long long> > res;
for (long long a = 2; a * a <= N; ++a) {
if (N % a != 0) continue;
long long ex = 0;
while (N % a == 0) {
++ex;
N /= a;
}
res.push_back({a, ex});
}
if (N != 1) res.push_back({N, 1});
return res;
}
int main() {
long long N;
cin >> N;
const int MOD = 1000000007;
vector<long long> ex(N+1, 0); // exp[p] := p の指数
for (long long n = 2; n <= N; ++n) {
const auto &res = prime_factorize(n); // n の素因数分解
for (auto p : res) ex[p.first] += p.second;
}
long long res = 1;
for (int p = 2; p <= N; ++p) {
res *= ex[p] + 1; // 約数の個数は (exp + 1) の積
res %= MOD;
}
cout << res << endl;
}
6-3. 素数を分け合う
こんなシチュエーションを考えてみましょう。$3$ つの整数 $a, b, c$ の積が $600$ となるような、整数 $a, b, c$ の組はどんなものが考えられるでしょうか??$600 = 2^3 \times 3^1 \times 5^2$ ですので、
a \times b \times c = 2^3 \times 3^1 \times 5^2
となります。このような場面では、素因数分解がとても活躍します。$600$ を素因数分解しておくことで、とても見やすくなるのです。実はこんな風に考えることができます。
- 「2」が 3 個
- 「3」が 1 個
- 「5」が 2 個
あります。これらの合計 6 個の品物を、$a$ 君、$b$ 君、$c$ 君で分け合う方法はどんなものが考えられるでしょうか?
たとえば、
- a 君が「2」を 1 個だけ
- b 君が「2」を 1 個、「3」を 1 個、「5」を 1 個
- c 君が「2」を 1 個、「5」を 1 個
という風に分配したとき、$a = 2, b = 30, c = 10$ となります。具体的に分配方法が何通りあるかについては、ABC 110 D - Factorization などで出題されています。
ここで重要なのは、素数は「もうこれ以上分割できないものである」ということです。つまり、「2」や「3」や「5」はそれ以上分割することができないので、そのまま分配するしかないのです。このことを利用して、以下の問題を解いてみましょう。
問題 8: CADDi 2018 C - Product and GCD (300 点)
$N$ 個の未知なる正の整数 $a_1, a_2, \dots, a_N$ が $a_1 a_2 \dots a_N = P$ を満たすことがわかっている。
$a_1, a_2, \dots, a_N$ の最大公約数として考えられる最大値を求めよ。
- $1 \le N, P \le 10^{12}$
(数値例)
・$N = 3$
・$P = 24$
答え: 2
$a_1 = 2, a_2 = 2, a_3 = 6$ のとき、最大公約数は $2$ となる
今回のように「(整数の積) = (整数)」という形の式を見たら、もう条件反射で素因数分解を考えてしまってよいと思います。$P$ を素因数分解しましょう。
a_1 a_2 \dots a_N = p_{1}^{e_{1}} p_{2}^{e_{2}} \dots p_{K}^{e_{K}}
そうすると、
- $e_1$ 個の $p_1$
- $e_2$ 個の $p_2$
- ...
- $e_K$ 個の $p_K$
を $a_1, a_2, \dots, a_N$ の $N$ 人で分け合う、という問題設定になります。そして $a_1, a_2, \dots, a_N$ の最大公約数をなるべく大きくするためには、素数をなるべく均等に分配すればよいということになります。
ここで注意したいことは、「各素因数ごとに独立に考えて良い」ということです!つまり、素因数は $p_1, p_2, \dots, p_K$ とありますが、
- まず $p_1$ を、$a_1, a_2, \dots, a_N$ になるべく均等に振り分け
- $p_2$ を、$a_1, a_2, \dots, a_N$ になるべく均等に振り分け
- ...
- $p_K$ を、$a_1, a_2, \dots, a_N$ になるべく均等に振り分ける
といったように、各素因数 $p_1, p_2, \dots, p_K$ について個別に考えれば良いです。$p_1$ をどのように振り分けたとしても、それは $p_2$ の振り分け方とは関係ないのです。このように「独立に考える」という発想は、AtCoder ではメチャクチャ多いですね。
- 二次元平面上の問題だけど、X 座標と Y 座標は独立に考えて良い
- 「期待値の線形性」が成り立つから、各要素ごとに確率を求めれば良い
といったアイディアも頻出です。少しそれてしまいましたが、独立に考えれば良いということで、
「$e$ 個の素数 $p$ を、$a_1, a_2, \dots, a_N$ に均等に振り分ける」
という方法を考えましょう。これはもう簡単な算数になっています。23 個のお菓子を 5 人に均等に振り分けたら、「23 ÷ 5 = 4 あまり 3」となります。つまり「4 個」が最大です。
今回の問題の解法を整理すると、以下のようになります。
- $P = p_{1}^{e_{1}} p_{2}^{e_{2}} \dots p_{K}^{e_{K}}$ と素因数分解する
- 各素因数 $p_i$ について、$e_i / N$ を計算する (あまりは切り捨て)
- その個数だけ $p_i$ を掛け算する
計算量は $O(\sqrt{P})$ となります。
# include <iostream>
# include <vector>
using namespace std;
vector<pair<long long, long long> > prime_factorize(long long N) {
vector<pair<long long, long long> > res;
for (long long a = 2; a * a <= N; ++a) {
if (N % a != 0) continue;
long long ex = 0;
while (N % a == 0) {
++ex;
N /= a;
}
res.push_back({a, ex});
}
if (N != 1) res.push_back({N, 1});
return res;
}
int main() {
int N;
long long P;
cin >> N >> P;
const auto &pf = prime_factorize(P);
long long res = 1;
for (auto p : pf) {
for (int j = 0; j < p.second/N; ++j) res *= p.first;
}
cout << res << endl;
}
6-4. 約数の構造を知る
まだまだ続きます!
問題 9: ABC 142 D - Disjoint Set of Common Divisors (400 点)
二つの正の整数 $A, B$ が与えられる。$A, B$ の公約数から何個か整数を選ぶことを考える。
選んだ整数からどの二つをとっても、それらが互いに素になるようにしたい。選べる個数の最大値を求めよ。
- $1 \le A, B \le 10^{12}$
(数値例)
・$A = 60$
・$B = 72$
答え: 3
60 と 72 の公約数は 1, 2, 3, 4, 6, 12 の 6 個ですが、このうち 1, 3, 4 を選ぶと「どの二つも互いに素」となっています。
まず、上でも見たとおり「公約数とは、最大公約数の約数」です。よってこの問題は、元々は二つの整数 $A, B$ に関する問題でしたが、$A$ と $B$ の最大公約数を $G$ とすると、次のような問題になるのです。
正の整数 $G$ が与えられる。
$G$ の約数の中から、「どの二つも互いに素となるように」いくつか選びたい。選べる個数の最大値を求めよ。
たった一つの整数に関する問題に帰着されました。こういう風に、元の問題をより簡単なものに帰着するケースは非常に多く見られます。なお、最大公約数を求めるアルゴリズムについては次回記事に書きます。
改めて $G$ を素因数分解しましょう。たとえば $G = 60$ のとき、
$60 = 2^2 \times 3^1 \times 5^1$
となります。そしてここが重要ポイントですが、$60$ の約数は、すべて
- $2^a \times 3^b \times 5^c$ ($a = 0, 1, 2$, $b = 0, 1$, $c = 0 1$)
という形をしています。たとえば $a = 2, b = 0, c = 1$ とすると、$2^2 \times 5^1 = 20$ です。この形をした $12$ 個の約数の中から、できるだけ多くの整数を選びつつ、それらが互いに素になるようにしなければなりません。
ここで「互いに素」の意味を考えてみましょう。互いに素というのは「同じ素因数を持たない」と同じことです。たとえば $20$ と $3$ は
- $20 = 2^2 \times 5^1$
- $3 = 3^1$
となって、同じ素因数を持たないので互いに素になっています。一方、$20$ と $6$ は
- $20 = 2^2 \times 5^1$
- $6 = 2^1 \times 3^1$
となり、「2」という素因数を共有しているので、互いに素ではありません。以上の考察から、$2^a \times 3^b \times 5^c$ という形をした整数の中から、互いに素になるように多く選ぼうと思うと、
- $2$ のみを素因数に持つ約数: $2$ とか
- $3$ のみを素因数に持つ約数: $3$ とか
- $5$ のみを素因数に持つ約数: $5$ とか
を選んでいくと良いことがわかります。$6$ とかを選んでしまうと、一気に「2」も「3」も使ってしまうので良くないです。例外として「$1$」は、まったく素因数を持たない数なので、好きに付け加えてよいです。よって $G = 60$ の場合の答えは、以下の $4$ 個です6。
- $1, 2, 3, 5$ と選ぶ場合の $4$ 個
一般の場合を考えてみましょう。
G = p_1^{e_{1}} p_2^{e_{2}} \dots p_K^{e_{K}}
という風に素因数分解できるとき、同じように素因数を 1 個ずつ選べば良いことがわかります。よって答えは
- $1, p_1, p_2, \dots, p_K$ と選ぶ場合の $K+1$ 個
となります。計算量は $O(\max(\sqrt{A}, \sqrt{B}))$ となります。
# include <iostream>
# include <vector>
using namespace std;
// 最大公約数を求める
long long GCD(long long x, long long y) {
return y ? GCD(y, x%y) : x;
}
// 素因数分解
vector<pair<long long, long long> > prime_factorize(long long N) {
vector<pair<long long, long long> > res;
for (long long a = 2; a * a <= N; ++a) {
if (N % a != 0) continue;
long long ex = 0;
while (N % a == 0) {
++ex;
N /= a;
}
res.push_back({a, ex});
}
if (N != 1) res.push_back({N, 1});
return res;
}
int main() {
long long A, B;
cin >> A >> B;
// 最大公約数を求める
long long G = GCD(A, B);
// G を素因数分解して、「素因数の個数 + 1」が答え
const auto &pf = prime_factorize(G);
cout << pf.size() + 1 << endl;
}
6-5. p で何回割れるのかに着目
最後に、難しめの問題に挑戦してみましょう!本記事で初めての水色 difficulty 問題 (しかも限りなく青色に近い) です。
整数 $N$ を素因数分解して
N = p_1^{e_{1}} p_2^{e_{2}} \dots p_K^{e_{K}}
と表したとき、素因数 $p_i$ に対する指数 $e_i$ という値に着目することで、問題が見通し良く解けることがあります。これは数学オリンピックでは超頻出のテクニックですが、競プロでも時々見かけます。なお、整数 $N$ の素因数 $p$ に対する指数を ${\rm ord}_{p} N$ と表します。大学受験では教わることがほとんどない記号ですが、とても便利です。対数 $\log$ との類似性があり、
{\rm ord}_{p} ab = {\rm ord}_{p} a + {\rm ord}_{p} b
といった関係が成り立ちます。素因数分解を考えればこの等式は明らかでしょう。
問題 10: ABC 150 D - Semi Common Multiple (400 点)
$N$ 個の偶数 $a_{1}, a_{2}, \dots, a_{N}$ と整数 $M$ が与えられる。
任意の $i$ に対して以下の条件を満たす正の整数 $X$ を $a_{1}, a_{2}, \dots, a_{N}$ の「半公倍数」とよぶことにする。
- $X = a_{i} \times (p + 0.5)$ を満たす負でない整数 $p$ が存在する。
$1$ 以上 $M$ 以下の整数のうちの $a_{1}, a_{2}, \dots, a_{N}$ の半公倍数の個数を求めよ。
(制約)
- $1 \le N \le 10^{5}$
- $1 \le M \le 10^{9}$
- $a_{i}$ は $2$ 以上の偶数
(数値例)
・$M = 50$
・$A = (6, 10)$
答え: 2
15 と 45 はともに 6 と 10 の半公倍数です。50 以下の整数のうち、6 と 10 の半公倍数は 15 と 45 のみです。
どこから手をつけたらいいかわからない難問に思えるかもしれません。ひとまず、$a_{i} \times (p + 0.5)$ という数式についてですが、$a_i$ は偶数なので、整数 $b_i$ を用いて $a_i = 2b_i$ とおくことができて、
a_{i} \times (p + 0.5) = 2b_i (p + 0.5) = b_i(2p + 1)
となります。よって問題は次のように言い換えられます:
$N$ 個の整数 $b_1, b_2, \dots, b_N$ が与えられる。以下の $N$ 個の条件をすべて満たす $X$ の個数を求めよ。
- $X = b_1 p_1$ を満たす 0 以上の奇数 $p_1$ が存在する
- $X = b_2 p_2$ を満たす 0 以上の奇数 $p_2$ が存在する
- $\dots$
- $X = b_N p_N$ を満たす 0 以上の奇数 $p_N$ が存在する
平たく言えば、$N$ 個の系列
- $b_1, 3b_1, 5b_1, \dots$
- $b_2, 3b_2, 5b_2, \dots$
- $\dots$
- $b_N, 3b_N, 5b_N, \dots$
にすべて含まれるような $X$ が $M$ 以下の範囲で何個あるかを求めよ、ということになります。具体例として $N = 2, b = (12, 20)$ の場合を考えると、二つの系列
- $12, 36, 60, 84, 108, 132, 156, 180, \dots$
- $20, 60, 100, 140, 180, 220, \dots$
に共通する数は $60, 180, 300, 420, \dots$ となります。この時点で、$b$ の最小公倍数を $L$ として、$L, 3L, 5L, 7L, \dots$ が答えになりそうだとエスパーした方も多いかもしれません。
一方、$N = 2, b = (24, 36)$ の場合を考えると、二つの系列
- $24, 72, 120, 168, \dots$
- $36, 108, 180, \dots$
に共通する数は出てきそうにありません。その理由を考えます。上の系列と下の系列のそれぞれについて「2 に関する指数」を考えてみましょう。
まず上の系列の $24, 72, 120, 168, \dots$ はすべて、$2$ に関する指数が $3$ になっています。一方、下の系列の $36, 108, 180, \dots$ はすべて、$2$ に関する指数が $2$ となっています。${\rm ord}_{2}$ の値が異なる系列同士が、同じ値を共有することはありえません。以上より
- $b_1, b_2, \dots, b_N$ は ${\rm ord}_{2}$ の値がすべて等しくないとき: 求める $X$ の個数は $0$ 個
ということがわかりました。逆にこの条件を満たすならば、$b_1, b_2, \dots, b_N$ の最小公倍数を $L$ としたとき、$X = L$ は条件を満たします。さらに、$L, 3L, 5L, \dots$ も条件を満たします。ただし、$X = 2L, 4L, 6L, \dots$ などが条件を満たさないことに注意しましょう。なぜなら、たとえば $X = 2L$ としてしまうと、
- $2L = b_1 p_1$
- $2L = b_2 p_2$
- $\dots$
- $2L = b_N p_N$
と表したときに、$p_1, p_2, \dots, p_N$ が奇数にならないためです。
以上をまとめると、この問題は次のようにして解くことができます。
- $b_i = \frac{a_i}{2}$ とする
- $b_1, b_2, \dots, b_N$ の $2$ に関する指数が等しくなければ、$0$ を返す
- 等しければ、これらの最小公倍数を $L$ としたとき、$X = L, 3L, 5L, \dots$ が条件を満たすことがわかるので、そのうち $M$ 以下のものを数える。
計算量は $O(N \log{A})$ となります ($A$ は登場する値の最大値)。
# include <iostream>
# include <vector>
using namespace std;
long long GCD(long long x, long long y) {
if ( y == 0) return x;
else return GCD(y, x % y);
}
long long solve(int N, long long M, vector<long long> &a) {
// 2 で割れるだけ割る (割れる回数が異なったらダメ)
bool same = true;
while (a[0] % 2 == 0) {
for (int i = 0; i < N; ++i) {
if (a[i] % 2 != 0) return 0;
a[i] /= 2;
}
M /= 2;
}
for (int i = 0; i < N; ++i) if (a[i] % 2 == 0) return 0;
// lcm
long long lcm = 1;
for (int i = 0; i < N; ++i) {
long long g = GCD(lcm, a[i]);
lcm = lcm / g * a[i];
if (lcm > M) return 0;
}
return (M / lcm + 1) / 2;
}
int main() {
int N; long long M;
cin >> N >> M;
vector<long long> a(N);
// あらかじめ a は一回 2 で割っておく
for (int i = 0; i < N; ++i) cin >> a[i], a[i] /= 2;
cout << solve(N, M, a) << endl;
}
7. おわりに
本記事で登場したアルゴリズムは、ただ 1 つでした!
- 整数 $N$ に対して、$a = 1, 2, \dots, \sqrt{N}$ で試し割りする
というだけです!本当にこれだけでした!
たったこれだけのアイディアで信じられないくらい、色んなことができることを見てきました。一つテンプレとなるアイディアを覚えると、次から次へと色んな工夫ができることが、整数分野の大きな魅力だと思います。
次回は最大公約数についてやります!!!!!
8. 問題集
見つけた問題を並べてみます。
8-1. 素数判定
8-2. 約数列挙
- ARC 026 B - 完全数 (約数列挙して総和を求めればよいでしょう)
- ABC 106 B - 105 (200 点) (N が小さいので愚直な方法でも大丈夫です)
- ABC 112 D - Partition (400 点) (少し難しいかもしれませんが、最終的に約数列挙に)
- ABC 136 E - Max GCD (500 点) (Partition をさらに発展させた問題です)
8-3. オイラー関数
8-4. 素因数分解: 素数を分け合う
- ARC 032 A - ホリドッグ
- ABC 069 C - 4-adjacent (300 点)
- ABC 169 D - Div Game (400 点)
- プログラミングバトル 本戦 BCU30 A - 球 (100 点) (気づけば一瞬です!)
- ABC 110 D - Factorization (400 点) (重複組合せの考え方も使います)
8-5. 素因数分解: 約数の構造
8-6. 素因数分解: p で何回割れるか
- ABC 148 E - Double Factorial (500 点) (5 で何回割れるかを考えましょう)
- Codeforces Round #586 D. Alex and Julian (2 で何回割れるのかがポイントです)
- JOI 春合宿 2007 day1-2 factorial - 階乗 (問題文はここにあります)
-
「形式的べき級数」で一斉を風靡した maspy さんも「形式的べき級数は問題を殴るライブラリとしてだけでなく、問題の考察のための道具として有効だという側面を伝えたい」と言っていますね。 ↩
-
ここでは学校教育に合わせる形で、正の整数のみを考えています。しかし本当は $-2$ や $-7$ なども素数と考えるのが自然です。 ↩
-
どうしても sqrt を使いたい場合には、s = (int)(sqrt(i) + 0.5) といったように、「0.5」といった適当な値を足した上で整数型に丸めると良いでしょう。 ↩
-
この性質は本来は「素因数分解の一意性」を使わずに示すべきものです。先にこういった考察を積み上げることで、素因数分解の一意性を示すのが本筋です。 ↩
-
他にも、1, 4, 3, 5 を選んで 4 個とする解もあります。 ↩