これは機械学習工学 / MLSE Advent Calendar 2018の6日目の記事です。
また「(続)テンソル分解を用いた教師無し学習による変数選択」を「機械学習の数理 Advent Calendar 2018」に書いたので合わせてよんでもらえると嬉しいです。
[Springerから本をだしました!]
(https://www.springer.com/jp/book/9783030224554)読んでもらえると嬉しいです!
はじめに
普通は論文とか手法の解説をするんだと思いますが、僕は自分の研究について書きます。僕は機械学習の専門家、というわけじゃなく、バイオインフォマティクスをやっています。ただ、自分の研究について書く、と言ってもバイオインフォマティクスの話をするわけじゃないです。
バイオインフォマティクスの分野のデータ解析は他の分野とはちょっと違っています。勿論、ゲノム科学をはじめとした大規模データ(網羅的解析)を扱う、ということもあるのですが、それ以上に、データ科学的な特徴があります。それはいわゆるlarge $p$ small $n$問題、つまり変数$p$の数に比べてサンプル数$n$が圧倒的に少ない、ということです。それも少ない、と言ってもちょっと半端じゃなく、$p$が2万次元なのに$n$は10個以下、とか普通にあります。これだと普通のデータ科学の方法を使うのはとっても難しくなってしまいます。
今回、僕が紹介するのは、この様な場合に特化した、僕自身が提案している手法である「テンソル分解を用いた教師無し学習による変数選択」についてです。今流行りのモデルベースの研究とは随分と違うのですが、楽しんで頂けると幸いです。
テンソル
この記事を読もうという人にテンソルの説明とか要らないかもしれませんが、一応、軽く説明しておきます。$x_{ijk} \in \mathbb{R}^{N \times M \times K}$を三階のテンソルとします。テンソル分解にはいろいろありますがここではTucker分解を採用するものとします。
$$
x_{ijk} = \sum_{\ell_1=1}^N \sum_{\ell_2=1}^M \sum_{\ell_3=1}^K G(\ell_1,\ell_2,\ell_3) u_{\ell_1i}u_{\ell_2j}u_{\ell_3k}
$$
ここで$G \in \mathbb{R}^{N \times M \times K}$はコアテンソル、$u_{\ell_1i} \in \mathbb{R}^{N \times N}, u_{\ell_2j} \in \mathbb{R}^{M \times M} u_{\ell_3k} \in \mathbb{R}^{K \times K}$は特異値行列で、すべて直交行列であるとします。$G$と$x_{ijk}$の数が同じなので、この様な展開がいつも可能なのは明らかです。基本、$G$の絶対値が大きいなるべく少ない数に限った和で右辺と左辺の差が少なくなるような特異値行列をいかに求めるか、という問題になります。この問題に対する解は僕が知る限り知られていません。経験的に比較的うまく行くことが知られているアルゴリズムがあるだけです。ここではその中でも一番単純なHOSVDというアルゴリズムを採用します。
問題設定
これを使って変数選択をします。まず、添え字$i$が変数を表し、$j,k$の組がサンプルを表すとします。つまり、$N$変数の測定を$M\times K$個のサンプルに対して行った、とします。$j,k$はサンプルの属性に関係しているものとします。話が分かりにくいので具体例をあげます。あなたは、銀行員です。融資先の企業を見つけたいです。企業には$N$個の指標(例;従業員数、利益率、資本金、退職金平均額、設立からの経過年数などなど)が与えられています。あなたがもっているデータは「会社は倒産したか?」と「利益率は高かったか?」という過去のデータです。ここでは簡単のため、「倒産したが利益率が高かった会社」「倒産したが利益率が低かった会社」「倒産せず利益率も高かった会社」「倒産しなかったが利益率が低かった会社」が$\frac{MK}{4}$社ずつあったとしましょう。その場合、
| $1 \leq j \leq \frac{M}{2}$ | $\frac{M}{2} < j \leq M$ | |
|---|---|---|
| $1 \leq k \leq \frac{K}{2}$ | 倒産せず利益率も高かった会社 | 倒産しなかったが利益率が低かった会社 |
| $ \frac{K}{2} < k \leq K $ | 倒産したが利益率が高かった会社 | 倒産したが利益率が低かった会社 |
の様な形で全$MK$社に$j,k$の番号を割り当てることが可能になります。
あなたはこのデータを使って今後の融資先を決めるのに事前にその会社がこの四分類のどれに該当するか知りたい、としましょう。しかし、困ったことに$N \gg MK$なので全部の変数を使ってしまうと必ず予測ができるように式が作れてしまうので変数の数を減らしたい、としましょう。変数選択については幸いなことにこのカレンダーの12/3の分「混合整数計画法による変数選択」にいろいろ書かれているのでそこを見てください。ここではテンソル分解をどう使って変数選択するか、だけを説明します。
ここでは以下のような模擬データを使用します。
$$
x_{ijk} \sim
\mathcal{N} (\mu,\sigma), ; j \leq \frac{M}{2}, k \leq \frac{K}{2}, i \leq N_1
$$
及び
$$
x_{ijk} \sim \mathcal{N} (0,\sigma), ; \mbox{otherwise}
$$
ここで$\mathcal{N}(\mu,\sigma)$は平均が$\mu$で標準偏差が$\sigma$の正規分布。上記の式の意味は、$N$個の変数のうち最初の$N_1$個だけが$j,k$依存性をもっていて、それは「倒産せず利益率も高かった会社」と「それ以外」という区別だ、ということです。目的はこの$N_1$個の変数をうまく選ぶことです。
まずはデータを実際に準備して単純にテンソル分解をしてみましょう。$N=1000,M=K=6,N_1=10,\mu=2,\sigma=1$とします。
N<-1000
M<-6
N1<-10
s<-2
set.seed(0)
x <- array(NA,c(M,M,N)) #計算の都合上、本文とは違い添え字の順番がx_{jki}の純になっています。
x[1:(M/2),1:(M/2),1:N1] <- rnorm(N1*(M/2)*(M/2),s)
x[is.na(x)]<- rnorm(sum(is.na(x)))
require(rTensor)
HOSVD <- hosvd(as.tensor(x),c(min(10,M),min(10,M),10))
jpeg(file="fig.jpg",width=960,height=480)
par(mfrow=c(1,2))
plot(rep(1:2,each=3),HOSVD$U[[1]][,1],col=rep(1:2,each=3),xlim=c(0.5,2.5),cex=2,lwd=2,main="u21",xlab="",cex.axis=2,,ylab="",cex.lab=2,cex.main=2,xaxt="n")
mtext(c("j<M/2","j>M/2"),at=1:2,side=1,las=3,cex=2)
plot(rep(1:2,each=3),HOSVD$U[[2]][,1],col=rep(1:2,each=3),xlim=c(0.5,2.5),cex=2,lwd=2,main="u31",xlab="",cex.axis=2,,ylab="",cex.lab=2,cex.main=2,xaxt="n")
mtext(c("k<K/2","k>K/2"),at=1:2,side=1,las=3,cex=2)
par(mfrow=c(1,1))
dev.off()
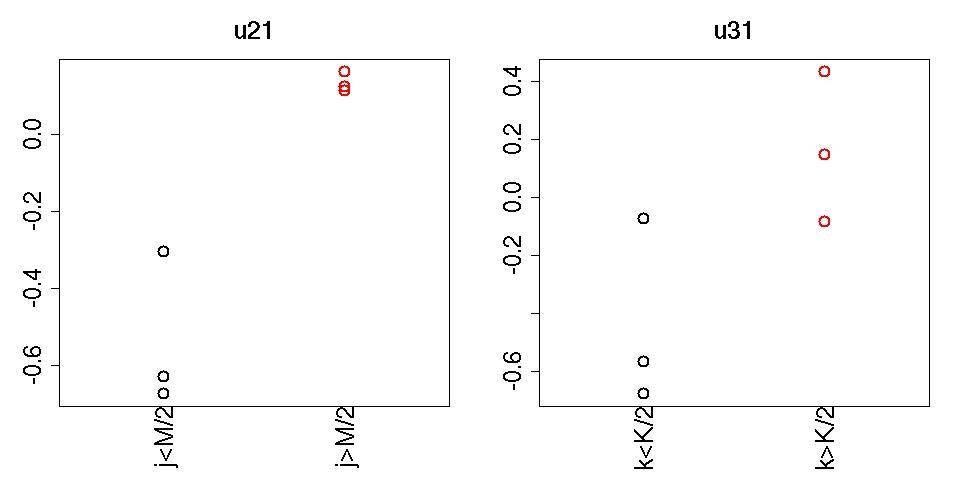
それぞれ$u_{2j}$と$u_{3k}$が描かれています。明らかに$j> \frac{M}{2}$と$j \leq \frac{M}{2}$、$k> \frac{K}{2}$と$k \leq \frac{K}{2}$で値に差があることがわかる。テンソル分解をするときに、この様な事前情報は一切、与えていないが、これが教師無し学習の醍醐味でデータが勝手に「こうなっていますよ」と教えてくれる。
次にこれを使って変数選択をしたい。$\ell_2=\ell_3=1$が重要、とわかったので$G(\ell_1,1,1)$の値を見て、絶対値が大きい$\ell_1$を探す。これはテンソル分解ではコアテンソルが一種の「重み」みたいになっているので$G(\ell_1,1,1)$の絶対値が大きい$\ell_1$である$u_{\ell_1i}$が$j> \frac{M}{2}$と$j \leq \frac{M}{2}$、$k> \frac{K}{2}$と$k \leq \frac{K}{2}$の区別に関係した変数のはずだからである。
-sort(-abs(HOSVD$Z@data[,1,1]))
[1] 23.828186 9.997571 4.959145 4.473892 2.431507 1.973123
| $\ell_1$ | 1 | 2 | 3 | 4 | 5 |
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
| $ \mid G(\ell_1,1,1) \mid$ | 23.8 | 10.00 | 4.96 | 4.47 | 2.43 |
上表の様に、$\ell_1=1$が最も大きな絶対値を持っていることがわかる。そこで$u_{1i}$を見てみよう。
jpeg(file="fig1.jpg",width=960,height=480)
plot(HOSVD$U[[3]][,1],cex=2,lwd=2,main="u11",xlab="i",cex.axis=2,ylab="",cex.lab=2,cex.main=2,col=c(rep(2,10),rep(1,990)))
abline(0,0,col=4,lty=2,lwd=2)
dev.off()
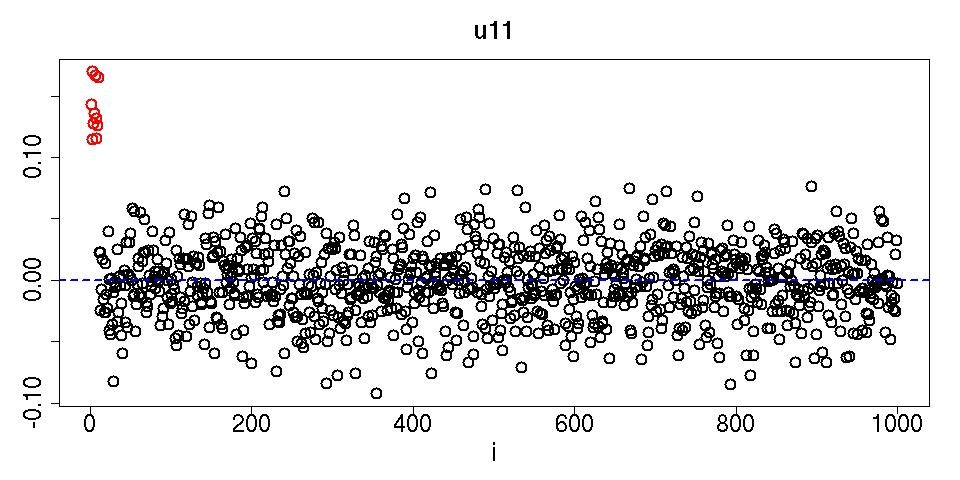
赤く描かれた$i \leq N_1$だけが$i> N_1$に比べて明らかに大きな値を付与されている。このように、ちゃんと$j,k$依存性がある変数だけ選ばれるのである。
ここで重要なことはこのプロセスは教師無し学習だ、ということである。テンソル分解をするときに、どの会社が倒産したとか、利益率が高かったとかそういうことは全く使われていない。いわばデータ駆動型の解析で変数選択までできてしまうのがだいご味である。
まあ、これでほぼ終わりなのだが、もうちょっと先をやってみよう。まず、ちゃんと数値的な基準をあたえてきっちり変遷選択したい、としよう。その場合、なんらかの帰無仮説を想定して$i$に$P$値を付与し、十分小さな値(例えば0.05以下)の物のみを選ぶという方法が考えられる。ここでは帰無仮説として「$u_{1i}$は正規分布している」というものを採用しよう。ちゃんとした数学的な証明はないが、$x_{ijk}$が有限な値の乱数の場合、中心極限定理を考えると$u_{1i}$は正規分布になると期待されるからである。その場合、この帰無仮説に基づく$P$値はχ二乗分布をつかって
$$
P_i = P_{\chi^2} \left [ > \left( \frac{u_{1i}}{\sigma_1}\right)^2\right]
$$
で与えられるだろう。ここで$\sigma_1$は$u_{1i}$の標準偏差、であり$u_{1i}$は平均がゼロになるように変換してから標準偏差を計算して上記の式に代入するものとする(まあ、そこまでやらなくても平均は最初っからほぼゼロなのですが)。$P_{\chi^2}[>x]$は引数が$x$より大きい場合のχ二乗分布の累積確率とします。この$P$値をBenjamini-Hochberg法で多重比較補正してから0.05以下の$i$を探すとちゃんと$i\leq N_1$が選択されます。
P <- pchisq(scale(HOSVD$U[[3]][,1])^2,1,lower.tail=F)
table(p.adjust(P,"BH")<0.05,c(rep(T,10),rep(F,990)))
FALSE TRUE
FALSE 990 0
TRUE 0 10
その意味で、テンソル分解を用いた教師無し学習による変数選択は普通の統計検定試験と同じように扱うことができるわけです。
他の手法との比較
これは論文じゃないのでこれで終わってもいいのですが、普通の教師あり学習と比べてみます。$k,j$と二つ変数があるのでいわゆる二群間の比較は使えません。ここではカテゴリ回帰を使った方法をためしましょう(これはいわゆるANOVAと同じことです)。カテゴリ回帰は
$$
x_{ijk} = a_i + b_i\sum_{s=1}^2 \delta_{js} + c_i\sum_{s=1}^2\delta_{ks}
$$
という式です。$a_i, b_i,c_i$は回帰係数です。$\delta_{js},\delta_{ks}$は、$j$や$k$が「倒産したかしないか」と「高利益率だったかどうか」の二群($s=1,2$)に属しているかどうかで$0,1$の値をとる関数です。
全ての$i$でこの回帰計算を実行し、$P_i$を計算し、同様に多重比較補正した$P$値が0.05以下かどうかで変数選択します。すると補正$P$値が0.05以下の$i$は1つもないことがわかります。
x1<-x
dim(x1)<- c(M*M,N)
cc1 <- matrix(0,M,M)
cc2 <- matrix(0,M,M)
cc1[1:(M/2),]<-1
cc2[,1:(M/2)]<-1
LM1 <- lm(x1~factor(cc1)+factor(cc2))
SLM1 <- summary(LM1)
fs1 <- t(data.frame(lapply(SLM1,"[",10)))
P1 <- pf(fs1[,1],fs1[,2],fs1[,3],lower.tail=F)
table(p.adjust(P1,"BH")<0.05,c(rep(T,10),rep(F,990)))
FALSE TRUE
FALSE 990 10
教師あり学習が教師無し学習に負けるなんて変だ、と思うかもしれません。これにはいろいろな原因があります。まず、この回帰計算では$j$と$k$をそれぞれ二群に分けているので四群のカテゴリ回帰になってしまっています。しかし、実際は「倒産せず利益率も高かった会社」と「それ以外」の二群だったわけです。それを正しくモデルに反映できていないので、結果がわるくなってしまいました。実際、最初っからこの二群であると仮定してカテゴリ回帰できればちゃんと変数選択できるのです。しかし、事前にそんなことはわかるわけがありません。ここに教師あり学習の限界があります。表の様なラベルがあれば人間はそれに応じたモデル化をするしかありません。解析する前に「二群だろう」と思うことはできないのです。教師あり、と言ってもそれは人間が勝手にラベルをつけただけです。実際にデータがそれに従って分布しているとは限りません。その意味で教師無し学習は教師あり学習より現実に即したよい戦略だと言えるでしょう。
また、別の問題として、カテゴリ回帰は$i$ごとに独立に$P$値を計算するのでネガティブデータ(この場合、$j,k$依存性がない$i>N_1$の変数)の数が増えれば増えるほど多重比較補正の効果が効いて小さな$P$値を得にくくなることがあげられます。実際$N=100$にしてあげればちゃんとカテゴリ回帰でも正しい変数選択ができるんですよね。一方、変数の数が増えると多重比較補正が効いて小さな$P$値が出にくくなる、ということ自体は、「テンソル分解を用いた教師なし学習による変数選択」の場合も同じですが、「テンソル分解を用いた教師なし学習による変数選択」では変数の数が増えると有利になる効果もあります。それは$\sigma_1$の値です。ネガティブデータが増えればそこは$u_{1i}$の期待値がゼロの部分だから$\sigma_1$はどんどん小さくなります。その結果、$i \leq N_1$の部分については、$\frac{u_{1i}}{\sigma_1}$の絶対値が大きくなることが期待でき、その結果、$P_i$も小さくなることが期待されます。だから、うまく行けば、変数が増えることで多重比較補正のせいで小さな$P$値がでにくいという効果を打ち消すことができるんですよね。
この「テンソル分解を用いた教師無し学習による変数選択」という方法は変数の数がサンプル数よりとても大きく、かつ、カテゴリと変数の関係が事前にはわからないくらい複雑な場合にしか機能を発揮できません。これは両方とも、たまたま、バイオインフォマティクスによく当てはまります。これが多分、この方法が世間であまり注目されてない理由だと思います。
もしまだ興味がもてるなら、「機械学習の数理 Advent Calendar 2018」に書いた「(続)テンソル分解を用いた教師無し学習による変数選択」も読んでくれると嬉しいです。
以下に僕がこの方法を使って書いたバイオインフォの論文があるので見てみてください。
参考文献
[1]Y-.H. Taguchi, Tensor decomposition-based unsupervised feature extraction identifies candidate genes that induce post-traumatic stress disorder-mediated heart diseases. BMC Med. Genomics, 10(S4):67, 2017. doi:10.1186/s12920-017-0302-1
[2]Y. h. Taguchi, Identification of candidate drugs using tensor-decomposition-based unsupervised feature extraction in integrated analysis of gene expression between diseases and DrugMatrix datasets. Scientific Reports, 7(1):13733, oct 2017. doi:10.1038/s41598-017-13003-0 (この内容を紹介した記事がQiitaにあります。)
[3]Y.-H. Taguchi, Drug candidate identification based on gene expression of treated cells using tensor decomposition-based unsupervised feature extraction for large-scale data. BMC Bioinformatics, 2019. doi:10.1186/s12859-018-2395-8 (この内容を紹介した記事がQiitaにあります。)
[4]Y h. Taguchi, Tensor decomposition-based unsupervised feature extraction applied to matrix products for multi-view data processing. PLOS ONE, 12(8):e0183933, aug 2017.doi:10.1371/journal.pone.0183933
[5]Y h. Taguchi, One-class differential expression analysis using tensor decomposition-based unsupervised feature extraction applied to integrated analysis of multiple omics data from 26 lung adenocarcinoma cell lines. pages 131–138, 2017. IEEE 17th International Conference on Bioinformatics and Bioengineering. doi:10.1109/BIBE.2017.00-66
[6]Y.-H. Taguchi, Tensor decomposition-based and principal-component-analysis-based unsupervised feature extraction applied to the gene expression and methylation profiles in the brains of social insects with multiple castes. BMC Bioinformatics, 19(S4):99, may 2018. [doi:10.1186/s12859-018-2068-7] (http://dx.doi.org/10.1186/s12859-018-2068-7)
[7]Y.-H. Taguchi, Tensor decomposition-based unsupervised feature extraction can identify the universal nature of sequence-nonspecific off-target regulation of mRNA mediated by MicroRNA transfection. Cells, 7(6):54, jun 2018. doi:10.3390/cells7060054
[8]Y h. Taguchi and Ka-Lok Ng. Tensor decomposition–based unsupervised feature extraction for integrated analysis of TCGA data on microRNA expression and promoter methylation of genes in ovarian cancer. pages 195–300, 2018. IEEE 18th International Conference on Bioinformatics and Bioengineering. [doi:10.1109/BIBE.2018.00045] (http://dx.doi.org/10.1109/BIBE.2018.00045) preprint version: doi:10.1101/380071
[9] Y-h. Taguchi, Multiomics Data Analysis Using Tensor Decomposition Based Unsupervised Feature Extraction. In: Huang DS., Bevilacqua V., Premaratne P. (eds) Intelligent Computing Theories and Application. ICIC 2019. Lecture Notes in Computer Science, vol 11643. Springer, Cham. doi:0.1007/978-3-030-26763-6_54 Preprint version: doi.org/10.1101/591867 (この内容を紹介した記事がQiitaにあります。)
[10] Y-h. Taguchi, Unsupervised Feature Extraction Applied to Bioinformatics
A PCA Based and TD Based Approach, (2019) Springer International, XVIII+321 pages,
https://doi.org/10.1007/978-3-030-22456-1
こちらはこれまでの研究の集大成ともいえる単著の英語の解説書です。
おまけ
一応、100回繰り返して平均とった結果です(行が正解、列が予想の混同行列)。
テンソル分解を用いた教師無し学習による変数選択
| $j,k$依存あり | $j,k$依存なし | |
|---|---|---|
| $i \leq N_1$ | 8.03 | 1.97 |
| $i> N_1 | 0 | 990 |
カテゴリ回帰(四群仮定)
| $j,k$依存あり | $j,k$依存なし | |
|---|---|---|
| $i \leq N_1$ | 1.55 | 8.45 |
| $i> N_1 | 0 | 990 |
カテゴリ回帰(二群仮定)
| $j,k$依存あり | $j,k$依存なし | |
|---|---|---|
| $i \leq N_1$ | 8.85 | 1.15 |
| $i> N_1 | 0 | 990 |
「テンソル分解を用いた教師無し学習による変数選択」は二群を仮定した教師あり学習の性能にも肉薄しているとわかると思います。
N<-1000
M<-6
N1<-10
s<-2
t1 <- NULL
t2 <- NULL
t3 <- NULL
for (i in c(1:100))
{
cat(i,"\n")
x <- array(NA,c(M,M,N))
x[1:(M/2),1:(M/2),1:N1] <- rnorm(N1*(M/2)*(M/2),s)
# x[(M/2+1):M,(M/2+1):M,1:N1] <- rnorm(N1*(M/2)*(M/2),-s)
x[is.na(x)]<- rnorm(sum(is.na(x)))
require(rTensor)
HOSVD <- hosvd(as.tensor(x),c(min(10,M),min(10,M),10))
P <- pchisq(scale(HOSVD$U[[3]][,1])^2,1,lower.tail=F)
t1 <- cbind(t1,p.adjust(P,"BH")<0.05)
x1<-x
dim(x1)<- c(M*M,N)
cc1 <- matrix(0,M,M)
cc2 <- matrix(0,M,M)
cc1[1:(M/2),]<-1
cc2[,1:(M/2)]<-1
LM1 <- lm(x1~factor(cc1)+factor(cc2))
SLM1 <- summary(LM1)
fs1 <- t(data.frame(lapply(SLM1,"[",10)))
P1 <- pf(fs1[,1],fs1[,2],fs1[,3],lower.tail=F)
t2 <- cbind(t2,p.adjust(P1,"BH")<0.05)
cc <- matrix(0,M,M)
cc[1:(M/2),1:(M/2)] <- 1
LM <- lm(x1~factor(cc))
SLM <- summary(LM)
fs <- t(data.frame(lapply(SLM,"[",10)))
P2 <- pf(fs[,1],fs[,2],fs[,3],lower.tail=F)
t3 <- cbind(t3,p.adjust(P2,"BH")<0.05)
}
TP <- sum(rowSums(t1)[1:10])/100
FN <- 10-TP
FP <- sum(rowSums(t1)[11:990])/990
TN <- 990-FP
matrix(c(TP,FP,FN,TN),2)
[,1] [,2]
[1,] 8.03000000 1.9700
[2,] 0.01010101 989.9899
TP <- sum(rowSums(t2)[1:10])/100
FN <- 10-TP
FP <- sum(rowSums(t2)[11:990])/990
TN <- 990-FP
matrix(c(TP,FP,FN,TN),2)
[,1] [,2]
[1,] 1.55000000 8.4500
[2,] 0.01313131 989.9869
TP <- sum(rowSums(t3)[1:10])/100
FN <- 10-TP
FP <- sum(rowSums(t3)[11:990])/990
TN <- 990-FP
matrix(c(TP,FP,FN,TN),2)
[,1] [,2]
[1,] 8.85000000 1.1500
[2,] 0.04747475 989.9525