はじめに
最近、私はテンソル分解を用いた教師なし学習による変数選択のマルチビューデータへの応用(論文)を提案し、その中ではマルチオミックスデータへの応用も行った。しかし、タイトルにマルチオミックスが入っていなかったせいか、この点を強調した最近のmixOmicsパッケージの論文にアピール力で結構負けている気がする。そこで自己の手法の宣伝もかねてmixOmicsで性能が試されているデータセットにテンソル分解を用いた教師なし学習による変数選択のマルチビューデータへの応用を適用した場合の性能比較を行いたいと思う。
追記
DIABLOの原著論文が刊行になりました。また、この内容をプレプリにして投稿しました。このプレプリは国際会議のプロシーディングとして刊行されました。
mixOmicsについて
mixOmcsはその名の通り、マルチオミックスデータの解析に特化したRのパッケージでありBioconductorで公開されており、普通に
if (!requireNamespace("BiocManager", quietly = TRUE))
install.packages("BiocManager")
BiocManager::install("mixOmics")
でインストール可能である。いろいろな手法が含まれているがここではDIABLOと名付けられた彼らがもっとも先進的であるとみなしている手法との性能比較を行う。DIABLOはプレプリントの図1が一番わかりやすのだが、複数のマルチオミックスデータをペアワイズで積を取ってから和をとるというやり方で変数を作成し、その変数で線形演算の範囲で予測子を構成して多クラス判別を行う手法(教師あり学習)である。数式を用いたちゃんとした説明はmixOmicsの論文のText S1の4節に詳しく掲載されている。DIABLO法の詳しい説明に立ち入るのは本稿の趣旨ではなので詳細はここでリンクを張った諸論文を参照されたい
DIABLO実行例
上記プレプリントまたはDIABLO実行例のページにはTCGAのデータを使ってmRNA,miRNA,proteomicsの三種のデータの統合解析を行った例について書かれている。
このデータはDIABLO実行例のページの
## $mRNA
## [1] 150 200
##
## $miRNA
## [1] 150 184
##
## $proteomics
## [1] 150 142
という部分からわかるように150サンプルに対して200個のmRNA,184個のmiRNA,142個のプロテオミクスデータから出発している。また150サンプルはDIABLO実行例のページの
## Basal Her2 LumA
## 45 30 75
という部分からわかるようにぞれぞれ45,30,75サンプルの3つのサブクラスのデータから構成されている。
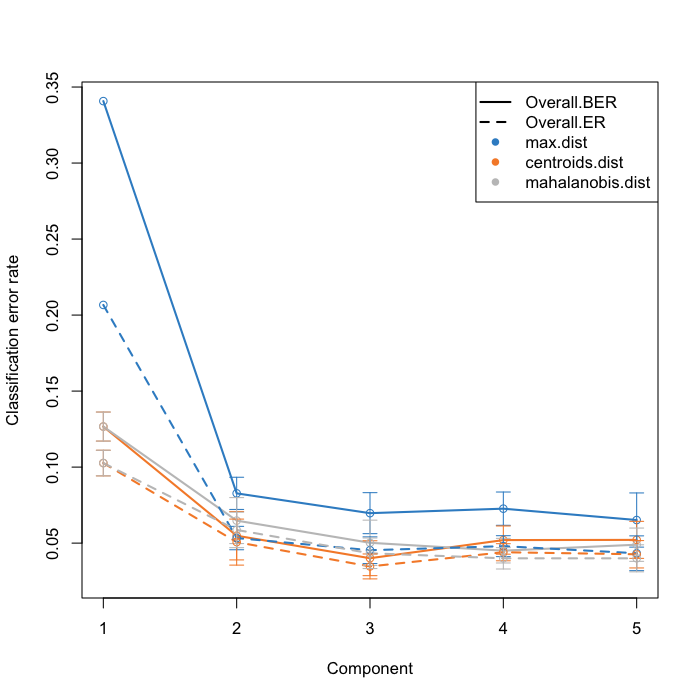
上図は3クラスの判別性能がDIABLOで作成された成分の何番目までを用いるとよい性能が得られるか、という税能評価である。縦軸はエラーレートであるが、最初の2成分で十分な性能が得られている。また、この空間への全150サンプルの付置は
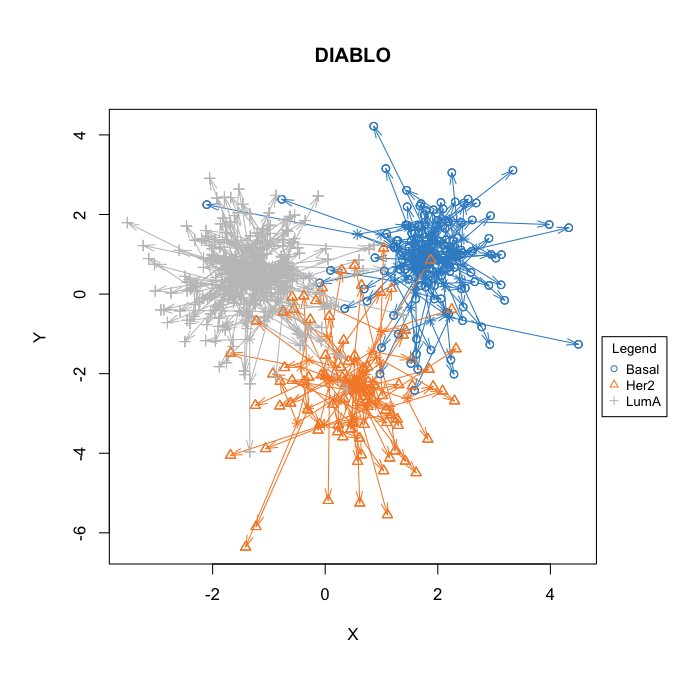
上図の様になっており、平面で十分によく分けられてクラスタリングされていることがわかる(変な矢印がついてい見にくいがそこは無視してください)。またDIABLOには変数選択の機能も実装されている。
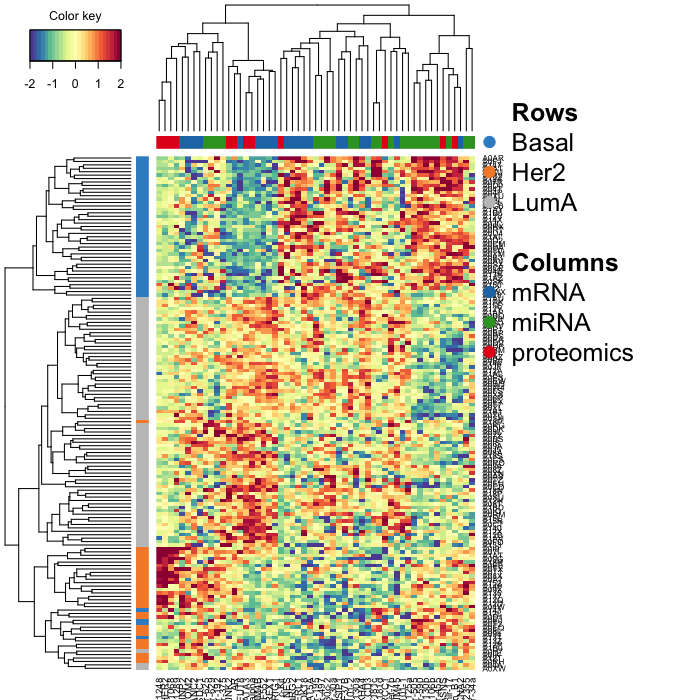
上図はDIABLOで選択された変数のheatmapである。行がサンプル、列が(選択された)オミックスデータという構成だが、いちいち多変量解析を持ちださなくても階層的クラスタリングだけで十分に3クラスが判別できるよい変数選択がオミックスデータに対して行えていることがよくわかる。
テンソル分解を用いた教師無し学習による変数選択のマルチビューデータ解析の応用を用いた場合
さて、上記データセットにテンソル分解を用いた教師無し学習による変数選択のマルチビューデータ解析の応用を用いよう。論文でいうとType IのCase Iに相当する。ここで$x_{i_1,j} \in \mathbb{R}^{200 \times 150}$は$i_1$番目のmRNAの$j$番目のサンプルにおける発現量を、$x_{i_2,j} \in \mathbb{R}^{184 \times 150}$は$i_2$番目のmiRNAの$j$番目のサンプルにおける発現量を、$x_{i_3,j} \in \mathbb{R}^{142 \times 150}$は$i_3$番目のプロテオミクスの$j$番目のサンプルにおける発現量を、それぞれ表すとすると、テンソル$x_{i_1,i_2,i_3,j}$は
$$
x_{i_1i_2i_3j} \equiv x_{i_1,j} \cdot x_{i_2,j} \cdot x_{i_3,j}
$$
と定義できる。これをHOSVDでテンソル分解して
$$
x_{i_1i_2i_3j} = \sum_{\ell_1,\ell_2,\ell_3,\ell_4} G(\ell_1,\ell_2,\ell_3,\ell_4) x_{\ell_1i_1}x_{\ell_2i_2}x_{\ell_3i_3}x_{\ell_4j}
$$
を得る。
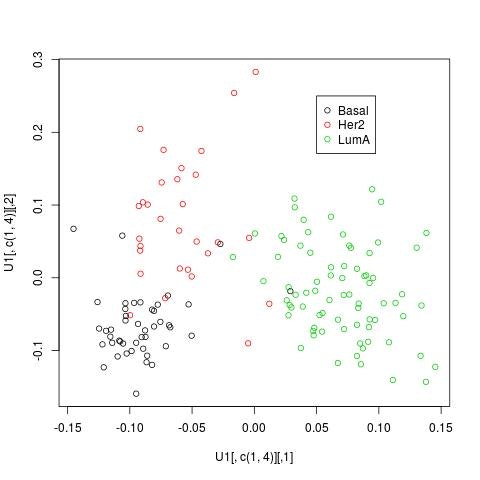
上図は$x_{\ell_4j}$の$\ell_4=1,4$で構成された平面での150サンプルの分布の様子である。3サブクラスが問題なくよく分かれて配置されているのが見て取れる。実際、この2成分を使った場合の線形判別で94%の判別性能が達成できる。
| Basal | Her2 | LumA | |
|---|---|---|---|
| Basal | 42 | 4 | 0 |
| Her2 | 2 | 25 | 2 |
| LumA | 1 | 1 | 73 |
上表はconfusion matrix(列がサブクラス、行が予測)である。
また、これを用いて変数選択を行った。$G(\ell_1,\ell_2,\ell_3,\ell_4)$に対して、$\ell_4=1,4$の時に$ G $の絶対値が大きい$\ell_1,\ell_2,\ell_3$を選ぶことで変数選択が可能になる。
| rank | $\ell_1$ | $\ell_2$ | $\ell_3$ | $\ell_4$ | $G(\ell_1,\ell_2,\ell_3,\ell_4)$ |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | -407857.582 |
| 2 | 1 | 1 | 4 | 4 | -209720.615 |
| 3 | 2 | 1 | 1 | 4 | -20452.480 |
| 4 | 2 | 1 | 3 | 1 | -11677.505 |
| 5 | 2 | 1 | 4 | 1 | -10428.742 |
| 6 | 2 | 1 | 2 | 1 | 10157.467 |
| 7 | 1 | 1 | 2 | 1 | -8973.774 |
| 8 | 1 | 2 | 1 | 4 | 8360.976 |
| 9 | 2 | 1 | 5 | 4 | -6628.467 |
| 10 | 1 | 1 | 3 | 4 | 6623.046 |
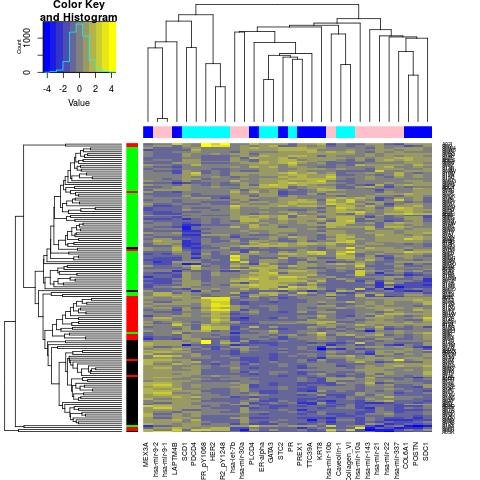
上表は上位10位までであるがこのことから$\ell_1=1,2,\ell_2=1,2,\ell_3=1,2,3,4$を選ぶのが妥当であろうと思われる。そこでさらにこれらの$x_{\ell_1i_1},x_{\ell_2i_2},x_{\ell_3i_3}$が多重正規分布をしているという帰無仮説を用いて、$i_1,i_2,i_3$に対して$P$値を付与し、上位10位ずつを選択してheatmapを描いた。
行がサンプル(黒がBasel,赤がHer2,緑がLuma)、列がオミックスデータ(青がmRNA,ピンクがmiRNA,水色がプロテオミクス)である。DIABLOの場合と遜色ない程度に、階層的クラスタリングだけで3つのサブクラスを判別できる変数が選べていることが見て取れる。
結論
DIABLOはかなり複雑な計算であり、自分でマルチオミックスデータをどう組み合わせるかというdesign matrixを作成しなくてはいけない上に、ラベル情報を使っている教師あり学習である。これに対してテンソル分解は教師なし学習であり,やっていることは単純である。実際、末尾にRの実行コードを上げておいたが拍子抜けするほど単純である。これでDIABLOと同じ性能がでているかと思うとちょっと信じがたい感じではある。しかし、DIABLOもマルチオミックスデータ間の積を考え、線形の判別を行っていると意味ではそんなに方向はずれていないのではないかとも思う。
テンソル分解にはテンソルが巨大になってしまう(今の場合、150×200×184×142個の要素がある)ので計算時間がかかるという欠点がある。実際、DIABLOはノーパソでも実行可能であるがテンソル分解は数十ギガのメモリーがあるサーバ機でなくては実行できない。それでも今後、マルチオミックスデータの解析にはテンソル分解は頻繁に使われていくのではないだろうか。
今回の計算の実行コード
install.packages("mixOmics") #mixOmicsパッケージインストール
require(mixOmics) #mixOmicsパッケージ読み込み
data('breast.TCGA') #TCGAデータの読み込み
data = list(mRNA = breast.TCGA$data.train$mrna,
miRNA = breast.TCGA$data.train$mirna,
proteomics = breast.TCGA$data.train$protein)
install.packages("rTensor") #rTensorパッケージインストール
require(rTensor) #rTensorパッケージ読みこみ
# テンソル作成
Z <- array(NA,c(150,200,184,142))
for (i in c(1:150))
{cat(i," ")
Z[i,,,] <-data.matrix(outer(outer(data$mRNA[i,],data$miRNA[i,],"*"),data$proteomics[i,],"*"))}
# テンソル分解
HOSVD <- hosvd(as.tensor(Z))
U1 <- HOSVD$U[[1]] #x_{\ell_4,J}
U2 <- HOSVD$U[[2]] #x_{\ell_1,i_1}
U3 <- HOSVD$U[[3]] #x_{\ell_2,i_2}
U4 <- HOSVD$U[[4]] #x_{\ell_3,i_3}
# 150サンプルの付置 (x_{\ell_4,j})
plot(U1[,c(1,4)],col=breast.TCGA$data.train$subtype)
legend(0.05,0.25,names(summary(breast.TCGA$data.train$subtype)),col=1:3,pch=1)
require(MASS) #MASSパッケージ読み込み
LD <- lda(U1[,c(1,4)],breast.TCGA$data.train$subtype,CV=T,prior=rep(1/3,3)) #線形判別
table(LD$class,breast.TCGA$data.train$subtype) #confusion matrix
ZZ <-order(-abs(HOSVD$Z@data[c(1,4),,,]))
[1:20];data.frame(arrayInd(ZZ,dim(HOSVD$Z@data[c(1,4),,,])),HOSVD$Z@data[c(1,4),,,][ZZ]) #Gの絶対値が大きい順に上位
P2 <- pchisq(rowSums(scale(U2[,1:2])^2),2,lower.tail=F) #x_{\ell_1,i_1},\ell=1,2に多重ガウス分布仮定してi_1にP値付与
P3 <- pchisq(rowSums(scale(U3[,1:2])^2),2,lower.tail=F) #x_{\ell_2,i_2},\ell=1,2に多重ガウス分布仮定してi_1にP値付与
P4 <- pchisq(rowSums(scale(U4[,1:4])^2),4,lower.tail=F) #x_{\ell_3,i_3},\ell=1,2,3,4に多重ガウス分布仮定してi_1にP値付与
U <- cbind(data$mRNA[,order(P2)[1:10]],cbind(data$miRNA[,order(P3)[1:10]],data$proteomics[,order(P4)[1:10]])) #上位10ずつをまとめる
install.packages("gplots") #gplotsパッケージインストール
require(gplots) #gplotパッケージ読み込み
# heatmap描画
heatmap.2(scale(U),col=rgb(seq(0,1,by=0.1),seq(0,1,by=0.1),seq(1,0,by=-0.1)),RowSideColors=c(rep("black",45),rep("red",30),rep("green",75)),hclustfun=function(x){hclust(x,method="average")},trace="none",ColSideColors=c(rep("blue",10),rep("pink",10),rep("cyan",10)))