こちらは創薬 Advent Calendar 2018(#souyakuAC2018)1日目の記事です。
また、創薬 Advent Calendar 2017(#souyakuAC2017)に投稿した「テンソル分解を用いて遺伝子発現プロファイルからインシリコ創薬」の前日譚です。こっちが先だったのですが論文が通らなくて研究順序と発表が逆になってしまいました(笑)。
「インシリコ創薬の課題」「インシリコ創薬の2大潮流」「インシリコ創薬の新潮流」及び、「教師なし学習によるインシリコ創薬」の中の「テンソル分解」までは前回の繰り返しになるので、そちらを見てください。そこまで読んだら「薬物投与培養細胞遺伝子発現プロファイルから薬物選択」にGO!
インシリコ創薬の課題
インシリコ創薬の2大潮流
インシリコ創薬の新潮流
教師なし学習によるインシリコ創薬
テンソル分解
薬物投与培養細胞遺伝子発現プロファイルから薬物選択
上述のテンソル分解を用いて、薬物投与されたがん由来の培養細胞の遺伝子発現プロファイルから、どの薬が効きそうか選択することを考えよう。データセットはLINCSから持ってきた。LINCSはThe Library of Integrated Network-Based Cellular Signaturesの略で、その名の通り、ネットワークベースで細胞間相互作用を理解しようというプロジェクトである。その中で多数の低分子化合物を多数の培養細胞にシステマティックに投与した場合の遺伝子発現プロファイルを測定、公開している。今回、用いたのはLINCS Phase II Dataと呼ばれるデータでGene Expression Omnibus (GEO)のGSE70138にて公開されている。多数の培養細胞に、多数の低分子化合物を複数の濃度で投与した場合のデータが公開されているという意味では非常に有用なのであるが、978遺伝子の発現しか計測されていないという欠点がある。
このデータを我々は、培養細胞ごとに$j$番目の化合物を$i$番目の濃度で投与した時の$\ell$番目の遺伝子の発現量を$x_{ij\ell} \in \mathbb{R}^{6 \times J \times 978}$という三階のテンソルの形にフォーマットした($J$は各培養細胞に投与された化合物の総種類数である)。そして、このテンソルをHOSVDアルゴリズムでタッカー分解した。結果、
$$
x_{ij\ell} = \sum_{k_1 k_2 k_3} G(k_1,k_2,k_3) x_{k_1 i}x_{k_2 j} x_{k_3 \ell}
$$
を得た。ここで$G(k_1,k_2,k_3) \in \mathbb{R}^{6 \times J \times 978}$,$x_{k_1 i} \in \mathbb{R}^{6 \times 6}$,$x_{k_2j} \in \mathbb{R}^{J \times J}$,$x_{k_3\ell} \in \mathbb{R}^{978 \times 978}$である。ここで、$x_{k_1i}$は濃度依存性を、$x_{k_2j}$は化合物依存性を、$x_{k_3\ell}$は遺伝子依存性を表す特異値ベクトルである。
まずは、濃度依存性のある場合に注目したいので、濃度依存性のある$x_{k_1i}$を同定する必要がある。非常に驚いたことに、培養細胞や、投与化合物セットとは全く独立に、常に$k_1=2$の場合に$x_{k_1i}$が濃度依存性を持っていることが分かった。
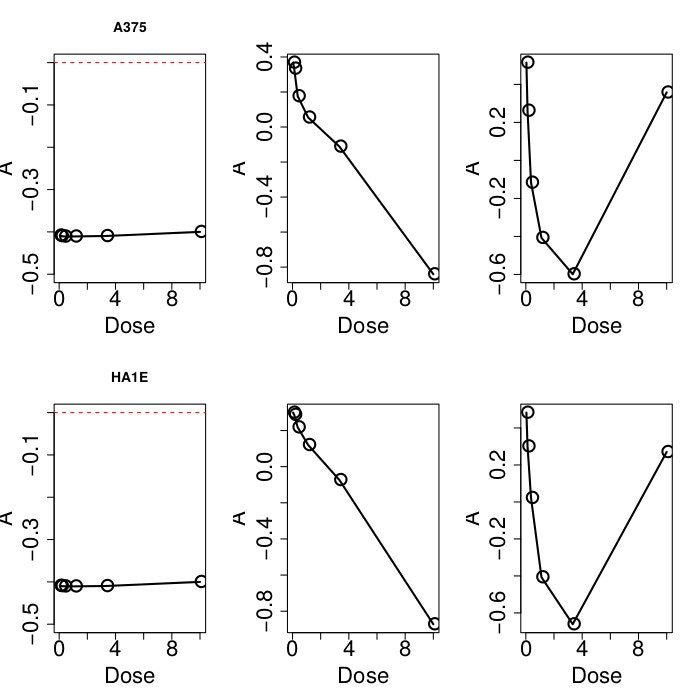
上図は13種類の対象とした培養細胞のうちの2つの例だけであるが、いずれも$k_1=2$の場合が$i$に対して単調性を持っていることがわかる。図は省略するが他の11種類の培養細胞にも同じ結果を得た。
その後の処理は以下の図のようになる。
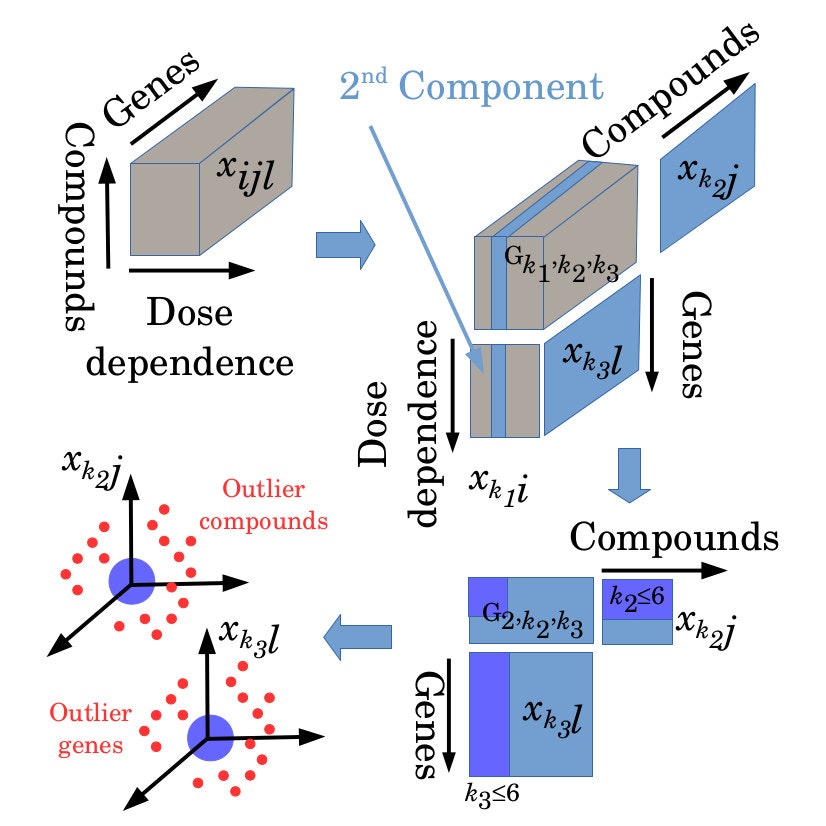
まずはテンソル$x_{ij\ell}$を用意し(左上)、テンソル分解して$k_1=2$が濃度依存性(Dose Dependence)を持っていることを確認する(右上)。次に$k_1=2$に固定したうちの$G(2,k_2,k_3)$の中で絶対値が大きい$(k_2,k_3)$の組み合わせを探す。これは上記テンソル分解の式で、$G(k_1,k_2,k_3)$は重みを表現しているので、濃度依存性を表現する$x_{k_2=2,i}$を含んだ右辺の項の中で寄与の大きい組み合わせに含まれる$x_{k_2j}$と$x_{k_3\ell}$が濃度依存性を伴った化合物依存性や遺伝子依存性を表現しているからである。その結果、$1 \leq k_2, k_2 \leq 6$の$G(2,k_2,k_3)$の絶対値が大きいことが分かった(右下)。次に$1 \leq k_2, k_2 \leq 6$の$x_{k_2j},x_{k_3\ell}$を用いて、化合物と遺伝子の選択を行う。そのために、以下の式で$j$番目の化合物と$\ell$番目の遺伝子にP値を付与する。
$$
P_j = P_{\chi^2} \left [> \sum_{k_2 \leq 6} {\left ( \frac{x_{k_2 j}}{\sigma_{k_2}}\right )^2} \right ]
$$
及び
$$
P_\ell = P_{\chi^2} \left [> \sum_{k_3 \leq 6} {\left ( \frac{x_{k_3 \ell}}{\sigma_{k_3}}\right )^2} \right ]
$$
但し、$x_{k2j}$や$x_{k_3\ell}$は平均ゼロにしてあるものとする。これらの式の心は、$x_{k2j}$や$x_{k_3\ell}$が多重正規分布しているということを帰無仮説とするということである。実際の$x_{k2j}$や$x_{k_3\ell}$の分布は$x_{ij\ell}$が正規分布に従う乱数である場合の$x_{k2j}$や$x_{k_3\ell}$の分布を使用するべきであるが、これはランダム行列の理論的な問題であり、まだそこまで議論できるほど理論が進んでいないため、やむなく正規分布を仮定した。P値は化合物や遺伝子が多数個あるために小さな$P$値が出やすくなってしまうという多重比較の問題を回避するため、Benjamini–Hochberg procedureで多重比較補正を行う。最後に補正された$P_j$や$P_\ell$が十分小さく(具体的には0.01以下)、ガウス分布には従っていないと思われる化合物と遺伝子を選択する(左下)。
表1
| 培養細胞 | BT20 | HS578T | MCF10A | MCF7 | MDAMB231 | SKBR3B | A549 | HCC515 |
|---|---|---|---|---|---|---|---|---|
| ガン種 | 乳がん | 乳がん | 乳がん | 乳がん | 乳がん | 乳がん | 肺がん | 肺がん |
| 予測遺伝子 | 41 | 57 | 42 | 55 | 41 | 46 | 45 | 46 |
| 予測化合物 | 4 | 3 | 2 | 6 | 5 | 6 | 8 | 5 |
| 全化合物 | 110 | 106 | 106 | 108 | 108 | 106 | 265 | 270 |
| 予測標的 | 418 | 576 | 476 | 480 | 560 | 423 | 428 | 352 |
| 培養細胞 | HA1E | HEPG2 | HT29 | PC3 | A375 |
|---|---|---|---|---|---|
| ガン種 | 腎臓がん | 肝臓がん | 大腸がん | 前立腺がん | 黒色腫 |
| 予測遺伝子 | 48 | 54 | 50 | 63 | 43 |
| 予測化合物 | 7 | 2 | 2 | 9 | 6 |
| 全化合物 | 262 | 269 | 270 | 270 | 269 |
| 予測標的 | 423 | 396 | 358 | 439 | 421 |
上表1はその結果である。13種の対象とした培養細胞が元のがん種と共に記されている。予測遺伝子、予測化合物がそれぞれ補正した$P_\ell,P_j$が0.01以下という基準で選択された個数となる。全化合物の行はそれぞれの培養細胞に投与された化合物の数を表現している。
さて、ここで予測遺伝子として選ばれた遺伝子は、化合物を投与した時に発現の変化が濃度依存性を持っていた遺伝子ではあっても、化合物の標的ではない。化合物は一般にタンパクに作用するのであって転写物には作用しないので、直接の標的タンパクをコーディングしている遺伝子の転写物の量に変化が現れることは期待できない。そこでこの問題を解決するために以下の様なことを考えた。
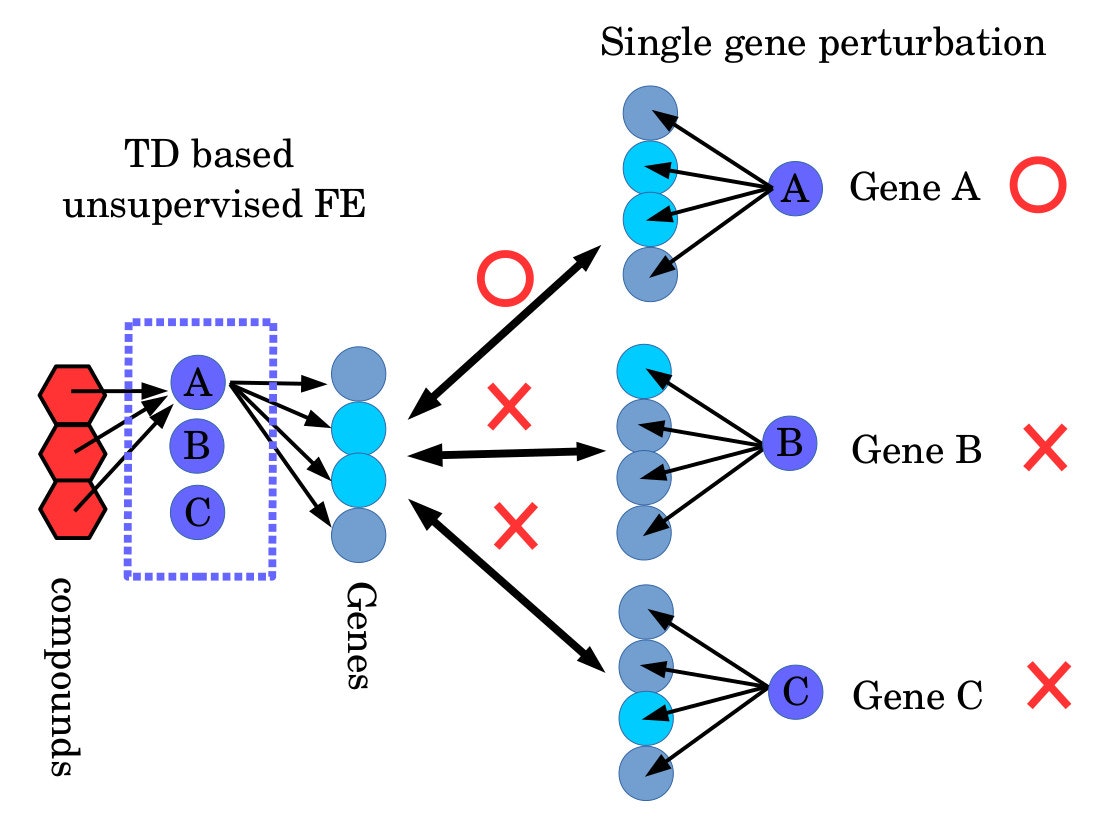
上図の左端の赤い正六角形が予測化合物、その右のGenesと書かれた4つの円の内の2つの水色の円が予測遺伝子である。化合物が作用しているのは点線の長方形で囲われたA,B,Cが記入された〇で表現されるタンパクである。しかし、ここは判らない。そこで予測遺伝子として選ばれた遺伝子と、同じ遺伝子の転写物が変化することが知られている遺伝子ノックアウト/オーバーエクスプレッション実験を探す。化合物がタンパクに結合してその作用を抑制・強化するならば、その効果はその遺伝子をノックアウト/オーバーエクスプレッションしたときと同じはずだからだ。具体的にはこれを実行するために予測遺伝子として選ばれた遺伝子のgene symbolをEnrichrというサーバにアップロードする。Enrichrはアップロードされた遺伝子のリストから様々なエンリッチメント解析を実行してくれる。この中でCrowdカテゴリの下にある、Single Gene Perturbations category from GEO upを選択する。ここを見るアップロードした遺伝子のリストと同じ遺伝子の発現が変化する遺伝子ノックアウト/オーバーエクスプレッションのリストがP値付きで得られる。ここではEnrichrが与える補正されたP値が0.01以下の遺伝子を選んだ。これが表の中の予測標的の数になる。LINCSのデータセットには978遺伝子しか含まれていないが、Enrichrを介することで観測されていない遺伝子が標的であるかどうかの予測までできるところがこの手法の肝になる。
既知の標的タンパクとのオーバーラップ
さて、この様な方法で求まった標的は本当に正しいのだろうか?実験をすることは(僕には)できないので確かめようがない。しかし、既知のデータベースと比較することは可能だ。
表2
|培養細胞|BT20|HS578T|MCF10A|MCF7|MDAMB231|SKBR3B|A549|HCC515|HA1E|HEPG2|HT29|PC3|A375|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|Dabrafenib|||||||||||||〇|
||||||||||||||〇|
|Dinaciclib|||||||〇|〇|〇|〇|〇|〇|〇|
||||||||〇|〇|〇|〇|〇|〇|〇|
|CGP-60474|||〇|〇|〇|〇|〇||〇|||〇|〇|
||||×|×|×|×|×||×|||×|〇|
|LDN-193189|〇||||〇||||||||〇|
||〇||||〇||||||||〇|
|OTSSP167|||||||ー|ー||ー||ー|ー|
||||||||〇|〇||〇||〇|〇|
|WZ-3105||ー||ー|ー||ー|ー|ー|||ー|ー|
|||〇||〇|〇||〇|〇|〇|||〇|〇|
|AT-7519||||〇||〇||〇|〇|||〇||
|||||〇||〇||〇|〇|||〇||
|BMS-387032||||〇||〇|〇||〇|||||
|||||〇||〇|〇||〇|||||
|JNK-9L|||||||||〇|||||
||||||||||〇|||||
|Alvocidib|〇|〇|〇|〇|〇|〇|||〇||||
||ー|ー|ー|ー|ー|ー|||ー||||
|GSK-2126458|||||||ー|||||ー||
||||||||ー|||||ー||
|NVP-BEZ235|||||||〇|||||〇||
||||||||×|||||×||
|Torin-2|||||||×|||||×||
||||||||〇|||||〇||
|NVP-BGT226|||||ー|||ー|||ー|ー||
||||||ー|||ー|||ー|ー||
|QL-XII-47|ー|||||||||||||
||ー|||||||||||||
|Celastrol|〇|||||||||||||
||ー|||||||||||||
|A443654||〇||〇||||||||||
|||〇||〇||||||||||
|NVP-AUY922|||||×|〇||||||||
||||||ー|ー||||||||
|Radicicol||||||〇||||||||
|||||||ー||||||||
上表2は2つのデータベースdrug2gene.com(2018年12月1日現在、アクセス不可)とDSigDBとの比較である(各化合物で上段がdrug2gene.com、下段が、DSigDBである)。〇はフィッシャーの正確確率検定で計算したオーバーラップのP値が0.05以下のもの、×はその条件を満たさないもの、-は化合物がデータセットに存在しないもの、である。多重比較補正をしていないので甘い評価にはなってしまっているが大多数の予測が既知のデータベースとオーバーラップしている。従来の遺伝子発現プロファイルからの創薬は教師あり学習であるため既知の有効化合物を必要としたがそれなしでも遺伝子発現プロファイルからの創薬が可能であることが示された。
結言
本記事では昨年の記事に続いて、テンソル分解を用いて遺伝子発現プロファイルからインシリコ創薬する方法について提案を行った。今後、遺伝子発現プロファイルをはじめとするオミックスデータの計測はどんどん安価に高速になって行くことが期待できる。このようなデータを用いて本記事で触れたような方法で創薬が進むことを願っている。
付記
本研究はInCob2018で発表済みであり、Oral Presentation Award(Consolation(残念賞(笑)))を受賞している。また、BMC Bininformatics誌に同国際会議のプロシーディングスとして刊行済み(https://doi.org/10.1186/s12859-018-2395-8)である。そこにより詳しい解析が記述されているので興味ある場合はご覧いただきたい。