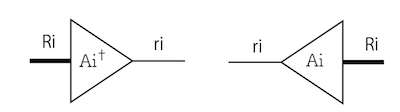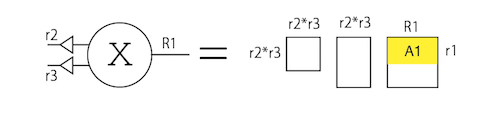はじめに
テンソルを、低いランクのテンソル(コアテンソル)と行列の組に分解することをTucker分解と呼ぶ。その手法のうち、HOSVD (higher order singular value decomposition)と、HOOI (higher orthogonal iteration of tensors)を使って、画像の低ランク近似をしてみる。
ソースコードは
https://github.com/kaityo256/hooi_sample
においてある。
テンソルのTucker分解
例えば、3階のテンソル$X$があり、それぞれの足の次元が$R_1, R_2, R_3$であるとする。この時、足の次元が$r_1, r_2, r_3$であるような3階のテンソル$\chi$と、$r_i$行$R_i$列の行列$A_i (i=1,2,3)$に分解する。この行列$A_i$は、コアテンソルの$i$番目の足と縮約を取ると、次元が$r_i$から$R_i$になる、つまり$A_i$はコアテンソルから元のテンソルに戻す「復元行列」となる。逆に、元のテンソルの$i$番目の足と$A_i^\dagger$の縮約を取ると、足の次元が$R_i$から$r_i$になる、つまり$A_i^\dagger$は射影行列である。それぞれ図示するとこんな感じ。
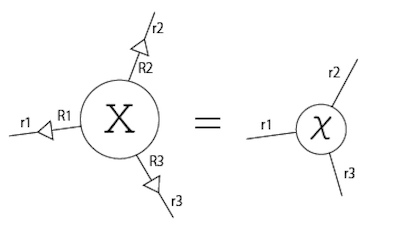
まず、元のテンソル$X$のそれぞれの足に射影行列をかけたものが、コアテンソル$\chi$になる。
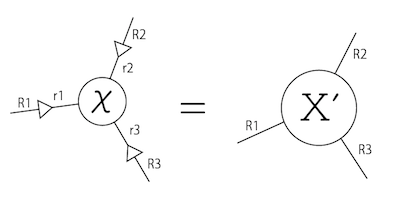
また、コアテンソル$\chi$の足それぞれに復元行列をかけたものが、元のテンソルを近似したテンソル$X'$となる。
もともとのテンソルの情報量は$R_0 R_1 R_2$であったが、コアテンソルの要素数が$r_0 r_1 r_2$、$A_i$行列の要素数が$R_i r_i$なので、圧縮した後の要素数は$r_0 r_1 r_2 + R_0 r_0 + R_1 r_1 + R_2 r_2$となる。
Tucker分解とは、元のテンソル$X$と、コアテンソルの次元が与えられた時、なるべく元のテンソルを精度よく近似する射影行列の組$A_i$を求めなさい、という問題となる。これを、画像の低ランク近似を題材に、HOSVDとHOOIという二つの方法でやってみよう。
HOSVD
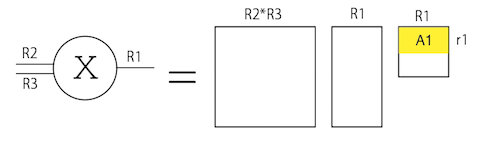
HOSVD (higher order singular value decomposition)では、まず足が沢山あるテンソルを、注目する足と、それ以外の足の二本足にしてしまう。するとこれは行列であるから、SVD(singular value decomposition)が適用できる。SVDした後に右側の行列の上位のランクを取ってきたものを、注目する足の復元行列とする。これを全ての足について繰り返し行う手続きがHOSVDである。
上の図では、3本の足を持つテンソル$X$のうち、1番目の足に注目し、2番目と3番目の足をまとめて$R_2 R_3\times R_1$の行列とみなしてSVDする。すると左側に$R_2 R_3 \times R_2 R_3$、右側に$R_1 \times R_1$の正方行列が現れるが、右側の上位$r_1$行をとったものが1番目の足の復元行列$A_1$となる。同様に$A_2$、$A_3$を求めることができる。
HOOI
さて、HOSVDは最良の近似を与えないことが知られている。これをイタレーションにより改善するのがHOOI (higher orthogonal iteration of tensors)である。
まず、復元行列$A_i$を最初はランダムに用意しておく。そして、注目する足(例えば1番)以外について、元のテンソルの足を$A_i (i \neq 1)$を使って潰してやる。その上でHOSVDと同様に注目する足とそれ以外の足の行列にしてSVDをかけ、できた行列の上位$r_1$個をとったものを新たな$A_1$とする。
注目する足以外は射影行列をつかって次元を落としてしまっているため、SVDに必要な計算量が大幅に落ちていることに注意。
これを全ての足について実行したものを1ループとし、このループを回すことで精度を改善する。
画像の低ランク近似
二次元画像は、x座標、y座標、色(RGB)を指定すればピクセル値が決まるので、(高さ, 幅, 3)の次元を持つ3階のテンソルとみなすことができる。このうち、高さと幅を潰す行列をHOSVD, HOOIにより求め、画像を低ランク近似してみる。HOSVDについては過去記事を参照。
幅$w$、高さ$h$の画像について、幅の次元を$r1$に、高さの次元を$r2$に潰すことを考える。
求めたいのは、幅、高さを潰す射影行列である。これを$a_1^\dagger, a_2^\dagger$とする。色については次元が3しかないので潰さないことにする。
最初に、$a_1, a_2$の初期値を用意する必要がある。初期値はなんでも良いが1、各行は直交している必要がある。よい与え方を思いつかなかったので、$w \times w$、$h \times h$のランダムな行列を用意して、それをSVDし、上位$r_1, r_2$行をとってくることで初期値としてみた。
X1 = np.random.rand(w,w)
X2 = np.random.rand(h,h)
U,s,A1 = linalg.svd(X1)
U,s,A2 = linalg.svd(X2)
a1 = A1[:r1, :]
a2 = A2[:r2, :]
後の便利のために、$a_1, a_2$を使って圧縮、復元したテンソルを与える関数を用意しておこう。
def restored_tensor(X,a1,a2):
pa1 = a1.T.dot(a1)
pa2 = a2.T.dot(a2)
X2 = np.tensordot(X,pa1,(1,0))
X3 = np.tensordot(X2,pa2,(0,0))
return X3.transpose(2,1,0)
これは、$X$に$a_i^\dagger$をかけてコアテンソルを作ってから、$a_i$をかけて復元したテンソルを返す関数になっている。
後は、
- 高さの足(2番)を$a_2^\dagger$でつぶしてから色とまとめてSVDして、幅をつぶす行列$a_1^\dagger$を更新
- 幅の足(1番)を$a_1^\dagger$でつぶしてから色とまとめてSVDして、高さをつぶす行列$a_2^\dagger$を更新
を繰り返せばよい。それを実装したのが以下のコードとなる。
for i in range(10):
X1 = np.tensordot(X,a2.T,(0,0)).transpose(2,1,0).reshape(r2*3,w)
U,s,A1 = linalg.svd(X1)
a1 = A1[:r1, :]
X2 = np.tensordot(X,a1.T,(1,0)).transpose(2,1,0).reshape(r1*3,h)
U,s,A2 = linalg.svd(X2)
a2 = A2[:r2, :]
結果
元のテンソル$X$にについて、その近似テンソル$X'$が与えられた時、その残差$r$を
$$
r = \frac{|X - X'|}{|X|}
$$
で定義する。ただし$|X|$は$X$のフロベニウスノルムである。
適当な画像を入力として、幅、高さの次元それぞれを20%に圧縮する変換を考えよう。入力画像として、たまたま手元にあったItanium2精霊馬の写真を用いる。
これを、HOSVDで近似したものが以下の画像となる。
残差は0.966415890942であった。
HOOIを10ステップ回すと、残差は以下のように減っていく。
1.28857987024
0.97532217632
0.95714093422
0.952636586271
0.950770629606
0.949809071863
0.949257702502
0.948920613334
0.948705104294
0.948562468306
最初の行は全く最適化をしていない場合の値である。そこから2回ループをまわすと残差はHOSVDよりも小さくなる。10回まわした後の画像は以下の通り。
この画像の残差は0.948562468306であり、HOSVDよりも2%弱改善されているが、その違いを目で区別するのは(少なくとも私には)困難である。
まとめ
画像を3階のテンソルだと思って、HOSVD、HOOIの二通りの方法で低ランク近似を行ってみた。$(w,h)$のサイズの画像について、幅を$r_1$に、高さを$r_2$に潰す場合、HOSVDでは$(3h, w)$と$(3w,h)$の二つの行列を一回ずつSVDする必要があるが、HOOIは$(3r_2, w)$と$(3r_1, w)$と、かなり小さい行列をSVDすればよいかわりに何度かループを回す必要がある。ただし、画像で試した範囲では数回も回せばHOSVDよりも残差が小さくなったので、元のテンソルの次元が大きい場合、全体の計算量はHOOIの方が小さいものと思われる。
-
HOSVDの近似を改良したい、という目的では、初期値としてHOSVDの結果を使うというのは有効である。しかし、HOSVDよりも計算のオーダーを落としたい、ということであれば、初期値はランダムに用意して良い。いずれにせよ、数回もイタレーションをまわせば十分な精度を得る。 ↩