Go to Qiita Advent Calendar 2024 Top
LoginSignup
8
5

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

POV-Rayによる数学お絵かき入門Advent Calendar 2017Day 15
@Hyrodium(Yuto Horikawa)in株式会社Rist

POV-Rayで描く「2重振り子」

Last updated at Posted at 2017-12-15

はじめに

これは POV-Rayによる数学お絵かき入門 Advent Calendar 2017 の15日目の記事です.

作例3回目となる今回は「2重振り子のアニメーション」を描きます.
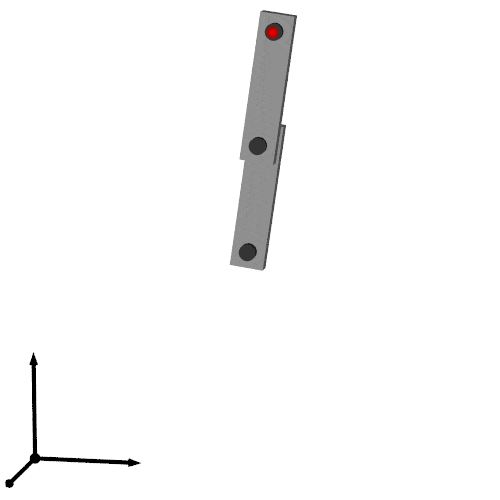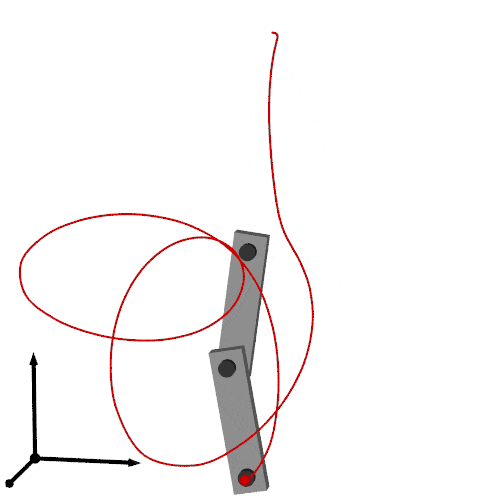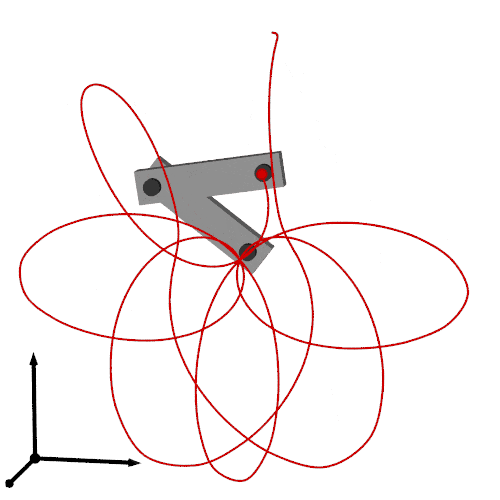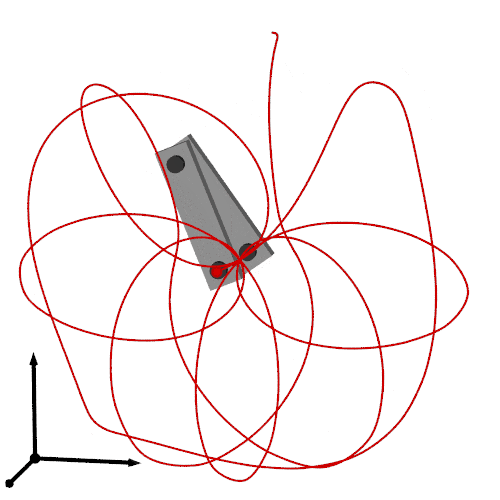
最終的な出力は次です.

方針

以下の方針でアニメーションを作成していきます.

  1. Wolfram言語を用いて運動方程式の近似解を出力.
  2. POV-Rayでテキストデータを読み込み, 連番画像を生成.
  3. 連番画像をgifアニメーションに変換.

運動方程式を解く

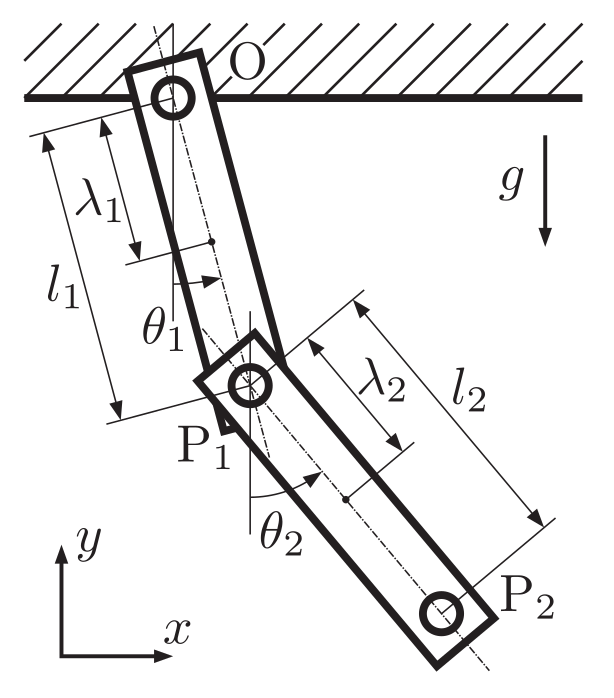
次の図のような2重振り子を考えます.

この振り子の運動の近似解をLagrangeの運動方程式から求めましょう.
各振り子の重心座標は次で与えられます.

\begin{align}
	(x_1,y_1)
	&=\lambda_1(\sin\theta_1,-\cos\theta_1) \\
	(x_2,y_2)
	&=l_1(\sin\theta_1,-\cos\theta_1)+\lambda_2(\sin\theta_2,-\cos\theta_2)
\end{align}

$m_1, m_2$を各振り子の質量とすれば系の位置エネルギーは次で与えられます.

\begin{align}
	U
	&=g(m_1y_1+m_2y_2) \\
	%&=-g(m_1(\lambda_1\cos\theta_1)+m_2(l_1\cos\theta_1\lambda_2\cos\theta_2))
\end{align}

$I_1, I_2$を各振り子の慣性モーメントとすれば系の運動エネルギーは次で与えられます.

\begin{align}
	K
	=\frac{1}{2}m_1(\dot{x_1}^2+\dot{y_1}^2)
	+\frac{1}{2}m_2(\dot{x_2}^2+\dot{y_2}^2)
	+\frac{1}{2}I_1\dot{\theta_1}^2
	+\frac{1}{2}I_2\dot{\theta_2}^2
\end{align}

Lagrange運動方程式は$L=K-U$とおいて

\begin{align}
\frac{d}{dt}\frac{\partial L}{\partial\dot{\theta_i}}-\frac{\partial L}{\partial\theta_i}=0
\end{align}

で与えられるのでした.
ここではWolfram言語を用いて運動方程式の近似解を求めます.
Wolfram言語を使えば, 上の微分方程式の面倒な展開をも任せて近似解を得ることが出来ます.
以下のWolfram Programming LabのTry It Yourselfから登録/課金なしで, Wolfram言語の実行が可能です.
https://lab.open.wolframcloud.com/app/

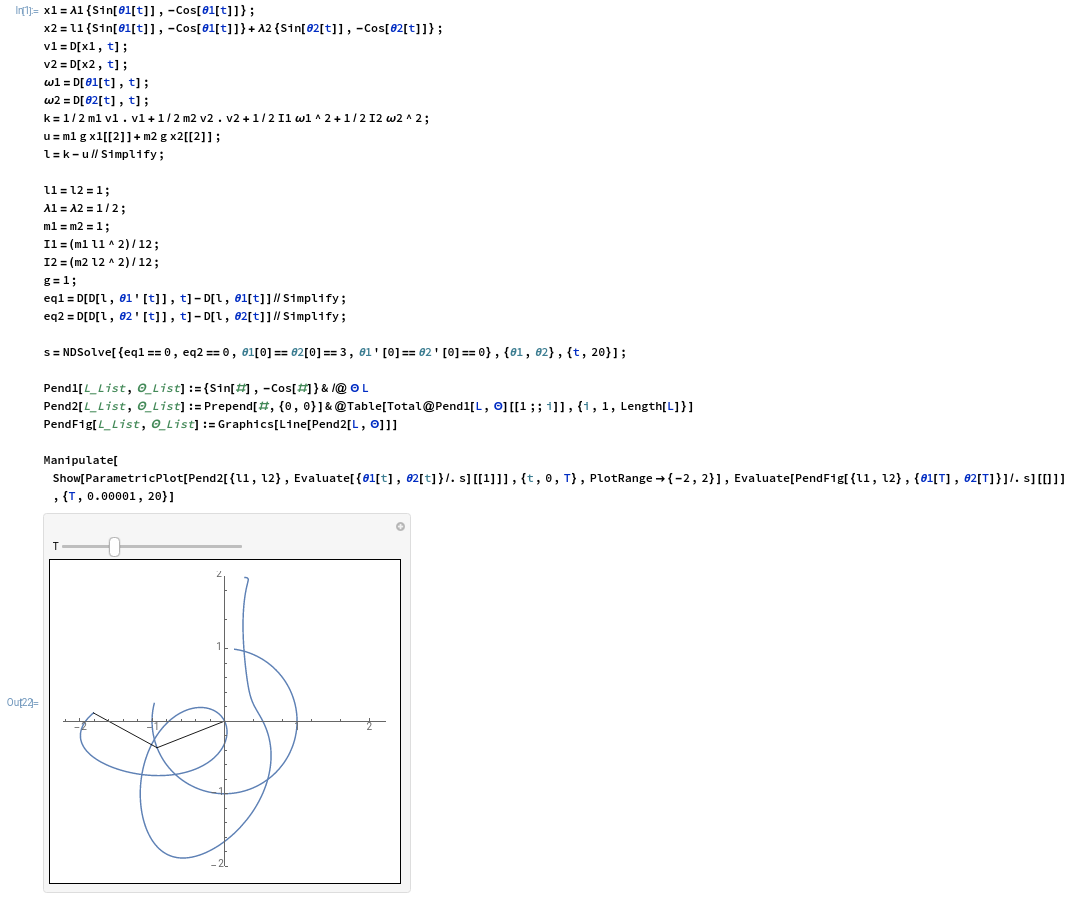
上計算と近似解を求めるためのWolfram言語のコードは次です.
ただし$m_1=m_2=1$, $l_1=l_2=1$, $\lambda_1=\lambda_2=1/2$, $I_1=I_2=m_1{l_1}^2/12$, $g=1$としました.

x1=\[Lambda]1{Sin[\[Theta]1[t]],-Cos[\[Theta]1[t]]};
x2=l1{Sin[\[Theta]1[t]],-Cos[\[Theta]1[t]]}+\[Lambda]2{Sin[\[Theta]2[t]],-Cos[\[Theta]2[t]]};
v1=D[x1,t];
v2=D[x2,t];
\[Omega]1=D[\[Theta]1[t],t];
\[Omega]2=D[\[Theta]2[t],t];
k=1/2 m1 v1.v1+1/2 m2 v2.v2+1/2 I1 \[Omega]1^2+1/2 I2 \[Omega]2^2;
u=m1 g x1[[2]]+m2 g x2[[2]];
l=k-u//Simplify;

l1=l2=1;
\[Lambda]1=\[Lambda]2=1/2;
m1=m2=1;
I1=(m1 l1^2)/12;
I2=(m2 l2^2)/12;
g=1;
eq1=D[D[l,\[Theta]1'[t]],t]-D[l,\[Theta]1[t]]//Simplify;
eq2=D[D[l,\[Theta]2'[t]],t]-D[l,\[Theta]2[t]]//Simplify;

s=NDSolve[{eq1==0,eq2==0,\[Theta]1[0]==\[Theta]2[0]==3,\[Theta]1'[0]==\[Theta]2'[0]==0},{\[Theta]1,\[Theta]2},{t,20}];

Pend1[L_List,\[CapitalTheta]_List]:={Sin[#],-Cos[#]}&/@\[CapitalTheta] L
Pend2[L_List,\[CapitalTheta]_List]:=Prepend[#,{0,0}]&@Table[Total@Pend1[L,\[CapitalTheta]][[1;;i]],{i,1,Length[L]}]
PendFig[L_List,\[CapitalTheta]_List]:=Graphics[Line[Pend2[L,\[CapitalTheta]]]]

Manipulate[
Show[ParametricPlot[Pend2[{l1,l2},Evaluate[{\[Theta]1[t],\[Theta]2[t]}/.s][[1]]],{t,0,T},PlotRange->{-2,2}],Evaluate[PendFig[{l1,l2},{\[Theta]1[T],\[Theta]2[T]}]/.s][[]]]
,{T,0.00001,20}]

実行結果を次に示します.
出力のスライダを動かせば振り子の動く様子が確認できます.

これをPOV-Rayが読めるように次のように出力してファイルに保存します.
会員登録なしのWolfram Programming Labからはファイル出力が使えないため, クリップボードを経由することになります.


ExportString[List@Flatten@Table[Evaluate[{\[Theta]1[t],\[Theta]2[t]}/.s][[1]],{t,0,20,0.1}],"CSV"]

結果のデータだけ欲しい方は以下からダウンロード出来ます.↓
https://gist.github.com/hyrodium/413417a5083711006db5acbcc5478aef

POV-Rayのレンダリング

カメラ等の設定

第8回を参考に, 次のようにカメラ等を設定します.

#version 3.7;
global_settings{assumed_gamma 1.0}

#macro SCS(lng,lat) <cos(radians(lat))*cos(radians(lng)),cos(radians(lat))*sin(radians(lng)),sin(radians(lat))> #end

#declare Lng=10;
#declare Lat=10;
#declare Pers=0.1;
#declare Zoom=0.45;
#declare LookAt=<0,0,0>;

#declare AspectRatio=image_width/image_height;
#declare Z=SCS(Lng,Lat);
#declare X=<-sin(radians(Lng)),cos(radians(Lng)),0>;
#declare Y=vcross(Z,X);
#declare Loc=LookAt+SCS(Lng,Lat)/(Zoom*Pers);
camera{
    perspective
    location Loc
    right -2*X*sqrt(AspectRatio)/Zoom
    up 2*Y/(sqrt(AspectRatio)*Zoom)
    direction Z/(Zoom*Pers)
    sky Y
    look_at LookAt
}
light_source{
    Loc
    color rgb<1,1,1>
}
background{rgb<1,1,1>}

外部ファイルの読み込み

第13回を参考に外部ファイルを読み込みます.
時刻$t$を0.1刻みで0から20まで出力したので, 201組の$(\theta_1,\theta_2)$のデータを読み込みます.
ここでは読み込むついでに$(x_2,y_2)$の座標も配列P2に計算しています.

#fopen MyFile "DoublePendulum.txt" read
#declare M=200;
#declare T1=array[M];
#declare T2=array[M];
#declare P2=array[M];

#declare i=0;
#while(i<M)
	#read (MyFile,t1)
	#read (MyFile,t2)
	#declare T1[i]=t1;
	#declare T2[i]=t2;
	#declare P2[i]=<0.5,sin(t1)+sin(t2),-cos(t1)-cos(t2)>;
	#declare i=i+1;
#end

振り子の描画

まず, 振り子1節分のobjectを次で描画します.

#declare h=0.15;
#declare rod=union{
	box{<h/2,h,h>,<-h/2,-h,-1-h> pigment{rgb<0.4,0.4,0.4>}}
	cylinder{<h,0,0>,<-h,0,0>,0.075 pigment{rgb<0.05,0.05,0.05>}}
	cylinder{<h,0,-1>,<-h,0,-1>,0.075 pigment{rgb<0.05,0.05,0.05>}}
};
rod

第7回で解説したrotate, translateを使って次のようにします.

#declare N=frame_number;
object{rod rotate<degrees(T1[N]),0,0>}
object{rod rotate<degrees(T2[N]),0,0> translate<0,sin(T1[N]),-cos(T1[N])> translate<0.3,0,0>}

ここでflame_numberは第9回で解説した整数で, アニメーションのフレーム番号なのでした.
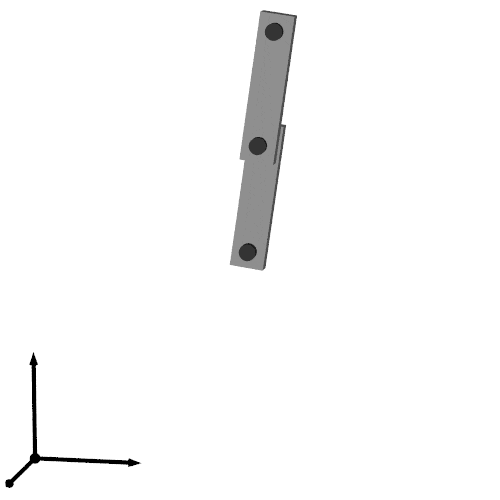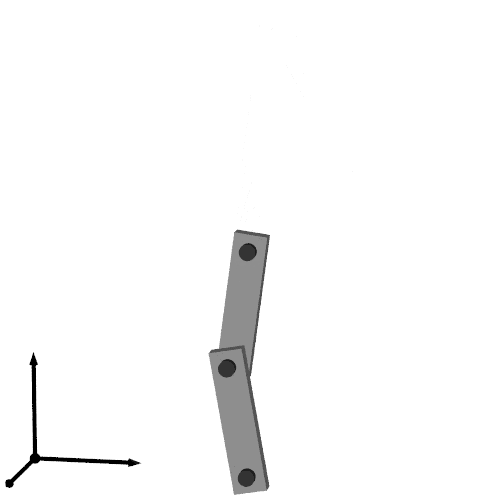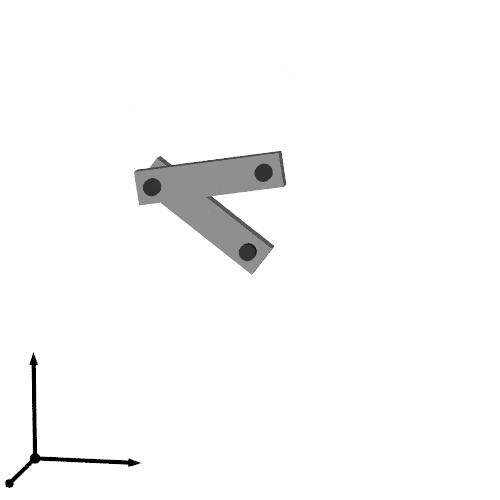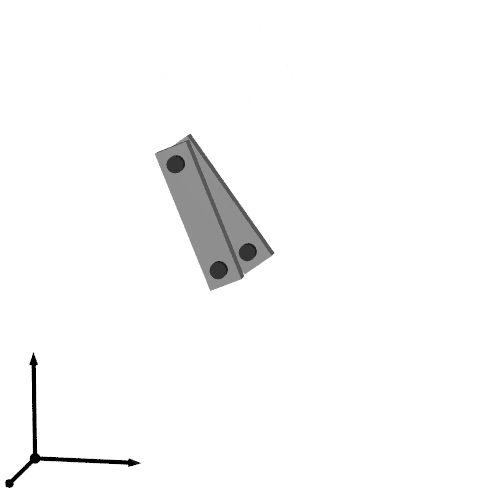
以上で次のような出力が得られます.

座標軸の描画

このままでは, 斜め上から振り子を見ていることが分かりにくいので, 座標軸の方向を表す矢印を描画します.
矢印を表すためのマクロを次のように書きます.

#macro Arrow(a,b,r)
	union{
		difference{
			cylinder{a,b,r}
			cylinder{b-6*r*vnormalize(b-a),2*b-a,2*r}
		}
		cone{b-6*r*vnormalize(b-a),2*r,b,0}
	}
#end

これでaを始点, bを終点, rを半径とする矢印が描画できます.
これを用いて左下に3方向に矢印を配置します.

union{
	sphere{<0,0,0>,0.05}
	object{Arrow(<0,0,0>,<1,0,0>,0.02)}
	object{Arrow(<0,0,0>,<0,1,0>,0.02)}
	object{Arrow(<0,0,0>,<0,0,1>,0.02)}
	translate <0,-2,-2>
}

これで冒頭に置いた1つ目のアニメーションが出来ました.

軌跡の描画

次は配列P2を元に軌跡を表す曲線を描画します.
曲線を書くには前回説明したsphere_sweepを使います.
天下り的ですが, 以下のように書きます.

#if(N>4)
	sphere_sweep {
	    cubic_spline
	    N+2,
	    #declare i=0;
	    #while(i<N+2)
		    P2[i],0.01
		    #declare i=i+1;
	    #end
	    pigment{rgb<1,0,0>}
	}
#end

sphere{<0.5,sin(T1[N])+sin(T2[N]),-cos(T1[N])-cos(T2[N])>,0.05 pigment{rgb<1,0,0>}}

以下に箇条書きで解説します.

  • 離散点を滑らかに繋ぎたいのでcubic_splineを使っています
  • cubic_splineを使うには少なくとも4点必要なので#ifで囲んでいます.
  • Nが小さい時は描画されない問題がありますが, 最後のsphereで隠れるのであまり問題になりません.

以上を合わせてレンダリングすれば以下のアニメーションが得られます.

8
5
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
5

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?