はじめに
これは POV-Rayによる数学お絵かき入門 Advent Calendar 2017 の14日目の記事です.
今日の記事では次のような曲線の描き方について書きます.
公式ドキュメントでは以下が近いです.
http://www.povray.org/documentation/3.7.0/r3_4.html#r3_4_5_1_13
愚直な方法
この節ではmacroで定義した曲線を折れ線近似して曲線を描きます.
具体例として常螺旋$(\cos(t),\sin(t),t/5)$を次のように描きます.
ここでa, bはパラメータの動く範囲を表し, Nは曲線の分割数を表しています.
rは曲線の半径です.
# macro p(w)
<cos(w),sin(w),w/5>
# end
# declare a=0;
# declare b=2*pi;
# declare N=12;
# declare r=0.03;
merge{
#declare i=0;
#while(i<N)
#declare w=a+i*(b-a)/N;
sphere{p(w),r}
cylinder{p(w),p(w+(b-a)/N),r}
#declare i=i+1;
#end
sphere{p(b),r}
pigment{rgb<1,0,0>}
}
分割数Nを十分に増やせば次のような滑らかな曲線が得られます.
ここでは$N=96$としました.
linear_spline
実はPOV-Rayにはsphere_sweepと呼ばれるオブジェクトが用意されており, 折れ線を描くには次のような構文になります.
sphere_sweep {
linear_spline
NUM_OF_SPHERES,
CENTER, RADIUS,
CENTER, RADIUS,
...
CENTER, RADIUS
}
RADIUSの後のカンマ,はあっても無くても構いません.
具体例1
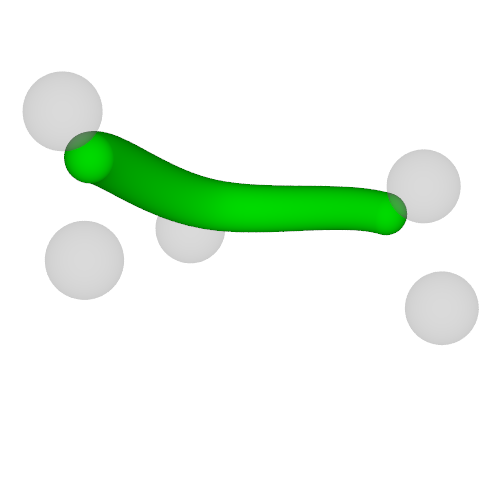
5つの点を繋ぐ折れ線は次のように書けます.
各点での半径をも指定する事が可能で, 折れ線の各線分では半径が線形補間されます.
# declare a1=<-1,.3,-.4>;
# declare a2=<-1,0,.2>;
# declare a3=<0,-1,-.4>;
# declare a4=<1,0,1>;
# declare a5=<1,.3,.3>;
sphere{a1,0.2 pigment{rgbft<.5,.5,.5,.5,.5>}}
sphere{a2,0.2 pigment{rgbft<.5,.5,.5,.5,.5>}}
sphere{a3,0.2 pigment{rgbft<.5,.5,.5,.5,.5>}}
sphere{a4,0.2 pigment{rgbft<.5,.5,.5,.5,.5>}}
sphere{a5,0.2 pigment{rgbft<.5,.5,.5,.5,.5>}}
sphere_sweep {
linear_spline
5,
a1,0.15
a2,0.1
a3,0.15
a4,0.15
a5,0.05
pigment{rgb<0,1,0>}
}
具体例2
これを使えば, 先程の愚直な方法をより簡潔に次のように書く事が出来ます.
# macro p(w)
<cos(w),sin(w),w/5>
# end
# declare a=0;
# declare b=2*pi;
# declare N=12;
# declare r=0.03;
sphere_sweep {
linear_spline
N+1,
#declare i=0;
#while(i<N+1)
p(a+i*(b-a)/N),r
#declare i=i+1;
#end
pigment{rgb<1,0,0>}
}
b_spline
Bスプライン曲線の解説
Bスプライン曲線とは, 簡単に述べれば「節点で出来る限り滑らかに繋げた区分多項式曲線」の事です.
一般のBスプライン曲線はde Boor Coxの漸化式によって定義されますが, POV-Rayでは一様な3次Bスプライン曲線のみが扱えます.
この一様3次Bスプライン曲線を定めるためには$n$個の制御点$\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\in\mathbb{R}^d$を与える必要があります.
ここでは一般の定義には触れずに, 一様3次Bスプライン曲線の定義を述べましょう.
まず関数$f(t)$を次で定義します.
\begin{align}
f(t)
=
\begin{cases}
\frac{1}{6}t^3 &(0\le t <1) \\
-\frac{1}{2}t^3+2t^2-2t+\frac{2}{3} &(1\le t <2) \\
\frac{1}{2}t^3-4t^2+10t-\frac{22}{3} &(2\le t <3) \\
-\frac{1}{6}t^3+2t^2-8t+\frac{32}{3} &(3\le t <4) \\
0 &\text{(otherwise)}
\end{cases}
\end{align}
$f$は$C^2$級に多項式を繋いだ関数で, そのグラフは次の黒実線になります.
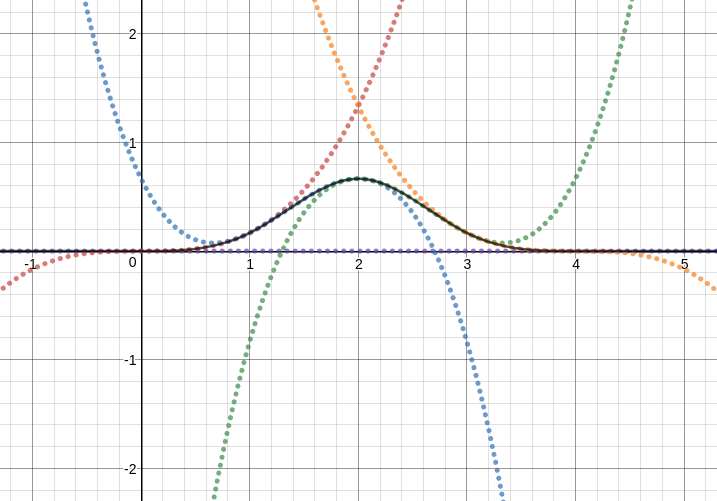
https://www.desmos.com/calculator/gpqwa1ebap
関数$f$を元に基底関数と呼ばれる$n$個の関数を次で定義します.
\begin{align}
f_1(t)&=f(t) \\
f_2(t)&=f(t-1) \\
&\cdots \\
f_n(t)&=f(t-n+1)
\end{align}
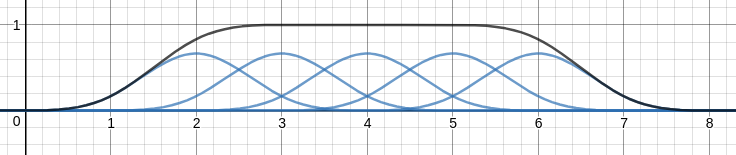
$n=5$では基底関数は次のようになります.
これらの基底関数を$n$個の制御点を掛けて足しあげて得られる曲線がBスプライン曲線$\boldsymbol{p}(t)$です.
\begin{align}
\boldsymbol{p}(t)=\sum_{i=1}^n f_i(t)\boldsymbol{a}_i
\end{align}
これをDesmosで描いたものが次の曲線です.
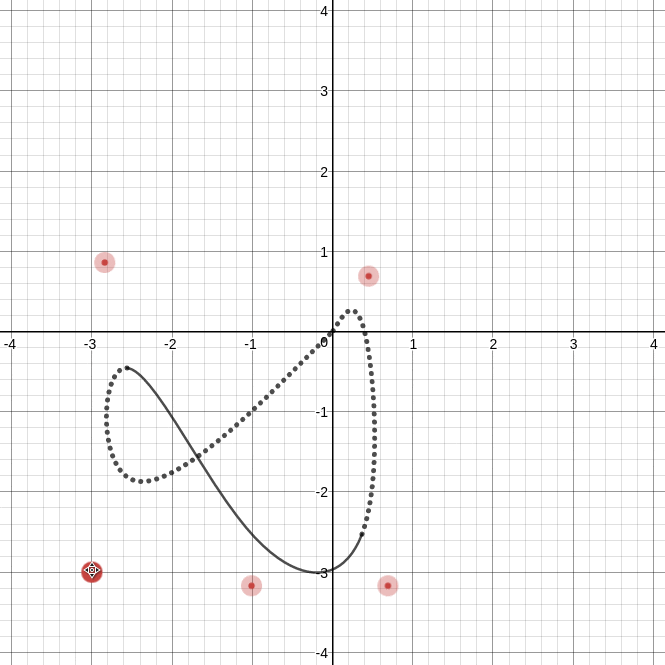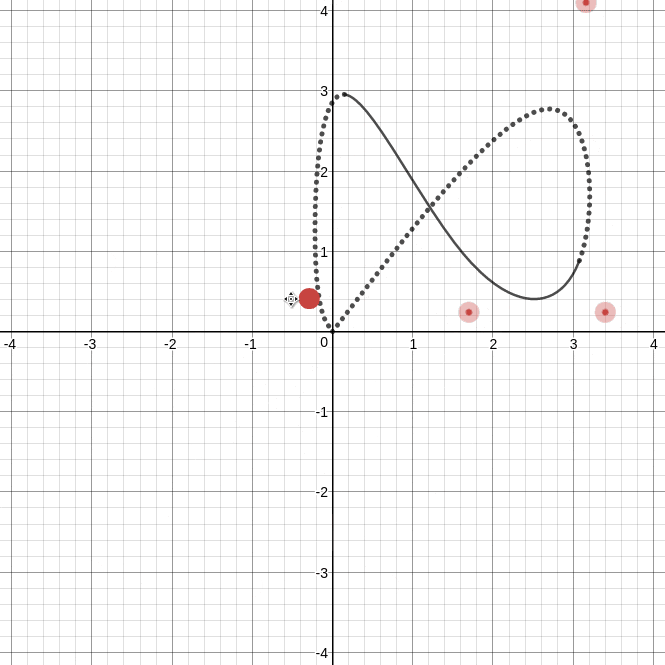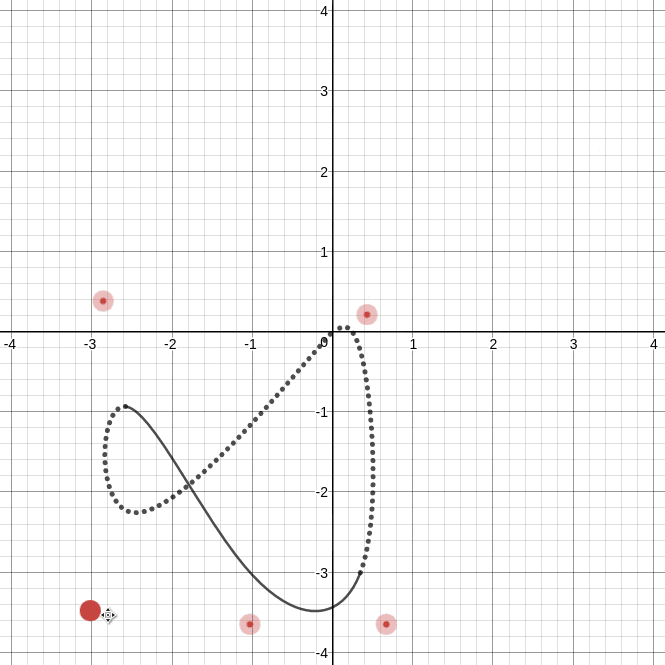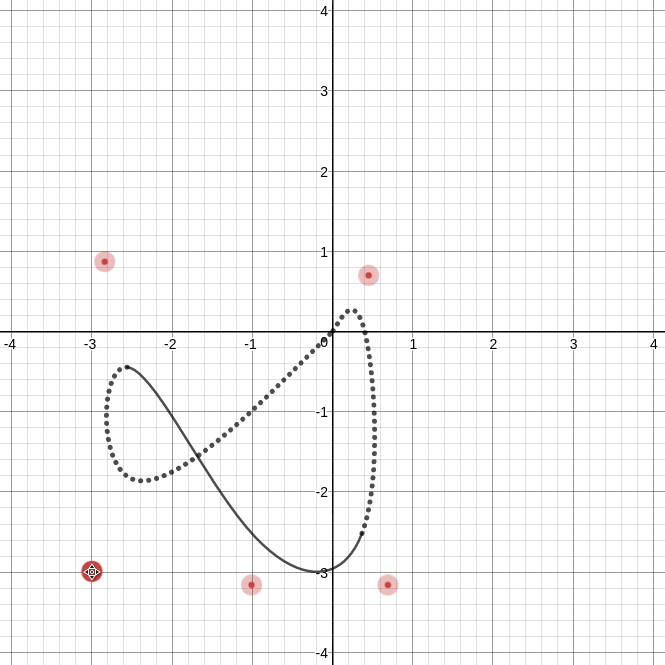
https://www.desmos.com/calculator/1wdbuoy859
上gifを見れば分かるように, 曲線は制御点$\boldsymbol{a}_i$の平行移動で一緒に平行移動する部分(実線 $t\in [3,5]$ )と変形する部分(点線 $t\notin [3,5]$ )に分かれます.
これの違いは基底関数の和$\sum_{i=1}^n f_i(t)$を見れば明らかで, 制御点$\boldsymbol{a}_i$の平行移動で一緒に平行移動する部分ではこの和が$1$になっています.
POV-RayでのBスプライン曲線の扱い
Bスプライン曲線を描くにはlinear_splineの代わりにb_splineを指定します.
POV-RayでBスプライン曲線を描くには折れ線の時と同様に次のようにします.
sphere_sweep {
b_spline
NUM_OF_SPHERES,
CENTER, RADIUS,
CENTER, RADIUS,
...
CENTER, RADIUS
}
この場合は曲線だけでなく, 半径に対してもBスプライン補完が適用されます.
つまり, 半径も曲線に(正確には媒介変数に)沿って$C^2$級に変化します.
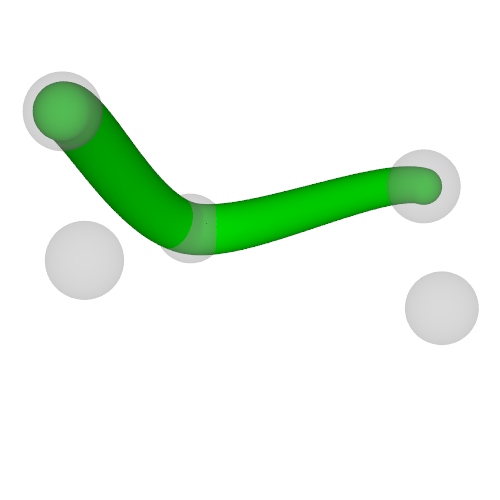
次に具体例を挙げます.
sphere_sweep {
b_spline
5,
a1,0.15
a2,0.1
a3,0.15
a4,0.15
a5,0.05
pigment{rgb<0,1,0>}
}
cubic_spline
b_splineで指定したは制御点を通る曲線を通るとは限りませんでしたが, cubic_splineを指定すれば与えた点列を通る曲線を描画する事が出来ます.
少し調べましたが, 具体的な曲線描画アルゴリズムを筆者は良く分かっていません.
とにかく, 与えた点列を良しなに繋いでくれるオブジェクトとしてcubic_splineは便利です.
こちらも同様に次のような構文です.
sphere_sweep {
cubic_spline
NUM_OF_SPHERES,
CENTER, RADIUS,
CENTER, RADIUS,
...
CENTER, RADIUS
}
ただし, b_splineと同様に曲線を描くには最低4つの制御点が必要で, 例外的に両端点となる2点を曲線は通りません.
これらは端点での速度ベクトルを指定するために使われます.
具体例
sphere_sweep {
cubic_spline
5,
a1,0.15
a2,0.1
a3,0.15
a4,0.15
a5,0.05
pigment{rgb<0,1,0>}
}