【機械学習】VITSでアニメ声へ変換できるボイスチェンジャー&読み上げ器を作った話

はじめに

DiscordやVRChatなど、オンラインでの会話を楽しむプラットフォームが近年賑わいを見せています。
そんな中で「さまざまな声質の音声で会話ができたら面白いだろう」と思い立ち、音声間での声質の変換ができる機械学習モデルを実装してみました。例えば以下の紹介動画のように変換できます。

機械学習の一手法「VITS」でアニメ声(つくよみちゃん)へ変換できるボイスチェンジャーを実装しました。https://t.co/LX0TV13uAD pic.twitter.com/vVWcDbUSpn

— zassou (@zassouEX) February 25, 2022

また、今回用いたモデルではテキストの読み上げを実行することもできます。

読み上げを行うこともできます。
(こちらに関してはもう少しファインチューニングが必要そうです。) pic.twitter.com/xKPhTL7A0E

— zassou (@zassouEX) February 25, 2022

実装したコードはこちら
以下ではこれに用いた手法について解説します。

データセット

今回はデータセットとして「JVS corpus」と「つくよみちゃんコーパス」を用いました。
JVS corpusは100人の俳優/声優によるテキストの読み上げ(.wav形式)と、発話内容といったラベルが付与されたデータセットです。
つくよみちゃんコーパスはアニメ声によるテキストの読み上げと、対応するラベルがつけられたデータセットです。

✨つくよみちゃんコーパス公開！✨

■Vol.1 声優統計コーパス（JVSコーパス準拠）
⇒https://t.co/tfqAFxQEds

高音ウィスパー系の14歳前後のアニメキャラクター風ボイスを目指して作りました。

一部の言葉にふりがなやアクセント記号を追加した台本も同梱しています。（詳しい説明もあります） pic.twitter.com/VtJ6ji2Qu3

— つくよみちゃん®【フリー素材キャラクター】 (@TYC_Project) February 26, 2021

JVS corpusとつくよみちゃんコーパスから成る合計101人の発話音声と、対応するテキスト(セリフ)をデータセットとします。
今回使用するモデルは発話内容を音素の形式で利用するため、データセットに付属しているテキストを音素に変換する必要があります。 これにはpyopenjtalkを用いました。これによって日本語文章を合計40種類の音素からなる音素列へと分解します。

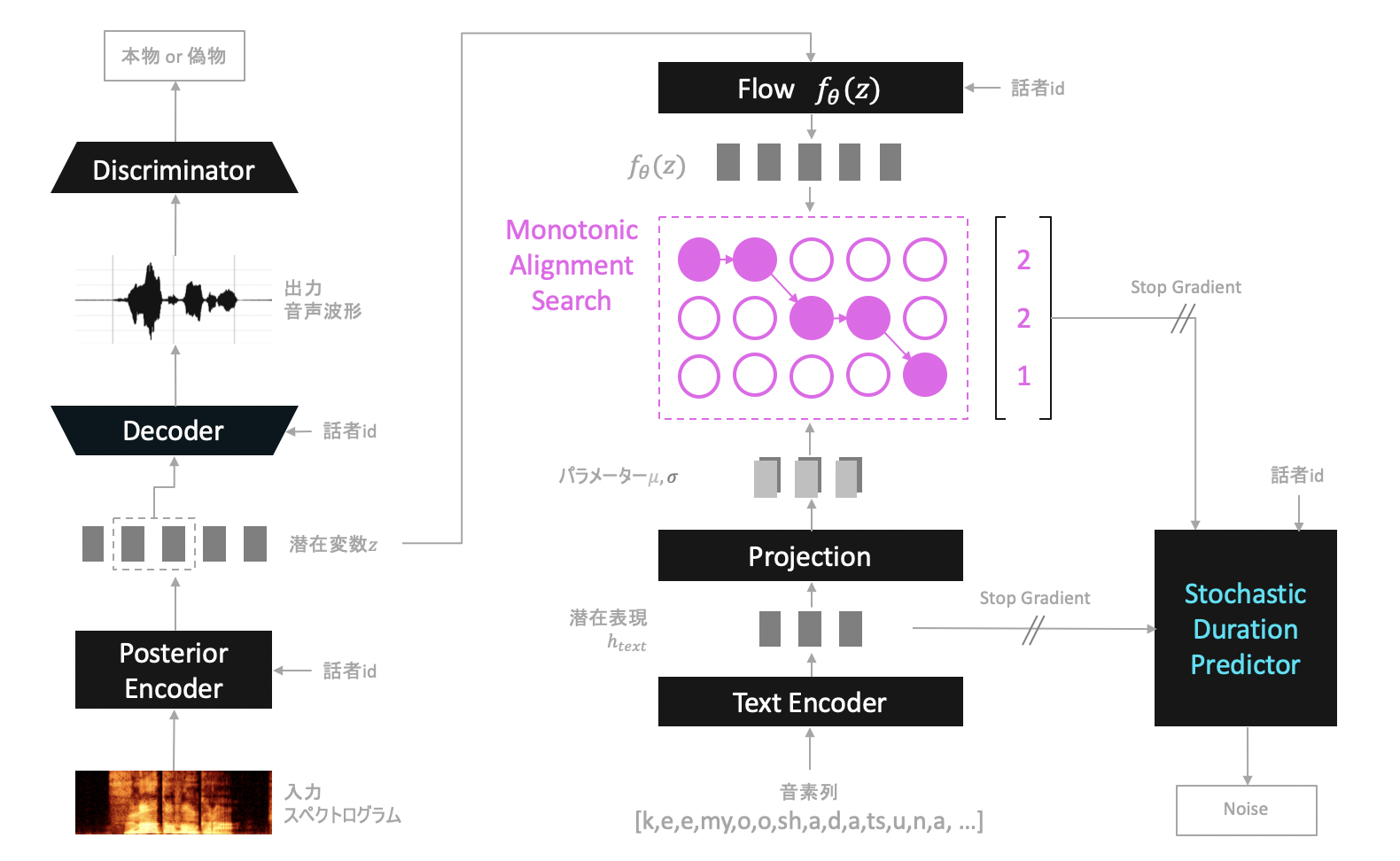
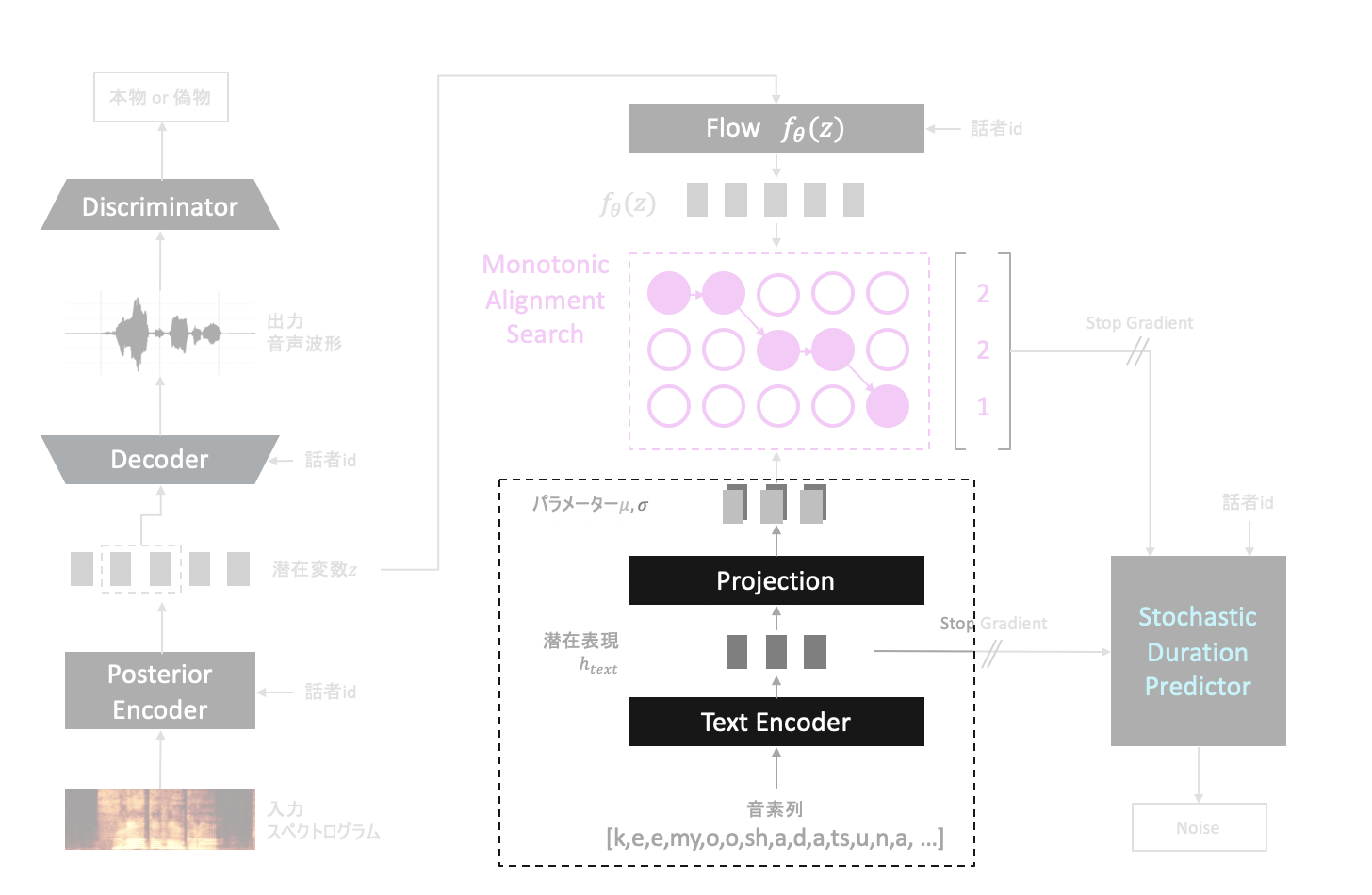
VITS

今回は音声変換にはVITSというモデルを用いました。VITSは

• テキストから音声の生成(読み上げ、Text-to-Speechなどとも呼ばれる)
• 音声の声質の変換

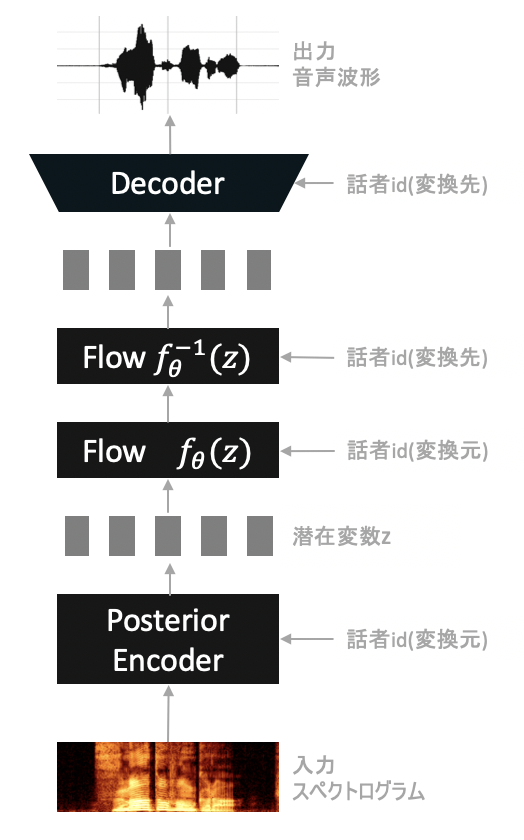
の2つが行えるモデルであり、学習時は以下のような構成を取ります(推論時については後述します)。

以下ではVITSを構成する各ネットワークについて順番に解説します。

Variational Autoencoder(VAE)

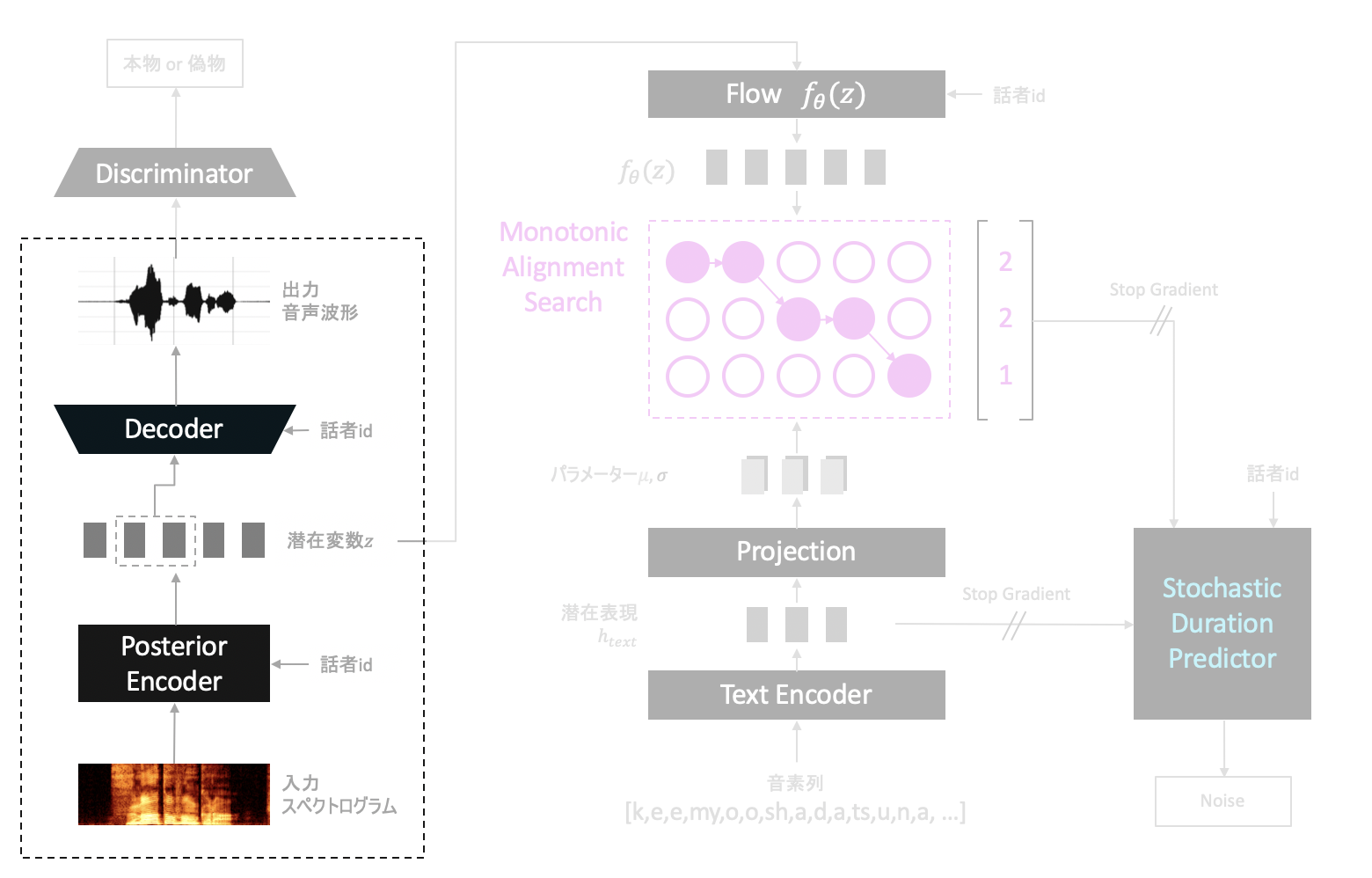
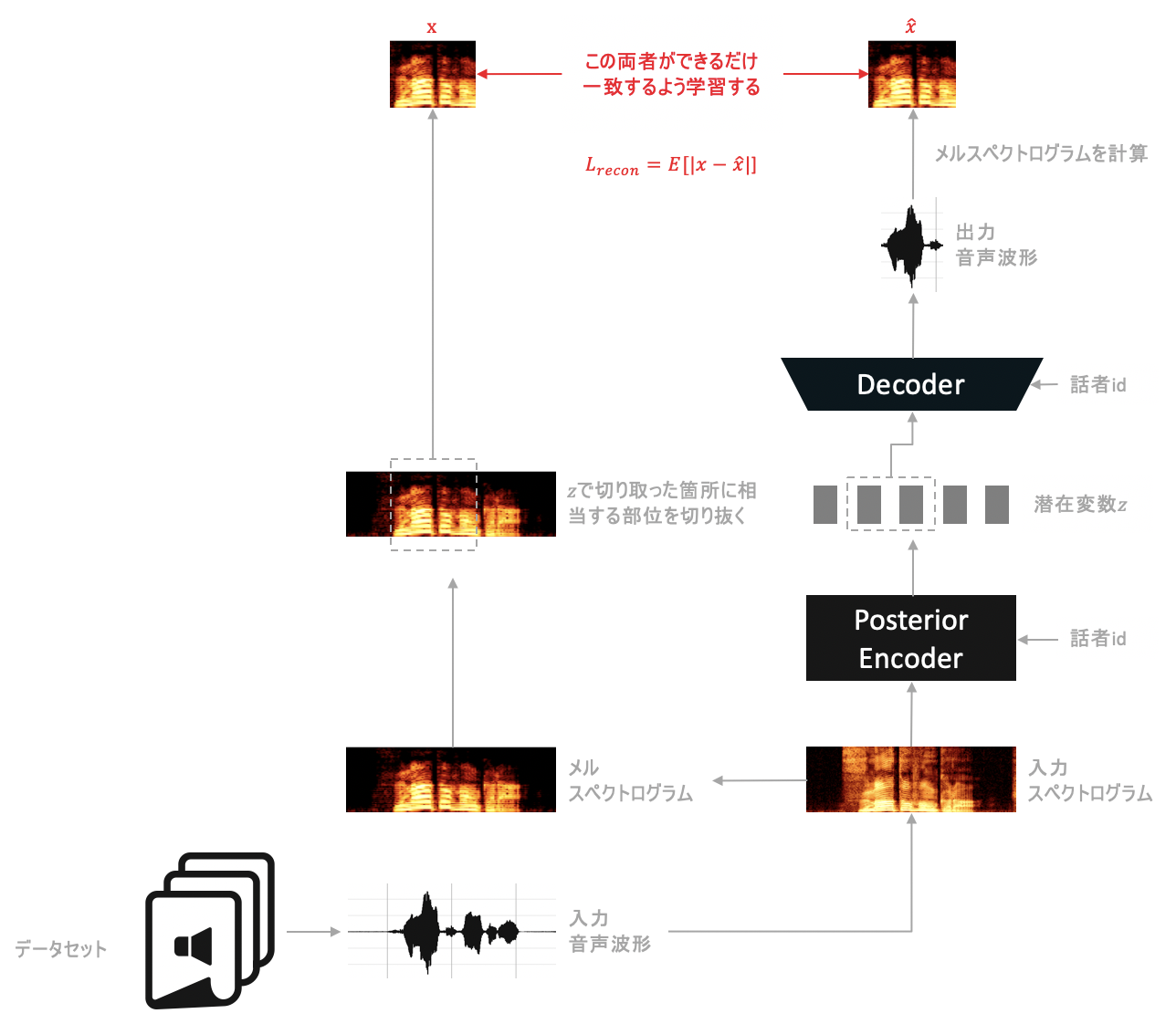
Posterior EncoderとDecoderからなる構造はVariational Autoencoder(VAE)と呼ばれるモデルをベースにしています。

Posterior Encoderは入力音声のスペクトログラムを入力にとり、入力音声を入力音声たらしめている特徴を抽出、潜在変数$z$として出力するためのネットワークです。
一方Decoderは抽出された特徴$z$を入力にとり、音声を波形という形で復元できるよう学習します。
「入力スペクトログラム→$z$→音声波形」と変換したとき、うまく元の音声を復元できるように目指し学習を進めます。

また、学習時はメモリ節約のため、Decoderへの入力は$z$全体ではなく、$z$から数サンプル分ランダムな箇所から切り取ったものとします。(推論時は$z$全体を入力とします。)
$z$で切り取った箇所に相当する部位の情報を復元できるようになるのを目標に学習を行います。

スペクトログラムの横軸は時刻、縦軸は周波数です。一方メルスペクトログラムはこれに少しアレンジを加えたような方式で、縦軸が対数スケールのようになっており、低い周波数の情報ほど詳細に図示することができます。メルスペクトログラムは、人間の聴覚は周波数の低い音に対して敏感で、周波数の高い音に対して鈍感であるという性質から考案された方式であり、これを入力と出力で一致させるよう目指すことでより自然な音声の生成が可能となるようです。

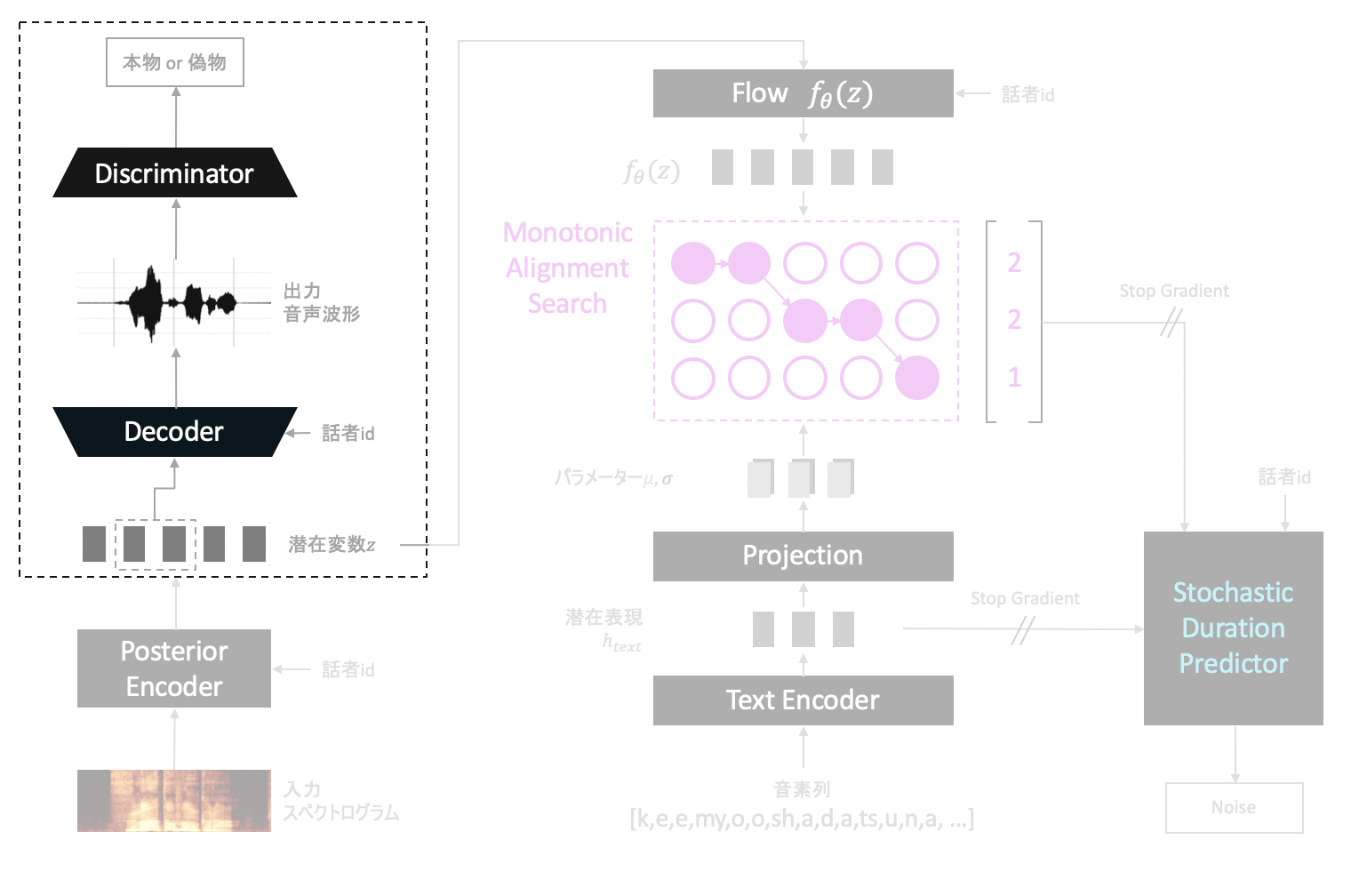
Generative adversarial networks(GAN)

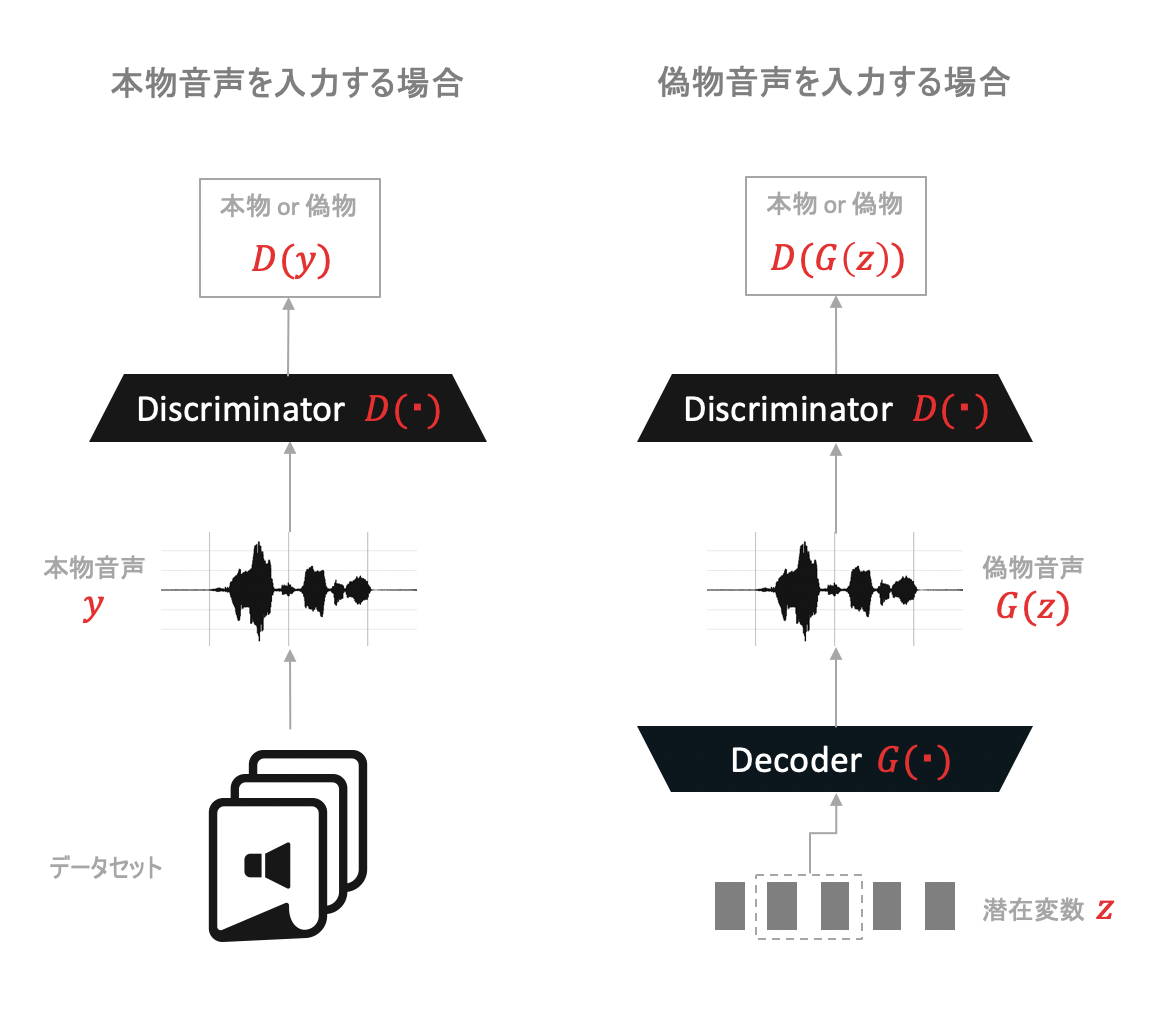
DiscriminatorとDecoderからなる構造はGenerative adversarial networks(GAN)という仕組みがベースとなっています。これは2つのネットワークを競わせるようにして学習する方式であり、VITSにおいては以下のようにして利用します。

Discriminatorはデータセット中の音声波形(本物音声と呼ぶことにします)と、上で述べたDecoderによって出力された音声波形(偽物音声と呼ぶことにします)の2種類を入力にとり、それらが本物か偽物かを正しく識別できるように目指し学習を進めます。
一方でDecoderは生成した音声によって、Discriminatorを本物音声だと騙せるよう目指し学習を進めます。

DiscriminatorとDecoderが互いに鍛え合うようにして学習を進めることで、Decoderはより本物音声に近い音声を生成できるようになっていきます。

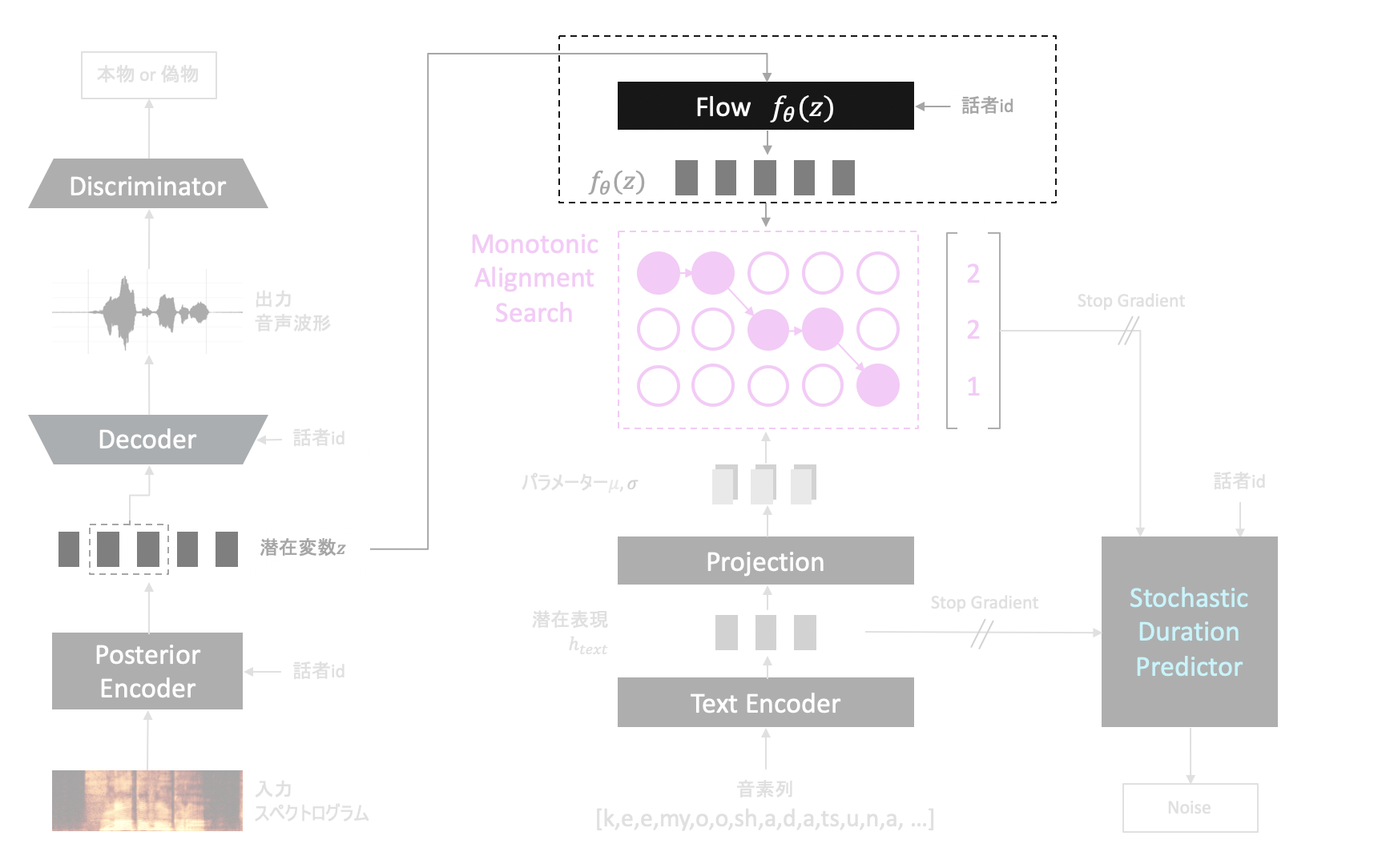
Flow

Flowとは、入力と出力が可逆という特徴を持つ種類のネットワークです。

VITSで用いられているFlowは、学習時は$z$と話者idの情報を入力にとり、$z$から話者の情報をできるだけ取り除き、発音に関する情報$z_p$を抽出する役割を果たします。

Flowなので逆を行うこともできます。$z_p$に対し別の話者の情報を付加し$z$を生成することもできます。

以降では順方向のFlowを$f_{\theta}(\cdot)$とし、逆方向のFlowを$f_{\theta}^{-1}(\cdot)$と表記します。

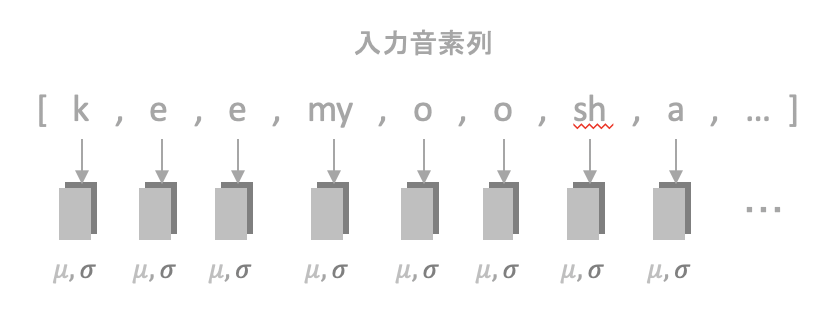
Text Encoder

Text Encoderは入力音素列に対し、Transformerのような形状のネットワークを用いてそれらを潜在表現$h_{text}$へと変換する役割をします。
Projectionでは畳み込みを用いて、$h_{text}$からパラメーター$\mu$と$\sigma$を生成します。各音素に対し、対応する$\mu$と$\sigma$が生成されるようなイメージです。
VITSではこれらのパラメーターを用い後述する処理を行うことで、音声と音素の関連付けを行います。

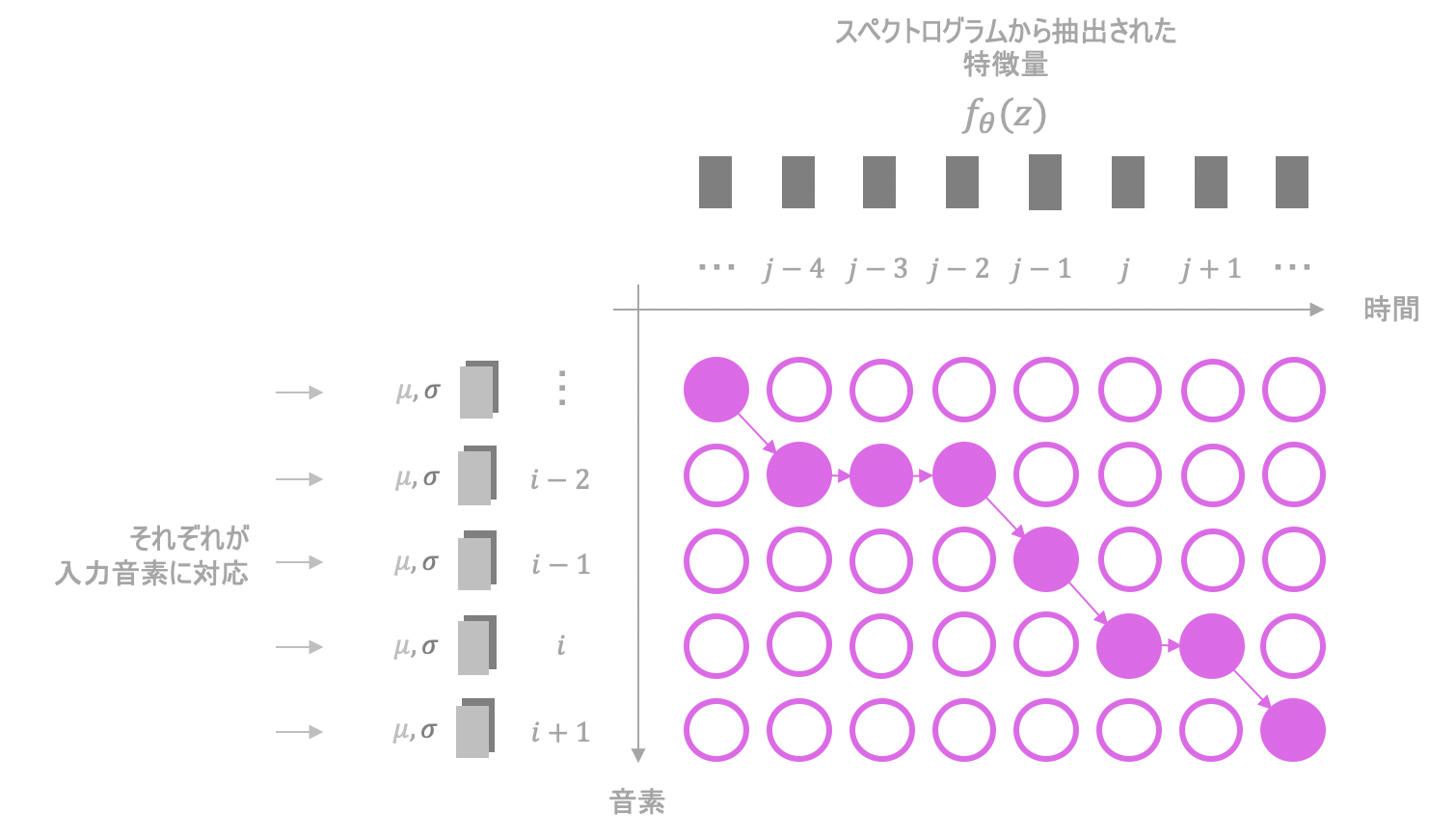
Monotonic Alignment Search(MAS)

Monotonic Alignment Search(MAS)では音声の情報と音素の情報の関連付けを行います。

Monotonic Alignment

Monotonic Alignmentとは

• 戻らない
• 飛ばさない
• 最後まで到達する

を満たすpathです。

MASではMonotonic Alignmentを求めることによって音声の情報と音素の情報の関連付けを行います。

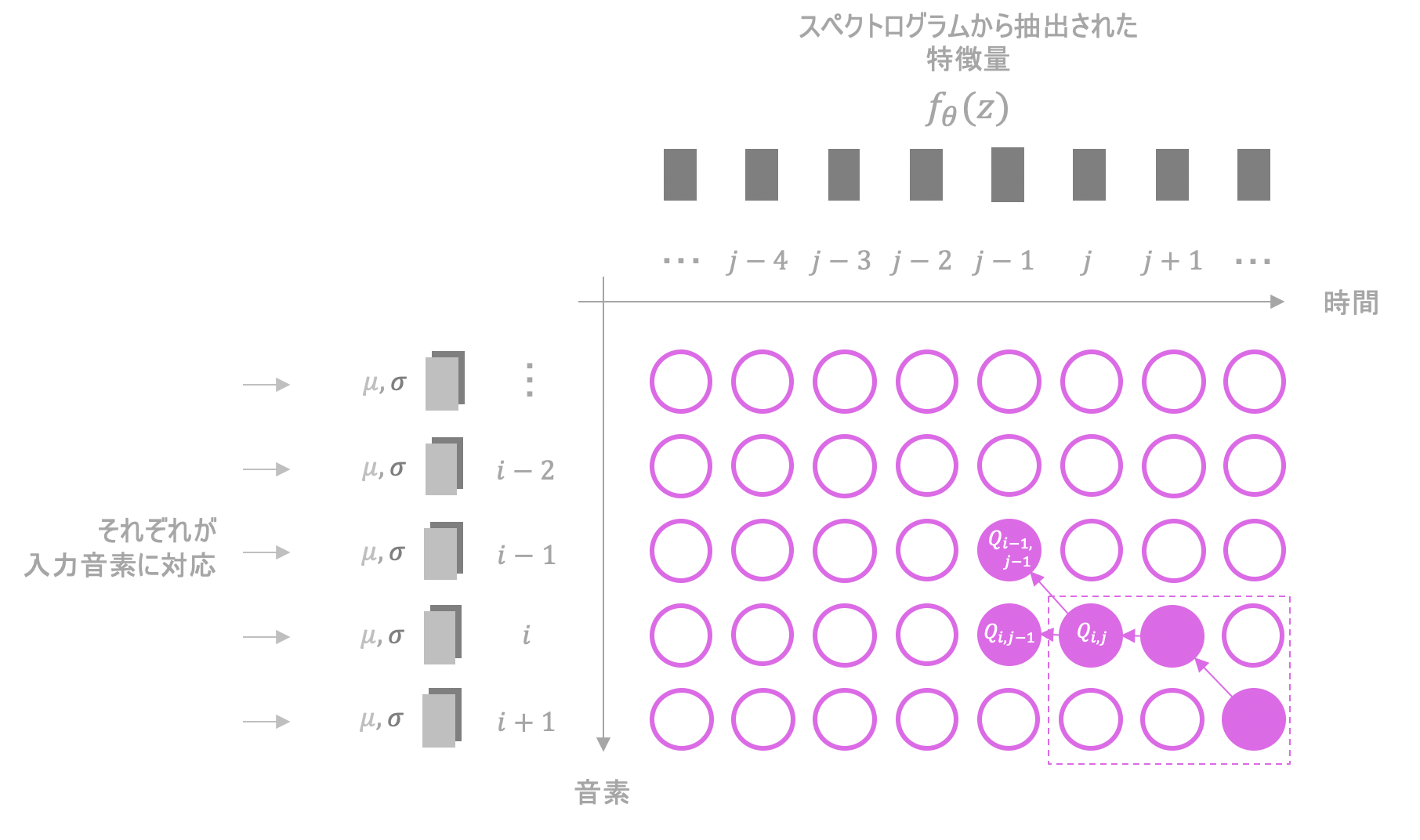
例えば、上の図ではMonotonic Alignmentによって、入力の(i-2)番目の音素が、音声の情報のうち時刻=(j-4),(j-3),(j-2)の要素と関連付けられています。
入力音声のうち、どの時刻からどの程度の間、何を発音しているかを関係付けているようなイメージです。

各ノードの尤度

MASではpathを、対数尤度の累積和が最大となるようにDP(動的計画法)で求めます。

$i$行目$j$列目のノードの対数尤度$L_{i,j}$は次のようにして求めることができます。

$$L_{i,j} = log\{N(f_{\theta}(z)[j]; \mu[i],\sigma[i])\}$$

ただし$N$は正規分布、$f_{\theta}(z)[j]$は$f_{\theta}(z)$の$j$番目の値、$\mu[i],\sigma[i]$はそれぞれ$i$番目の音素に対応する$\mu,\sigma$です。

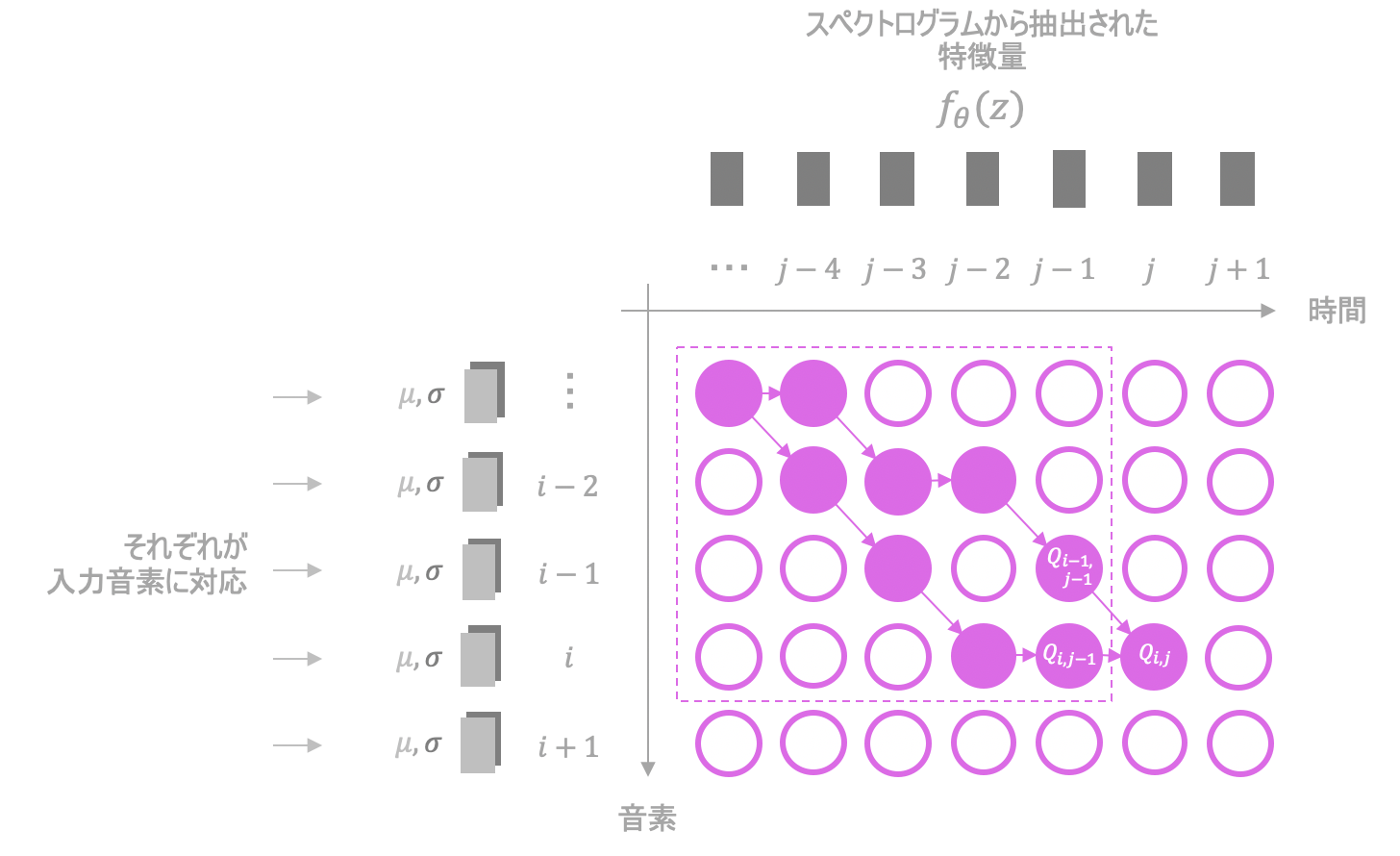
DPの実行

対数尤度の累積和が最大となるようにpathを求めます。

$Q_{i,j}=\max ( Q_{i-1,j-1}, Q_{i,j-1} ) + L_{i,j} $を繰り返し実行し、尤度の累積和の最大値を求めます。$(i,j)$にたどり着くような無数のpathがそれぞれ持つ累積和の中から、最も大きいものが$Q_{i,j}$に順次格納されていくイメージです。

これで対数尤度の累積和の最大値は求まりますが、まだpathそのものは求めることができていません。そこで、来たであろう道を逆向きに辿って求めます。

座標$(i,j)$から$(i-1,j-1)$もしくは$(i,j-1)$どちらに進むか考えているとします。この時両者のうち求めた累積和の大きい方を選び、その座標へと移動します。例えば、$Q_{i-1,j-1}$と$Q_{i,j-1}$のうち、後者の方が大きいならば$(i,j-1)$へと移動します。
これを繰り返し、通った箇所を記録していくことでpathを求めることができます。

Stochastic Duration Predictor

Stochastic Duration PredictorはText-to-Speechの推論時、各音素がどの程度間発音されているかを予測するためのネットワークです。

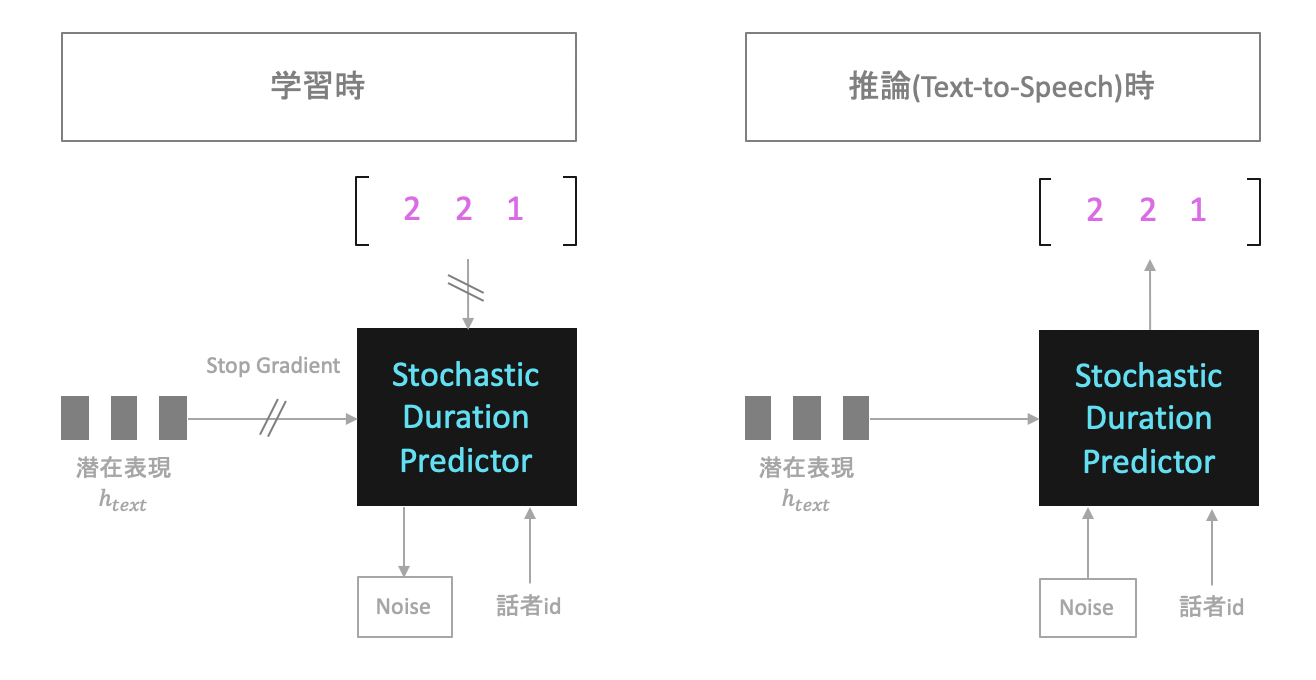
学習時

学習時は上の画像のように、以下の情報3つを入力にとり、それらの分布を変形して正規分布へと落とし込むことを目標とします。

• 話者id
• $h_{text}$
• Duration

Durationは各音素がどの程度の時間発音されたかを表す数値で、MASで求めたpathから計算します。
例えば、下の図であれば(i-2)番目の音素に対応するDurationは3です。i番目の音素に対応するDurationは2です。

推論時

推論時は、入力された音素の情報$c$(図では$h_{text}$に相当)とNoiseを用いて、Duration(その音素がどの程度の間発音されていたか)$d$を推定することを目的とします。

アーキテクチャ

ここで、各音素に対しDurationを推定するのには、以下の理由から一工夫必要になります。

1. Durationが離散整数値であるために、そのままではFlowでの連続最適化が難しい
2. また、1次元であるために、高次元の分布へと落とし込むのが難しい

1.と2.をそれぞれ以下の手法で解決します。

• variational dequantization
  入力する離散整数値に、乱数$u\in{[0,1)}$を加算して連続値へと変える手法

• variational data augmentation
  入力データと、追加で生成したデータ$v$をセットにして処理することでデータの次元を増やす手法

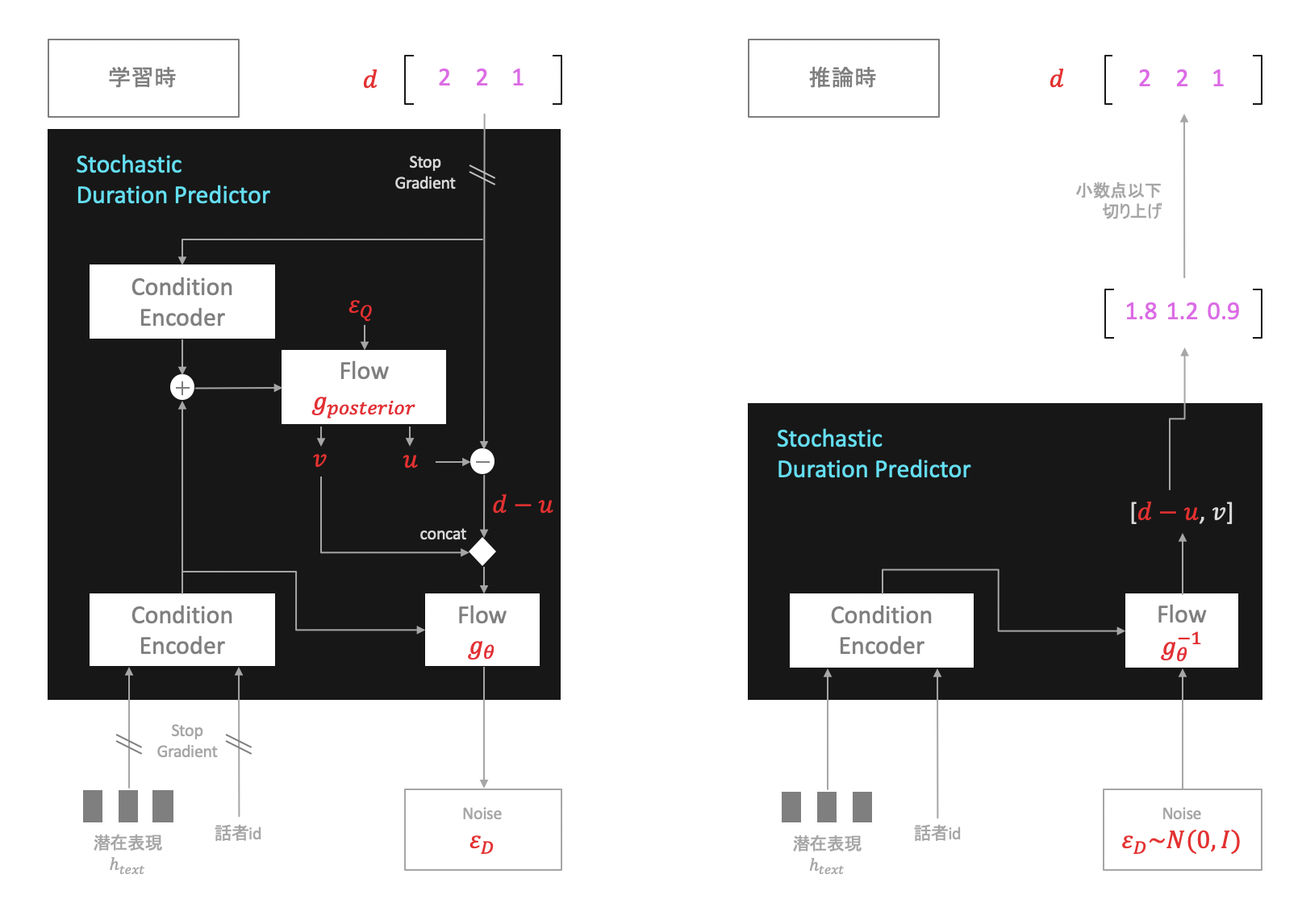
これらを踏まえた上で、Stochastic Duration Predictorは以下のようなアーキテクチャとなります。

• 学習時
  Stochastic Duration Predictorは構成要素として2種類のFlow(図の$g_{posterior}$と$g_{\theta}$)を含んでいますが、このうち$g_{posterior}$は学習時にのみ用います。
  $g_{posterior}$は正規分布からサンプリングされた乱数$\epsilon_{Q}$を入力にとり、それを用いて$v$と$u$を生成します。次に$d-v$を計算、$u$とセットで$g_{\theta}$へ入力します。$g_{\theta}$の出力$\epsilon_{D}$が正規分布$N(0,I)$にできるだけ従うよう学習します。

• 推論時
  正規分布$N(0,I)$から乱数$\epsilon_{D}$をサンプリング、$g_{\theta}^{-1}$への入力とし$d-v$と$u$を出力させます。さらに、連続値$d-v$の小数点以下を切り上げることによって離散値$d$へと変換します。
  このようにして各音素の潜在表現(図の$h_{text}$)に対しそれぞれのDurationを推定します。$\epsilon_{D}$を用いてDurationに確率的な変動を持たせることでより高品質な音声を合成できるようです。

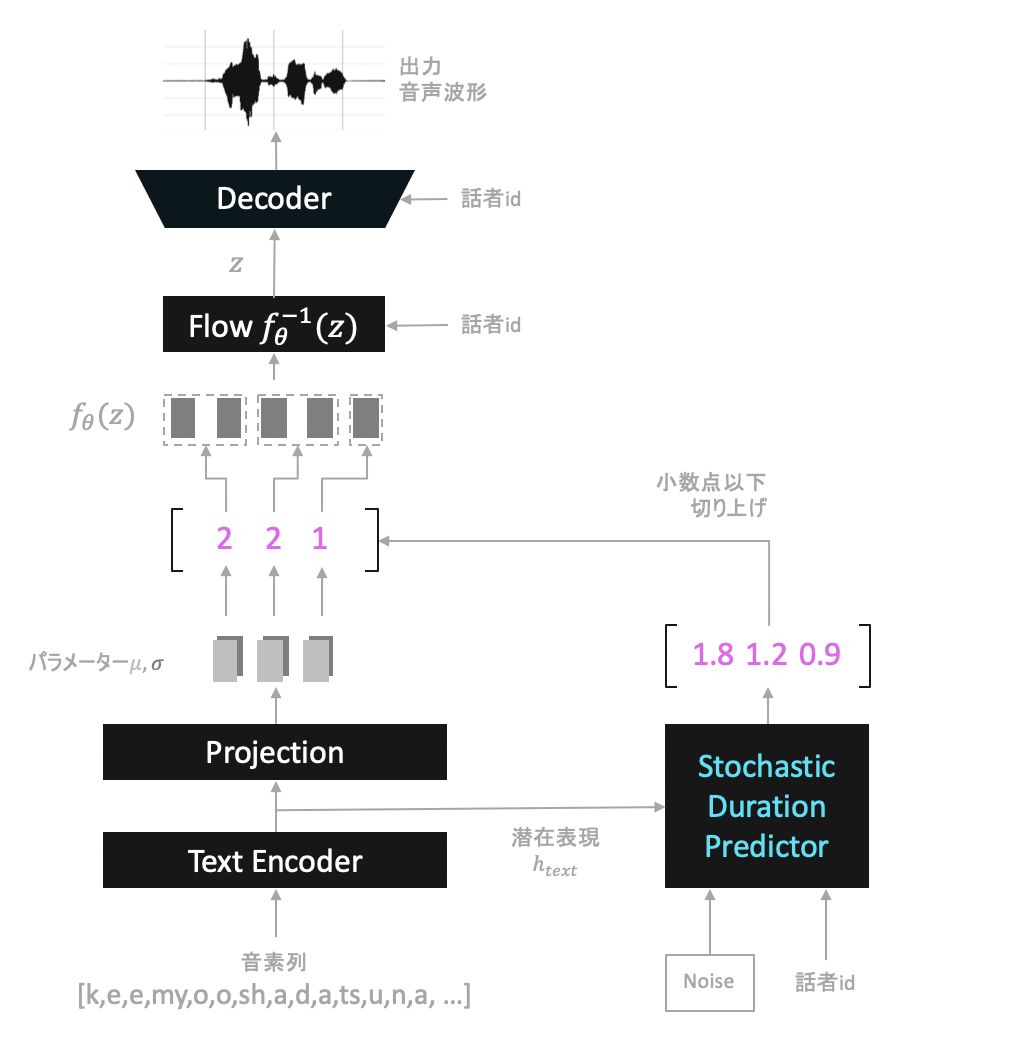
推論時(テキスト読み上げ)

学習時と推論時でVITSは違ったネットワーク構成をとります。
テキストから音声の生成時は次のようになります。

入力された各音素をそれぞれ潜在表現に変換し、それらに対しDuration(整数値)を求め音声の合成を行います。

推論時(音声変換)

音声変換時は次のような構成をとります。

学習時と違い、音声変換の推論においてはテキストの情報は一切必要としません。そのためStochastic Duration Predictorが不要となります。

損失関数

VITSでは以下の、大きく分けて3種類の損失関数を用います。

1. VAEによるloss
   • Reconstruction loss
     $$L_{rec} = E [ |x_{mel}-\hat{x}_{mel}| ]$$
   • KL divergence loss
     $$L_{kl} = E [ \log { \sigma_{te}(x) } - \log { \sigma_{pe}(x) } - \frac{1}{2} + \frac{(f_{\theta}(z) - \mu_{te}(x))^{2}}{2(\sigma_{te}(x))^{2}} ]$$
2. GANによるloss
   • Adversarial loss
     $$L_{adv}(D) = E[ (D(y)-1)^2 + (D(G(z)))^2 ]$$
     $$L_{adv}(G) = E[ (D(G(z))-1)^2 ]$$
   • Feature matching loss
     $$L_{fm} = E[ \sum_{l=1}^{T} \frac{1}{N_{l}} |D^{l}(y) - D^{l}(G(z))|_1 ]$$
3. Duration loss

\begin{align}

L_{dur} = E_{q_{\phi}(u,v|d,c)}[&\frac{1}{2}(\log (2\pi) + \epsilon_{D}^{2} )\\ -& \frac{1}{2}(\log (2\pi) + \epsilon_{Q}^{2} )\\ -& \log \left\vert \frac{\partial g_{\theta}}{\partial (d-u,v)}  \right\vert\\ -& \log \left\vert \frac{\partial g_{posterior}}{\partial \epsilon_{Q}}  \right\vert] \\

\end{align}

(ただし$E$はバッチ内で平均をとる操作に相当します。)

これらの損失関数について順番に解説していきます。

VAEによるloss

$x$を生成したい音声とします。この時音声の分布$p(x)$が分かれば$x$を生成することができます。

学習時に、モデルを動かした時に音声$x$が出力されたとします。このとき尤度は$p(x)$となります。VITS(VAE)ではこれの対数尤度$\log p(x)$を最大化するよう目指すことで、モデルが音声の生成を学習します。

対数尤度の計算

具体的にどのようにすれば対数尤度$\log p(x)$を求め、実装に落とし込めるか考えます。

まず潜在変数$z$を導入します。音声を音声たらしめている特徴が格納された変数のようなイメージです。
$z$は、データセットの音声$x$を入力にとり、特徴を抜き出し$z$を出力してくれる都合の良いモデルがあれば求まりそうな気がします。これは先ほど説明したPosterior Encoderに相当するモデルで、$q(z|x)$とおきます。この時対数尤度$\log p(x)$は次のように変形できます。

\begin{align}

\log p(x) &= \log \{ p(x)\} \int q(z|x) dz \\
&= \int q(z|x) \log \{ p(x) \} dz \\
&= \int q(z|x) \log \{ p(x)\frac{p(z|x)}{p(z|x)} \} dz \\
&= \int q(z|x) \log \{ \frac{p(x,z)}{p(z|x)} \} dz \\
&= \int q(z|x) \log \{ \frac{p(x,z)}{p(z|x)} \frac{q(z|x)}{q(z|x)} \} dz \\
&= \int q(z|x) \log \{ \frac{q(z|x)}{p(z|x)} \frac{p(x,z)}{q(z|x)} \} dz \\
&= \int q(z|x) \{ \log \{ \frac{q(z|x)}{p(z|x)} \} + \log \{ \frac{p(x,z)}{q(z|x)} \} \} dz \\
&= \int q(z|x) \log \{ \frac{q(z|x)}{p(z|x)} \} + \int q(z|x) \log \{ \frac{p(x,z)}{q(z|x)} \} dz \\

\end{align}

このうち、第1項は$q(z|x)$と$p(z|x)$の間のKLダイバージェンスの形となっています。KLダイバージェンスとは2つの分布がどれだけ似ているかを表す指標で、同じ分布間では0となる、常に0を含む正の値となるといった性質を持ちます。

第2項は**Evidence Lower Bound(ELBO)**と呼ばれる値で、次のように定義します。
$$\mathcal{L} = \int q(z|x) \log { \frac{p(x,z)}{q(z|x)} } dz$$

第1項は事後分布を含むため計算が困難です。しかしKLダイバージェンスは常に0を含む正の値となるという性質を持ちます。そのため対数尤度は第2項のELBOで下から抑えることができます。

$$\log p(x)\geq\mathcal{L}$$

VAEではこのELBOを最大化するよう学習します。
実装上の都合のため、以降ではELBOの最大化を$-\mathcal{L}$の最小化と言い換えて話を進めます。

ELBOは次のように変形できます。

\begin{align}

-\mathcal{L} &= -\int q(z|x) \log \{ \frac{p(x,z)}{q(z|x)} \} dz \\
&= -\int q(z|x) \log \{ \frac{p(x|z)p(z)}{q(z|x)} \} dz \\
&= - \int q(z|x) \log \{ p(x|z) \} dz + \int q(z|x) \log \{ \frac{q(z|x)}{p(z)} \} dz \\

\end{align}

ここで、VITSでは上の式の事前分布$p(z)$の箇所を$p(z|c)$に置き換え、$z$の事前分布を音素列$c$に関連付けます。

\begin{align}

-\mathcal{L} 
&= - \int q(z|x) \log \{ p(x|z) \} dz + \int q(z|x) \log \{ \frac{q(z|x)}{p(z|c)} \} dz \\

\end{align}

このうち第1項がReconstruction loss、第2項がKL divergence lossです。以後それぞれ$L_{recon}$, $L_{kl}$と置くことにします。

Reconstruction loss

ELBOの第1項である、

L_{recon} = - \int q(z|x) \log \{ p(x|z) \} dz

はReconstruction lossと呼ばれています。$L_{recon}$を最小化するよう学習することで、Encoder→Decoderを経た時に音声を正しく復元できるよう目指します。

VITSでは、潜在変数$z$が与えられている時の、音声$x$の分布がラプラス分布に従うと仮定します。すなわち

p(x|z) = A\exp(-|x - \hat{x}|)

とします。ただし$x$は入力音声、$\hat{x}$はDecoderから出力される音声、$A$は定数です。
これを用いて$L_{recon}$は以下のように変形できます。

\begin{align}

L_{recon} &= - \int q(z|x) \log \{ p(x|z) \} dz \\
&= -E_{q(z|x)} [ \log \{ p(x|z) \} ] \\
&= -E_{q(z|x)} [ \log \{ A\exp(-|x - \hat{x}|) \} ] \\
&= E_{q(z|x)} [|x - \hat{x}|] + A \\

\end{align}

$E_{q(z|x)}$はバッチごとに平均をとる操作に相当します。また、定数$A$は学習時、勾配に影響を及ぼさないので無視できます。

以上で求めたReconstruction lossを以下の図のようにして実装に落とし込みます。

$L_{recon}$を最小化するよう学習することで、Posterior Encoder→Decoderの過程で音声を正しく復元できるよう目指し学習します。

KL divergence loss

ELBOの第2項である、

L_{kl} = \int q(z|x) \log \{ \frac{q(z|x)}{p(z|c)} \} dz

はKLダイバージェンスの形をしているためKL divergence lossと呼ばれています。学習によってこれの最小化を目指します。
音声$x$を入力にとり潜在変数$z$を出力するモデル(Posterior Encoder)に相当する$q(z|x)$を、音素列$c$が与えられた上での$z$の分布$p(z|c)$にできるだけ近くなるようにし、音声と音素を関連付けているようなイメージです。

$L_{kl}$は以下のように変形できます。

\begin{align}

L_{kl} &= \int q(z|x) \log \{ \frac{q(z|x)}{p(z|c)} \} dz \\
&= \int q(z|x) \{ \log \{ q(z|x) \} - \log \{p(z|c) \} \} dz \\
&= \int q(z|x) \{ \log \{ q(z|x) \} \} dz - \int q(z|x) \{ \log \{p(z|c) \} \} dz \\
&= E_{q(z|x)} [ \log \{ q(z|x) \} ] - E_{q(z|x)} [ \log \{p(z|c) \} ] \\

\end{align}

KL divergence loss 第1項

まず第1項

E_{q(z|x)} [ \log \{ q(z|x) \} ]

について考えます。

$q(z|x)$はPosterior Encoderのことです。音声$x$を入力にとり、潜在変数$z$を出力します。

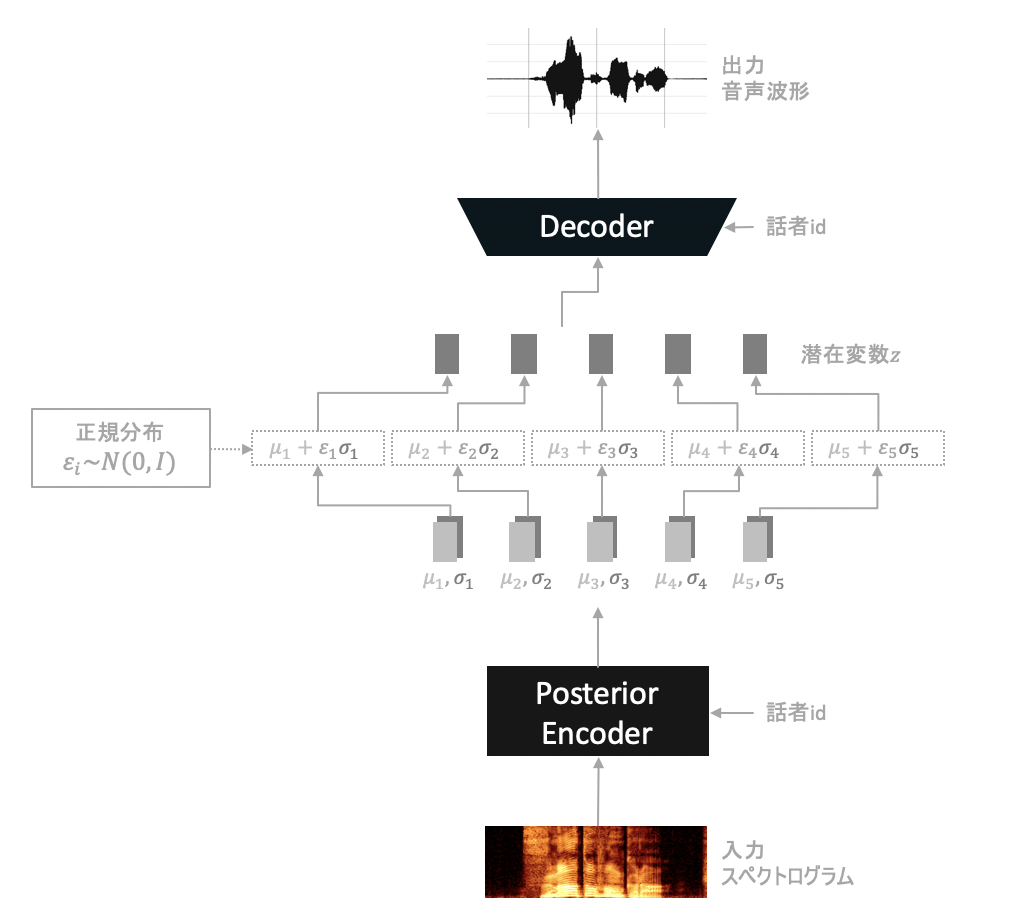
ここで、潜在変数$z$の各要素$z_{i}$は実装では以下のようにして確率的に生成します。

1. 各$\epsilon_{i}$をそれぞれ正規分布$N(0, I)$からサンプリング
2. 入力音声$x$をPosterior Encoderに入力し、パラメーター$\mu_{i}$と$\sigma_{i}$を得る
3. $z_{i} = \epsilon\sigma_{i} + \mu_{i}$を計算

言い換えると$z$の各要素は平均$\mu_{i}$、分散$\sigma_{i}$の正規分布からサンプリングされた値だと考えることができます。
したがって、$x$を入力とし以上の手順を経て生成された平均値を$\mu_{pe}(x)$、分散を$\mu_{pe}(x)$と表記することで次のように表すことができます。

z \sim q(z|x) = N(z;\mu_{pe}(x),\sigma_{pe}(x))

ただし$N(z;\mu_{pe}(x),\sigma_{pe}(x))$は平均$\mu_{pe}(x)$、分散$\sigma_{pe}(x)$の正規分布とします。$z \sim q(z|x)$は$z$を確率分布$q(z|x)$からサンプリングする操作です。

これよりKL divergence lossの第1項は定数Aを用いて

\begin{align}

E_{q(z|x)} [ \log \{ q(z|x) \} ] &= E_{q(z|x)} [ \log \{ N(z;\mu_{pe}(x),\sigma_{pe}(x)) \} ] \\
&= E_{q(z|x)} [ \log \{ A(\sigma_{pe}(x))^{-1} exp \{ - \frac{(z - \mu_{pe}(x))^{2}}{2(\sigma_{pe}(x))^{2}} \} \} ] \\
&= E_{q(z|x)} [ \log \{ A \} + \log \{ (\sigma_{pe}(x))^{-1} \} + \log \{ exp \{ - \frac{(z - \mu_{pe}(x))^{2}}{2(\sigma_{pe}(x))^{2}} \} \} ] \\
&= A - E_{q(z|x)} [ \log \{ \sigma_{pe}(x) \} ] + E_{q(z|x)} [ - \frac{(z - \mu_{pe}(x))^{2}}{2(\sigma_{pe}(x))^{2}} ] \\
&= A - E_{q(z|x)} [ \log \{ \sigma_{pe}(x) \} ] - E_{q(z|x)} [ \frac{z^2 - 2z\mu_{pe}(x) + (\mu_{pe}(x))^{2}}{2(\sigma_{pe}(x))^{2}} ] \\
&= A - E_{q(z|x)} [ \log \{ \sigma_{pe}(x) \} ] - \frac{ E_{q(z|x)} [z^2] - 2E_{q(z|x)} [z] \mu_{pe}(x) + (\mu_{pe}(x))^{2}}{2(\sigma_{pe}(x))^{2}} \\
&= A - E_{q(z|x)} [ \log \{ \sigma_{pe}(x) \} ] - \frac{ ((\sigma_{pe}(x))^{2} + \mu_{pe}(x))^{2}) - 2 (\mu_{pe}(x))^{2} + (\mu_{pe}(x))^{2}}{2(\sigma_{pe}(x))^{2}} \\
&= A - E_{q(z|x)} [ \log \{ \sigma_{pe}(x) \} ] - \frac{1}{2} \\

\end{align}

となります。

KL divergence loss 第2項

次に第2項

E_{q(z|x)} [ \log \{p(z|c) \} ]

について考えます。

$p(z|c)$は音素$c$が与えられた上での、潜在変数$z$の分布です。VITSでは$z$が正規分布$N=(z;\mu_{te}(x)$,$\sigma_{te}(x))$に従うと仮定して学習します。(ただし$\mu_{te}(x)$と$\sigma_{te}(x)$は音素列の情報を基に、Projectionから出力されるパラメーターとする)

p(z|c) = N(z;\mu_{te}(x),\sigma_{te}(x))

また、一度$z$をFlow$f_{\theta}$に入力して$f_{\theta}(z)$を得て、これを用いて最適化を行うことでより自然な音声の生成が可能となるようです。

p(z|c) = N(f_{\theta}(z);\mu_{te}(x),\sigma_{te}(x)) \left\vert  \frac{\partial f_{\theta}(z)}{\partial z} \right\vert

ここで、Flow$f_{\theta}$は体積保存な変換に制限します。これにより確率変数の変数変換に必要な、ヤコビアンを次のように固定できます。

\left\vert \frac{\partial f_{\theta}(z)}{\partial z} \right\vert = 1

以上を用いてKL divergence lossの第2項は定数Aを用いて次のように変形できます。

\begin{align}

E_{q(z|x)} [ \log \{p(z|c) \} ] &= E_{q(z|x)} [ \log \{N(f_{\theta}(z);\mu_{te}(x),\sigma_{te}(x)) \left\vert \frac{\partial f_{\theta}(z)}{\partial z} \right\vert \} ] \\
&= E_{q(z|x)} [ \log \{ A(\sigma_{te}(x))^{-1} exp \{ - \frac{(f_{\theta}(z) - \mu_{te}(x))^{2}}{2(\sigma_{te}(x))^{2}} \} \} ] \\
&= E_{q(z|x)} [ \log \{ A\} + \log \{ (\sigma_{te}(x))^{-1} \} + \log \{ exp \{ - \frac{(f_{\theta}(z) - \mu_{te}(x))^{2}}{2(\sigma_{te}(x))^{2}} \} \} ] \\
&= A + E_{q(z|x)} [ - \log \{ \sigma_{te}(x) \} - \frac{(f_{\theta}(z) - \mu_{te}(x))^{2}}{2(\sigma_{te}(x))^{2}} ] \\

\end{align}

KL divergence lossの全体像

以上よりKL divergence lossである$L_{kl}$は以下のように求められます。

\begin{align}

L_{kl} &= E_{q(z|x)} [ \log \{ q(z|x) \} ] - E_{q(z|x)} [ \log \{p(z|c) \} ] \\
&= (- E_{q(z|x)} [ \log \{ \sigma_{pe}(x) \} ] - \frac{1}{2}) - (E_{q(z|x)} [ - \log \{ \sigma_{te}(x) \} - \frac{(f_{\theta}(z) - \mu_{te}(x))^{2}}{2(\sigma_{te}(x))^{2}} ]) \\
&= E_{q(z|x)} [ \log \{ \sigma_{te}(x) \} - \log \{ \sigma_{pe}(x) \} - \frac{1}{2} + \frac{(f_{\theta}(z) - \mu_{te}(x))^{2}}{2(\sigma_{te}(x))^{2}} ]

\end{align}

(KL divergence lossの$\frac{1}{2}$は定数として無視してしまっても良さそうに思えましたが、公式実装ではlossにこの項が含まれていたため、それに倣ってこのような記述としています。)

GANによるloss

Adversarial loss

Adversarial lossは下のように定義される、DecoderとDiscriminatorが互いに鍛え合うために必要なlossです。

L_{adv}(D) = E[(D(y)-1)^2 + (D(G(z)))^2] \\
L_{adv}(G) = E[(D(G(z))-1)^2]

Discriminatorは$L_{adv}(D)$を最小化するよう目指すことで、本物らしい音声ほど1に近い値を出力し、Decoderによって生成された偽物の音声らしいほど0に近い値を出力できるよう学習します。Decoderに騙されないよう精度をあげるよう学習を進めます。

一方でDecoderは$L_{adv}(G)$を最小化するよう目指し、生成した音声でDiscriminatorを本物だと騙せるよう学習します。

Feature matching loss

Feature matching lossは、本物音声と偽物音声をそれぞれDiscriminatorへ入力とした場合における、中間層の出力の統計量を、両者の分布間で近づけるための損失関数です。
この損失関数の最小化を目標にすることによって学習の安定化を図り、生成音声の質の向上を狙います。

$$L_{fm} = E[ \sum_{l=1}^{T} \frac{1}{N_{l}} |D^{l}(y) - D^{l}(G(z))|_1 ]$$

ただし$T$はDiscriminatorを構成する層の数とします。

Decoderは、生成した偽物音声をDiscriminatorに入力した場合における中間層の出力を、本物音声を入力した場合のものに近づくよう学習します。

自分的な解釈ですが、恐らくDecoderがDiscriminatorの全体としての出力だけでなく、中間層1つ1つをも欺くことができるようにしているイメージだと思われます。

Duration loss

\begin{align}

L_{dur} = E_{q_{\phi}(u,v|d,c)}[&\frac{1}{2}(\log (2\pi) + \epsilon_{D}^{2} )\\ -& \frac{1}{2}(\log (2\pi) + \epsilon_{Q}^{2} )\\ -& \log \left\vert \frac{\partial g_{\theta}}{\partial (d-u,v)}  \right\vert\\ -& \log \left\vert \frac{\partial g_{posterior}}{\partial \epsilon_{Q}}  \right\vert] \\

\end{align}

Stochastic Duration Predictorの目的は、入力された音素の情報$c$(図では$h_{text}$に相当)からDuration(その音素がどの程度の間発音されていたか)$d$を推定することです。また、$d$の推定時には確率的な揺らぎを与えることによってより自然な音声の生成を目指します。

Stochastic Duration Predictorは、$c$(音素の情報)が分かっている時の$d$(Duration)の対数尤度

\begin{align}

\log p(d|c)

\end{align}

をできるだけ最大化したいです。ELBOを求めた時と同様にして、$\log p(d|c)$の変分下限は以下のように求められます。

\begin{align}

\log p(d|c) \geq E_{q_{\phi}(u,v|d,c)}[\log\frac{p_{\theta}(d-u,v|c)}{q_{\phi}(u,v|d,c)}]

\end{align}

$E_{q_{\phi}(u,v|d,c)}$はミニバッチ内の平均を取る操作に相当します。

VITSではこの変分下限(上の式の右辺)を最大化するよう目指すことで学習します。実装上は変分下限の最大化を、負の変分下限の最小化と言い換えます。

\begin{align}

L_{dur} &= -E_{q_{\phi}(u,v|d,c)}[\log\frac{p_{\theta}(d-u,v|c)}{q_{\phi}(u,v|d,c)}]

\end{align}

ここで、上のネットワーク図より$\epsilon_{D}=g_{\theta}(d-u,v;c)$、$(u,v)=g_{posterior}(\epsilon_{Q};d,c)$です。従って確率変数の変数変換を用いて次のようにできます。

\begin{align}

L_{dur} &= -E_{q_{\phi}(u,v|d,c)}[\log\frac{p_{\theta}(d-u,v|c)}{q_{\phi}(u,v|d,c)}] \\
&= -E_{q_{\phi}(u,v|d,c)}[\log\frac{p(\epsilon_{D}) \left\vert \frac{\partial g_{\theta}}{\partial (d-u,v)}  \right\vert}{p(\epsilon_{Q}) \left\vert \frac{\partial g_{posterior}}{\partial \epsilon_{Q}}  \right\vert ^{-1}}] \\
&= E_{q_{\phi}(u,v|d,c)}[-\log p(\epsilon_{D}) + \log p(\epsilon_{Q}) - \log \left\vert \frac{\partial g_{\theta}}{\partial (d-u,v)}  \right\vert - \log \left\vert \frac{\partial g_{posterior}}{\partial \epsilon_{Q}}  \right\vert] \\

\end{align}

ここで、$\epsilon_{D}$は標準正規分布に従うよう学習したいため$p(\epsilon_{D})=N(\epsilon_{D};0,I)$とします。また、$\epsilon_{Q}$は標準正規分布からサンプリングされた値です。
これらより次のように変形できます。

\begin{align}

L_{dur} &= E_{q_{\phi}(u,v|d,c)}[-\log p(\epsilon_{D}) + \log p(\epsilon_{Q}) - \log \left\vert \frac{\partial g_{\theta}}{\partial (d-u,v)}  \right\vert - \log \left\vert \frac{\partial g_{posterior}}{\partial \epsilon_{Q}}  \right\vert] \\
&= E_{q_{\phi}(u,v|d,c)}[-\log N(\epsilon_{D};0,I) + \log N(\epsilon_{Q};0,I) - \log \left\vert \frac{\partial g_{\theta}}{\partial (d-u,v)}  \right\vert - \log \left\vert \frac{\partial g_{posterior}}{\partial \epsilon_{Q}}  \right\vert] \\
&= E_{q_{\phi}(u,v|d,c)}[-\log (\frac{1}{\sqrt{2\pi}}exp\{-\frac{\epsilon_{D}}{2}\}) + \log (\frac{1}{\sqrt{2\pi}}exp\{-\frac{\epsilon_{Q}}{2}\}) - \log \left\vert \frac{\partial g_{\theta}}{\partial (d-u,v)}  \right\vert - \log \left\vert \frac{\partial g_{posterior}}{\partial \epsilon_{Q}}  \right\vert] \\
&= E_{q_{\phi}(u,v|d,c)}[\frac{1}{2}(\log (2\pi) + \epsilon_{D}^{2} ) - \frac{1}{2}(\log (2\pi) + \epsilon_{Q}^{2} ) - \log \left\vert \frac{\partial g_{\theta}}{\partial (d-u,v)}  \right\vert - \log \left\vert \frac{\partial g_{posterior}}{\partial \epsilon_{Q}}  \right\vert] \\

\end{align}

以上が実装するDuration lossとなります。

損失関数の全体像

以上で紹介した$L_{rec}, L_{kl}, L_{adv}(D), L_{adv}(G), L_{fm}, L_{dur}$を用いて、損失関数$L$は全体として以下のように表せます。

$$L = L_{rec} + L_{kl} + L_{adv}(D) + L_{adv}(G) + L_{fm} + L_{dur}$$

$L$を最小化するよう目指し学習します。

生成結果

以下はiteration数=1200000回学習した際のモデルによる生成結果です。

個人的には音声変換に関してはかなりうまくいっているように聞こえました。
一方で読み上げに関してはイントネーションにやや難があり、さらなるデータセットの増量、ファインチューニングなどが必要そうに思われました。

機械学習の一手法「VITS」でアニメ声(つくよみちゃん)へ変換できるボイスチェンジャーを実装しました。https://t.co/LX0TV13uAD pic.twitter.com/vVWcDbUSpn

— zassou (@zassouEX) February 25, 2022

読み上げを行うこともできます。
(こちらに関してはもう少しファインチューニングが必要そうです。) pic.twitter.com/xKPhTL7A0E

— zassou (@zassouEX) February 25, 2022

まとめ

VITSでボイスチェンジャーと読み上げ器を作成しました。
本記事の内容に関しては万全を期して作成しておりますが、間違った点などがありましたらご指摘いただけると非常に助かります。

ソースコード

実装したコードはこのリポジトリにあります。
https://github.com/zassou65535/VITS
公開しているコードは簡単のため、JVSコーパスにのみの対応としています。

参考

[1]Conditional Variational Autoencoder with Adversarial Learning for End-to-End Text-to-Speech
[2]VITS: Conditional Variational Autoencoder with Adversarial Learning for End-to-End Text-to-Speech
[3]Variational Autoencoder徹底解説
[4]深層生成モデルを巡る旅(2): VAE
[5]深層生成モデルを巡る旅(1): Flowベース生成モデル
[6]Glow-TTS: A Generative Flow for Text-to-Speech via Monotonic Alignment Search
[7]自然言語の指示による画像操作システム
[8]音響特徴量「メルスペクトル」と「MFCC（メル周波数ケプストラム係数）」の解説と実例紹介
[9]ベイズの公式は地味に難しいので、確率の乗法公式を2回使おう
[10]正規分布間のKLダイバージェンス
[11]Variational Inference with Normalizing Flows
[12]【統計検定１級対策】確率変数の変数変換の具体例
[13]ラプラス分布の期待値と分散の求め方
[14]Improved Techniques for Training GANs
[15]VFlow: More Expressive Generative Flows with Variational Data Augmentation
[16]Flow++: Improving Flow-Based Generative Models with Variational Dequantization and Architecture Design
[17]VITS Slides