深層生成モデルを巡る旅(1): Flowベース生成モデル

はじめに

Flowベース生成モデルという深層生成モデルをご存知でしょうか？
他の深層生成モデルであるGANやVAEなどと比べると知名度は劣りますが, 以下のような特徴があります.

• データの尤度が求められる
• その尤度を直接最大化することで学習ができる
• 逆変換ができる

詳しくはこれから述べていきますが, これらの特徴が有用になる場面もあるでしょう.
ということで, 本記事ではそんなFlowベース生成モデルについて調べた結果をまとめます.
「Flowベース生成モデル」と毎回書くのは長いので, 以下では単に「Flow」と書かせてください.
扱うのは導入の他, 以下のFlowたちです.

• Coupling Flows
• Residual Flows
• ODE-based Flows
• Autoregressive Flows

最近ではGraphNVPのようなグラフデータに適用したFlowなどもありますが, 本記事では主に画像のドメインに注目することとします.

間違いや質問などがございましたら遠慮なくコメントをください（にわか者なのできっとどこかに間違いがあります…）.

Flowの基本

生成モデルの基本的な考え方やFlowへの導入は[3]が詳しいです.
詳細はこちらにお任せするとして簡単にまとめると, Flowは, データの分布を学習させる関数$p_\theta(\cdot)$に訓練データ$x$を入れた時の尤度の期待値$\underset{x}{\mathbb{E}}[p_\theta(x)]$を最大化することにより, $p_\theta(\cdot)$を学習させます（c.f., 最尤推定）. これを実現するためには「尤度を求められること」が条件となりますが, この条件を担保するための工夫がFlowのポイントです.

Flowのイメージ

FlowはGANやVAEと同じく, 潜在変数$z$を利用します. 潜在変数$z$からデータ$x$を生成する関数を$f$としましょう.

$$
\boldsymbol{x} := f(\boldsymbol{z})
$$

Flowでは, $z$の次元は$x$と同じとし, この$f$を逆変換可能な関数とします. したがって, データから潜在変数への変換は次式で求められます.

$$
\boldsymbol{z} = f^{-1}(\boldsymbol{x})
$$

潜在変数$z$には勾配計算やサンプリングが容易な多変量正規分布を仮定します. 一方, データ$x$は一般には複雑な分布に従うので, これらの間を結ぶ関数を逆変換可能な形で設計するのは簡単ではありません. そこで, Flowモデルでは逆変換可能な（単純な）関数$f_i \in {f_1,...,f_K}$を繰り返し適用することで$f$を設計します.

$$
f = f_1 \circ f_2 \circ ... \circ f_K
$$

[1]のイメージ図が分かりやすいので引用します.

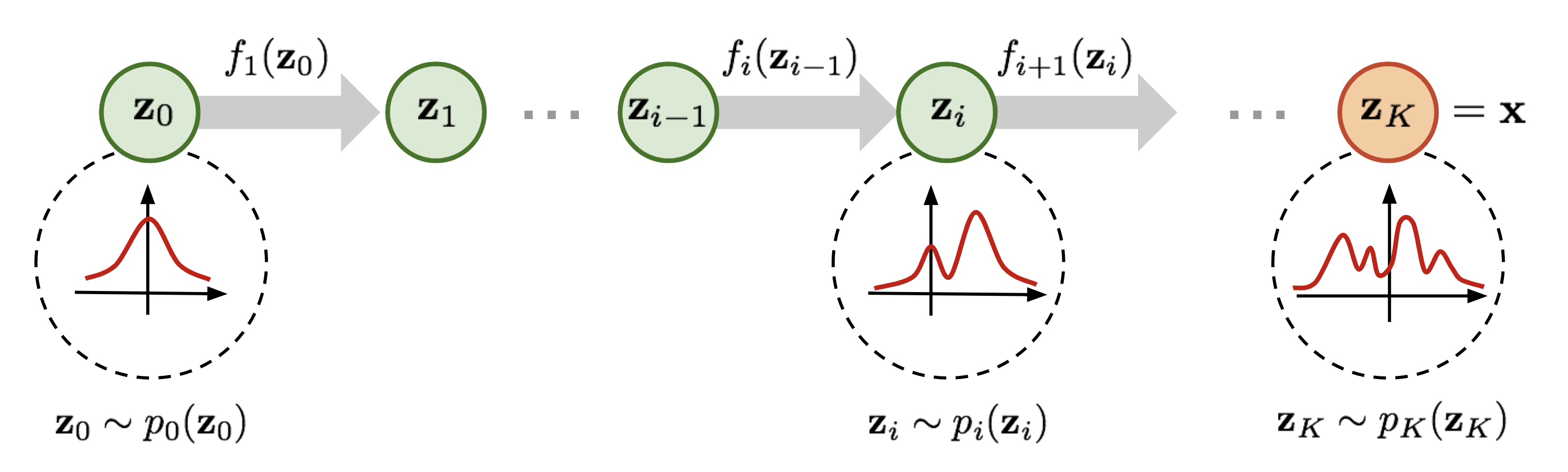
[1] L. Weng. "Flow-based Deep Generative Models."

このように, 生成時に潜在変数からデータに向かって$f_i$が順番に適用されていく流れをFlowと呼びます. また, 逆（推論）方向に見ると複雑な分布を単純な分布に少しずつ変換していることからNormalizing Flowと呼ばれることもあります（元の変分推論におけるNormalizing Flowとは意味が異なって広まっているようです）.

動画で見るとより分かりやすいです. Densityが2次元の正規分布からGitHubの公式キャラクター「Octcat」のシルエットに移っていく様子がFlowらしいですよね.
Vector Fieldは, サンプリングされた各点の動きをベクトルで示したものです.

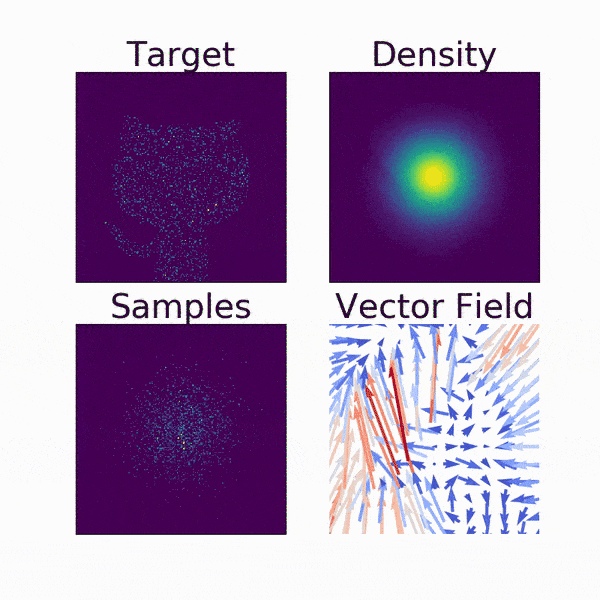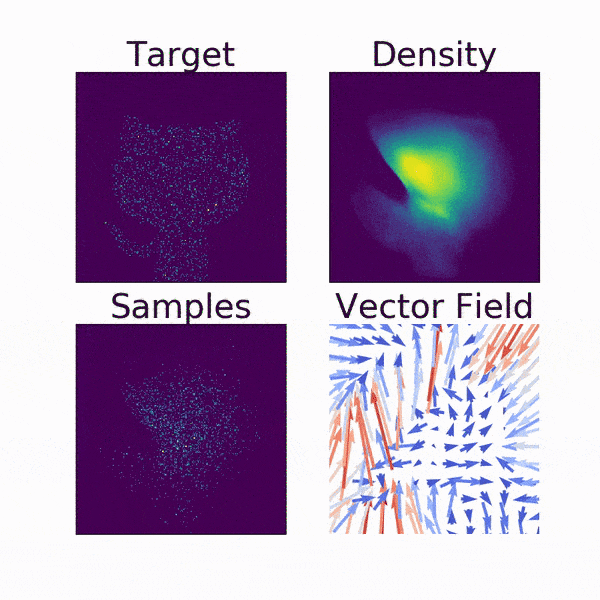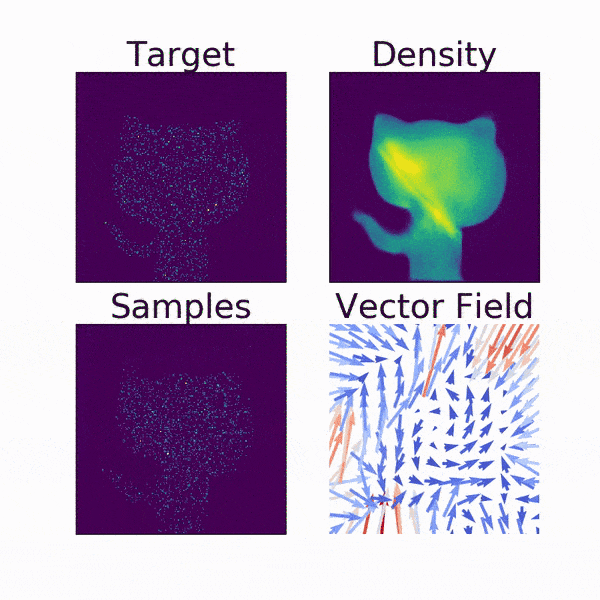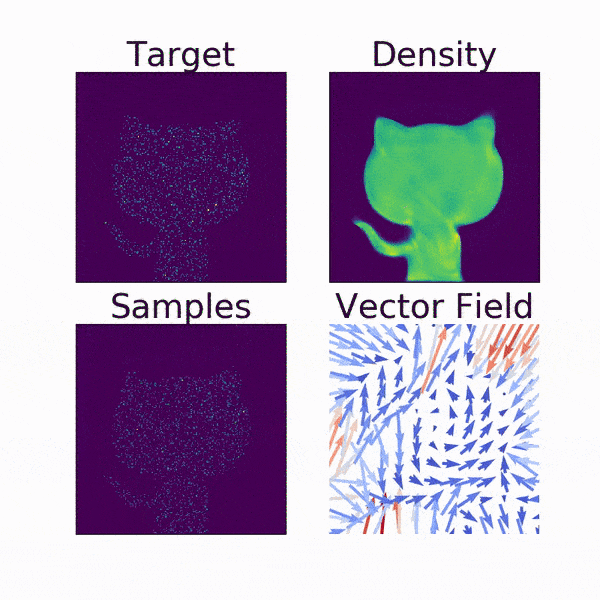
rtqichen/ffjord: code for "FFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Models".

確率変数の変換

お気持ちを説明したところで, 実際の話に移ります.
いきなりですが, 確率変数の変換の式を導入します. これはFlowの論文を読むと必ずと言って良いほど出てくる重要な式で, $x$の確率密度を$z$の確率密度に変換するのに使います.

$$
p_x(\boldsymbol{x}) = p_z(\boldsymbol{z}) \left \vert \det \frac{\mathrm{d} f^{-1}}{\mathrm{d} \boldsymbol{x}} \right\vert
$$

式の導出は[4]が分かりやすいです. 1次元の場合に簡単に説明すると, $x$と$z$は1対1で対応しているので,

\begin{eqnarray}
p_x(x)\mathrm{d}x = p_z(z)\mathrm{d}z\\
p_x(x) = p_z(z)\frac{\mathrm{d}z}{\mathrm{d}x}\\
p_x(x) = p_z(z)\frac{\mathrm{d}f^{-1}}{\mathrm{d}x}
\end{eqnarray}

となります. これを$N$次元に拡張するとJacobianの行列式が出てきます.

目的関数

以上のお気持ちと変数変換を踏まえると, Flowの目的関数が導入できます.
Flowでは, 尤度$p_x(\boldsymbol{x})$を最大化する代わりに, 同値な操作として負の対数尤度 (NLL; negative log likelihood) を損失関数として最小化します（その方が計算上都合が良いため）.
変数変換と$f = f_1 \circ f_2 \circ ... \circ f_K$ を使って, $\boldsymbol{x}$のNLLを計算していくと,

\begin{eqnarray}
-\log p_x(\boldsymbol{x}) &=& -\log p_K(\boldsymbol{z}_K)\\
 &=& -\log p_{K-1}(\boldsymbol{z}_{K-1}) + \log\left \vert \det \frac{\mathrm{d} f_K}{\mathrm{d} \boldsymbol{z}_{K-1}} \right\vert \\
&=& -\log p_{K-2}(\boldsymbol{z}_{K-2}) + \log\left \vert \det \frac{\mathrm{d} f_K}{\mathrm{d} \boldsymbol{z}_{K-1}} \right\vert + \log\left \vert \det \frac{\mathrm{d} f_{K-1}}{\mathrm{d} \boldsymbol{z}_{K-2}} \right\vert\\
&=&...\\
&=& -\log p_z(\boldsymbol{z}) + \sum_{i=1}^K \log\left \vert \det \frac{\mathrm{d} f_i}{\mathrm{d} \boldsymbol{z}_{i-1}} \right\vert
\end{eqnarray}

となり, $z$のNLLとJacobianの行列式の対数 (ここではlog-detと呼びます)に分解できます.
$p_z(\cdot)$は正規分布なので, 第1項は簡単に計算できます.

log-det

ただし, サイズが$D\times D$のJacobianの行列式の計算には$O(D^3)$の計算量が必要なので, $D$が大きくなるとlog-detが計算時間のボトルネックになります. 実際, Glowで生成しているCelebAの画像は$D=256\times256\times3\simeq200,000$次元です. したがって, 現実的にはJacobian行列式を高速に計算するための工夫が必要になります. 詳しくは後で述べますが, Jacobianが三角行列になるような工夫をしたり, log-det自体をtraceによって近似したりといったアプローチがあります.

GAN・VAEとの比較

[1]の図がわかりやすいので引用させていただきます.
* Flowの$f$と$f^{-1}$がこれまでの定式化と逆になっています. 文脈によってどちらが$f$になるかが変わることが多いので注意してください.

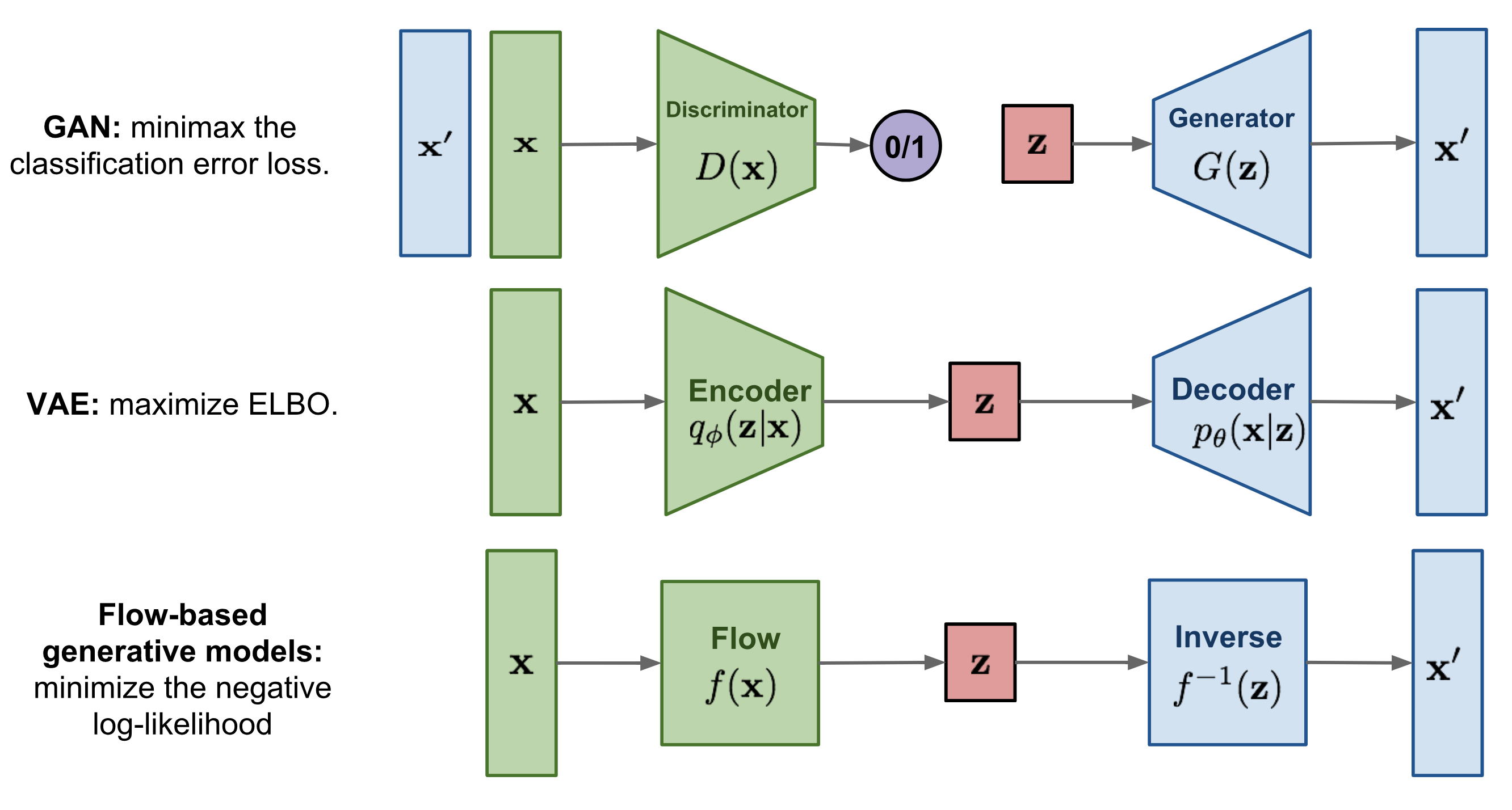
[1] L. Weng. "Flow-based Deep Generative Models."

GANもVAEも, Generator/Decoderで低次元の潜在変数$z$からデータ$x'$（画像など）を生成します.
GANはこれに加えてDiscriminatorを用意して, Generatorとの間でミニマックス最適化を行います. データを潜在変数に落とすEncoderは基本的にありません.
一方, VAEはEncoderを持ち, データ$x$の対数尤度の変分下限 (ELBO; evidence lower bound) の最大化によりパラメータを学習します.

Flowはまず, GANのGenerator/DiscriminatorやVAEのEncoder/Decoderのように2つのモデルを用意する必要がありません. $f$で生成をして$f^{-1}$で推論（密度推定）を行います.
それから, 対数尤度を直接最大化できます. これは損失関数がモデルの性能の直接的な指標として使えるということです. GANでは生成された画像をどう評価するかということが問題になりますが, FlowではNLL (bit/dim)でモデル間の性能比較ができます.
また, 逆変換を保障するために, 潜在空間で次元を落とさない点（モジュールが台形ではなく長方形）や, VAEのサンプリングのような確率的な操作を持たない点も特徴的です. これは一長一短で, $x$と$z$をexactに対応させられる一方, 次元を落とさない分メモリが必要になってしまいます.

様々なFlow

それでは, 様々なFlowを系統立てて紹介していきます.

Coupling Flow

log-detの計算の工夫として, Jacobianが三角行列になるように各層をカップリング によりモデル化し, 行列式の計算を$O(N)$で行うFlowがCoupling Flowです. Flowの中で最も有名な種類です.

NICE [Dinh+, 2015]

NICE (non-linear independent component estimation) は元祖Flowとも言える最もシンプルなCoupling Flowで, 各層では学習させる関数(ニューラルネットなど任意)を$m$として加法カップリングで変換を行います.
$D$次元の$\boldsymbol{x}$を$d$と$D-d$次元に分割して, 前半はそのままとします. 推論方向の式はこちらです.

\begin{cases}
\boldsymbol{y}_{1:d} = \boldsymbol{x}_{1:d}\\
\boldsymbol{y}_{d+1:D} = \boldsymbol{x}_{d+1:D} + m(\boldsymbol{x}_{1:d})
\end{cases}

このように定めると, データ生成は$m^{-1}$を使わずに求められます.

\begin{cases}
\boldsymbol{x}_{1:d} = \boldsymbol{y}_{1:d}\\
\boldsymbol{x}_{d+1:D} = \boldsymbol{y}_{d+1:D} - m(\boldsymbol{y}_{1:d})
\end{cases}

さらに, Jacobianが次のような三角行列になります.

\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} = 
\left[
\begin{array}{cc}
\mathbb{I}_d & O \\
\frac{\partial \boldsymbol{y}_{d+1:D}}{\partial \boldsymbol{x}_{1:d}} & \mathbb{I}_{D-d} 
\end{array}
\right]

この行列式は$1$（log-detは0）ですね.
NICEは計算が簡単な一方, 全ての次元間での関係性を取り込むために, 各層で分割を交換するという操作が必要になります.
また, 画像生成の結果はMNISTでもまだ微妙です.

NICE: Non-linear Independent Components Estimation

RealNVP [Dinh+, 2017]

NICEのlog-detは0でvolume preservingでしたが, スケーリング関数$s$を含むアフィンカップリング で定めたものがReal NVP (real-valued non-volume preserving) です.

\begin{cases}
\boldsymbol{y}_{1:d} = \boldsymbol{x}_{1:d}\\
\boldsymbol{y}_{d+1:D} = \boldsymbol{x}_{d+1:D} \odot \exp(s(\boldsymbol{x}_{1:d})) + t(\boldsymbol{x}_{1:d})
\end{cases}

逆変換に$s^{-1}, t^{-1}$は不要です.

\begin{cases}
\boldsymbol{x}_{1:d} = \boldsymbol{y}_{1:d}\\
\boldsymbol{x}_{d+1:D} = (\boldsymbol{y}_{d+1:D} - t(\boldsymbol{y}_{1:d})) \odot \exp(-s(\boldsymbol{y}_{1:d}))
\end{cases}

さらに, Jacobianが三角行列になります.

\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} = 
\left[
\begin{array}{cc}
\mathbb{I}_d & O \\
\frac{\partial \boldsymbol{y}_{d+1:D}}{\partial \boldsymbol{x}_{1:d}} & \mathrm{diag} (\exp(s(\boldsymbol{x}_{1:d})))
\end{array}
\right]

log-detはNICEと同じく$O(D)$で求められますが, スケーリングができるのでNICEよりも高い表現能力を持つと言えます.

この他にReal NVPでは, 全ての次元間での関係性を取り込むために市松模様状に次元を分割したり, 画像にスケールさせるために階層的な構造(multi-scale architecture)を持たせたりといった工夫をしています.

[Density Estimation Using Real NVP](https://arxiv.org/abs/1605.08803)

Glow [Kingma+, 2018]

Glow (generative flow) は, Real NVPのカップリング層の前に1x1畳込みを入れて画像のチャネル間の関係性を取り込んだものです. 1x1畳込みの逆変換は, 逆行列をがんばって計算します.
また, 小さいバッチサイズでも学習できるように, バッチ正規化の代わりにActNormというチャネル方向の正規化を採用しています.

シンプルな改良ですが, 256x256の画像を綺麗に生成できるようになりました.

ここで, temperatureという生成時のパラメータについて補足しておきます.
$z$は正規分布からサンプリングする乱数ですが, そのときの分散に乗ずる値がtemperatureです. 分散を小さくすると自然な画像に, 大きくすると多様な画像に, というように自然さと多様性のトレードオフを調節するために指定できるパラメータです.

Glow: Generative Flow with Invertible 1x1 Convolutions

Flow++ [Ho+, 2019]

Flow++ は, さらに2点の改良を加えています.

• これまでの一様分布のdequantizationに代わるvariational dequnatization
• 累積分布関数とself-attentionを使った, より複雑なカップリング層

これにより, Flowの中で最も良いbits/dimを達成しました.
bits/dimは, 次元数で割ったNLLの底を2にするためにさらに$\log{2}$で割った指標で, 小さい方が良いとされます.
手法の詳細は論文をご参照ください.

Flow++: Improving Flow-Based Generative Models with Variational Dequantization and Architecture Design

Residual Flow

Residual Flow は, ResNetを可逆にすることでカップリング（次元分割）を使わずにFlowを構築するというアプローチです.

i-ResNet [Behrmann+, 2019]

i-ResNet (invertible residual network) は, ResNetにスペクトル正規化を加えてLipschitz定数を1未満に抑えることで, 不動点反復により逆変換を計算します.
推論方向の計算は通常のResNetと同じです.
生成時は, ResBlockの出力を$\boldsymbol{y}=F(\boldsymbol{x})=\boldsymbol{x}+g(\boldsymbol{x})$として, 逆変換を次のアルゴリズムで求めます.

ResNetの形とLipschitz制約はlog-detの計算にも役立ちます. いろいろな近似（Hutchinson's trickなど）を使うと, log-detはべき乗法で十分高速に求められます.

[Invertible Residual Networks](https://arxiv.org/abs/1811.00995)

Residual Flow [Chen+, 2019]

i-ResNetのlog-detの推定にはバイアスがあります. そこで, べき乗法で近似するときの反復回数を毎回のBernoulli試行で決めることで不偏推定を実現したものがResidual Flow です. この方法は論文中で"Russian roulette estimator"と呼ばれています.

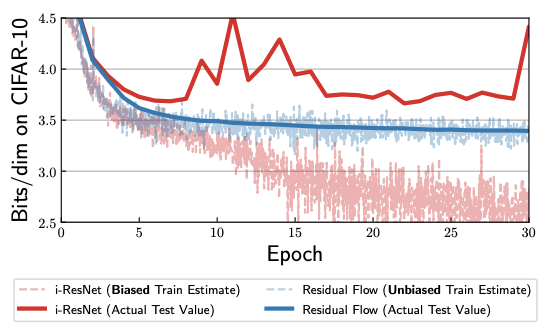[Residual Flows for Invertible Generative Modeling](https://arxiv.org/abs/1906.02735)

ODE-based Flows

ここで紹介するFlowは, NeurIPS 2018のBest Paperに選ばれたNeural ODEを元に構築したFlowです. こちらについては[6]が詳しいです.

Neural ODE [Chen+, 2018]

Neural ODE (neural ordinary differential equation) は, ResNetとEuler法の形が似ていることから, ResNetの層を連続化したものを常微分方程式 (ODE) として解くというものです. Neural ODEの学習では, 誤差逆伝搬の代わりに, 計算グラフを使わないadjoint methodというODE解法を使います.
この論文自体は新しいモデル及び学習方法の提案をしていますが, 密度推定のためのNormalizing Flowに応用する実験も行われています.

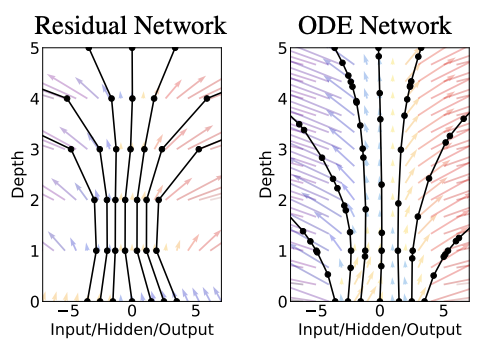[Neural Ordinary Differential Equations](https://arxiv.org/abs/1806.07366)

FFJORD [Grathwohl+, 2019]

Neural ODEを生成モデルに拡張したのがFFJORD (free-form Jacobian of reversible dynamics) です. 逆変換はNeural ODEと同様にadjoint methodで計算します.
ここでも, log-detの計算の高速化にHutchinson's trickを利用しています.
CIFAR-10の画像生成では, Glowの2%以下のパラメータ数で同程度の品質の画像を生成できたとしています.

[FFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Models](https://arxiv.org/abs/1810.01367)

Autoregressive Flows

尤度を自己回帰モデルのように条件付き分布の積で表したFlowがAutoregressive Flowです.

$$
p(\boldsymbol{x}) = \prod_{i=1}^D p(x_i|x_1,...,x_{i-1})
$$

このようにすると, 尤度を計算できると同時に, Jacobianが三角行列になってlog-detを高速に計算できます. 一方, 自己回帰部分の計算がsequentialになり計算に時間がかかるという欠点があります.

MADE [Germain+, 2015]

MADE (masked autoencoder for density estimation) は, 全結合のAutoencoderに適当なマスクをかけて, 次元間の条件付き分布を扱えるようにしました.

MADE: Masked Autoencoder for Distribution Estimation

MAF [Papamakarios+, 2017]

MADEを元にFlowを構築したのがMAF (masked autoregressive flow) です.
$\sigma, \mu$の計算にMADEを使って, 尤度の計算を一度にできます.

p(\boldsymbol{x}) = \prod_{i=1}^D p(x_i|\boldsymbol{x}_{1:i-1})\\
p(x_i|\boldsymbol{x}_{1:i-1}) = z_i \odot \sigma_i(\boldsymbol{x}_{1:i-1}) + \mu_i(\boldsymbol{x}_{1:i-1})

一方, データ生成は$x_i$を順番に生成するため時間がかかります.

x_i \sim p(x_i|\boldsymbol{x}_{1:i-1}) = z_i \odot \sigma_i(\boldsymbol{x}_{1:i-1}) + \mu_i(\boldsymbol{x}_{1:i-1})

Coupling Flowと似た形になっていますね.

Masked Autoregressive Flow for Density Estimation

IAF [Kingma+, 2016]

IAF (inverse autoregressive flow) は, MAFの密度推定とデータ生成を逆にして, 高速にデータ生成を行えるようにしたものです. 密度推定はsequentialな処理となり遅くなります.

x_i \sim p(x_i|\boldsymbol{z}_{1:i-1}) = z_i \odot \sigma_i(\boldsymbol{z}_{1:i-1}) + \mu_i(\boldsymbol{z}_{1:i-1})

Improving Variational Inference with Inverse Autoregressive Flow

MAFとIAFのデータ生成時の振る舞いを比較した図が[1]にあります. IAFは, 最初にサンプリングする$\boldsymbol{z}$のみから$x_i$を生成しています.
* 図中IAFの式に$\boldsymbol{x}_{1:i-1}$

が含まれていますが, おそらく$\boldsymbol{z}_{1:i-1}$の誤りです.

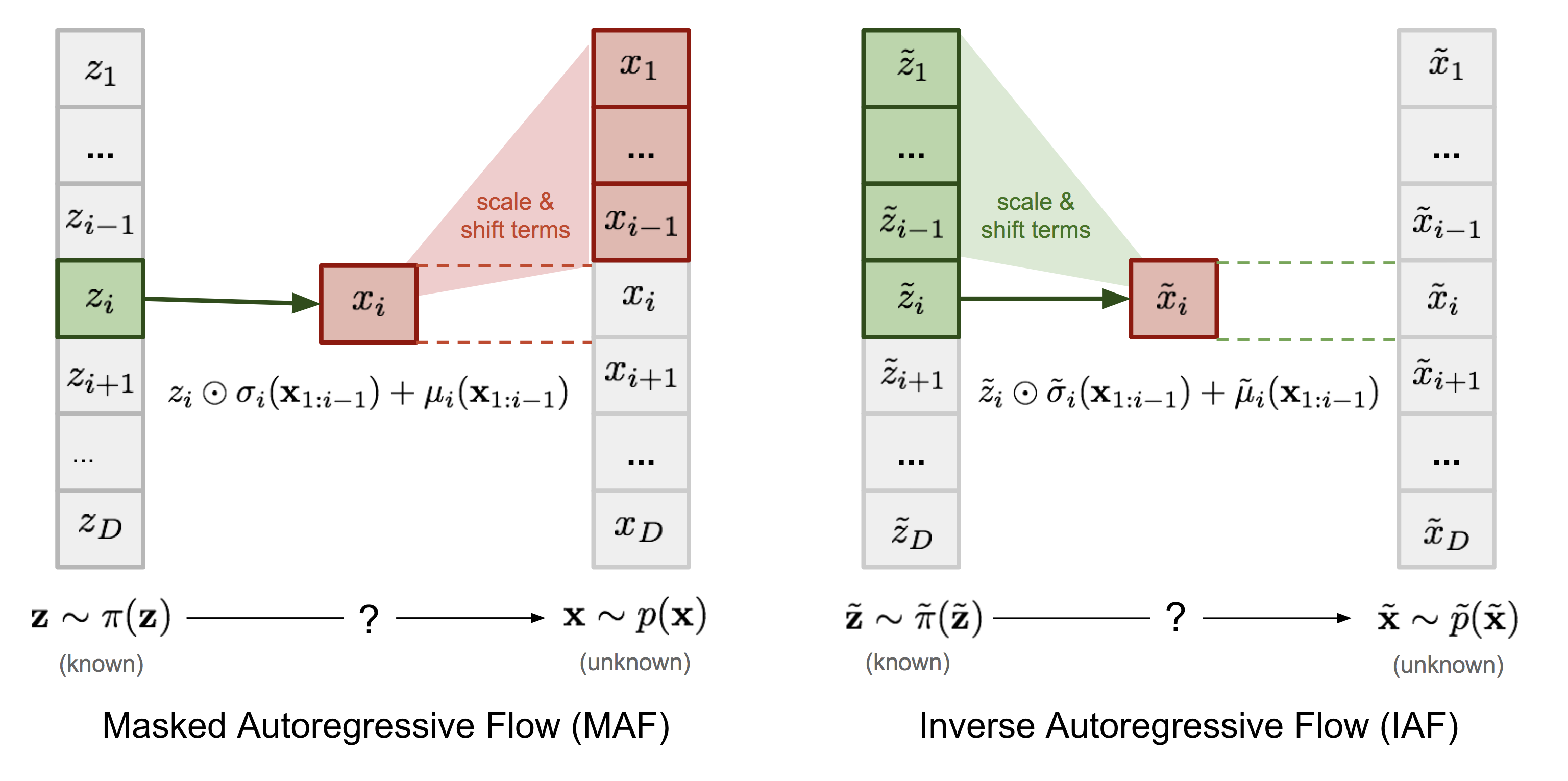
[1] L. Weng. "Flow-based Deep Generative Models."

おわりに

かなり長くなってしまいましたが, 最後までお読みいただきありがとうございます！
FlowはGANと比べると画像の品質はまだ劣っていますが, 生成画像のコントロールしやすさなどの利点もあり, 今後の発展が見込まれるテーマだと思います.
また, 数学の理論やテクニックが随所に見られて, 数学好きの方にも魅力的なテーマではないでしょうか？

タイトルを『深層生成モデルを巡る旅(1)』と続編を期待させるものにしてしまったので, 時間を見つけつつGANやVAEについても調べてまとめたいと思っています. 気長にお待ちいただければ幸いです.

（追記）
2019/11/3: 次回はVAEです.

参考文献

[1] Lilian Weng. "Flow-based Deep Generative Models." 2018.
線形代数の復習から書いてある, とても親切なサーベイ記事です. オリジナルの図も豊富で, 本記事でも引用させていただきました.

[2] Ivan Kobyzev et al. "Normalizing Flows: Introduction and Ideas." 2019.
Flowの最新サーベイ論文です.

[3] Masahiro Suzuki. "[DL輪読会]Flow-based Deep Generative Models." 2019.
Flowを基礎から各論まで解説したスライドです. 日本語の資料では最もわかりやすいと思います.

[4] Eric Jang, "Normalizing Flows Tutorial, Part 1: Distributions and Determinants." 2018.
Flowの基礎をTensorFlowの簡単なコード付きで紹介しています.

[5] Eric Jang "Normalizing Flows Tutorial, Part 2: Modern Normalizing Flows." 2018.
[4]の続編で, 各モデルの紹介をしています.

[6] Joji Toyama. "[DL輪読会]Neural Ordinary Differential Equations." 2019.
ODE-based Flowの詳しい解説スライドです.