目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
| リンク | 説明 |
|---|---|
| marubatsu.py | Marubatsu、Marubatsu_GUI クラスの定義 |
| ai.py | AI に関する関数 |
| test.py | テストに関する関数 |
| util.py | ユーティリティ関数の定義。現在は gui_play のみ定義されている |
| tree.py | ゲーム木に関する Node、Mbtree クラスの定義 |
| gui.py | GUI に関する処理を行う基底クラスとなる GUI クラスの定義 |
AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。
ミニマックス法による探索の実装方法の種類
前回の記事では、引き分けの局面の最善手の優劣を計算するために、ミニマックス法で計算した評価値を修正する方法を紹介しましたが、評価値を修正する方法を考慮すると今回の記事で取り上げる話の内容が複雑になってしまうので、今回の記事から は ミニマックス法のみで評価値を計算する場合の説明 を行います。
探索とは何か
ミニマックス法 によるゲーム木のノードの 評価値の計算 は、そのノードの局面から お互いが最善手を着手し続けた結果 到達する、決着がついた局面 を表すリーフノードを 探してその評価値を計算する というものです。このような、特定のデータ の中から 特定の条件を満たすデータ を 見つける処理 の事を 探索 と呼びます。
探索に関する重要な用語を以下の表にまとめます。
| 用語 | 意味 |
|---|---|
| 探索 | データの中から 条件にあうデータを見つける作業 |
| 探索空間 | 探索の対象 となる データの集合(集まり) |
| 探索条件 | 探索するデータの 条件 |
| 探索アルゴリズム | 探索を行うための 手順 |
| 解(かい) | 探索アルゴリズムによって 探索されたデータ |
探索は日常でも頻繁に行われています。例えば、東京駅から新宿駅まで電車を使って最も安くたどり着けるルートを探すのは探索です。この場合の探索空間は「電車の路線」、探索条件は「値段が最も安いこと」、探索アルゴリズムは「目的のルートを探す手順」、解は「探索アルゴリズムで得られたルート」です。
探索アルゴリズム には、探索空間 と 探索条件 の 性質 によって さまざまな種類 があり、ミニマックス法 は 二人零和有限確定完全情報ゲーム に対して、最善手を求めるために必要 なゲーム木の ノードの評価値を計算 するための 探索アルゴリズム です。同じ目的の探索アルゴリズムとしては、今後の記事で紹介する αβ(アルファベータ)法などがあります。
探索アルゴリズムには数多くの種類があるので、本記事では以降は、〇×ゲームの AI を作成する際に必要 となる、ゲーム木の探索アルゴリズムに限定 して話を進めることにします。
ミニマックス法を利用した〇×ゲームの AI など、探索を行う処理 は 様々な方法で実装 することができ、それぞれ 利点と欠点がある ため 状況によって使い分ける 必要があります。
探索結果を記録した静的なデータを作成する実装方法
一般的に 探索には時間がかかります。そのため あらかじめ全ての状況に対する探索 を行い、結果を記録しておく ことができれば、探索を素早く行う ことができるようになります。
このような、様々な状況に対する何らかの計算をあらかじめ行い、結果をまとめたものを 計算表 や 数表 と呼びます。代表的な計算表には九九の表があり、九九の表を暗記することで 1 桁の掛け算の答えをすぐに求めることができます。
電卓が発明される前は、三角関数などの様々な数学で必要となる計算結果をまとめた数表の事典が作られ、実際に利用されていました。筆者は子供の頃祖父の家でそのような事典を見た記憶があります。また、Google で検索した所、数表小事典という事典の写真が掲載されている個人のブログが見つかりましたので紹介します。
また、コンピューターが作られたきっかけの一つが、第二次世界大戦でアメリカ軍が大砲の弾を命中させるための計算表を作るためだと言われています。
以前の記事で紹介した メモ化 による処理の効率化と似ていると思った人がいるかもしれませんが、メモ化は プログラムの実行中に計算した結果を記録 して後で利用するという点が、あらかじめすべてのデータを計算して記録する方法と 異なります。
これまでの記事で作成した、ゲーム木を利用して着手を選択する AI は、下記のような方法で着手を選択します。この中で AI の関数が行う処理は手順 4、5 です。
- 〇×ゲームのゲーム木を作成する
- ゲーム木の全てのノードの評価値をミニマックス法で計算する
- 局面と最善手の対応表を作成する
- その対応表から現在の局面の最善手の一覧を計算する
- 最善手の一覧からランダムに着手を選択する
上記の 手順 1 ~ 3 は、AI の関数が手順 4、5 で着手を選択する処理を行うより前 に、あらかじめ実行して作成 します。このような、 プログラムを実行する前 にあらかじめ 作成しておいたデータ のことを 静的なデータ と呼びます。
探索結果を記録した静的なデータを作成 する方法には、下記のような 利点と欠点 があるため、常に利用できるわけではありません。
利点
この方法の利点の一つは、すべてのノードの評価値を計算するので、正確な解(評価値)が計算 され、強解決の AI を作成できる というものです。後述しますが、探索アルゴリズムの中には 100 % 正確な解(評価値)を計算できないものがあります。
もう一つの利点は、探索の処理 が あらかじめ完了している ため、探索の結果が記録された対応表から最善手の一覧を取り出して 素早く計算することができる というものです。
そのことを確認するために ゲーム開始時の局面 に対して、(ミニマックス法ではありませんが)子ノードの評価値を AI の関数の中で計算 して着手を選択する ai14s と、局面と最善手の対応表の 静的なデータを利用 して着手を選択する ai_gt7 の 処理速度 を %%timeit を利用して 比較 してみることにします。
まず、下記のプログラムで必要なデータを変数に代入します。
from marubatsu import Marubatsu
from ai import ai14s, ai_gt7
from util import load_bestmoves
mb = Marubatsu()
data = load_bestmoves("../data/bestmoves_and_score_by_board_sv_rd.dat")
下記のプログラムでゲーム開始時の局面に対する ai14s の処理速度の平均を計測 すると、実行結果のように 約 500 μs(マイクロ(100 万分の一)秒)であることがわかります。
%%timeit
ai14s(mb)
実行結果
514 µs ± 1.34 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
下記のプログラムでゲーム開始時の局面に対する ai_gt7 の処理速度の平均を計測すると、実行結果のように 約 1 μs(1 ns(ナノ秒)= 1000 μs です) であることから、静的なデータを利用した AI の処理速度の方が 約 500 倍も速い ことがわかります。
%%timeit
ai_gt7(mb, bestmoves_and_score_by_board=data)
実行結果
971 ns ± 5.04 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
欠点
探索結果を記録した静的なデータをあらかじめ作成する方法の 欠点 は、ゲーム木の ノードの数が多くなる と、ゲーム木を 作成することが困難または不可能になる点 です。〇×ゲームのようなノードが少ないゲームの場合は問題はありませんが、オセロ、将棋、囲碁などのゲームのゲーム木はノードの数が多すぎて ゲーム木を作成することは現実的には不可能 です1。また、仮にゲーム木のデータを作成できたとしても、データの量が多すぎる ためコンピューターのハードディスクやメモリ内に記録して 保存することは不可能 です2。そのため、多くのゲーム では この方法を利用することはできません。
〇×ゲームの場合はこの欠点はあてはまらないため、この方法を利用して 高速に処理を行う強解決の AI を作成 することができます。一方、多くのゲームでは利用できない ので、本記事を読んで 〇×ゲームより複雑なゲームの AI を作成 しようと思った場合は 別の方法が必要になります。そのため、別の方法を説明し、実際にその方法で AI を実装することにします。
評価値を動的に計算する実装方法
あらかじめゲーム木を作成することが不可能な場合は、AI が処理を行う際 にミニマックス法を実際に行って子ノードの 評価値をその場で計算 する必要があります。そのような、プログラムの実行時に計算 するデータの事を 動的なデータ と呼びます。ただし、評価値を動的に計算したからといって、ゲーム木のノードの数が減るわけではありません。そのため、ゲーム木のノードの数が多すぎる場合に生じる「ゲーム木の作成が不可能」、「データの記録が不可能」という問題に対しては、以下のような方法で対処する必要があります。
探索空間を狭める
「ゲーム木の作成が不可能」という問題に対しては、行う 探索の性質を考慮した何らかの方法 で 探索空間(探索するデータの範囲)を狭める という手法がとられます。例えば、「最も身長が高い日本人を探す」という探索の問題に対して、「全世界から探す」という方法は大変すぎます。そこで、ほとんどの日本人が日本に住んでいる ことや、日本の中で東京の人口が最も多い ことを考慮して、「日本の中だけで探す」や「東京都の中だけで探す」ように 探索の範囲を狭める ことで、探索の手間と時間を大幅に減らす ことができます。探索の範囲を狭めることを、探索の絞り込み と呼びます。
探索空間を狭める ことと、探索空間を狭めるように 探索の条件を変更 することは 同じ意味 を持ちます。例えば「日本の中」から「最も身長が高い日本人を探す」という探索と、「世界の中」から「日本にいる最も身長が高い日本人を探す」という探索は、同じ探索です。
探索の条件に完全に一致 するデータの事を 最適解 と呼びます。探索の範囲を狭める ことで 探索の範囲外のデータが無視される ことになるので、上記の例では 最も背の高い日本人が日本の国外にいた場合 は、その人を 見つけることはできません。探索の範囲を狭めた場合に見つかる解のように、最適解でない可能性が生じる解 のことを 近似解 と呼びます。最適解と近似解の差 の事を 誤差 と呼び、誤差が少ない ことを 精度が高いと 呼びます。
探索の範囲を狭める という手法は、日常生活でも良く行われています。例えば警察が殺人事件の容疑者を調べる際に、犯行時刻のアリバイがある容疑者を除外するのは探索の範囲の絞り込みです。
探索範囲を狭めて 近似解を求める ということは、探索に必要な 処理時間を短くする代わり に正確でない解で 妥協する ということです。ただし、同じ妥協するにしても、近似解の 精度が高いほうが望ましい ことは言うまでもないでしょう。
絞り込みを適切に行う ことで得られた近似解の 精度を向上 させることができます。日本人のほとんどが日本にいることを考慮すれば、先程の「日本の中だけで探す」という絞り込みによってかなり精度の高い近似解を得ることができるでしょう。また、絞り込みの方法 によっては近似解ではなく、最適解を得ることができる 場合もあります。例えば 1 ~ 100 までの素数を探索する際に、2 以外の偶数を探索範囲から除外するという方法で探索範囲を絞り込むことで、最適解を得ることができます。
ミニマックス法を利用した AI の場合は、ノードの局面の 最善手 を 子ノードの評価値の最大値(または最小値)で計算 します。ミニマックス法では、ノードの評価値は そのノードの すべての子孫ノードの評価値を計算 することで求めるので、探索空間から それ以外のノードを削除 しても 最適解の評価値を得る ことができます。
従って、ミニマックス法 で 特定のノードの評価値を計算 する際には、探索空間をゲーム木全体から、そのノードをルートノード とするゲーム木の 部分木に狭める ことができます。その結果、残念ながらルートノードの評価値は全てのゲーム木のノードの評価値を計算する必要がありますが、深さが深いノードほど 、子孫ノードの数が減る ため 探索空間をより大きく狭める ことができます。
他にも、ゲーム木のノードの評価値を求める際に、上記とは別の方法で 探索の範囲を狭めた上 でミニマックス法と同じ 最適解を求める ことができる αβ法 という 効率の良い探索アルゴリズム があります。αβ法については、次回の記事で紹介します。
必要なノードのデータのみを記録する
探索の範囲を狭めた結果、現実的な時間で探索の処理を行うことが可能になった場合でも、探索時に計算したすべてのデータ をコンピューターの メモリやファイルに記録 するには データの量が大きすぎる 場合があります。そのような場合は、必要が無くなったデータ を 破棄しながら計算を行う 必要があります。
そのような計算は特に珍しいものではありません。例えば下記の 1 から 10 までの合計を計算するプログラムは、途中で 1 までの合計、2 までの合計のような値を計算して total に代入していますが、total の値を次の合計の値で上書きして破棄する という処理を行います。
total = 0
for i in range(1, 11):
total += i
print(total)
ミニマックス法で計算した探索結果を記録した静的なデータを作成する場合は、ゲーム木のすべてのノードの評価値を記録しておく必要がありますが、特定のノードの評価値を動的に計算する 場合は、計算の過程で作成したノードのデータ をずっと 記録し続けておく必要はありません。わかりづらいと思いますので、具体例を挙げて説明します。
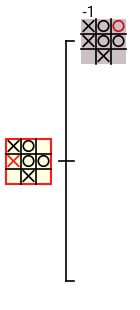
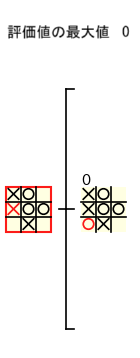
例えば、下図の赤枠のノードの評価値を計算するためには、3 つの子ノードの評価値のデータが必要 となります。

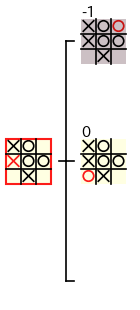
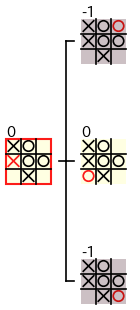
赤枠のノードの評価値は、下図のような手順で 子ノードの評価値のデータのみを使って計算される ので、子ノードの評価値が計算された後 では、子孫ノードのデータは必要ありません。従って、ミニマックス法 では、計算の過程で あるノードの評価値が計算された後 では、その 子孫ノードのデータを破棄 することができます。
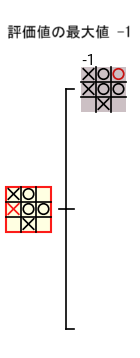
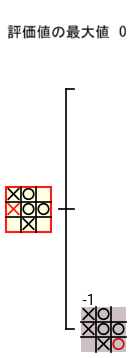
さらに、ミニマックス法でノードの評価値を計算する際に必要となるのは、子ノードの 評価値だけ なので、子ノードのデータも破棄 することができます。具体的には、下図のように 〇 の手番のノードの評価値を計算する際には 子ノードの評価値の最大値を記録 しておけばよいので、子ノードのデータを破棄 することができます。
上記から、ミニマックス法で N というノード の評価値を計算する際に 記録する必要があるノード は、ノード N から、ミニマックス法の処理の途中で 評価値を計算中のノードまで のノードだけであることがわかります。〇×ゲームのゲーム木のノードの深さは最大で 9 なので、ノード N の深さが n の場合は、最大でも 10 - n 個3 のノードのデータだけを記録しておけば充分で、他の途中で計算した大量のノードの情報はすべて破棄 することができます。
深さ優先探索によるミニマックス法の実装
ミニマックス法 は 幅優先アルゴリズム と 深さ優先アルゴリズム の 2 種類のアルゴリズムで実装することができますが、ミニマックス法で評価値を 動的に計算する場合 は、深さ優先アルゴリズム を利用するのが 一般的 です。
その理由は、幅優先アルゴリズム では、計算の過程で 同じ深さのノード の情報を すべて記録する必要がある ため、ゲーム木の ノードが深くなるほど 記録しなければならない ノードの数が大きく増えてしまう からです。
深さ優先アルゴリズムで探索を行うアルゴリズムの事を、深さ優先探索(depth first search) と呼びます。そこで、ミニマックス(mini max)法を深さ優先探索で行い、最善手を選択する ai_mmdfs という AI の関数を定義 する事にします。
ai_mmdfs が行う処理は、Mbtree クラスで深さ優先アルゴリズムでゲーム木を作成する create_tree_by_df と、評価値を計算する calc_score_by_df と よく似ています が、ゲーム木のノードの children 属性 に子ノードのデータを 記録しない 点が 大きく異なります。
Python では、以前の記事で説明したように、利用できなくなったオブジェクト を 自動的に削除 する ガーベジコレクション という処理が行われます。作成した 子ノード を children 属性に記録しない ようにすることで、そのノードの 評価値の計算の処理が行われた後で、子ノードの情報が どこからも参照されなくなって 利用できなくなる ので、ガーベジコレクションによって 自動的に削除されて廃棄される ようになります。
局面を表すデータを代入する 仮引数 mb と、デバッグ表示を行うかどうかを表す 仮引数 debug を持ち、ミニマックス法で その局面の評価値 を計算して 返す関数 として ai_mmdfs を定義 することで、以前の記事で定義した ai_by_score のデコレーター を使って AI の関数を定義 する事ができます。
なお、決着がついている リーフノードの評価値 は最初にミニマックス法で評価値の計算を行う際に設定した以下の表のように計算することにします。最も早く勝利できる合法手を選択するような評価値を計算する場合については、今後の記事で実装します。
| 局面の状況 | 〇 の勝利の評価値 |
|---|---|
| 〇 の勝利 | 1 |
| 引き分け | 0 |
| × の勝利 | -1 |
下記は、ai_mmds の定義です。
-
5 行目:仮引数
mbと仮引数debugを持つ関数としてai_mmdfsを定義する -
6 行目:ミニマックス法による探索を深さ優先アルゴリズムで計算する際に、再帰呼び出しを行う関数
mm_searchをローカル関数として定義する。この関数が行う処理は、create_tree_by_dfやcalc_score_by_dfと同様に、評価値を計算する局面のノードを代入するnodeを仮引数として持ち、計算した評価値を返すという処理を行う。ローカル関数として定義したのは、この関数をai_mmdfs以外で利用することはないからである - 7 ~ 12 行目:リーフノードの場合の評価値を計算し、返り値として返す
-
14、15 行目:リーフノードでない場合は合法手の一覧を計算し、子ノードの評価値を記録する
score_listを空の list で初期化する - 16 ~ 20 行目:それぞれの合法手に対する繰り返し処理を行う
-
17、18 行目:
nodeの局面をコピーしたデータに対して合法手の着手を行う -
19、20 行目:子ノードのデータを作成し、そのデータを実引数に記述して
mm_searchを再帰呼び出しし、その子ノードの評価値を表す返り値をscore_listの要素に追加する。なお、mm_searchでは、親ノードのデータやノードの深さのデータを利用しないので、ノードを作成する際にそれらに関する実引数は省略した -
21 ~ 24 行目:繰り返し処理の結果、
score_listに子ノードの評価値の一覧のデータを要素として持つ list が代入されるので、ミニマックス法に従って、手番によってそれらの最大値または最小値を計算して返り値として返す -
26、27 行目:
ai_mmdfsの処理として、評価値を計算するmbの局面を表すノードを作成し、そのノードを実引数に記述してmm_searchを呼び出すことで、この局面の評価値を計算する。また、計算した評価値を返り値として返す処理を行う
1 from marubatsu import Marubatsu
2 from tree import Node
3 from copy import deepcopy
4
5 def ai_mmdfs(mb, debug=False):
6 def mm_search(node):
7 if node.mb.status == Marubatsu.CIRCLE:
8 return 1
9 elif node.mb.status == Marubatsu.CROSS:
10 return -1
11 elif node.mb.status == Marubatsu.DRAW:
12 return 0
13
14 legal_moves = node.mb.calc_legal_moves()
15 score_list = []
16 for x, y in legal_moves:
17 mb = deepcopy(node.mb)
18 mb.move(x, y)
19 childnode = Node(mb)
20 score_list.append(mm_search(childnode))
21 if node.mb.turn == Marubatsu.CIRCLE:
22 return max(score_list)
23 else:
24 return min(score_list)
25
26 node = Node(mb)
27 return mm_search(node)
行番号のないプログラム
from marubatsu import Marubatsu
from tree import Node
from copy import deepcopy
def ai_mmdfs(mb, debug=False):
def mm_search(node):
if node.mb.status == Marubatsu.CIRCLE:
return 1
elif node.mb.status == Marubatsu.CROSS:
return -1
elif node.mb.status == Marubatsu.DRAW:
return 0
legal_moves = node.mb.calc_legal_moves()
score_list = []
for x, y in legal_moves:
mb = deepcopy(node.mb)
mb.move(x, y)
childnode = Node(mb)
score_list.append(mm_search(childnode))
if node.mb.turn == Marubatsu.CIRCLE:
return max(score_list)
else:
return min(score_list)
node = Node(mb)
return mm_search(node)
上記の定義後に、下記のプログラムを実行して ゲーム開始時の局面の評価値 を ai_mmdfs で計算すると、実行結果のように引き分けの局面を表す 0 という正しい評価値が計算される ことが確認できます。なお、ai_mmdfs で ゲーム開始時の局面の評価値を計算 すると、ゲーム木を作成する際と同様にゲーム木の 全てのノードを作成して評価値を計算する処理 が行われるので、ゲーム木を作成する際と同様に 約 30 秒ほどの処理時間 がかかります。
mb = Marubatsu()
print(ai_mmdfs(mb))
実行結果
0
ai_mmdfs が正しく実装されているかどうかを確認するために、下図の (1, 1)、(1, 0) に着手した 〇 の必勝の局面の評価値を計算 することにします。

下記のプログラムを実行すると、実行結果のように 1 という正しい評価値が計算される ことが確認できます。こちらの場合は、深さ 2 のノードをルートノードとする部分木を作成する処理 と同様の処理が行われ、その場合の 部分木のノードの数 はゲーム木全体のノードの数よりも 大幅に少ない ので 1 秒未満で計算が終了 します。
mb.move(1, 1)
mb.move(1, 0)
print(ai_mmdfs(mb))
実行結果
1
ゲーム開始時の局面 で着手を選択する際に、約 30 秒もかかってしまう のは 時間がかかりすぎ で、この AI と対戦するのは苦痛でしょう。そのため、何らかの工夫 を行って、この AI の 処理時間を短くする工夫が必要 になります。その工夫は次回の記事で紹介します。
探索範囲の絞り込みの確認
先程、「ミニマックス法 で 特定のノードの評価値を計算 する際には、探索空間をゲーム木全体から、そのノードをルートノード とするゲーム木の 部分木に狭める ことができます」という説明を行いました。そこで、実際に どれくらい狭めることができているかを確認 できるように ai_mmdfs を修正することにします。具体的には、ai_mmdfs では、mm_search を呼び出すたび に 1 つのノードの評価値を計算する ので、mm_search を呼び出した回数を数える ことで、実際に 探索を行ったノードの数を数える ことができます。
下記は、そのように ai_mmdfs を修正したプログラムで、仮引数 debug に True が代入 されている場合に 数えた回数を表示 しています。
-
4 行目:
mm_searchが呼び出された回数を数えるai_mmdfsのローカル変数countを0で初期化する -
6 行目:
ai_mmdfsのローカル変数countは、ai_mmdfsの ローカル関数mm_searchにとっての クロージャー変数 である。以前の記事で説明したように、クロージャー変数は値を参照することはできるか、nonlocal クロージャー変数名を実行しないと 代入処理を行うことはできない ので、nonlocal countを記述 している -
7 行目:
mm_searchが呼び出されたので、countに 1 を足す -
9 行目:
ai_mmdfsの中でmm_searchを呼び出した後で、countを表示する必要があるので、mm_searchの返り値をscoreに代入するように修正する -
10 行目:
dprintを利用してdebugがTrueの場合にcountの値を表示する -
11 行目:
scoreをai_mmdfsの返り値として返す
1 from ai import dprint
2
3 def ai_mmdfs(mb, debug=False):
4 count = 0
5 def mm_search(node):
6 nonlocal count
7 count += 1
元と同じなので省略
8 node = Node(mb)
9 score = mm_search(node)
10 dprint(debug, "count =", count)
11 return score
行番号のないプログラム
from ai import dprint
def ai_mmdfs(mb, debug=False):
count = 0
def mm_search(node):
nonlocal count
count += 1
if node.mb.status == Marubatsu.CIRCLE:
return 1
elif node.mb.status == Marubatsu.CROSS:
return -1
elif node.mb.status == Marubatsu.DRAW:
return 0
legal_moves = node.mb.calc_legal_moves()
score_list = []
for x, y in legal_moves:
mb = deepcopy(node.mb)
mb.move(x, y)
childnode = Node(mb)
score_list.append(mm_search(childnode))
if node.mb.turn == Marubatsu.CIRCLE:
return max(score_list)
else:
return min(score_list)
node = Node(mb)
score = mm_search(node)
dprint(debug, "count =", count)
return score
修正箇所
+from ai import dprint
def ai_mmdfs(mb, debug=False):
+ count = 0
def mm_search(node):
+ nonlocal count
+ count += 1
元と同じなので省略
node = Node(mb)
- return mm_search(node)
+ score = mm_search(node)
+ dprint(debug, "count =", count)
+ return score
上記の修正後に下記のプログラムを実行すると、実行結果のように ゲーム開始時の局面 に対して ai_mmdfs を呼び出すと、549946 個 のノードの評価値が計算されることが確認できます。これは、以前の記事で確認した 〇×ゲームのゲーム木のノードの数と一致 します。
mb.restart()
print(ai_mmdfs(mb, debug=True))
実行結果
count = 549946
0
続けて下記のプログラムで (1, 1)、(1, 0) に着手した局面に対して ai_mmdfs を呼び出すと、7046 個 のノードの評価値が計算されることが確認できます。このように、深さ 2 のノードの局面の場合の 探索空間を大幅に減らすことができる ことが確認できました。その結果、処理時間 もゲーム開始時の局面と比べて 大幅に減らす ことができます。
mb.move(1, 1)
mb.move(1, 0)
print(ai_mmdfs(mb, debug=True))
実行結果
count = 7064
1
ノードを作成しない実装方法
先程定義した ai_mmdfs では、下記のプログラムの 3、6 行目のように、局面を表す mb から局面の ノードを表す Node クラスのインスタンスを作成 し、それを mm_search の実引数に記述して呼び出す という処理を行っています
1 def ai_mmdfs(mb, debug=False):
2 def mm_search(node):
略
3 childnode = Node(mb)
4 score_list.append(mm_search(childnode))
略
5
6 node = Node(mb)
7 return mm_search(node)
ゲーム木を実際に作成する Mbtree クラスの create_tree_by_df では、作成した子ノードのデータ を Node クラスのインスタンスの children 属性に記録する という処理を行っていたので、ノードのデータを作成する必要 がありました。
しかし、mm_serach では 子ノードの情報を記録していません。また、仮引数 node に代入された ノードのデータの中で、実際に mm_search の中で 利用しているのは mb 属性の値だけ なので、局面のデータから ノードのデータをわざわざ作成する必要はありません。
そのため、mm_search の仮引数 を Marubatsu クラスのインスタンスを代入する mborig に修正 することができ、そうすることで Node クラスのインスタンスを作成するという 無駄な処理を省く ことができます。下記は、そのように ai_mmdfs を修正したプログラムです。
-
3 行目:仮引数
nodeをmborigに修正する -
6、8、10、13、16、19 行目:
node.mbをmborigに修正する - 18 行目と 24 行目の前にあった Node クラスのインスタンスを作成する処理を削除する
-
18、24 行目:
mm_searchの実引数をmbに修正する
1 def ai_mmdfs(mb, debug=False):
2 count = 0
3 def mm_search(mborig):
4 nonlocal count
5 count += 1
6 if mborig.status == Marubatsu.CIRCLE:
7 return 1
8 elif mborig.status == Marubatsu.CROSS:
9 return -1
10 elif mborig.status == Marubatsu.DRAW:
11 return 0
12
13 legal_moves = mborig.calc_legal_moves()
14 score_list = []
15 for x, y in legal_moves:
16 mb = deepcopy(mborig)
17 mb.move(x, y)
18 score_list.append(mm_search(mb))
19 if mborig.turn == Marubatsu.CIRCLE:
20 return max(score_list)
21 else:
22 return min(score_list)
23
24 score = mm_search(mb)
25 dprint(debug, "count =", count)
26 return score
行番号のないプログラム
def ai_mmdfs(mb, debug=False):
count = 0
def mm_search(mborig):
nonlocal count
count += 1
if mborig.status == Marubatsu.CIRCLE:
return 1
elif mborig.status == Marubatsu.CROSS:
return -1
elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
score_list = []
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score_list.append(mm_search(mb))
if mborig.turn == Marubatsu.CIRCLE:
return max(score_list)
else:
return min(score_list)
score = mm_search(mb)
dprint(debug, "count =", count)
return score
修正箇所
def ai_mmdfs(mb, debug=False):
count = 0
- def mm_search(node):
+ def mm_search(mborig):
nonlocal count
count += 1
- if node.mb.status == Marubatsu.CIRCLE:
+ if mborig.status == Marubatsu.CIRCLE:
return 1
- elif node.mb.status == Marubatsu.CROSS:
+ elif mborig.status == Marubatsu.CROSS:
return -1
- elif node.mb.status == Marubatsu.DRAW:
+ elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
score_list = []
for move in legal_moves:
- mb = deepcopy(node.mb)
+ mb = deepcopy(mborig)
x, y = move
mb.move(x, y)
- childnode = Node(mb)
- score_list.append(mm_search(childnode))
+ score_list.append(mm_search(mb))
- if node.mb.turn == Marubatsu.CIRCLE:
+ if mborig.turn == Marubatsu.CIRCLE:
return max(score_list)
else:
return min(score_list)
- node = Node(mb)
- score = mm_search(node)
+ score = mm_search(mb)
dprint(debug, "count =", count)
return score
上記の修正後に下記のプログラムを実行すると、実行結果のように修正前と同じ結果が表示されます。なお、Node クラスのインスタンスを作成する処理を無くしても 処理時間はほとんど変化しません。その理由は、Node クラスのインスタンスを作成する処理時間 が、ai_mmdfs で行う処理時間の ごく一部に過ぎない からです。
mb.restart()
print(ai_mmdfs(mb, debug=True))
実行結果
count = 549946
0
また、下記のプログラを実行すると、実行結果のように修正前と同じ結果が表示されます。
mb.move(1, 1)
mb.move(1, 0)
print(ai_mmdfs(mb, debug=True))
実行結果
count = 7064
1
ミニマックス法 によるノードの 動的な評価値の計算の処理 では、ゲーム木を実際に作成する必要はなく、局面を表すデータだけを使って処理を行う ことができます。
AI の関数としての ai_mmdfs の定義
ai_mmdfs を 局面の評価値を計算する関数 として定義したので、@ai_by_score のデコレータ式を ai_mmdfs の定義の直前の行に記述することで、AI の関数を定義できます。ただし、その前に ai_mmdfs に対して修正を行う必要があります。どのような修正を行う必要があるかについて少し考えてみて下さい。
ai_mmdfs の修正
ai_by_score のデコレータは、その中で定義されたラッパー関数 wrapper の中の下記のプログラムの 3 行目のように、最大の評価値 を持つ子ノードになる合法手を候補手の一覧として計算します。つまり、ai_by_score を利用するため には、局面の評価値を計算する関数 が、その局面の 手番に関わらず 常に 候補手 として計算する合法手を着手した 局面の評価値が最大になる ように評価値を計算する必要があります。
1 def ai_by_score(eval_func):
略
2 def wrapper(mb_orig, debug=False, *args, rand=True, analyze=False, **kwargs):
略
3 if best_score < score:
4 best_score = score
5 best_moves = [move]
略
しかし、ai_mmdfs が計算する 評価値 は、〇 の勝利の局面の評価値を 1、× の勝利の局面の評価値を -1 と計算するので、× の手番の局面 では候補手として計算する合法手を着手した 〇 の手番の局面の評価値 が、最小の評価値として計算される という問題があります。
この問題を解決するためには、下記のプログラムの 5、6 行目のように、ai_mmdfs の 返り値 を 〇 の手番の局面 の場合は -1 を乗算 して 正負を反転させる ことで、最小値を最大値に変換する処理を行う 必要があります。なお、下記のプログラムでは @ai_by_score のデコレーター式を 3 行目に記述して、ai_mmdfs を AI の関数として利用 できるようにしています。
1 from ai import ai_by_score
2
3 @ai_by_score
4 def ai_mmdfs(mb, debug=False):
元と同じなので省略
5 if mb.turn == Marubatsu.CIRCLE:
6 score *= -1
7 return score
行番号のないプログラム
from ai import ai_by_score
@ai_by_score
def ai_mmdfs(mb, debug=False):
count = 0
def mm_search(mborig):
nonlocal count
count += 1
if mborig.status == Marubatsu.CIRCLE:
return 1
elif mborig.status == Marubatsu.CROSS:
return -1
elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
score_list = []
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score_list.append(mm_search(mb))
if mborig.turn == Marubatsu.CIRCLE:
return max(score_list)
else:
return min(score_list)
score = mm_search(mb)
dprint(debug, "count =", count)
if mb.turn == Marubatsu.CIRCLE:
score *= -1
return score
修正箇所
+ from ai import ai_by_score
+ @ai_by_score
def ai_mmdfs(mb, debug=False):
元と同じなので省略
+ if mb.turn == Marubatsu.CIRCLE:
+ score *= -1
return score
上記の修正後に下記のプログラムを実行して、先程の (1、1)、(1, 0) に着手を行った mb の局面に対して ai_mmdfs を実行すると、実行結果のように 最善手の中からランダムな着手が選択される ことが確認できます。
print(ai_mmdfs(mb))
実行結果(実行結果はランダムなので下記と異なる場合があります)
(0, 2)
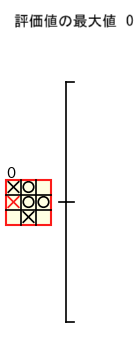
なお、この局面は下図のように (1, 2) 以外の合法手が最善手なので、(1, 2) が選択されることはありません。

下記のプログラムで debug=True を実引数に記述して呼び出すと、実行結果のように デバッグ表示が行われる ことが確認できます。
print(ai_mmdfs(mb, debug=True))
実行結果
Start ai_by_score
Turn o
.X.
.o.
...
legal_moves [(0, 0), (2, 0), (0, 1), (2, 1), (0, 2), (1, 2), (2, 2)]
略
Finished
best score 1
best moves [(0, 0), (2, 0), (0, 1), (2, 1), (0, 2), (2, 2)]
(2, 2)
下記のプログラムで rand=False を実引数に記述して呼び出すと、実行結果のように上記の best moves の 最初の候補手 である (0, 0) が 常に表示 されます。
print(ai_mmdfs(mb, rand=False))
実行結果
(0, 0)
下記のプログラムで analyze=True を実引数に記述して呼び出すと、実行結果のように 候補手の一覧 と、それぞれの合法手に着手した局面の 評価値の一覧 が表示されることが確認できます。また、最善手でない (1, 2) を着手した場合の評価値が他の評価値より小さな 0 として正しく計算されていることが確認できます。
from pprint import pprint
pprint(ai_mmdfs(mb, analyze=True))
実行結果
{'candidate': [(0, 0), (2, 0), (0, 1), (2, 1), (0, 2), (2, 2)],
'score_by_move': {(0, 0): 1,
(0, 1): 1,
(0, 2): 1,
(1, 2): 0,
(2, 0): 1,
(2, 1): 1,
(2, 2): 1}}
強解決の AI であるかの確認
下記のプログラムで、ai_mmdfs が 強解決の AI であるか を確認します。実行結果から強解決の AI であることが確認できました。
from util import Check_solved
Check_solved.is_strongly_solved(ai_mmdfs)
実行結果
100%|██████████| 431/431 [00:15<00:00, 28.19it/s]
431/431 100.00%
(True, [])
今回の記事のまとめ
今回の記事では、ミニマックス法で 評価値を動的に計算 し、それを利用して着手を選択する ai_mmdfs を定義 しました。ただし、現状では ゲーム開始時の局面 で ai_mmdfs が 着手を選択 すると 約 30 秒 もの時間がかかってしまうので、この AI で対戦を行うのは 長時間待たされる という苦痛を伴うことになります。そこで、次回の記事では、ai_mmdfs の 処理速度を向上させる方法 について紹介します。
本記事で入力したプログラム
| リンク | 説明 |
|---|---|
| marubatsu.ipynb | 本記事で入力して実行した JupyterLab のファイル |
| ai.py | 本記事で更新した ai_new.py |
次回の記事