0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@ysgeso

Pythonで〇×ゲームのAIを一から作成する　その112　弱解決の AI であるかの判定と枝狩りによる探索の効率化

0
Last updated at Posted at 2024-09-01

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク 説明
marubatsu.py Marubatsu、Marubatsu_GUI クラスの定義
ai.py AI に関する関数
test.py テストに関する関数
util.py ユーティリティ関数の定義。現在は gui_play のみ定義されている
tree.py ゲーム木に関する Node、Mbtree クラスの定義
gui.py GUI に関する処理を行う基底クラスとなる GUI クラスの定義

AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。

弱解決の AI であるかどうかの判定

以前の記事では、〇× ゲームの AI が 弱解決の AI であるか どうかを、ランダムな着手を行う ai2s と十分な回数だけ対戦 させ、一度も敗北しないかどうかで判定 を行いました。この判定方法は 判定したい AI に ai2s が勝利する着手が存在する場合 に、その着手を 偶然選択しない可能性が 0 にはならない ので、AI が 弱解決の AI であるかどうかを 100 % 判定することはできません。そこで、今回の記事では別の方法で 弱解決の AI であるかどうかを 100 % 判定する処理を実装 する事にします。

以前の記事で説明したように、弱解決の定義 は、「ゲームの開始時の局面の状態が判明しており、どのような相手と対戦しても、その 局面の状況以上の結果になる合法手を選択する方法が判明 しているゲームのこと」です。〇×ゲームは ゲーム開始時の局面の状況 は 引き分けの局面 なので、ゲーム開始時の局面から対戦を行った場合に、どのような相手と対戦しても 敗北しないこと が弱解決の AI の条件です。その条件をどのように判定すればよいかについて少し考えてみて下さい。

上記では、敗北しないことが条件であると説明しましたが、その AI がゲーム開始時の局面から対戦を行った場合に 出現する全ての局面で最善手を選択する という条件で判定できるのではないかと 思った人がいるかもしれません。しかし、その方法は弱解決の AI であるかを判定する方法としては 厳密には正しくありません。

以前の記事で説明しましたが、〇×ゲームのような引き分けのゲームの場合は、必ず引き分け以上の結果になる ことが弱解決の条件です。従って、相手が最善手を選択しなかった結果、必勝の局面になった場合に最善手を選択せず に引き分けになったとしても、弱解決の AI の条件を満たします。

出現する全ての局面で最善手を選択するという条件は、弱解決の条件よりも 厳しい条件 です。従って、その条件を満たす場合は、必ず弱解決の AI であることが保証されますが、その逆は必ずしも正しくはありません。

本記事では実装しませんが、出現する全ての局面で最善手を選択するという条件を判定する処理を記述することもできます。興味がある方は実装してみて下さい。

判定のアルゴリズムとゲーム木の探索

どのような相手と対戦しても敗北しないということは、AI がゲーム開始時の局面から着手を行った際に出現する局面の中に、AI が敗北する局面が一つも存在しない ということです。

AI がゲーム開始時の局面から着手を行った際に出現する局面は、ゲーム木のルートノードから、下記の条件を満たす子ノードを辿って出現するノード の局面です。

  • AI の手番の場合は、その AI が行う可能性のあるすべての合法手に対応する子ノード
  • AI の手番でない場合は、全ての合法手に対応する子ノード

従って、ゲーム木の中で、上記の条件を満たす部分木 のノードをすべて調べ、その中に AI が敗北する局面が存在しない場合 に弱解決の AI であると判定することができます。

以下は、弱解決であるかどうかを判定する下記のアルゴリズムです。

  1. 〇 の担当と × の担当の両方で下記の手順で判定を行い、両方で弱解決であると判定 された場合に、弱解決の AI であると判定する
  2. ゲーム開始時の局面から以下の着手を行うすべての局面を調べ。AI が敗北する局面が 1 つも存在しなければ、担当した手番では弱解決の AI であると判定する
    • AI が担当する手番では、その AI が行う可能性のあるすべての合法手を着手する
    • AI が担当しない手番では、すべての合法手を着手する

プログラミングに慣れた方で、もっと効率的なアルゴリズムを思いついた人がいるかもしれませんが、最初は上記の愚直なアルゴリズムから紹介し、もっと効率的なアルゴリズムについては今回の記事の後半で紹介します。

このような、ゲーム木の中のノードの中からから 特定の条件を満たすノードを探す ことを ゲーム木の探索 と呼びます。

また、ゲーム木に限らず、数多くのデータの中から 特定の条件を満たすデータを探す処理 のことを 探索 と呼び、探索を幅優先アルゴリズムで行うことを 幅優先探索、深さ優先アルゴリズムで行うことを 深さ優先探索 と呼びます。

上記の手順 2 は、ゲーム木のルートノードから、条件を満たす 全ての子ノードを辿っていく処理 になるので、再帰呼び出しによる深さ優先アルゴリズム で記述することができます。また、手順 1 から 〇 と × の担当で異なる処理を行う必要がある ことがわかります。

強解決の AI であるかの判定を Check_solved のメソッドとして定義したので、弱解決の AI であるかの判定も同様に Check_solved のメソッドとして下記のように定義する事にします1。深さ優先アルゴリズムで処理を行うので、このメソッドは 深さ優先探索 を行う処理です。

名前：弱解決（weakly solved）であるかを判定するので is_weakly_solved とする
処理：指定した手番を担当した場合に AI が弱解決であるかを再帰呼び出しを使って判定する
入力：下記の仮引数にデータを代入する

  • node：判定を行うゲーム木のノード
  • ai：判定を行う AI の関数
  • turn：判定を行う AI が担当する手番
  • params：AI が必要とするパラメーター

出力：弱解決と判定された場合は True、そうでない場合は False を返す

calc_legal_moves の修正

上記のアルゴリズムの手順 2 では、AI が担当しない手番では すべての合法手を着手する ので、合法手の一覧を計算する Marubatsu クラスの calc_legal_moves メソッドを利用します が、このメソッドには以下のような 問題点がある ことに気が付きましたので修正します。

ゲーム木を作成する create_tree_by_df では、ノード N に対して、全ての子ノードを計算する処理を行います。その際に、下記のプログラムの 2 行目のように、ゲーム中であるという条件が満たされる場合 に calc_legal_moves を利用して 合法手の一覧を計算 しました。

1  def create_tree_by_df(self, N):
2      if N.mb.status == Marubatsu.PLAYING:
3          legal_moves = N.mb.calc_legal_moves()
4          for x, y in legal_moves:
以下略

このような処理が必要となるのは、Marubatsu クラスの calc_legal_moves が、下記のプログラムのように 空いているマスの一覧を計算する という処理 だけ を行っているため、ゲームの 決着がついた局面でも複数の合法手を返す 可能性があるからです。

def calc_legal_moves(self):
    legal_moves = [(x, y) for y in range(self.BOARD_SIZE) 
                        for x in range(self.BOARD_SIZE)
                        if self.board[x][y] == Marubatsu.EMPTY]
    return legal_moves

しかし、よく考えると ゲームの決着がついている局面 には 合法手は存在しない ので 空の list を返すようにするべき です。また、そのように calc_legal_moves 修正することで、create_tree_by_df の 4 行目の for 文の繰り返し処理が一度も実行されなくなる ので、2 行目 のゲームの決着がついているかどうかの 判定を行う必要が無くなります。

そこで、calc_legal_moves を下記のように修正します。

  • 4、5 行目：ゲームの決着がついている場合は、空の list を返すように修正する
 1  from marubatsu import Marubatsu
 2
 3  def calc_legal_moves(self):
 4      if self.status != Marubatsu.PLAYING:
 5          return []
 6      legal_moves = [(x, y) for y in range(self.BOARD_SIZE) 
 7                          for x in range(self.BOARD_SIZE)
 8                          if self.board[x][y] == Marubatsu.EMPTY]
 9      return legal_moves
10
11  Marubatsu.calc_legal_moves = calc_legal_moves
行番号のないプログラム 
from marubatsu import Marubatsu

def calc_legal_moves(self):
    if self.status != Marubatsu.PLAYING:
        return []
    legal_moves = [(x, y) for y in range(self.BOARD_SIZE) 
                        for x in range(self.BOARD_SIZE)
                        if self.board[x][y] == Marubatsu.EMPTY]
    return legal_moves

Marubatsu.calc_legal_moves = calc_legal_moves
修正箇所 
from marubatsu import Marubatsu

def calc_legal_moves(self):
+   if self.status != Marubatsu.PLAYING:
+       return []
    legal_moves = [(x, y) for y in range(self.BOARD_SIZE) 
                        for x in range(self.BOARD_SIZE)
                        if self.board[x][y] == Marubatsu.EMPTY]
    return legal_moves

Marubatsu.calc_legal_moves = calc_legal_moves

次に、create_tree_by_df を下記のプログラムのように修正します。

  • 4 行目の下にあった if 文を削除し、削除した if 文のインデントを全て無くす
1  from tree import Mbtree, Node
2  from copy import deepcopy
3
4  def create_tree_by_df(self, N):
5      legal_moves = N.mb.calc_legal_moves()
インデント以外は元と同じなので略
6
7  Mbtree.create_tree_by_df = create_tree_by_df
行番号のないプログラム 
from tree import Mbtree, Node
from copy import deepcopy

def create_tree_by_df(self, N):
    legal_moves = N.mb.calc_legal_moves()
    for x, y in legal_moves:
        mb = deepcopy(N.mb)
        mb.move(x, y)
        node = Node(mb, parent=N, depth=N.depth + 1)
        N.insert(node)
        self.nodelist.append(node)
        self.nodelist_by_depth[node.depth].append(node)
        self.nodenum += 1
        self.create_tree_by_df(node)

Mbtree.create_tree_by_df = create_tree_by_df
修正箇所 
from tree import Mbtree, Node
from copy import deepcopy

def create_tree_by_df(self, N):
-   if N.mb.status == Marubatsu.PLAYING:
-        legal_moves = N.mb.calc_legal_moves()
+   legal_moves = N.mb.calc_legal_moves()
インデント以外は元と同じなので略

Mbtree.create_tree_by_df = create_tree_by_df

上記の修正後に下記のプログラムを実行して、create_tree_by_df を利用してゲーム木を作成し、draw_subtree で作成したゲーム木のルートノードから深さ 1 までの部分木を表示すると、実行結果のように正しく表示されることが確認できます。

mbtree = Mbtree(algo="df")
mbtree.draw_subtree(mbtree.root, maxdepth=1)

実行結果

なお、calc_legal_moves を上記のように修正しても、これまで calc_legal_moves を利用しているプログラムを 修正する必要はありません。その理由は、これまでのプログラムでは ゲームの決着がついた局面で calc_legal_moves の値を利用することがなかったからです。

従って、create_tree_by_df 以外でも、if N.mb.status == Marubatsu.PLAYING: のような if 文の判定を削除することができる場所がいくつかありますが、そのままでも正しい処理が行われるのでそれらについては修正しないことにします。修正したい人は calc_legal_moves でプログラムを検索してそのような個所を探し出して修正すると良いでしょう。

is_weakly_solved の定義

is_weakly_solved は 再帰呼び出し によって計算を行うので、仮引数 node から辿れる部分木 の中に、一つでも相手が勝利するノードがあれば False を、そうでなければ True を返すという処理を行います。

また、node の局面 が 決着がついているか どうかで、下記の処理を行います。

  • 決着がついている場合は、相手が勝利していれば False を、いなければ True を返す
  • 決着がついていない場合は、下記に対応するすべての子ノードに対して再帰呼び出しを行う。再帰呼び出しの返り値が False になる場合 は、子ノードの中に相手が勝利する局面が存在する ことを意味するので、すべての再帰呼び出しの返り値が True の場合は True を、そうでなければ False を返す
    • AI が担当する手番では、その AI が行う可能性のあるすべての合法手を着手する
    • AI が担当しない手番では、すべての合法手を着手する

また、決着がついていない場合の処理は、前後の式が両方共 True の場合に True を計算する and 演算子 を使って、下記のアルゴリズムで計算できます。

  • 結果を計算する変数を用意し、True で初期化 する
  • 再帰呼び出しの返り値とその変数を and 演算子で演算 し、その変数に代入する

上記の計算を行うことで、一つでも再帰呼び出しの返り値が False になった場合は、結果を計算する変数が False になります。

下記は、上記のアルゴリズムに従って、is_weakly_solved を定義したプログラムです。

  • 3 行目：is_strongly_solved と同様に、静的メソッドとして定義する
  • 4 行目：先程説明した 4 つの仮引数を持つ関数として is_weakly_solved を定義する。その際に params の実引数を省略できるようにデフォルト値が None の仮引数とする
  • 5、6 行目：params が None の場合に空の dict を代入する
  • 7、8 行目：node の局面が AI の勝利か引き分けの場合は True を返す
  • 9、10 行目：ゲーム中でない場合は相手が勝利しているので、False を返す。11 行目以降の処理は、ゲーム中の場合のみ行われる
  • 12、13 行目：node の局面が AI が担当する手番の場合は、ai が選択する着手の一覧を計算して moves に代入する
  • 14、15 行目：node の局面が相手が担当する手番の場合は、合法手の一覧を計算して moves に代入する
  • 16 行目：決着がついていない場合の返り値（return value）を計算する変数 retval の値を True で初期化する
  • 17 行目：moves 内に記録されたそれぞれの着手に対する繰り返し処理を行う
  • 18、9 行目：children_by_moves 属性を使って move の着手を行った子ノードを計算し、その子ノードに対する is_weakly_solved の再帰呼び出しを行う。再帰呼び出しの返り値と retval を and 演算子で計算し、retval に代入する
  • 19 行目：retval を返り値として返す
 1  from util import Check_solved
 2
 3  @staticmethod
 4  def is_weakly_solved(node, ai, turn, params=None):
 5      if params is None:
 6          params = {}
 7      if node.mb.status == turn or node.mb.status == Marubatsu.DRAW:
 8          return True
 9      elif node.mb.status != Marubatsu.PLAYING:
10          return False
11
12      if turn == node.mb.turn:
13          moves = ai(node.mb, candidate=True, **params) 
14      else:
15          moves = node.mb.calc_legal_moves()
16      retval = True
17      for move in moves:
18          childnode = node.children_by_move[move]
19          retval = Check_solved.is_weakly_solved(childnode, ai, turn, params) and retval
20      return retval
21
22  Check_solved.is_weakly_solved = is_weakly_solved
行番号のないプログラム 
from util import Check_solved

@staticmethod
def is_weakly_solved(node, ai, turn, params=None):
    if params is None:
        params = {}
    if node.mb.status == turn or node.mb.status == Marubatsu.DRAW:
        return True
    elif node.mb.status != Marubatsu.PLAYING:
        return False
        
    if turn == node.mb.turn:
        moves = ai(node.mb, candidate=True, **params) 
    else:
        moves = node.mb.calc_legal_moves()
    retval = True
    for move in moves:
        childnode = node.children_by_move[move]
        retval = Check_solved.is_weakly_solved(childnode, ai, turn, params) and retval
    return retval

Check_solved.is_weakly_solved = is_weakly_solved

上記のプログラムを実行後に弱解決の AI ではない ai2s と、弱解決の AI である ai14s と、強解決の AI である ai_gt6 を is_weakly_solved を利用して計算することにします。

下記のプログラムの実行結果から、ai2s は 〇 を担当した場合と × を担当した場合のいずれも False になり、弱解決の AI ではないことが確認できます。

from ai import ai2s, ai14s, ai_gt6

print(Check_solved.is_weakly_solved(mbtree.root, ai2s, Marubatsu.CIRCLE))
print(Check_solved.is_weakly_solved(mbtree.root, ai2s, Marubatsu.CROSS))

実行結果

False
False

下記のプログラムの実行結果から、ai14s は 〇 を担当した場合と × を担当した場合のいずれも True になり、弱解決の AI であることが確認できます。

print(Check_solved.is_weakly_solved(mbtree.root, ai14s, Marubatsu.CIRCLE))
print(Check_solved.is_weakly_solved(mbtree.root, ai14s, Marubatsu.CROSS))

実行結果

True
True

下記のプログラムの実行結果から、ai_gt6 は 〇 を担当した場合と × を担当した場合のいずれも True になり、弱解決の AI であることが確認できます。強解決の AI のほうが 弱解決の AI よりも条件が厳しいので、これは当然の結果です。

from util import load_bestmoves

bestmoves = load_bestmoves("../data/bestmoves_by_board.dat")
params = {"bestmoves_by_board": bestmoves}
print(Check_solved.is_weakly_solved(mbtree.root, ai_gt6, Marubatsu.CIRCLE, params))
print(Check_solved.is_weakly_solved(mbtree.root, ai_gt6, Marubatsu.CROSS, params))

実行結果

True
True

再帰呼び出しを開始する処理を行う関数の定義

上記のプログラムでは、弱解決であるかどうかを判定する際に、〇 の手番と × の手番で 2 回 is_weakly_solved を呼び出す必要がある 点が面倒です。また、is_weakly_solved を呼び出す際に mbtree.root と 手番を表すデータ を 毎回記述する必要がある 点も面倒です。

再帰呼び出しによる処理を行う際は、再帰呼び出しを開始する処理を行う関数を別に定義する ことで、プログラムの 記述を簡潔にする ことができるのでその方法を紹介します。

再帰呼び出しを開始する処理を行う 関数やメソッドの名前 は、再帰呼び出しの関数とは 別の名前にする 必要がありますが、その 2 つには 似たような名前を付けるのが一般的 です。良く使われるのが、再帰呼び出しの関数名の語尾に _ や、_r2 などを付け加えるというものです3。今回の場合は 再帰呼び出しを開始するメソッド の名前を is_weakly_solved に、再帰呼び出しのメソッド の名前を is_weakly_solved_r とすることにします。

まず、下記のプログラムのように、再帰呼び出しのメソッドである is_weakly_solved の名前を is_weakly_solved_r という名前に変更します。

  • 2 行目：メソッドの名前を is_weakly_solved_r に修正する。なお、params の値が None の場合に行う処理 は、この関数を呼び出す is_weakly_solved で行う ので、is_weakly_solved_r で 改めて行う必要はない。そのため、params を通常の仮引数とし、2 行目の下にあった params に対する処理は削除した
  • 5 行目：再帰呼び出しで呼び出すメソッドの名前を is_weakly_solved_r に修正する
1  @staticmethod
2  def is_weakly_solved_r(node, ai, turn, params):
元と同じなので省略
3      for move in moves:
4          childnode = node.children_by_move[move]
5          retval = Check_solved.is_weakly_solved_r(childnode, ai, turn, params) and retval
6      return retval
7
8  Check_solved.is_weakly_solved_r = is_weakly_solved_r
行番号のないプログラム 
@staticmethod
def is_weakly_solved_r(node, ai, turn, params):
    if node.mb.status == turn or node.mb.status == Marubatsu.DRAW:
        return True
    elif node.mb.status != Marubatsu.PLAYING:
        return False
        
    if turn == node.mb.turn:
        moves = ai(node.mb, candidate=True, **params) 
    else:
        moves = node.mb.calc_legal_moves()
    retval = True
    for move in moves:
        childnode = node.children_by_move[move]
        retval = Check_solved.is_weakly_solved_r(childnode, ai, turn, params) and retval
    return retval

Check_solved.is_weakly_solved_r = is_weakly_solved_r
修正箇所 
@staticmethod
-def is_weakly_solved(node, ai, turn, params=None):
+def is_weakly_solved_r(node, ai, turn, params):
-   if params is None:
-       params = {}
元と同じなので省略
    for move in moves:
        childnode = node.children_by_move[move]
-       retval = Check_solved.is_weakly_solved(childnode, ai, turn, params) and retval
+       retval = Check_solved.is_weakly_solved_r(childnode, ai, turn, params) and retval
    return retval

Check_solved.is_weakly_solved_r = is_weakly_solved_r

次に、is_weakly_solved を下記のように再定義します。元の is_weakly_solved には、ノードと手番を代入する仮引数が必要でしたが、AI が弱解決であるかどうか を調べるために 必要なデータ は AI の関数とそのパラメータだけ のはずです。それは、強解決の AI であるかを判定する is_strongly_solved の仮引数が ai と params だけであることからもわかります。

実際に is_weakly_solved に必要な仮引数も ai と params だけで、元々あった node と turn は下記のように is_weakly_solved のプログラムの中に記述することができます。

なお、せっかくなので、仮引数 verbose を追加し、verbose が True の場合は 〇 の手番、× の手番、全体のそれぞれで弱解決の AI であるかを表示するようにしてみました。ただし、返り値は全体の結果のみを返すことにします。

  • 2 行目：仮引数を、AI と AI のパラメータと、デフォルト値を True とする verbose を仮引数とするように修正する
  • 5 行目：ゲーム木のデータをファイルから読みこむ
  • 6 行目：ルートノードを root に代入する
  • 7、8 行目：〇 の手番と × の手番のそれぞれで is_weakly_solved_r を呼び出して弱解決の AI であるかどうかを計算し、結果を変数に代入する
  • 9 行目：AI が弱解決の AI あるかを計算する
  • 10 ~ 13：verbose が True の場合に結果を print で表示する
  • 14 行目：結果を返り値として返す
 1  @staticmethod
 2  def is_weakly_solved(ai, params=None, verbose=True):
 3      if params is None:
 4          params = {}
 5      mbtree = Mbtree.load("../data/aidata")
 6      root = mbtree.root
 7      circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params)
 8      cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params)
 9      result = circle_result and cross_result
10      if verbose:
11          print("   o", circle_result)
12          print("   x", cross_result)
13          print("Both", result)
14          return result
15
16  Check_solved.is_weakly_solved = is_weakly_solved
行番号のないプログラム 
@staticmethod
def is_weakly_solved(ai, params=None, verbose=True):
    if params is None:
        params = {}
    mbtree = Mbtree.load("../data/aidata")
    root = mbtree.root
    circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params)
    cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params)
    result = circle_result and cross_result
    if verbose:
        print("   o", circle_result)
        print("   x", cross_result)
        print("Both", result)
    return result

Check_solved.is_weakly_solved = is_weakly_solved

上記を実行後に下記のプログラムで ai2s を判定すると、実行結果に先程と同様に 〇、×、両方のいずれも False が表示されることが確認できました。先ほどのプログラムと比較して、1 行で実引数を 1 つだけ記述すれば良い のでかなり 簡潔に記述 できます。

print(Check_solved.is_weakly_solved(ai2s))

実行結果

   o False
   x False
Both False
False

is_weakly_solved の改良

上記のプログラムを実行すると、筆者のパソコンでは 約 45 秒ほど時間がかかりましたが、そのうちの何秒かは is_weakly_solved を実行するたびに行われる、25 MB もの大きさ がある aidata.mbtree からデータを読み込む処理に費やされた時間 です。そこで、is_strongly_solved で行っているように、aidata.mbtree から 読み込んだデータ を mbtree というクラス属性に代入する ことでファイルからのデータの読み込みを 最初の 1 回だけで済ませる という工夫を行うことにします。

aidata.mbtree のデータを代入するクラス属性の名前を mbtree とし、下記のプログラムのように is_wealky_solved を修正します。

  • 4、5 行目：Check_solved クラスのクラス属性 mbtree 属性が None の場合にファイルからデータを読み込んで、mbtree 属性に代入する
  • 6 行目：root の計算を Check_solved.mbtree.root に修正する
 1  def is_weakly_solved(ai, params=None, verbose=True):
 2      if params is None:
 3          params = {}
 4      if Check_solved.mbtree is None:
 5          Check_solved.mbtree = Mbtree.load("../data/aidata")
 6      root = Check_solved.mbtree.root
 7      circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params)
 8      cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params)
元と同じなので省略
 9
10  Check_solved.is_weakly_solved = is_weakly_solved
行番号のないプログラム 
@staticmethod
def is_weakly_solved(ai, params=None, verbose=True):
    if params is None:
        params = {}
    if Check_solved.mbtree is None:
        Check_solved.mbtree = Mbtree.load("../data/aidata")
    root = Check_solved.mbtree.root
    circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params)
    cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params)
    result = circle_result and cross_result
    if verbose:
        print("   o", circle_result)
        print("   x", cross_result)
        print("Both", result)
    return result

Check_solved.is_weakly_solved = is_weakly_solved
修正箇所 
def is_weakly_solved(ai, params=None, verbose=True):
    if params is None:
        params = {}
-   mbtree = Mbtree.load("../data/aidata")
+   if Check_solved.mbtree is None:
+       Check_solved.mbtree = Mbtree.load("../data/aidata")
-   root = mbtree.root
+   root = Check_solved.mbtree.root
    circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params)
    cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params)
元と同じなので省略

Check_solved.is_weakly_solved = is_weakly_solved

次に、mbtree というクラス属性を None で初期化 する必要があります。本当は下記のプログラムの 4 行目のように、Check_solved クラスの定義の中で初期化処理を記述する必要がある のですが、marubatsu.ipynb の中でクラスを定義し直すと、先程修正したメソッドの記述を全て行う必要がある点がかなり面倒です。

1  class Check_solved:
2      bestmoves_by_board = None
3      mblist_by_board = None
4      mbtree = None
元と同じなので省略

そこで、本記事では、下記のプログラムで直接 Check_solved のクラス属性に None を代入して初期化することにします。なお、この 初期化処理は必ず必要になる ので、次回以降の記事で Check_solved を util.py からインポートして利用する際には、上記の修正を util.py に記述した Check_solved の定義に必ず記述しておく必要がある 点に注意して下さい。

Check_solved.mbtree = None

実行結果は同じなので省略しますが、上記の実行後に、下記のプログラムで ai2s に対して is_weakly_solved を実行すると、mbtree 属性にまだファイルから読み込んだデータが代入されていないので処理に 45 秒ほど時間がかかります。

print(Check_solved.is_weakly_solved(ai2s))

その後、もう一度同じプログラムを実行すると、今度は mbtree 属性にデータが代入されているので約 2/3 の 30 秒ほどで処理が完了します。

print(Check_solved.is_weakly_solved(ai2s))

続けて、下記のプログラムで ai14s と ai_gt6 のチェックを行うとこちらは処理がすぐに完了します。ai2s と比較して処理時間が短い理由についてはこの後で説明します。また、実行結果から正しく処理が行われることが確認できます。

print(Check_solved.is_weakly_solved(ai14s))
print(Check_solved.is_weakly_solved(ai_gt6, params))

実行結果

   o True
   x True
Both True
True
   o True
   x True
Both True
True

枝狩りによる処理の効率化

上記で弱解決の AI であるかを判定する処理は実装できていますが、ai2s に対して is_weakly_solved　の処理を行うと約 30 秒もの時間がかかってしまいます。その理由は is_weakly_solved_r が 効率の悪い処理を行っているから なので、処理を効率化します。

まず、改良後と比較を行うことができるようにするために、下記のプログラムで ai2s、ai14s、ai_gt6 のそれぞれに対する処理時間を %%timeit で計測します。その際に、verbose=False を記述しないとメッセージが大量に表示されてしまう点に注意して下さい。

なお、下記の処理は、約 30 秒かかる処理が 7 回行われるので 3 分以上かかります。

%%timeit
Check_solved.is_weakly_solved(ai2s, verbose=False)

実行結果

28.7 s ± 85.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

%%timeit
Check_solved.is_weakly_solved(ai14s, verbose=False)

実行結果

306 ms ± 2.95 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

%%timeit
Check_solved.is_weakly_solved(ai_gt6, params, verbose=False)

実行結果

179 ms ± 1.44 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

下記はそれぞれの処理時間を表にまとめたものです。その際に、わかりやすいように単位をミリ秒に統一しました。

AI 処理時間
ai2s 28700 ms
ai14s 306 ms
ai_gt6 179 ms

相手が勝利した局面を発見した場合の枝狩り

is_weakly_solved_r では、AI がゲーム開始時から着手を行った場合に出現する全てのノードをチェックする処理を行いますが、チェックの際に 相手が勝利する局面が見つかった時点 で 弱解決の AI であることが確定する ので、残りのノードをチェックするのは無駄 です。

木構造のデータの探索の際に 途中で結果が判明した場合など で、必要のない探索を行わないようにする ことを 枝狩り と呼び、枝狩りを行うことで 探索するノードの数を減らし、処理時間を短くする ことができるようになります。

例えば is_weakly_solved は深さ優先アルゴリズムで探索の処理を行う過程で、左のノードから赤い矢印の順番で再帰呼び出しの処理を行うと、太い赤枠の × が勝利している局面のノードをチェックした時点 で、その AI が 弱解決の AI ではないことが確定 します。そのため、図の 暗い色で表示された残りのノードを探索する必要はなくなります。暗い色のノードの探索を行わないという処理が、ゲーム木から暗い色の ノードの枝を刈り取る様子に似ている ことから、この処理に 枝狩り（pruning）という名前が付けられたようです。

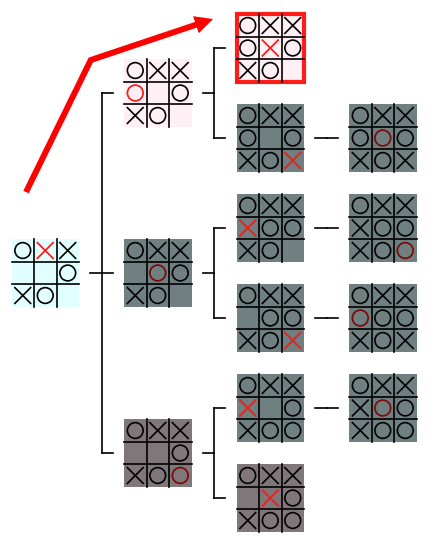
再帰呼び出しが行われた回数を数えるための修正

まず、枝狩りの効果を実感できるようにする ために、再帰呼び出しが何回行われたかを数える ように、is_weakly_solved_r と is_weakly_solved を修正することにします。

具体的には下記の方法で再帰呼び出しの回数を数えます。

  • Check_solved の count というクラス属性で再帰呼び出しの回数を数える
  • count 属性は is_weakly_solved で処理を開始する際に 0 で初期化する。なお、初期化処理は is_weakly_solved 内で行うので、先程の mbtree 属性のように、Check_solved の定義の最初で初期化処理を行う必要はない
  • is_weakly_solved_r の最初で count 属性を 1 増やすことで再帰呼び出しの回数を数える

まず、is_weakly_solved を下記のプログラムのように修正します。

  • 3 行目：最初に count 属性を 0 で初期化する
1  @staticmethod
2  def is_weakly_solved(ai, params=None, verbose=True):
3      Check_solved.count = 0
元と同じなので省略
4
5  Check_solved.is_weakly_solved = is_weakly_solved
行番号のないプログラム 
@staticmethod
def is_weakly_solved(ai, params=None, verbose=True):
    Check_solved.count = 0
    if params is None:
        params = {}
    if Check_solved.mbtree is None:
        Check_solved.mbtree = Mbtree.load("../data/aidata")
    root = Check_solved.mbtree.root
    circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params)
    cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params)
    result = circle_result and cross_result
    if verbose:
        print("   o", circle_result)
        print("   x", cross_result)
        print("Both", result)
    return result

Check_solved.is_weakly_solved = is_weakly_solved
修正箇所 
@staticmethod
def is_weakly_solved(ai, params=None, verbose=True):
+   Check_solved.count = 0
元と同じなので省略

Check_solved.is_weakly_solved = is_weakly_solved

次に、is_weakly_solved_r を下記のプログラムのように修正します。

  • 3 行目：最初に count 属性を 1 増やす
1  @staticmethod
2  def is_weakly_solved_r(node, ai, turn, params):
3      Check_solved.count += 1
元と同じなので省略
4
5  Check_solved.is_weakly_solved_r = is_weakly_solved_r
行番号のないプログラム 
@staticmethod
def is_weakly_solved_r(node, ai, turn, params):
    Check_solved.count += 1
    if node.mb.status == turn or node.mb.status == Marubatsu.DRAW:
        return True
    elif node.mb.status != Marubatsu.PLAYING:
        return False
        
    if turn == node.mb.turn:
        moves = ai(node.mb, candidate=True, **params) 
    else:
        moves = node.mb.calc_legal_moves()
    retval = True
    for move in moves:
        childnode = node.children_by_move[move]
        retval = Check_solved.is_weakly_solved_r(childnode, ai, turn, params) and retval
    return retval

Check_solved.is_weakly_solved_r = is_weakly_solved_r
修正箇所 
@staticmethod
def is_weakly_solved_r(node, ai, turn, params):
+   Check_solved.count += 1
元と同じなので省略

Check_solved.is_weakly_solved_r = is_weakly_solved_r

上記の修正後に下記のプログラムを実行し、ai2s、ai14s、ai_gt6 のそれぞれに対して何回再帰呼び出しが行われたかを表示します。

下記の実行結果から、ai2s の場合は 1099892 回も再帰呼び出しが行われる ことが確認できます。これは、ゲーム木のノードの数の 549946 の 2 倍で、〇 の担当と × の担当の両方でルートノードからゲーム木を探索しているからです。100 万回以上もの再帰呼び出しが行われていることが、この 処理に時間がかかる理由 です。

Check_solved.is_weakly_solved(ai2s)
print(Check_solved.count)

実行結果

   o False
   x False
Both False
1099892

下記の実行結果から ai14s の場合は 3244 回しか再帰呼び出しが行われていないことが確認できます。これは 多くの局面 で ai14s が行う着手が 合法手の一覧よりも少ないため です。

Check_solved.is_weakly_solved(ai14s)
print(Check_solved.count)

実行結果

   o True
   x True
Both True
3244

下記の実行結果から ai_gt6 の場合は 92128 回の再帰呼び出しが行われる確認できます。ai14s よりも回数が多いのは、ai_gt6 が全ての最善手を選択する のに対し、ai14s は最善手の中の 一部しか選択しない場合がある からです。例えばゲーム開始時の局面では、9 つの全ての合法手が最善手ですが、ai14s は真ん中のマスしか選択しません。

Check_solved.is_weakly_solved(ai_gt6, params)
print(Check_solved.count)

実行結果

   o True
   x True
Both True
92128

下記は先ほどの表に再帰呼び出しの回数を加えたものです。再帰呼び出しの回数 と 処理時間 に 関係がある ことがわかります。なお、ai_gt6 のほうが ai14s より再帰呼び出しの回数多いのに処理時間が短いのは、ai14s そのものの処理時間 が、ai_gt6 の処理時間よりも かなり長いから です。

AI 処理時間 回数
ai2s 28700 ms 1099892
ai14s 306 ms 3244
ai_gt6 179 ms 92128

is_weakly_solved_r の修正

相手が勝利した際の枝狩り は、下記のプログラムのように is_weakly_solved_r の繰り返し処理の中で、再帰呼び出しの返り値が False の場合 に、残りの繰り返し処理を実行せずに 即座に False を返す ようにすることで行うことができます。

  • 2 行目の前にあった retval = True は必要が無くなったので削除する
  • 4、5 行目：再帰呼び出しの返り値が False の場合に False を返すように修正する
  • 6 行目：繰り返し処理が終了した時点で、全ての再帰呼び出しの返り値が True であることが確定するので、True を返すように修正する
1  @staticmethod
元と同じなので省略
2      for move in moves:
3          childnode = node.children_by_move[move]
4          if not Check_solved.is_weakly_solved_r(childnode, ai, turn, params):
5              return False
6      return True
7
8  Check_solved.is_weakly_solved_r = is_weakly_solved_r
行番号のないプログラム 
@staticmethod
def is_weakly_solved_r(node, ai, turn, params):
    Check_solved.count += 1
    if node.mb.status == turn or node.mb.status == Marubatsu.DRAW:
        return True
    elif node.mb.status != Marubatsu.PLAYING:
        return False
        
    if turn == node.mb.turn:
        moves = ai(node.mb, candidate=True, **params) 
    else:
        moves = node.mb.calc_legal_moves()
    for move in moves:
        childnode = node.children_by_move[move]
        if not Check_solved.is_weakly_solved_r(childnode, ai, turn, params):
            return False
    return True

Check_solved.is_weakly_solved_r = is_weakly_solved_r
修正箇所 
@staticmethod
元と同じなので省略
-   retval = True
    for move in moves:
        childnode = node.children_by_move[move]
-       retval = Check_solved.is_weakly_solved_r(childnode, ai, turn, params) and retval
+       if not Check_solved.is_weakly_solved_r(childnode, ai, turn, params):
+           return False
-   return retval
+   return True

Check_solved.is_weakly_solved_r = is_weakly_solved_r

上記の修正後に下記のプログラムで ai2s、ai14s、ai_gt6 のそれぞれに対して何回再帰呼び出しが行われたかを表示すると、実行結果のように ai2s の回数 が 58 のように劇的に削減された ことが確認できます。これは、ai2s は全ての合法手を選択するので、すぐに敗北するノードが探索されるから です。一方、ai14s と ai_gt6 は 敗北することがない ので、再帰呼び出しの回数は変化しません。

Check_solved.is_weakly_solved(ai2s)
print(Check_solved.count)
Check_solved.is_weakly_solved(ai14s)
print(Check_solved.count)
Check_solved.is_weakly_solved(ai_gt6, params)
print(Check_solved.count)

実行結果

   o False
   x False
Both False
58
   o True
   x True
Both True
3244
   o True
   x True
Both True
92128

次に、下記のプログラムでそれぞれの処理時間を計測します。

%%timeit
Check_solved.is_weakly_solved(ai2s, verbose=False)

実行結果

28.6 s ± 117 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

%%timeit
Check_solved.is_weakly_solved(ai14s, verbose=False)

実行結果

313 ms ± 3.04 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

%%timeit
Check_solved.is_weakly_solved(ai_gt6, params, verbose=False)

実行結果

190 ms ± 1.69 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

下記は修正前と修正後の処理時間と再帰呼び出しの回数をまとめたものです。A が修正前、B が修正後を表します。表から ai2s の処理速度が劇的に減り、それ以外は回数が変わらないのでほとんど変化しないことがわかります。

AI 処理時間A 回数A 処理時間B 回数B
ai2s 28700 ms 1099892 3.15 ms 58
ai14s 306 ms 3244 305.00 ms 3244
ai_gt6 179 ms 92128 191.00 ms 92128

2024/09/02 追記

実は、下記のプログラムの 3 行目のように、and 演算子の前に retval を記述する ように修正しても、相手が勝利した局面を発見した場合の枝狩りを行えます。

これは、以前の記事で説明した、and 演算子の前に記述された式が False になった場合は、and 演算子の後ろの式が実行されないという、短絡評価が行われる ことが原因です。具体的には、下記のような処理によって枝狩りが行われます。

  • is_weakly_solved_r の返り値が False になると、retval の値が False になる
  • その後の繰り返し処理では、下記の計算が行われ、短絡評価により後ろの再帰呼び出しは実行されない
    retval = False and Check_solved.is_weakly_solved_r(略) 
for move in moves:
    childnode = node.children_by_move[move]
    retval = retval and Check_solved.is_weakly_solved_r(childnode, ai, turn, params)
修正箇所 
for move in moves:
    childnode = node.children_by_move[move]
-   retval = Check_solved.is_weakly_solved_r(childnode, ai, turn, params) and retval
+   retval = retval and Check_solved.is_weakly_solved_r(childnode, ai, turn, params)

上記のプログラムでも問題はないのですが、短絡評価より return False のほうが残りの処理が行われなくなることが明確になる ので本記事では上記は採用しません。

board 属性の値が同じ局面に対する枝狩り

〇×ゲームのゲーム木には、ゲーム盤の状況を表す board 属性の値が同じ局面が多数存在する ので、is_weakly_solved_r でゲーム木を探索する際に、既にチェック済 の board 属性の値を持つノードを 再び探索する ことが 良くあります。

同じ board 属性 の値を持つ局面に対して AI が行う着手の一覧は同じになる ので、is_weakly_solved_r の返り値の値も同じ になります。従って、探索の際に 既にチェック済 の board 属性の値を持つノードを 再び探索した場合 は、そのノードの子ノードの探索を省略する という、枝狩りを行うことができます。

また、先程 相手が勝利したノードを探索した時点で False を返す ように is_weakly_solved_r を修正したので、新しいノードを探索 した時点で、それまでに探索した全てのノード に対する is_weakly_solved_r の 返り値は True になります。従って、既にチェック済 のノードに対する is_weakly_solved_r の 返り値は True になります。

ノードがチェック済であるかの判定は、前回の記事と同様の方法で、registered_board という変数に代入した set を利用する ことで行うことができます。具体的には、is_weakly_solved_r を下記のプログラムのように修正します。

  • 2 行目：仮引数に registered_boards を追加する
  • 3 行目：ノードの局面の board 属性を文字列に変換する
  • 4、5 行目：変換した文字列が registered_boards に登録されている場合は、このノードはチェック済なので True を返す。このノードは探索しない ので、この処理は 6 行目の count 属性の値を 1 増やす処理の前に行う必要がある
  • 7 行目：登録されていない場合は、局面を表す文字列を registered_boards に追加する
  • 10 行目：再帰呼び出しの際の実引数に registered_boards を追加する
 1  @staticmethod
 2  def is_weakly_solved_r(node, ai, turn, params, registered_boards):
 3      txt = node.mb.board_to_str()
 4      if txt in registered_boards:
 5          return True
 6      Check_solved.count += 1
 7      registered_boards.add(txt)
元と同じなので省略 
 8      for move in moves:
 9          childnode = node.children_by_move[move]
10          if not Check_solved.is_weakly_solved_r(childnode, ai, turn, params, registered_boards):
11              return False
12      return True
13
14  Check_solved.is_weakly_solved_r = is_weakly_solved_r
行番号のないプログラム 
@staticmethod
def is_weakly_solved_r(node, ai, turn, params, registered_boards):
    txt = node.mb.board_to_str()
    if txt in registered_boards:
        return True
    Check_solved.count += 1
    registered_boards.add(txt)
    if node.mb.status == turn or node.mb.status == Marubatsu.DRAW:
        return True
    elif node.mb.status != Marubatsu.PLAYING:
        return False
        
    if turn == node.mb.turn:
        moves = ai(node.mb, candidate=True, **params) 
    else:
        moves = node.mb.calc_legal_moves()
    for move in moves:
        childnode = node.children_by_move[move]
        if not Check_solved.is_weakly_solved_r(childnode, ai, turn, params, registered_boards):
            return False
    return True

Check_solved.is_weakly_solved_r = is_weakly_solved_r
修正箇所 
@staticmethod
-def is_weakly_solved_r(node, ai, turn, params):
+def is_weakly_solved_r(node, ai, turn, params, registered_boards):
+   txt = node.mb.board_to_str()
+   if txt in registered_boards:
+       return True
    Check_solved.count += 1
+   registered_boards.add(txt)
元と同じなので省略
    for move in moves:
        childnode = node.children_by_move[move]
-       if not Check_solved.is_weakly_solved_r(childnode, ai, turn, params):
+       if not Check_solved.is_weakly_solved_r(childnode, ai, turn, params, registered_boards):
            return False
    return True
    
Check_solved.is_weakly_solved_r = is_weakly_solved_r

次に、is_weakly_solved の中で is_weakly_solved を呼び出す処理を下記のプログラムのように修正します。

  • 3 ~ 6 行目：is_weakly_solved_r の実引数の最後に空の set を追加する
1  @staticmethod
2  def is_weakly_solved(ai, params=None, verbose=True):
元と同じなので省略
3      circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE,
4                                                     params, set())
5      cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS,
6                                                     params, set())
元と同じなので省略
7
8  Check_solved.is_weakly_solved = is_weakly_solved
行番号のないプログラム 
@staticmethod
def is_weakly_solved(ai, params=None, verbose=True):
    Check_solved.count = 0
    if params is None:
        params = {}
    if Check_solved.mbtree is None:
        Check_solved.mbtree = Mbtree.load("../data/aidata")
    root = Check_solved.mbtree.root
    circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params, set())
    cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params, set())
    result = circle_result and cross_result
    if verbose:
        print("   o", circle_result)
        print("   x", cross_result)
        print("Both", result)
    return result

Check_solved.is_weakly_solved = is_weakly_solved
修正箇所 
@staticmethod
def is_weakly_solved(ai, params=None, verbose=True):
元と同じなので省略
-   circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params)
+   circle_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CIRCLE, params, set())
-   cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params)
+   cross_result = Check_solved.is_weakly_solved_r(root, ai, Marubatsu.CROSS, params, set())
元と同じなので省略

Check_solved.is_weakly_solved = is_weakly_solved

上記の修正後に下記のプログラムで ai2s、ai14s、ai_gt6 のそれぞれに対して処理を行うと、実行結果のように 弱解決であるかを正しく判定できている ことが確認できます。また、それぞれの処理の回数が減っている ので、枝狩りの効果があった ことが確認できます。

Check_solved.is_weakly_solved(ai2s, verbose=False)
print(Check_solved.count)
Check_solved.is_weakly_solved(ai14s, verbose=False)
print(Check_solved.count)
Check_solved.is_weakly_solved(ai_gt6, params, verbose=False)
print(Check_solved.count)

実行結果

   o False
   x False
Both False
45
   o True
   x True
Both True
1366
   o True
   x True
Both True
5700

次に、下記のプログラムでそれぞれの処理時間を計測します。

%%timeit
Check_solved.is_weakly_solved(ai2s, verbose=False)

実行結果

2.83 ms ± 9.52 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%%timeit
Check_solved.is_weakly_solved(ai14s, verbose=False)

実行結果

178 ms ± 13.9 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

%%timeit
Check_solved.is_weakly_solved(ai_gt6, params, verbose=False)

実行結果

35.3 ms ± 427 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

下記は修正前と修正後の処理時間と再帰呼び出しの回数をまとめたものです。C が board 属性が同じノードを枝狩りした場合を表します。表からいずれの回数も減っており、特に ai_gt6 の回数と処理時間が大幅に減っている ことが確認できます。

AI 処理時間A 回数A 処理時間B 回数B 処理時間C 回数C
ai2s 28700 ms 1099892 3.15 ms 58 2.83 ms 45
ai14s 306 ms 3244 305.00 ms 3244 178.00 ms 1366
ai_gt6 179 ms 92128 191.00 ms 92128 35.30 ms 5700

このように、枝狩りを行うことで、探索の回数を減らすことができ、処理時間を減らすことができます。

さらなる枝狩りのアイディア

is_weakly_solved の処理は、枝狩りを行うことでいずれの場合も 1 秒未満で行うことができるようになりました。別の枝狩りを行うことでさらに処理時間を減らす ことができますが、この処理時間で不満はないの で、本記事ではこれ以上の枝狩りは行わないことにします。

以下に、さらなる枝狩りのアイディアをいくつか紹介しますので、興味がある方は実装してみて下さい。

同一局面による枝狩り

前回の記事で説明したように、〇×ゲームには同一局面が多数存在するので、同一局面による枝狩りを行うこともできます。ただし、同一局面による枝狩りは、AI が選択する着手の一覧 が、同一局面に対しても同じだけ回転、反転した着手の一覧に一致する場合 のみ行うことができる点に注意が必要です。例えば、その条件を満たさない ai1 に対しては正しい判定を行うことはできません。

ノードの評価値を使った枝狩り

上記のプログラムでは、決着がついた局面のノードを使って判定を行っていますが、ゲーム木の各ノードに計算された 評価値を使った枝狩り を行うことができます。例えば AI が 〇 を担当する場合 は、評価値が -1 のノードが探索 されると、そのノードから相手が最善手を選択し続けると敗北することになるので、その時点で弱解決の AI ではないことが確定 します。なお、AI が × を担当する場合は評価値が 1 のノードが探索された場合に弱解決の AI ではないことが確定します。

なお、弱解決の AI を判定する場合は評価値が -1 のノードが探索されることはない ので、この枝狩りによって再帰呼び出しの回数を減らす効果は得られません。

is_strongly_solved の修正

前回の記事で、is_strongly_solved を 同一局面を考慮 した mblist_by_board_min.dat を利用して判定するように修正 しましたが、それでは ai1 に対する正しい判定を行うことができない という欠点が生じます。そこで、同一局面を考慮しない mblist_by_board2.dat と考慮する mblist_by_board_min.dat のどちらを使って判定するかを 選択できるように修正 することにします。

具体的には、下記のプログラムのように修正します。

  • 5 行目：デフォルト値を True とする、同一局面を考慮する（consider）かどうかを表す仮引数 consider_samedata を追加する
  • 8 ~ 10、12 ~ 14 行目：consider_samedata が True の場合は、mblist_by_board_min.dat を、そうでない場合は mblist_by_board2.min からファイルから読み込むように修正する
  • 11、15、20、27 行目：ファイルから読み込んだデータを mblist というローカル変数に代入し、それを使って処理を行うように修正する
 1  from tqdm import tqdm
 2  from util import load_bestmoves, load_mblist
 3
 4  @staticmethod
 5  def is_strongly_solved(ai, params=None, consider_samedata=True):
 6      if Check_solved.bestmoves_by_board is None:
 7          Check_solved.bestmoves_by_board = load_bestmoves ("../data/bestmoves_by_board.dat")
 8      if consider_samedata:
 9          if Check_solved.mblist_by_board_min is None:
10              Check_solved.mblist_by_board_min = load_mblist("../data/mblist_by_board_min.dat")
11          mblist = Check_solved.mblist_by_board_min
12      else:
13          if Check_solved.mblist_by_board2 is None:
14              Check_solved.mblist_by_board2 = load_mblist("../data/mblist_by_board2.dat") 
15          mblist = Check_solved.mblist_by_board2        
16      if params is None:
17          params = {}
18      count = 0
19      incorrectlist = []
20      for mb in tqdm(mblist):
21          candidate = set(ai(mb, candidate=True, **params))
22          bestmoves = set(Check_solved.bestmoves_by_board[mb.board_to_str()])
23          if candidate <= bestmoves:
24              count += 1
25          else:
26              incorrectlist.append((mb, candidate, bestmoves))
27      nodenum = len(mblist)
28      print(f"{count}/{nodenum} {count/nodenum*100:.2f}%")
29      return count == nodenum, incorrectlist
30
31  Check_solved.is_strongly_solved = is_strongly_solved
行番号のないプログラム 
from tqdm import tqdm
from util import load_bestmoves, load_mblist

@staticmethod
def is_strongly_solved(ai, params=None, consider_samedata=True):
    if Check_solved.bestmoves_by_board is None:
        Check_solved.bestmoves_by_board = load_bestmoves ("../data/bestmoves_by_board.dat")
    if consider_samedata:
        if Check_solved.mblist_by_board_min is None:
            Check_solved.mblist_by_board_min = load_mblist("../data/mblist_by_board_min.dat")
        mblist = Check_solved.mblist_by_board_min
    else:
        if Check_solved.mblist_by_board2 is None:
            Check_solved.mblist_by_board2 = load_mblist("../data/mblist_by_board2.dat") 
        mblist = Check_solved.mblist_by_board2        
    if params is None:
        params = {}
    count = 0
    incorrectlist = []
    for mb in tqdm(mblist):
        candidate = set(ai(mb, candidate=True, **params))
        bestmoves = set(Check_solved.bestmoves_by_board[mb.board_to_str()])
        if candidate <= bestmoves:
            count += 1
        else:
            incorrectlist.append((mb, candidate, bestmoves))
    nodenum = len(mblist)
    print(f"{count}/{nodenum} {count/nodenum*100:.2f}%")
    return count == nodenum, incorrectlist

Check_solved.is_strongly_solved = is_strongly_solved
修正箇所 
from tqdm import tqdm
from util import load_bestmoves, load_mblist

@staticmethod
-def is_strongly_solved(ai, params=None):
+def is_strongly_solved(ai, params=None, consider_samedata=True):
    if Check_solved.bestmoves_by_board is None:
        Check_solved.bestmoves_by_board = load_bestmoves ("../data/bestmoves_by_board.dat")
-   if Check_solved.mblist_by_board_min is None:
-       Check_solved.mblist_by_board_min = load_mblist("../data/mblist_by_board_min.dat")
+   if consider_samedata:
+       if Check_solved.mblist_by_board_min is None:
+           Check_solved.mblist_by_board_min = load_mblist("../data/mblist_by_board_min.dat")
+       mblist = Check_solved.mblist_by_board_min
+   else:
+       if Check_solved.mblist_by_board2 is None:
+           Check_solved.mblist_by_board2 = load_mblist("../data/mblist_by_board2.dat") 
+       mblist = Check_solved.mblist_by_board2        
    if params is None:
        params = {}
    count = 0
    incorrectlist = []
-   for mb in tqdm(Check_solved.mblist_by_board):
+   for mb in tqdm(mblist):
        candidate = set(ai(mb, candidate=True, **params))
        bestmoves = set(Check_solved.bestmoves_by_board[mb.board_to_str()])
        if candidate <= bestmoves:
            count += 1
        else:
            incorrectlist.append((mb, candidate, bestmoves))
-   nodenum = len(Check_solved.mblist_by_board)
+   nodenum = len(mblist)
    print(f"{count}/{nodenum} {count/nodenum*100:.2f}%")
    return count == nodenum, incorrectlist

Check_solved.is_strongly_solved = is_strongly_solved

上記の修正後に、下記のプログラムで ai14s が強解決の AI であるかを、同一局面を考慮する場合と考慮しない場合で判定すると、実行結果のように異なるノード数で正しい判定が行われることが確認できます。

なお、下記のプログラムでは、先ほどと同様にクラス属性に直接 None を代入していますが、これらのクラス属性の初期化処理は util.py の Check_solved の定義の中に記述する必要があります。

Check_solved.mblist_by_board_min = None
Check_solved.mblist_by_board2 = None
result, incorrectlist = Check_solved.is_strongly_solved(ai14s)
print(result)

実行結果

100%|██████████| 431/431 [00:00<00:00, 2191.99it/s]
424/431 98.38%
False

result, incorrectlist = Check_solved.is_strongly_solved(ai14s, consider_samedata=False)
print(result)

実行結果

100%|██████████| 3191/3191 [00:01<00:00, 2895.01it/s]
3139/3191 98.37%
False

今回の記事のまとめ

今回の記事では、弱解決の AI であるかを判定する処理を実装しました。

また、その際にゲーム木の探索について説明し、枝狩りという処理によって探索を効率的に行う手法について説明しました。

本記事で入力したプログラム

今回の記事で定義した calc_same_boardtexts は util.py に保存することにします。

リンク 説明
marubatsu.ipynb 本記事で入力して実行した JupyterLab のファイル
marubatsu_new.py 今回の記事で更新した marubatsu.py
tree_new.py 今回の記事で更新した tree.py
util_new.py 今回の記事で更新した util.py

次回の記事

更新履歴

更新日時 更新内容
2024/09/02 is_weakly_solved_r の修正にノートを追記しました

  1. 以前の記事でこのクラスの名前を Chekc_strongly_solved のようにしなかったのは、弱解決の AI であるかの判定を行うメソッドを定義する予定だったからです ↩

  2. _r の r は、再帰呼び出し（recursive call）の英語の頭文字です ↩

  3. これ以外にも、様々な名前の付け方があります ↩

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?