LoginSignup
0
0
@ysgeso

Pythonで〇×ゲームのAIを一から作成する　その99　深さ優先アルゴリズムによるゲーム木の生成

Last updated at Posted at 2024-07-18

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク 説明
marubatsu.py Marubatsu、Marubatsu_GUI クラスの定義
ai.py AI に関する関数
util.py ユーティリティ関数の定義。現在は gui_play のみ定義されている
tree.py ゲーム木に関する Node、Mbtree クラスの定義
gui.py GUI に関する処理を行う基底クラスとなる GUI クラスの定義

ルールベースの AI の一覧

ルールベースの AI の一覧については、下記の記事を参照して下さい。

Mbtree のインスタンスの保存と読込

今回の記事では、ゲーム木を深さ優先アルゴリズムで作成する方法を紹介しますが、その前に Mbtree クラスのインスタンスをファイルに保存できるようにします。

Mbtree クラスのインスタンスの作成には 30 秒ほど時間がかかります。これまでの記事では、毎回 Mbtree クラスのインスタンスの作成を作成していたため、毎回 30 秒ほど待たされることになっていましたが、Mbtree クラスのインスタンスをファイルに保存 し、ファイルから読み込むことができるようにすれば、待たされる時間を減らす ことができます。

save メソッドの実装

Mbtree クラスのインスタンスのファイルへの保存は、以前の記事で説明した pickle モジュールを使って行うことができるので、下記のようなメソッドを定義する事にします。

名前：保存（save）を行うので、save という名前にする
処理：Mbtree クラスのインスタンスをファイルに保存する
入力：保存するファイルのパスを仮引数 fname に代入する。ただし、ファイルのパスに拡張子は含めないものとする
出力：なし

下記は、save メソッドの定義です。セーブファイルの拡張子は、他の pickle で保存したデータと区別ができる ように .mbtree としました。

  • 5 行目：with を使って、fname の末尾に拡張子である .mbtree を加えたファイルを、書き込みとバイナリモードで開く
  • 6 行目：自分自身のインスタンスを pickle.dump を使ってファイルに保存する
  • 7 行目：保存が完了したことを表すメッセージを表示する
1  from tree import Mbtree 
2  import pickle
3
4  def save(self, fname):
5      with open(f"{fname}.mbtree", "wb") as f:
6          pickle.dump(self.root, f)
7          print("save completed.")
8        
9  Mbtree.save = save
行番号のないプログラム 
from tree import Mbtree 
import pickle

def save(self, fname):
    with open(f"{fname}.mbtree", "wb") as f:
        pickle.dump(self, f)
        print("save completed.")
        
Mbtree.save = save

上記の実行後に、下記のプログラムを実行することで、Mbtree クラスのインスタンスをファイルに保存することができます。幅優先（breadth first）アルゴリズムで作成したゲーム木を保存するので、ファイルの名前は bftree としました。

mbtree = Mbtree()
mbtree.save("bftree")

実行結果

ゲーム木の生成時の表示は省略
save completed

上記の実行後に、プログラムが記述されている marubatsu.ipynb が保存されているフォルダの中に、bftree.mbtree という名前のファイルが保存されていることを確認して下さい。

load メソッドの定義

次に、保存したファイルを読み込む下記のようなメソッドを定義します。

名前：読み込み（load）を行うので、load という名前にする
処理：ファイルから Mbtree クラスのインスタンスを読み込む
入力：読み込むファイルのパスを仮引数 fname に代入する。ただし、ファイルのパスに拡張子は含めないものとする
出力：ファイルから読み込まれた Mbtree クラスのインスタンス

下記は load メソッドの定義です。ファイルから Mbtree クラスのインスタンスを読み込む処理に 必要な情報は fname だけ なので、このメソッドを 静的メソッド としました。

  • 1 行目：静的メソッドとして定義する
  • 3 行目：with を使って fname の末尾に拡張子である .mbtree を加えたファイルを、読み込みとバイナリモードで開く
  • 4 行目：pickle.load でファイルを読み込み、得られた Mbtree クラスのインスタンスを return 文で返り値として返す
1  @staticmethod
2  def load(fname):
3      with open(f"{fname}.mbtree", "rb") as f:
4          return pickle.load(f)
5
6  Mbtree.load = load
行番号のないプログラム 
@staticmethod
def load(fname):
    with open(f"{fname}.mbtree", "rb") as f:
        return pickle.load(f)

Mbtree.load = load

上記の実行後に、下記のプログラムの 2 行目を実行することで、Mbtree クラスのインスタンスをファイルから読み込むことができます。実行結果は省略しますが、ファイルが正しく読み込まれているかどうかを確認するために、3 行目でアニメーションを行いましたので、アニメーションが正しく行われることを確認して下さい。

from tree import Mbtree_Anim
mbtree_bf = Mbtree.load(fname="bftree")
mbtree_anim = Mbtree_Anim(mbtree_bf)

load メソッドを定義するのではなく、下記のように __init__ メソッドを修正することで、Mbtree(fname="bftree") のように Mbtree のインスタンスの作成時にファイルを読み込むことができるようにすれば良いと思った人がいるかもしれません。

  • __init__ メソッドの仮引数に、デフォルト値が None のデフォルト引数 fname を追加する
  • fname が None の場合はファイルからデータを読み込んで、その返り値を返す

具体的には下記のようなプログラムですが、このプログラムは正しく動作しません。

def __init__(self, fname=None):
    if fname is None:
        Node.count = 0
        self.root = Node(Marubatsu())
        self.create_tree_by_bf()
    else:
        with open(f"{fname}.mbtree", "rb") as f:
            return pickle.load(f)  

Mbtree.__init__ = __init__

上記の修正後に、下記のプログラムを実行すると、実行結果のようなエラーが発生します。エラーが発生する理由は、__init__ メソッド では、return 文で None 以外のデータを返すとエラーが発生する ようになっているからです。そのことは、__init__ は None を返す（return）べき（should）であるという意味のエラーメッセージにも表記されています。

mbtree = Mbtree("bftree")

実行結果

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[6], line 1
----> 1 mbtree_bf = Mbtree("bftree")

TypeError: __init__() should return None, not 'Mbtree'

ファイルの圧縮

bftree.mbtree には、50 万以上のノードの情報が記録される ので、ファイルのサイズは約 100 MB の大きさになります。そのことを実際に確認してみて下さい。下図は、Windows のエクスプローラで bftree.mbtree を表示したものです1。

このような大きなファイルには以下のような問題があります。

  • 保存や読み込みに時間がかかる。筆者のパソコンでは bftree.mbtree の保存と読み込みにそれぞれ約 10 秒かかった
  • 大きなファイルを数多く作成すると、ハードディスクなどの 記憶装置の容量を圧迫する

デジタルデータを、その内容を変更せず2に 小さくする処理 のことを 圧縮 と呼びます。また、圧縮されたデジタルデータを 元に戻す処理 のことを 展開 や、解凍 と呼びます。上記のような大きなデータをファイルに保存する際は、圧縮して保存することで上記の問題に対処するのが一般的です。

Python には、ファイルを圧縮 して保存したり、圧縮された ファイルを展開 して読み込むための gzip というモジュールが用意されています。gzip の使い方は簡単で、gzip モジュールをインポートした後 で、ファイルを開く際に open の代わりに gzip.open を記述する だけで行えます。

gzip の詳細については、下記のリンク先を参照して下さい。

下記は、ファイルを圧縮するように save と load メソッドを修正したプログラムです。

  • 4、12 行目：open を gzip.open に修正する
 1  import gzip
 2
 3  def save(self, fname):
 4      with gzip.open(f"{fname}.mbtree", "wb") as f:
 5          pickle.dump(self, f)
 6          print("save completed.")
 7       
 8  Mbtree.save = save 
 9
10  @staticmethod
11  def load(fname):
12      with gzip.open(f"{fname}.mbtree", "rb") as f:
13          return pickle.load(f)
14
15  Mbtree.load = load
行番号のないプログラム 
import gzip

def save(self, fname):
    with gzip.open(f"{fname}.mbtree", "wb") as f:
        pickle.dump(self, f)
        print("save completed.")
        
Mbtree.save = save 

@staticmethod
def load(fname):
    with gzip.open(f"{fname}.mbtree", "rb") as f:
        return pickle.load(f)

Mbtree.load = load
修正箇所 
import gzip

def save(self, fname):
-   with open(f"{fname}.mbtree", "wb") as f:
+   with gzip.open(f"{fname}.mbtree", "wb") as f:
        pickle.dump(self, f)
        print("save completed.")
        
Mbtree.save = save 

@staticmethod
def load(fname):
-   with open(f"{fname}.mbtree", "rb") as f:
+   with gzip.open(f"{fname}.mbtree", "rb") as f:
        return pickle.load(f)

Mbtree.load = load

上記の修正後に、下記のプログラムでファイルを保存し、作成された bftree.mbtree のファイルのサイズを確認すると、ファイルのサイズが下図の 12077 KB のように、約 1/10 に減った ことが確認できます。なお、上記の修正により、元の bftree.mbtree のファイルは利用できなくなる ので、下記では 同じ名前のファイルにデータを上書き しました。

mbtree.save("bftree")

下記は、新しい bftree.mbtree を load メソッドで読み込み、正しく読み込めていることを確認するためにアニメーションを表示するプログラムです。実行結果は省略しますが、正しく読み込めていることを確認してみて下さい。

mbtree_bf = Mbtree.load("bftree")
mbtree_anim = Mbtree_Anim(mbtree_bf)

ファイルが gzip で圧縮されていることを明確にしたい場合は、ファイルの拡張子として .gz が良く使われます。本記事で保存するファイルが gzip で圧縮されていることを明確にする必要はないと思いましたので、拡張子は .mbtree のままにしました

大きなファイルを圧縮、展開 すると、処理に時間がかかります。上記でファイルを約 1/10 に圧縮したにもかかわらず、保存、読み込みの時間が 1/10 にならない のはそのためです。

ファイルの サイズが大きくない場合 は、保存の際に 圧縮する必要はない でしょう。

深さ優先アルゴリズムによるゲーム木の作成

幅優先（breadth first）アルゴリズムは、以下の手順で、ノードの 深さの浅い順番 で、子ノードを作成する というものでした。

  1. ゲーム開始時の局面を表すノードを、ルートノードとするゲーム木を作成 する
  2. 子ノードを作成する処理を行う ノードの深さ d を 0 に設定 する
  3. 深さ d のノードが存在しない場合は、ゲーム木が完成しているので処理を終了する
  4. 深さ d のノードが存在する場合は、それらの全てのノードに対して子ノードを作成する
  5. 深さ d に 1 を足して 手順 3 に戻る

一方、深さ優先（depth first）アルゴリズム は、以下の手順で、次のノードを作成する際 に、深いノードから 優先的 にノードを作成します。わかりづらいかもしれませんが、深さの深い順に作成するわけではない点に注意して下さい。

  1. ゲーム開始時の局面を表すノードを、ルートノードとするゲーム木を作成する3
  2. 子ノードを作成する 処理を行う ノードを N と表記 し、N を ルートノードで初期化 する
  3. N にまだ 作成していない子ノードが存在するか を判定する
    1. 作成していない子ノードが 存在する場合 は、その子ノードを作成 し、作成した子ノードを N として手順 3 に戻る
    2. 作成していない子ノードが 存在しない場合 は、親ノードが存在するか を判定する
      1. 親ノードが 存在する場合 は、親ノードを N として手順 3 に戻る
      2. 親ノードが 存在しない場合 は、ゲーム木が完成しているので 処理を終了する

おそらく、この説明では意味がわからないと思いますので、具体例を挙げて説明します。

深さ優先アルゴリズムによるゲーム木の作成の例

上記では、ゲーム開始時の局面をルートノードとするゲーム木を作成しますが、深さ優先アルゴリズムで、任意のノードをルートノード とする 部分木を作成 することもできます。

具体的には上記の 手順 1 を下記のように修正します。

  1. 任意の局面を表すノードを、ルートノードとするゲーム木を作成 する

これは、前回の記事で、ゲーム開始時以外の局面をルートノード とする 部分木の各ノードの高さ を、幅優先アルゴリズムで計算 したのと似ています。

そこで、下図の左のノードをルートノードとする部分木を、深さ優先アルゴリズムで作成する手順を説明します。なお、以降の図ではノードを下記のように表記します。

  • 赤枠で表示 されたノードが、先程のアルゴリズムの中の、子ノードを作成する処理を行う ノード N を表す
  • 暗い色のノード が、今後追加される予定のノード を表す

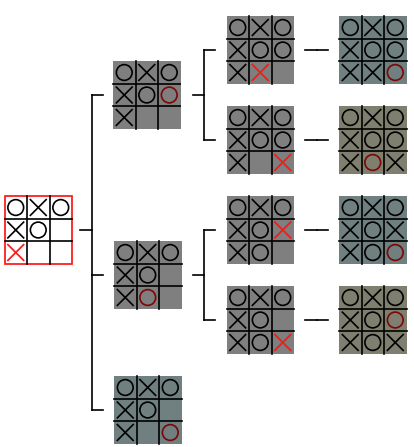
上図 は、下記の深さ優先アルゴリズムの 手順 1、2 を行った状態 なので、上図に対して手順 3 の処理を行っていくことにします。

1 回目の手順 3 の処理

手順 3 では「N にまだ作成していない子ノードが存在するか」を判定します。下図左の赤枠の N には作成していない子ノードが 3 つ存在します。

存在する場合は手順 3-1 の「作成していない子ノードが存在する場合は、その子ノードを作成し、作成した子ノードを N として手順 3 に戻る」という作業を行うので、下図右のように 赤枠の子ノードを作成 し、そのノードを N として手順 3 に戻ります。

　

2、3 回目の手順 3 の処理

上図右の赤枠の N には作成していない子ノードが存在するので、上記と同様の手順 で左下図の赤枠の子ノードが作成され、そのノードを N とします。同様の手順で右下図の赤枠の子ノードが作成され、そのノードを N とします。

　

4、5 回目の手順 3 の処理

上図右の赤枠の N には作成していない子ノードが 存在しない ので、左下図のようにその 親ノードが N になります。左下図の赤枠の N にも作成していない子ノードが存在しないので、右下図のようにその親ノードが N になります。4、5 回目の手順 3 の処理では 子ノードは作成されず、N が親ノードへ移動するだけの処理 が行われます。

　

6、7 回目の手順 3 の処理

上図右の赤枠の N には作成していない子ノードが存在するので、先程と同様の手順で左下図の赤枠の子ノードが作成され、そのノードを N とします。同様の手順で右下図の赤枠の子ノードが作成され、そのノードを N とします。

　

ノードが作成される順番

以後は同様 なので、それぞれの回の手順 3 で行われる処理の説明は省略し、ノードが作成される順番 を、画像を並べて示すことにします。右下の画像で すべてのノードが追加された後 で、N がルートノード になり、ルートノードには作成していない子ノードが存在せず、親ノードも存在しないので 部分木が完成して処理が終了 します。

　　　　　

　　　　　　

下図は、N が移動する順番 を表しています。赤い矢印 は 子ノードを作成 した後で N が移動する場合、紫の矢印 は ノードを作成せず に親ノードへ N が移動する場合を表します。

図からわかるように、深さ優先アルゴリズムでは、深いノードが優先 してノードが作成されるので、深さ優先 アルゴリズムと名付けられました。

下図は、幅優先アルゴリズム でノードを 作成する順番 を矢印で表したものです。本記事ではゲーム木の表示幅が横に広がりすぎるため、ゲーム木のノードを左から右に浅い順に表示してきましたが、木構造は 一般的 に 上から下に深さが浅い順にノードを表示 するので、下図ではそのようにしました。

図からわかるように、幅優先アルゴリズムでは、横幅を優先 しながらゲーム木を作成するように見えるので、幅優先 アルゴリズムと名付けられました。

2 つのアルゴリズムの違いと使い分け

〇×ゲームの ゲーム木を作成する場合 は、幅優先と深さ優先の どちらのアルゴリズムを使っても、問題なくゲーム木を 作成することができます。この 2 つのアルゴリズムの違いは、ゲーム木を使って評価値を計算する、探索と呼ばれる処理 を行う際などで 違いが生じます。また、どちらのアルゴリズムにも 長所と短所がある ため、適切に 使い分ける必要があります。それらに関しては、今後の記事で具体例を挙げて紹介する予定です。

深さ優先アルゴリズムによるプログラムの記述は、今後の記事で様々な場面で利用することになるので、深さ優先アルゴリズムを用いたゲーム木の作成を行うことにします。

再起呼び出しを使用しない深さ優先アルゴリズムを用いたゲーム木の作成

深さ優先アルゴリズムをプログラムで記述する際には、次回の記事で説明する 再起呼び出し という方法を使うのが一般的ですが、再起呼び出しは説明が必要なので、先に 再起呼び出しを使わず に深さ優先アルゴリズムでゲーム木を作成する方法を紹介します。

Mbtree クラスの __init__ メソッドの修正

現状の Mbtree クラスは、幅優先アルゴリズムでゲーム木を作成するようになっているので、__init__ メソッドを下記のプログラムのように、ゲーム木を 作成するアルゴリズム を インスタンスの作成時に選択できる ように修正します。

  • 4 行目：デフォルト値を、幅優先（breadth first）アルゴリズムを表す "bf" とする、アルゴリズム（algorithm）の略である仮引数 algo を追加する
  • 5 行目：algo を同名の属性に代入する
  • 8、9 行目：self.algo が "bf" の場合は、create_tree_by_bf を呼び出して 幅優先アルゴリズム でゲーム木を作成する
  • 8、9 行目：self.algo が "bf" 以外の場合 は、create_tree_by_df を呼び出して 深さ優先アルゴリズム でゲーム木を作成する。なお、このメソッドはこの後で定義する
 1  from tree import Node, Mbtree
 2  from marubatsu import Marubatsu
 3
 4  def __init__(self, algo="bf"):
 5      self.algo = algo
 6      Node.count = 0
 7      self.root = Node(Marubatsu())
 8      if self.algo == "bf":  
 9          self.create_tree_by_bf()
10      else:
11          self.create_tree_by_df()
12        
13  Mbtree.__init__ = __init__
行番号のないプログラム 
from tree import Node, Mbtree
from marubatsu import Marubatsu

def __init__(self, algo="bf"):
    self.algo = algo
    Node.count = 0
    self.root = Node(Marubatsu())
    if self.algo == "bf":  
        self.create_tree_by_bf()
    else:
        self.create_tree_by_df()
        
Mbtree.__init__ = __init__
修正箇所 
from tree import Node, Mbtree
from marubatsu import Marubatsu

def __init__(self, algo="bf"):
+   self.algo = algo
    Node.count = 0
    self.root = Node(Marubatsu())
-   self.create_tree_by_bf()
+   if self.algo == "bf":  
+       self.create_tree_by_bf()
+   else:
+       self.create_tree_by_df()
        
Mbtree.__init__ = __init__

上記のプログラムでは、algo に "bf" 以外が代入されていた場合は深さ優先アルゴリズムにしましたが、algo に "df" が代入されていた場合のみ 深さ優先アルゴリズムにするという実装も考えられます。ただし、その場合は、algo に "bf" と "df" 以外の値が代入 された場合は、エラーが発生する ようにプログラムを記述する必要がある点に注意して下さい。

create_tree_by_df の定義

次に、深さ優先アルゴリズムでゲーム木を作成する create_tree_by_df を定義します。なお、このメソッドの名前の df は、深さ優先を表す depth first の頭文字です。

行う処理は、先程説明した下記のアルゴリズムです。

  1. ゲーム開始時の局面を表すノードを、ルートノードとするゲーム木を作成する
  2. 子ノードを作成する 処理を行う ノードを N と表記 し、N を ルートノードで初期化 する
  3. N にまだ 作成していない子ノードが存在するか を判定する
    1. 作成していない子ノードが 存在する場合 は、その子ノードを作成 し、作成した子ノードを N として手順 3 に戻る
    2. 作成していない子ノードが 存在しない場合 は、親ノードが存在するか を判定する
      1. 親ノードが 存在する場合 は、親ノードを N として手順 3 に戻る
      2. 親ノードが 存在しない場合 は、ゲーム木が完成しているので 処理を終了する

また、その際に、create_tree_by_bf で計算した、下記のデータも計算するようにします。

属性名 意味
nodelist ゲーム木に登録された順番で、ノードを要素に持つ list
nodelist_by_depth それぞれの深さのノードの一覧を表す list
nodenum ゲーム木のノードの総数

手順 1 の実装

手順 1 のルートノードの作成は __init__ メソッド内の下記のプログラムで実装済なので、特に何も記述する必要はありません。

self.root = Node(Marubatsu())

nodelist 属性の初期化

次に、上記の表の 3 つの属性の値を初期化する処理を記述します。

まず、nodelist の初期化処理について説明します。

幅優先アルゴリズムでは、ゲーム木のノードを 深さが浅い順で作成 したので、create_tree_by_df では下記のプログラムのように、nodelist をゲーム木の 作成が完了した後 で、各深さのノードの一覧を結合 することで計算することができましたが、深さ優先アルゴリズムでは、ノードは 深さが浅い順に作成されない ので、下記の方法で nodelist を計算することはできません。

self.nodenum = 0
self.nodelist = []
for nodelist in self.nodelist_by_depth:
    self.nodenum += len(nodelist)
    self.nodelist += nodelist

深さ優先アルゴリズムの場合は、ノードを登録するたび に nodelist に append メソッドで登録した ノードを追加 する必要があります。従って、下記のプログラムの 2 行目のように、最初に nodelist を、既にゲーム木に追加されている ルートノードを要素とする list で初期化 する必要があります。

def create_tree_by_df(self):
    self.nodelist = [self.root]

Mbtree.create_tree_by_df = create_tree_by_df

nodelist_by_depth 属性の初期化

幅優先アルゴリズムでは、nodelist_by_depth の各要素は、下記のプログラムのように、各深さのノードの一覧を計算した後 で、append メソッドで 追加する ことで計算できましたが、深さ優先アルゴリズムでは 異なる深さのノードが次々に追加される ので、この方法では計算することはできません。どのように計算できるかについて少し考えてみて下さい。

while len(nodelist) > 0:
    # 深さが depth の子ノードの一覧を計算する
    childnodelist = [] 
    for node in nodelist:
        if node.mb.status == Marubatsu.PLAYING:
            node.calc_children()
            childnodelist += node.children
    # 深さが depth の子ノードの一覧を nodelist_by_depth に追加する
    self.nodelist_by_depth.append(childnodelist)
    nodelist = childnodelist
    depth += 1

nodelist_by_depth は下記の方法で計算することができます。

  • nodelist_by_depth の 各深さの要素 に 空の list を代入 しておく
  • ゲーム木に ノードを追加するたび に、nodelist_by_depth の 対応する深さのノードの要素 に、その ノードを追加 する

下記は、そのように create_tree_by_df を修正したプログラムです。ルートノードはゲーム木に追加済 なので 4 行目の処理を記述し忘れないように注意して下さい。

  • 3 行目：nodelist_by_depth には、深さが 0 ~ 9 まで 10 種類 の深さに対応するノードの一覧の情報を記録するので、リスト内包表記を利用して、10 個の空の list を要素として持つ list として初期化する。なお、[[]] * 10 と記述してはいけない点に注意すること
  • 4 行目：nodelist_by_depth の 深さ 0 のノードの一覧 に、ルートノードを追加 する
1  def create_tree_by_df(self):
2      self.nodelist = [self.root]
3      self.nodelist_by_depth = [[] for _ in range(10)]
4      self.nodelist_by_depth[0].append(self.root)
5    
6  Mbtree.create_tree_by_df = create_tree_by_df
行番号のないプログラム 
def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
    
Mbtree.create_tree_by_df = create_tree_by_df
修正箇所 
def create_tree_by_df(self):
    self.nodelist = [self.root]
+   self.nodelist_by_depth = [[] for _ in range(10)]
+   self.nodelist_by_depth[0].append(self.root)
    
Mbtree.create_tree_by_df = create_tree_by_df

nodenum 属性の初期化

nodenum は、create_tree_by_bf では、ゲーム木の完成後に nodelist_by_depth から nodelist を計算する処理の中でその計算を行いましたが、nodelist_by_depth から nodelist を計算する処理が無くなったので、以下のような方法で計算することにします。

  • ルートノードは登録済なので、最初に nodenum を 1 で初期化する
  • ゲーム木にノードを追加する度に nodenum に 1 を足す

下記はそのように create_tree_by_df を修正したプログラムです。

  • 5 行目：nodenum 属性を 1 で初期化する
1  def create_tree_by_df(self):
2      self.nodelist = [self.root]
3      self.nodelist_by_depth = [[] for _ in range(10)]
4      self.nodelist_by_depth[0].append(self.root)
5      self.nodenum = 1
6    
7  Mbtree.create_tree_by_df = create_tree_by_df
行番号のないプログラム 
def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
    self.nodenum = 1
    
Mbtree.create_tree_by_df = create_tree_by_df
修正箇所 
def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
+   self.nodenum = 1
    
Mbtree.create_tree_by_df = create_tree_by_df

なお、create_tree_by_bf と同様の方法で nodenum を計算することもできるので、そちらが良いと思った方はその方法を採用して下さい。

手順 2 の実装

下記の手順 2 は、下記のプログラムのように記述できます。

2. 子ノードを作成する処理を行うノードを N と表記し、N を ルートノードで初期化する

  • 2 行目：ローカル変数 N にルートノードを代入する。変数の名前がわかりづらいと思った方は、N を別の名前に変更しても良い
def create_tree_by_df(self):
元と同じなので省略
    N = self.root
    
Mbtree.create_tree_by_df = create_tree_by_df
行番号のないプログラム 
def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
    self.nodenum = 0

    N = self.root
    
Mbtree.create_tree_by_df = create_tree_by_df
修正箇所 
def create_tree_by_df(self):
元と同じなので省略
+   N = self.root
    
Mbtree.create_tree_by_df = create_tree_by_df

手順 3 の実装

下記の手順 3 を判定する方法について少し考えてみて下さい。

3. N にまだ作成していない子ノードが存在するかを判定する

完成したゲーム木では、ゲームの 決着がついていない ノードには、合法手の数だけ子ノードが存在 します。従って、上記の手順 3 は、以下の方法で判定することができます。

  • ゲームの 決着がついている場合 は、そもそも子ノードは存在しないので、まだ作成していない子ノードは 存在しない
  • 決着が ついていない場合 で、N の 子ノードの数 が 合法手の数よりも少ない場合 は、まだ作成していない子ノードは存在し、そうでなければ存在しない

下記は、create_tree_by_df に手順 3 の判定を追加したプログラムです。

  • 2 行目：N の局面の合法手の一覧を計算する
  • 3 行目：N の子ノードの数を計算する
  • 4 行目：ゲーム中であり、N の子ノードの数が合法手の数より小さいことを判定する
  • 5 行目：ここに手順 3.1 の処理を記述する
  • 7 行目：ここに手順 3.2 の処理を記述する
1  def create_tree_by_df(self):
元と同じなので省略
2      legal_moves = N.mb.calc_legal_moves()
3      childnum = len(N.children)
4      if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
5          pass
6      else:
7          pass
8    
9  Mbtree.create_tree_by_df = create_tree_by_df
行番号のないプログラム 
def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
    self.nodenum = 0
    
    N = self.root
    
    legal_moves = N.mb.calc_legal_moves()
    childnum = len(N.children)
    if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
        pass
    else:
        pass
    
Mbtree.create_tree_by_df = create_tree_by_df
修正箇所 
def create_tree_by_df(self):
元と同じなので省略
+   legal_moves = N.mb.calc_legal_moves()
+   childnum = len(N.children)
+   if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
+       pass
+   else:
+       pass
    
Mbtree.create_tree_by_df = create_tree_by_df

手順 3.1 の実装

下記の手順 3.1 の処理を実装する方法について少し考えてみて下さい。

3.1. 作成していない子ノードが存在する場合は、その子ノードを作成し、作成した子ノードを N として手順 3 に戻る

手順 3.1 の処理を行った後で 手順 3 に戻る必要がある ので、繰り返し処理 を記述する必要があります。また、手順 3.1 では 必ず手順 3 に戻る という処理を行うので、while 文による 無限ループ を記述することにします。なお、手順 3.2 の中に、ゲーム木の完成による 無限ループの終了の条件がある ので、無限ループを記述しても問題はありません。

N の子ノードは、合法手の一覧である legal_moves の 要素の順で作成する ことにします。その場合は、N の 作成済の子ノードの数を childnum とすると、legal_moves の中で、0 ~ childnum 未満 のインデックスの合法手を着手した 子ノードが作成済である ことを意味します。従って、次は legal_move[childnum] の合法手の着手を行った局面を表す ノードを作成 して N の 子ノードに追加 すればよいことがわかります。

子ノードの作成と追加の処理は Node クラスのインスタンスを作成し、insert メソッドを使って N の子ノードに作成したノードを追加する処理を行います。

その後、nodelist、nodelist_by_depth、nodenum の値を更新する処理を行う必要がある点を忘れないように注意して下さい。

下記は、そのように create_tree_by_df を修正したプログラムです。

  • 4 行目：while True: のブロックの中に手順 3.1、3.2 の処理を記述することで、無限ループを行うように修正する
  • 8 行目：追加する子ノードに対応する合法手の座標を計算する
  • 9、10 行目：N のノードの Marubatsu クラスのインスタンスの深いコピーを行い、それに対して合法手を着手して、子ノードの局面を表すデータを作成する
  • 11、12 行目：mb を局面、N を親ノード、深さを N のノードの深さ + 1 とするノードを作成し、N の子ノードに追加する
  • 13 ~ 15 行目：nodelist、nodelist_by_depth、nodenum の値を更新する
  • 16 行目：N を、作成した子ノードである node で更新する
 1  from copy import deepcopy
 2
 3  def create_tree_by_df(self):
元と同じなので省略
 4      while True:
 5          legal_moves = N.mb.calc_legal_moves()
 6          childnum = len(N.children)
 7          if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
 8              x, y = legal_moves[childnum]
 9              mb = deepcopy(N.mb)
10              mb.move(x, y)
11              node = Node(mb, parent=N, depth=N.depth + 1)
12              N.insert(node)
13              self.nodelist.append(node)
14              self.nodelist_by_depth[N.depth + 1].append(node)
15              self.nodenum += 1
16              N = node
17          else:
18              pass
19    
20  Mbtree.create_tree_by_df = create_tree_by_df
行番号のないプログラム 
from copy import deepcopy

def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
    self.nodenum = 0
    
    N = self.root
    
    while True:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
            x, y = legal_moves[childnum]
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            self.nodelist.append(node)
            self.nodelist_by_depth[N.depth + 1].append(node)
            self.nodenum += 1
            N = node
        else:
            pass
    
Mbtree.create_tree_by_df = create_tree_by_df
修正箇所（while True によるインデントの修正は省略します） 
from copy import deepcopy

def create_tree_by_df(self):
元と同じなので省略
+   while True:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
+           x, y = legal_moves[childnum]
+           mb = deepcopy(N.mb)
+           mb.move(x, y)
+           node = Node(mb, parent=N, depth=N.depth + 1)
+           N.insert(node)
+           self.nodelist.append(node)
+           self.nodelist_by_depth[N.depth + 1].append(node)
+           self.nodenum += 1
+           N = node
        else:
            pass
    
Mbtree.create_tree_by_df = create_tree_by_df

子ノードを作成する処理は、Node クラスの calc_children メソッドで行うことができるのではないかと思った人がいるかもしれませんが、このメソッドは名前が children のように複数形になっていることからわかるように、ノードの 全ての子ノードを作成する処理を行う ので、深さ優先アルゴリズムでは利用できません。

手順 3.2 の実装

下記は手順 3.2 を再掲したものです。

3.2. 作成していない子ノードが存在しない場合は、親ノードが存在するかを判定する
3.2.1. 親ノードが存在する場合は、親ノードを N として手順 3 に戻る
3.2.2. 親ノードが存在しない場合は、ゲーム木が完成しているので処理を終了する

手順 3.2 下記のプログラムのように実装できます。なお、幅優先アルゴリズムでは、作成したノードの深さを表示することで途中経過を表現しましたが、深さ優先アルゴリズムでは途中経過をうまく表示することができない ので、最後に作成したノードの数だけを表示するようにしました。

  • 4、5 行目：親ノードが存在しない場合は、break 文で無限ループを抜ける
  • 6、7 行目：そうでなければ、N に親ノードである N.parent を代入する
  • 9 行目：ゲーム木の作成が完了したので、作成したノードの数を表示する
 1  def create_tree_by_df(self):
元と同じなので省略
 2          if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
元と同じなので省略
 3          else:
 4              if N.parent is None:
 5                  break
 6              else:
 7                  N = N.parent
 8
 9      print(f"total node num = {self.nodenum}")
10
11  Mbtree.create_tree_by_df = create_tree_by_df
行番号のないプログラム 
def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
    self.nodenum = 0
    
    N = self.root
    
    while True:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
            x, y = legal_moves[childnum]
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            self.nodelist.append(node)
            self.nodelist_by_depth[N.depth + 1].append(node)
            self.nodenum += 1
            N = node
        else:
            if N.parent is None:
                break
            else:
                N = N.parent

    print(f"total node num = {self.nodenum}")
    
Mbtree.create_tree_by_df = create_tree_by_df
修正箇所 
def create_tree_by_df(self):
元と同じなので省略
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
元と同じなので省略
        else:
-           pass
+           if N.parent is None:
+               break
+           else:
+               N = N.parent

+   print(f"total node num = {self.nodenum}")
    
Mbtree.create_tree_by_df = create_tree_by_df

プログラムの改良

上記のような while True: による無限ループのプログラムは、無限ループから 抜ける条件かがわかりづらい という 欠点 があります。create_tree_by_df の無限ループから抜ける条件は、手順 3.2 で N.parent が None になる場合 ですが、以下の事から、while 文の条件式 を N が None ではない という条件式に修正することができます。

  • 最初は N にはルートノードが代入されるので、None ではない
  • 手順 3.1 では N に作成した子ノードが代入されるので N は None にはならない
  • 手順 3.2 では、N に親ノードが存在する場合だけ N に親ノードを代入するので、N は None にはならない
  • 上記から、現状のプログラムでは N に None が代入されることはない
  • 手順 3.2 で N の親ノードが None の場合に無限ループから抜けるが、無限ループから抜ける代わりに N に N.parent を代入 すると、N に None が代入 される。従って、そのように修正し、while 文の 条件式を N is not None に修正 することでも、ゲーム木が完成した際に無限ループから抜けることができる

下記は、そのように create_tree_by_df を修正したプログラムです。先ほどと比べて、while 文の 繰り返しが終了する条件がわかりやすくなった ことを確認して下さい。

  • 2 行目：while 文の条件式を、N が None ではないという条件に修正する
  • 7 行目：手順 3.2 の処理を、常に N に親ノードを代入する処理に修正する
 1  def create_tree_by_df(self):
元と同じなので省略
 2      while N is not None:
 3          legal_moves = N.mb.calc_legal_moves()
 4          childnum = len(N.children)
 5          if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
元と同じなので省略
 6          else:
 7              N = N.parent
 8               
 9      print(f"total node num = {self.nodenum}")
10    
11  Mbtree.create_tree_by_df = create_tree_by_df
行番号のないプログラム 
def create_tree_by_df(self):
    self.nodelist = [self.root]
    self.nodelist_by_depth = [[] for _ in range(10)]
    self.nodelist_by_depth[0].append(self.root)
    self.nodenum = 0
    
    N = self.root
    
    while N is not None:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
            x, y = legal_moves[childnum]
            mb = deepcopy(N.mb)
            mb.move(x, y)
            node = Node(mb, parent=N, depth=N.depth + 1)
            N.insert(node)
            self.nodelist.append(node)
            self.nodelist_by_depth[N.depth + 1].append(node)
            self.nodenum += 1
            N = node
        else:
            N = N.parent
                
    print(f"total node num = {self.nodenum}")
    
Mbtree.create_tree_by_df = create_tree_by_df
修正箇所 
def create_tree_by_df(self):
元と同じなので省略
    while N is not None:
        legal_moves = N.mb.calc_legal_moves()
        childnum = len(N.children)
        if N.mb.status == Marubatsu.PLAYING and childnum < len(legal_moves):
元と同じなので省略
        else:
            N = N.parent
                
    print(f"total node num = {self.nodenum}")
    
Mbtree.create_tree_by_df = create_tree_by_df

この修正を行わなくても、create_tree_by_df は正しく動作しますが、プログラムはわかりやすく記述したほうが良いと思いましたので修正しました。

動作の確認

上記の修正後に、下記のプログラムで深さ優先アルゴリズムでゲーム木を作成すると、実行結果から 幅優先アルゴリズムと同じ 549945 個のノードが作成された ことが確認できます。

mbtree_df = Mbtree(algo="df")

実行結果

total node num = 549945

実際には algo="bf" 以外を記述すれば深さ優先アルゴリズムでゲーム木が作成されますが、わかりやすさを重視して algo="df" を記述しました。

次に、下記のプログラムで作成したゲーム木を視覚化します。実行結果は幅優先アルゴリズムで作成したゲーム木を視覚化した場合と同じなので省略しますが、様々な操作を行い、正しく視覚化できることを確認して下さい。

from tree import Mbtree_GUI
mbtree_gui = Mbtree_GUI(mbtree_df)

ゲーム木の生成の過程のアニメーションの修正

次に、下記のプログラムで深さ優先アルゴリズムで作成したゲーム木の生成過程のアニメーションを表示してみることにします。実際にアニメーションを確認してみて下さい。

mbtree_anim = Mbtree_Anim(mbtree_df)

実行結果（右図は 0 ~ 19 フレームまでのアニメーションの繰り返しです）

実行結果から、深さ優先アルゴリズムでのゲーム木の生成過程がうまくアニメーションで表示されるように見えますが、少しわかりづらい と思った人はいないでしょうか？そう思った方は、どこがわかりづらいかを少し考えてみて下さい。

その原因の一つは、選択されたノード の 子ノードが表示されない 点にあります。

幅優先アルゴリズム の場合は、選択されたノードの 子ノード がゲーム木に 追加されるのは一般的にかなり先のフレーム になります。そのため、選択されたノードの子ノードが表示されていなくてもわかりづらくはありませんし、子ノードを表示してしまうと親ノードの兄弟ノードが表示されなくなってしまうので、表示しないほうがわかりやすくなります。

一方、深さ優先アルゴリズム の場合は、選択されたノードの 子ノード は、次のフレームで作成 されますが、上記のアニメーションでは、表示されていなかった子ノード が 次のフレームで表示されて選択される 点がわかりづらさの原因になっています。

そこで、深さ優先アルゴリズムの場合は、中心となるノード と 選択されたノード を 同じノードに修正 することにします。ただし、深さが 7 以上のノードが選択状態になった場合は、深さ 6 のノードを中心となるノードにする点は変更しません。

選択されたノードの深さが浅い場合は、アニメーションのゲーム木の表示がフレームごとに大きく変化するので、どうしてもアニメーションがわかりにくくなると思いますが、これは現状のアニメーションの方法ではどうしようもないと思います。

深さが 6 以上のノードが選択されたノードになった場合は、アニメーションのゲーム木の表示がフレームごとにほとんど変化しなくなるので、わかりやすくなると思います。深さ優先アルゴリズムの生成の過程を理解するためには、そのようなノードが選択されたフレームの挙動を見ると良いでしょう。

下記は、そのように Mbtree_Anim クラスの update_gui を修正したプログラムです。

  • 5 ~ 7 行目：ゲーム木を作成したアルゴリズムが幅優先アルゴリズムを表す "bf" の場合のみ、中心となるノードを選択されたノードの親ノードにするように修正する
1  import matplotlib.patches as patches
2
3  def update_gui(self):
元と同じなので省略
4      self.centernode = self.selectednode
5      if self.mbtree.algo == "bf":
6          if self.centernode.depth > 0:
7              self.centernode = self.centernode.parent
元と同じなので省略
8
9  Mbtree_Anim.update_gui = update_gui
行番号のないプログラム 
import matplotlib.patches as patches

def update_gui(self):
    self.ax.clear()
    self.ax.set_xlim(-1, self.width - 1)
    self.ax.set_ylim(0, self.height)   
    self.ax.invert_yaxis()
    self.ax.axis("off")   
    
    self.selectednode = self.mbtree.nodelist[self.play.value]
    self.centernode = self.selectednode
    if self.mbtree.algo == "bf":
        if self.centernode.depth > 0:
            self.centernode = self.centernode.parent
    while self.centernode.depth > 6:
        self.centernode = self.centernode.parent
    if self.centernode.depth <= 4:
        maxdepth = self.centernode.depth + 1
    elif self.centernode.depth == 5:
        maxdepth = 7
    else:
        maxdepth = 9
    self.mbtree.draw_subtree(centernode=self.centernode, selectednode=self.selectednode, ax=self.ax, maxdepth=maxdepth)
    for rect, node in self.mbtree.nodes_by_rect.items():
        if node.id > self.play.value:
            self.ax.add_artist(patches.Rectangle(xy=(rect.x, rect.y), width=rect.width, height=rect.height, fc="black", alpha=0.5))

Mbtree_Anim.update_gui = update_gui
修正箇所 
import matplotlib.patches as patches

def update_gui(self):
元と同じなので省略
    self.centernode = self.selectednode
-   if self.centernode.depth > 0:
-      self.centernode = self.centernode.parent
+   if self.mbtree.algo == "bf":
+       if self.centernode.depth > 0:
+           self.centernode = self.centernode.parent
元と同じなので省略

Mbtree_Anim.update_gui = update_gui

上記の修正後に、下記のプログラムでアニメーションを実行すると、実行結果の左図のように、修正前の右図と比較してアニメーションが少しわかりやすくなったことを確認して下さい。ただし、今回の修正で劇的にわかりやすさがかわることはありません。修正前の方がわかりやすいと思う人がいれば、元に戻して下さい。

mbtree_anim = Mbtree_Anim(mbtree_df)

実行結果（0 ~ 19 フレームまでのアニメーションの繰り返しです。なお、左図と右図は連動していないので、表示されるフレームがずれる場合があります）

　

データの保存

下記のプログラムで深さ優先アルゴリズムで作成されたゲーム木をファイルに保存します。

mbtree_df.save("dftree")

また、先程 Mbtree に algo という属性を加えた ので、下記のプログラムのように、幅優先アルゴリズムで作成したゲーム木のアニメーションを行おうとすると、実行結果のように algo という属性がないという意味のエラーが発生します。

Mbtree_Anim(mbtree_bf)

実行結果

略
Cell In[22], line 12
     10 self.selectednode = self.mbtree.nodelist[self.play.value]
     11 self.centernode = self.selectednode
---> 12 if self.mbtree.algo == "bf":
     13     if self.centernode.depth > 0:
     14         self.centernode = self.centernode.parent

AttributeError: 'Mbtree' object has no attribute 'algo'

そのため、実行結果は省略しますが、下記のプログラムで幅優先探索アルゴリズムでゲーム木を作成し直し、ファイルに保存し直す必要があります。

mbtree_bf = Mbtree()
mbtree_bf.save("bftree")

なお、bftree.mbtree や dftree.mbtree は、ファイルのサイズが大きい ので、それらを 利用しない回 では、github にそれらのファイルをアップロードしない ことにします。

今回の記事のまとめ

今回の記事では、最初にゲーム木をファイルに保存するようにしました。

次に、深さ優先アルゴリズムによるゲーム木の生成方法について説明し、これまでに学んだ方法で深さ優先アルゴリズムでゲーム木を作成するプログラムを実装しました。

次回の記事では、深さ優先アルゴリズムを実装する際に一般的に使われる、再起呼び出しについて説明します。

本記事で入力したプログラム

リンク 説明
marubatsu.ipynb 本記事で入力して実行した JupyterLab のファイル
tree_new.py 今回の記事で更新した tree.py
bftree.mbtree 幅優先探索アルゴリズムで作成したゲーム木の保存ファイル
dftree.mbtree 深さ優先探索アルゴリズムで作成したゲーム木の保存ファイル

次回の記事

  1. 1 MB = 1000 KB です ↩

  2. 圧縮には、データを完全に元に戻すことができる可逆圧縮と、データが完全に戻らない非可逆圧縮があります。非可逆圧縮は、可逆圧縮に比べてデータをより小さくすることができるので、画像や動画など、完全に元に戻らなくても大きな問題が発生しない場合に良く使われます ↩

  3. 手順 1 の、ゲーム開始時の局面をルートノードとするゲーム木から作成を開始するという点だけは、幅優先アルゴリズムと同じです ↩

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0