Pythonで〇×ゲームのAIを一から作成する その90 幅優先アルゴリズムによる任意の深さのゲーム木の作成と部分木の視覚化

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

ルールベースの AI の一覧

ルールベースの AI の一覧については、下記の記事を参照して下さい。

幅優先アルゴリズムによる任意の深さのゲーム木の作成

前回の記事では、下記の、幅優先アルゴリズム による、深さ 2 までのゲーム木の作成と視覚化を行いましたが、その際に記述した手法でを深さ 3 以上のゲーム木を作成すると、プログラムの記述が大変であるという問題があることを示しました。

1. ゲーム開始時の局面 を表すノードを ルートノード とする ゲーム木を作成 する
2. 子ノードを作成する処理を行う ノードの深さ d を 0 に設定 する
3. 深さ d のノードが存在しない場合は、ゲーム木が完成しているので処理を終了する
4. 深さ d のノードが存在する場合は、それらの 全てのノードに対して子ノードを作成 する
5. 深さ d に 1 を足して 手順 3 に戻る

下記は、前回の記事の最後で記述した、深さ 4 のゲーム木を作成するプログラムです。このプログラムの問題点は、深さ d のノードを作成する際に、for 文を深さの分だけ入れ子にして記述する必要がある というものです。

def create_tree_by_bf(self):
    # 深さ 1 のノードの作成
    self.root.calc_children()
    # 深さ 2 のノードの作成
    for childnode in self.root.children:
        childnode.calc_children()
        # 深さ 3 のノードの作成
        for grandchildnode in childnode.children:
            grandchildnode.calc_children()
            # 深さ 4 のノードの作成
            for greatgrandchildnode in grandchildnode.children:
                greatgrandchildnode.calc_children()

実は、上記のプログラムでは、深さ 2 のノードを すべて作成する前 に、深さ 3 のノードを 作成しはじめている ので、上記の 幅優先アルゴリズムの手順でゲーム木を作成していません。上記のプログラムが行う処理は、今後の記事で説明する深さ優先アルゴリズムと幅優先アルゴリズムを組み合わせたものです。

なお、深さ 2 までのゲーム木を作成する下記のプログラムでは、深さ 1 のノードをすべて作成してから深さ 2 のノードを作成するので、幅優先アルゴリズムのみが使われています。

def create_tree_by_bf(self):
    # 深さ 1 のノードの作成
    self.root.calc_children()
    # 深さ 2 のノードの作成
    for childnode in self.root.children:
        childnode.calc_children()

子ノードの一覧の記録

幅優先アルゴリズムで、深さ 3 以上のゲーム木を作成するためには、子ノードを作成する際に、作成した子ノードの一覧を list などで記録しておく 必要があります。具体的には、下記のアルゴリズムの手順 4 で、作成した深さ d + 1 の子ノードの一覧を記録しておくことで、手順 3 に戻った時に、記録しておいた子ノードの一覧を、次の深さのノードの一覧として利用 することができます。

1. ゲーム開始時の局面 を表すノードを ルートノード とする ゲーム木を作成 する
2. 子ノードを作成する処理を行う ノードの深さ d を 0 に設定 する
3. 深さ d のノードが存在しない場合は、ゲーム木が完成しているので処理を終了する
4. 深さ d のノードが存在する場合は、それらの 全てのノードに対して子ノードを作成 する
5. 深さ d に 1 を足して 手順 3 に戻る

具体的には、下記のプログラムのように create_tree_by_bf を修正します。なお、修正の際に、create_tree_by_bf に下記のような工夫を行いました。また、create_tree_by_bf は全面的に内容が変化したので、修正箇所は省略します。

• それぞれの深さ の ノードの一覧の情報 は、この後でノードの描画や、ノードを描画した際の高さを計算する際に必要となるので、nodelist_by_depth という属性に、list の形式で記録する。nodelist_by_depth には、深さ 0 のノードの一覧から順番に要素を追加するので、インデックスの番号がノードのリストの深さに等しくなる
• ゲーム木を作成 する処理には 時間がかかる ので、途中経過の報告 として、各深さのノードの作成が完了した時点で、作成した その深さのノードの数を表示 する
• 作成した ノードの総数を計算 して nodenum 属性に代入し、その 数を表示する

下記は、プログラムの説明です。

• それぞれの ローカル変数 は以下の意味を持つ
  • nodelist：手順 4 で子ノードを作成する、深さ depth のノードの一覧
  • depth：nodelist に記録された ノードの深さ
  • childlist：手順 4 で作成した、深さ depth + 1 のノードの一覧
• 5、6 行目：nodelist を、深さ 0 のノードの一覧を表す list で初期化し、nodelist の深さを表す depth を 0 で初期化する
• 11 行目：nodelist の中身が空になるまで繰り返し処理を行う（手順 3）
• 12 行目：手順 4 で作成する子ノードの一覧を記録する childnodelist を空の list で初期化する
• 13 ~ 15 行目：nodelist のそれぞれの子ノードに対して、14 行目で子ノードを作成する処理を行い、15 行目で childnodelist に、作成された子ノードの list を += 演算子で拡張する処理を行う
• 16 行目：深さ depth の全てのノードの子ノードを計算する処理が完了したので、node_list_by_depth 属性の要素に、作成した子ノードの list を追加する。この処理によって、depth + 1 番の要素に深さ depth + 1 のノードの list が代入される
• 17、18 行目：次の繰り返し処理では、childnodelist に代入された、depth + 1 の深さのノードに対して処理を行うので、nodelist に childnodelist を代入し、depth に 1 を加算する
• 19 行目：作成した深さ depth の子ノードの数を表示する。なお、各深さのノードの数の最大値は 6 桁の数値になるので、書式指定を表す :>6 を使って、6 桁の数値を右揃えで表示するように工夫した
• 21 ~ 24 行目：nodelist_by_depth 内の要素の数の合計を計算して nodenum 属性に代入し、24 行目でゲーム木のノードの総数を表示する

 1  from tree import Mbtree
 2
 3  def create_tree_by_bf(self):
 4      # 深さ 0 のノードを、子ノードを作成するノードのリストに登録する
 5      nodelist = [self.root]
 6      depth = 0
 7      # 各深さのノードのリストを記録する変数を初期化する
 8      self.nodelist_by_depth = [ nodelist ]
 9   
10      # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
11      while len(nodelist) > 0:
12          childnodelist = [] 
13          for node in nodelist:
14              node.calc_children()
15              childnodelist += node.children
16          self.nodelist_by_depth.append(childnodelist)
17          nodelist = childnodelist
18          depth += 1
19          print(f"{len(nodelist):>6} depth {depth} node created")
20        
21      self.nodenum = 0
22      for nodelist in self.node_list_by_depth:
23          self.nodenum += len(nodelist)
24      print(f"total node num = {self.nodenum}")
25
26  Mbtree.create_tree_by_bf = create_tree_by_bf

行番号のないプログラム

from tree import Mbtree

def create_tree_by_bf(self):
    # 深さ 0 のノードを、子ノードを作成するノードのリストに登録する
    nodelist = [self.root]
    depth = 0
    # 各深さのノードのリストを記録する変数を初期化する
    self.nodelist_by_depth = [ nodelist ]
    
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            node.calc_children()
            childnodelist += node.children
        self.nodelist_by_depth.append(childnodelist)
        nodelist = childnodelist
        depth += 1
        print(f"{len(nodelist):>6} depth {depth} node created")
        
    self.nodenum = 0
    for nodelist in self.nodelist_by_depth:
        self.nodenum += len(nodelist)
    print(f"total node num = {self.nodenum}")

Mbtree.create_tree_by_bf = create_tree_by_bf

上記の修正後に、下記のプログラムを実行すると、実行結果から下記の事がわかります。

• 深さ 9 までのノードが作成された
• 9 手目の局面を表す 深さ 9 のノード が 362880 個 もある
• 〇×ゲームの 局面の総数 を表す、ゲーム木の ノードの総数 が 986410 個 もある

ノードを作成する際に、deepcopy で Marubatsu クラスのインスタンスを複製する処理を行うため、この処理は 約 100 万回もの deepcopy による複製の処理 が行われます。そのため、上記の処理には時間がかかり、筆者のパソコンでは 約 60 秒 の時間がかかりました。

mbtree = Mbtree()

実行結果

     9 depth 1 node created
    72 depth 2 node created
   504 depth 3 node created
  3024 depth 4 node created
 15120 depth 5 node created
 60480 depth 6 node created
181440 depth 7 node created
362880 depth 8 node created
362880 depth 9 node created
     0 depth 10 node created
total node num = 986410

なお、着手の順番によって 異なるノードが完全に同じ局面 になる¹場合がありますが、現時点では それらは別々のノードとして扱う ことにします。また、以前の記事で説明した 同一局面 も 考慮に入れません。従って、ゲーム木には、数多くの完全に同じ局面や、同一局面のノードが存在しますが、最強の AI を作成する際に、処理の効率の面を除けば、そのことは問題にはなりません。同一局面などについては、今後の記事で考慮に入れる予定です。

間違った各深さのノードの数の計算方法

実は、〇×ゲームのゲーム木の ノードの数 は 約 100 万 ではありません。その理由は、create_tree_by_bf に一つ大きなバグがあるからです。そのバグが何であるかについて少し考えてみて下さい。

まず、各深さのノードの数を計算する 間違った方法の考え方 について説明します。

〇×ゲームでは、最初は 9 つのマスが開いているので合法手の数は 9 です。従って 1 手目の着手の種類は 9 通りあります。

〇×ゲームは、着手を行うたびにゲーム盤のマスが 1 つ埋まる ので、2 手目を着手する局面の合法手の数は 8 です。従って、2 手目までの着手の組み合わせは 9 * 8 = 72 通りあります。3 手目も同様で、3 手目までの着手の組み合わせは 9 * 8 * 7 = 504 になります。

下記は、1 ~ 9 手目の着手の組み合わせの数の計算式と計算結果を表にしたものです。計算結果 と先程の 実行結果 に表示された数字が 一致する ことを確認して下さい。

手数	着手の組み合わせの数の計算式	計算結果
1	$9$	9
2	$9 × 8$	72
3	$9 × 8 × 7$	504
4	$9 × 8 × 7 × 6$	3024
5	$9 × 8 × 7 × 6 × 5$	15120
6	$9 × 8 × 7 × 6 × 5 × 4$	60480
7	$9 × 8 × 7 × 6 × 5 × 4 × 3$	181440
8	$9 × 8 × 7 × 6 × 5 × 4 × 3 × 2$	362880
9	$9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1$	362880

9 手目までの着手の組み合わせの式のように、1 から特定の整数までの数を掛け算する という計算を 階乗 と呼び、数学では $9!$ のように、! の記号を使って表現します。

上記のそれぞれの式は、下記の表の式のように階乗を使って記述することができるので、d 手目までの着手の組み合わせの数は $\frac{9!}{(9-d)!}$ で計算することができます。なお、9 手目の式には 0 の階乗 を表す $0!$ がありますが、数学では $0! = 1$ と 定義されている²のでこの式で正しく計算することができます。

手数	式	階乗を使った式
1	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}$	$ \frac{9!}{8!}$
2	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{7 × 6 × 5 × 4 × 3 × 2 × 1}$	$ \frac{9!}{7!}$
3	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{6 × 5 × 4 × 3 × 2 × 1}$	$ \frac{9!}{6!}$
4	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{5 × 4 × 3 × 2 × 1}$	$ \frac{9!}{5!}$
5	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{4 × 3 × 2 × 1}$	$ \frac{9!}{4!}$
6	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{3 × 2 × 1}$	$ \frac{9!}{3!}$
7	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{2 × 1}$	$ \frac{9!}{2!}$
8	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{1}$	$ \frac{9!}{1!}$
9	$\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{1}$	$ \frac{9!}{0!}$

正しい各深さのノードの数の計算方法

上記の考え方は一見正しいように見えるかもしれませんが、決着がついた局面 には 合法手が存在しない ことを考慮していない点が間違っています。

従って、create_tree_by_bf の問題点は、ゲームの決着がついていた場合でも子ノードを計算してしまう ことなので、下記のプログラムのように修正する必要があります。

• 8 ~ 10 行目：node の局面が決着がついていない場合のみ子ノードを計算するようにする

 1  from marubatsu import Marubatsu
 2
 3  def create_tree_by_bf(self):
元と同じなので省略
 4      # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
 5      while len(nodelist) > 0:
 6          childnodelist = [] 
 7          for node in nodelist:
 8              if node.mb.status == Marubatsu.PLAYING:
 9                  node.calc_children()
10                  childnodelist += node.children
元と同じなので省略
11
12  Mbtree.create_tree_by_bf = create_tree_by_bf

行番号のないプログラム

from marubatsu import Marubatsu

def create_tree_by_bf(self):
    # 深さ 0 のノードを、子ノードを作成するノードのリストに登録する
    nodelist = [self.root]
    depth = 0
    # 各深さのノードのリストを記録する変数を初期化する
    self.nodelist_by_depth = [ nodelist ]
    
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            if node.mb.status == Marubatsu.PLAYING:
                node.calc_children()
                childnodelist += node.children
        self.nodelist_by_depth.append(childnodelist)
        nodelist = childnodelist
        depth += 1
        print(f"{len(nodelist):>6} depth {depth} node created")
        
    self.nodenum = 0
    for nodelist in self.nodelist_by_depth:
        self.nodenum += len(nodelist)
    print(f"total node num = {self.nodenum}")

Mbtree.create_tree_by_bf = create_tree_by_bf

修正箇所

from marubatsu import Marubatsu

def create_tree_by_bf(self):
元と同じなので省略
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
-           node.calc_children()
-           childnodelist += node.children
+           if node.mb.status == Marubatsu.PLAYING:
+               node.calc_children()
+               childnodelist += node.children
元と同じなので省略

Mbtree.create_tree_by_bf = create_tree_by_bf

上記以外にも、下記のような修正方法があります。

• calc_children のほうで、決着がついた局面の場合は、子ノードを計算しないようにする
• 決着がついた局面で、合法手を返さないように calc_legal_moves を修正する

上記の修正後に、下記のプログラムを実行すると正しいゲーム木が作成されます。

mbtree = Mbtree()

実行結果

     9 depth 1 node created
    72 depth 2 node created
   504 depth 3 node created
  3024 depth 4 node created
 15120 depth 5 node created
 54720 depth 6 node created
148176 depth 7 node created
200448 depth 8 node created
127872 depth 9 node created
     0 depth 10 node created
total node num = 549946

また、上記の実行結果から下記の事がわかります。

• 深さ 9 のノード は、先程の約 1/3 の 127872 個 である
• ゲーム木の ノードの総数 は先ほどの約半数の 549946 個 である
• 〇×ゲームは、〇 の 3 回目の着手が行われる 5 手目までは決着がつかないので、深さ 5 までのノードの数は先ほどと変わらない

また、ノードの数が約半数に減少したので、筆者のパソコンでは上記の処理は、先程の約半分の約 35 秒かかりました。

表示範囲を限定したゲーム木の部分木の視覚化

上記の実行結果からわかるように、〇×ゲームのゲーム木は、最もノードの数が多い 深さが 8 のノードが 20 万以上 もあります。これまで行ってきたゲーム木の視覚化では、ゲーム盤 を 縦方向に y 座標が 4 おきに描画 していたので、その方法でゲーム盤を描画すると、縦方向の画像のサイズ が 4 * 約 20 万 = 約 100 万という途方もない大きさ になるので、ゲーム木のすべてを描画 するのは 現実的ではありません。

深さ 8 のノードの数が 20 万以上になるということに驚いている人がいるかもしれませんが、〇×ゲームのゲーム木の規模は、オセロや将棋などの、他の多くのゲームのゲーム木と比較すれば、非常に小さいです。

例えば、将棋のゲーム木の場合は、7 手目までの合法手の組み合わせの数を表す、深さ 7 のノードの数はこちらのページによると 約 150 億もあるようです。また、同一局面のノードを同じノードとみなした場合の将棋のゲーム木のノードの総数は、こちらの論文によると $10^{68}$ ~ $10^{69}$ もあるそうです。

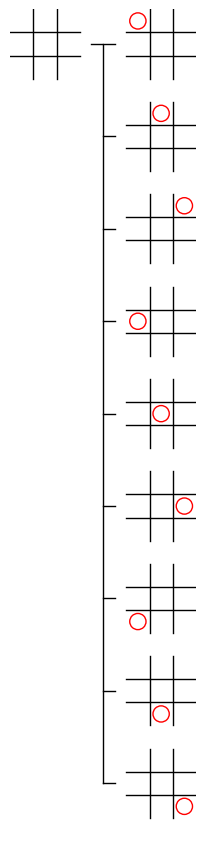
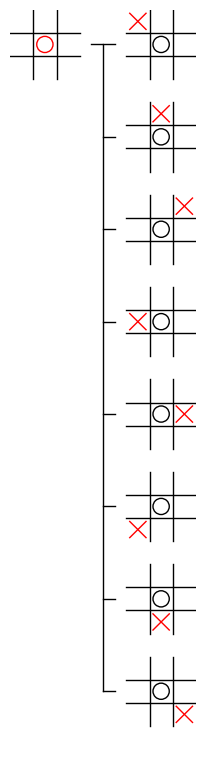
木構造の一部 のうち、それ自体が 木構造を持つもの のことを 部分木 と呼びます。例えば、下図左の、ルートノードから深さ 1 までのノードとそれらをつなぐエッジを取り出したものは、木構造を持つのでゲーム木の部分木です。下図右の、(1, 1) に着手を行ったノードから、その子ノードとそれらをつなぐエッジを取り出したものも部分木です。

　

部分木は木の一部なので、ゲーム木の部分木を描画する処理を実装 する事で、表示範囲を限定した、現実的な大きさのゲーム木を描画 することができるようになります。

ルートノードからの深さを限定した部分木の描画

ルートノードから、特定の深さまで のノードとそれらをつなぐエッジを 取り出したものは部分木になる ので、最初にそのような部分木を描画する処理を実装することにします。

最初に、表示する 木の深さ を代入する maxdepth という仮引数を draw_tree に追加することで、特定の深さまでの、ゲーム木の一部だけを描画する処理を実装することにします。

特定の深さまでのノードの高さを計算する処理の実装

draw_tree で maxdepth までの深さのノードを描画するためには、maxdepth までの深さ のそれぞれの ノードの高さを計算する必要 があります。そこで、ノードの高さを計算する calc_node_height の仮引数に、高さを計算するノードの深さの最大値を代入する maxdepth を追加 して、指定した深さまでのノードの高さだけを計算 するように修正します。なお、元の calc_node_height から全面的な修正が行われたので修正箇所は省略します。

• 1 行目：ノードの深さの最大値を代入する仮引数 maxdepth を追加する
• 2 行目：ノードの高さは、深い順に計算する必要があるので、range の step に -1 を設定することで、maxdepth から 0 まで、深さを 1 ずつ減らしながら ノードの高さを計算する。なお、繰り返し処理で range から得られる整数は、range の 2 つ目の実引数の値は含まない ので、maxdepth から 0 まで 1 ずつ数値を減らしながら繰り返しを行いたい場合は、2 つ目の実引数に -1 を記述する必要がある 点に注意する事
• 3 行目：深さ depth のノードの一覧が代入されている self.node_list_by_depth[depth] から順番にノードを取り出す繰り返し処理を行う
• 4、5 行目：深さが maxdepth のノード は、その 子ノードを描画しない ので、子ノードが存在しているかどうかに関わらず 高さを表す height 属性に 4 を代入 する
• 6、7 行目：それ以外の場合は、calc_height を使ってノードの高さを計算する

1  def calc_node_height(self, maxdepth):
2      for depth in range(maxdepth, -1, -1):
3          for node in self.nodelist_by_depth[depth]:
4              if depth == maxdepth:
5                  node.height = 4
6              else:
7                  node.calc_height()
8
9  Mbtree.calc_node_height = calc_node_height

行番号のないプログラム

def calc_node_height(self, maxdepth):
    for depth in range(maxdepth, -1, -1):
        for node in self.nodelist_by_depth[depth]:
            if depth == maxdepth:
                node.height = 4
            else:
                node.calc_height()

Mbtree.calc_node_height = calc_node_height

上記の修正後に、下記のプログラムを実行すると、実行結果のように、深さ 2 までの各ノードを描画した際の高さが正しく計算されていることが確認できます。

mbtree.calc_node_height(maxdepth=2)
for depth in range(3):
    for node in mbtree.nodelist_by_depth[depth]:
        print(f"depth {depth} height {node.height}")

実行結果（長いのでクリックして表示して下さい）

depth 0 height 288
depth 1 height 32
depth 1 height 32
depth 1 height 32
depth 1 height 32
depth 1 height 32
depth 1 height 32
depth 1 height 32
depth 1 height 32
depth 1 height 32
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4
depth 2 height 4

下記は、深さ 9 までの、すべてのノードを描画する場合の高さを計算し、ルートノードの高さのみを表示するプログラムです。実行結果から、ゲーム木全体を描画する場合は、高さが 100 万を超えるようなサイズになることが確認できました。

mbtree.calc_node_height(maxdepth=9)
print(mbtree.root.height)

実行結果

1020672

特定の深さまでの部分木を描画する処理の実装

次に、下記のプログラムのように、ルートノードから特定の深さまでの部分木を描画する ように draw_tree を修正します。なお、深さ 3 以上の部分木を描画すると高さが非常に長くなるので、深さを表す実引数を省略した場合は深さ 2 の部分木を描画するようにしました。

• 3 行目：描画する部分木の深さの最大値を代入する仮引数 maxdepth を、デフォルト値を 2 とするデフォルト引数として追加する
• 4 行目：maxdepth までの深さのノードの高さを計算する
• 5 行目：ゲーム盤とゲーム盤の横の間隔を 2 としたので、前回の記事で説明したように、Figure の横幅は 5 * (maxdepth + 1) - 2³ で計算できる。ただし、式を簡潔にするために、ここでは 5 * (maxdepth + 1) とした
• 13 行目：深さ 0 から maxdepth - 1 まで順にノードを描画する。なお、深さ maxdepth のノード は、深さ maxdepth - 1 のノードを描画する際に、子ノードとして描画される ので maxdepth - 1 の深さまでの描画を行えば良い
• 14 行目：ノードを描画する y 座標を表す dy を 0 で初期化する
• 15 ~ 17 行目：深さ depth のノードを順番に描画する。深さ depth のノードの座標は (5 * depth, dy) である。また、描画を行うたびに dy に描画したノードの高さを加算する⁴

 1  import matplotlib.pyplot as plt
 2
 3  def draw_tree(self, size=0.25, lw=0.8, maxdepth=2):
 4      self.calc_node_height(maxdepth)
 5      width = 5 * (maxdepth + 1)
 6      height = self.root.height
 7      fig, ax = plt.subplots(figsize=(width * size, height * size))
 8      ax.set_xlim(0, width)
 9      ax.set_ylim(0, height)   
10      ax.invert_yaxis()
11      ax.axis("off")        
12    
13      for depth in range(maxdepth):
14          dy = 0
15          for node in self.nodelist_by_depth[depth]:
16              node.draw_node(ax=ax, size=size, lw=lw, dx=depth*5, dy=dy)
17              dy += node.height
18        
19  Mbtree.draw_tree = draw_tree

行番号のないプログラム

import matplotlib.pyplot as plt

def draw_tree(self, size=0.25, lw=0.8, maxdepth=2):
    self.calc_node_height(maxdepth)
    width = 5 * (maxdepth + 1)
    height = self.root.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
    for depth in range(maxdepth):
        dy = 0
        for node in self.nodelist_by_depth[depth]:
            node.draw_node(ax=ax, size=size, lw=lw, dx=depth*5, dy=dy)
            dy += node.height
        
Mbtree.draw_tree = draw_tree

修正箇所

import matplotlib.pyplot as plt

-def draw_tree(self, size=0.25, lw=0.8):
+def draw_tree(self, size=0.25, lw=0.8, maxdepth=2):
-   self.calc_node_height()
+   self.calc_node_height(maxdepth)
-   width = 13
+   width = (maxdepth + 1) * 5
    height = self.root.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
-   # 深さ 0 のノードの描画
-   self.root.draw_node(ax=ax, size=size, lw=lw)
-   dy = 0
-   # 深さ 1 のノードの描画
-   for childnode in self.root.children:
-       childnode.draw_node(ax=ax, size=size, lw=lw, dx=5, dy=dy)
-       dy += childnode.height
+   for depth in range(maxdepth):
+       dy = 0
+       for node in self.nodelist_by_depth[depth]:
+           node.draw_node(ax=ax, size=size, lw=lw, dx=depth*5, dy=dy)
+           dy += node.height
        
Mbtree.draw_tree = draw_tree

描画処理の確認

下記のプログラムを実行すると、実行結果のように、深さ 2 までの部分木が描画されます。なお、実行結果は前回の記事で行った描画と同じ内容になります。

mbtree.draw_tree(maxdepth=2)

実行結果（長いのでクリックした表示して下さい）

また、下記のプログラムを実行すると、実行結果のように深さ 3 までの部分木を描画することができます。なお、そのままだと画像が大きくなりすぎるので、size と lw を使ってゲーム盤を小さく描画しました。

mbtree.draw_tree(size=0.1, lw=0.4, maxdepth=3)

実行結果（長いのでクリックした表示して下さい）

上図で、深さ 1、2 のノードが濃く描画されるのは目の錯覚ではありません。今回の記事の後半で説明しますが、それらのノードは 2 回描画されるため濃くなります。

下記のプログラムで 深さ 4 まで の部分木の描画を行おうとすると、実行結果のようなエラーが発生します。これは、matplotlib では、作成できる 画像のピクセルのサイズの最大値が 65536⁵ で、それを超えるような 120960 ピクセルの高さの画像を作成しようとしたことが原因です。size の値をさらに小さくすれば深さ 4 くらいまでであれば描画することは可能ですが、それ以上の深さのゲーム木を描画しようとすると、ゲーム盤が小さすぎて肉眼で確認できなくなる点と、処理に非常に長い時間がかかるという問題が発生します。

mbtree.draw_tree(size=0.1, lw=0.4, maxdepth=4)

実行結果

略
     68 self.width = width
     69 self.height = height
---> 70 self._renderer = _RendererAgg(int(width), int(height), dpi)
     71 self._filter_renderers = []
     73 self._update_methods()

ValueError: Image size of 250x120960 pixels is too large. It must be less than 2^16 in each direction.

特定のノードから特定の深さまでの部分木の描画

上記のように、ルートノードから深いノードまでの部分木を描画しようとすると、画像が大きくなりすぎて表示が困難になるという問題があるため、このままではゲーム木の 深いノードを描画することは困難 です。そこで、ゲーム木の 特定のノードから、特定の深さまで の部分木を描画するように draw_tree を修正することにします。

そのために draw_tree に、描画を開始（start）する 部分木のルートノード を代入する startnode という属性を追加します。ただし、startnode に対応する実引数を省略した場合は、ルートノードから描画されるようにするようにします。

下記は、修正前の draw_tree のプログラムです。このプログラムに修正を加えていきます。

def draw_tree(self, size=0.25, lw=0.8, maxdepth=2):
    self.calc_node_height(maxdepth)
    width = 5 * (maxdepth + 1)
    height = self.root.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
    for depth in range(maxdepth):
        dy = 0
        for node in self.nodelist_by_depth[depth]:
            node.draw_node(ax=ax, size=size, lw=lw, dx=depth*5, dy=dy)
            dy += node.height

描画を開始する部分木のルートノードを代入する仮引数の追加

まず、下記のプログラムのように、描画を開始する部分木のルートノードを代入する仮引数 startnode に関する処理を追加します。

• 1 行目：デフォルト値を None とする仮引数 startnode を追加する
• 2、3 行目：startnode が None の場合に、startnode にルートノードを代入する

1  def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
2      if startnode is None:
3          startnode = self.root
元と同じなので省略
4        
5  Mbtree.draw_tree = draw_tree

行番号のないプログラム

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
    if startnode is None:
        startnode = self.root
    self.calc_node_height(maxdepth)
    width = 5 * (maxdepth + 1)
    height = self.root.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
    for depth in range(maxdepth):
        dy = 0
        for node in self.nodelist_by_depth[depth]:
            node.draw_node(ax=ax, size=size, lw=lw, dx=depth*5, dy=dy)
            dy += node.height
        
Mbtree.draw_tree = draw_tree

修正箇所

-def draw_tree(self, size=0.25, lw=0.8, maxdepth=2):
+def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
+   if startnode is None:
+       startnode = self.root
元と同じなので省略
        
Mbtree.draw_tree = draw_tree

描画するノードの高さの計算

startnode から、深さ maxdepth までの部分木を描画する際には、これまでと同様に、描画するノードの高さを計算 する必要がありますが、その高さを計算する self.calc_node_height(maxdepth) を修正する必要はありません。

例えば深さ 1 の、(0, 0) に 〇 が配置されたノードから、深さ 2 までのノードの部分木を描画する場合のことを考えてみて下さい。そのような部分木は、下図のルートノードから深さ 2 までのノードを描画した場合の画像の中の、赤枠で囲った部分と同じになります。

別の言葉で説明すると、startnode から深さ maxdepth までのノードまでの部分木は、上図の赤い枠の部分のように、ルートノードから深さ maxdepth までのノードの部分木に 必ず含まれ、同じ大きさで描画する ので、self.calc_node_height(maxdepth) によって、startnode から深さ maxdepth までのノードの高さを すべて計算することができます。

self.calc_node_height(maxdepth) によって、上図の赤い枠の外にある、実際には描画しないノードの高さを計算するという、無駄な処理が行われてしまうという点が気になっている人がいるかもしれません。確かにそのような無駄な処理が行われてしまいますが、〇×ゲームのゲーム木のような小規模なゲーム木の場合は、そのような 無駄な計算 は人間が知覚できないほど 短い時間で行える ので、無駄な処理が行われることを 気にする必要はない でしょう。なお、どうしてもそのような無駄な処理が行われることが気になる方は、cal_node_height に仮引数 startnode を追加し、無駄な処理が行われないように cal_node_height を修正して下さい。

オセロや将棋のような大規模なゲーム木の場合はそのような無駄な処理によって、人間が知覚できるほどの処理時間の違いが生じる可能性があります。そのような場合は、無駄な処理が行われないように calc_node_height を修正する必要があります。

ノードの深さを表す Node クラスの depth 属性の計算

次に、部分木を描画する Figure のサイズを計算 する必要があります。Figure の縦幅は、startnode の height 属性に代入されているので簡単ですが、横幅を計算 するためには、startnode の ノードの深さを知る必要 があります。

Node クラスには、現時点では深さの情報は記録されていないので、Node クラスに ノードの深さを表す depth という属性を追加 することにします。

下記は、Node クラスの __init__ メソッドの修正したプログラムです。Node クラスの インスタンスを作成する際 に、実引数でノードの深さを指定 するようにしました。

• 1 行目：作成するノードの深さを表す、デフォルト値が 0 の仮引数 depth を追加する
• 5 行目：depth 属性に、仮引数 depth を代入する

1  from tree import Node
2
3  def __init__(self, mb, depth=0):       
4      self.mb = mb
5      self.depth = depth
6      self.children = []
7
8  Node.__init__ = __init__

行番号のないプログラム

from tree import Node

def __init__(self, mb, depth=0):       
    self.mb = mb
    self.depth = depth
    self.children = []

Node.__init__ = __init__

修正箇所

from tree import Node

-def __init__(self, mb, depth=0):
+def __init__(self, mb):       
    self.mb = mb
+   self.depth = depth
    self.children = []

Node.__init__ = __init__

ノードの深さ は、親ノードの深さ + 1 になります。また、子ノードは calc_children メソッドを使って作成します。従って、下記のような処理を行うことで、ゲーム木の全てのノードに深さの情報を記録することができます。

• ルートノード を作成する際に 深さ 0 を設定 する
• 子ノードを作成 する際に、子ノードの深さを 自身のノードの深さ + 1 に設定 する

先程、Node クラスの __init__ メソッドの仮引数 depth を、デフォルト値が 0 のデフォルト引数としたので、ルートノードを作成する処理 では、深さ 0 のノードが作成 されます。そのため、上記の 2 つ目の処理を実装することで、ゲーム木の全てのノードに深さの情報を記録することができます。

下記は、子ノードを作成する calc_children を修正するプログラムです。

• 8 行目：子ノードを作成する際に、self.depth + 1 を実引数に記述することで、自分よりも 1 つ深いノードとして子ノードを作成する。

 1  from copy import deepcopy
 2
 3  def calc_children(self):
 4      self.children = []
 5      for x, y in self.mb.calc_legal_moves():
 6          childmb = deepcopy(self.mb)
 7          childmb.move(x, y)
 8          self.insert(Node(childmb, self.depth + 1))
 9
10  Node.calc_children = calc_children

行番号のないプログラム

from copy import deepcopy

def calc_children(self):
    self.children = []
    for x, y in self.mb.calc_legal_moves():
        childmb = deepcopy(self.mb)
        childmb.move(x, y)
        self.insert(Node(childmb, self.depth + 1))

Node.calc_children = calc_children

修正箇所

from copy import deepcopy

def calc_children(self):
    self.children = []
    for x, y in self.mb.calc_legal_moves():
        childmb = deepcopy(self.mb)
        childmb.move(x, y)
-       self.insert(Node(childmb))
+       self.insert(Node(childmb, self.depth + 1))

Node.calc_children = calc_children

Node クラスに 属性を追加した ので、下記のプログラムで mbtree を作り直す必要があります。下記のプログラムの 2、3 行目では、ルートノードと、深さ 9 のノードの depth 属性を表示しており、実行結果から depth 属性に正しい値が代入されることが確認できます。

mbtree = Mbtree()
print(mbtree.root.depth)
print(mbtree.nodelist_by_depth[9][0].depth)

実行結果

     9 depth 1 node created
    72 depth 2 node created
   504 depth 3 node created
  3024 depth 4 node created
 15120 depth 5 node created
 54720 depth 6 node created
148176 depth 7 node created
200448 depth 8 node created
127872 depth 9 node created
     0 depth 10 node created
total node num = 549946
0
9

上記のプログラムを記述した後で、ノードの深さ は 手数と同じ なので、Marubatsu クラスの move_count 属性に代入されている ことに気が付きましたが、ノードの depth 属性を追加したほうが、プログラムがわかりやすくなる と思いましたので、上記のプログラムをそのまま採用することにします。

Figure のサイズの計算

startnode のノードの深さがわかるようになったので、Figure のサイズを計算する処理は、下記のプログラムのように記述できます。

• 5 行目：Figure の横幅を、maxdepth から startnode の深さを引いて、1 を足した値⁶から計算するように修正する
• 6 行目：Figure の縦幅を、startnode の高さに修正する

1  def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
2      if startnode is None:
3          startnode = self.root
4      self.calc_node_height(maxdepth)
5      width = 5 * (maxdepth - startnode.depth + 1)
6      height = startnode.height
元と同じなので省略
7        
8  Mbtree.draw_tree = draw_tree

行番号のないプログラム

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
    if startnode is None:
        startnode = self.root
    self.calc_node_height(maxdepth)
    width = 5 * (maxdepth - startnode.depth + 1)
    height = startnode.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
    for depth in range(maxdepth):
        dy = 0
        for node in self.nodelist_by_depth[depth]:
            node.draw_node(ax=ax, size=size, lw=lw, dx=depth*5, dy=dy)
            dy += node.height
        
Mbtree.draw_tree = draw_tree

修正箇所

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
    if startnode is None:
        startnode = self.root
    self.calc_node_height(maxdepth)
-   width = 5 * (maxdepth + 1)
+   width = 5 * (maxdepth - startnode.depth + 1)
-   height = self.root.height
+   height = startnode.height
元と同じなので省略
        
Mbtree.draw_tree = draw_tree

ノードの描画の処理の実装

元のプログラムは、深さ 0 のノードから、深さの浅い順に、その深さのすべてのノードを順番に描画していましたが、今回は以下の点で描画するノードが異なります。

• 深さ startnode.depth の startnode から描画 する
• 描画するのは、startnode の 子孫ノードだけ である

ノードから 子ノードを辿っていく ことでたどり着くことができるノードの事を、子孫（decendant）ノード と呼びます。逆に、親ノードを辿っていく ことでたどり着くことができるノードの事を 先祖（ancestor）ノード と呼びます。

create_node_by_df では、幅優先アルゴリズムで、ルートノードの子孫ノードを、深さが 0 のノードから、深さが浅い順に作成しました。startnode の子孫ノードの描画 も同様に、幅優先アルゴリズム で、下記の手順で描画することができます。

1. 次に描画を行う、深さ startnode.depth のノードの一覧を [startnode] に設定する
2. 次に描画を行うノードの深さ d を startnode.depth に設定する
3. 描画する深さ d のノードが存在しない、または d が maxdepth 以上の場合は部分木の描画の処理が完了しているので処理を終了する
4. 描画する深さ d のノードが存在する場合は、それらの 全てのノードを描画 し、その子ノードを次に描画を行う深さ d + 1 のノードの一覧に追加する
5. 深さ d に 1 を足して 手順 3 に戻る

create_node_by_df との主な違いは、以下の通りです。

• 最初の深さ が 0 ではなく、startnode.depth である
• 最初 に処理を行う ノードの一覧 が [self.root] ではなく、[startnode] である
• 深さ d に対して行う処理が、深さ d の全てのノードに対する処理ではなく、深さ d の startnode の子孫ノードに対する処理だけ である
• 行う処理 が子ノードの作成ではなく、ノードの 描画処理 である

下記は、上記のアルゴリズムで draw_tree を修正したプログラムです。行っている処理は creat_node_by_df とかなり似ているので、興味がある方は比べてみて下さい。なお、creat_node_by_df で行っていた、部分木のそれぞれの深さのノードの list を nodelist_by_depth 属性に記録する処理は必要がないので行っていません。

• 2 行目：最初に描画するノードの一覧を [startnode] で初期化する
• 3 行目：最初に描画するノードの深さを startnode.depth で初期化する
• 4、9、12 行目：元の draw_tree では、ノードの描画位置を 5 * depth で計算していたが、その方法では、ノードの描画位置が 5 * (maxdepth - depth) という式になり、見た目がわかりづらくなる。そこで、ノードの描画位置の y 座標と同様の方法で、ノードの描画位置の x 座標を dx で表し、以下のような処理を行うように修正した
  • 4 行目：startnode の描画の x 座標を 0 で初期化する
  • 9 行目：x 座標が dx の位置にノードを描画する
  • 12 行目：次の深さのノードを描画する前に、dx に 5 を加算する
• 5 行目：nodelist に要素が存在し、なおかつ depth が maxdepth 未満の場合に nodelist を描画するように修正する
• 7 行目：描画する次の深さのノードの一覧を表す childnodelist を空の list で初期化する
• 8 行目：nodelist 内のすべてのノードを描画する
• 13、14 行目：次に描画するノードの深さを表す depth に 1 を足し、nodelist に childnodelist を代入する

 1  def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
元と同じなので省略
 2      nodelist = [startnode]
 3      depth = startnode.depth
 4      dx = 0
 5      while len(nodelist) > 0 and depth < maxdepth:        
 6          dy = 0
 7          childnodelist = []
 8          for node in nodelist:
 9              node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
10              dy += node.height
11              childnodelist += node.children
12          dx += 5
13          depth += 1
14          nodelist = childnodelist
15        
16  Mbtree.draw_tree = draw_tree

行番号のないプログラム

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
    if startnode is None:
        startnode = self.root
    self.calc_node_height(maxdepth)
    width = 5 * (maxdepth - startnode.depth + 1)
    height = startnode.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
    nodelist = [startnode]
    depth = startnode.depth
    dx = 0
    while len(nodelist) > 0 and depth < maxdepth:        
        dy = 0
        childnodelist = []
        for node in nodelist:
            node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
            dy += node.height
            childnodelist += node.children
        dx += 5
        depth += 1
        nodelist = childnodelist
        
Mbtree.draw_tree = draw_tree

修正箇所

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
元と同じなので省略
+   nodelist = [startnode]
+   depth = startnode.depth
+   dx = 0
-   for depth in range(maxdepth):
+   while len(nodelist) > 0 and depth < maxdepth:        
        dy = 0
+       childnodelist = []
-       for node in self.nodelist_by_depth[depth]:
+       for node in nodelist:
-           node.draw_node(ax=ax, size=size, lw=lw, dx=depth*5, dy=dy)
+           node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
            dy += node.height
+           childnodelist += node.children
+       dx += 5
+       depth += 1
+       nodelist = childnodelist
        
Mbtree.draw_tree = draw_tree

draw_tree の処理の確認と修正

上記の修正後に、いくつかのゲーム木の部分木を描画して、draw_tree が正しく実装されているかどうかを確認することにします。

下記は、ルートノードから深さ 2 までのノードを描画するプログラムです。実行結果から正しく描画されることが確認できます。

mbtree.draw_tree(maxdepth=2)

実行結果（長いのでクリックして表示して下さい）

下記は、深さ 6 のノードの一覧を表す mbtree.nodelist_by_depth[6] の中に記録されている最初のノードから深さ 9 までのノードを描画するプログラムです。実行結果から正しく描画されいそうなことが確認できます。

mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)

実行結果

上記で 正しく描画されていそう と記述したのは、実際には正しく描画されていない からです。ただし、そのことを 実行結果を見てすぐに気づくことは非常に難しい と思います。どこが間違っているかについては今回の記事の最後で説明しますが、興味がある方は、上図のどこが間違っているかを探してみて下さい。

うまく実装できていそうな気はしますが、上記だけでは確信が持てない ので、深さ 5 のノードの一覧を表す mbtree.nodelist_by_depth[5] の中に記録されている最初のノードから深さ 9 までのノードを描画してみることにします。実行結果から、一見するとうまくいっているように見えるかもしれませんが、図を少し眺めれば 明らかに何かがおかしい ことがわかります。どこがおかしいかについて少し考えてみて下さい。

mbtree.draw_tree(mbtree.nodelist_by_depth[5][0], maxdepth=9)

実行結果

問題の検証

真っ先に気づく部分としては、下図の 赤い枠 で囲った部分で、ゲーム盤の (2, 1) と (1, 2) のマスに 〇 と × の両方が描画 されている点が挙げられるでしょう。

また、下記の局面でも赤枠と同様のおかしな局面が表示されます。

• 赤枠の 1 つ上に表示される局面で、(0, 2) と (2, 0) に赤い × が描画される
• 赤枠の 2 つ下に表示される局面でも赤枠と同様の変な局面が描画される

また、気づきづらい点として、上図の 緑の枠 で囲った部分が挙げられます。2 つある緑の枠で囲った部分の 左の局面 は、いずれも 〇が 3 つ並んでいるので、〇 が勝利している局面で す。従って、その局面に子ノードは存在しない はずですが、図の緑の枠の部分のように 右にノードが描画されています。

緑枠の部分に関しては、そのおかしさに気が付かない可能性があるので、一目でおかしいことがわかる、赤枠の局面 に おかしな描画が行われる原因を推測する ことにします。

まず、赤枠の部分では (2, 1) のマスなどに 〇 と × の両方が描画されている ことから、複数の局面が同じ場所に描画されている ことが推測されます。そのため、同じ場所に複数の局面が描画される原因を調べることが、このバグの原因を突き止めるための鍵になりそうです。

同じ場所に複数の局面が描画される原因

draw_tree では、深さの浅い順に、draw_node を使って ノード と 子ノード の関係を 描画 しますが、これはよく考えると、深さ d のノードを 描画する際 に、深さ d と 深さ d + 1 のノードを描画する ことを意味します。

例えば、深さ 0 から 深さ 3 までのノードを draw_tree で描画する場合は、draw_node によって下記のような深さの局面が処理が行われます。

draw_node を呼び出すノードの深さ	描画する局面のノードの深さ
0	0 と 1
1	1 と 2
2	2 と 3

上記の表から、draw_tree では、深さが 1 と 2 のノード が、draw_node によって、2 回描画される ことがわかります。また、表から 最も浅い ノードと 最も深い ノードである、深さが 0 と 3 のノードは 1 度だけ描画される こともわかります。

従って、先ほどの図の赤枠の部分が変だった原因は、おそらく赤枠がある 深さ 8 の局面のノード が、以下の 2 つの場合で 2 度描画 された際に、y 座標が異なる位置に描画されたため であることが推測されます。

• 深さ 7 のノードを draw_node で描画した際に、そのノードの 子ノードとして描画 する
• 深さ 8 のノードを draw_node で描画した際に、そのノードを描画 する

このうちの、いずれかまたは両方で、間違った位置に深さ 8 のノードが描画された可能性が高いので、次はそのことを検証することにします。

draw_node で子ノードとして描画された 深さ 8 のノードの検証

先程 draw_tree では、最も深いノードが 1 度しか描画されない 事がわかったので、下記のプログラムで深さ 5 のノードから 深さ 8 までの部分木を描画 することで、実行結果のように、深さ 8 のノードを 1 度だけ描画するようにすることができます

mbtree.draw_tree(mbtree.nodelist_by_depth[5][0], maxdepth=8)

実行結果

上図で描画された 深さ 8 のノード は、「深さ 7 のノードを draw_node で描画した際に、そのノードの 子ノードとして描画」したものです。上図の描画におかしな点は見られないことから、先程のおかしな局面の図は、もう一つの「深さ 8 のノードから draw_node で描画した際」に行われた可能性が高いことが推測されます。

深さ 8 のノードから draw_node で描画された深さ 8 のノードの検証

深さ 8 のノードから draw_node で描画された深さ 8 のノードの描画の検証は、下記のプログラムのように、子ノードを描画しないように draw_node を修正することで行えます。

• 8 行目の下にあった子ノードを描画する処理を削除する。なお、エッジを描画する処理は必要 なので削除してはいけない点に注意すること

 1  from marubatsu import Marubatsu_GUI
 2
 3  def draw_node(self, ax, size=0.25, lw=0.8, dx=0, dy=0):
元と同じなので省略
 4      # 子ノードが存在する場合に、エッジの線と子ノードを描画する
 5      if len(self.children) > 0:   
 6          plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + edgeheight], c="k", lw=lw)
 7          for childnode in self.children:
 8              # この下にあった子ノードを描画する処理を削除する
 9              plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
10              dy += childnode.height
11            
11  Node.draw_node = draw_node

行番号のないプログラム

from marubatsu import Marubatsu_GUI

def draw_node(self, ax, size=0.25, lw=0.8, dx=0, dy=0):
    width = 8
    if ax is None:
        height = len(self.children) * 4
        fig, ax = plt.subplots(figsize=(width * size, height * size))
        ax.set_xlim(0, width)
        ax.set_ylim(0, height)   
        ax.invert_yaxis()
        ax.axis("off")
        for childnode in self.children:
            childnode.height = 4
        if len(self.children) > 0:
            edgeheight = height - 4
    else:
        if len(self.children) > 0:
            edgeheight = self.height - self.children[-1].height
    
    # 自分自身のノードを (dx, dy) に描画する
    Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
    # 子ノードが存在する場合に、エッジの線と子ノードを描画する
    if len(self.children) > 0:   
        plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + edgeheight], c="k", lw=lw)
        for childnode in self.children:
            plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
            dy += childnode.height
            
Node.draw_node = draw_node

修正箇所

from marubatsu import Marubatsu_GUI

def draw_node(self, ax, size=0.25, lw=0.8, dx=0, dy=0):
元と同じなので省略
    # 子ノードが存在する場合に、エッジの線と子ノードを描画する
    if len(self.children) > 0:   
        plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + edgeheight], c="k", lw=lw)
        for childnode in self.children:
-           Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy, lw=lw)
            plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
            dy += childnode.height
            
Node.draw_node = draw_node

上記の修正後に下記のプログラムで再び深さ 5 のノードから深さ 9 までの部分木を描画すると、実行結果のような画像が描画されます。draw_node で子ノードを描画しなくなったので、深さ 9 のノードが描画されなくなりますが、その点についてはこの後で修正します。

mbtree.draw_tree(mbtree.nodelist_by_depth[5][0], maxdepth=9)

実行結果

比較による原因の検証

下図は、左から下記の方法で深さ 8 のノードを描画した場合の上部を並べたものです。

• 深さ 7 の子ノードとして draw_node で描画した場合
• 深さ 8 のノードから draw_node で描画した場合
• 上記の両方を描画した場合

左の 2 つの図を重ね合わせる と、確かに 右の図になる ので、おかしな図が描画される原因が、同じ深さの局面を異なる位置に 2 回描画した 事であることが確認できました。

問題の修正

問題の原因が同じ深さの局面を 2 度描画したことにあるので、どちらか 片方の方法だけで局面を描画する ように修正することにします。どちらの方法で局面を描画すべきであるかについて少し考えてみて下さい。

draw_node で子ノードとして局面を描画する方法を採用してしまうと、深さ 0 のノードを描画することができなくなってしまうので、そちらの方法は採用することができません。

draw_node で子ノードを描画しないようにする修正は先程行いましたが、そのように修正したため、最も深いノードが描画されなくなった ので、その問題を修正することにします。

この問題は、下記のプログラムのように、draw_tree で、深さ 0 から maxdepth - 1 ではなく、maxdepth まで の深さのノードを draw_node で描画する ようにすることで解決できます。最も深いノードのエッジが描画されてしまうのではないかと思う人がいるかもしれませんが、前回の記事で、子ノードが存在しない場合は、エッジと子ノードを描画しないように draw_node を修正したので、この方法で問題はありません。

• 2 行目：depth が maxdepth 未満ではなく、以下を判定するように修正する

1  def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
元と同じなので省略
2      while len(nodelist) > 0 and depth <= maxdepth:        
元と同じなので省略
3        
4  Mbtree.draw_tree = draw_tree

行番号のないプログラム

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
    if startnode is None:
        startnode = self.root
    self.calc_node_height(maxdepth)
    width = 5 * (maxdepth - startnode.depth + 1)
    height = startnode.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
    nodelist = [startnode]
    depth = startnode.depth
    dx = 0
    while len(nodelist) > 0 and depth <= maxdepth:        
        dy = 0
        childnodelist = []
        for node in nodelist:
            node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
            dy += node.height
            childnodelist += node.children
        dx += 5
        depth += 1
        nodelist = childnodelist
        
Mbtree.draw_tree = draw_tree

修正箇所

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
元と同じなので省略
-   while len(nodelist) > 0 and depth < maxdepth:        
+   while len(nodelist) > 0 and depth <= maxdepth:        
元と同じなので省略
        
Mbtree.draw_tree = draw_tree

上記の修正後に下記のプログラムを実行すると、実行結果のように、深さ 9 のノードが描画されるようになります。ただし、深さ 8 のノードの描画位置は間違ったままなので、修正する必要があります。

mbtree.draw_tree(mbtree.nodelist_by_depth[5][0], maxdepth=8)

実行結果

局面の描画位置の間違いの検証

描画位置の 間違いを検証 する際には、正しく描画された図と比較す ると良いでしょう。

下図左は、上図の上部を抜粋したもので、下図右は、正しい位置に深さ 8 の局面が描画された場合の図です。

左右の図を比較すると右図の正しい位置に描画される深さ 8 の局面は、一部で 間を空けて描画される ことが分かります。また、その 間が空く部分 は、左図の赤枠の局面のように、決着が付いた局面の右 であることがわかります。

つまり、左図の問題は、決着がついた局面の右 に、紫の枠の局面の部分のように、間を空けずに上から詰めて描画してしまったこと が原因で発生したことがわかります。

そのことを踏まえて draw_tree のプログラムを検証することにします。draw_tree では、下記のプログラムの 7 行目ように、描画したノードの子ノードを childnodelist に追加 する処理を行います。そして、次の深さのノードを描画 する際に、childnodelist に登録されていたノード を Figure の 上端から順番に描画する という処理を行います。

1  while len(nodelist) > 0 and depth < maxdepth:        
2      dy = 0
3      childnodelist = []
4      for node in nodelist:
5          node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
6          dy += node.height
7          childnodelist += node.children

上記を元に、下図の 深さ 7 の赤と紫枠のノードを描画した際に行われる処理を検証します。

赤枠と紫枠のノードを描画する際には、下記の手順で処理が行われます。

1. 赤枠のノードはこの深さの最初のノードなので、このノードを描画する前の childnodelist には 空の list が代入される
2. 赤枠のノードは決着がついた局面で、子ノードは存在しないので、node.children には空の list が代入されている。従って、赤枠のノードの描画後に、childnodelist + node.children を実行しても childnodelist の内容は空の list のままである
3. 紫枠のノードは決着がついていないので、子ノードが存在する。そのため、紫枠のノードの描画後に childnodelist には、紫枠のノードの子ノードが追加される

上記から、深さ 7 のノードが すべて描画された後 では、childnodelist の先頭 には、紫枠 のノードの 子ノードが代入 されることになります。そのため、次の 深さ 8 のノードを描画する際には、紫枠 のノードの 子ノード が、Figure の 上から順に描画 され、上図のように、間を空ける必要がある場所 に 詰めてその局面が描画 されてしまうことになります。

このことから、子ノードが存在しないノードを描画した場合 でも、childnodelist には、そこに 何も描画しないことを表す何らかのデータを追加する必要がある ことがわかります。従って、下記のようにプログラムを修正することで、この問題を解決することができます。

• 子ノードが存在しない場合は、childnodelist にそこに何も描画しないことを表す None を追加 する
• ノードを描画する際に nodelist の要素に None が代入 されていた場合は、何も描画せず、次のノードを一つ下に描画する ために、dy の座標を 4 増やす 処理を行う

下記は、そのように draw_tree を修正したプログラムです。

• 6 行目：nodelist から取り出した node の値が None の場合は、何も描画せずに、dy を 4 増やす処理だけを行う
• 11 ~ 14 行目：子ノードが存在する場合はこれまでと同じ処理を行うが、子ノードが存在しない場合は childnodelist に None を追加するように修正する

 1  def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
元と同じなので省略
 2      while len(nodelist) > 0 and depth <= maxdepth:        
 3          dy = 0
 4          childnodelist = []
 5          for node in nodelist:
 6              if node is None:
 7                  dy += 4
 8              else:
 9                  node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
10                  dy += node.height
11                  if len(node.children) > 0:  
12                      childnodelist += node.children
13                  else:
14                      childnodelist.append(None)
元と同じなので省略
15        
16  Mbtree.draw_tree = draw_tree

行番号のないプログラム

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
    if startnode is None:
        startnode = self.root
    self.calc_node_height(maxdepth)
    width = 5 * (maxdepth - startnode.depth + 1)
    height = startnode.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
    nodelist = [startnode]
    depth = startnode.depth
    dx = 0
    while len(nodelist) > 0 and depth <= maxdepth:        
        dy = 0
        childnodelist = []
        for node in nodelist:
            if node is None:
                dy += 4
            else:
                node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
                dy += node.height
                if len(node.children) > 0:  
                    childnodelist += node.children
                else:
                    childnodelist.append(None)
        dx += 5
        depth += 1
        nodelist = childnodelist
        
Mbtree.draw_tree = draw_tree

修正箇所（else のインデントの修正は省略します）

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
元と同じなので省略
    while len(nodelist) > 0 and depth <= maxdepth:        
        dy = 0
        childnodelist = []
        for node in nodelist:
+           if node is None:
+               dy += 4
+           else:
                node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
                dy += node.height
-               childnodelist += node.children
+               if len(node.children) > 0:  
+                   childnodelist += node.children
+               else:
+                   childnodelist.append(None)
元と同じなので省略
        
Mbtree.draw_tree = draw_tree

上記の修正後に、下記のプログラムを実行すると、実行結果から深さ 8 のノードが正しい位置に描画されるようになることが確認できますが、深さ 9 のノードの描画位置が正しく描画されないという問題があることがわかります。この問題の原因と修正方法について少し考えてみて下さい。

mbtree.draw_tree(mbtree.nodelist_by_depth[5][0], maxdepth=9)

実行結果

深さ 9 のノードの描画位置のバグの検証

深さ 9 のノードの描画位置の問題点は、上図から先程と同様に、決着がついた局面の右に詰めて局面が描画される ことであることがわかります。

このようなことが起きる原因は、下記のプログラムのように、node が None だった場合 に、次のノードを描画する座標を 下にずらす処理しか行っていない からです。

            if node is None:
                dy += 4

従って、下記のプログラムの 8 行目のように、node が None の場合は、childnodelist に None を追加することで、一つ下の深さの同じ場所に何も表示されないようになります。

また、この処理は その下のすべての深さでも行われる ようになるので、決着がついた局面の右 には、どの深さでも 局面が描画されなくなります。

 1  def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
元と同じなので省略
 2      while len(nodelist) > 0 and depth <= maxdepth:        
 3          dy = 0
 4          childnodelist = []
 5          for node in nodelist:
 6              if node is None:
 7                  dy += 4
 8                  childnodelist.append(None)
元と同じなので省略
 9        
10  Mbtree.draw_tree = draw_tree

行番号のないプログラム

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
    if startnode is None:
        startnode = self.root
    self.calc_node_height(maxdepth)
    width = 5 * (maxdepth - startnode.depth + 1)
    height = startnode.height
    fig, ax = plt.subplots(figsize=(width * size, height * size))
    ax.set_xlim(0, width)
    ax.set_ylim(0, height)   
    ax.invert_yaxis()
    ax.axis("off")        
    
    nodelist = [startnode]
    depth = startnode.depth
    dx = 0
    while len(nodelist) > 0 and depth <= maxdepth:        
        dy = 0
        childnodelist = []
        for node in nodelist:
            if node is None:
                dy += 4
                childnodelist.append(None)
            else:
                node.draw_node(ax=ax, size=size, lw=lw, dx=dx, dy=dy)
                dy += node.height
                if len(node.children) > 0:  
                    childnodelist += node.children
                else:
                    childnodelist.append(None)
        dx += 5
        depth += 1
        nodelist = childnodelist
        
Mbtree.draw_tree = draw_tree

修正箇所

def draw_tree(self, startnode=None, size=0.25, lw=0.8, maxdepth=2):
元と同じなので省略
    while len(nodelist) > 0 and depth <= maxdepth:        
        dy = 0
        childnodelist = []
        for node in nodelist:
            if node is None:
                dy += 4
+               childnodelist.append(None)
元と同じなので省略
        
Mbtree.draw_tree = draw_tree

上記の修正後に、先程と同じ下記のプログラムを実行することで、実行結果のようにバグが修正されたことが確認できます。

mbtree.draw_tree(mbtree.nodelist_by_depth[5][0], maxdepth=9)

実行結果

深さが 6 のノードからの部分木の描画の確認

さきほど、深さ 6 のノードからの部分木の描画が間違っていると説明しましたので、下記のプログラムで修正後にその部分木を描画してみることにします。実行結果の左図が修正後のもの、右図修正前のものです。

mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)

実行結果

　

右図では、決着が付いた局面の右に局面が描画されますが、左図では正しく描画されることが確認できます。ただし、右図を一目見て間違っていることを認識することは簡単ではないでしょう。このように、プログラムが 正しく実装されているかどうかを確認 する際には、間違っていることが簡単にはわからないような場合が良くあります。そのため、確認の作業を行う際は、様々な状況で確認を行う 必要があることを覚えて解いてください。

今回の記事のまとめ

今回の記事では、幅優先アルゴリズムで任意の深さのゲーム木を作成し、ゲーム木の部分木を描画する処理を実装しました。

部分木を描画する処理では、見つけづらく、初心者には修正が難しそうなバグが発生しましたが、このような見つけづらく修正しづらいバグは、実際に良く発生するので、今回のバグの修正方法が参考なれば幸いです。

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

以下のリンクは、今回の記事で更新した tree.py です。

次回の記事

1. 例えば、(0, 0)、(1, 1)、(2, 2) の順で着手を行った場合と、(2, 2)、(1, 1)、(0, 0) の順で着手を行った場合は、完全に同じ局面になります ↩

2. 0 の階乗は直観的に 0 であると思う人が多いかもしれませんが、数学で 0 の階乗が 1 に定義されている理由は、そのように定義すると都合が良いからです。実際に 0 の階乗が 1 であれば、n 手目までの着手の組み合わせが 1 つの式で表現できます ↩

3. 深さ 0 のノードも含むので、深さの数は maxdepth + 1 になります ↩

4. dy に関する処理の意味を忘れた方は、前回の記事を復習して下さい ↩

5. キリの悪い数字に見えるかもしれませんが、これは 2 進数 では $2^{16}$ という キリの良い数字 です ↩

6. 1 を足す理由は、例えば、startnode の深さと maxdepth が等しい場合は、1 を足さないと Figure の幅が 0 になってしまう からです ↩