目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
ルールベースの AI の一覧
ルールベースの AI の一覧については、下記の記事を参照して下さい。
ゲーム木全体の視覚化の方針
〇×ゲームに限った話ではありませんが、多くのゲームのゲーム木は、規模が大きすぎてその 全体を詳細に表示するようなゲーム木の図を描画することは困難 です。実際に〇×ゲームの場合は、以前の記事で示したように、最もノードの数が多い深さ 8 のノードの数が約 20 万もあるため、ゲーム木を図示した場合にとんでもない高さの画像が必要になります。
このような場合は、ゲーム木の一部である 部分木を描画 し、キーボードやマウスなどの操作によって 表示する部分木を移動する ことで、全体像を把握する ということが良く行われます。例えば、コンピューターの ファイルシステム は、ゲーム木と同様の 木構造 になっており、フォルダ が木構造の ノードに対応 します。Windows の場合は、エクスプローラというアプリを使って、下記のような方法でハードディスクなどの記憶装置の中に保存されたファイルシステムの一部を表示しています。
- 特定のフォルダの中身を表示することで、全体の一部を表示する
- フォルダのアイコンをダブルクリックすることで、表示するフォルダを移動する
- ↑ ボタンをクリックすることで、親のフォルダに表示を移動する
そこで、本記事では下記のような方法で〇×ゲームのゲーム木を視覚化し、全体像を把握できるようにする処理を実装することにします。
- 特定のノードを中心とした部分木 を表示する
- ボタンなどの GUI や、カーソルキーなどの操作によって 表示する部分木を移動 する
部分木の描画に関する問題点とその解決方法
前回の記事では、下図のような、特定のノードから特定の深さまでの部分木 を表示する処理を実装しましたが、上記のようなゲーム木の視覚化を下図のような部分木で行うと、部分木の表示範囲 を原因とするいくつかの問題が発生します。どのような問題があるかについて少し考えてみて下さい。
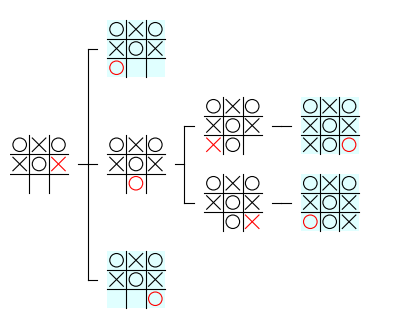
先祖ノードの局面の表示
ゲーム木を使ってゲームの分析を行う際に、どのような着手を行った結果、その局面に至ったか の情報は重要です。しかし、上図のゲーム木の部分木には、どのような着手を行った結果、一番左の局面に至ったかについての情報が表示されていません。
そこで、draw_tree で startnode に 特定の局面を指定して部分木を描画 する際に、ゲーム開始時の局面から、startnode の局面に至るまでの間の局面も表示 するように修正することにします。そのような、ノードの 親ノードを辿っていく ことでたどり着くことができるノードの事を 先祖(ancestor)ノード と呼びます。Figure の中で、どのような位置に先祖ノードを表示すればよいかについて少し考えてみて下さい。
例えば、Windows のエクスプローラーでは、下図の赤丸の部分のような方法で、現在表示しているフォルダを表示するまでに開かなければならないフォルダを表示します。

エクスプローラーでは上部に表示しますが、draw_tree の場合は startnode の左に、下図のような形で先祖ノードを並べて表示するという方法が考えられます。先祖ノードに 子ノードがいくつあっても、エッジは右に 1 本だけ表示 することにします。本記事ではこの方法を採用しますが、他の方法が良いと思った方は自由に変更して下さい。

ノードへの親ノードの情報の記録
上図のような描画を行うためには、ルートノード から startnode に至るまでの先祖ノードの情報を知る必要があります。現状の Node には子ノードの情報しか記録されていませんが、親ノードの情報を記録 するようにすれば、startnode から 親ノードを順に辿っていく ことで すべての先祖ノード を 深い順に辿る ことができます。
ノードの mb 属性に代入されている Marubatsu クラスのインスタンスの record 属性に、ルートノードからそのノードの局面に至るまでの着手が記録されているので、その情報を使ってルートノードからそのノードに至るまでの先祖ノードを調べて表示する処理を記述することも可能です。
そこで、Node クラスを下記のように修正することにします。
- 親ノードを表す
parentという属性を追加する - 親ノードが存在しないルートノードの場合は
parentにNoneを代入する - 親ノードは、Node クラスのインスタンスを作成する際に実引数で指定する
まず、__init__ メソッドを下記のプログラムのように修正することで、Node クラスのインスタンスを作成する際に、親ノードを指定 できるようにします。なお、親ノードを表す実引数を省略した場合は、親ノードが存在しないルートノードが作成されるようにしました。
-
3 行目:デフォルト値を
Noneとするデフォルト引数parentを追加する -
5 行目:
parent属性に仮引数parentを代入する
1 from tree import Node
2
3 def __init__(self, mb, parent=None, depth=0):
4 self.mb = mb
5 self.parent = parent
6 self.depth = depth
7 self.children = []
8
9 Node.__init__ = __init__
行番号のないプログラム
from tree import Node
def __init__(self, mb, parent=None, depth=0):
self.mb = mb
self.parent = parent
self.depth = depth
self.children = []
Node.__init__ = __init__
修正箇所
from tree import Node
-def __init__(self, mb, depth=0):
+def __init__(self, mb, parent=None, depth=0):
self.mb = mb
+ self.parent = parent
self.depth = depth
self.children = []
Node.__init__ = __init__
次に、下記のプログラムの 8 行目のように、子ノードを作成する処理を行う calc_children を、作成する 子ノードの親ノード が 自分のノードを表す self になる ように修正します。
1 from copy import deepcopy
2
3 def calc_children(self):
4 self.children = []
5 for x, y in self.mb.calc_legal_moves():
6 childmb = deepcopy(self.mb)
7 childmb.move(x, y)
8 self.insert(Node(childmb, parent=self, depth=self.depth + 1))
9
10 Node.calc_children = calc_children
行番号のないプログラム
from copy import deepcopy
def calc_children(self):
self.children = []
for x, y in self.mb.calc_legal_moves():
childmb = deepcopy(self.mb)
childmb.move(x, y)
self.insert(Node(childmb, parent=self, depth=self.depth + 1))
Node.calc_children = calc_children
修正箇所
from copy import deepcopy
def calc_children(self):
self.children = []
for x, y in self.mb.calc_legal_moves():
childmb = deepcopy(self.mb)
childmb.move(x, y)
- self.insert(Node(childmb, self.depth + 1))
+ self.insert(Node(childmb, parent=self, depth=self.depth + 1))
Node.calc_children = calc_children
下記のプログラムの 3 行目のように Mbtree クラスのインスタンスを作成し、4 行目で ルートノードの子ノードの親ノードの局面1 を表示すると、実行結果のように ルートノードの局面が表示される ので、Node に親ノードを表す属性が追加されたことが確認できます。
from tree import Mbtree
mbtree = Mbtree()
print(mbtree.root.children[0].parent.mb)
実行結果
9 depth 1 node created
72 depth 2 node created
504 depth 3 node created
3024 depth 4 node created
15120 depth 5 node created
54720 depth 6 node created
148176 depth 7 node created
200448 depth 8 node created
127872 depth 9 node created
0 depth 10 node created
total node num = 549946
Turn o
...
...
...
先祖ノードの局面の表示
次に、先祖ノードの局面をどこに描画するか を決める必要がありますが、startnode の左に並べて描画するのが自然でしょう。
すべての先祖ノードに対して行うという処理は、ルートノードにたどり着くまで親ノードを順番に辿る という手順で行うことができます。この処理は、先祖ノードを 深い順に辿って行う という処理であり、下記のプログラムのように記述することができます。
-
1 行目:
nodeに親ノードが存在しない場合はルートノードであることを表すので、親ノードが存在しない間、繰り返しの処理を行う -
2 行目:
nodeに親ノードであるnode.parentを代入する -
3 行目:
nodeに関する処理を記述することで、親ノードの処理を行う
while node.parent is not None:
node = node.parent
# node に関する処理を行う
従って、startnode のすべての先祖ノードを startnode の左に並べて描画するという処理は、下記のプログラムのように記述できます。
-
8 行目:Figure の左端にルートノードを描画することになったので、描画するノードの深さは 0 ~
maxdepthになる。従って、Figure の幅 は5 * (maxdepth + 1)で計算できる -
11 行目:左端に描画するノードが
startnodeからルートノードに変わったので、startnodeの描画位置の x 座標 はその 深さ * 5 だけ右にずれる ことになる。そのためstartnodeの描画位置の x 座標表すdxを、0からstartnode.depth * 5に修正する -
15 ~ 21 行目:
startnodeの先祖ノードを深い順に、先程示した方法で繰り返しを使ってゲーム盤を描画する処理を行う -
16 行目:最初に表示する先祖ノードは、
startnodeの親ノードなので、その深さであるstartnode.depth - 1を使って描画位置の x 座標を計算してdxに代入する -
17 行目:
startnodeの 先祖ノード は、いずれもstartnodeと同じ y 座標に描画 する。また、その座標はstartnodeと同様に、Figure の上下のちょうど真ん中に描画するので、前回の記事で説明したように、(startnode.height - 3) / 2という式で計算できる -
20 行目:(dx, dy) の位置に、
draw_boardを使ってnodeのノードの局面を描画する -
21 行目:
nodeの親ノードの局面は、一つ左に描画するのでdxから5を引く
1 from marubatsu import Marubatsu_GUI
2 import matplotlib.pyplot as plt
3
4 def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
5 if startnode is None:
6 startnode = self.root
7 self.calc_node_height(maxdepth)
8 width = 5 * (maxdepth + 1)
9 height = startnode.height
10 fig, ax = plt.subplots(figsize=(width * size, height * size))
元と同じなので省略
11 dx = 5 * depth
12 while len(nodelist) > 0 and depth <= maxdepth:
13 dy = 0
元と同じなので省略
14
15 node = startnode
16 dx = 5 * (node.depth - 1)
17 dy = (startnode.height - 3) / 2
18 while node.parent is not None:
19 node = node.parent
20 Marubatsu_GUI.draw_board(ax, node.mb, show_result=True, dx=dx, dy=dy, lw=lw)
21 dx -= 5
22
23 Mbtree.draw_tree = draw_tree
行番号のないプログラム
from marubatsu import Marubatsu_GUI
import matplotlib.pyplot as plt
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
nodelist = [startnode]
depth = startnode.depth
dx = 5 * depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
childnodelist = []
for node in nodelist:
if node is None:
dy += 4
childnodelist.append(None)
else:
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
dx += 5
depth += 1
nodelist = childnodelist
node = startnode
dx = 5 * (node.depth - 1)
dy = startnode.height / 2 - 1.5
while node.parent is not None:
node = node.parent
Marubatsu_GUI.draw_board(ax, node.mb, show_result=True, dx=dx, dy=dy, lw=lw)
dx -= 5
Mbtree.draw_tree = draw_tree
修正箇所
from marubatsu import Marubatsu_GUI
import matplotlib.pyplot as plt
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
- width = 5 * (maxdepth - startnode.depth + 1)
+ width = 5 * (maxdepth + 1)
height = startnode.height
fig, ax = plt.subplots(figsize=(width * size, height * size))
元と同じなので省略
- dx = 0
+ dx = 5 * depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
元と同じなので省略
+ node = startnode
+ dx = 5 * (node.depth - 1)
+ dy = startnode.height / 2 - 1.5
+ while node.parent is not None:
+ node = node.parent
+ Marubatsu_GUI.draw_board(ax, node.mb, show_result=True, dx=dx, dy=dy, lw=lw)
+ dx -= 5
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行すると、実行結果のように startnode の左にルートノードから startnode に至るまでの祖先ノードの局面が描画されるようになります。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
実行結果

先祖ノードのエッジの描画
上記のプログラムでは、startnode の 先祖ノードにエッジが描画されない という問題があります。この問題は、draw_node 内で行っていたノードのエッジを描画する処理を draw_tree 内の先祖ノードを描画する処理にも記述すれば解決できますが、同じような処理を draw_node と draw_tree の両方で記述するのはあまりよい方法であるとは言えません。
先祖ノードの描画 で行いたい処理は、ノードの描画とその右に伸びる 1 本だけのエッジ です。また、そのようなノードとエッジの描画の処理は、前回の記事で、「部分木の最も深いノードに子ノードが存在する場合の表示」として 実装済 です。従って、その処理をうまく利用する ことで、先祖ノードとそのエッジの描画を 簡潔に記述 することができます。どのように記述すれば良いかについて少し考えてみて下さい。
「部分木の最も深いノードに子ノードが存在する場合の表示」の処理は、draw_node に対して、下記のような実引数を記述した場合に行われます。
-
draw_nodeで描画する ノードの深さとmaxdepthが等しい -
draw_nodeで描画するノードが 子ノードを持つ
startnode の 先祖ノード は、先祖であることから 必ず子ノードを持つ ので、上記の 2 つ目の条件は必ず満たします。従って、draw_node を呼び出す際に、キーワード引数 maxdepth にそのノードの深さを代入 するようにすれば、その ノードとその右に伸びる 1 本だけのエッジを描画 することができます。
その処理の実装は、下記のプログラムのように draw_node を修正すれば良いと思った方がいるかもしれませんが、このプログラムではうまくいきません。
-
4 行目の下 にあった
dyを計算する処理は必要が無くなったので削除する -
7 行目:
draw_nodeの キーワード引数maxdepthに、描画するノードの深さを代入 することで、そのノードと右に伸びる 1 本のエッジを描画するように修正する。なお、先祖ノードは Figure の上下方向の真ん中に描画 するので、ノードを描画する y 座標の基準 となるdyには Figure の 上端を表す0で初期化する 必要がある点に注意する事
1 def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
2 node = startnode
3 dx = 5 * (node.depth - 1)
4 # この下にあった dy を計算する処理は必要が無くなったので削除する
5 while node.parent is not None:
6 node = node.parent
7 node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
8 dx -= 5
9
10 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
nodelist = [startnode]
depth = startnode.depth
dx = 5 * depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
childnodelist = []
for node in nodelist:
if node is None:
dy += 4
childnodelist.append(None)
else:
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
dx += 5
depth += 1
nodelist = childnodelist
node = startnode
dx = 5 * (node.depth - 1)
while node.parent is not None:
node = node.parent
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
dx -= 5
Mbtree.draw_tree = draw_tree
修正箇所
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
node = startnode
dx = 5 * (node.depth - 1)
- dy = (startnode.height - 3) / 2
while node.parent is not None:
node = node.parent
- Marubatsu_GUI.draw_board(ax, node.mb, show_result=True, dx=dx, dy=dy, lw=lw)
+ node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
dx -= 5
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行すると、実行結果のように startnode の先祖ノードが描画されなくなります。その理由について少し考えてみて下さい。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
実行結果

バグの原因の検証と修正
ノードが描画されなくなったので、draw_node 内で ノードの描画 を行う下記のプログラムを 検証する ことにします。
# 自分自身のノードを真ん中の位置になるように (dx, dy) からずらして描画する
y = dy + (self.height - 3) / 2
Marubatsu_GUI.draw_board(ax, self.mb, show_result=True, lw=lw, dx=dx, dy=y)
上記のプログラムでは、dy + (self.height - 3) / 2 という式でノードのゲーム盤を描画する y 座標を計算 しています。このうち dy には node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0) によって draw_node を呼び出していることから 0 が代入されている ので、self.height の値がおかしい可能性が高い でしょう。
そこで、下記のプログラムのように、ルートノードの height 属性を表示 してみると、実行結果から 約 100 万という値が代入されている ことがわかります。従って、ルートノードは、Figure の 表示の範囲外に描画 されたため、表示されないように見えてしまいます。
print(mbtree.root.height)
実行結果
1020672
startnode と同じ y 座標 に先祖ノードを描画するためには、先祖ノードの height 属性の値を startnode の height 属性と同じ値にする 必要があります。従って、下記のプログラムのように draw_tree を修正することで、この問題を解決することができます。
-
7 行目:先祖ノードの
height属性にstartnodeのheight属性を代入する
1 def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
2 node = startnode
3 dx = 5 * (node.depth - 1)
4 # この下にあった dy を計算する処理は必要が無くなったので削除する
5 while node.parent is not None:
6 node = node.parent
7 node.height = startnode.height
8 node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
9 dx -= 5
10
11 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
nodelist = [startnode]
depth = startnode.depth
dx = 5 * depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
childnodelist = []
for node in nodelist:
if node is None:
dy += 4
childnodelist.append(None)
else:
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
dx += 5
depth += 1
nodelist = childnodelist
node = startnode
dx = 5 * (node.depth - 1)
while node.parent is not None:
node = node.parent
node.height = startnode.height
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
dx -= 5
Mbtree.draw_tree = draw_tree
修正箇所
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
node = startnode
dx = 5 * (node.depth - 1)
while node.parent is not None:
node = node.parent
+ node.height = startnode.height
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
dx -= 5
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行すると、実行結果のように startnode の先祖ノードとその右に 1 本のエッジだけが描画されるようになります。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
実行結果
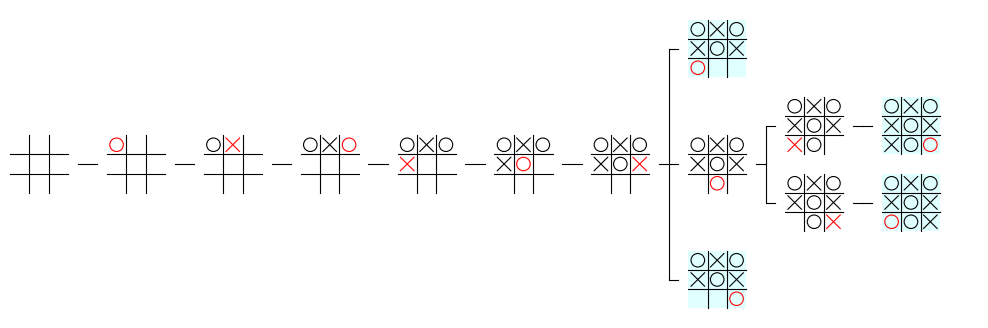
dx の計算方法の改良
上記のプログラムでは、最初のノードを描画する x 座標 を dx という変数に代入 し、ノードを描画する度に dx の値から 5 を引く ことで 次のノードの描画位置を計算 しています。このように記述した理由は、dx を一つの計算式で計算する場合は、その計算式の見た目が少し複雑になりプログラムがわかりづらくなってしまうためでした。
しかし、今回の修正によって、必ず ルートノードから ゲーム木の部分木を 描画するようになった ことで、ノードの描画の x 座標 は、ノードの深さ * 5 というシンプルで わかりやすい式で計算できる ようになります。そこで、下記のプログラムのように dx の計算をその式で行うようにすることにします。
- 4、18 行目の下にあった、
dxを初期化する処理を削除する - 13 行目の下にあった、
dxに 5 を加算する処理を削除する - 24 行目の下にあった、
dxに 5 を減算する処理を削除する -
6、22 行目:
dxを、描画するノードの深さを使った式で計算するように修正する
1 def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
2 nodelist = [startnode]
3 depth = startnode.depth
4 # この下にあった `dx` の初期化処理を削除する
5 while len(nodelist) > 0 and depth <= maxdepth:
元と同じなので省略
6 dx = 5 * node.depth
7 node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
8 dy += node.height
9 if len(node.children) > 0:
10 childnodelist += node.children
11 else:
12 childnodelist.append(None)
13 # この下にあった `dx` に 5 を加算する処理を削除する
14 depth += 1
15 nodelist = childnodelist
16
17 node = startnode
18 # この下にあった `dx` の初期化処理を削除する
19 while node.parent is not None:
20 node = node.parent
21 node.height = startnode.height
22 dx = 5 * node.depth
23 node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
24 # この下にあった `dx` に 5 を減算する処理を削除する
25
26 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
nodelist = [startnode]
depth = startnode.depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
childnodelist = []
for node in nodelist:
if node is None:
dy += 4
childnodelist.append(None)
else:
dx = 5 * node.depth
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
depth += 1
nodelist = childnodelist
node = startnode
while node.parent is not None:
node = node.parent
node.height = startnode.height
dx = 5 * node.depth
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
Mbtree.draw_tree = draw_tree
修正箇所
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
nodelist = [startnode]
depth = startnode.depth
- dx = 5 * depth
while len(nodelist) > 0 and depth <= maxdepth:
元と同じなので省略
+ dx = 5 * node.depth
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
- dx -= 5
depth += 1
nodelist = childnodelist
node = startnode
- dx = 5 * (node.depth - 1)
while node.parent is not None:
node = node.parent
node.height = startnode.height
+ dx = 5 * node.depth
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
- dx -= 5
Mbtree.draw_tree = draw_tree
実行結果は先ほどと同じなので省略しますが、上記の修正後に、下記のプログラムを実行して正しい描画が行われることを確認して下さい。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
兄弟ノードの描画
上記の修正で、先祖ノードの描画を行うことができるようになりましたが、ゲーム木を使ってゲームの分析を行う際には、startnode の 親ノードの局面で合法手を着手した局面、すなわち 親ノードの子ノードの一覧 の情報も重要になります。
木構造で、同じノードの子ノード のことを 兄弟(sibling)ノード と呼びます。従って、上記の、親ノードの局面の合法手を着手した局面は、startnode の兄弟ノードを表します。
ただし、draw_tree を startnode の親のノードから maxdepth までの深さの部分木を描画 するようにしてしまうと、描画する ノードの数が大幅に増えてしまう 場合があるという問題が発生します。
例えば、先程は深さ 6 のノードから深さ 9 までの部分木を描画しましたが、下記のプログラムのように、その親のノードから深さ 9 までの部分木を描画 すると実行結果からわかるように、画像の縦幅が大幅に増えてしまいます。
この問題をうまく解決する方法について少し考えてみて下さい。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][0].parent, maxdepth=9)
修正箇所
-mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
+mbtree.draw_tree(mbtree.nodelist_by_depth[6][0].parent, maxdepth=9)
実行結果

描画するノードの絞り込み
この問題は、startnode の 兄弟ノードに対してまで、深さ 9 までのノードを描画 しているためにおきるので、兄弟ノードの場合はその子ノードを描画しない という工夫をすることで、描画する Figure の画像の縦幅を大幅に削減することができます。例えば、深さ 6 のノードから深さ 9 までの部分木を draw_tree で描画する場合は、下図のように描画します。
図の赤い丸が startnode で、水色の枠のノードが startnode の兄弟ノードです。先ほどの画像と比べて Figure の縦幅は 水色の兄弟ノードの分だけしか増えない ので、Figure の縦幅が大幅に短くなります。

このような工夫で Figure の縦幅が大幅に減るのは、縦幅を計算する式 が、掛け算 で行われるのと 足し算 で行われることによる違いが原因です。
わかりづらいと思いますので、具体例を挙げて説明します。
深さ 2 のノードから深さ 3 まで の部分木を描画する場合は、深さ 2 のノードには合法手が 7 つ存在するので、Figure には 縦に 7 つ分 のゲーム盤が描画されます。
深さ 2 のノードの親ノードである、深さ 1 のノードから深さ 3 まで の部分木を描画する場合は、下記から Figure には 縦に 8 * 7 = 56 個分 のゲーム盤が描画されます。
- 深さ 1 のノードはそれぞれ合法手を 8 つ持つ
- 深さ 2 のノードはそれぞれ合法手を 7 つ持つ
深さ 2 のノードの 兄弟ノードだけを追加して描画 する場合は、兄弟ノードの数である 7 個分のゲーム盤を縦に追加して描画 する必要があるので、Figure には 縦に 7 + 7 = 14 個分 のゲーム盤が描画されます。
下記の性質から、特に浅いノードを draw_tree で描画する場合は Figure の縦幅に大幅な差が生じることになります。
- 深さが浅いほど合法手の数が増える
- 足し算と掛け算では数が大きい程、計算結果に大きな差が生じる
Figure の縦幅の計算
この方針で Figure を描画するためには、Figure の縦幅のサイズを計算 する必要があります。どのようにして計算すればよいかについて少し考えてみて下さい。
下図の 赤枠の部分 は、元々描画されていた部分木 で、この部分の 縦幅は startnode の height 属性に代入 されています。また、水色の矢印の長さ は 兄弟ノードの数 * 4 で計算できます。兄弟ノードの数は、「startnode の親ノードの子ノードの数 - 1」なので、len(startnode.parent.children) - 1 という式で計算することができます。

従って、Figure の縦幅の計算は下記のプログラムで計算することができます。ただし、このプログラムには一つ重要な問題があります。それが何かについて少し考えてみて下さい。
height = startnode.height + (len(startnode.parent.children) - 1) * 4
問題は startnode がルートノードの場合 に発生します。その場合は、startnode.parent に None が代入 されているので、startnode.parent.children を計算しようとすると エラーが発生 します。従って、高さの計算は下記のプログラムのように、startnode.height を基準 とし、親ノードが存在する場合だけ増やす ように記述する必要があります。
height = startnode.height
parent = startnode.parent
if parent is not None:
height += (len(parent.children) - 1) * 4
下記は、そのように draw_tree を修正するプログラムです。なお、下記のプログラムでは、parent という変数に startnode の親ノードを代入しました。そこで、以後は startnode の親ノードの事を parent と表記する ことにします。
- 7 ~ 9 行目:親ノードが存在する場合だけ、高さを増やす
1 def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
2 if startnode is None:
3 startnode = self.root
4 self.calc_node_height(maxdepth)
5 width = 5 * (maxdepth + 1)
6 height = startnode.height
7 parent = startnode.parent
8 if parent is not None:
9 height += (len(parent.children) - 1) * 4
元と同じなので省略
10
11 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
parent = startnode.parent
if parent is not None:
height += (len(parent.children) - 1) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
nodelist = [startnode]
depth = startnode.depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
childnodelist = []
for node in nodelist:
if node is None:
dy += 4
childnodelist.append(None)
else:
dx = 5 * node.depth
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
depth += 1
nodelist = childnodelist
node = startnode
while node.parent is not None:
node = node.parent
node.height = startnode.height
dx = 5 * node.depth
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
Mbtree.draw_tree = draw_tree
修正箇所
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
parent = startnode.parent
if parent is not None:
height += (len(parent.children) - 1) * 4
元と同じなので省略
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行すると、実行結果のように Figure の縦幅が、startnode の兄弟ノードの分だけ増えることが確認できます。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
実行結果

親ノードの描画処理の修正
次に、startnode の親ノードである parent と、parent の子ノードへの エッジの描画 を行う処理を実装することにします。parent に対しては、その子ノードへのエッジをすべて描画 する必要があり、その処理は draw_node で行うことができます。
ただし、その際に startnode の兄弟ノード は子ノードが存在しているかどうかに関わらず、高さを 4 で描画する必要がある 点を忘れないようにして下さい。また、parent の高さ は、startnode.height ではなく、startnode.height に 兄弟ノードの高さを加えた値にする 必要がある点にも注意が必要です。
これらを忘れると、先程の 先祖ノードの描画の高さと height 属性の値が異なっていた ため、先祖ノードが描画されなかったバグ と同じ理由で parentが Figure の表示範囲内に描画されなくなったり、エッジがおかしな位置に描画されるようになります。
兄弟ノードの height 属性に 4 を代入する処理は、parent の children 属性に対する繰り替えし処理 で行いますが、その際に children 属性の要素に含まれる startnode の height 属性を 4 に変更してはいけない 点に注意が必要です。Python では 同一のオブジェクトであるかの判定 は == 演算子ではなく、is 演算子 を使って行う必要があります。同様にオブジェクトが 同一でない事の判定 は != 演算子ではなく is not 演算子 を使って行います。これらの違いについては以前の記事を参照して下さい。
上記から、parent のエッジの描画処理は、下記のプログラムのように draw_tree を修正することで実装することができます。
- 10 行目:親ノードが存在する場合は、親ノードの高さを Figure と同じサイズにする
- 12 ~ 17 行目:親ノードが存在する場合に、親ノードを描画する処理を行う
-
13 ~ 15 行目:
startnodeのそれぞれの兄弟(sibling)ノードの高さを4にする。ただし、startnodeの高さを変えてはいけないので、14 行目でその判定を行う -
16、17 行目:親ノードの描画を行う。
startnodeの兄弟ノードへのエッジをすべて描画する必要があるので、キーワード引数maxdepthを省略したり、parent.depthを代入してはいけない点に注意すること。なお、maxdepthにはstartnodeの深さよりも大きな値が代入されているはずなので、maxdepth=maxdepthを記述することで、startnodeの深さと異なる値を設定することができる -
19 ~ 24 行目:親ノードの先祖ノードを描画する。親ノードは描画済 なので、親ノードの親ノードから描画を行うようにするために19 行目では
nodeにstartnodeではなく、parentを代入 するように修正した
1 def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
2 if startnode is None:
3 startnode = self.root
4 self.calc_node_height(maxdepth)
5 width = 5 * (maxdepth + 1)
6 height = startnode.height
7 parent = startnode.parent
8 if parent is not None:
9 height += (len(parent.children) - 1) * 4
10 parent.height = height
11 fig, ax = plt.subplots(figsize=(width * size, height * size))
元と同じなので省略
12 if parent is not None:
13 for sibling in parent.children:
14 if sibling is not startnode:
15 sibling.height = 4
16 dx = 5 * parent.depth
17 parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
18
19 node = parent
20 while node.parent is not None:
21 node = node.parent
22 node.height = startnode.height
23 dx = 5 * node.depth
24 node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
25
26 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
parent = startnode.parent
if parent is not None:
height += (len(parent.children) - 1) * 4
parent.height = height
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
nodelist = [startnode]
depth = startnode.depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
childnodelist = []
for node in nodelist:
if node is None:
dy += 4
childnodelist.append(None)
else:
dx = 5 * node.depth
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
depth += 1
nodelist = childnodelist
if parent is not None:
for sibling in parent.children:
if sibling is not startnode:
sibling.height = 4
dx = 5 * parent.depth
parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
node = parent
while node.parent is not None:
node = node.parent
node.height = startnode.height
dx = 5 * node.depth
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
Mbtree.draw_tree = draw_tree
修正箇所
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
parent = startnode.parent
if parent is not None:
height += (len(parent.children) - 1) * 4
+ parent.height = height
fig, ax = plt.subplots(figsize=(width * size, height * size))
元と同じなので省略
+ if parent is not None:
+ for sibling in parent.children:
+ if sibling is not startnode:
+ sibling.height = 4
+ dx = 5 * parent.depth
+ parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
- node = startnode
+ node = parent
- while node.parent is not None:
- node = node.parent
- node.height = startnode.height
- dx = 5 * node.depth
- node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
+ while node.parent is not None:
+ node = node.parent
+ node.height = startnode.height
+ dx = 5 * node.depth
+ node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行すると、実行結果のように parent が Figure の上下の真ん中に描画され、parent のエッジが描画されるようになります。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
実行結果

親ノードの先祖ノードの描画位置の修正と、兄弟ノードの描画
先程のプログラムには、上図のように、親ノードの先祖ノードの描画位置 と、兄弟ノードが描画されない という問題があります。
親ノードの先祖ノードの描画位置がおかしいのは、Figure の高さが変化した にも関わらす、それらのノードの height 属性に startnode の height 属性を代入 しているからなので、Figure の高さを表す height を代入 することで修正することができます。
兄弟ノードの描画は、兄弟ノードの高さに 4 を代入する際 に、draw_node を使って描画 すると良いでしょう。兄弟ノードに子ノードが存在する場合は 1 本だけエッジを描画する 必要があるので、キーワード引数 maxdepth に兄弟ノードの深さを代入 して呼び出します。
なお、その際に startnode を描画 してしまうと、startnode を 2 回描画する ことになる点に注意して下さい。ただし、9 行目の、次の兄弟ノードの描画位置の y 座標を計算する処理 は、startnode に対しても行う必要がある 点にも注意が必要です。
下記は、そのように draw_tree を修正したプログラムです。
-
3 行目:兄弟ノードの描画位置の y 座標を表す
dyを0で初期化する - 7 行目:兄弟ノードの描画位置の x 座標を計算する
-
8 行目:キーワード引数
maxdepthに兄弟ノードの深さを代入 して呼び出すことで、子ノードが存在した場合に エッジを 1 本だけ描画する ように兄弟ノードを描画する -
9 行目:次の兄弟ノードの描画位置 を
sibling.heightだけ下にずらす。なお、この処理はsiblingにstartnodeが代入されている場合でも行う必要がある ため、5 行目の if 文のブロックの外に記述 する必要がある点に注意すること - 16 行目:親ノードの先祖ノードの高さに Figure の高さを代入するように修正する
1 def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
2 if parent is not None:
3 dy = 0
4 for sibling in parent.children:
5 if sibling is not startnode:
6 sibling.height = 4
7 dx = 5 * sibling.depth
8 sibling.draw_node(ax, maxdepth=sibling.depth, size=size, lw=lw, dx=dx, dy=dy)
9 dy += sibling.height
10 dx = 5 * parent.depth
11 parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
12
13 node = parent
14 while node.parent is not None:
15 node = node.parent
16 node.height = height
17 dx = 5 * node.depth
18 node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
19
20 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
parent = startnode.parent
if parent is not None:
height += (len(parent.children) - 1) * 4
parent.height = height
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
nodelist = [startnode]
depth = startnode.depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
childnodelist = []
for node in nodelist:
if node is None:
dy += 4
childnodelist.append(None)
else:
dx = 5 * node.depth
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
depth += 1
nodelist = childnodelist
if parent is not None:
dy = 0
for sibling in parent.children:
if sibling is not startnode:
sibling.height = 4
dx = 5 * sibling.depth
sibling.draw_node(ax, maxdepth=sibling.depth, size=size, lw=lw, dx=dx, dy=dy)
dy += sibling.height
dx = 5 * parent.depth
parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
node = parent
while node.parent is not None:
node = node.parent
node.height = height
dx = 5 * node.depth
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
Mbtree.draw_tree = draw_tree
修正箇所
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
if parent is not None:
+ dy = 0
for sibling in parent.children:
if sibling is not startnode:
sibling.height = 4
+ dx = 5 * sibling.depth
+ sibling.draw_node(ax, maxdepth=sibling.depth, size=size, lw=lw, dx=dx, dy=dy)
+ dy += sibling.height
dx = 5 * parent.depth
parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
node = parent
while node.parent is not None:
node = node.parent
- node.height = startnode.height
+ node.height = height
dx = 5 * node.depth
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行すると、実行結果のように親ノードの先祖ノードと、兄弟ノードが正しく描画されることが確認できます。なお、このプログラムには重大なバグがあります。それが何かについて少し考えてみて下さい。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
実行結果
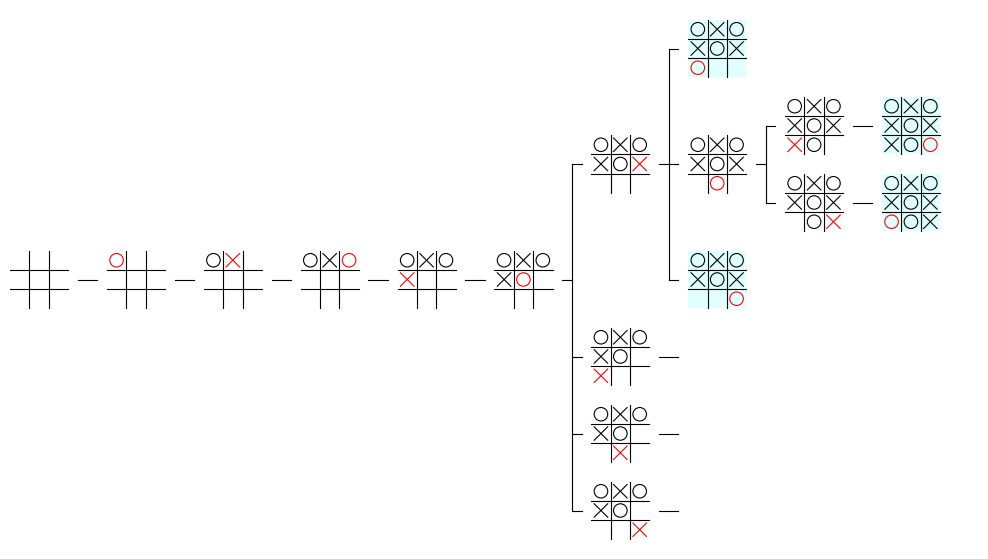
startnode の描画位置のバグの検証と修正
そのバグは、下記のプログラムの実行結果ように、startnode が、親ノードの子ノードの 先頭のノードでない場合 は、startnode の描画位置がおかしくなる というものです。具体的には、下記の場合は startnode とその子孫の部分木が上にずれて描画されています。このようなことが起きる原因について少し考えてみて下さい。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][1], maxdepth=9)
修正箇所
-mbtree.draw_tree(mbtree.nodelist_by_depth[6][0], maxdepth=9)
+mbtree.draw_tree(mbtree.nodelist_by_depth[6][1], maxdepth=9)
実行結果

このバグの原因は、下記のプログラムの 4 行目のように、startnode とその子孫の部分木を描画する y 座標の基準を表す dy に、Figure の上端を表す 0 に設定しているからです。
nodelist = [startnode]
depth = startnode.depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
startnode とその子孫の部分木 は、startnode が親ノードの 何番目の子ノードであるか によって、下にずらして描画する必要があります。具体的には startnode より前に兄弟ノードが存在する場合 は、その数 * 4 だけ下にずらして描画 する必要があります。上図の場合は、startnode の前に一つ兄弟ノードが存在するので 4 だけずらす必要があります。
ずらす量は、startnode が parent の children 属性の i 番のインデックスの要素に代入 されている場合は、i * 4 という式で計算できます。例えば 0 番のインデックスの要素に代入されている場合は、startnode より前に兄弟ノードは存在しないので 0 * 4 = 0 で、ずらす必要はありません。2 番のインデックスの要素に代入されている場合は、startnode より前に 2 つ兄弟ノードが存在するので 2 * 4 = 8 だけずらす必要があります。
list などのシーケンス型には、実引数で指定したオブジェクトが、list の何番のインデックスの要素に代入されているか を計算する、index というメソッドがあるので、それを利用することで、下記のプログラムのように draw_tree を修正することができます。
-
6、7 行目:親ノードが存在する場合、
dyにstartnodeが代入されているparent.childrenのインデックス * 4 を計算して代入する
1 def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
2 nodelist = [startnode]
3 depth = startnode.depth
4 while len(nodelist) > 0 and depth <= maxdepth:
5 dy = 0
6 if parent is not None:
7 dy = parent.children.index(startnode) * 4
元と同じなので省略
8
9 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
if startnode is None:
startnode = self.root
self.calc_node_height(maxdepth)
width = 5 * (maxdepth + 1)
height = startnode.height
parent = startnode.parent
if parent is not None:
height += (len(parent.children) - 1) * 4
parent.height = height
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
nodelist = [startnode]
depth = startnode.depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
if parent is not None:
dy = parent.children.index(startnode) * 4
childnodelist = []
for node in nodelist:
if node is None:
dy += 4
childnodelist.append(None)
else:
dx = 5 * node.depth
node.draw_node(ax=ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=dy)
dy += node.height
if len(node.children) > 0:
childnodelist += node.children
else:
childnodelist.append(None)
depth += 1
nodelist = childnodelist
if parent is not None:
dy = 0
for sibling in parent.children:
if sibling is not startnode:
sibling.height = 4
dx = 5 * sibling.depth
sibling.draw_node(ax, maxdepth=sibling.depth, size=size, lw=lw, dx=dx, dy=dy)
dy += sibling.height
dx = 5 * parent.depth
parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
node = parent
while node.parent is not None:
node = node.parent
node.height = height
dx = 5 * node.depth
node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
Mbtree.draw_tree = draw_tree
修正箇所
def draw_tree(self, startnode=None, size:float=0.25, lw:float=0.8, maxdepth=2):
元と同じなので省略
nodelist = [startnode]
depth = startnode.depth
while len(nodelist) > 0 and depth <= maxdepth:
dy = 0
if parent is not None:
dy = parent.children.index(startnode) * 4
元と同じなので省略
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行すると、実行結果のように startnode とその子孫の部分木が正しい位置に描画されるようになることが確認できます。
mbtree.draw_tree(mbtree.nodelist_by_depth[6][1], maxdepth=9)
実行結果
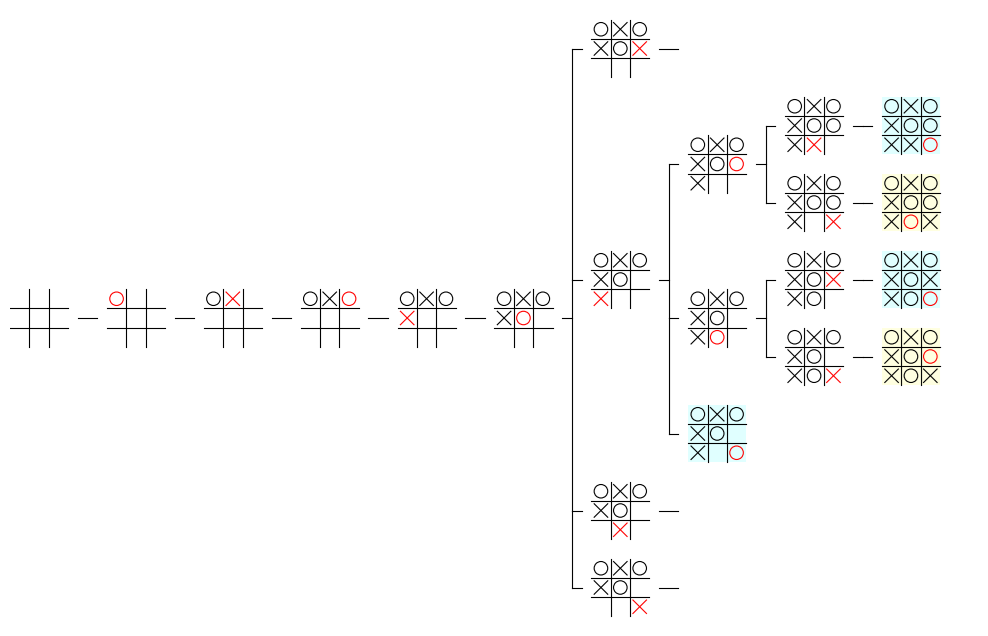
シーケンス型の index メソッドの詳細に関しては、下記のリンク先を参照して下さい。
今回の記事のまとめ
今回の記事では、ゲーム木全体の視覚化を行うために必要となる、ゲーム木の部分木の表示範囲の改良を行いました。次回の記事で、ゲーム木全体の視覚化の処理を実装する予定です。
本記事で入力したプログラム
以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。
以下のリンクは、今回の記事で更新した tree.py です。
次回の記事
-
ややこしいですが、親の子なので、自分自身、すなわちルートノードの事を表します ↩