Pythonで〇×ゲームのAIを一から作成する その103 複数の項で表される漸化式のトップダウンな再帰呼び出しによる計算

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
util.py	ユーティリティ関数の定義。現在は gui_play のみ定義されている
tree.py	ゲーム木に関する Node、Mbtree クラスの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

ルールベースの AI の一覧については、下記の記事を参照して下さい。

漸化式に対する繰り返し処理の説明の訂正

前回の記事では、以下のような説明を行いましたが、正確ではなかったので訂正 します。なお、深刻な間違いではないような気がするので、過去の記事の内容はそのままにします。

• 直前の計算結果のみ で表される 漸化式 の計算は、ボトムアップとトップダウンの どちらの手順でも直線的な繰り返し処理 によって計算を行うことができる

• 漸化式 の計算は、ボトムアップ な手順で 必ず直線的な繰り返し処理 によって計算を行うことができる

• 直前以外 の計算結果を利用する漸化式を、トップダウン な手順で計算すると、 繰り返し処理が分岐する

上記では、直前の計算結果のみ で表されるかどうかで分類していますが、厳密には 直前 である必要はなく、以前の 1 つの計算結果のみ で表されるかどうかがで分類します。

例えば、下記は以下のような計算を行う漸化式です。

$x_n = x_{n-2} + n$、$x_0 = 0$、$x_1 = 1$

• $n$ が偶数の場合は 0 から $n$ までの偶数の合計を計算する
• $n$ が奇数の場合は 1 から $n$ までの奇数の合計を計算する

この漸化式は 以前の 1 つの計算結果のみ で表され、ボトムアップとトップダウンのどちらの手順でも直線的な繰り返し処理によって計算を行うことができます。

従って、上記の説明を下記のように訂正することにします。なお、$x_n$ のような、漸化式で計算されるもののことを 項 と呼び、漸化式は 以前の項を使った式 で記述されるので、以後は 以前の計算結果 を単に 項 と表記することにします。

• 1 つの項のみ で表される 漸化式 の計算は、ボトムアップとトップダウンの どちらの手順でも直線的な繰り返し処理 によって計算を行うことができる

• 漸化式 の計算は、ボトムアップ な手順で 必ず直線的な繰り返し処理 によって計算を行うことができる

• 複数の項 で表される漸化式を トップダウン な手順で計算すると、 繰り返し処理が分岐する

分岐する繰り返し処理を行う再帰呼び出し

前回の記事では直線的な繰り返し処理を行う再帰呼び出しを紹介しましたので、次に 分岐する繰り返し処理 を行う 再帰呼び出し を紹介します。

今回の記事では、分岐する繰り返し処理の中で、複数の項で表される漸化式を、トップダウンな再帰呼び出しによる計算で行う方法について説明します。

複数の項で表される漸化式の、トップダウンな再帰呼び出しによる計算

分岐する繰り返し処理 を 再帰呼び出しで記述する例 として 良く取り上げられる のが、下記の漸化式で表される フィボナッチ数 $F_n$ の計算 です。

$F_n = F_{n-1}+F_{n-2}$、$F_0 = 0$、$F_1 = 1$

前回の記事では $F_n$ をボトムアップな再帰呼び出しによって、直線的な繰り返し処理で計算する方法を紹介しました。一方、$F_n$ を トップダウン な再帰呼び出しで計算すると 分岐する繰り返し処理 になります。そのことを以下で示します。

fib_by_tr の定義

まず、トップダウン な再帰呼び出しで $F_n$ を計算する関数を定義することにします。関数の名前は、再帰呼び出し（recursive call）をトップダウン（topdown）で行うことから、fib_by_tr とします。

fib_by_tr で行う処理は、前回の記事で定義した sum_by_tr と 同様 で、$F_n$ を計算する漸化式を表す処理をそのまま記述します。

具体的には、fib_by_tr を sum_by_tr と同様の、以下のような考え方で定義します。

• fib_by_tr が正しく定義できていれば、fib_by_tr(n) によって $F_n$ が計算できる
• 同様に $F_{n - 1}$ は fib_by_tr(n - 1) で計算できる
• 同様に $F_{n - 2}$ は fib_by_tr(n - 2) で計算できる
• $F_n$ は、$F_n = F_{n-1}+F_{n-2}$ という式で計算できるので、fib_by_tr の中では、fib_by_tr(n - 1) + fib_by_tr(n - 2) を計算し、返り値として返す処理を行う
• ただし、$F_0 = 0$、$F_1 = 1$ から、n が 0 と 1 の場合は、それぞれ 0 と 1 を返す

下記は、そのように fib_by_tr を定義したプログラムです。プログラムを見ればわかるように、この関数では、漸化式を表す処理をそのまま記述 しているので、for 文やボトムアップな再帰呼び出しと比較して、簡潔にプログラムを記述 することができます。

• 2 ~ 5 行目：n が 0 と 1 の場合は $F_0 = 0$、$F_1 = 1$ なので、その値を返す
• 7 行目：$F_n = F_{n-1} + F_{n-2}$ を表す式を計算し、その計算結果を返り値として返す

1  def fib_by_tr(n):
2      if n == 0:
3          return 0
4      elif n == 1:
5          return 1   
6
7      return fib_by_tr(n - 1) + fib_by_tr(n - 2)

行番号のないプログラム

def fib_by_tr(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1   
        
    return fib_by_tr(n - 1) + fib_by_tr(n - 2)

下記の for 文を使った fib_by_f の定義と比較してみて下さい。共通する 2 ~ 5 行目 の n が 0 と 1 の場合の処理を 除いた処理 は、圧倒的に fib_by_tr のほうが簡潔 です。

def fib_by_f(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
    fib_p2 = 0
    fib_p1 = 1
    for i in range(2, n + 1):
        fib = fib_p1 + fib_p2
        fib_p2 = fib_p1
        fib_p1 = fib
    return fib

下記のプログラムを実行することで、$F_0$ ~ $F_9$ を fib_by_f と fib_by_tr で計算し、計算結果を並べて表示します。実行結果からどちらも同じ計算を行うことが確認できます。

for i in range(10):
    print(f"fib({i}) = {fib_by_f(i)}, {fib_by_tr(i)}")

実行結果

fib(0) = 0, 0
fib(1) = 1, 1
fib(2) = 1, 1
fib(3) = 2, 2
fib(4) = 3, 3
fib(5) = 5, 5
fib(6) = 8, 8
fib(7) = 13, 13
fib(8) = 21, 21
fib(9) = 34, 34

fib_by_f との違い

前回の記事の再掲になりますが、for 文や while 文 と、再帰呼び出し では、データの管理の方法 が下記のように 異なります。管理すべきデータを減らすことができる 分だけ、再帰呼び出しでは 処理の記述を減らす ことができます。

• for 文や while 文では、計算に必要なデータをすべて自分で管理する必要がある
• 再帰呼び出し では、関数の中では 以下のデータのみを管理 すれば良い
  • 仮引数で受け取った、その関数での繰り返し処理に必要なデータ
  • 再帰呼び出しで、次の繰り返し処理に実引数で渡すデータ
  • 再帰呼び出しからの返り値のデータ

$F_n$ を計算するトップダウンな再帰呼び出しでは、$F_n = F_{n-1}+F_{n-2}$ を 計算するために必要な $F_{n-1}$ と $F_{n-2}$ の計算を、再帰呼び出しによって別の関数に委託 し、その 結果を返り値で受け取ることで計算を行う ため、$F_{n-1}$ と $F_{n-2}$ を計算するためのデータを 管理する必要はありません。それが、プログラムを簡潔に記述できる理由です。

fib_by_br の違い

下記のプログラムのように、トップダウンな再帰呼び出しを行う fib_by_tr は、ボトムアップな再帰呼び出しを行う fib_by_br と比べても 簡潔に、見た目が わかりやすく プログラムを記述することができます。その理由について少し考えてみて下さい。

def fib_by_tr(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1   
        
    return fib_by_tr(n - 1) + fib_by_tr(n - 2)
    
def fib_by_br(n, i=2, fib_p1=1, fib_p2=0):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
    if i <= n:
        return fib_by_br(n, i + 1, fib_p1 + fib_p2, fib_p1)
    else:
        return fib_p1

漸化式をそのまま記述できる

fib_by_tr のほうが わかりやすく見える理由 は、return fib_by_tr(n - 1) + fib_by_tr(n - 2) のように、プログラムの中に 漸化式と同じ式をそのまま記述できる点 でしょう。また、この式 が $F_n = F_{n-1} + F_{n-2}$ を 計算している ことは、一目瞭然 でしょう。

一方、fib_by_br では、再帰呼び出しを表す fib_by_br(n, i + 1, fib_p1 + fib_p2, fib_p1) の実引数の中の fib_p1 + fib_p2 が $F_n = F_{n-1} + F_{n-2}$ を 計算しています が、そのことは 実引数が 4 つもある ため直観的には わかりづらい のではないかと思います。

仮引数が 1 つだけで済む

fib_by_br の仮引数が 4 つ必要になる理由は、以下の通りです。なお、$F_0$ と $F_1$ の計算は両者で同じなので、下記は $n$ が 2 以上の $F_n$ を計算する場合の説明です。

• ボトムアップな処理では、$F_2$ から順番に $F_n$ までの計算を行うが、その際に、何番目を計算しているかを記録 する必要がある。それが i という仮引数である
• 再帰呼び出しの処理を $F_n$ で 終わらせるため には、$n$ の値が必要 になる。それが n という仮引数と、if i <= n: という条件分岐である。なお、fib_by_tr と異なり、fib_by_br の再帰呼び出しの処理の中で n の値は変化しない 点に注意すること
• $F_n$ を計算するためには、$F_{n-1}$ と $F_{n-2}$ の値が必要になる。それが fib_p1 と fib_p2 という仮引数である

一方、fib_by_tr の仮引数が 1 だけで済む理由は、以下の通りです。

• トップダウンな処理では、$F_n$ から順番に計算を行うが、その際に $F_{n-1}$ と $F_{n-2}$ を計算する再帰呼び出しの処理を行う
• 上記から n が小さくなりながら 再帰呼び出しが行われるが、$F_0 = 0$ と $F_1 = 1$ なので、n が 0 または 1 になった時点で 再帰呼び出しを行う必要がなくなる。そのため、fib_by_br のように、再帰呼び出しを終わらせるための仮引数は必要がない
• $F_n = F_{n-1} + F_{n-2}$ の計算は、fib_by_br のように仮引数に代入されたデータを使うのではなく、$F_{n-1}$ と $F_{n-2}$ を計算する 再帰呼び出しの返り値を使って行う ので、そのための仮引数は必要がない

上記のように、fib_by_tr では、$F_n$ を計算する際に必要となる $F_{n-1}$ と $F_{n-2}$ の計算結果を 直接管理していない ことが、簡潔に記述できる理由です。

再帰呼び出しの末端の処理の違い

他にも、fib_by_tr では、if i <= n: という 条件文によって、再帰呼び出しを行うかどうかを 判定している 点がわかりづらく見えるかもしれません。このような違いが生じるのは、再帰呼び出しの末端で行われる処理 が、fib_by_tr と fib_by_br で 異なる からです。

fib_by_tr では、再帰呼び出しを行うたびに、仮引数 n に代入される値が 減っていきます。そのため、再帰呼び出しの 末端 では、n が 0 または 1 になり、再帰呼び出しではない return 0 または return 1 が実行されます。従って、n が 0 または 1 の場合の処理は、再帰呼び出しの計算の中で 必ず実行されます。

fib_by_br では、再帰呼び出しを行うたびに、仮引数 i に代入される値が 増えていきます。そのため、n が 2 以上の場合は、再帰呼び出しを止めるための条件式を記述 する必要があります。それが、if i <= n: という条件文で、再帰呼び出しの 末端 ではこの条件式が False になるため、再帰呼び出しではない return total が実行されます。また、n が 2 以上 の場合は return 0 と return 1 は決して実行されません。

計算速度の問題

fib_by_tr にはプログラムを簡潔に記述できるという利点がありますが、その一方で 重大な欠点 があります。それは $n$ が 大きくなる と、$F_n$ 数を計算する 処理時間が急激に増える という問題です。

例えば、$F_{40}$ を下記のプログラムで fib_by_tr で計算すると、筆者のパソコンでは約 20 秒の時間がかかりました。また、もっと大きな $n$ で $F_n$ を計算すると、具体的な処理時間についてはこの後で説明しますが、急激に処理時間が増える ようになります。

print(fib_by_tr(40))

実行結果

102334155

一方、同じ $F_{40}$ を下記のプログラムで fib_by_f や fib_by_bf で計算すると、同じ結果が表示されますが、どちらも一瞬で計算が終了します。

print(fib_by_f(40))
print(fib_by_br(40))

実行結果

102334155
102334155

fib_by_tr の処理の流れ

このような大きな差が生じる理由を理解するためには、$F_n$ をトップダウンな再帰呼び出しで計算を行った際の 処理の流れを理解する 必要があります。そこで、処理の流れを print で表示するように fib_by_tr を修正することにします。この修正は、前回の記事で sum_by_tr に対して行ったものとほぼ同じです。

ただし、今回は以下のような工夫を行いました。

• fib_by_tr と表記するのは長いので、メッセージでは fib と表記する
• 再帰呼び出しの 深さだけ メッセージを 2 文字ずつインデント して右にずらして表示する。インデントを行うことで、メッセージを表示した 再帰呼び出しの深さが明確になる
• + 演算子は 先頭から計算が行われる ので、fib_by_tr(n-1) + fib_by_tr(n-2) という式は、先頭の fib_by_tr(n-1) から順 に再帰呼び出しが行われる。そこで fib_by_tr(n-1) と fib_by_tr(n-2) の再帰呼び出しを 順番に別々に行い、その前後 に計算の 途中経過と結果を表すメッセージを表示 するようにした

再帰呼び出しで 深さを考慮に入れた計算 を行う場合は、深さを表す仮引数を用意 し、再帰呼び出しを行う際に、深さに 1 を足した実引数を記述 することで行います。

下記はそのように fib_by_tr を修正したプログラムです。

• 1 行目：再帰呼び出しの深さを表す仮引数 depth を追加する。最初に呼び出された関数の深さは 0 なので、デフォルト値を 0 とするデフォルト引数とした
• 2 行目：2 文字の半角の空白 に * depth を計算することで、インデントを表す 深さの数 * 2 文字分の半角の空白 を計算し、indent に代入する
• 4、7 行目：n が 0 と 1 の場合の計算結果をインデントの後に表示する
• 10、12 行目：fib_by_tr の再帰呼び出しを行う際に、次の深さを表す depth + 1 を実引数に記述するようにする
• 10、12、13 行目：計算の途中経過を表示できるように、fib_by_tr(n-1) と fib_by_tr(n-2) のそれぞれの返り値と、合計の計算結果を変数に代入する
• 9、11、14 行目：計算の途中経過と結果を、インデントの後に表示する

 1  def fib_by_tr(n, depth=0):
 2      indent = "  " * depth
 3      if n == 0:
 4          print(f"{indent}fib(0) = 0")
 5          return 0
 6      elif n == 1:
 7          print(f"{indent}fib(1) = 1")
 8          return 1   
 9      print(f"{indent}fib({n}) = fib({n - 1}) + fib({n - 2})")
10      r1 = fib_by_tr(n - 1, depth + 1)
11      print(f"{indent}fib({n}) = {r1} + fib({n - 2})")
12      r2 = fib_by_tr(n - 2, depth + 1)
13      retval = r1 + r2
14      print(f"{indent}fib({n}) = {r1} + {r2} = {retval}")
15      return retval

行番号のないプログラム

def fib_by_tr(n, depth=0):
    indent = "  " * depth
    if n == 0:
        print(f"{indent}fib(0) = 0")
        return 0
    elif n == 1:
        print(f"{indent}fib(1) = 1")
        return 1   
    print(f"{indent}fib({n}) = fib({n - 1}) + fib({n - 2})")
    r1 = fib_by_tr(n - 1, depth + 1)
    print(f"{indent}fib({n}) = {r1} + fib({n - 2})")
    r2 = fib_by_tr(n - 2, depth + 1)
    retval = r1 + r2
    print(f"{indent}fib({n}) = {r1} + {r2} = {retval}")
    return retval

修正箇所

-def fib_by_tr(n):
+def fib_by_tr(n, depth=0):
+   indent = "  " * depth
    if n == 0:
+       print(f"{indent}fib(0) = 0")
        return 0
    elif n == 1:
+       print(f"{indent}fib(1) = 1")
        return 1   
-   return fib_by_tr(n - 1) + fib_by_tr(n - 2)
+   print(f"{indent}fib({n}) = fib({n - 1}) + fib({n - 2})")
+   r1 = fib_by_tr(n - 1, depth + 1)
+   print(f"{indent}fib({n}) = {r1} + fib({n - 2})")
+   r2 = fib_by_tr(n - 2, depth + 1)
+   retval = r1 + r2
+   print(f"{indent}fib({n}) = {r1} + {r2} = {retval}")
+   return retval

下記は、上記の fib_by_tr を使って $F_4$ を計算するプログラムで、実行結果のように計算の途中経過が表示されます。なお、コメントの部分は筆者が加筆したものです。

print(fib_by_tr(4))

実行結果

fib(4) = fib(3) + fib(2)       # fib(4) の 9 行目の表示
  fib(3) = fib(2) + fib(1)     # fib(4) から呼び出された fib(3) の 9 行目の表示 
    fib(2) = fib(1) + fib(0)
      fib(1) = 1
    fib(2) = 1 + fib(0)
      fib(0) = 0
    fib(2) = 1 + 0 = 1
  fib(3) = 1 + fib(1)          # fib(4) から呼び出された fib(3) の 11 行目の表示 
    fib(1) = 1
  fib(3) = 1 + 1 = 2           # fib(4) から呼び出された fib(3) の 13 行目の表示 
fib(4) = 2 + fib(2)            # fib(4) の 11 行目の表示
  fib(2) = fib(1) + fib(0)     # fib(4) から呼び出された fib(2) の 9 行目の表示 
    fib(1) = 1
  fib(2) = 1 + fib(0)          # fib(4) から呼び出された fib(2) の 11 行目の表示 
    fib(0) = 0
  fib(2) = 1 + 0 = 1           # fib(4) から呼び出された fib(2) の 13 行目の表示 
fib(4) = 2 + 1 = 3             # fib(4) の 13 行目の表示

実行結果では、同じ深さ の再帰呼び出しの メッセージのインデントは同じ になります。また、再帰呼び出しが行われるたびに、2 文字分の半角の空白のインデントが追加され、再帰呼び出しの処理が終了するたびにインデントが戻ります。従って、例えば fib(4) から呼び出された 再帰呼び出しの処理 では、fib(4) のメッセージよりも インデントが多いメッセージが表示 され、再帰呼び出しの処理がすべて終了した時点で、次の fib(4) のメッセージが表示されます。

上記の実行結果の処理の流れは以下のようになります。

• fib(4) が呼び出され、fib(3) + fib(2) の計算を開始する。+ 演算子は先頭から処理が行われる ので、fib(3) を先に計算する
  • fib(3) が呼び出され、fib(2) + fib(1) の計算を開始する。fib(2) を先に計算する
    • fib(2) が呼び出され、fib(1) + fib(0) の計算を開始する。fib(1) を先に計算する
      • fib(1) が呼び出され、1 が返る（再帰呼び出しの末端）
    • fib(2) の fib(1) + fib(0) が 1 + fib(0) になる。残りの fib(0) を計算する
      • fib(0) が呼び出され、0 が返る（再帰呼び出しの末端）
    • fib(2) の 1 + fib(0) が 1 + 0 = 1 になり、1 が返る
  • fib(3) の fib(2) + fib(1) が 1 + fib(1) になる。残りの fib(1) を計算する
    • fib(1) が呼び出され、1 が返る（再帰呼び出しの末端）
  • fib(3) の 1 + fib(1) が 1 + 1 = 2 になり、2 が返る
• fib(4) の fib(3) + fib(2) が 2 + fib(2) になる。残りの fib(2) を計算する
  • 上記と同様の手順で fib(2) が計算され、1 が返る
• fib(4) の 2 + fib(2) が 2 + 1 = 3 になり、3 が返る

fib_by_tr で複数の再帰呼び出しが行われる際には、下記のような処理が行われます。

• 複数の再帰呼び出しが、記述された順番 に行われる
• 行われた再帰呼び出しの 処理がすべて完了してから 、次の再帰呼び出しが行われる

また、fib_by_tr の再帰呼び出しの処理では、fib_by_tr(1) と fib_by_tr(0) が呼び出された場合に 再帰呼び出しが行われない ので、それらは 再帰呼び出しの末端 になります。上記のように、fib_by_tr で行われる再帰呼び出しの処理には、複数の末端が存在 します。

行われた処理の流れを式だけで表すと以下のようになります。下記では、関数が呼び出された場合に計算される式を、その下に () で囲って記述しました。例えば、1 行目の fib(3) によって計算される式は、2 行目の () で囲った (fib(2) + fib(1)) です。

fib(4) =   fib(3)                     + fib(2)
       =  (fib(2)           + fib(1)) + fib(2)              
       = ((fib(1) + fib(0)) + fib(1)) + fib(2)
       = ((1      + fib(0)) + fib(1)) + fib(2)
       = ((1      + 0     ) + fib(1)) + fib(2)
       = ( 1                + fib(1)) + fib(2)
       = ( 1                + 1     ) + fib(2)
       =   2                          + fib(2)
       =   2                          + (fib(1) + fib(0))
       =   2                          + (1      + fib(0))
       =   2                          + (1      + 0     )
       =   2                          +  1
       =   3

下図は、処理の流れを図に表したものです。赤い矢印が関数呼び出しを、青い矢印が返り値を返す処理を、数字が処理が行われた順番を表します。

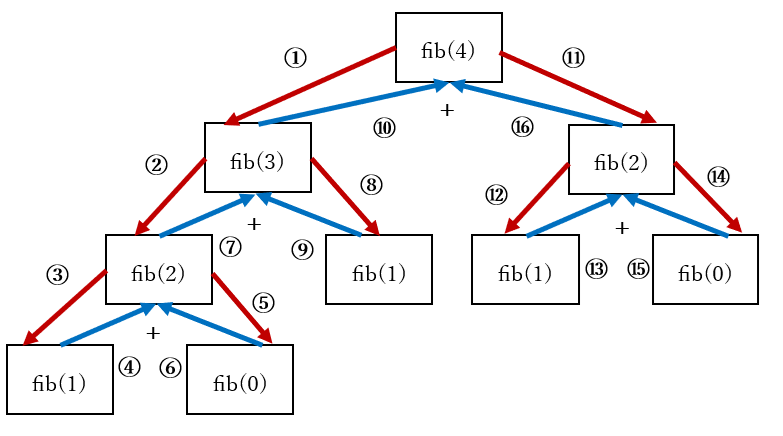
上図のように、トップダウンな再帰呼び出しによる $F_n$ の計算は、関数内で $F_{n-1}$ と $F_{n-2}$ を計算する 2 つの再帰呼び出しが行われる ので、分岐する繰り返し処理 が行われます。

同様の理由で、複数の項で表される漸化式 を トップダウンな再帰呼び出しで計算 すると、分岐する繰り返し処理 が行われます。

分岐する繰り返し処理の処理時間

一般的に、分岐する繰り返し処理 では、繰り返しの 回数が増える と 処理の数が爆発的に増える という性質があります。例えば、繰り返しのたびに 2 つに分岐 する場合は、1 回目の繰り返しで 2 回の処理が、2 回目の繰り返しで 2 * 2 = 4 回の処理が、n 回目の繰り返しで $2^n$ 回 の処理が必要になります。このような $x$ を $y$ 回乗算する $x^y$ という計算を 指数関数 と呼び、指数関数は $x > 1$ の場合に $y$ が増加すると、爆発的に増えていく という性質があります¹。例えば $2^{10} = 約 1000$、$2^{20} = 約 100 万$、$2^{30} = 約 10 憶$ になります。

下図は $0 ≦ x ≦ 9$ の整数の範囲で $y=x$、$y=2^x$、$y=3^x$ をグラフにしたものです。グラフから $y=x$ と比較して、$y=2^x$ や $y=3^x$ が爆発的に増えていく様子がわかります。

上記のグラフは matplotlib を使って下記のプログラムで描画しました。なお、matplotlib でのグラフの描画方法については今後の記事で説明する予定なので、今回の記事では下記のプログラムの説明は行いません。

また、numpy というモジュールを使えばもっと簡潔にプログラムを記述することができますが、numpy はまだ説明していないので利用していません。

import matplotlib.pyplot as plt
import japanize_matplotlib

x_list = [x for x in range(10)]
exp2_list = [ 2 ** x  for x in range(10)]
exp3_list = [ 3 ** x  for x in range(10)]

plt.plot(x_list, x_list, label="$y=x$")
plt.plot(x_list, exp2_list, label="$y=2^x$")
plt.plot(x_list, exp3_list, label="$y=3^x$")
plt.ylim(0, 1000)
plt.legend()
plt.show()

何故そのようになるかについての説明は省略しますが、$F_n$ の計算に必要な処理は n が 1 つ増える と 約 1.6 倍 になります。従って、$n$ が $k$ 増えると処理時間は約 $1.6^k$ 倍 になります。先ほどの $F_{40}$ の計算に 2 分もの時間がかかったのは、$1.6^{40} = 1.5 億$ という非常に大きな数になるからです。$n$ を増やしていくと、すぐに $F_n$ の計算が数年かけても計算が終わらないようになります。

別の分岐する繰り返し処理の例として、〇× ゲームの ゲーム木を作成する処理 が挙げられます。ゲーム木の作成では、深さ 0 のルートノードからはじめ、「深さ d のすべてのノードに対して子ノードを作成し、d に 1 を足す」という繰り返し処理を行います。そのため、複数の子ノードが存在するノード では、この 繰り返し処理は分岐します。そのため、〇×ゲームのゲーム木の 深さは 9 しかありませんが、全体の ノードの数は 50 万以上 にもなります。

一方、直線的な繰り返し処理 の場合は、一般的に繰り返しの 回数に比例した処理時間 がかかります。そのため、fib_by_f を使って $F_{40}$ を計算した際にかかる時間は、$F_1$ の 約 40 倍 にしかなりません。そのため、fib_by_f では、下記のプログラムのように、かなり大きな $n$ でも $F_n$ を計算することができます。なお、fib_by_br では、再帰呼び出しの繰り返しの回数に制限があるという別の理由から、大きな $n$ の $F_n$ を計算することはできません。

print(fib_by_f(10000))

実行結果（とてつもなく大きな数字になります）

33644764876431783266621612005107543310302148460680063906564769974680081442166662368155595513633734025582065332680836159373734790483865268263040892463056431887354544369559827491606602099884183933864652731300088830269235673613135117579297437854413752130520504347701602264758318906527890855154366159582987279682987510631200575428783453215515103870818298969791613127856265033195487140214287532698187962046936097879900350962302291026368131493195275630227837628441540360584402572114334961180023091208287046088923962328835461505776583271252546093591128203925285393434620904245248929403901706233888991085841065183173360437470737908552631764325733993712871937587746897479926305837065742830161637408969178426378624212835258112820516370298089332099905707920064367426202389783111470054074998459250360633560933883831923386783056136435351892133279732908133732642652633989763922723407882928177953580570993691049175470808931841056146322338217465637321248226383092103297701648054726243842374862411453093812206564914032751086643394517512161526545361333111314042436854805106765843493523836959653428071768775328348234345557366719731392746273629108210679280784718035329131176778924659089938635459327894523777674406192240337638674004021330343297496902028328145933418826817683893072003634795623117103101291953169794607632737589253530772552375943788434504067715555779056450443016640119462580972216729758615026968443146952034614932291105970676243268515992834709891284706740862008587135016260312071903172086094081298321581077282076353186624611278245537208532365305775956430072517744315051539600905168603220349163222640885248852433158051534849622434848299380905070483482449327453732624567755879089187190803662058009594743150052402532709746995318770724376825907419939632265984147498193609285223945039707165443156421328157688908058783183404917434556270520223564846495196112460268313970975069382648706613264507665074611512677522748621598642530711298441182622661057163515069260029861704945425047491378115154139941550671256271197133252763631939606902895650288268608362241082050562430701794976171121233066073310059947366875

• 直線的な繰り返し処理 の場合は、繰り返しの 回数に比例した処理時間 がかかる
• 分岐する繰り返し処理 の場合は、繰り返しの回数が増えると、指数関数 に従って処理時間が 爆発的に増える

プログラムの処理時間は、計算量という概念で表現されます。ただし、計算量の話をすると長くなるので、その話は今後の記事で紹介しようと思います。

計算時間に差が出る理由

同じ計算を行っている にも関わらず sum_by_f や sum_by_br と sum_by_tr の 処理時間が大きく異なる 点が気になっている人がいるかもしれません。このような差は、sum_by_tr が 無駄な計算を大量に行っている ことが原因です。

先程の下記の実行結果を見て下さい。3 ~ 7 行目 で fib(2) の計算が行われていますが、全く同じ fib(2) の計算が 12 ~ 16 行目 で行われていることがわかります。

 1  fib(4) = fib(3) + fib(2)
 2    fib(3) = fib(2) + fib(1)
 3      fib(2) = fib(1) + fib(0)
 4        fib(1) = 1
 5      fib(2) = 1 + fib(0)
 6        fib(0) = 0
 7      fib(2) = 1 + 0 = 1
 8    fib(3) = 1 + fib(1)
 9      fib(1) = 1
10    fib(3) = 1 + 1 = 2
11  fib(4) = 2 + fib(2)
12    fib(2) = fib(1) + fib(0)
13      fib(1) = 1
14    fib(2) = 1 + fib(0)
15      fib(0) = 0
16    fib(2) = 1 + 0 = 1
17  fib(4) = 2 + 1 = 3

先程の図を使ってそのことを表すと下図のようになります。下図の 紫色の枠 で囲まれた部分が fib(2) を計算する処理 で、全く同じ処理が 2 回行われている ことがわかります。

このような無駄な処理が行われる理由は、以前の記事で説明したように、再帰呼び出しでは自分自身と同じ処理を行う、新しい別の関数を呼び出す という処理が行われるからです。従って、再帰呼び出しで呼び出された fib_by_tr は、それぞれが 独立した処理 を行います。例えば、再帰呼び出しが行われている過程で、fib_by_tr(2) が複数回呼び出された としても、それらは独立して処理を行うため、過去に fib_by_tr(2) が呼び出されて $F_2$ が 計算済であったとしても、その値を 別の fib_by_tr(2) が利用することはできません。そのため、fib_by_tr(2) が呼び出されるたびに、同じ計算が何度も行われる という無駄が生じます。現実の世界に例えると、協力して仕事を行わない 2 人の部下に全く同じ指示を与える ことに相当します。

以前の記事で説明したように、全く同じ計算を行う 場合でも、計算の手順を表す アルゴリズムによって、計算の速度などの 性質が大きく変わる ことが 良くあります。

再帰呼び出しの計算を行う例として、フィボナッチ数 $F_n$ の計算が良く取り上げられますが、$F_n$ は確かに プログラムの記述 は fib_by_tr のようにトップダウンな再帰呼び出しで 簡潔に行えます が、$n$ が 40 を超えたあたりから 計算時間が長くなりすぎる という重大な欠点があります。そのため、実際には $F_n$ を計算するアルゴリズムとして、トップダウンな再帰呼び出しは向いていない と言えます。これは、$F_n$ に限った話ではなく、複数の項で表される漸化式 でも同様です。

複数の項で表される漸化式は、ボトムアップな方法で計算したほうが効率が良い。

メモ化による処理の効率化

上記で説明した重大な欠点があるとはいえ、漸化式をトップダウンな再帰呼び出しで 簡潔に記述できる という点は 便利 です。そこで、同じ処理を大量に行うトップダウンな再帰呼び出しの処理を、効率的に行う手法 について紹介します。

問題の原因は、再帰呼び出しによって呼び出された関数の処理が 独立して行われる という点なので、再帰呼び出しで行われる処理が、過去に行われた計算の結果を共有 することができれば、この問題を解決することができるようになります。

そのような手法の一つに メモ化（memoization）²という手法があります。メモ化とは、後から利用される可能性がある計算を行った際に、その 計算結果を記録しておき、再利用する という手法です。

メモ化は、後で利用する可能性があるデータを記憶して取っておく、キャッシュ（cache）という 処理の高速化の技術の一種 です。

メモ化を行う方法の一つに、list や dict などの ミュータブルなデータに計算結果を記録 し、そのデータを再帰呼び出しの関数の 仮引数に代入して共有する という方法があります³。

メモ化で利用する dict や list のように、ある値を、別の値に置換（変換）するための表のようなデータの事を、置換表（transposition table）と呼びます。

$F_n$ の場合は、メモ化を行う dict には、キーに $F_n$ の $n$ を、そのキーの値に $F_n$ を記録します。下記は、メモ化を行うように fib_by_tr を修正するプログラムです。

下記は、メモ化を利用するように fib_by_tr を修正したプログラムです。

• 1 行目：計算済の $F_n$ を記録する仮引数 memo を追加する。デフォルト値を空の dict にすることで、再帰呼び出しの処理を開始する際に、実引数を記述せずに fib_by_tr を呼び出すことで、memo が空の dict で初期化される
• 3 ~ 8 行目：n が 0 または 1 の場合は、0 または 1 を返すだけで良いので、メモ化を利用したほうが処理が多くなる。そのため、この部分は 元のプログラムから変更しない
• 9 ~ 11 行目：memo に n をキーとする要素が存在する場合は、$F_n$ は計算済で memo[n] に代入されているので、それを返り値として返す。その際に、memo からデータを取り出したことを明確にするためにメッセージに (memo) を表示するようにした
• 13, 15 行目：fib_by_tr を呼び出す際にキーワード引数 memo=memo を追加する
• 19 行目：新しく計算した $F_n$ を memo[n] に代入して記録する

 1  def fib_by_tr(n, depth=0, memo={}):
 2      indent = "  " * depth
 3      if n == 0:
 4          print(f"{indent}fib(0) = 0")
 5          return 0
 6      elif n == 1:
 7          print(f"{indent}fib(1) = 1")
 8          return 1   
 9      if n in memo:
10          print(f"{indent}fib({n}) = {memo[n]} (memo)")
11          return memo[n]
12      print(f"{indent}fib({n}) = fib({n - 1}) + fib({n - 2})")
13      r1 = fib_by_tr(n - 1, depth + 1, memo=memo)
14      print(f"{indent}fib({n}) = {r1} + fib({n - 2})")
15      r2 = fib_by_tr(n - 2, depth + 1, memo=memo)
16      retval = r1 + r2
17      print(f"{indent}fib({n}) = {r1} + {r2} = {retval}")
18      memo[n] = retval
19      return retval

行番号のないプログラム

def fib_by_tr(n, depth=0, memo={}):
    indent = "  " * depth
    if n == 0:
        print(f"{indent}fib(0) = 0")
        return 0
    elif n == 1:
        print(f"{indent}fib(1) = 1")
        return 1   
    if n in memo:
        print(f"{indent}fib({n}) = {memo[n]} (memo)")
        return memo[n]
    print(f"{indent}fib({n}) = fib({n - 1}) + fib({n - 2})")
    r1 = fib_by_tr(n - 1, depth + 1, memo=memo)
    print(f"{indent}fib({n}) = {r1} + fib({n - 2})")
    r2 = fib_by_tr(n - 2, depth + 1, memo=memo)
    retval = r1 + r2
    print(f"{indent}fib({n}) = {r1} + {r2} = {retval}")
    memo[n] = retval
    return retval

修正箇所

-def fib_by_tr(n, depth=0):
+def fib_by_tr(n, depth=0, memo={}):
    indent = "  " * depth
    if n == 0:
        print(f"{indent}fib(0) = 0")
        return 0
    elif n == 1:
        print(f"{indent}fib(1) = 1")
        return 1   
+   if n in memo:
+       print(f"{indent}fib({n}) = {memo[n]} (memo)")
+       return memo[n]
    print(f"{indent}fib({n}) = fib({n - 1}) + fib({n - 2})")
    r1 = fib_by_tr(n - 1, depth + 1, memo=memo)
    print(f"{indent}fib({n}) = {r1} + fib({n - 2})")
    r2 = fib_by_tr(n - 2, depth + 1, memo=memo)
    retval = r1 + r2
    print(f"{indent}fib({n}) = {r1} + {r2} = {retval}")
+   memo[n] = retval
    return retval

上記の修正後に、下記のプログラムで $F_4$ を計算すると、実行結果の 12 行目のように、一度計算された fib(2) を memo から取り出すようになったことが確認できます。

print(fib_by_tr(4))

実行結果（行番号とコメントを追記しました）

 1  fib(4) = fib(3) + fib(2)
 2    fib(3) = fib(2) + fib(1)
 3      fib(2) = fib(1) + fib(0)
 4        fib(1) = 1
 5      fib(2) = 1 + fib(0)
 6        fib(0) = 0
 7      fib(2) = 1 + 0 = 1
 8    fib(3) = 1 + fib(1)
 9      fib(1) = 1
10    fib(3) = 1 + 1 = 2
11  fib(4) = 2 + fib(2)
12    fib(2) = 1 (memo)          # ここでの fib(2) の値はメモ化されたデータを利用している
13  fib(4) = 2 + 1 = 3

また、下記のプログラムで $F_{40}$ を計算すると、メッセージからメモ化の利用が何度も行われることが確認できます。また、先程と異なり一瞬で計算が行われることが確認できます。

print(fib_by_tr(40))

実行結果

fib(40) = fib(39) + fib(38)
  fib(39) = fib(38) + fib(37)
    fib(38) = fib(37) + fib(36)
      fib(37) = fib(36) + fib(35)
        fib(36) = fib(35) + fib(34)
略
                                                          fib(6) = fib(5) + fib(4)
                                                            fib(5) = fib(4) + fib(3)
                                                              fib(4) = 3 (memo)
                                                            fib(5) = 3 + fib(3)
                                                              fib(3) = 2 (memo)
略
    fib(37) = 24157817 (memo)
  fib(39) = 39088169 + 24157817 = 63245986
fib(40) = 63245986 + fib(38)
  fib(38) = 39088169 (memo)
fib(40) = 63245986 + 39088169 = 102334155
102334155

仮引数 memo に関する補足

以前の記事で、デフォルト引数のデフォルト値 を、list や dict のような ミュータブルなデータにするのは避けたほうが良い と説明しました。また、以前の記事ではデフォルト値をミュータブルなデータにしたことによるバグを紹介しました。その理由は、ミュータブルなデータをデフォルト値に設定すると、その 仮引数に要素を追加 したり、要素の内容を変更 すると、デフォルト値が変更されてしまう からです。

ただし、fib_by_tr の仮引数 memo の場合は、この性質が 逆に有効 になります。その理由は、fib_by_tr で $F_n$ の計算を何度も行う場合 は、過去の fib_by_tr で行った計算の結果を 再利用できると効率が良い からです。例えば、先程 fib_by_tr(40) を計算した際に、2 ~ 40 まで の $F_n$ を計算したので、memo のデフォルト値にはそれらのデータが記録 されています。そのため、下記のプログラムのようにもう一度 fib_by_tr(40) を実行すると、実行結果から memo からデータを取り出すことで計算が行われたことが確認できます。

print(fib_by_tr(40))

実行結果

fib(40) = 102334155 (memo)
102334155

また、下記のプログラムでまだ計算していない $F_{41}$ を計算した場合は、memo のデフォルト値に記録された $F_{40}$ と $F_{39}$ を使って、すぐに計算を行うことができることが確認できます。

print(fib_by_tr(41))

実行結果

fib(41) = fib(40) + fib(39)
  fib(40) = 102334155 (memo)
fib(41) = 102334155 + fib(39)
  fib(39) = 63245986 (memo)
fib(41) = 102334155 + 63245986 = 165580141
165580141

fib_by_tr の memo のデフォルト値に大量のデータが記録してしまうと、メモリの消費が問題となる場合があります。そのような問題が起きることを防ぎたい場合は、下記のプログラムのように fib_by_tr を修正して下さい。

def fib_by_tr(n, depth=0, memo=None):
     if memo is None:
         memo = {}
元と同じなので省略

プログラム全体

def fib_by_tr(n, depth=0, memo=None):
     if memo is None:
         memo = {}
    indent = "  " * depth
    if n == 0:
        print(f"{indent}fib(0) = 0")
        return 0
    elif n == 1:
        print(f"{indent}fib(1) = 1")
        return 1   
    if n in memo:
        print(f"{indent}fib({n}) = {memo[n]} (memo)")
        return memo[n]
    print(f"{indent}fib({n}) = fib({n - 1}) + fib({n - 2})")
    r1 = fib_by_tr(n - 1, depth + 1, memo=memo)
    print(f"{indent}fib({n}) = {r1} + fib({n - 2})")
    r2 = fib_by_tr(n - 2, depth + 1, memo=memo)
    retval = r1 + r2
    print(f"{indent}fib({n}) = {r1} + {r2} = {retval}")
    memo[n] = retval
    return retval

修正箇所

-def fib_by_tr(n, depth=0, memo={}):
+def fib_by_tr(n, depth=0, memo=None):
+    if memo is None:
+        memo = {}
元と同じなので省略

メモ化を行った場合の計算速度

メモ化を行うことで fib_by_tr の計算速度は劇的に向上しますが、それでも メモ化の処理を行わなければならない分だけ、ボトムアップな繰り返し処理を行う fib_by_f や fib_by_bf よりも 計算に時間がかかります。

そのことを確認するために、実際に計算速度を %%timeit で比較することにします。

まず、print があると %%timeit でうまく計測を行えないので、下記のプログラムのように fib_by_tr から print を削除してメッセージの表示を行わないように修正します。

def fib_by_tr(n, memo={}):
    if n == 0:
        return 0
    elif n == 1:
        return 1   
    if n in memo:
        return memo[n]
        
    memo[n] = fib_by_tr(n - 1, memo=memo) + fib_by_tr(n - 2, memo=memo)
    return memo[n]

修正箇所

def fib_by_tr(n, depth=0, memo={}):
-   indent = "  " * depth
    if n == 0:
-       print(f"{indent}fib(0) = 0")
        return 0
    elif n == 1:
-       print(f"{indent}fib(1) = 1")
        return 1   
    if n in memo:
-       print(f"{indent}fib({n}) = {memo[n]} (memo)")
        return memo[n]
-   print(f"{indent}fib({n}) = fib({n - 1}) + fib({n - 2})")
-   r1 = fib_by_tr(n - 1, depth + 1, memo=memo)
-   print(f"{indent}fib({n}) = {r1} + fib({n - 2})")
-   r2 = fib_by_tr(n - 2, depth + 1, memo=memo)
-   retval = r1 + r2
-   print(f"{indent}fib({n}) = {r1} + {r2} = {retval}")
-   return retval
+   memo[n] = fib_by_tr(n - 1, memo=memo) + fib_by_tr(n - 2, memo=memo)
+   return memo[n]

fib_by_tr は今後はもう利用しないので上記のように修正しましたが、途中経過を表示する fib_by_tr を今後も利用したい場合は、以前の記事で紹介した方法で、途中経過を表示するかどうかを表す仮引数 debug を追加すると良いでしょう。

下記は、fib_by_f、fib_by_br、fib_by_tr のそれぞれで $F_{40}$ の計算時間を %%timeit で計測するプログラムです。なお、fib_by_tr では、メモ化を最初から行った場合の処理時間を計測したいので、memo={} を記述して、memo の値を空の dict で初期化しています。

%%timeit
fib_by_f(40)

実行結果

1.57 µs ± 28.9 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

%%timeit
fib_by_br(40)

実行結果

4 µs ± 22.4 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

%%timeit
fib_by_tr(40, memo={})

実行結果

11.6 µs ± 87.5 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

下記は実行結果をまとめたものです。実行結果から、実際に fib_by_tr が最も計算時間がかかることがわかります。なお、fib_by_br のほうが fib_by_f よりも時間がかかっているのは、関数呼び出しの処理に時間がかかるからです。

	計算時間の平均
fib_by_f	1.57 μs
fib_by_br	4.00 μs
fib_by_tr	11.60 μs

メモ化の欠点

既に気づいている人がいるかもしれませんが、メモ化は、以前の記事で 0 から 5 までの整数の合計を表す $x_5$ 計算する下記のプログラムで、$x_0$ から $x_5$ を dict に記録 していたのと 同様の処理を行っています。そのため、大きな $n$ の $F_n$ を計算すると メモリが大量に消費される という欠点が生じます。特に、同様の計算を何度も行うことが明らかでない場合は、メモ化によるメモリの消費が大きなデメリットになる場合があるので、常にメモ化を行えば良いというわけではありません。

x = {}
x[0] = 0
for n in range(1, 6):
    x[n] = x[n - 1] + n

上記のように、メモ化の処理はボトムアップによる $F_n$ の計算でも利用できます。

以前の記事で説明したように、再帰呼び出しによる繰り返し処理は、繰り返しの回数に制限があるため、fib_by_tf で $F_{10000}$ のような計算を行おうとすると RecursionError が発生します。そのため、fib_by_tf の場合はメモ化で記録できる $F_n$ の数が少ないので、メモリが大量に消費されることはありません。

ただし、メモ化を行う際に大量のメモリが消費されることは実際に良くあります。そのため、メモ化を行う際には、どれくらいの量のデータがメモ化されるかについて考慮する必要がある点に注意して下さい。

メモ化の他の欠点としては、メモ化の処理を記述 する分だけ、プログラムが複雑になる 点です。人によっては、メモ化の処理を含めた場合は、ボトムアップな再帰呼び出しの処理のほうが簡潔に記述できると感じる人がいるかもしれません。

漸化式を計算するアルゴリズムの選択

ここまでで扱った 複数の項で表される漸化式 の計算は以下のような性質を持ちます。

• ボトムアップな 繰り返し処理の場合は、直線的 な繰り返し処理で行える
• トップダウンな 繰り返し処理の場合は、分岐 する繰り返し処理で行える

このように、アルゴリズム によって直線的な繰り返し処理と、分岐する繰り返し処理を 選択できる場合 は、基本的に 直線的な繰り返し処理を選んだほうが処理が高速 になります。

従って、漸化式 を計算するアルゴリズムは、以下の性質を考えて選択すると良いでしょう。

• for 文や while 文で記述すると、記述が少し面倒だが、最も計算時間が短くなる。また、$n$ の大きさに制限はない
• ボトムアップな再帰呼び出しで記述すると、for 文や while 文よりも少し簡潔に記述を行えるが、再帰呼び出しの性質から処理が若干遅くなり、大きな $ n$ に対する $x_n$ の計算もできない
• トップダウンな再帰呼び出しで記述すると、プログラムの記述は最も簡単だが、処理が分岐する場合はメモ化などの工夫を行わないと処理時間が非常に長くなる。また再帰呼び出しの性質から、大きな $n$ に対する $x_n$ の計算もできない

上記のように、トップダウンな再帰呼び出しには欠点が多いですが、プログラムを簡潔に記述できるという点は確かに魅力的ではあるので、小さい $n$ でしか計算しないことがあらかじめわかっている場合などでは利用しても良いのではないかと思います。

分岐が必須となる繰り返し処理

ここまでで説明した漸化式の性質から、直線的な繰り返し処理になるかどうかは、ボトムアップであるかトップダウンであるかによって決まると誤解した人がいるかもしれませんが、そのような決まりはありません。例えば、〇×ゲームのゲーム木を作成する処理は、ルートノードからボトムアップな繰り返し処理で行う必要がありますが、その際に繰り返しの処理が分岐します。

漸化式の場合はそうではありませんが、世の中には 分岐が必須となる繰り返し処理 が 多数あります。その代表例としては、〇×ゲームのゲーム木のような、木構造で表現されるデータに対する処理 が挙げられます。そのようなデータに対する処理は、ボトムアップ、トップダウンのいずれの方法でも分岐する繰り返し処理を記述する必要があります。

そこで、次回の記事では分岐が必須となる繰り返し処理について説明することにします。

fib_by_f の記述の簡略化

最後に、fib_by_f を もう少し簡潔に記述できる ことに気が付きましたので紹介します。

下記は、元の fib_by_f の定義です。

このプログラムでは、for 文のブロックで以下のような手順で処理を行います。

1. $F_i$ を fib_p1 + fib_p2 で計算し、fib に代入する
2. $F_{i-1}$ を表す fib_p1 は、次の繰り返し処理で計算する $F_{i+1}$ の 2 つ前の項なので、fib_p2 に代入する
3. $F_{i}$ を表す fib は、次の繰り返し処理で計算する $F_{i+1}$ の 1 つ前の項なので、fib_p1 に代入する

def fib_by_f(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
    fib_p2 = 0
    fib_p1 = 1
    for i in range(2, n + 1):
        fib = fib_p1 + fib_p2
        fib_p2 = fib_p1
        fib_p1 = fib
    return fib

fib_by_f の修正

上記のプログラムは、下記のように修正できます。修正された箇所は 10、11 行目です。

 1  def fib_by_f(n):
 2      if n == 0:
 3          return 0
 4      elif n == 1:
 5          return 1
 6    
 7      fib_p2 = 0
 8      fib_p1 = 1
 9      for i in range(2, n + 1):
10          fib_p1, fib_p2 = fib_p1 + fib_p2, fib_p1
11      return fib_p1

行番号のないプログラム

def fib_by_f(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
    fib_p2 = 0
    fib_p1 = 1
    for i in range(2, n + 1):
        fib_p2, fib_p1 = fib_p1, fib_p1 + fib_p2
    return fib_p1

修正箇所

def fib_by_f(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
    fib_p2 = 0
    fib_p1 = 1
    for i in range(2, n + 1):
-       fib = fib_p1 + fib_p2
-       fib_p2 = fib_p1
-       fib_p1 = fib
+       fib_p2, fib_p1 = fib_p1, fib_p1 + fib_p2
-   return fib
+   return fib_p1

下記は、修正後のプログラムの 10 行目のプログラムです。このプログラムは、元のプログラムから fib に $F_n$ を代入する処理を省略 したのと同じ処理が行われます。

fib_p2, fib_p1 = fib_p1, fib_p1 + fib_p2

よくある勘違い

上記のプログラムは、下記のプログラムと同じ処理が行われるように見えるかもしれませんが、そうではありません。下記のプログラムでは、1 行目で fib_p2 に fib_p1 が代入される ので、2 行目 の式では fib_p1 = fib_p1 + fib_p1 が計算されることになります。

fib_p2 = fib_p1
fib_p1 = fib_p1 + fib_p2

一方、下記の修正前のプログラムの 2 行目では、上記の 1 行目と同じ処理が行われますが、3 行目 では、2 行目で fib_p1 が代入される前の fib_p2 の値を使って fib_p1 + fib_p2 を計算した値が代入される点が異なります。1 行目で fib という変数に fib_p1 + fib_p2 の式の結果を代入した理由 は、2 行目の計算で fib_p1 の値が必要になる からです。

fib = fib_p1 + fib_p2
fib_p2 = fib_p1
fib_p1 = fib

修正後の 10 行目で行われる処理

修正後のプログラムの 10 行目の処理の 右辺は tuple を表しており、下記のプログラムの tuple の () が省略された ものです。従って、右辺の計算を行うと、0 番の要素に fib_p1 が、1 番の要素に fib_p1 + fib_p2 が代入された tuple が作成 されます。

その後、以前の記事で説明した 反復可能オブジェクトの展開 が行われ、fib_p2 と fib_p1 に上記で作成された tuple の 0 番の要素と 1 番の要素の値が代入されます。

fib_p2, fib_p1 = (fib_p1, fib_p1 + fib_p2)

従って上記のプログラムは、fib_p2 と fib_p1 に、修正前のプログラムと同様に、この代入文の計算が行われる前の fib_p1 と fib_p2 の値で計算された式の計算結果が代入されます。その際に tuple に必要なデータが記録 されているため、元のプログラムの fib は必要ありません。

元の式では、fib に $F_n$ の計算結果を代入していましたが、上記のプログラムでは fib_p1 にその値が代入される ようになりました。そのため、最後の 11 行目の return 文は、下記のプログラムのように fib の代わりに fib_p1 を返す ように修正する必要があります。

return fib_p1

さらなる修正

最後の文が return fib_p1 なのはわかりづらいので、fib_p2 と fib_p1 の名前をそれぞれ fib_p1 と fib に変更することにします。変更した名前は以下のような意味を表します。

• 修正前は fib_p1 + fib_p2 を計算する前の値の意味を表す
  • fib_p2：$F_i$ を計算する際に必要な 2 つ前の $F_{i-2}$ の値
  • fib_p1：$F_i$ を計算する際に必要な 1 つ前の $F_{i-1}$ の値
• 修正後は fib_p1 + fib_p2 を計算した後の値の意味を表す
  • fib_p1：次の $F_{i+1}$ を計算する際に必要な 2 つ前の $F_{i-1}$ の値
  • fib：次の $F_{i+1}$ を計算する際に必要な 1 つ前の $F_{i}$ の値

下記は、そのように fib_by_f を修正したプログラムです。最後の行が return fib になる点が少しわかりやすくなっています。

 1  def fib_by_f(n):
 2      if n == 0:
 3          return 0
 4      elif n == 1:
 5          return 1
 6    
 7     fib_p1 = 0
 8     fib = 1
 9     for i in range(2, n + 1):
10         fib_p1, fib = fib, fib + fib_p1
11     return fib

行番号のないプログラム

def fib_by_f(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
    fib_p1 = 0
    fib = 1
    for i in range(2, n + 1):
        fib_p1, fib = fib, fib + fib_p1
    return fib

修正箇所

def fib_by_f(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
-   fib_p2 = 0
+   fib_p1 = 0
-   fib_p1 = 1
+   fib = 1
    for i in range(2, n + 1):
-       fib_p2, fib_p1 = fib_p1, fib_p1 + fib_p2
+       fib_p1, fib = fib, fib + fib_p1
-   return fib_p1
+   return fib

下記のプログラムを実行することで、$F_0$ ~ $F_9$ を fib_by_f と fib_by_tr で計算し、計算結果を並べて表示します。実行結果からどちらも同じ計算を行うことが確認できます。

for i in range(10):
    print(f"fib({i}) = {fib_by_f(i)}, {fib_by_tr(i)}")

実行結果

fib(0) = 0, 0
fib(1) = 1, 1
fib(2) = 1, 1
fib(3) = 2, 2
fib(4) = 3, 3
fib(5) = 5, 5
fib(6) = 8, 8
fib(7) = 13, 13
fib(8) = 21, 21
fib(9) = 34, 34

上記の fib_by_f であれば、ボトムアップな再帰呼び出し の fib_by_br とプログラムの 複雑さはほぼ同じになる ので、ボトムアップな再帰呼び出しで記述するメリットはほとんどないかもしれません。

変数の値の交換

上記のような tuple と反復可能オブジェクトの展開の利用 は、2 つの変数の値を交換（swap） するプログラムを記述する際にも良く使われます。

例えば、a と b の変数の値を交換する際に、下記のようなプログラムを記述すると、4 行目 の処理で a に代入されていた値がなくなってしまう ためうまくいきません。下記のプログラムを実行すると、a と b の値が実行結果のように どちらも 2 になってしまいます。

1  a = 1
2  b = 2
3
4  a = b
5  b = a
6  print(a)
7  print(b)

行番号のないプログラム

a = 1
b = 2

a = b
b = a
print(a)
print(b)

実行結果

2
2

下記のプログラムの 4、6 行目のように、片方の変数を別の変数に代入して取っておき、後でもう 片方の変数に代入する ことでうまく交換できるようになります。なお、一時的（temporary） にデータを取っておく変数の名前には tmp や temp が良く使われます。

1  a = 1
2  b = 2
3
4  tmp = a
5  a = b
6  b = tmp
7  print(a)
8  print(b)

行番号のないプログラム

a = 1
b = 2

tmp = a
a = b
b = tmp
print(a)
print(b)

修正箇所

a = 1
b = 2

+tmp = a
a = b
-b = a
+b = tmp
print(a)
print(b)

実行結果

2
1

Python では、先程説明した tuple と 反復可能オブジェクトの展開 を利用すること、下記のプログラムの 4 行目のように 変数の値の交換 を 1 行で簡潔に記述 することができるので 良く使われます。tuple でデータを記録する ことで、tmp を用意する必要が無くなります。

1  a = 1
2  b = 2
3
4  a, b = b, a
5  print(a)
6  print(b)

行番号のないプログラム

a = 1
b = 2

a, b = b, a
print(a)
print(b)

修正箇所

a = 1
b = 2

-tmp = a
-a = b
-b = tmp
+a, b = b, a
print(a)
print(b)

実行結果

2
1

今回の記事のまとめ

今回の記事では、複数の項で表される漸化式をトップダウンな再帰呼び出しによる計算すると繰り返し処理が分岐することを説明しました。また、その際に行われる処理の性質について説明し、処理を効率化するためのメモ化という手法について説明しました。

本記事で入力したプログラム

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル

次回の記事

1. $0 < x < 1$ の場合は急激に 0 に近づいていきます ↩

2. Wikipedia によると memorization は、大事なことをメモするという memo の正式名称である memorandom から作られた造語とのことです ↩

3. 数値型や文字列型などのイミュータブルなデータを仮引数に代入して共有することはできますが、その場合は仮引数の値を変更した場合に、共有した他の関数の仮引数の値が変化しません ↩