Pythonで〇×ゲームのAIを一から作成する　その180　水平線効果と誤差の蓄積によるバグ

Posted at 2025-07-13

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
test.py	テストに関する関数
util.py	ユーティリティ関数の定義
tree.py	ゲーム木に関する Node、Mbtree クラスなどの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。

深さの上限を増やすと AI が強くなる理由のまとめ

ここまでの記事で、ミニマックス法 による 深さ制限探索 で最善手を選択する AI が、深さの上限を増やすことで強くなる理由 について以下のような説明を行いました。

以前の記事で説明したように、深さの上限をゲーム木の深さ以上に設定する ことで、ゲームの決着がついた局面 に対する 正確な評価値を元に計算 できるようになるため
一般的に ゲームが進行するにつれて勝敗の形勢がはっきりする ため、深さの上限を増やすことでより多くゲームが進行した 形勢判断をしやすい局面 に対する近似値が計算される可能性が高くなる。形勢判断をしやすい局面では、近似値の誤差の精度とばらつきの精度が高まる ため、より正確な似値のミニマックス値が計算される可能性が高まる
前回の記事で説明したように、深さの上限を増やすほど 計算される近似値のミニマックス値の 誤差の精度を大きく落とさず に、ばらつきの精度を高める ことができるため

上記以外の理由として、水平線効果の影響を受けづらくなる というものがあります。今回の記事ではその説明を行います。

参考までに水平線効果の wikipaeida と Chess programming wiki のリンクを示します。

用語

今回の記事でも前回の記事に引き続き下記の表の用語を用いることにします。

用語と記号	意味
正確なミニマックス値	深さの制限がないゲーム木の探索によって計算される、局面の正確なミニマックス値のこと
近似値	静的評価関数が計算する正確なミニマックス値とは異なる不正確な値が計算される場合がある評価値のこと
近似値のミニマックス値	深さ制限探索によって計算される、静的評価関数が計算する近似値に対するミニマックス値のこと

水平線効果とは何か

水平線効果（horizon effect）¹とは、深さ制限探索 アルゴリズムを利用した際に発生する現象です。水平線効果は ゲーム木の探索以外の場合でも発生 しますが、本記事では ミニマックス法 による 深さ制限探索 でのゲーム木の探索での 水平線効果の説明 を行います。

深さ制限探索 では、深さの上限まで しか探索を行わないため、それ以上の深さのノードを考慮しません。残念ながら 静的評価関数 は、形勢判断を 100 % 正確に行うことができない ため、形勢判断を大きく誤る 場合があります。形勢判断を大きく誤る原因 の中で、深さの制限 を行うことによって発生するものを 水平線効果 と呼びます。

水平線効果という 名前の由来 は、ルートノードから 特定の深さのノードまでしか探索を行わない ことによって引き起こされる 形勢判断の誤り が、海上で 水平線までの見える範囲の情報 を元に航海を行うことによる 判断の誤り に似ているからです。例えば航海中では 水平線の向こう にある島や陸地は 見えない ため、難破中に水平線の向こうに陸地があったとしても 間違った方向に進んでしまう ことがあります。

言葉だけではわかりづらいと思いますので、水平線効果の具体例をいくつか紹介します。

水平線効果の例 1

以前の記事で説明したように、ルール 11 で着手を選択する静的評価関数を利用した ai11s は、下図左の局面で下図右のように (0, 2)または² に着手を行います。

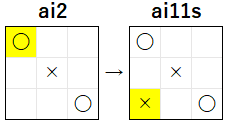
下記は上記左の局面で ai11s が着手を選択するプログラムで、実際に (0, 2)² を選択することが確認できます。

from marubatsu import Marubatsu
from ai import ai11s

mb = Marubatsu()
mb.move(2, 2)
mb.move(1, 1)
mb.move(0, 0)
print(ai11s(mb))

実行結果

(0, 2)

しかしその後で下図のように、お互いが最善手の着手を行うと × が敗北してしまう ため、この着手は 最善手ではありません。

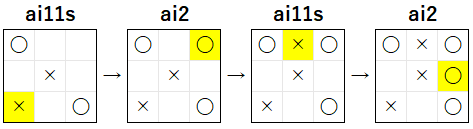
この問題は ルール 11 に基づいた計算によって選択された着手が 最善手のように見える が、その次の相手の着手までを検証すると最善手ではない ことが原因なので、ai11s を用いて 深さの上限を 2 とした 深さ制限探索 を行うことでこの問題を解決することができます。

下記はそのことを深さ制限探索を行う ai_abs_dls を利用して確認するプログラムで、最善手である (0, 1)³ が計算されたことが確認できます。なお、以前の記事で説明したように、ai_abs_dls を利用する際は ai11s がミニマックス値を計算する ように eval_params= {"minimax": True} を実引数に記述する必要がある点に注意して下さい。

from ai import ai_abs_dls

print(ai_abs_dls(mb, maxdepth=2, eval_func=ai11s, eval_params={"minimax": True}))

実行結果

(0, 1)

また、ai11s は弱解決の AI ではありません が、ai11s を用いて 深さの上限を 2 とした深さ制限探索を行うことで 弱解決の AI になります。下記は Check_solved の is_weakly_solved でそのことを確認するプログラムで、実行結果から弱解決の AI であることが確認できます。

from util import Check_solved

Check_solved.is_weakly_solved(ai11s)
Check_solved.is_weakly_solved(ai_abs_dls, params={"maxdepth": 2, "eval_func": ai11s,
                                                  "eval_params": {"minimax": True}})

実行結果

   o True
   x False
Both False
   o True
   x True
Both True

将棋の簡単な説明と静的評価関数の設定

他の水平線効果の具体例として 将棋の場合の例 を紹介します。なお、将棋のルールの詳細な説明は非常に長くなるので省略しますが、本記事の説明を理解するだけであれば、下記の点だけを理解しておけば充分 です。

〇× ゲームと同様に二人零和有限確定完全情報ゲームである
9 × 9 の正方形で区切られたゲーム盤の上に駒を配置して遊ぶゲームである
先手と後手が交互に 1 つの駒を動かす
必ず 1 つの駒を動かす必要があり、パスすることはできない
駒には様々な種類があり、それぞれ動かせる場所が決まっている。本記事の例で紹介する駒は下記の場所に移動できる
- 歩：1 つ前にのみ移動できる
- 香車：前方向に好きなだけ移動できる
- 角：斜め 4 方向に好きなだけ移動できる
- 飛車：上下左右に好きなだけ移動できる
- 王：周囲の 8 マスのいずれかに移動できる
基本的には駒を移動する際に、他の駒を跳び越すことはできない⁴
自分の駒があるマスに移動することはできない
相手の駒があるマスに移動することで相手の駒を取って自分のものにすることができる
相手の王という駒を取ることが勝利条件である

本当は将棋は全部で 40 個の駒を使って遊ぶゲームですが、本記事で例示する局面では 説明に不必要な駒は配置しない ことにします。また、将棋には 持ち駒 と成りというルールがありますが、本記事では 持ち駒も成りも行わない ものとします。

数多くの例外はありますが、将棋では 相手の駒を取ることで有利になることが多い ので、以下の説明では 駒を取ることを考慮した近似値を計算 する 下記の静的評価関数 を利用することにします。なお、もちろん実際の強い将棋の静的評価関数は下記のような単純なものではありませんが、水平線効果を理解するためには十分 だと思います。

紹介する例の 最初の局面では近似値を 0 として計算する
駒の種類に応じて下記の点数を設定 する。点数は 駒の強さによって設定 した。例えば飛車は最も強い駒なので 10 点を、歩は最も弱い駒なので 1 点とした。その他の駒は今回の記事の説明では出現しないので点数を設定しない
- 歩は 1 点
- 香車 2 点
- 角は 9 点
- 飛車は 10 点
先手が後手の駒を取った場合 の 局面の近似値 は、直前の局面の近似値に対してその 駒の点数を加算 する。後手が先手の駒を取った場合 は減算する

水平線効果の例 2

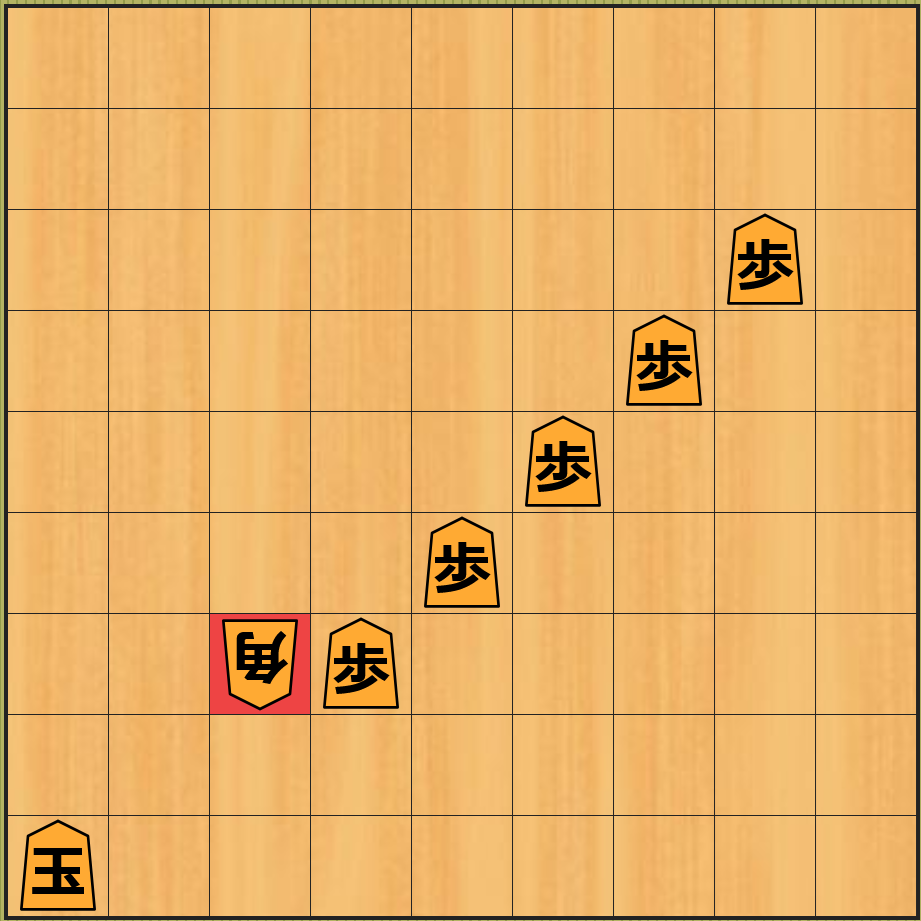
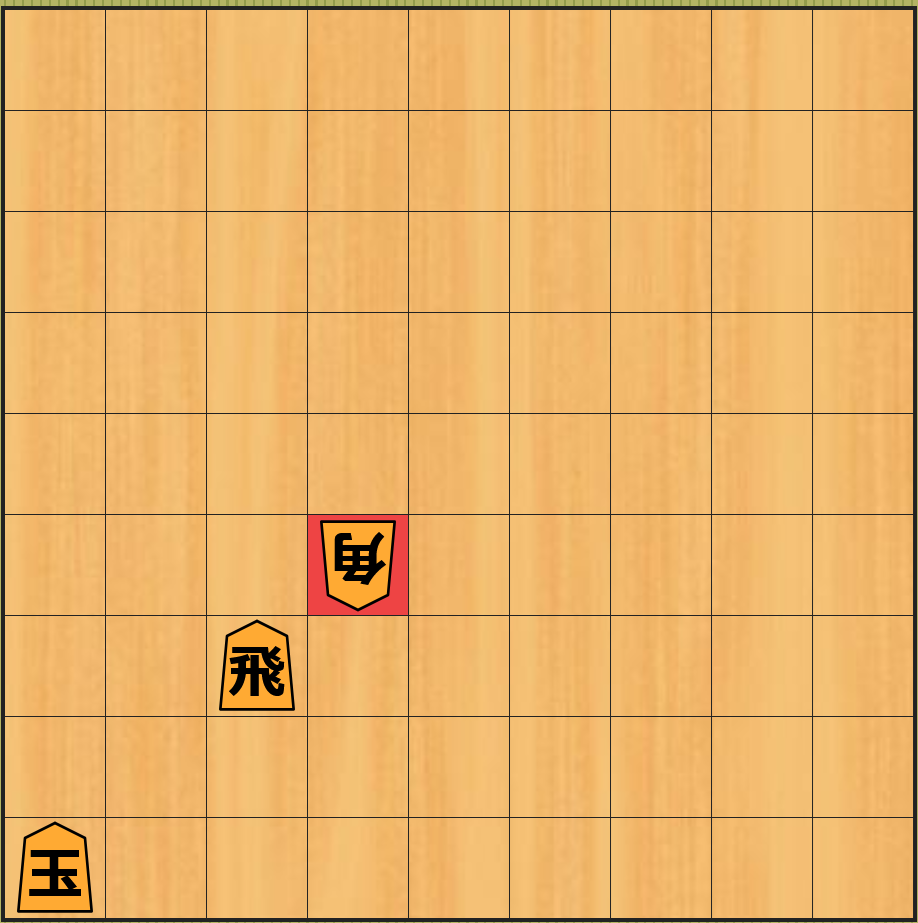
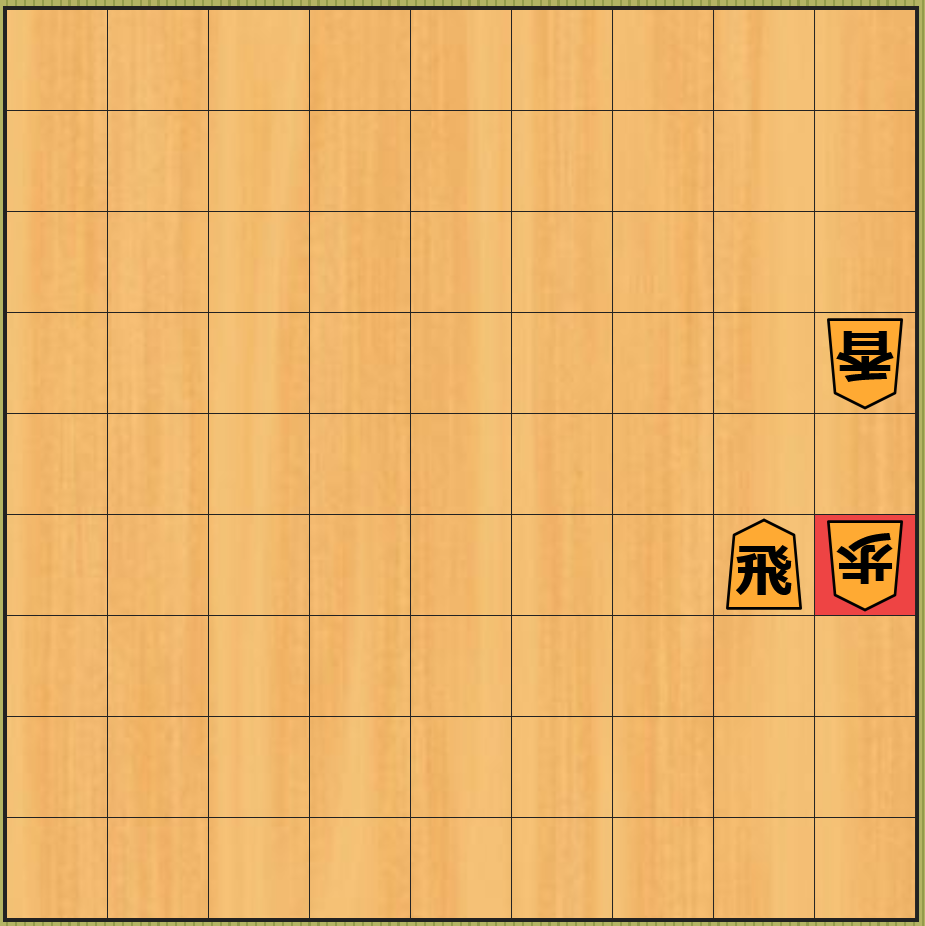
下図の局面 $N$ は 先手の局面 です。先ほど説明したように 最初の局面の近似値は 0 です。

将棋盤の画像の作成は、こちらのサイトを利用させていただきました。マスの中の漢字が駒の種類を表しており、後手の駒は上下を逆に表示します⁵。

前回の記事と同様に最初の局面を $N$、その子ノードの局面を $A$、$B$、$C$、・・・、$A$ の子ノードの局面を $AA$、$AB$、$AC$、・・・のように表記することにします。

深さの上限を 1 とした場合

局面 $N$ では 先手の駒は飛車しかない ので、先手の合法手 は上下左右方向に好きなだけ移動できる 飛車を移動する合法手だけ です。

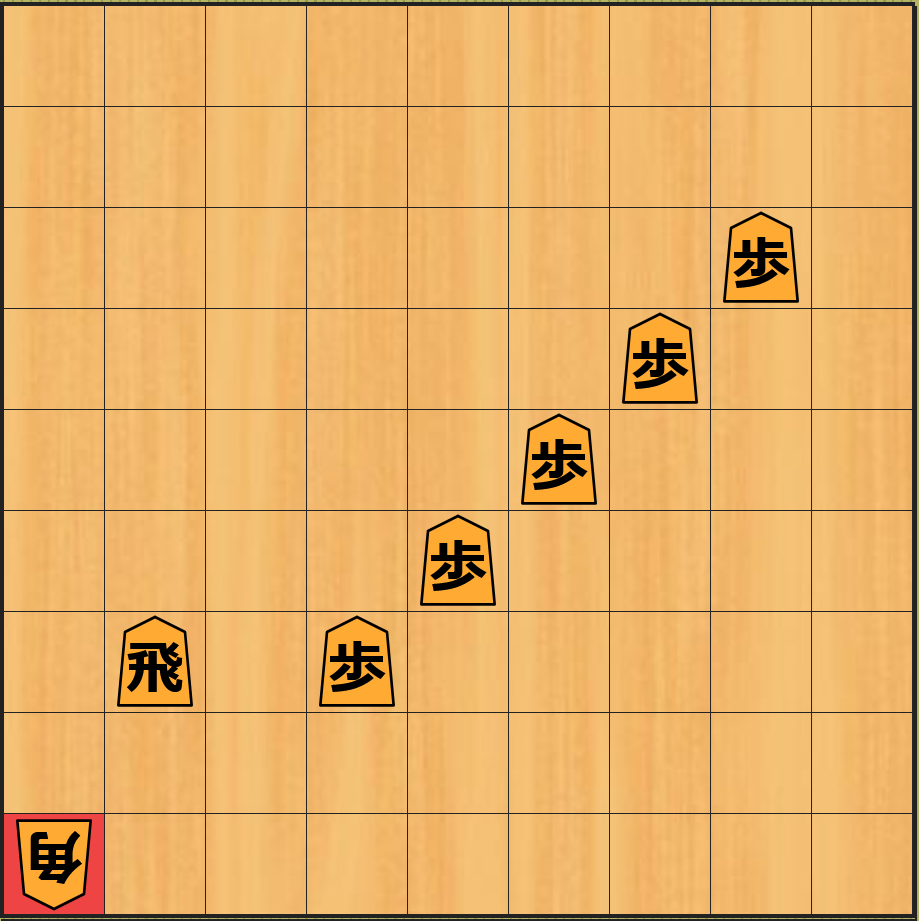
飛車を 1 つ前に動かす ことで、下図の局面 $A$ ように 先手が 1 点である相手の歩を取る ので $A$ の局面の 近似値は 1 になります。なお、赤色のマス は そのマスに駒を移動 したことを表します。

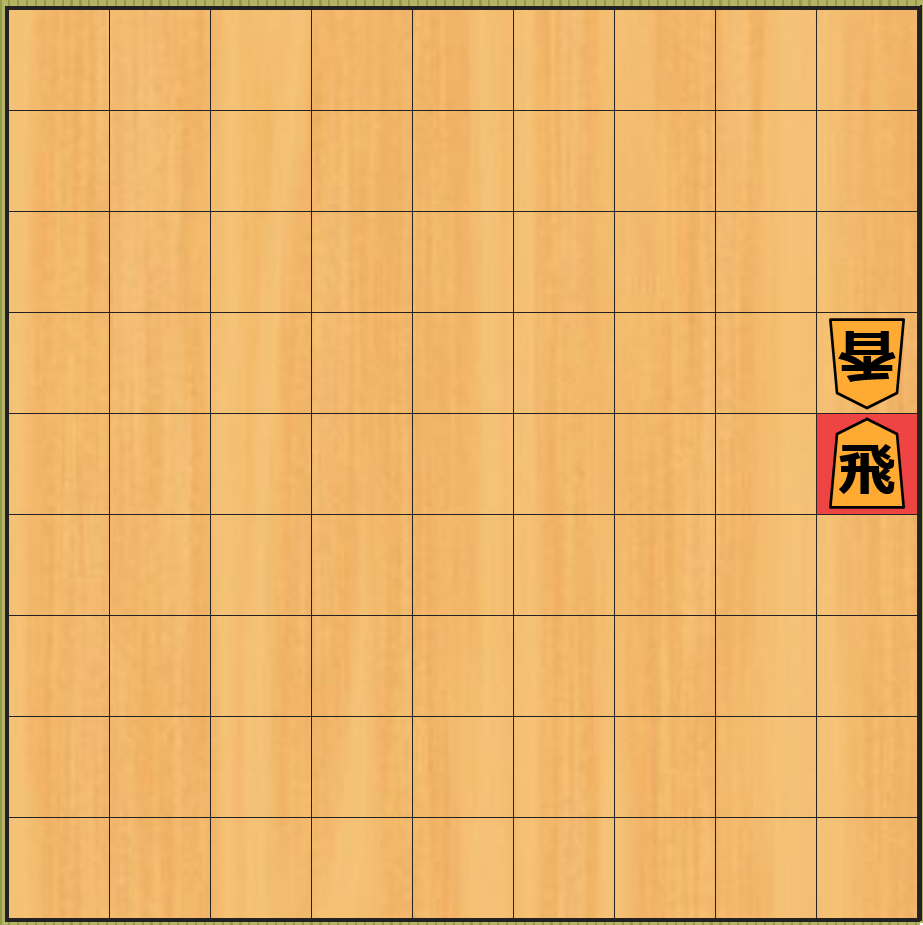
下図の局面 $B$ のように、飛車を 1 つ前以外に移動 した場合は、相手の 駒を取ることができない ので $B$ の局面の 近似値は 0 のまま です。他のマスに飛車を移動 した場合の局面 $C$、$D$、・・・も同様に局面の 近似値は 0 となります。

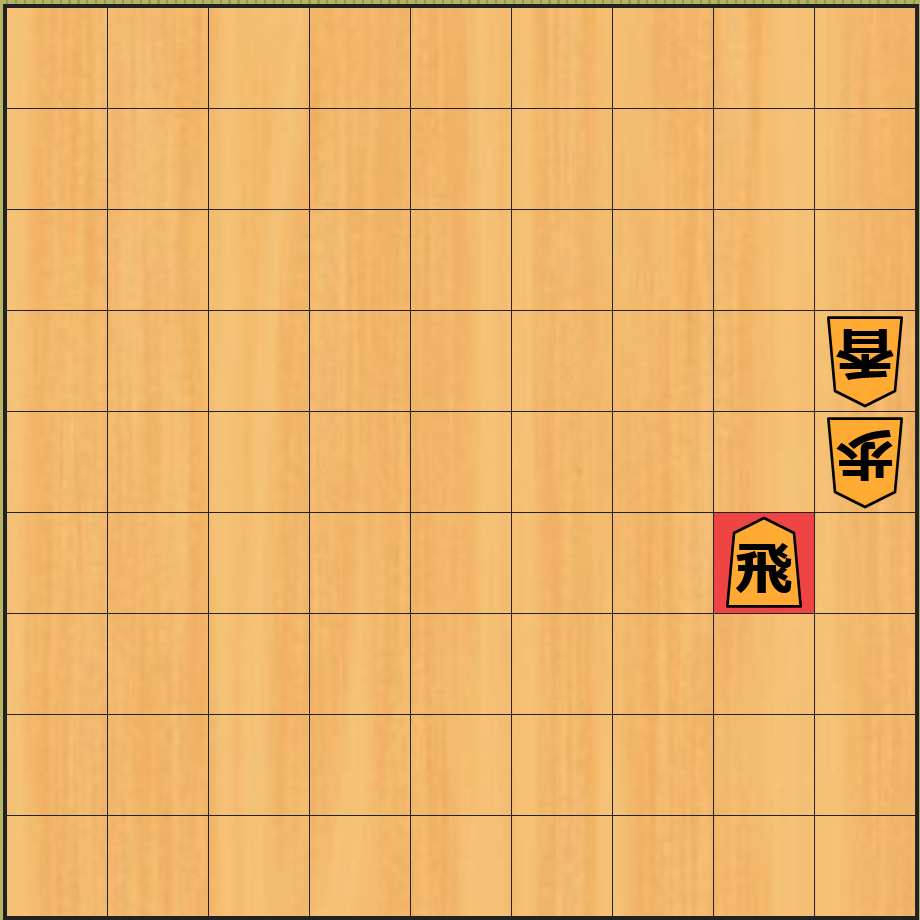
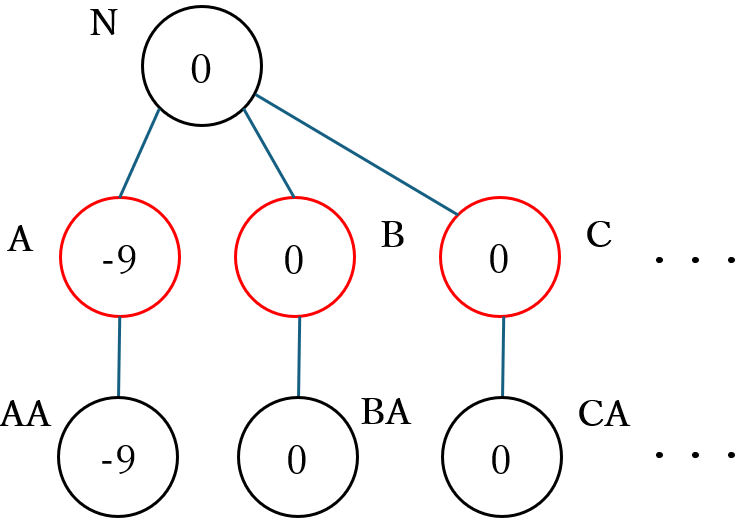
従って、深さの上限を 1 とした場合の ミニマックス法 では、下図のように局面 $\boldsymbol{N}$ の子ノード の中で局面 $\boldsymbol{A}$ の近似値が最大値 となるので局面 $A$ になる 飛車を一つ前に移動 する合法手が 最善手として計算 されます。下図では黒丸が先手の手番の max ノード、赤丸が後手の手番の min ノード、丸の中の数値が近似値のミニマックス値を表します。

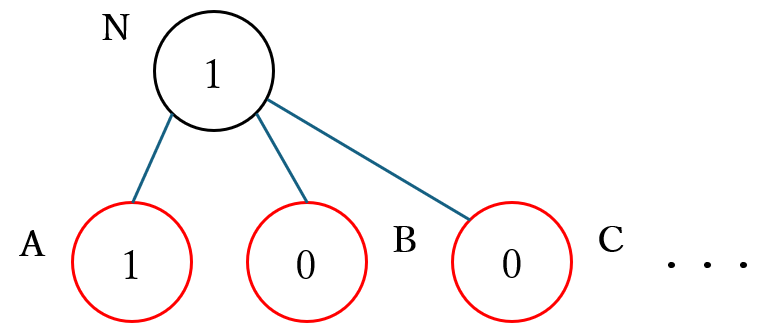
深さの上限を 2 とした場合

次に、深さの上限を 2 とした場合のことを考えます。

先程の下図の局面 $A$ では、後手の駒は香車しかない ので 後手の合法手 は前方向に好きなだけ移動できる 香車を移動する合法手だけ です。

香車は駒を跳び越すことはできない ので、局面 $A$ では下図の局面 $AA$ のように 香車を 1 つ前に移動して飛車を取る 合法手しかありません。飛車は 10 点の駒 なので局目 $AA$ の 近似値 は 1 -10 = -9 になります。

先程の下図の局面 $B$ では、後手の駒 には一つ前に移動できる歩と前方向に好きなだけ移動できる香車があります。

香車は駒を跳び越すことはできず、自分の駒である歩のマスに移動することもできないので、局面 $B$ では下図の局面 $BA$ のように 歩を 1 つ前に移動する合法手しかありません。駒を取ることはできない ので局面 $BA$ の 近似値は 0 のまま です。

$N$ の局面で 飛車が他の場所に移動した場合も同様 なので他の $C$、$D$、・・・の局面の 子ノード $CA$、$DA$、・・・の 近似値も 0 となります。

従って、深さの上限を 2 とした場合のミニマックス法では下図のように $\boldsymbol{A}$ の近似値のミニマックス値 は -9、$\boldsymbol{B}$ の近似値のミニマックス値 は 0 となります。

下記の表は 深さの上限を 1、2 とした場合の $N$、$A$、$B$、$C$、・・・に対して計算される 近似値のミニマックス値 と計算される最善手です。

深さの上限	$N$	$A$	$B$、$C$、・・・	最善手
1	1	1	0	$A$
2	0	-9	0	$B$、$C$、・・・

表から $\boldsymbol{A}$ に対して計算される値が大きく変わっている ことと、最善手 として計算される合法手が 変化した ことがわかります。

このように、深さの上限が 1 の場合は 飛車で歩を取る合法手が最善手 となりますが、深さの上限が 2 の場合は 飛車を香車で取り返される ため 最善手ではないことが判明 します。

上記の例の水平線効果を別の言葉で説明すると、先のことを深く考えずに 目先の利益を重視 した結果 後で大損をする ということに相当します。

水平線効果の例 3

上記の例のような、相手の駒を取った 直後の局面ですぐに取り返される という場合であれば、それを考慮した静的評価関数を作ることは充分に可能 だと思います。しかし、駒の取り合いを連続して繰り返す ような局面の場合は、駒の取り合いを始める前の局面 に対して 正しい形勢判断を表す近似値を計算する ような静的評価関数を作ることは困難です。

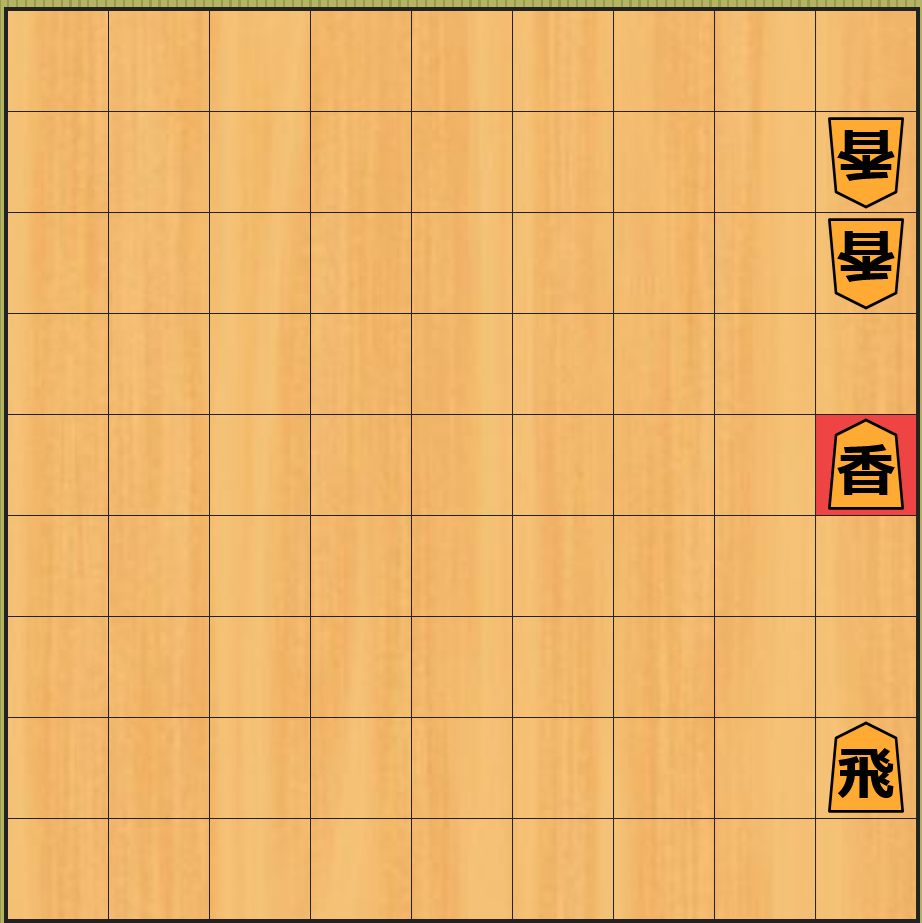
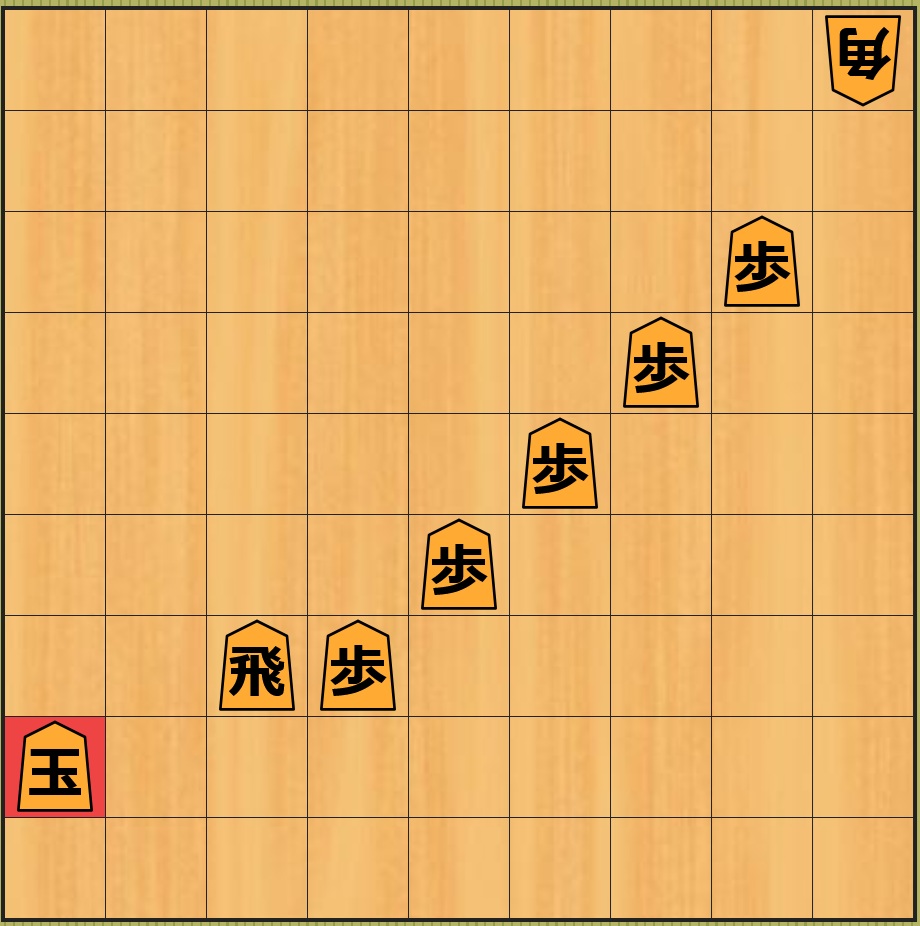
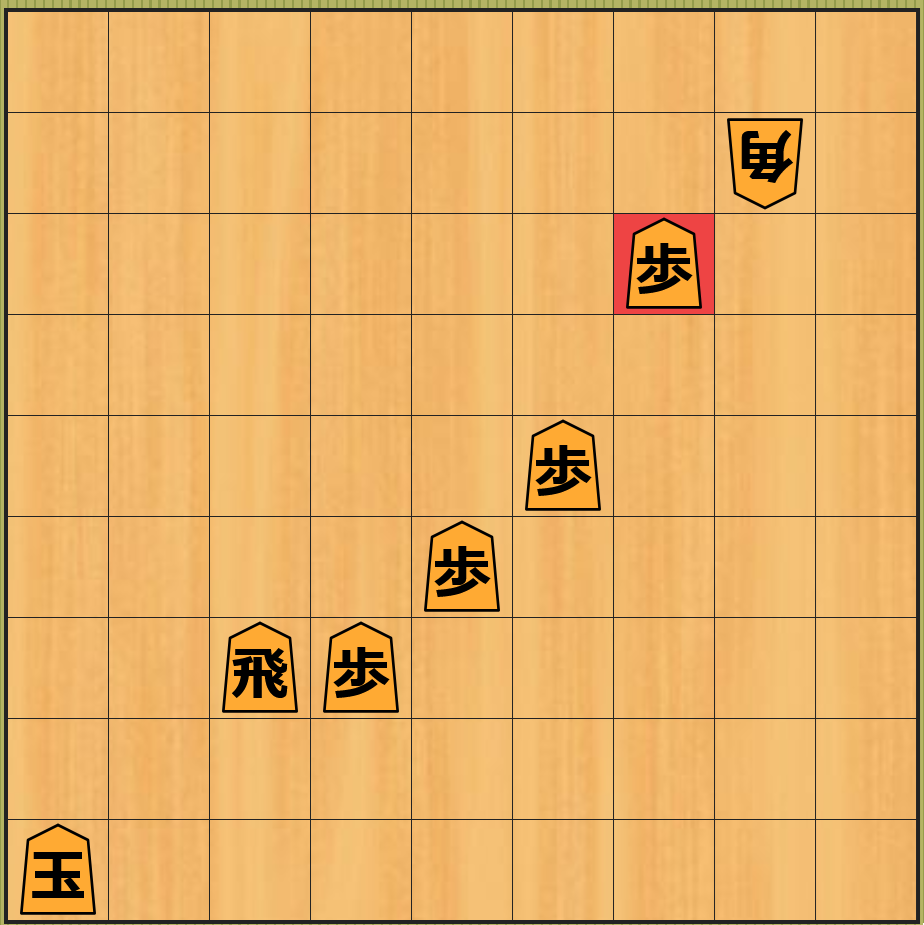
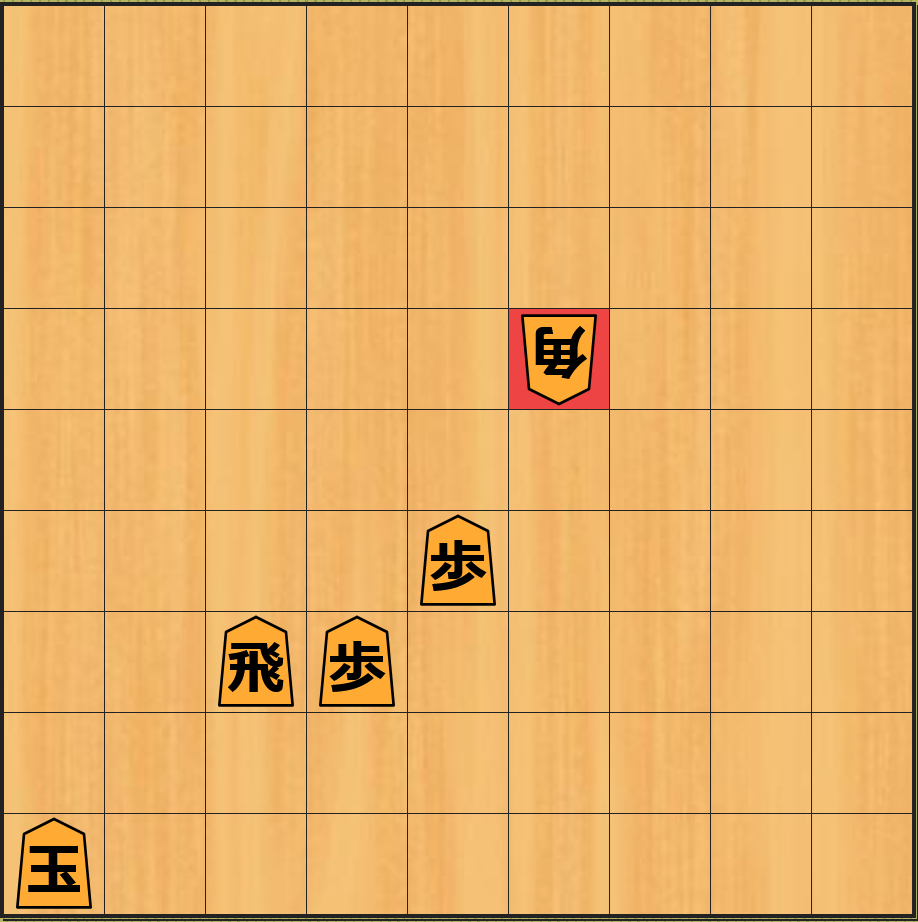
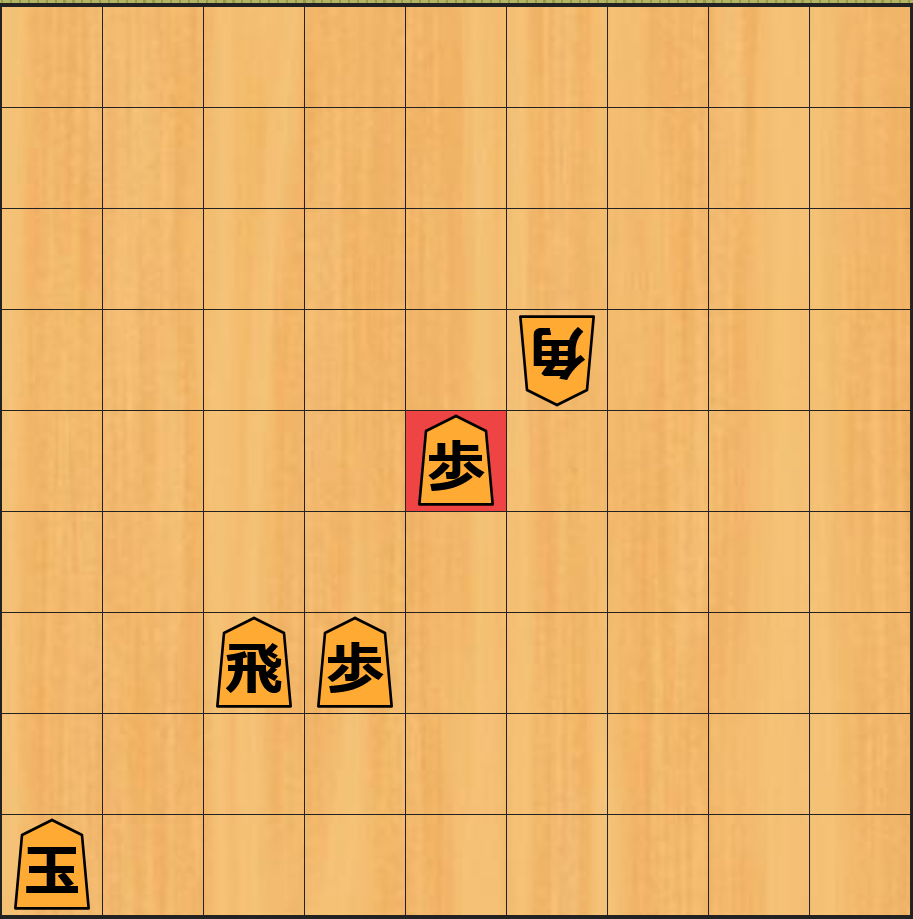
具体例を挙げて説明します。下記の 左上の図 の局面から お互いが駒を取り合う ことで 6 手目で一番下の図の局面 になります。

下記は上記の それぞれの局面 に対して 静的評価関数が計算する近似値 の表です。

手数	取った駒	近似値
0	なし	0
1	後手の歩(1 点)	1
2	先手の歩(-1 点)	0
3	後手の香車(2 点)	2
4	先手の香車(-2 点)	0
5	後手の香車(2 点)	2
6	先手の飛車(-10 点)	-8

上記の表から、この手順で着手を行った場合の 1 手目の局面の近似値のミニマックス値は、深さの上限を 5 以下 とした場合と 深さの上限を 6 とした場合で 近似値が 2 と -8 のように 大きく異なる ことがわかります。そのため、この局面で 深さの上限を 5 以下 とした深さ制限探索では 形勢判断を正しく行うことができない ことがわかります。

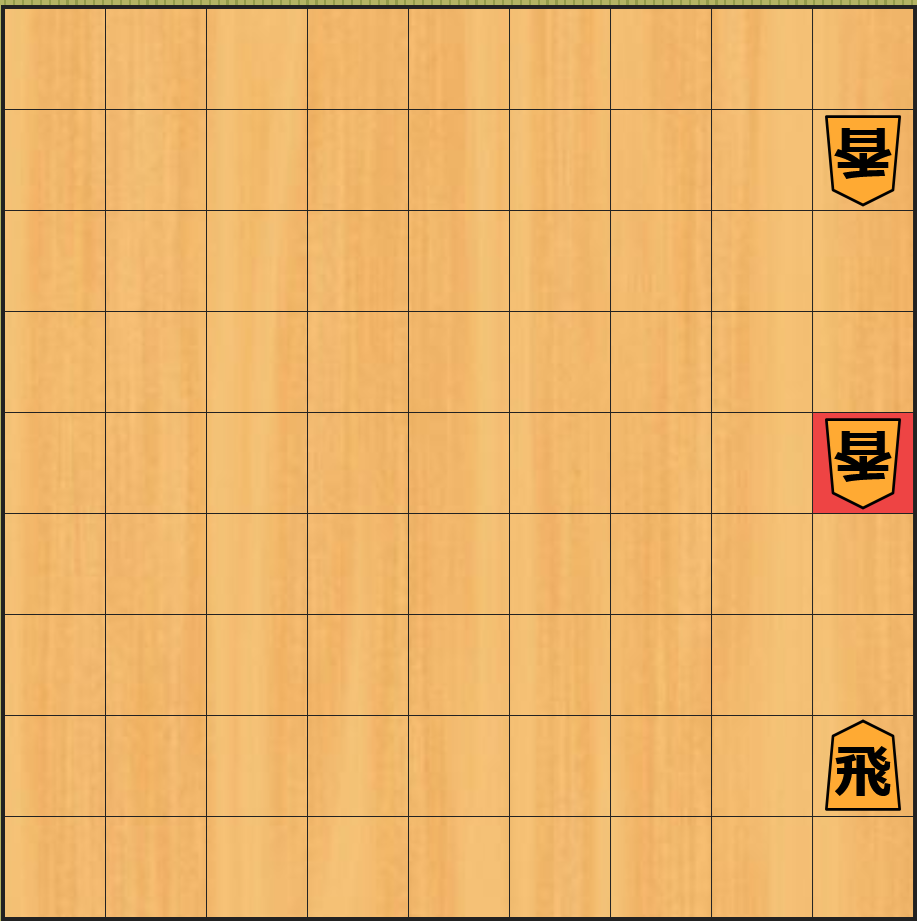
一方、先程の局面と比べて 後手の香車が一つ少ない 下図左の局面から 駒の取り合いを行う と、途中の局面は省略しますが、5 手後に下図右の局面 になります。

下記は上記の左図から 5 手までの局面に対して 静的評価関数が計算する近似値 の表で、この場合は 5 手後の局面の近似値は 2 になります。

手数	取った駒	近似値
0	なし	0
1	後手の歩(1 点)	1
2	先手の歩(-1 点)	0
3	後手の香車(2 点)	2
4	先手の香車(-2 点)	0
5	後手の香車(2 点)	2

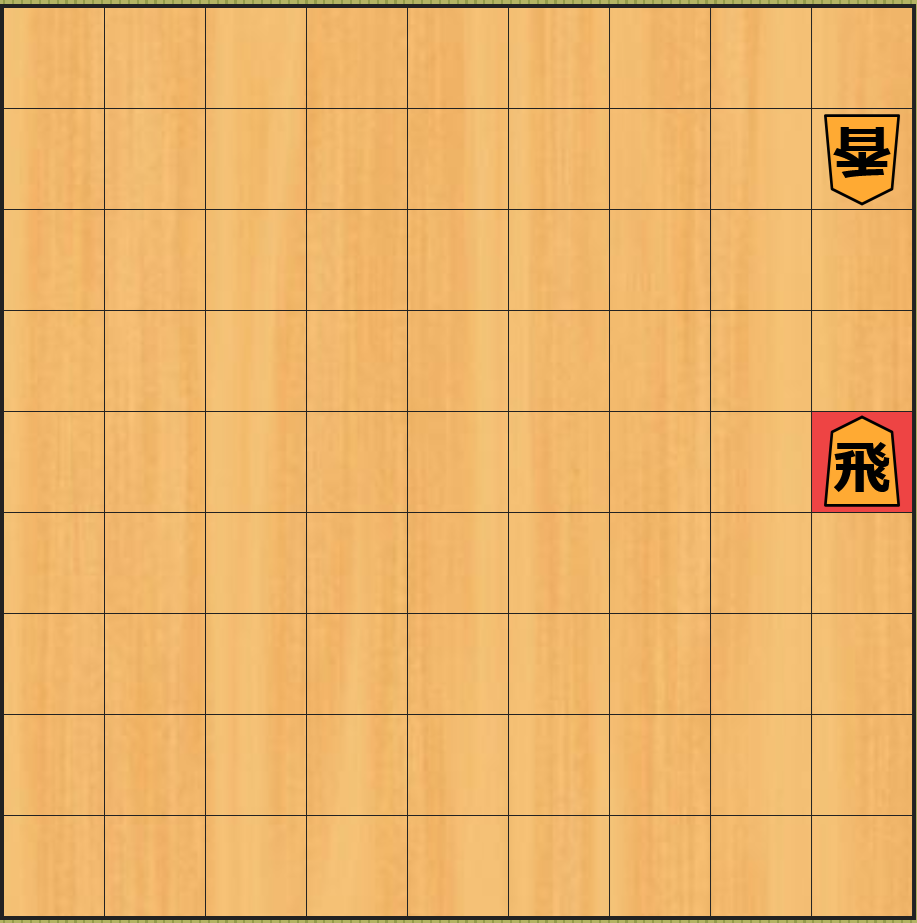
下図の 2 つの局面は良く似ていますが、後手の香車が多いかどうか で 形勢が大きく異なり ますが、そのことを 駒の取り合いを行う前の下図の局面 から 正しい形勢判断を行うことは困難 です。将棋に慣れている方であれば下図のような駒を決まった順番で取り合うだけの単純な局面であればどちらが有利かを簡単に判断することは可能かもしれませんが、駒の取り合いが複数パターン存在するような複雑な局面 であったり、駒の取り合いが 10 手以上続くような局面 の形勢判断は さらに困難に なります。

このように、将棋では 駒の取り合いが続く局面 では、駒の取り合いが終わるまでは形勢判断を行うことが困難 なため、水平線効果が発生する可能性が高く なります。

水平線効果の例 4

不利になる状況が避けられない 場合でも、不利な局面になるのを 先延ばしを行うことができる 場合があり、そのような場合に 水平線効果が発生 することがあります。Chess programming wiki ではチェスの局面での具体例が紹介されていますが、本記事では 将棋の局面で同様の具体例 を示します。

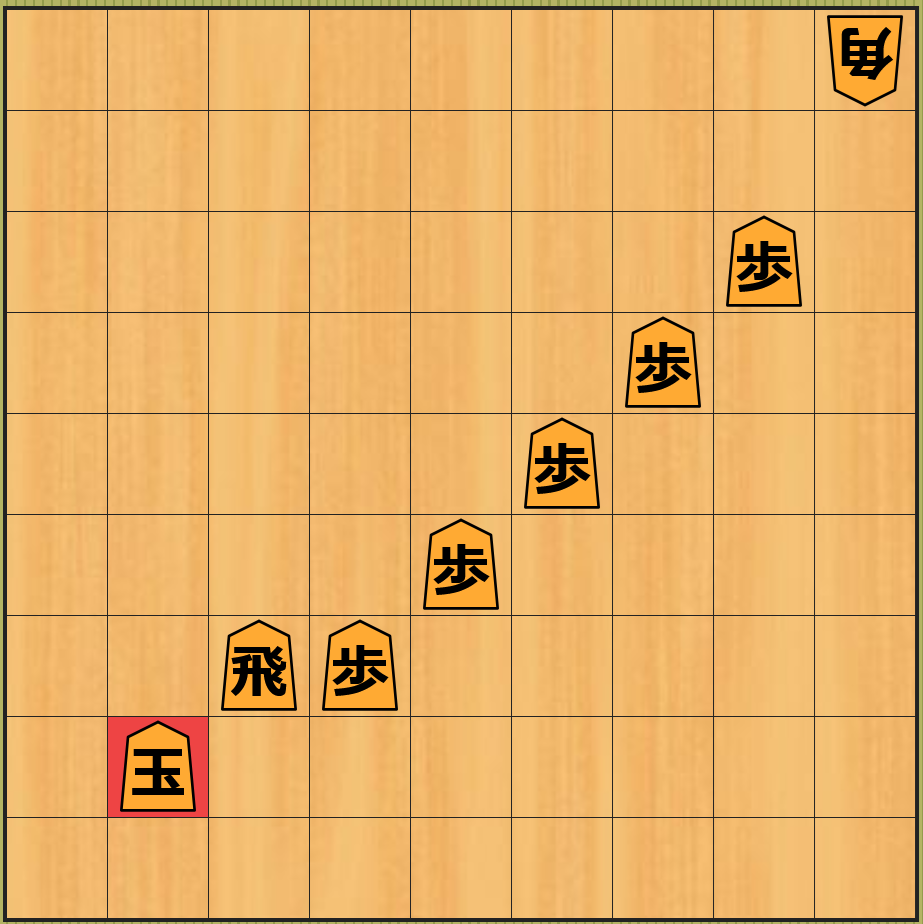
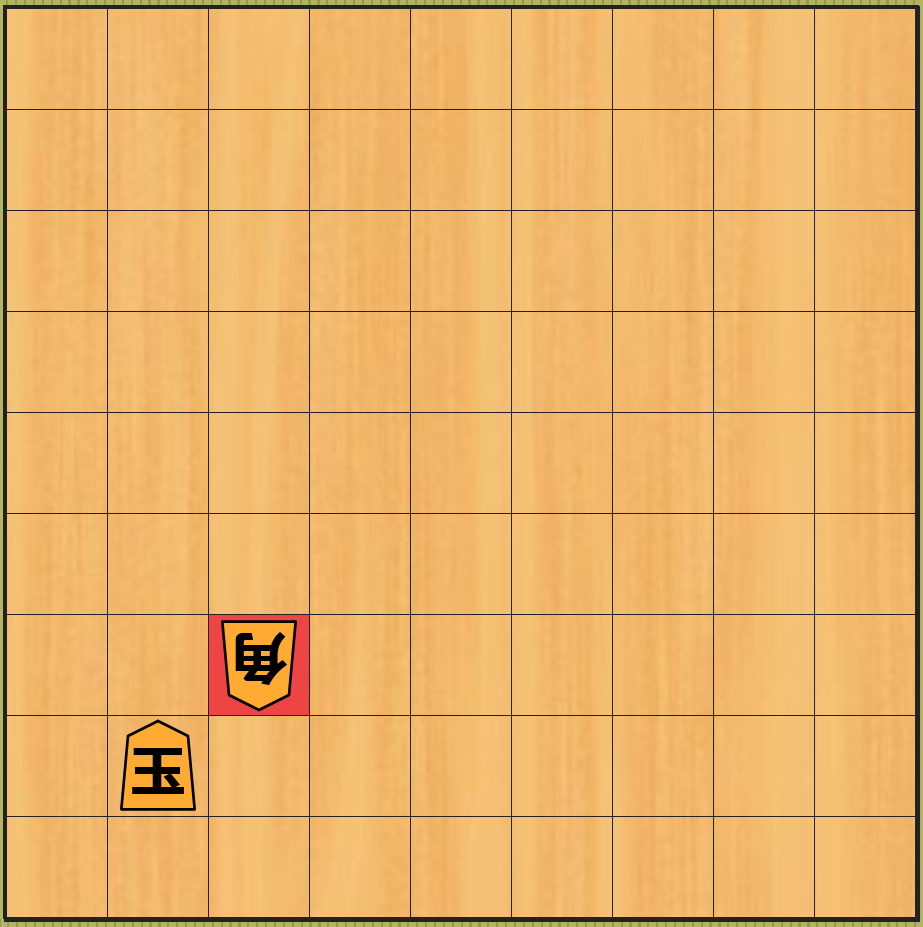
下図左は先手の局面で、このまま 先手が何もしないでいる と下図右のように 次の後手の手番 で斜めに移動できる角で 飛車を取られてしまいます⁶。

この局面での 先手の合法手 は以下の通りです。それぞれについて検討します。

5 つある歩のいずれかを前に移動する
飛車を移動する
王を前、右上、右のいずれかに移動する

飛車を移動する場合

このままでは飛車を取られてしまうので、飛車を移動する合法手について最初に検討することにします。飛車を取られないよう に下図左のように 移動する と、下図右のように次の後手の手番で角で 王を取られて負けてしまいます。他のマスに飛車を移動した場合も同様なので、この局面では 飛車を移動することはできません。

上図右は 2 手先の局面なので、このことは 深さの上限を 2 とした深さ制限探索を行うことで 計算することができます。

王を移動する場合

この局面での 最善手 は、下図左のように 王を右上に移動する というものです。そのように移動することで、その次の後手の手番で飛車を取られても下図右のように 王で角を取り返すことができる ので 下図右の局面の近似値 は -10 + 9 = -1 となります。このことは 深さの上限を 3 とした深さ制限探索を行うことで 計算することができます。

下図左のように 王を上に移動 した場合は、下図右のようにその次の後手の手番で角で飛車を取られることになります。下図右の局面 ではどの合法手を着手しても 角を取り返すことができない ので下図右の局面に対して先手が着手を行った局面の 近似値はすべて -10 となります。図は省略しますが王を右に移動した場合も同様です。下図右の局面で 角を取れないことを確認する必要がある ので、これらのことは 深さの上限を 3 とした深さ制限探索を行うことで 計算することができます。

歩を移動する場合

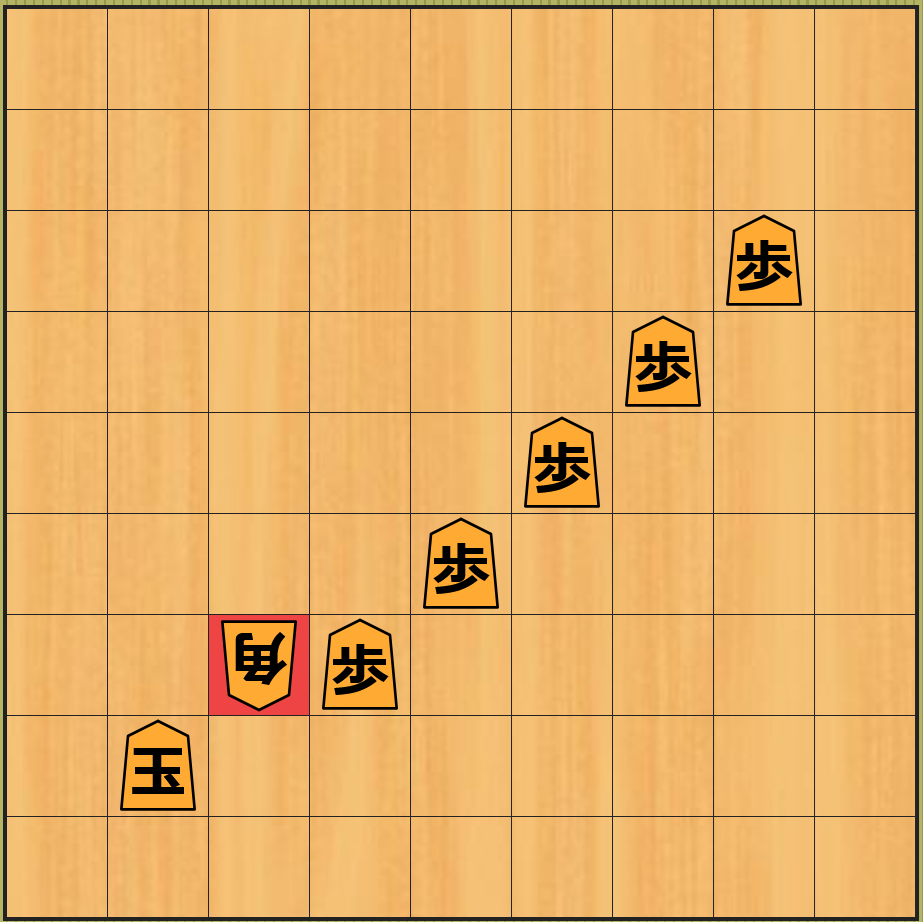
下図のように 一番右の歩を移動 した場合は、角は駒を跳び越すことができないので、次の相手の手番で飛車を取られることはなくなります。

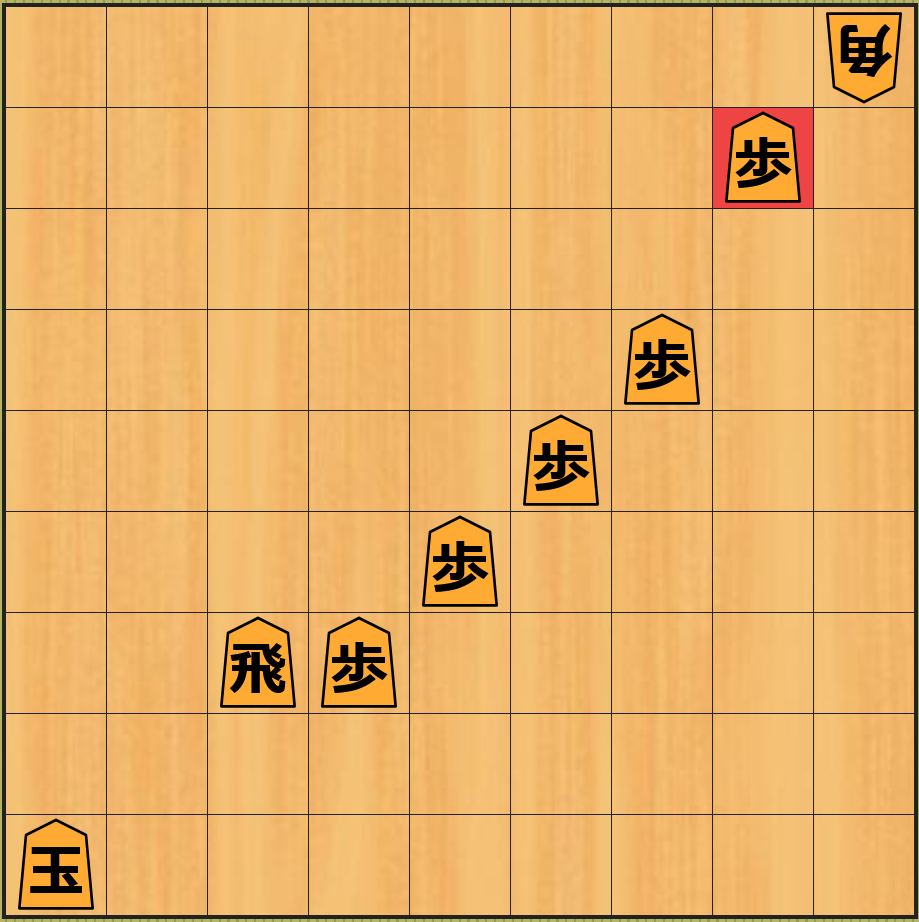
しかし、下図のように 後手の手番でその歩を取られた局面 では、相変わらず そのまま放っておくと 飛車を取られてしまう局面 になります。また、飛車を移動することができない という状況も 変わりません。従って上図の歩を移動するという着手は、飛車を取られること を 先延ばしにしている に過ぎないということです。また下図の局面の 近似値 は歩が後手に取られたので -1 になります。

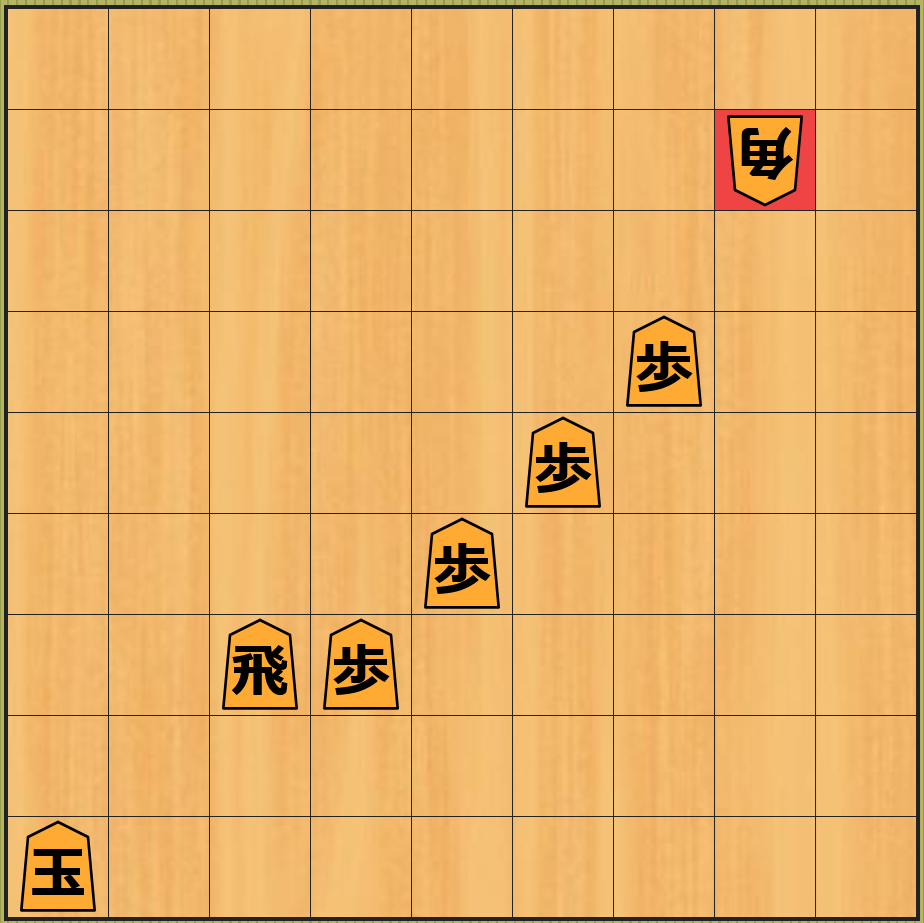
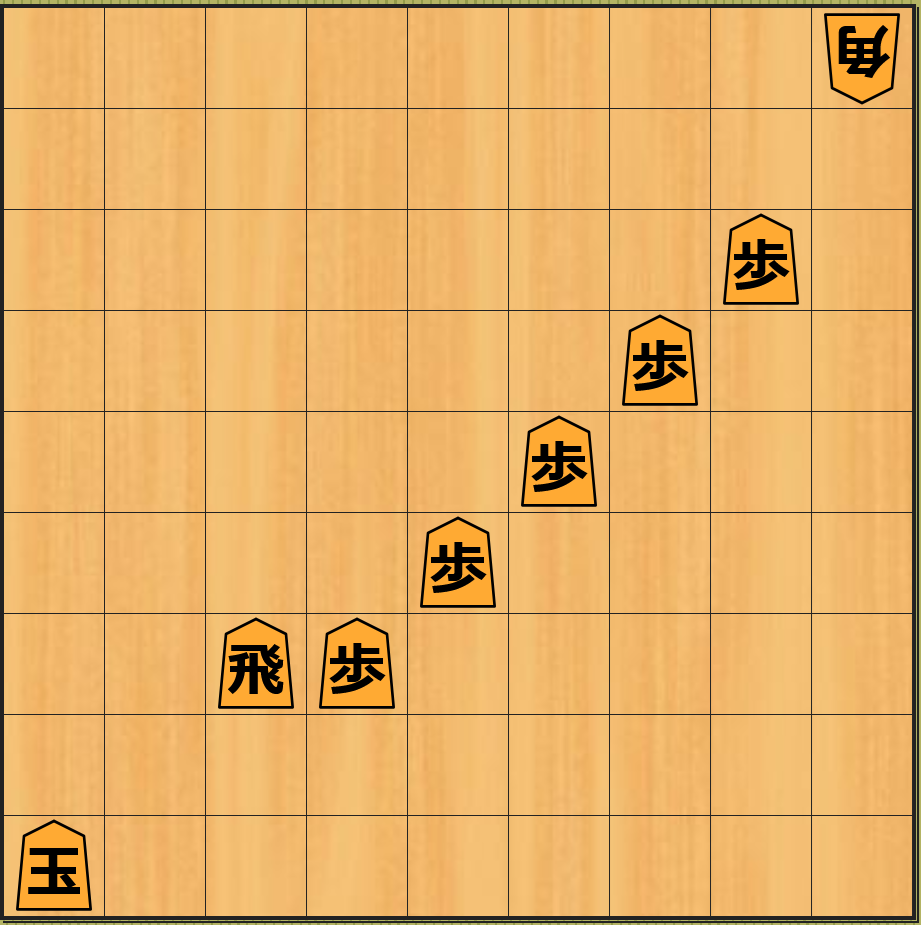
上図の局面で歩はまだ 4 つ残っているので、下図のように 同様の先延ばしを後 4 回繰り返す ことができます。

最初の局面から 10 手目の上の最後の図の局面では 歩が無くなった のでもう 先延ばしを行うことはできません。従って、その後は下図のように王を右上に移動、角で飛車を取る、王で角を取るという着手が最善手となります。

上図の最後の局面は最初の局面から 13 手後の局面 で、先手が角を 1 枚、後手が歩が 5 枚、飛車が 1 枚取っているので 近似値 は 9 - 5 - 10 = -6 となります。

上図は 最初に王を右上に移動 して角を取り返した場合の下図の 近似値が -1 の局面 と比べて近似値が 5 も小さい ので、先延ばしが悪影響を与える ことがわかります。また、先延ばしの結果がわかるまでに 13 手 もの手数がかかることから、先延ばしが悪影響を与えることを知る ためには 深さが 13 以上の深さ制限探索が必要 になることがわかります。

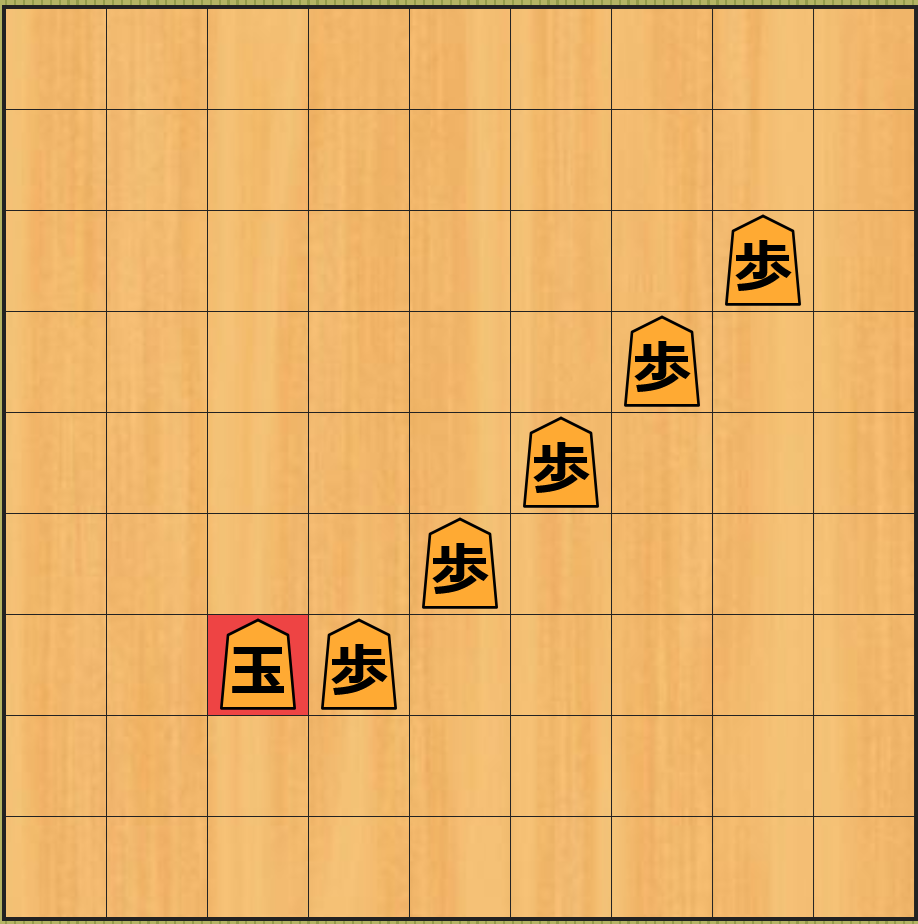
このように、不利な局面になることが避けられない が 先延ばしができる ような局面⁷では、先延ばしが無意味または状況が悪化することを知るために 大きな深さの上限が必要になる ことがあるため、水平線効果が発生する可能性が高く なります。

水平線効果の例 5

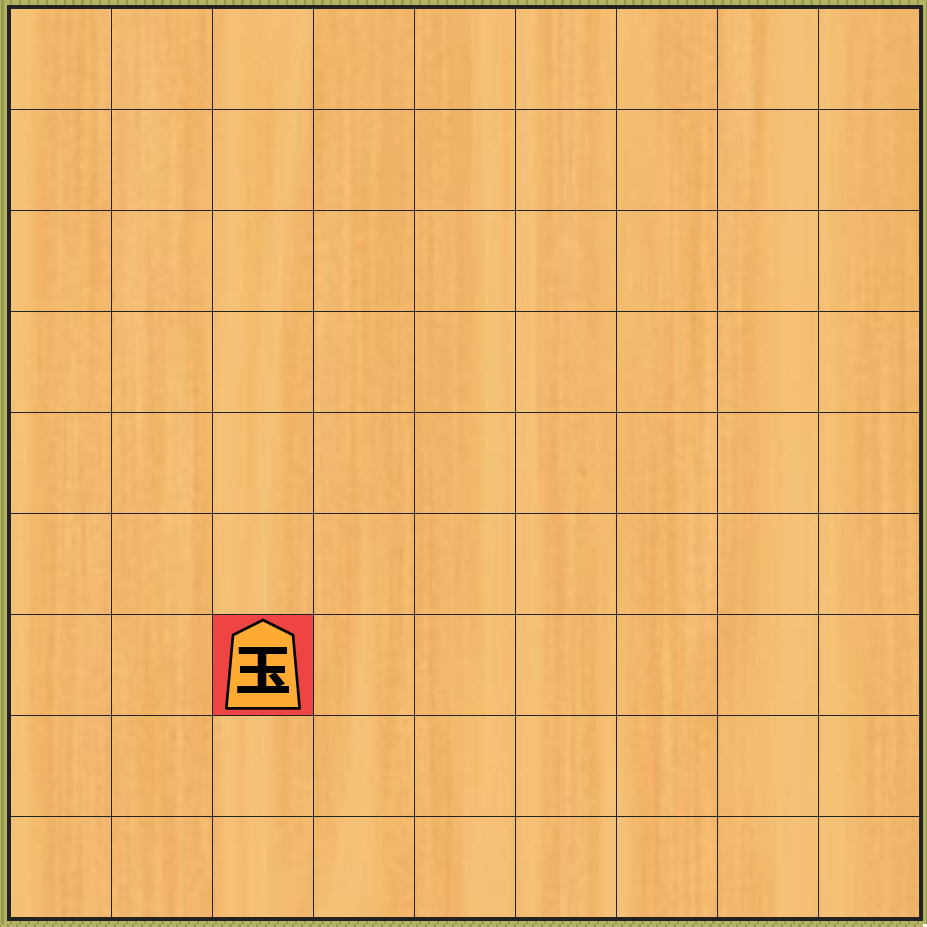
水平線効果は、駒の取り合いが起きない場合 や、不利な局面の先延ばしと関係ない 場合でも 発生することがあります。有名な具体例としては、2015 年に 将棋のプロ棋士と AI の対戦 が行われた 電王戦での対局 があります。この頃は AI の強さがプロ棋士を超え始めた時期 でしたが、現在と比べて 評価関数の精度が低く、深さ制限探索での 深さの上限も小さかった ため、水平線効果 によって AI が形勢判断を間違う ような 局面がある ことが知られていました。下記はその局面の図で、後手の AI が 後手が有利になると勘違いして先手の自陣に角を着手 した局面です。この局面から 先手が間違えずにしばらく着手を行う ことでこの 角が先手に取られてしまう ため、この局面は実際には 先手が大きく有利な局面 です。おそらく後手の AI は深さ制限探索の 深さの上限が足りなかった ため、 水平線効果 によってこの局面が自分にとって 不利であることがわからなかった のではないかと思います。

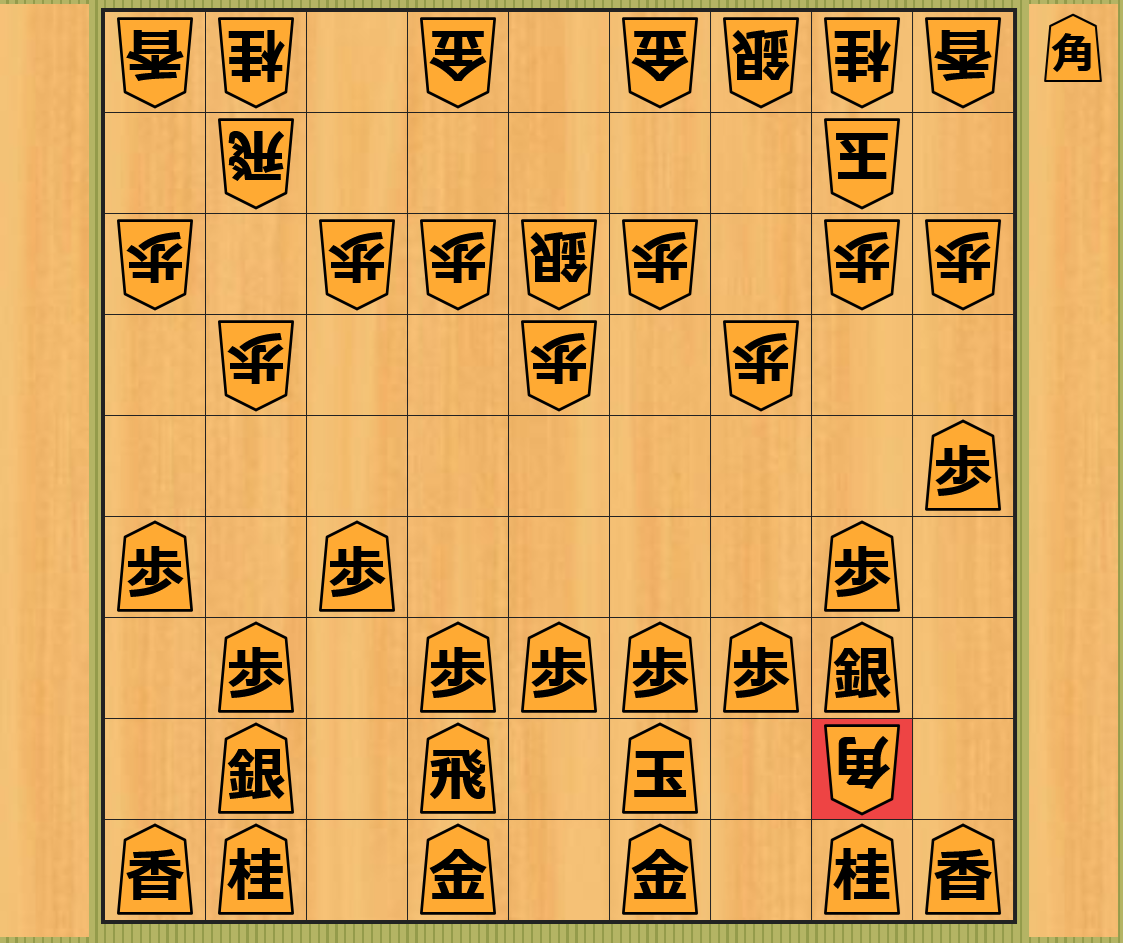
もちろんそれから 10 年たった現在の将棋の強い AI はこの局面で形勢判断を誤りませんが、現在の AI であっても依然として 水平線効果によって形勢判断を誤ることはあります。

参考までにこの対局に関する記事のリンクを下記に示します。

水平線効果の対策

水平線効果は、深さの上限が足りない ことによって起きるので、深さの上限を増やす ことで ある程度は解消 することができます。ただし、ゲームの 決着がついた局面まで探索しない限り、深さの上限をどこまで増やしても水平線効果の問題を 完全に解決することはできません。また、深さの上限を増やす ことで 処理時間が増えてしまう ので、深さの上限を 単純に増やすことでこの問題を解決することは困難 です。

また、先の局面まで考慮できる ような 精度の高い評価関数を作成 することでも水平線効果を ある程度は解消 することができますが、完全に解決することは困難です。

静止探索

水平線効果への 対策法の一つ に 静止探索（quiescence search）という手法があります。水平線効果の 主要な原因 は、駒の取り合いなどによって 静的評価関数が計算する 近似値 が着手を行うごとに 大きく動く ことにあります。実際に先程の 駒の取り合いの例 の場合は、下記の表のように 近似値 が 着手を行うごとに変動 します。

手数	取った駒	近似値
0	なし	0
1	後手の歩(1 点)	1
2	先手の歩(-1 点)	0
3	後手の香車(2 点)	2
4	先手の香車(-2 点)	0
5	後手の香車(2 点)	2
6	先手の飛車(-10 点)	-8

そこで、静止探索 では深さ制限探索で静的評価関数が近似値を計算する 深さの上限の局面 が、駒の取り合いの最中などによって 評価値が変動する局面であった場合 に、形勢が落ち着いて近似値の変動がほぼ 静止する局面 になるまで 深さの上限を増やす ことで、水平線効果が起こりにくいようにする という手法です。

静止探索には、深さの上限が増える ため 処理時間が増える という問題があります。細かい話になるので本記事では紹介しませんが、その問題を解決するための 枝狩りの手法 がいくつか考えられています。

参考までに静止探索の Chess programming wiki のリンクを下記に示します。

水平線効果の対策の限界

静止探索以外 にも様々な水平線効果に対する 対策が考えられています が、残念ながら 深さの上限がある限り、探索を行わない局面が生じてしまうため水平線効果の問題を 完全に解決する方法は見つかっていません。

なお、〇× ゲームのような深さが浅いゲーム木の場合は深さ制限探索を行う必要がないため水平線効果が発生しないようにすることができますが、ほとんど のゲームでは 水平線効果から完全に逃れることはできません。

誤差の蓄積によるバグ

前回の記事で定義した calc_pdistlist には 誤差の蓄積によるバグ があることが判明しましたので、その説明と修正を行います。

前回の記事では calc_pdistlist で 20 までの深さの上限 を計算しましたが、下記のプログラムで 50 までの深さの上限を計算 するとバグが発生します。

from tree import calc_pdistlist, draw_pdistlist

pdistlist = calc_pdistlist(maxdepth=100, std=5, area=20)

実行結果

(-2.349041216719884, 17.213367568249353, 4.148899561118508)
(-3.3306690738754696e-16, 25.08040342281806, 5.008033887946253)
(-3.3155263675920765, 14.289116783779123, 3.7800948114801463)
略
(2.310928032510741, 0.36410465169475975, 0.6034108481745748)
(3.3912666286262514, 4.1834925445817355, 2.0453587813832894)
(10.784657385689131, 446.8687632896369, 21.139270642329098)
(344.8948880209233, 21320266.678833306, 4617.387430012052)
(11341449.049151158, 7.656161987802852e+20, 27669770486.584908)
(4.01324040102822e+20, 3.396353242496722e+61, 5.827823987129949e+30)
(1.7864964707298612e+61, 2.992759592440811e+183, 5.470612024664892e+91)
---------------------------------------------------------------------------
OverflowError                             Traceback (most recent call last)
略
File c:\Users\ys\ai\marubatsu\180\tree.py:2103, in calc_stval(pdist)
   2101 var = 0
   2102 for s, p in pdist.items():
-> 2103     var += ((s - e) ** 2) * p
   2104 std = var ** 0.5
   2105 return e, var, std

OverflowError: (34, 'Result too large')

エラーメッセージの OverflowError は、計算結果が python が扱える数値の範囲を超えた（overflow）という意味で、結果が大きすぎるという意味を表す Result too large というメッセージからもそのことがわかります。

下記の エラーが発生する直前の実行結果 から平均、分散、標準偏差がいずれも 急激に大きくなっている ことがわかります。具体的には最後の平均、分散、標準偏差は $1.79 × 10^{61}$、$2.99 × 10^{183}$、$5.47 × 10^{91}$ という とんでもない大きな値 になっています。

(2.310928032510741, 0.36410465169475975, 0.6034108481745748)
(3.3912666286262514, 4.1834925445817355, 2.0453587813832894)
(10.784657385689131, 446.8687632896369, 21.139270642329098)
(344.8948880209233, 21320266.678833306, 4617.387430012052)
(11341449.049151158, 7.656161987802852e+20, 27669770486.584908)
(4.01324040102822e+20, 3.396353242496722e+61, 5.827823987129949e+30)
(1.7864964707298612e+61, 2.992759592440811e+183, 5.470612024664892e+91)

原因の検証

実行結果を数えた結果、エラーが発生する のは 深さの上限が 38 の場合 であることが分かったので、下記のプログラムでエラーが発生しない 深さの上限を 37 まで とした場合で計算し、計算した確率分布を検証 することにします。なお、実行結果はエラーが発生する直前までは先ほどと同じなので省略します。

pdistlist = calc_pdistlist(maxdepth=37, std=5, area=20)

次に、下記のプログラムで 深さの上限が 37 の場合の 確率分布を表示 すると、実行結果のように 確率変数が 0 ~ 4 の場合の確率が 1 を大きく超えている ことがわかります。

from pprint import pprint

pprint(pdistlist[37])

実行結果

defaultdict(<class 'int'>,
            {-20: 0.0,
             -19: 0.0,
             -18: 0.0,
             -17: 0.0,
             -16: 0.0,
             -15: 0.0,
             -14: 0.0,
             -13: 0.0,
             -12: 0.0,
             -11: 0.0,
             -10: 0.0,
             -9: 0.0,
             -8: 0.0,
             -7: 0.0,
             -6: 0.0,
             -5: 0.0,
             -4: 0.0,
             -3: 0.0,
             -2: 0.0,
             -1: 3.991041525101385e-61,
             0: 6.641991647843087e+46,
             1: 1.0550226605387531e+60,
             2: 8.156222531909125e+60,
             3: 1.658323276472035e+59,
             4: 5.486353835843315e+39,
             5: 1.458118061627133e-102,
             6: 0.0,
             7: 0.0,
             8: 0.0,
             9: 0.0,
             10: 0.0,
             11: 0.0,
             12: 0.0,
             13: 0.0,
             14: 0.0,
             15: 0.0,
             16: 0.0,
             17: 0.0,
             18: 0.0,
             19: 0.0,
             20: 0.0})

確率分布の確率の合計は 1 になる ので、この点は明らかに変です。そこで、下記のプログラムで それぞれの深さの上限 に対する確率分布の 確率の合計を表示 することにします。

for pdist in pdistlist:
    print(sum(pdist.values()))

実行結果

1.0
1.0000000000000009
1.0000000000000029
1.0000000000000089
1.0000000000000255
1.0000000000000755
1.0000000000002272
1.000000000000682
1.000000000002046
1.000000000006137
1.0000000000184108
1.0000000000552325
1.0000000001656972
1.0000000004970917
1.000000001491275
1.000000004473825
1.0000000134214755
1.0000000402644271
1.0000001207932863
1.0000003623799028
1.0000010871401026
1.000003261423853
1.00000978430347
1.0000293531976092
1.000088062177684
1.0002642097985759
1.0007928388346246
1.0023804027824998
1.0071582207878376
1.0216287495261822
1.0662997749864653
1.2123777367289046
1.782025269161202
5.659024499897169
181.22775996396462
5952154.112261737
2.1087374071559737e+20
9.377077520095147e+60

実行結果から、下記の事が確認できました。

深さの上限が 1 の時点 から確率分布の 確率の合計 がわずかに 1 を上回る
深さの上限が大きくなるにつれて 確率分布の 確率の合計が増えていき、最後の方では 急激に増える

誤差が発生する理由

深さの上限を 1 とした場合に 0.0000000000000009 のような 微小な誤差が発生する理由 は、以前の記事で説明したように、Python に限らず コンピュータが小数点を含んだ数値を正確に表現できない場合がある からです。例えば、下記のプログラムの実行結果のように 0.1 × 3 という小学生でも 0.3 と答えられるような計算を、Python は正しく計算することはできず、微小な誤差が発生 します。

print(0.1 * 3)

実行結果

0.30000000000000004

このような 誤差は多くの場合は非常に小さく、足し算と引き算しか行わない場合 は ほとんどの場合は無視しても問題はありません。一方、特に 掛け算や割り算 を 多数行った場合 は先ほどの計算結果のように 微小な誤差の積み重ね が 非常に大きな誤差 となって 計算結果が大きく間違う ようなことがあるため注意が必要です。このような 誤差の積み重ね によって 非常に大きな誤差が発生 することを 誤差の爆発 と呼びます。

コンピューターの計算で発生する誤差のことを 計算誤差 と呼びます。計算誤差には、丸め誤差、打切り誤差、情報落ち、桁落ちなどの 様々な種類 があり、いずれもそのような誤差が 大きな問題となることがある ので注意が必要です。先程の計算で発生した誤差は、丸め誤差によって発生したものです。

参考までに計算誤差の wikipedia のリンクを下記に記します。

誤差が爆発する理由

先程の計算で誤差が爆発する理由は、計算した確率分布の 確率の合計 が 深さの上限が 1 増える たびに 3 乗の値 になるからです。また、そのような計算が行われる理由は、calc_pdistlist が次の深さの上限の確率分布の計算する際に、3 つの確率分布の確率変数の組み合わせ に対して、掛け算を使って計算を行っている からです。

例えば max ノード $N$ の子ノード $A$、$B$、$C$ の確率分布が下記のように 誤差によって確率の合計が 2 になっている場合の $N$ の確率分布の計算を行ってみることにします。

$A$ の確率分布 { 0: 1, -1: 1 }
$B$ の確率分布 { -1: 1, -2: 1 }
$C$ の確率分布 { -2: 1, -3: 1 }

下記は 3 つの確率分布で計算される 確率変数の組み合わせ と、その確率 です。すべての確率変数に対する確率は 1 なので 3 つの確率変数の組み合わせの確率は $1^3 = 1$ になります。

$A$	$B$	$C$	確率
0	-1	-2	1
0	-1	-3	1
0	-2	-2	1
0	-2	-3	1
-1	-1	-2	1
-1	-1	-3	1
-1	-2	-2	1
-1	-2	-3	1

組み合わせは 8 通りなので $\boldsymbol{N}$ の確率分布の 確率の合計は 8 となり、これは $A$、$B$、$C$ の確率分布の合計の乗算である $\boldsymbol{2^3}$ と等しい ことがわかります。

なお、誤差が存在しなければ 確率分布の合計は 1 なので、次の深さの上限の確率分布の確率の合計は $1^3 = 1$ となり 1 から変化しないため問題は発生しません。

上記が正しいことは、深さの上限が 1 の場合の確率分布の 確率の合計 を 毎回 3 乗した値と比較 を行う下記のプログラムで確認することができます。実行結果から、2 つの計算結果がほぼ同じように増えていく ことが確認できます。なお、全く同じにならない のは深さの上限が 1 の場合で発生した 誤差が毎回発生する からです。

p = 1.0000000000000009
for pdist in pdistlist[1:]:
    print(sum(pdist.values()), p)
    p = p ** 3

実行結果

1.0000000000000009 1.0000000000000009
1.0000000000000029 1.0000000000000027
1.0000000000000089 1.000000000000008
1.0000000000000255 1.000000000000024
1.0000000000000755 1.000000000000072
1.0000000000002272 1.0000000000002158
1.000000000000682 1.0000000000006475
1.000000000002046 1.0000000000019424
1.000000000006137 1.0000000000058273
1.0000000000184108 1.000000000017482
1.0000000000552325 1.000000000052446
1.0000000001656972 1.0000000001573381
1.0000000004970917 1.0000000004720144
1.000000001491275 1.0000000014160433
1.000000004473825 1.0000000042481298
1.0000000134214755 1.0000000127443895
1.0000000402644271 1.000000038233169
1.0000001207932863 1.0000001146995117
1.0000003623799028 1.0000003440985745
1.0000010871401026 1.0000010322960788
1.000003261423853 1.0000030968914335
1.00000978430347 1.0000092907030729
1.0000293531976092 1.0000278723681708
1.000088062177684 1.0000836194351408
1.0002642097985759 1.0002508792826368
1.0007928388346246 1.0007528266849441
1.0023804027824998 1.0022601807255482
1.0071582207878376 1.0067958789733265
1.0216287495261822 1.0205265026937171
1.0662997749864653 1.0628521686011438
1.2123777367289046 1.2006559819957636
1.782025269161202 1.7308353916285395
5.659024499897169 5.1852213533910785
181.22775996396462 139.412560130275
5952154.112261737 2709603.2688953583
2.1087374071559737e+20 1.989377138084674e+19
9.377077520095147e+60 7.873201529448793e+57

最初の誤差を $x = 0.0000000000000009$ と表記すると、深さの上限が $d$ の場合の確率分布の合計は $(1 + x)^{3^d}$ という、指数関数の指数 という式で表されます。$(1 + x)^d$ という 指数関数 は、$x > 0
$ の場合に $d$ が大きくなると 急激に大きくなる という性質がありますが、$(1 + x)^{3^d}$ の場合はそれよりも さらに急激に大きくなる という性質があります。そのため、x が 0.0000000000000009 のような 非常に 0 に近い小さな誤差 であっても、深さの上限を増やすと途中から 誤差が急激に大きな値 となって 誤差の爆発 が発生します。

誤差の修正

今回のプログラムで発生する誤差は、確率分布の 確率の合計が 1 を超えることが原因 なので、この誤差は calc_pdist で 確率分布の計算を行う際 に、その 確率の合計が 1 になる ように確率分布の 計算結果を修正す ることで解消することができます。下記はそのような処理を行うように calc_pdist を修正したプログラムです。

17 行目：計算さいた確率分布の確率の合計を計算する
18、19 行目：確率分布のそれぞれの確率変数の確率を、上記で計算した確率の合計で割ることで、確率の合計が 1 になるように修正する

 1  from collections import defaultdict
 2  from itertools import product
 3  
 4  def calc_pdist(pdistlist, maxnode=True):   
 5      pdist = defaultdict(int)
 6      pdistlist = [pd.items() for pd in pdistlist]
 7      productdata = product(*pdistlist)
 8      for data in productdata:
 9          score, prob = data[0]
10          for s, p in data[1:]:
11              if maxnode:
12                  score = max(score, s)
13              else:
14                  score = min(score, s)
15              prob *= p
16          pdist[score] += prob
17      psum = sum(pdist.values())
18      for key in pdist:
19          pdist[key] /= psum
20      return pdist

行番号のないプログラム

from collections import defaultdict
from itertools import product

def calc_pdist(pdistlist, maxnode=True):   
    pdist = defaultdict(int)
    pdistlist = [pd.items() for pd in pdistlist]
    productdata = product(*pdistlist)
    for data in productdata:
        score, prob = data[0]
        for s, p in data[1:]:
            if maxnode:
                score = max(score, s)
            else:
                score = min(score, s)
            prob *= p
        pdist[score] += prob
    psum = sum(pdist.values())
    for key in pdist:
        pdist[key] /= psum
    return pdist

修正箇所

from itertools import product

def calc_pdist(pdistlist, maxnode=True):   
    pdist = defaultdict(int)
    pdistlist = [pd.items() for pd in pdistlist]
    productdata = product(*pdistlist)
    for data in productdata:
        score, prob = data[0]
        for s, p in data[1:]:
            if maxnode:
                score = max(score, s)
            else:
                score = min(score, s)
            prob *= p
        pdist[score] += prob
+   psum = sum(pdist.values())
+   for key in pdist:
+       pdist[key] /= psum
    return pdist

tree.py からインポートした calc_pdistlist は上記で修正した calc_pdist を利用しないので、calc_pdistlist の定義を実行し直します。プログラムは tree.py 内で定義された calc_pdistlist と同じなので折りたたみます。

calc_pdistlist のプログラム

from tree import calc_discrete_ndist, translate_pdist, calc_stval

def calc_pdistlist(maxdepth, std, area):
    maxnode = True
    pdistA = calc_discrete_ndist(0, s=std, area=area)
    print(calc_stval(pdistA))
    pdistlist = [pdistA]

    for _ in range(maxdepth):
        if maxnode:
            pdistB = translate_pdist(pdistA, -1)
            pdistC = translate_pdist(pdistA, -2)
        else:
            pdistB = translate_pdist(pdistA, 1)
            pdistC = translate_pdist(pdistA, 2)
        pdistA = calc_pdist([pdistA, pdistB, pdistC], maxnode=maxnode)
        print(calc_stval(pdistA))
        pdistlist.append(pdistA)
        maxnode = not maxnode

    return pdistlist

上記の実行後に下記のプログラムでで 100 までの深さの上限 の計算を行います。実行結果でエラーが発生しないことから、誤差の問題が解決された ことがわかります。

pdistlist = calc_pdistlist(maxdepth=100, std=5, area=20)

実行結果

(-3.3306690738754696e-16, 25.08040342281806, 5.008033887946253)
(3.3155263675920734, 14.289116783779107, 3.780094811480144)
(1.0574856958804537, 7.288277471989019, 2.6996809944860187)
略
(1.903315648692667, 0.0886226806456293, 0.2976956174444449)
(1.9033782396398788, 0.08857218891104862, 0.29761080106583604)
(1.90331568894469, 0.08849754678670865, 0.2974853723911625)

また、下記のプログラムで、すべての深さ の上限の確率分布の 確率の合計を表示 すると、実行結果からいずれも 1 または ほぼ 1 の値が表示 され、先程のように途中から急激に大きくなることが無くなったことが確認できます。なお、確率の合計が 1 になるように修正する計算 でも 誤差が発生する ため、結果が完全に 1 にならない場合があります。

for pdist in pdistlist:
    print(sum(pdist.values()))

実行結果

1.0
1.0
1.0
1.0000000000000002
1.0
1.0000000000000002
1.0
略

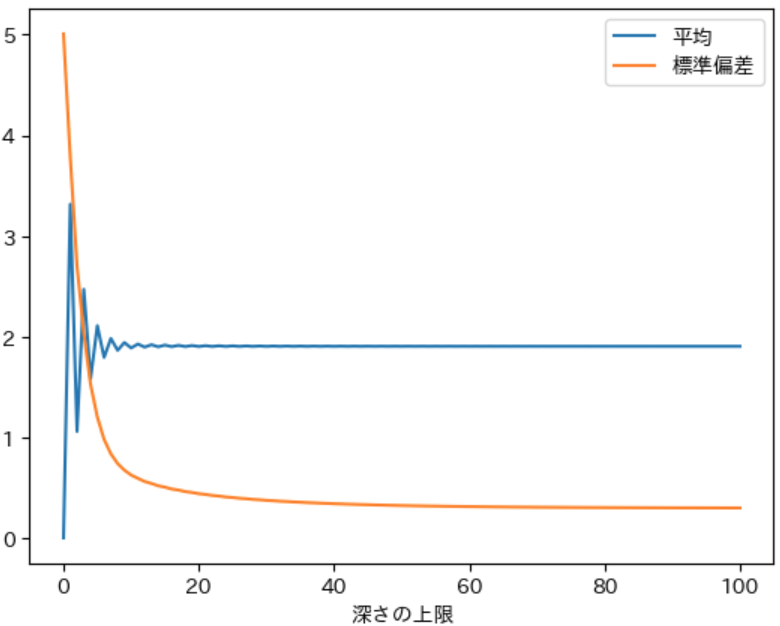
最後に下記のプログラムで計算した結果のグラフを表示します。グラフと先程の実行結果から深さの上限を増やすことで 平均が 2、標準偏差が 0.30 に収束する ことが確認できます。

from tree import draw_pdistlist

draw_pdistlist(pdistlist)

実行結果

今回の記事のまとめ

今回の記事では、水平線効果について説明し、深さの上限を増やした際に AI が強くなる理由の一つとして、水平線効果が発生しにくくなるという理由を説明しました。ただし、水平線効果はその性質から、深さ制限探索を行う限り完全に解消することはできません。

また、誤差の蓄積による爆発とその解消方法について説明しました。

本記事で入力したプログラム

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル
tree.py	本記事で更新した tree_new.py

次回の記事

近日公開予定です

horizon には地平線という意味もありますが、陸地では丘や山があると地平線が見えなくなる場合がよくあるため horizon effect の日本語訳は地平線効果ではなく、水平線効果となっているのではないかと思います ↩
(2, 0) に着手を行う場合もありますが、(0, 2) に着手を行った場合と同一局面になります ↩ ↩²
他の最善手である (1, 0)、(2, 1)、(1, 2) が計算される場合もあります ↩
桂馬という相手や自分の駒を跳び越すことができる特殊な駒がありますが、本記事の例では利用しません ↩
本記事では持ち駒は考慮しないので表示しません ↩
本記事では成りを考慮しないことにしたので、右図では後手の角を成っていません ↩
他にも敗北を先延ばしするために無意味な王手をかけ続けるような例があり、実際にそのようなことを行うプロ棋士よりも強い将棋の AI があります。また、囲碁ではシチョウと呼ばれる同様の無意味な先延ばしがあります ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その180 水平線効果と誤差の蓄積によるバグ

目次と前回の記事

これまでに作成したモジュール

深さの上限を増やすと AI が強くなる理由のまとめ

用語

水平線効果とは何か

水平線効果の例 1

将棋の簡単な説明と静的評価関数の設定

水平線効果の例 2

深さの上限を 1 とした場合

深さの上限を 2 とした場合

水平線効果の例 3

水平線効果の例 4

飛車を移動する場合

王を移動する場合

歩を移動する場合

水平線効果の例 5

水平線効果の対策

静止探索

水平線効果の対策の限界

誤差の蓄積によるバグ

原因の検証

誤差が発生する理由

誤差が爆発する理由

誤差の修正

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その180　水平線効果と誤差の蓄積によるバグ