グレースケール画像のうんちく

Last updated at 2023-12-31Posted at 2018-04-15

グレースケール変換の前提知識から具体的な変換アルゴリズムまで解説します。

カラー画像を元に白黒印刷したい場合や、最近だと機械学習の物体認識で輝度だけ使いたい等、グレースケール化の機会は意外とよくあります。
OpenCV や ImageMagick 等のグラフィックエンジンを使えばお任せ変換できますが、それが具体的にどういう処理をして、どのような選択肢があるのか、知っておいて損はないでしょう。

実際に、OpenCV や ImageMagick でグレースケール変換をしたい方は、こちらを参考にどうぞ。

グレースケールとは

画像を色味のない明るさの度合いだけで表現するのがグレースケールです。
似た言葉にモノクロ画像がありますが、こちらは下のカラー以外3つを含む広い概念です。白と黒のどちらかだけで中間のグレーがないバイナリ画像を指す事もありますし、セピア調のように色味をつけたモノトーンかもしれません。

カラー画像	グレースケール画像	バイナリ画像	セピア調モノクロ画像

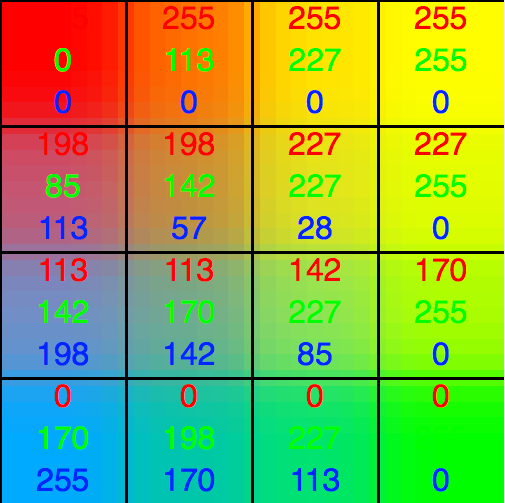
カラー画像は1つのピクセルの色を表すのに複数の値が必要で、R,G,Bの3つの値を用いる事が多いのですが、グレースケール画像だと１つのピクセルに1つです。
その1つの値に、モニタだと Y(輝度、CIE XYZ の Y軸)、L(Luminance、輝度)、印刷では K(Key 又は blacK)、より抽象的には V(Value、色価)、Intensity(強度)、Gray-Level(グレイレベル、濃度値)といった文字や用語がよく用いられます。

colourful pixel	grayscale pixel

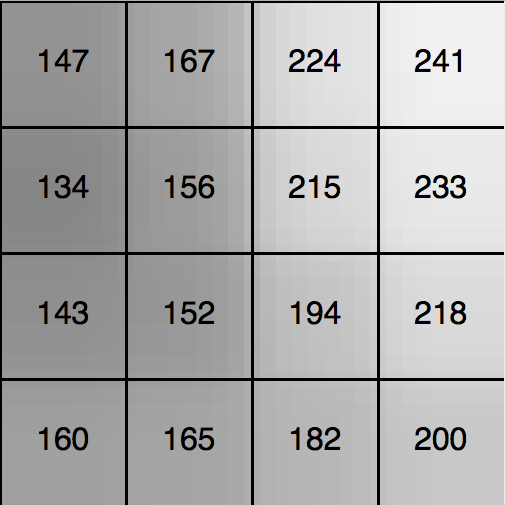(OpenCV の imshow 関数を使った表示)

つまり(基本的な)グレースケール変換は、色成分RGB(又はCMYK等)が持つその複数の値から人の眼が感じる色の強さを推定して1つの値にまとめる作業と言えます。

前提知識

R,G,B は同じ値でも見た目の明るさが違う

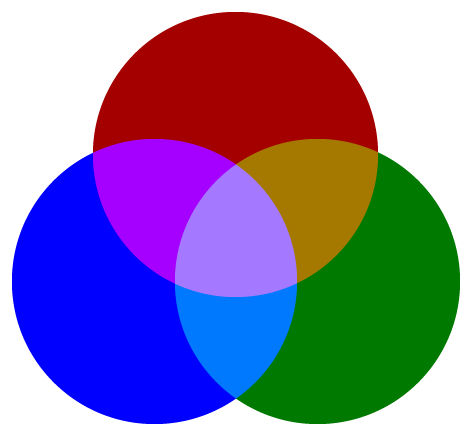
R,G,B は３つ同じ値で加色混合すると無彩色(黒〜グレー〜白)になるよう輝度がバランス調整されています。
一番左は R=G=B=255 真ん中は R=G=B=187 で揃えてますが、大抵の人にはG(緑)が明るく R(赤)は暗く B(青)はとても暗く見えます。
一番右のように、R,G,Bの値を同じにせず見た目の明るさで揃えて混ぜると青紫方向に色味がかります。

R=G=B=255	R=G=B=187(sRGBで輝度半分相当)	R:165,G:121,B:255(明るさを揃える)

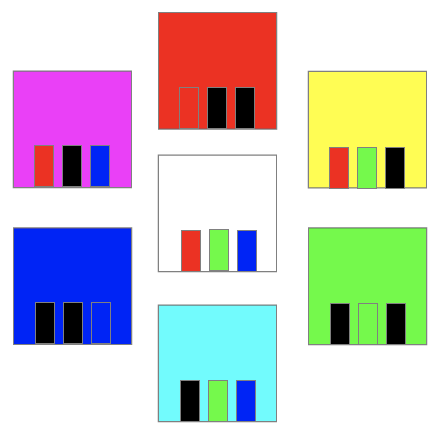
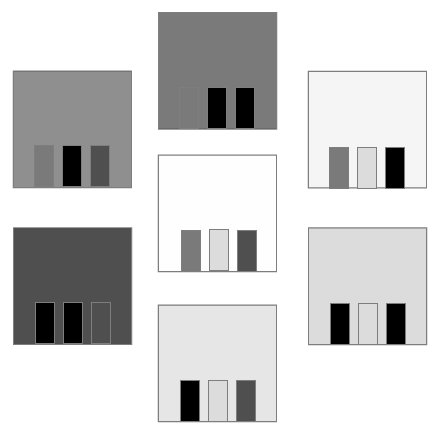
色成分R,G,B毎の明るさ（輝度)の違いを考慮した良いグレースケール変換と、考慮しない悪いグレースケール変換を並べてみます。

カラー画像	良いグレースケール (CIE XYZ)	悪いグレースケール (RGB平均)

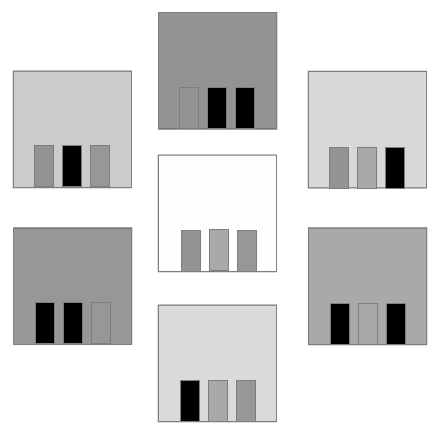この悪い方でも我慢できる事はあるので、性能優先で悪いグレースケールを使う事も多々あります。

ガンマ補正で平均が歪む

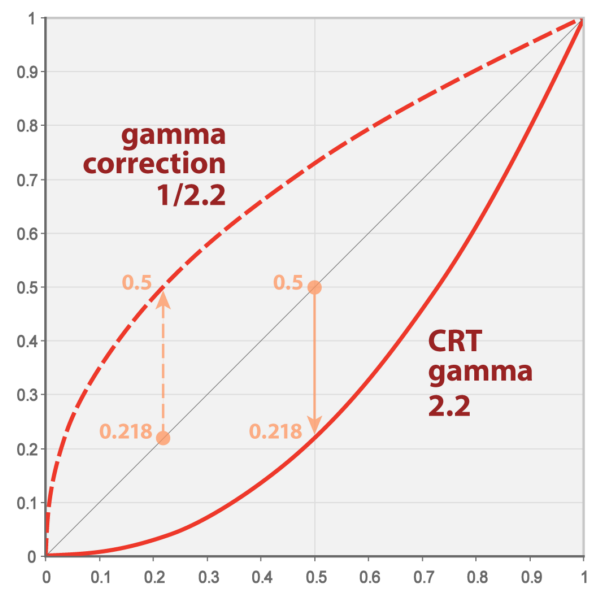
一般的な画像ファイルに記録される RGB 値はピクセルの物理的な輝度と素直に比例しません。昔のブラウン管テレビが入力信号の電圧に対して出力する輝度が比例しなかったので、信号側で補正する事にしたそうです。あと、低輝度に敏感な視覚特性に都合がよい事も勘案したと思われます。


(c) https://ja.wikipedia.org/wiki/ガンマ値

このグラフで言うと、入力信号に対して CRT gamma 曲線のように輝度が下に沈み込む特性を想定して、RGB値の方を gamma correction の点線のように釣り上げる補正をします。すると、CRT では何も補正せずとも輝度リニアに表示するという理屈です。

ガンマ補正のうんちく

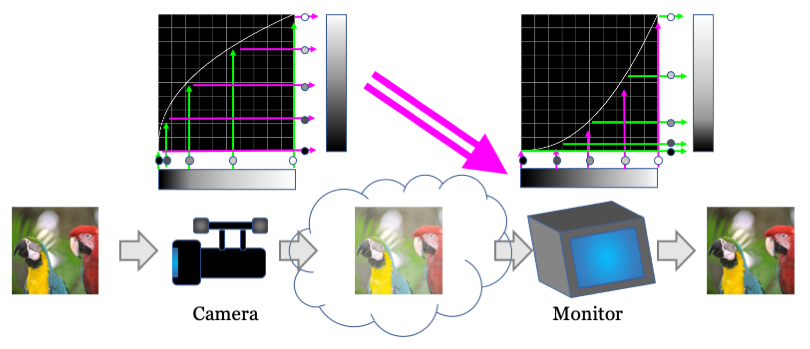https://qiita.com/yoya/items/122b93970c190068c752

このガンマ補正された R,G,B の値のまま平均を計算すると、本物の輝度の平均にはなりません。
以下の図は 1(最高輝度)と0(最低輝度)の真ん中の輝度を計算すると問題になる例です。

このように、ガンマ補正を考慮せずにR,G,Bの輝度値の平均をとると、期待する輝度よりも暗くなります。

カラー画像	嘘 CIE XYZ(ガンマ処理無し)	CIE XYZ(ガンマを考慮した版)

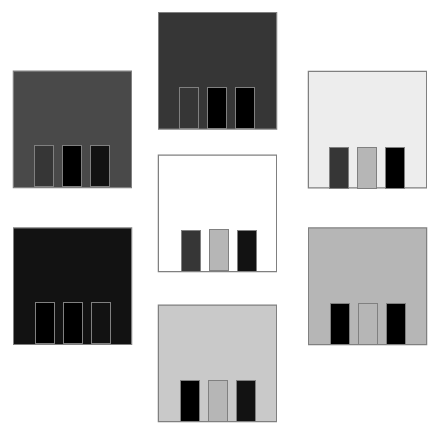この真中の図のように特に彩度が高い色に影響が現れます。以下のようにガンマ値解除の手続きをとる事で、右図のような結果に出来ます。

R,G,B値にかかっているガンマ補正を外して、物理的な輝度と比例の関係にする (linear-RGB 化)
やりたい輝度計算をする。(グレースケールだとR,G,Bを混ぜる計算)
その後またガンマ補正をかけ直して元に戻す

ちなみに、グレースケール以外でも回転やリサイズ等の座標変換で補間処理がある時にも同じ事が言えます。

ImageMagick リサイズ補間アルゴリズム -colorspace RGB (ガンマ補正の考慮)

情報量が減る

例えば、純粋に R だけの画像、G だけの画像、B だけの画像で明るさが同じ場合、グレースケールだと区別が出来ない事からも分かると思いますが、グレースケール化すると情報量がだいぶ落ちます。
精度的にもカラー画像が 24bit あるからと、そこから 8bit を超えるグレースケール画像を作る事は出来ません。画像形式的に 16bit で作ったとしても精度的に上位 8bit 以外の bit はゴミなので無意味です。
これはカラー画像 R,G,B に 8bit ずつ割り当てている為に、その時点で値が量子化(値を荒い精度で表現)されているからです。
ただし、元の映像に対する前提や、結果画像ファイルの使い方の条件次第では、元の情報を多少なりとも保ったグレースケールが得られる可能性はあります。

RGB からグレースケールへ変換

R,G,B 3つの値をどうやって 1つの値にまとめるのか。幾つか代表的な方法を紹介します。

RGB平均

V = (R + G + B) / 3.0

処理は単純ですが、前提知識で述べた２つの問題があって、実感と合わない結果になりがちです。

元画像	平均

右下の緑とか論外ですね。^^;

RGB平均 (ガンマ補正)

ガンマ補正を考慮した変換をしてみます。

(R',G',B') = 逆ガンマ補正(R,G,B)
V' = (R' + G' + B') / 3.0
V = ガンマ補正(V')

元画像	逆ガンマ補正	グレースケール変換	ガンマ補正

これで大分よくなりますが、それでも色々と食い違っています。特に左下が明るすぎます。

CIE XYZ の Y

CIE XYZ は人の眼の視覚特性を等色実験で調べて CIE(国際照明委員会)がまとめた規格で、RGB とは別の軸を持つ色空間です。
XYZ 軸の Y 軸が輝度(明るさ)で、XとZは無輝面で RGB への変換で色味に影響します。

詳しくはこちらを参考にどうぞ

XYZ色空間に迫る
- https://qiita.com/Ushio/items/203f16ad1e23fd42231c
- https://qiita.com/Ushio/items/7a5d80612796c4bcfca6

この CIE XYZ を使った方法だと、sRGB にかかっているガンマ補正を考慮した上、更に R,G,B を足す際に重み付けをする(加重平均)事で、前提知識にある問題を2つとも解決します。

(R',G',B') = 逆ガンマ補正(R,G,B)
V' = 0.2126*R' + 0.7152*G' + 0.0722*B'
V = ガンマ補正(V')

元画像	逆ガンマ補正	グレースケール変換	ガンマ補正

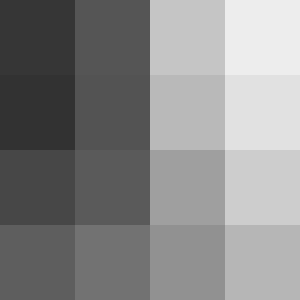人の眼の色の捉え方には個人差がありますが、おそらく多くの人はこのグレースケールに納得できるでしょう。
また、カラーマネジメントの観点でも sRGB 以外の P3 や AdobeRGB 、ProPhoto といった色域やガンマ値が異なる色空間でも XYZ への変換は ICC プロファイルで定義されているので、適切な CMM(カラーマネジメントモジュール) を使えば輝度は楽に取得できます。

デジタル放送の BT.709 も同じ加重平均ですし、sRGB (Webで流通している画像の殆どがこれ)も同じなので、これが決定版だ！ …と言いたいところですが、そうとも言い切れないので記事の最後で少し解説しておきます。

ITU-R Rec BT.601

V = 0.299*R + 0.587*G + 0.114*B

CIE XYZ と並んでメジャーな計算式を持つ BT.601 は SDTV の規格です。
ガンマ補正がかかったまま R,G,B を加重平均するので、今まで説明した通り微妙な結果になりますが、おそらく御家庭のテレビに複雑な処理をさせたくない都合でしょう。

CIE XYZ の Y のような色彩工学的に理想的な輝度ではない事から、Y を相対輝度、ビデオ業界で多用されるこの独特な輝度を **Luma(ルーマ)**と表現して区別するようです。

https://en.wikipedia.org/wiki/Luma_(video)

あと JPEG の YCbCr の Y を求める式としても有名です。

ガンマ補正をかけた場合と両方の結果を並べます。

元画像	BT.601(ガンマ補正のまま)	BT.601（ガンマ補正解除して計算）

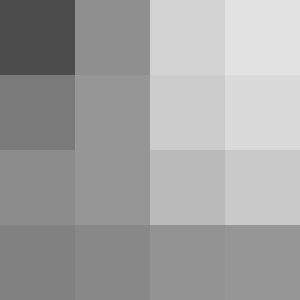ITU-R Rec BT.601
- https://www.itu.int/rec/R-REC-BT.601/en

標準テレビジョン放送(デジタル放送を除く。)に関する送信の標準方式

V = 0.30*R + 0.59G + 0.11*B

日本のアナログ放送の規格では、BT.601 より少し精度を落として定義されています。

元画像	日本のアナログ放送

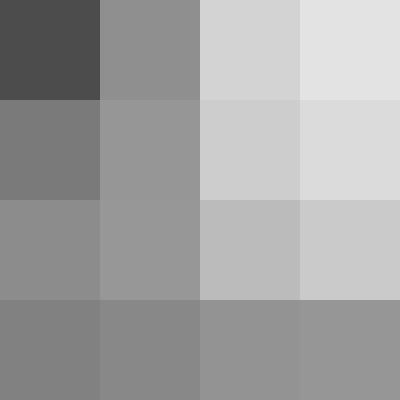標準テレビジョン放送(デジタル放送を除く。)に関する送信の標準方式
- http://www.tele.soumu.go.jp/horei/reiki_honbun/a72ab21051.html

BT.601 係数を更に粗くする

更に係数の精度を落とす処理もたまに見かけます。

V = 0.3*R + 0.6*G + 0.1*B

元画像	BT.601(ガンマ補正のまま)	粗い方

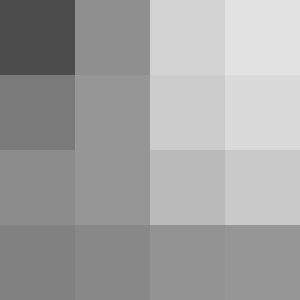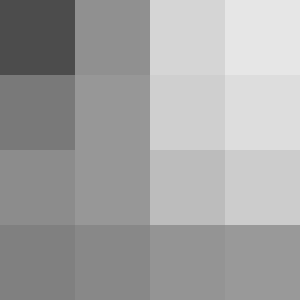精度についてはこんな感じで一見して違いが分からなかったりします。
あとこれもガンマ補正を解かず処理すると彩度の高い色ほど暗くなり、やはり良くない結果が出ます。

ITU-R Rec BT.709

V = 0.2126*R + 0.7152*G + 0.0722*B

BT.709 は HDTVの規格です。これはガンマ補正を解除すれば CIE XYZ と同じ処理です。また、sRGB も BT.709 相当です。

元画像	BT.709(ガンマ補正のまま)	BT.709(ガンマ補正を解除)

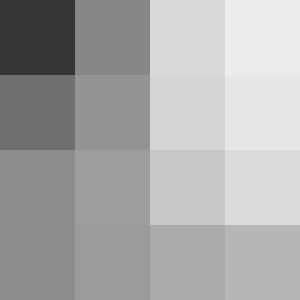ITU-R Rec BT.709
- https://www.itu.int/rec/R-REC-BT.709/en

標準テレビジョン放送等のうちデジタル放送に関する送信の標準方式

日本のデジタル放送の規格は BT.709 と同じ係数の計算式で精度も同じなので説明を省きます。

標準テレビジョン放送等のうちデジタル放送に関する送信の標準方式
- http://www.tele.soumu.go.jp/horei/reiki_honbun/72ab2104001.html

YCgCo の Y

V = R/4 + G/2 + B/4

YCgCo 色空間で使われる輝度(Y)の計算式です。
単純な計算ながらも G を強めに反映する事で、RGB平均よりは良い結果が期待できます。
ビット演算が使えるのも強みです。

V = (R>>2) + (G>>1) + (B>>2) 
  = (((R + B)>>1) + G)>>1

元画像	YCgCo

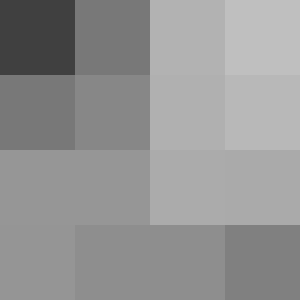YCgCo は動画圧縮の都合が優先で、人の視覚特性にあまり合っていないので、グレースケール化に使うことはあまりないですが、ビット演算で多少速度が稼げるのと計算誤差が把握しやすいメリットに対して一考の余地があります。

HSV の V (RGB の最大)

V = max(R,G,B)

R,G,B の一番明るい輝度を使います。これまで列挙した中では一番ハズレの方式かもしれません。
ただ、例えばイラスト画像等で色の使い方が独特な場合などで、都合の良い事もあります。

実例)

XYZ 変換(リニアRGBでBT709変換)の Y が理想ですが、ガンマ解くの大変なので sRGB 程度の色域だと BT601 が落とし所ですよね。尚、Max がいい感じになったのは具体的にはコレです。特殊すぎる状況ですが。
参考) https://t.co/c1fJobj5S7 pic.twitter.com/053i0ykfCm
— ＼助けよや／ (@yoya) 2017年10月19日

元画像	HSV

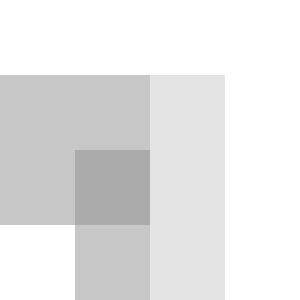HSL の L (RGB の最大と最小の中間)

V = (max(R,G,B) + min(R,G,B)) / 2

こちらも HSV 同様、特殊な状況でたまに使う事があります。

元画像	HSL

Gチャンネルonly

V = G

どうせ R,G,B のうち G の輝度が圧倒的(6割)なので、G だけで良いのでは？という方法です。

元画像	G

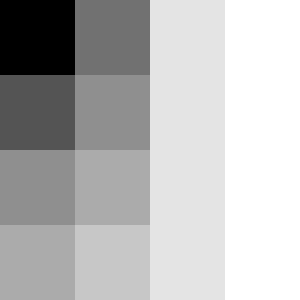The・雑という感じですが。画像によってはあまり違和感がなかったりします。
あと、人の目は暗がりだと緑に近い色がよく見えるので、夜間をイメージする画像としても良いかもしれません。(プルキンエ現象)
参考) https://qiita.com/yoya/items/96c36b069e74398796f3#comment-55b8dd0c13f313b8d708

Bチャンネルonly (特殊用途)

V = B

先ほどは G チャネルで。今度はB チャネルです。
見ての通り、一般的なグレースケール変換としては全然駄目です。

元画像	B

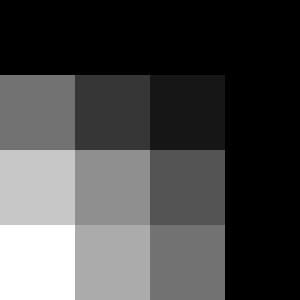ただモニタのテストといった使い道もあるようです。
YUV(YCbCr)として見た場合、人の眼は色味より輝度(Y)成分のノイズに敏感である事に注目すると、Y に対して RGB におよそ 3:6:1 〜 2:7:1 位の割合で振り分けられるので、B の値を R G に割り振りグレースケールとして使うと、ノイズが知覚的に10倍ちかく増やせる事もあり、視認が楽になります。

情報感謝！ > @toru_ver15

R, G, B の各チャネルに均一にノイズが乗っていた場合、Y成分の低いBの方がノイズ量は相対的（視覚的？）に多くなるので、BをRとGにコピーしてモノクロ画像として表示するとノイズが見やすくなる、と認識しています。
— toru (@toru_ver15) 2019年6月20日

中央値 (実験)

R,G,B の中央値を使う方法です。これはただの思いつきの実験です。実際に使う事はないでしょう。

V = [R,G,B].sort()[1] // Median

元画像	Median

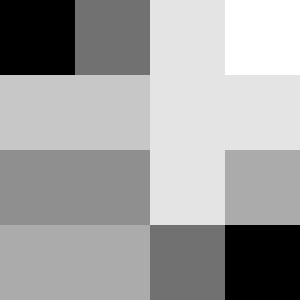駄目だこりゃ。。(;’ε‘)

マニュアル調整

グレースケール化すると色情報がなくなるので、見た目のコントラストはどうしても下がります。
それに対して、マニュアル調整で対処する事があります。

レベル補正

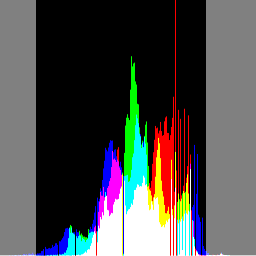
元画像	ヒストグラム	グレースケール

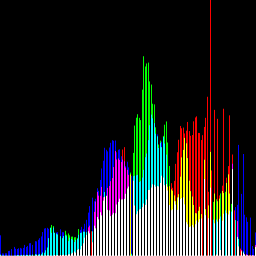
予め画像のコントラストを引き上げる事で、グレースケール画像が引き締まって見えます。

レベル補正	ヒストグラム	補正済みグレースケール

レベル補正 - コントラスト補正については以下の記事が参考になると思います

ImageMagick でコントラスト補正
- https://qiita.com/yoya/items/1da8e8e04881bab67015

カラーバランス

被写体に合わせて、R,G,B の係数を変えると見た目の良いグレースケールが得られます。
Adobe Photoshop だとチャンネルミキサーのカラーバランスで調整できます。
SB Creative の「Photoshop 10年使える逆引き手帖」初版第1刷 p195 から、実際のケースを引用します。

新緑の緑 - 緑を極端に強調します。

V = -0.1*R + 1.20*G + -0.1*B

自然の風景 - 少し緑多め

V = 0.2*R + 0.7*G + 0.1*B

ポートレート (人肌の多い画像) 赤味を強調します。青はゼロです。

V = 0.75*R + 0.25*G + 0*B

ノイズ感のある画像 - 青を強調

V = 0.3*R + 0*G + 0.7*B

要するに R,G,B のうち、特に見せたい色を強調してコントラストを上げる戦略です。

高度なグレースケール変換

Contrast Preserving Decolorization

こちらの論文で提案された、コントラストをなるべく維持する手法です。

http://www.cse.cuhk.edu.hk/~leojia/projects/color2gray/ (decolorization_iccp12.pdf)

今までの方法だと R G B を決まった係数で混ぜますが、それだと都合の悪い事があります。

元画像	BT.601 係数で足すだけ	BT.601 係数+ガンマ処理

BT.601係数処理+ガンマ処理の方が色の明るさ的には正しいのに、結果としてコントラスト(明暗の差)による境界がわかりにくく、BT.601係数で足すだけの方が画像の印象が良い。といったケースもありえます。

Contrast Preserving Decolorization の手法は、各色の正確な明るさよりも隣り合うピクセル間での輝度&色差コントラスト(Lab空間の距離)維持を優先します。

OpenCV は以下のコードで、この Decolor アルゴリズムを利用出来ます。

import cv2
_, infile, outfile = sys.argv
img = cv2.imread(infile)
img_gray, _ = cv2.decolor(img);
cv2.imwrite(outfile, img_gray)

元画像	decolor

水色で明るいグレースケールを使ってしまっているので、赤を黒とする事で、その差を際立たせています。

Salience-Preserving Color Removal

特徴が残るように色を消す手法だそうです。
色の本来の明るさをある程度犠牲にして、色による差をなるべく情報として残す点では Contrast Preserving Decolorization と同じです。

http://users.cs.northwestern.edu/~ago820/color2gray/

SIGGRAPH2005 での発表スライドから図を抜粋すると、

http://users.cs.northwestern.edu/~ago820/color2gray/Presentations/Gooch_Color2Grey.ppt

既存の方法だと、3次元の色空間を決まった軸にマッピングするに過ぎません。

(page 8) Simple Linear Mapping

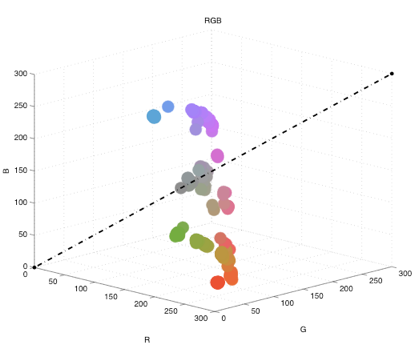PCA で軸を探してそこにマッピングすると一見良さそうですが、

(page 9) Principal Component Analysis (PCA)

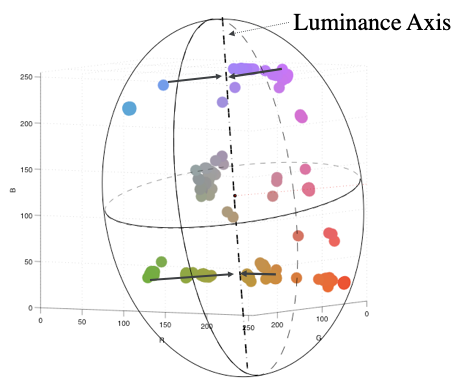同じ輝度で色相環上に配置するケースが苦手なので、

(page 10)	Problem with PCA
Worst case: Isoluminant Colorwheel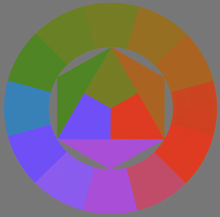

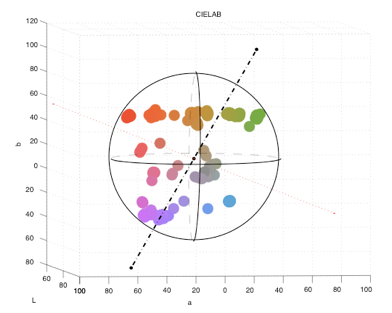(page 11) Non-linear mapping

一本の直線の軸にまとめるのこだわるのを辞めた。といった具合です。
Illuminance distance (輝度差) と Chrominance distance (色差)の両方がなるべく反映されるよう処理します。

興味のある方は論文をどうぞ。(57ページあります)

その他

ガンマ変換の注意

ポイントだけ並べます

リニア輝度は sRGB に比べて低輝度が潰れるので、8ビットのまま処理できない
- ref) https://qiita.com/yoya/items/dba7c40b31f832e9bc2a#ガンマ補正の注意点
ガンマ変換は浮動小数点の pow 関数を使うので結構重たい
sRGB ガンマを 2.2 ガンマで近似する事があるが、低輝度の値が結構違う。
- ref) https://qiita.com/yoya/items/122b93970c190068c752#sRGB のガンマ補正
そもそもガンマ変換を気にせず雑に四則演算する処理系が多い。

NTSC 係数(?)

BT.601 係数についてネットで検索すると NTSC coefficient(係数)の呼び方で、この式をよく見かけます。ただし日本語ばかりで英語の記事はほぼ見つかりません。

Y = 0.298912*R + 0.586611*G + 0.114478*B

そもそも合計が 1.000001 で輝度100% をオーバーシュートしてますね。

NTSC 係数のおそらく元ネタであろうページはこちらです。

http://www.scarse.org:80/docs/color_faq.html (web archive)

Finally, we have RGB -> CIE XYZccir601-1 (C illuminant):
    |X|   |0.606881 0.173505 0.200336|   |Red  |
    |Y| = |0.298912 0.586611 0.114478| * |Green|
    |Z|   |0.000000 0.066097 1.116157|   |Blue |

標準光源 C

ImageMagick で使っている Rec601 係数を紹介します。
海外の記事だとこちらの係数をよく見かけます。

* MagickCore/enhance.c (GrayscaleImage)
intensity=0.298839*red+0.586811*green+0.114350*blue;

こちらは標準光源 C での NTSC RGB Primary xyY の Y の値のようです。

参考までに2エントリ抜粋。

Name	Gamma	Reference White	Red Primary (x)	(y)	(Y)	Green Primary (x)	(y)	(Y)	Blue Primary (x)	(y)	(Y)	Volume (ΔE3)	Lab Gamut Efficiency %	Coding Efficiency %
NTSC RGB	2.2	C	0.6700	0.3300	0.298839	0.2100	0.7100	0.586811	0.1400	0.0800	0.114350	1,300,252	54.2	99.9
sRGB	≈2.2	D65	0.6400	0.3300	0.212656	0.3000	0.6000	0.715158	0.1500	0.0600	0.072186	832,870	35.0	100.0

http://www.brucelindbloom.com/index.html?WorkingSpaceInfo.html

恐らく NTSC の仕様から算出できる値だと思われます。

Paul Haeberli Luminance

若干怪しい方法ですが、古いプログラムで利用される事もあるので、一応取り上げます。

http://graficaobscura.com/matrix/index.html
Where rwgt is 0.3086, gwgt is 0.6094, and bwgt is 0.0820. This is the luminance vector. Notice here that we do not use the standard NTSC weights of 0.299, 0.587, and 0.114. The NTSC weights are only applicable to RGB colors in a gamma 2.2 color space. For linear RGB colors the values above are better.

NTSC の重み付けはガンマ 2.2 に合わせたもので、リニア RGB には以下の計算の方が良いと主張しています。

Y = 0.3086*R + 0.6094*G + 0.0820*B

BT.601, BT.709 の仕様書ではガンマ補正済みの R,G,B を元に Y,Cb,Cr に変換しますが、運用がそうなっていても、ガンマの非線形に合わせて係数を変えたとまでは記載されていません。(見落としてたらゴメンなさい)

https://itu.int/dms_pubrec/itu... BT.601 仕様書を読むとガンマ補正された状態で RGB=>YCbCr 変換してるように読めました。pre-corrected を補正前と誤解してて、よく考えたら事前に補正したって意味ですよね。
— ＼助けよや／ (@yoya) 2019年12月27日

そして、以下の掲示板を読むと、ちょっと怪しく見えてきます。

https://dsp.stackexchange.com/questions/27599/how-is-the-luminance-vector-calculated-for-these-linear-matrix-transforms
Those values appear to be approximations of 79, 156, and 21 all divided by 256. Paul Haeberli gave those integers already in code dated 1988 and posted in 1990 to the comp.graphics Usenet newsgroup, again without explanation or references for the numbers. Ask him? – Olli Niemitalo Dec

1990年が初出のようですが、その根拠は示されていないようです。

蛇足

GSDF (Grayscale Standard Display Function)

グレースケール化ではないので記事のスコープ外ですが、折角なのでうんちく。

レントゲン写真等、医療用途にてグレースケールは多用されますが、通常のモニタ表示ではモニタごとに表示が違う、そもそもアナログ写真と見た目が違う等で誤診を誘発しやすい問題があり、補正して特定のトーンカーブに合わせる規格があります。

詳しくはこちらを参照して下さい。

医用画像診断用モニターに求められるグレースケール表示とは

https://www.eizo.co.jp/products/tech/files/2004/wp_jp_04_001_grayscale.pdf

医⽤画像表⽰⽤モニタの精度管理

http://www.kanrigakkai.jp/img/housyasen/27-02.pdf

その特定のトーンカーブですが、物理輝度をどのように数値化するのか(輝度の量子化)はとても重要で、例えば sRGB のような単純なガンマ補正は輝度レベルによって階調の見易さがだいぶ異なるのでバンディングが起こりやすく階調特性的に不味いです。具体的には 10 と 11 を並べた場合と、100 と 101 を並べた時とで違いが片方だけ分かるというのは良くないので、DICOM のグレースケールは全輝度に渡って均等に違いが分かるように定義されます。

最後に

はじめに思いつく RGB 単純平均は悪手で、CIE XYZ が良い方法。という結論で大体合ってますが、実際にその辺のモニタで試すと BT.601 のガンマ補正解除版も良かったりするので、自分は BT.601 を使う事もあります。
幾つか心当たりがあります。

一般にRGB規格は標準光源 C 、D65 が基本だけど、一般の人のモニタは色温度を高めに設定するので、赤が暗くなりがちで BT.601 で赤の比重が高いので相殺分があるかも
XYZ といえば CIE1932 だけど被験者は17人でかつ人種の偏り(瞳の色が違うし住環境による文化の違いとか)もあるはずで、物差しとして絶対視するのは良いけど、その物差し自体が実際の利用状況に合うかは別の話。

https://twitter.com/yoya/status/694712509756878849CIE1931 は17人、CIE1964 は76人だけど、サンプルの偏差はどの位なんだろ。実験誤差もあるだろうけど個人の差の方が気になる。論文手に入らないのだろうか。
— ＼助けよや／ (@yoya) 2017年10月19日

赤を頑張れば、緑が犠牲になるといったトレードオフもあるので、結局、サンプルを作って実際に評価するのが良いでしょう。

あと、こちらに画像ファイルを放り込むと、列挙した方式を全部まとめて変換します。参考にして下さい。(注: 高度な方法は含まれません)