XYZ色空間に迫る(2)

XYZ色空間に迫る(1) からの続きになります。
いよいよ本題のXYZ色空間です。

イケてないRGB色空間

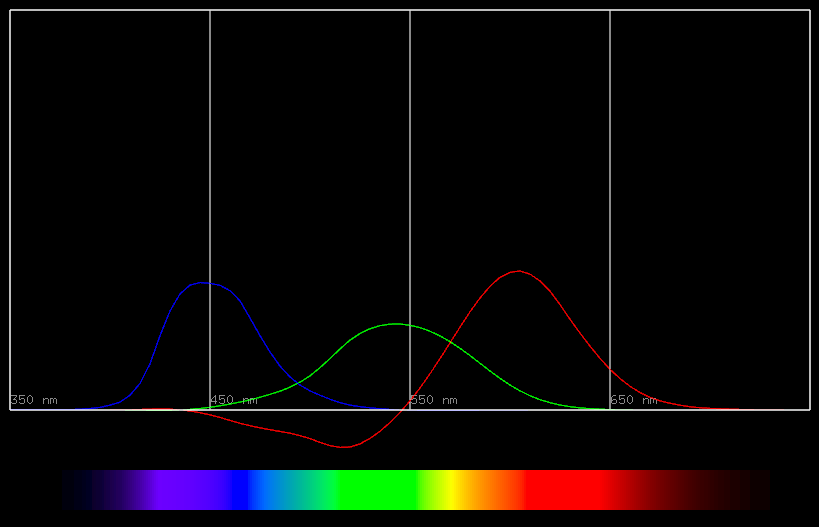
前回で1931 CIE RGB等色関数を手に入れました。そしてRGBの三値刺激は空間の座標と捉えることができ、それをCIE 1931 色空間と呼ぶのでした。

しかしながら、この空間、実は結構不便なところがあって、このままではあまり使われません。
実際にはこのデータを元にした、改良版が世界標準として使われています。

まずイケてないのは、マイナスです。特にRで顕著ですね。でも実はRだけではないのです。
実際にデータを見てみましょう。

波長	R	G	B
380	0.00003	-0.00001	0.00117
385	0.00005	-0.00002	0.00189
390	0.00010	-0.00004	0.00359
395	0.00017	-0.00007	0.00647
400	0.00030	-0.00014	0.01214
405	0.00047	-0.00022	0.01969
410	0.00084	-0.00041	0.03707
415	0.00139	-0.00070	0.06637
420	0.00211	-0.00110	0.11541
425	0.00266	-0.00143	0.18575
430	0.00218	-0.00119	0.24769
435	0.00036	-0.00021	0.29012
440	-0.0026	0.00149	0.31228
445	-0.0067	0.00379	0.31860
450	-0.0121	0.00678	0.31670
455	-0.0187	0.01046	0.31166
460	-0.0260	0.01485	0.29821
465	-0.0332	0.01977	0.27295
470	-0.0393	0.02538	0.22991
475	-0.0447	0.03183	0.18592
480	-0.0493	0.03914	0.14494
485	-0.0536	0.04713	0.10968
490	-0.0581	0.05689	0.08257
495	-0.0641	0.06948	0.06246
500	-0.0713	0.08536	0.04776
505	-0.0812	0.10593	0.03688
510	-0.0890	0.12860	0.02698
515	-0.0935	0.15262	0.01842
520	-0.0926	0.17468	0.01221
525	-0.0847	0.19113	0.00830
530	-0.0710	0.20317	0.00549
535	-0.0531	0.21083	0.00320
540	-0.0315	0.21466	0.00146
545	-0.0061	0.21487	0.00023
550	0.02279	0.21178	-0.00058
555	0.05514	0.20588	-0.00105
560	0.09060	0.19702	-0.00130
565	0.12840	0.18522	-0.00138
570	0.16768	0.17087	-0.00135
575	0.20715	0.15429	-0.00123
580	0.24562	0.13610	-0.00108
585	0.27989	0.11686	-0.00093
590	0.30928	0.09754	-0.00079
595	0.33184	0.07909	-0.00063
600	0.34429	0.06246	-0.00049
605	0.34756	0.04776	-0.00038
610	0.33971	0.03557	-0.00030
615	0.32265	0.02583	-0.00022
620	0.29708	0.01828	-0.00015
625	0.26348	0.01253	-0.00011
630	0.22677	0.00833	-0.00008
635	0.19233	0.00537	-0.00005
640	0.15968	0.00334	-0.00003
645	0.12905	0.00199	-0.00002
650	0.10167	0.00116	-0.00001
655	0.07857	0.00066	-0.00001
660	0.05932	0.00037	0.00000
665	0.04366	0.00021	0.00000
670	0.03149	0.00011	0.00000
675	0.02294	0.00006	0.00000
680	0.01687	0.00003	0.00000
685	0.01187	0.00001	0.00000
690	0.00819	0.00000	0.00000
695	0.00572	0.00000	0.00000
700	0.00410	0.00000	0.00000
705	0.00291	0.00000	0.00000
710	0.00210	0.00000	0.00000
715	0.00148	0.00000	0.00000
720	0.00105	0.00000	0.00000
725	0.00074	0.00000	0.00000
730	0.00052	0.00000	0.00000
735	0.00036	0.00000	0.00000
740	0.00025	0.00000	0.00000
745	0.00017	0.00000	0.00000
750	0.00012	0.00000	0.00000
755	0.00008	0.00000	0.00000
760	0.00006	0.00000	0.00000
765	0.00004	0.00000	0.00000
770	0.00003	0.00000	0.00000
775	0.00001	0.00000	0.00000
780	0.00000	0.00000	0.00000

そう、見た目にはあまりわかりませんでしたが、実際には至る所でマイナスが含まれています。
計算機で計算する分にはまだいいですが、当時1931年にはまだ手計算が主流で、計算尺など使っていたとのことで、マイナスの計算もなるべくしたくなかったというのも一つ大きなイケてないポイントでした。

次にイケてないポイントとしては、せっかく色が人間基準かつ定量的に扱えそうなのに、パート(1)で紹介した人間基準の明るさの単位、輝度などの測光量との対応がシンプルにいっていない点です。なんとか統一理論が欲しいと考えられました。

基底変換

これをなんとかするテクニックとして、線形代数の基底変換を使います。
というのも、先に述べてきたとおり、色は空間上の点であり、RGB色空間の座標は、

\begin{pmatrix} R \\ G \\ B \end{pmatrix}=R\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}+G\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}+B\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}

と基底ベクトルとの線形結合で表現できます。
なので、都合のよい基底ベクトルを選んでやっても、本質的に同じものを表していることになります。
例えば以下のように。

\begin{pmatrix} R \\ G \\ B \end{pmatrix}=X\begin{pmatrix} X_{ 1 } \\ X_{ 2 } \\ X_{ 3 } \end{pmatrix}+Y\begin{pmatrix} Y_{ 1 } \\ Y_{ 2 } \\ Y_{ 3 } \end{pmatrix}+Z\begin{pmatrix} Z_{ 1 } \\ Z_{ 2 } \\ Z_{ 3 } \end{pmatrix}

実際のところは、

\begin{pmatrix} R \\ G \\ B \end{pmatrix}=X\begin{pmatrix} 0.418466 \\ -0.091169 \\ 0.000921 \end{pmatrix}+Y\begin{pmatrix} -0.158661 \\ 0.252431 \\ -0.002550 \end{pmatrix}+Z\begin{pmatrix} -0.082835 \\ 0.015707 \\ 0.178599 \end{pmatrix}

という数字が来ます。
※数字には誤差が含まれていたりしますので、理想的には信頼のおけるソースか、導出することをおすすめします。この数字は、色彩工学入門 のRGB to XYZからの計算です。

これは当然行列でも表現でき、

\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 2.76883 & 1.75171\quad  & 1.13014 \\ 1.0 & 4.59061 & 0.06007 \\ 0.0 & 0.05651 & 5.59417 \end{pmatrix}\begin{pmatrix} R \\ G \\ B \end{pmatrix}\\ \begin{pmatrix} R \\ G \\ B \end{pmatrix}=\begin{pmatrix} 0.418466 & -0.158661\quad  & -0.082835 \\ -0.091169 & 0.252431 & 0.015707 \\ 0.000921 & -0.002550 & 0.178599 \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}

と相互に変換が可能です。
そして新しい基底で変換後の空間を、XYZ色空間と呼びます。

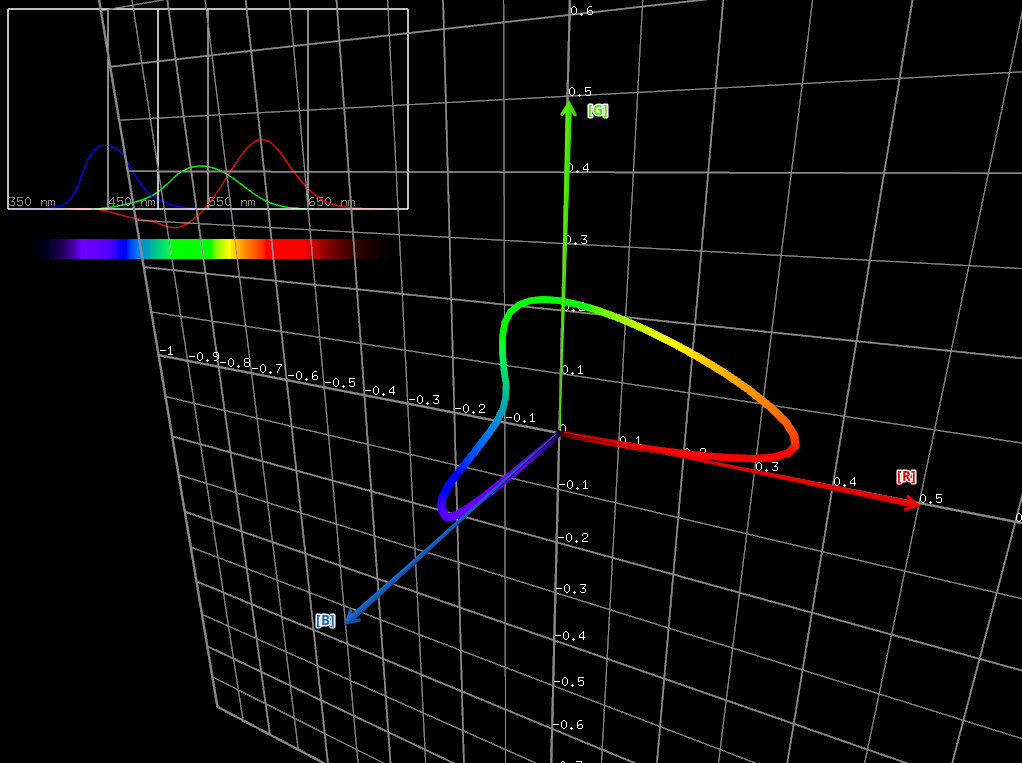
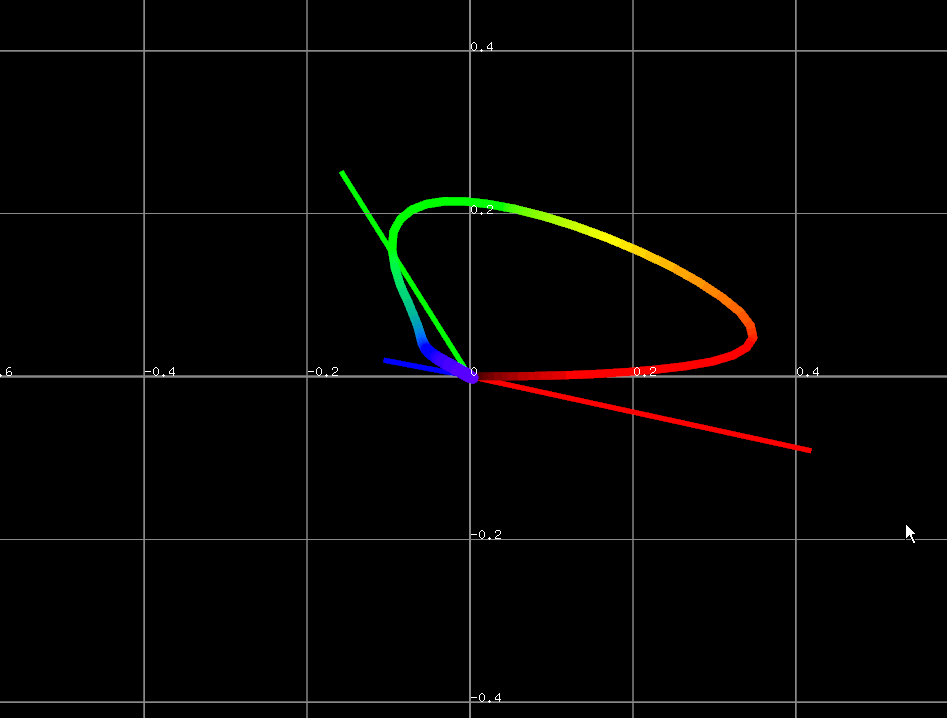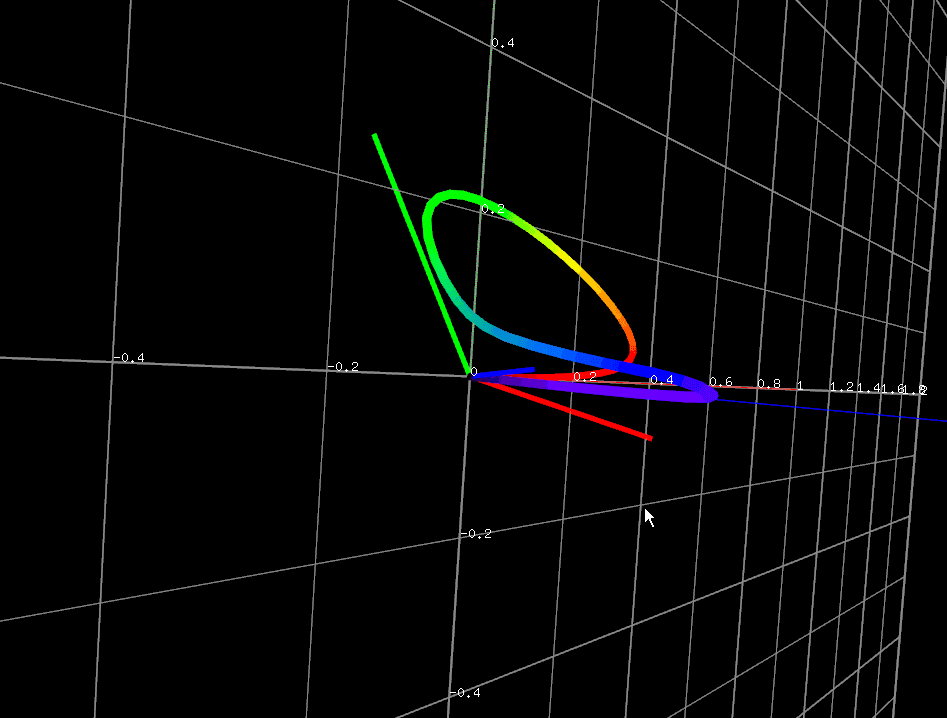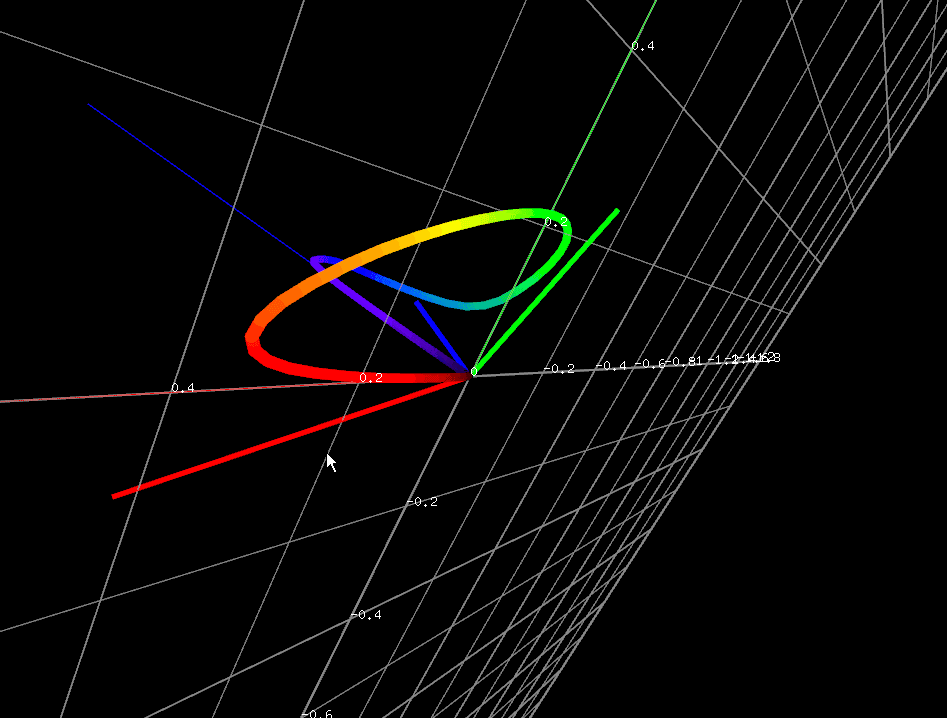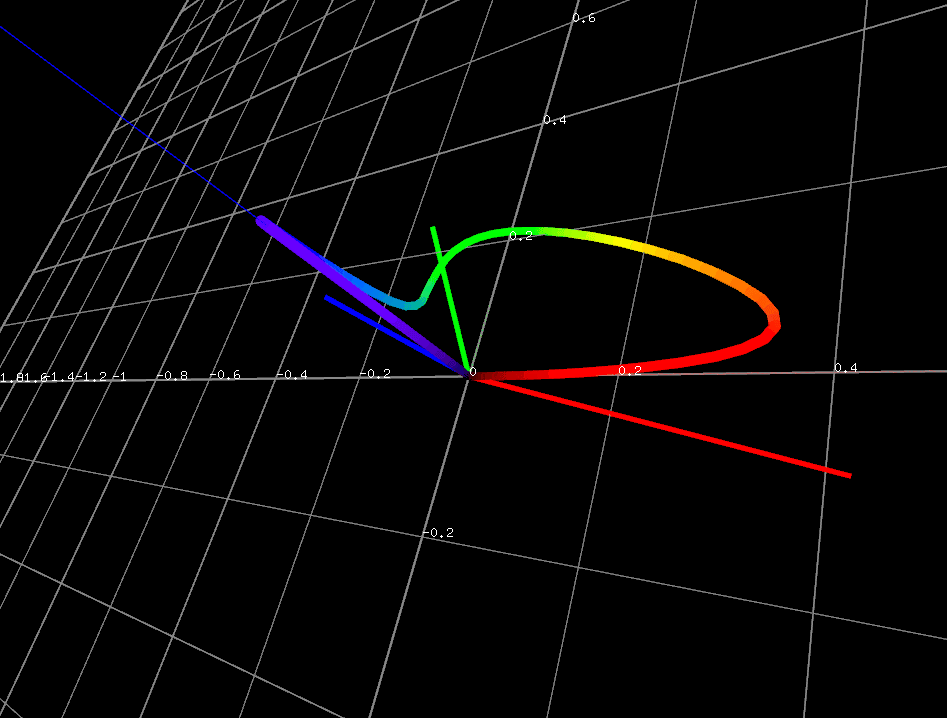
数値だけみてもややイメージがわかないため、空間的に見てみましょう。
XYZはもはやRGBではありませんが、便宜上、Xが赤、Yが緑、Zが青に着色しています。

直観的に、XYZの成分がすべて正の値を取るように基底ベクトルを選んでいることがわかります。
また、成分の数値が0.0~1.0付近にわりと集中しています。（Zだけはちょっとはみ出していますが

CIE 1931 XYZ等色関数

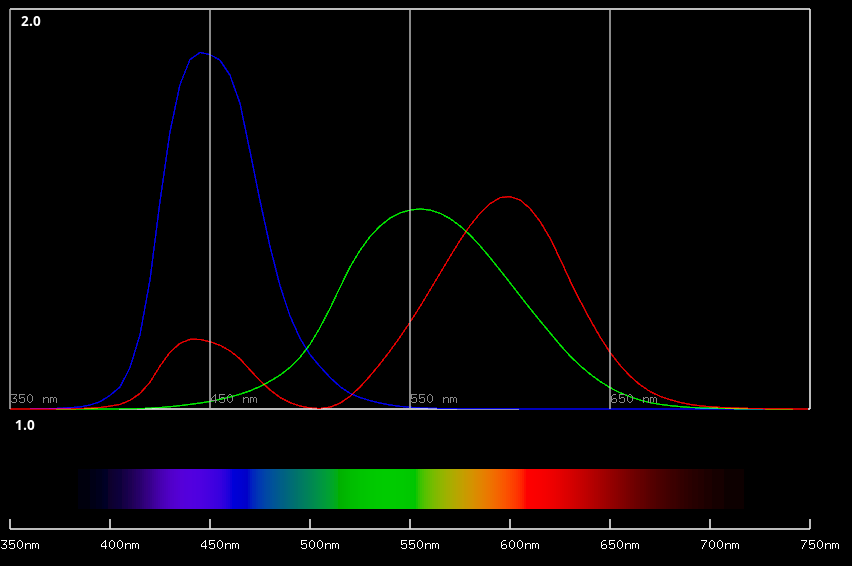
RGBからXYZ, XYZからRGBの変換方法だけはわかりました。では等色関数はどうなるかというと、RGB等色関数を、XYZ色空間で見たものを考えます。
具体的には、関数の値をまるごと変換します。

\begin{pmatrix} \overline { x } \left( \lambda  \right)  \\ \overline { y } \left( \lambda  \right)  \\ \overline { z } \left( \lambda  \right)  \end{pmatrix}=\begin{pmatrix} 2.76883 & 1.75171\quad  & 1.13014 \\ 1.0 & 4.59061 & 0.06007 \\ 0.0 & 0.05651 & 5.59417 \end{pmatrix}\begin{pmatrix} \overline { r } \left( \lambda  \right)  \\ \overline { g } \left( \lambda  \right)  \\ \overline { b } \left( \lambda  \right)  \end{pmatrix}

この $\overline { x } \left( \lambda \right), \overline { y } \left( \lambda \right) , \overline { z } \left( \lambda \right) $ をCIE 1931 XYZ等色関数と呼びます。

結果グラフとしてみると、

確かに負の部分が消えています。
実際数値としても、マイナスは存在しません。当時計算を担当している人も大喜びだったことでしょう。
数値はこちらでも確認することができます。
CIE 1931 2-deg, XYZ CMFs

ただし、ここで注意したいのは、すべての成分が正の値をとるようになったといっても、元々三値刺激で等色できなかった波長の色というのはXYZ色空間であっても引き続き等色できません。基底変換を行ったといっても本質的に表現している内容は同じというわけです。

測光量との対応

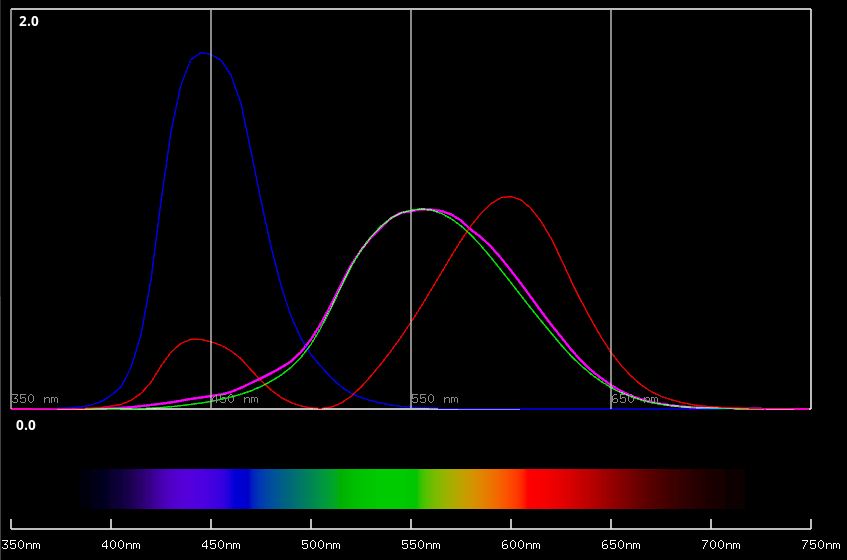
もう一つのわがまま、測光量との関係性です。とりあえず、XYZ等色関数と一緒に、分光視感効率 V(λ)をマゼンタ色で重ねてみてみます。

なんと、驚くべきことにXYZ等色関数の$ \overline { y } \left( \lambda \right) $ がほぼ一致しています。
これは例えば、パート(1)の任意の光の三値刺激 で紹介した同じ方法で、XYZ三値刺激を求めると、

\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\int _{ 0 }^{ \infty  }{ a\left( \lambda  \right) \begin{pmatrix} \overline { x } \left( \lambda  \right)  \\ \overline { y } \left( \lambda  \right)  \\ \overline { z } \left( \lambda  \right)  \end{pmatrix}d\lambda  } 

このときにYに最大視感効率(Km)をかけるだけで測光量になる ことを示しています。
これはもう当時計算を担当している人が喜んで踊りだしてもおかしくありませんね。

なぜこんなことができるのか？

なぜ $ \overline { y } \left( \lambda \right) $ は $ V\left(\lambda \right) $ と一致するんでしょうか？それはもちろんそうなるように変換を定義したので当たり前といえば当たり前なのですが、どういうアイディアなのかが気になります。

それに迫るために、まずはRGB原刺激の輝度はどういう扱いだったかというと、RGBそれぞれ比率が明らかでした。

$ l_r : l_g : l_b = 1 : 4.5907 : 0.0601 $

であるというのは、パート(1)で紹介しました。
したがって、輝度とRGBは以下のような関係があることがわかります。

$ L=R+4.5907G+0.0601B $

ところで $ Y $ が輝度になるというのは、言い換えれば、$ X, Z $ の輝度がゼロであると言い換えることもできます。そこで輝度がゼロとはどういうことかというと、数式上では、

$ 0=R+4.5907G+0.0601B $

と表現できます。これは結局平面の方程式と捉えることができます。この面を無輝面と呼びます。
イメージしにくいので、実際に見てみますと、

斜めった面がそれになります。なるほど確かに $ X, Z $ の軸がこの無輝面上にしっかり存在していることが確認できます。
じゃあY成分については？と先の変換行列を見てみますと、

\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 2.76883 & 1.75171\quad  & 1.13014 \\ 1.0 & 4.59061 & 0.06007 \\ 0.0 & 0.05651 & 5.59417 \end{pmatrix}\begin{pmatrix} R \\ G \\ B \end{pmatrix}\\ Y=1.0R+4.59061G+0.06007B

とほぼほぼ明度係数そのまんまになっています。なるほど、よくできています。

ところでYを求めるときの明度係数ですが、ある種ベクトルと捉えることもでき、空間に黄色で描画してみると、

※注意: みやすさのために、黄色ベクトルの長さを短めにしています。実際にはもっと長いです。

と図形的意味としては平面の法線を表しています。
そしてYを求める計算は内積と捉えることができます。

Y=1.0R+4.59061G+0.06007B\\ Y=\begin{pmatrix} 1.0 & 4.59061 & 0.06007 \end{pmatrix}\begin{pmatrix} R \\ G \\ B \end{pmatrix}

X, Yの軸はこのベクトルと直交しており、このことからもXY軸成分の輝度が0になることを理解できます。

以上より、XYZ色空間が大変洗練された色の表現方法であることがわかります。現在広く使われているsRGB色空間や、AdobeRGB色空間なども、このXYZ色空間の一部を切り出して使っているとも言えます。

xy色度図

パート(1)でのRGB色空間での平面的解釈でも紹介したやり方は、XYZ色空間でも有効です。
どうするかというと、やはり同様に、

\acute { X } =\frac { X }{ X+Y+Z } \\ \acute { Y } =\frac { Y }{ X+Y+Z } \\ \acute { Z } =\frac { Z }{ X+Y+Z } 

と変換して、zを潰してしまえば良いだけです。

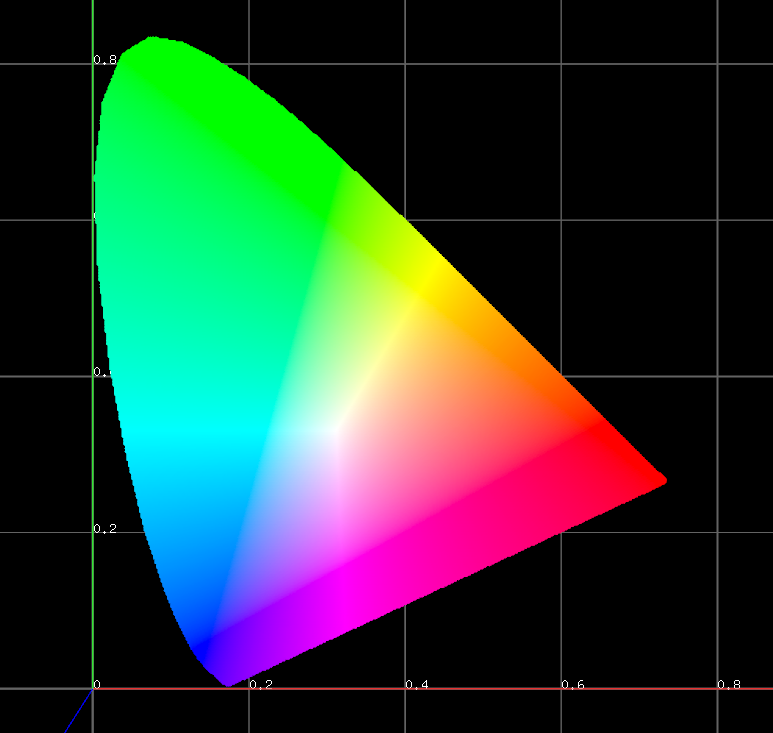
やっと見たことのある有名な色の図になりました。ちなみにこのXY色度図でも(0.333, 0.333)が白になるように、XYZ色空間への変換行列が調整されています。これまたよくできているものです。

まとめ

ひとまず目標だったXYZ色空間、およびXY色度図までたどり着くことができました。色の分野は本当に知識の幅が広く、大変ですし、まだ自分も勉強の途中ですが、一つの学習の軌跡として誰かの一部役にたつ・・・のを期待します。