目標
色は非常に私達の生活に密着していて、当たり前のように存在しているにも関わらず、いざ真面目に扱おうとするとよくわからなくなってしまうものではないでしょうか。
色の知見というのは非常に幅広く、無限に広がっていってしまう上、表色系周りの話では抽象的になりがちで難解です。そこで現状さまざまな基礎になるRGB表色系、XYZ表色系周辺の理解を目的として、寄り道をしながらもストーリー立ててまとめてみようと思います。
プログラムコードとしてはC++で記載します。(それほどでてきませんが)
色ってなんだろう?
色の正体を探してみましょう。
まず色を感じる体の部位というのはやはり目です。皮膚や耳や舌では感じられません。また、目を閉じてみると、強い明かりが周りになければ、真っ暗闇で色は見つけることはできません。
ここかやらやはり目が色にとっては重要なようです。
次に明かりを消してみます。するとまたもや色は消えていきます。明かりをつけると、色はまた戻ってきます。このことから、どうやら明るい所、すなわち光があるところに、私達は色を感じます。なにやら色は光に重要な関連があるようです。なのでまずは光について考えてみましょう。
ニュートンのプリズム分光実験
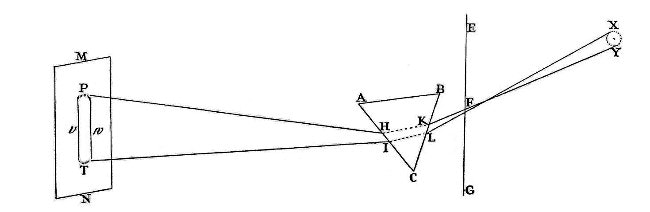
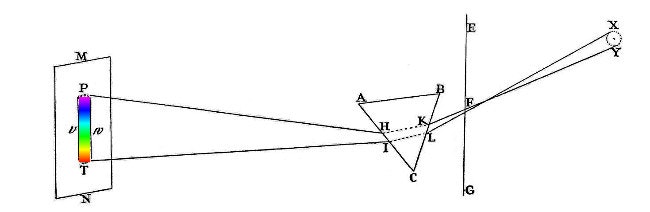
アイザック・ニュートンは、プリズム分光実験という有名な実験をしたことでも有名です。
彼の光学研究の著作「Opticks」の中で、太陽光のような白い光はあらゆる色の光が混ざったものである、と主張しました。
色によって屈折率が異なるため、プリズムによって光が分離されるというわけです。
屈折
屈折といえば、やはりスネルの法則が有名です。波動についての法則ですが、光も波動の性質を有しているため、この法則に従います。
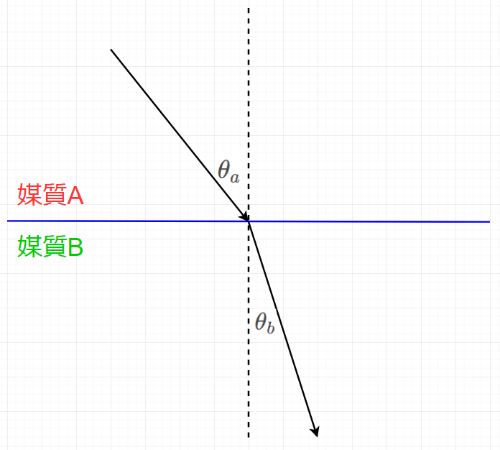
それによれば、波動が媒質Aと媒質Bの境界を通過するとき、その角度には以下のような関係があります。
\frac { \sin { \theta _{ a } } }{ \sin { \theta _{ b } } } =\frac { v_a }{ v_b }
ここで、$ v_a $ $ v_b $はそれぞれ物質の中での波の速度を示し、$ \frac { v_a }{ v_b } $ を屈折率(refraction index)とも呼びます
少し変形してやれば、
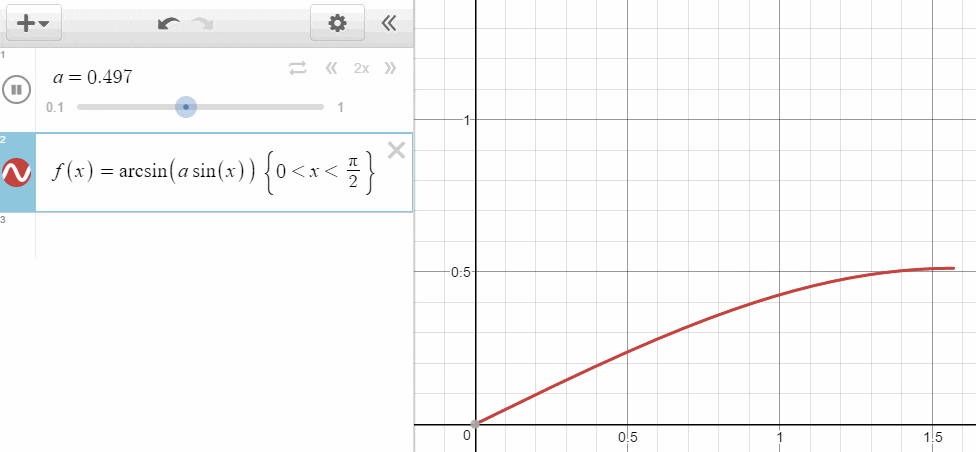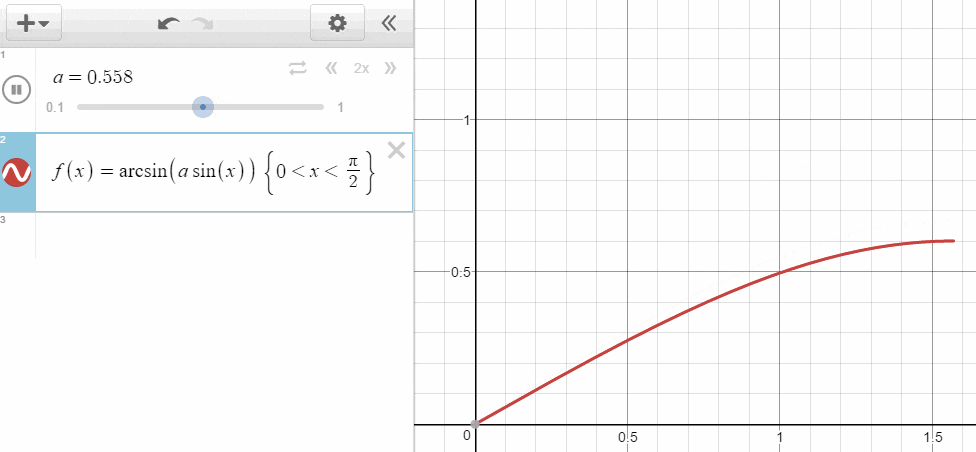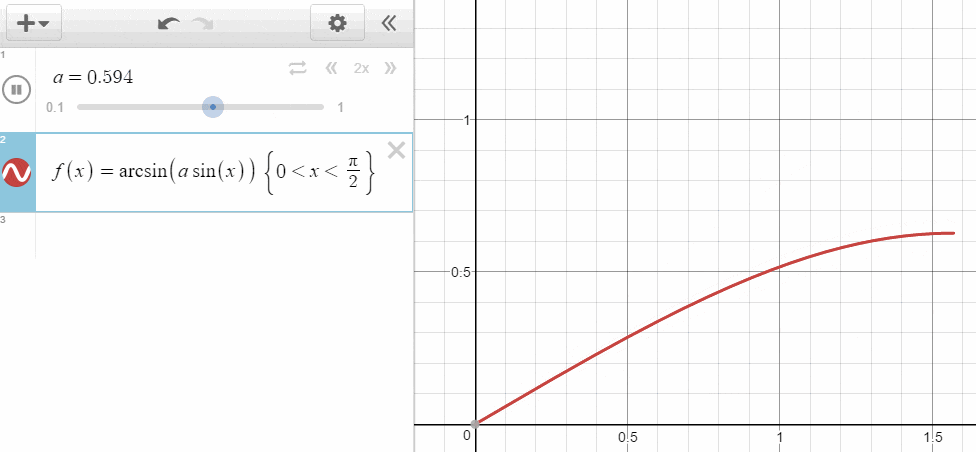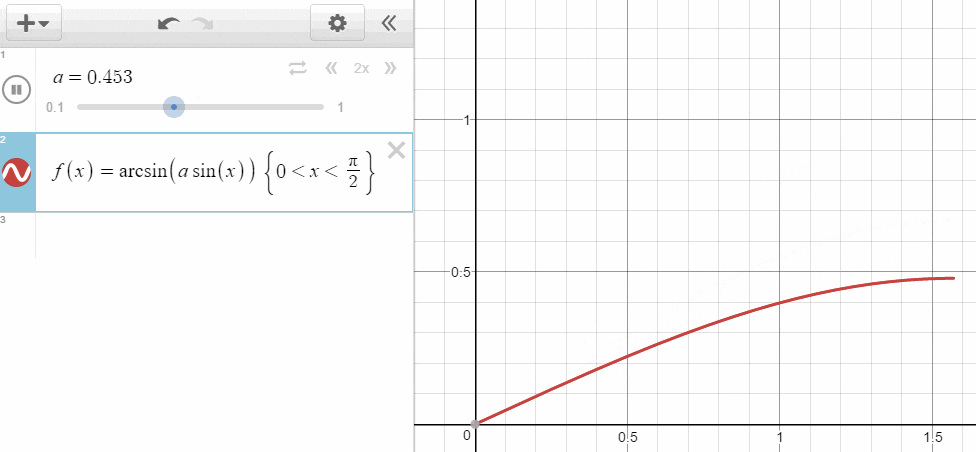
\frac { \sin { \theta _{ a } } }{ \sin { \theta _{ b } } } =\frac { v_{ a } }{ v_{ b } } \\ \sin { \theta _{ a } } =\frac { v_{ a } }{ v_{ b } } \sin { \theta _{ b } } \\ \frac { v_{ b } }{ v_{ a } } \sin { \theta _{ a } } =\sin { \theta _{ b } } \\ \theta _{ b }=\arcsin { \frac { v_{ b } }{ v_{ a } } \sin { \theta _{ a } } }
速度の比 $ \frac { v_a }{ v_b } $ が小さい、つまりより遅く進まざるを得ない物質に移動するとき、$ \theta_{ b } $ の角度は $ \theta_{ a } $ に対して小さくなるということです。そしてこの $ \frac { v_a }{ v_b } $ を相対屈折率と呼びます。
また、光が最も高速になるのは真空中であり、これを基準にした場合、つまり媒質Aが真空である場合は、$ \frac { v_a }{ v_b } $ を媒質Bの絶対屈折率と呼びます。
ちなみに、比が1である場合は、当然角度に変化はありません。
余談ですが、OpenGLに実装されているrefract関数なんかは、etaとして相対屈折率を引数に取ります。(臨界角の場合は正しく計算してくれませんが・・・)
https://www.khronos.org/registry/OpenGL-Refpages/gl4/html/refract.xhtml
プリズムの絶対屈折率
ニュートンも実験に使ったプリズムというのはどういう屈折率を持つのか、少し気になって来ました。
調べてみるとどうやら例えばBK7というのがプリズムに使われたりするようです。
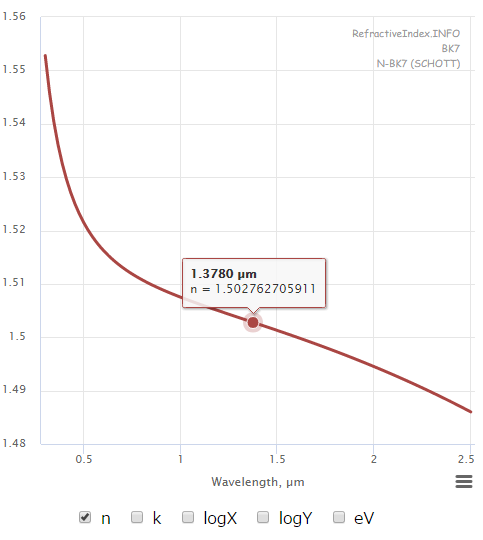
こちらのサイトでデータを見ることができます。[2]
https://refractiveindex.info/?shelf=glass&book=BK7&page=SCHOTT
※横軸: 真空中での波長, 縦軸: 絶対屈折率
おっと、横軸にWavelength、波長とあり、グラフが変化しています。
これがなぜかといえば、真空ではなく媒質の中においては、光速が振動数によって異なるためです。
※ただこれがなぜかというのは大変難しい原理のようです。
不正確ではありますが、その上で感覚的には振動数の大小によって媒質中での進行が妨げられ具合が変化するのは納得できることかと思います。
色と波長
以上をふまえると、先のプリズム分光実験で光が分断された原因は波長の違いによるものだと解釈できます。色と波長というのは切っても切れない関係性にあるわけです。
波長と色の対応はおおむね以下のようになっています。
では色は波長なんでしょうか?結論から言うとそうではありません。
ニュートンはこのことを「Opticks」の中で
"For the rays to speak properly are not coloured. In them there is nothing else than a certain power and distribution to stir up a sensation of this or that colour."
「正確にいうと、光線には色がついていない。光線の中にあるのは、この色あの色などという感覚を引き起こす、ある種の力や性質にほかならない」訳:[3]
と述べています。
これはさらにこのように続きます。
For as Sound in a Bell or musical String, or other sounding Body, is nothing but a trembling Motion, and in the Air nothing but that Motion propagated from the Object, and in the Sensorium 'tis a Sense of that Motion under the Form of Sound;
[1] [Pg 125]
「ベルや楽器の弦の音や他の音は振動の動きだけであり、空気の中では物体から動きだけが伝播し、知覚においては運動音の形態による運動を感覚として捉える」(訳:自分)
音の例はわかりやすいですね。音といっても物理的側面だけ見れば、それはただの空気などの振動です。人間の感覚器官である耳に入ったことで、それが音として感覚として脳に知覚されるわけです。
それと同様に、色も物理的側面だけ見れば、ただの粒子 or 波動です。それが人間の感覚である目に入ったことで、それが色として感覚として脳に知覚されるわけです。どうやら色は物理だけの話ではなさそうです。感覚の話が上がってきて、人間の知覚や認識あたりの話がからんできそうな気がしてきます。これは実際そうで、物理的に同じ光であっても違う色に見えたり、逆に違う光なのに同じ色に見えたりします。
色恒常性
同じ物理量なのに、違った色に感じてしまう一例として、立命館大学文学部人文学科心理学専攻 北岡 明佳 氏の見えない色、見えてしまう色 ~脳が感じる色のふしぎ~から画像を引用ですが、
下の女の子の目の色、違って見えます。しかし 全て同じ色 なのです。

にわかには信じられませんが、疑り深い方は画像エディタ等でピクセルの色を見てみてください。私は五度見くらいしました。
なんでこんなことがおこるのでしょうか? 私たちの目はポンコツだったんでしょうか?
私達をとりまく環境というのは、照明環境がとても変化しやすいです。朝・昼・夜でも違いますし、日陰や人工的な明かりによっても変化します。加えて、明かりの色がかわると当然あらゆる物体はその影響をうけます。例えばバナナに赤い光をあてると、やはりバナナは赤く見えるはずです。でもそれでは我々人間としては物体の本来の色を見分けるのには不便です。熟した果実をうっかり照明環境で未熟と勘違いスルーしちゃったらもったいないじゃないですか。そんなわけで脳の戦略としては、照明環境をキャンセルして、本来の物体の色がなんであったかを貪欲に捉えられるように 進化してきた結果なのです。
このように、照明光が変化しても、物体表面の色は変化せずに同じ色に見えることを、色恒常性 と呼びます。
先の画像では、赤・青のフィルターが、照明光だと脳が勘違いしたのですね。この例でもわかるように、正しい色を間違えたりと、色恒常性はまったく完璧ではありませんが、日常生活ではまあわりとうまく機能してくれているのではないでしょうか。
ちなみに何年か前に話題になった、「白と金」「青と黒」あのドレスの問題なんかも、この色恒常性が原因だと言われています。
このように我々は受けた光をそのまま見ているとは言い難く、光だけを分析していっても真実は見えず、受け取る側についても深い洞察や分析が必要であることがわかります。
三色説
光の波長と色との関係性を上記で考えてきましたが、光の三原色というのはやはり有名です。これによれば、3種類の原色を分量を変えて混ぜ合わせることで、多くの色を再現することができるというものです。ディスプレイや、白色LEDなどがこの性質を利用したものですね。
でも逆に言えば、特定の波長の色に似せて作った、原色を混ぜ合わせてできた"嘘の色"の区別が我々はできないということです。なんと騙されやすいことでしょう。
でも考えてみると不思議です。例えば音において短波長は高い音、長波長は低い音に対応します。が、音の三原音なんて言葉はありません。ためしに実際に高い音と低い音を混ぜて聞いてみましょう。
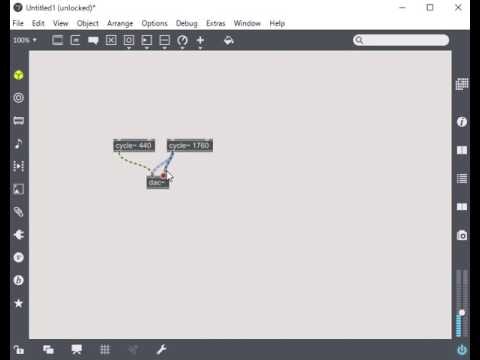
以下はMax MSPでの実験の様子です。
高い音・低い音がそれぞれ同時に鳴っているように聞こえるはずです。青の光と赤の光を同時に照らすとマゼンタに見えるのとは大違いです。どうしてちゃんと音を聞き分けられるのかといえば、それは耳の構造によるものです。
耳の中には蝸牛管(うずまき管)が存在していて、その中のコルチ器という管のような細長くうずまいた器官があります。先に行くほど細くなっており、細さにより共鳴する周波数が異なるため、複数の波長を別々の感覚として我々は感じることができるというわけです。
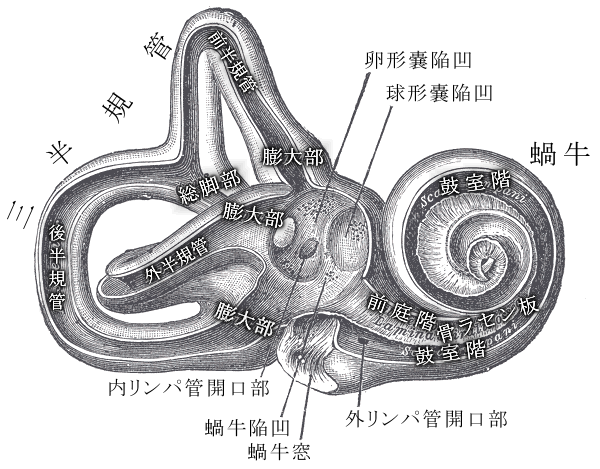
[wikipedia 蝸牛] (https://ja.wikipedia.org/wiki/%E8%9D%B8%E7%89%9B)より
もしも光にも同じことができて、波長ごとの成分を分離できるんだとしたら、色が混ざって違う色に見えることをうまく説明できません。そこで網膜には赤色専用センサー、青色専用センサー、緑色専用センサーの3種類だけ存在していて、その刺激のバランスが色ではないか?というアイディアが発展しました。それがヤング=ヘルムホルツの三色説です。
また、当時は細胞の感度というのはなかなか定量的に評価できませんでしたが、後に心理物理学的手法によりSmith & Pokorny らが錐体の波長ごとの感度(分光感度)を求めました。それをプロットしてみると、以下のようになります。
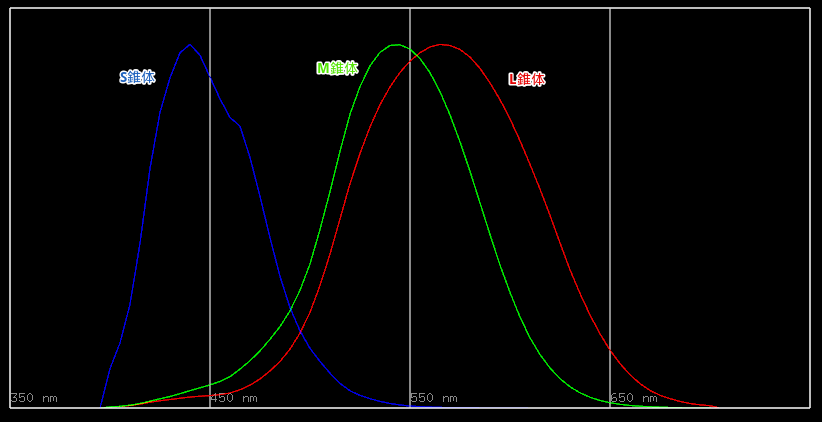
Smith & Pokorny normal trichromats colour matching functions are provided
at 5 nm steps. データは http://colour-science.org/ より。波長域を見るために、山の高さは意図的に揃えられてます。
S,M,Lというのは、それぞれ波長との対応から、S錐体, M錐体, L錐体と呼ばれます。(Short, Middle, Long )
それぞれの錐体細胞が担当するカバーする範囲を確認することができます。
我々はこの3種類の細胞によって、幅広い波長を結構大雑把に色として感じているということです。逆にこのセンサー3種をうまく刺激してやれば、目をうまく騙して特定の波長が見えているかのように我々を錯覚させることができるということですね。
反対色説
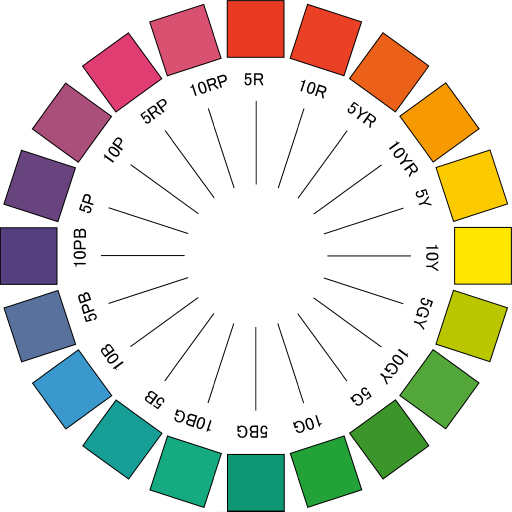
ところで色には補色という考え方があります。反対色とも呼ばれますが、反発しているような印象を受けける色の組み合わせが存在します。例えば下記の図の特に赤-緑・黄-青で顕著ですね。
この考え方はヘーリングの反対色説を元にしています。
これによれば、赤-緑, 黄-青の反応というのは、それぞれお互いに排除する関係にあり、そのバランスが色であるというのです。これはこれでなかなか感覚にマッチしているのではないでしょうか?
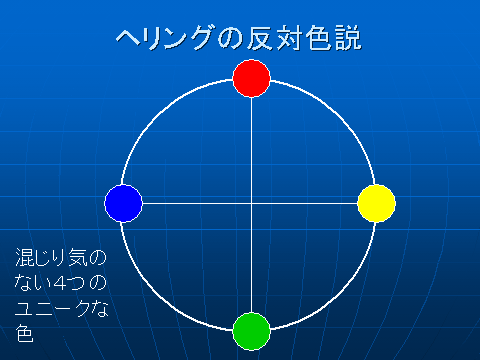
感覚の生理と心理 [6] より
しかしながら、先の三色説とは別の角度の考察であり、対立しているともいえます。
シュレーディンガーの指摘
三色説も反対色説も、それぞれの主張はもっともです。どうにかこの2つの統一したいものです。
そこで理論物理学者シュレーディンガー -量子力学で有名ですが- は、三原色を反対色に一次変換できると指摘しました。
それによれば、3色の刺激をそれぞれ $ r g b $、赤-緑 感覚を $ x_{ 1 } $ 黄-青 感覚を $ x_{ 2 } $ とすると、
x_{ 1 }=A\left( b-g \right) \\ x_{ 2 }=B\left( g-r \right)
※ A, Bは定数
で表現できるというのです。え?本当に???というのもあるので、ちょっと実際にやってみます。先程のSmith & Pokornyの分光感度のデータで試してみます。
コードはシンプルです。
auto lms = SmithPokorny(_lambdaNM);
double B_Y = _a * (lms.b - lms.g);
double G_R = _b * (lms.g - lms.r);
A=-0.7\\ B=-1.6
おお、確かに上の変換式によってある程度、赤-緑, 黄-青 感覚に変換することができました。
※この変換モデル線形変換だけではなく、いくつか研究されているそうです。
実はこの考察は、とてもよく現象を表したモデルであることが明らかになります。ここで細胞の構造を見てみましょう。
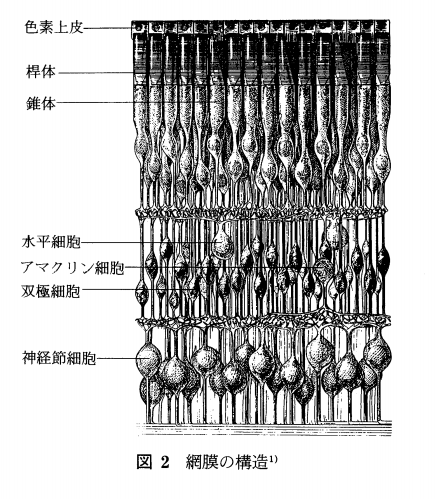
[7] カラー画像工学の基礎と応用 (第1回) 視覚と色 矢口 博久より
なにやら種類の違う細胞が層をなしています。
ちなみにこの図では光は下から来ます。
光があたるとまず錐体、および桿体(暗いところで働く光のセンサーであり、色は感じられない)でまず三原色ベースの光や強さを検知します。次に双極細胞につながっています。実験※1によれば、この細胞が反対色の反応を示すそうです。どうやら神経のつながりにより、一次変換などの変換が行われているようです。アマクリン細胞や水平細胞は横との通信用です。最後に神経節細胞細胞を通過し、神経は束ねられ盲点を経由して脳へ向かいます。盲点は神経の束が邪魔でそこだけ部分的に視覚情報が得られない場所として有名です。
このように網膜細胞は段階的な構造を持っており、三色説・反対色説はその段階の違いにすぎなかったということです。
これを段階説と呼びます。
※1
名古屋大学 御手洗玄洋らによる鯉の網膜単一細胞内電位を記録する研究、および実験
輝度
ここまでで、人間の感じる光というのは物理的な量と乖離があることがわかってきました。特に波長によって明るさは違ってみるというのは有名です。
光の明るさを表せる物理的な量としては、放射輝度 や放射照度などがあります。これらを放射量と呼びます。が、それが人間にとって直観的に明るさを表現しているかというと微妙です。例えば、可視光線の範囲であれば、ある程度はそうですが、赤外線や紫外線といった可視域の外にある光が大きな放射輝度を持っていたとしても、人間には見えないでしょう。
そんなわけで人間基準の単位があってもいいはずです。ようは人間にとってどのくらい明るく見えるか単位です。それがあれば、例えば部屋の明るさや、ライトの明るさをより直観的かつ定量的に扱うことができそうです。このような人間基準の量を、測光量と呼び、定義もきちんとあります。
測光量で大事なのは、特定の波長の光がどのくらい明るく見えるか?という点です。というのも可視域の外ではやはり明るさはゼロだし、緑は明るく見えるし、青や赤はそれよりも暗く見えます。
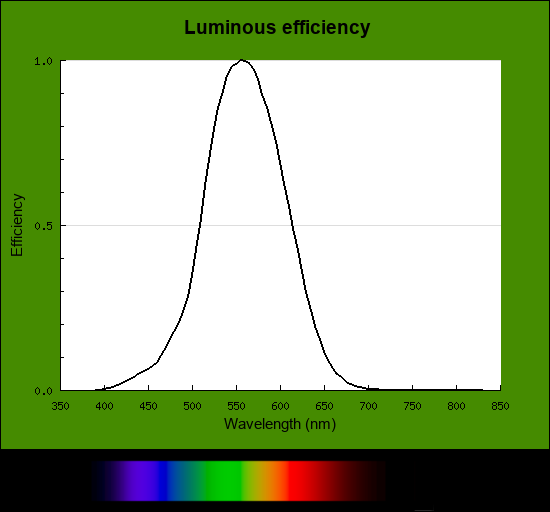
実際のところ波長ごとにどれだけ明るく見えるかは一般に、分光視感効率 V(λ) と波長の関数で表現されます。
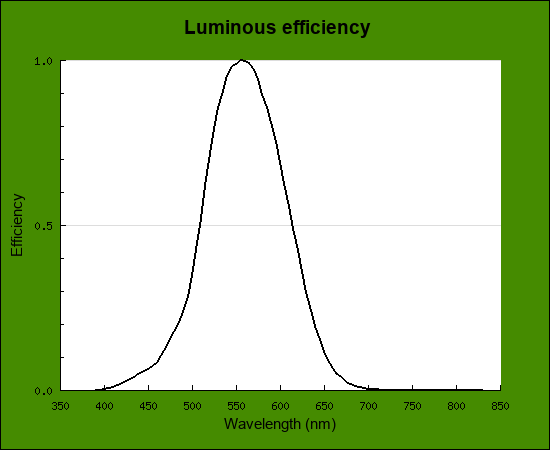
http://www.cvrl.org/lumindex.htm よりEnergy (linear), 5nm step.
なんとなく直感的にも納得できる形な気もします。
さて、この関数を使えば放射量と、"人間基準"の明るさである測光量の対応付けが定義できそうです。先のニュートンのプリズム分光実験でもわかるように、現実の光は複数の波長が混在しています。なので、細かく波長ごとに分光視感効率 V(λ)を掛けて足してあげればいいわけです。掛けて足すわけなので一般に積分を使ってこの対応は定義されます。
\Phi _{ v }=K_{ m }\int _{ 380 }^{ 780 }{ \Phi _{ e }\left( \lambda \right) V\left( \lambda \right) d\lambda }
ここで、 $ \Phi_{ e }\left( \lambda \right) $ は波長あたりの放射量、$ \Phi_{ v } $ が測光量です。
$ K_m $ については、最大視感効率と呼ばれる定数であり、 $ K_m=683 $[lm/W] となっています。
測光量: 光束(luminous flux) は放射量: 放射束(radiant flux)に対応する量です。W(ワット)からlm(ルーメン)に変換する量でもあるため、単位は[lm/W] となっています。
それぞれ放射量-測光量は以下のように対応して存在しています。
| 放射量 | 測光量 |
|---|---|
| 放射束(radiant flux) | 光束(luminous flux) |
| 放射照度(irradiance) | 照度(illuminance) |
| 放射発散度(radiant exitance) | 光束発散度(luminous exitance) |
| 放射輝度(radiance) | 輝度(luminance) |
それぞれすべて上の式で放射量 -> 測光量への変換が可能です。
世間にあふれる光に関する製品、例えばプロジェクターやら照明器具やらで、ルーメン(lm)-光束 やルクス(lx)-照度といった単位で製品のスペックを説明しているのにはこのような背景があるためなのですね。
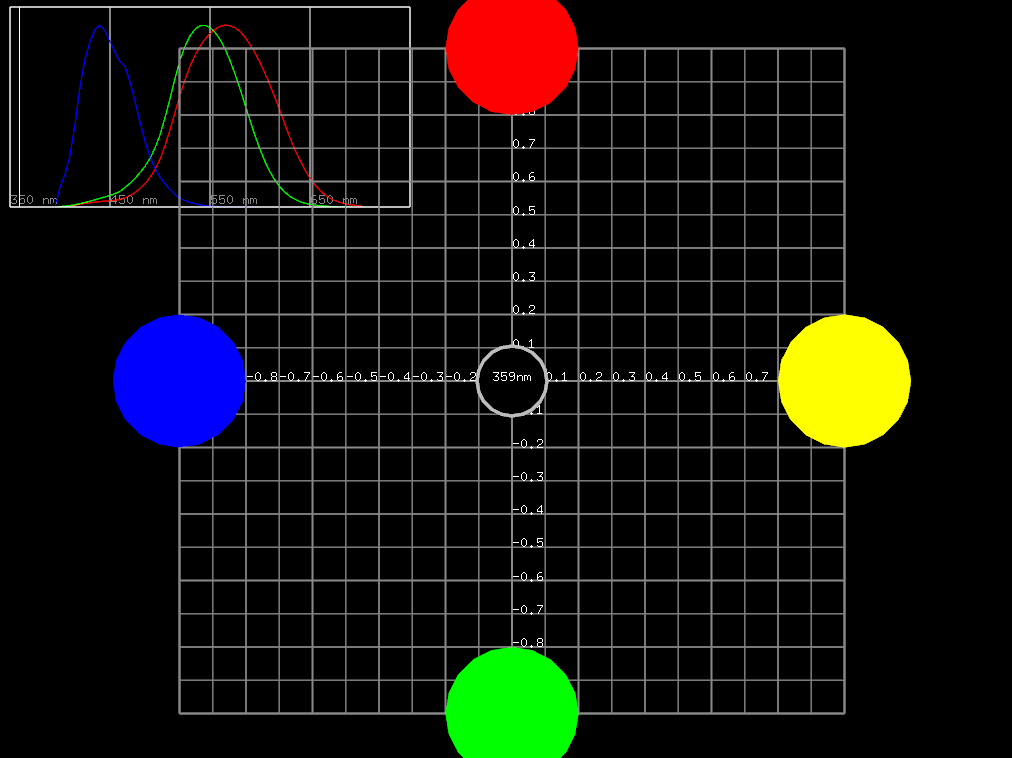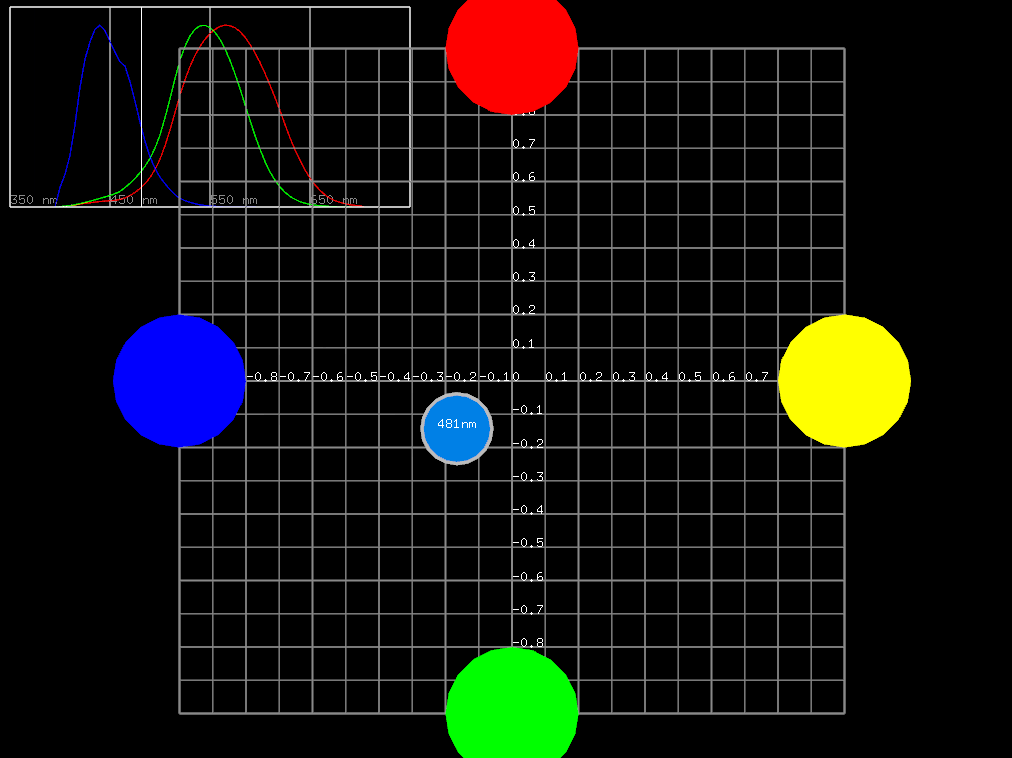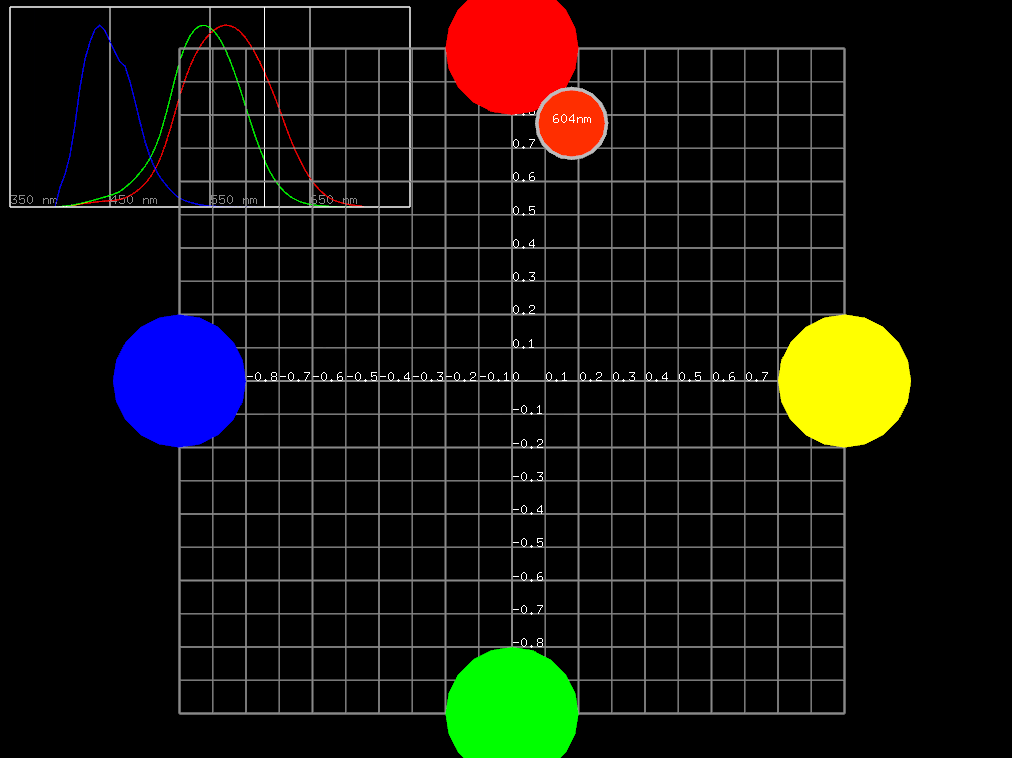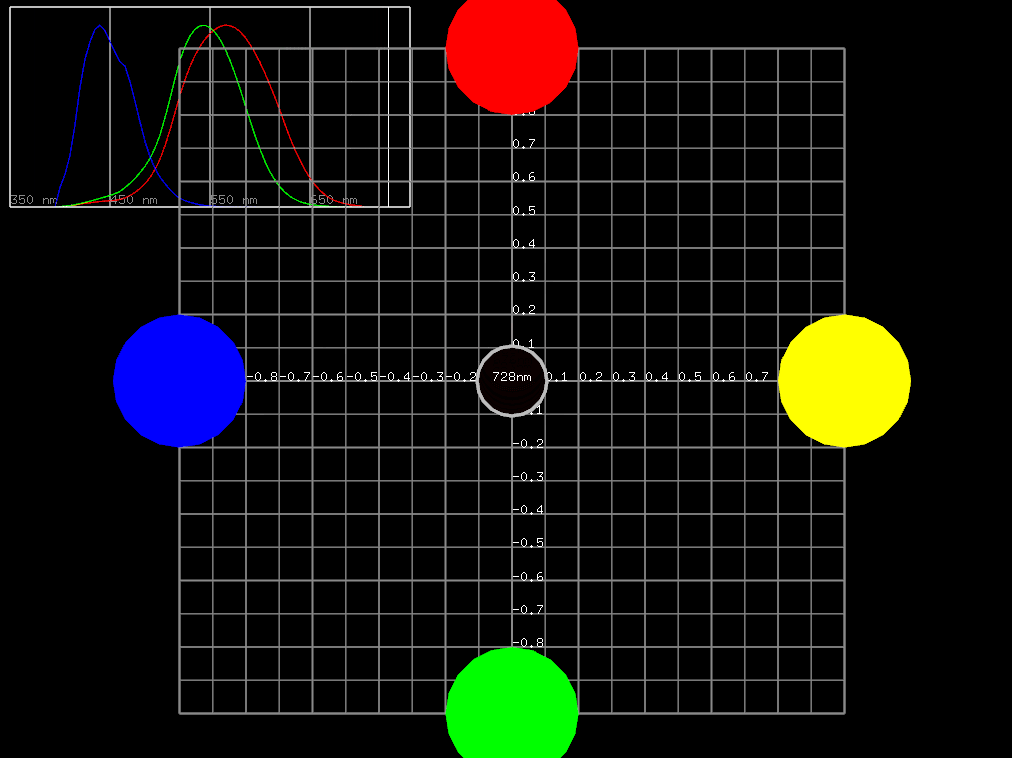
等色実験
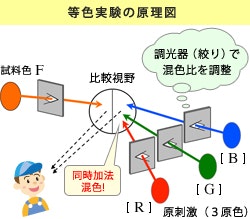
少し話がそれてしまいましたが、三原色それぞれの色の強さを調整し、LMS錐体細胞を自由に興奮させることができ、それによってさまざまな色を再現できるのはわかってきました。そこで実際に特定のスペクトルによる色と、赤・緑・青の光源を用意してきて、同じ色になるには赤・緑・青の光源の強さをどういう調整にすればいいかを調べたくなってきます。同じ色に見える、を等色するといい、このような実験を等色実験と呼びます。
現在ではWright と Guild’s の等色実験によって得られたデータが1931年にCIEで承認され、色について多くの事柄が標準化され、広く使われるようになっています。
シーエスエス株式会社 色の客観的な表現と伝達 (その4)より
同じ波長群をもつ光は、やはり同じ色に見え、これを完全等色(isomeric color match)と呼びます。
これは当たり前ですが、対して、違う波長群でも同じ色に見えることを条件等色(metameric color match)と完全等色と区別して呼びます。この等色実験というのは、条件等色を調べる実験であるということです。
特定のスペクトルによる光を $ \left[ C \right] $ と表し、特定の赤・緑・青を光源-それぞれ原刺激ともいいますがこれらを $ \left[ R \right], \left[ G \right], \left[ B \right] $ と表すことにします。
そして、$ \left[ C \right] $ の輝度を $ L_c $, $ \left[ R \right], \left[ G \right], \left[ B \right] $ の輝度を $ L_a, L_g, L_b $ とします。
このとき、$ L_a, L_g, L_b $ を調整して、特定のスペクトル光源と、特定の赤・緑・青を調整して混ぜた光源が同じ色に見えることを以下のように数式表現します。同じ色に見えるだけなのか、物理的に同じ量なのかを明確に区別して扱うということです。
(L_{ c })_{ \left[ C \right] }\equiv (L_{ r })_{ \left[ R \right] }+(L_{ g })_{ \left[ G \right] }+(L_{ b })_{ \left[ B \right] }
※$ \equiv $を等色記号として、同じ色に見える、条件等色と解釈します。通常の$ = $と区別します。
先の三色説によれば、上の式ですべての色が表現できそうです。
実験にあたって、$ \left[ R \right], \left[ G \right], \left[ B \right] $ の波長が気になります。CIEの定義では1931年の等色実験において、700 nm (赤)、546.1 nm (緑) および 435.8 nm (青)と規定されていますが、最初の実験当時、なかなか自由に特定の波長を手に入れるのが難しいという事情もあったそうで実際には、650 nm(赤)、530 nm (緑)、460nm (青) で実験が行われ、後にデータ処理として、700 nm, 546.1 nm, 435.8 nm に変換されました。
だいぶ700nmは見えるギリギリだったりしますが、刺激をなるべく分離すること、それによって手計算がメインだった当時は労力の短縮のメリットなどがあったことに起因するらしいです。
ところで、$ L_{ a }=L_{ g }=L_{ b } $ なら白なんでしょうか?
結論から言うとそうではなく、白になるように輝度を調整したものを $ l_r, l_g, l_b $ とするとその比率は、
$ l_r : l_g : l_b = 1 : 4.5907 : 0.0601 $
となることがわかっています。これを明度係数といいます。とすると、白を基準に $ \left[ R \right], \left[ G \right], \left[ B \right] $ の強さを定義したほうがシンプルになりそうです。そこで、
R= \frac {L_r}{l_r} \\
G= \frac {L_g}{l_g} \\
B= \frac {L_b}{l_b} \\
C_{ \left[ C \right] }\equiv \left( \frac { L_{ r } }{ l_{ r } } \right) _{ \left[ R \right] }+\left( \frac { L_{ g } }{ l_{ g } } \right) _{ \left[ G \right] }+\left( \frac { L_{ b } }{ l_{ b } } \right) _{ \left[ B \right] } \\
C_{ \left[ C \right] }\equiv R_{ \left[ R \right] }+G_{ \left[ G \right] }+B_{ \left[ B \right] }
と定義します。
このように定めると、$ R, G, B$ は白のときからの比率となり、単位も失われます。
さらに $ R, G, B $が比率になったことで、白と等色するときの $ R, G, B $ は、$ R = G = B $となり、非常に扱いやすくなりました!
大体なに、そろそろ実験した結果どうなったのか気になって来ました。
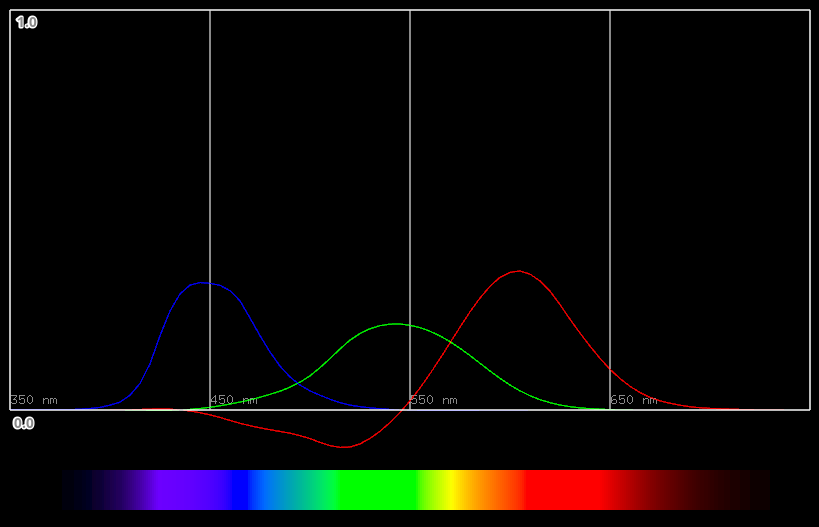
Wright & Guild 1931 2 Degree RGB 等色関数(CMF, color maching function)
早速見てみましょう。
Smith & Pokorny の錐体の分光感度によく似ていますが、大きな違いとしては、
- R-Gが少し離れている
- 赤が大きくマイナスになっている
といったところでしょうか。
1つ目については、細胞の感度と実際の色の感じ方の差でしょう。で2つ目はなんでしょうか?
例えば500nmのときの数値はそれぞれ、
| 刺激 | 数値 |
|---|---|
| R | -0.0926 |
| G | 0.17468 |
| B | 0.01221 |
となっています。式にすると、
C_{ \left[ C_{ 500nm } \right] }\equiv -0.0926_{ \left[ R \right] }+0.17468_{ \left[ G \right] }+0.01221_{ \left[ B \right] }
ということのようです。
どういうことかというと、
これだけ3種の原刺激でさまざまな色を再現できる、と述べておきながら恐縮なのですが、結論から言うと作り出せない色があったからです。
いくら $ R, G, B $を調整しても等色しなかったということです。
そこであきらめがつかないので、マイナスを許容することにしました。
先の式を移項しまして、
C_{ \left[ C_{ 500nm } \right] }+0.0926_{ \left[ R \right] }\equiv 0.17468_{ \left[ G \right] }+0.01221_{ \left[ B \right] }
これならわかります。つまり調べる任意の波長の光源のほうに、色を足しておく形です。
これでひとまずは辻褄があい、波長と$ R, G, B $の関係性が明らかになりました。
例えば、580nmの光なら、
| 刺激 | 数値 |
|---|---|
| R | 0.24562 |
| G | 0.13610 |
| B | -0.00108 |
C_{ \left[ C_{ 580nm } \right] }\equiv 0.24562_{ \left[ R \right] }+0.13610_{ \left[ G \right] }-0.00108_{ \left[ B \right] }\\ \begin{pmatrix} \frac { L_{ r } }{ l_{ r } } \\ \frac { L_{ r } }{ l_{ r } } \\ \frac { L_{ b } }{ l_{ b } } \end{pmatrix}=\begin{pmatrix} 0.24562 \\ 0.13610 \\ -0.00108 \end{pmatrix}\\ l_{ r }:l_{ g }:l_{ b }=1:4.5907:0.0601\\ \begin{pmatrix} L_{ r } \\ L_{ g } \\ L_{ b } \end{pmatrix}=\begin{pmatrix} 0.24562\times 1 \\ 0.13610\times 4.5907 \\ -0.00108\times 4.5907 \end{pmatrix}\\ =\begin{pmatrix} 0.24562 \\ 0.62479 \\ -0.00496 \end{pmatrix}
このようにどういう輝度で混色すれば等色できるかがわかるようになりました。
任意の光の三値刺激
上記の等色関数は、特定の波長の光はどういう比率で3種の原刺激をブレンドすれば等色できるのか?を表しています。しかし現実世界にあふれる光は、各波長が入り交じる形が普通です。特定の波長の光ではなく、波長が入り混じった光と等色するにはどうしたら良いでしょう?
心配は無用です。それぞれの波長を分離して刺激を計算すればいいのです。
例えば、ある光 $ [C] $ が、特定波長あたりの放射量 $ a\left( \lambda \right) $ を持っていた場合、波長ごとに分離を考えます。
C_{ \left[ C \right] }=...+\left\{ a\left( \lambda _{ 400nm } \right) \Delta \lambda \right\} _{ \left[ C_{ 400nm } \right] }+\left\{ a\left( \lambda _{ 401nm } \right) \Delta \lambda \right\} _{ \left[ C_{ 401nm } \right] }+\left\{ a\left( \lambda _{ 402nm } \right) \Delta \lambda \right\} _{ \left[ C_{ 402nm } \right] }+...\\ C_{ \left[ C \right] }=\sum _{ \lambda =0 }^{ \infty }{ \left\{ a\left( \lambda \right) \Delta \lambda \right\} _{ \left[ C_{ \lambda } \right] } }
すると、例えば400nmの光や、500nmなどの特定波長の光の三値刺激の割合は先程の等色関数により既知であることに気づきます。それぞれ個別に分量をはじき出して、合算してもうまくいくはずです。
R, G, Bの等色関数をそれぞれ $ \overline{r}\left( \lambda \right), \overline{g}\left( \lambda \right), \overline{b}\left( \lambda \right) $ とすると、
\begin{pmatrix} R \\ G \\ B \end{pmatrix}=\sum _{ \lambda =0 }^{ \infty }{ a\left( \lambda \right) \Delta \lambda \begin{pmatrix} \overline { r } \left( \lambda \right) \\ \overline { g } \left( \lambda \right) \\ \overline { b } \left( \lambda \right) \end{pmatrix} } =\int _{ 0 }^{ \infty }{ a\left( \lambda \right) \begin{pmatrix} \overline { r } \left( \lambda \right) \\ \overline { g } \left( \lambda \right) \\ \overline { b } \left( \lambda \right) \end{pmatrix}d\lambda }
といった計算によってどんな色の光でも等色関数によって三値刺激を定量的に求めることができるのです。等色関数がいかに強力なアイディアかを感じますね。
すべての波長が一定の放射量を保つ場合
すべての波長が一定の放射量を保つ場合を考えてみます。これは先の例でいうところの、特定波長あたりの放射量 $ a\left( \lambda \right) =1 $ みたいな定数のケースに該当します。すると、
\begin{pmatrix} R \\ G \\ B \end{pmatrix}=\int _{ 0 }^{ \infty }{ a\left( \lambda \right) \begin{pmatrix} \overline { r } \left( \lambda \right) \\ \overline { g } \left( \lambda \right) \\ \overline { b } \left( \lambda \right) \end{pmatrix}d\lambda } =\int _{ 0 }^{ \infty }{ \begin{pmatrix} \overline { r } \left( \lambda \right) \\ \overline { g } \left( \lambda \right) \\ \overline { b } \left( \lambda \right) \end{pmatrix}d\lambda }
単に等色関数の積分になります。これを実際に計算してみます。
glm::dvec3 area;
for (int i = 380; i <= 780; i +=5 ) {
area += cmf_rgb_1931(i) * 5.0;
}
※積分範囲が380~780になってしまっていますが、これは等色関数のデータがこの範囲だったためです。
結果は、
\begin{pmatrix} R \\ G \\ B \end{pmatrix}=\begin{pmatrix} 18.917849999999994 \\ 18.910100000000003 \\ 18.909999999999986 \end{pmatrix}
となりました。ほぼ $ R=G=B $になっています。つまりこれは結局白に見えるということですね。
色空間
さて、得られた等色関数の値ですが、先の式を見直してみます。
C_{ \left[ C \right] }\equiv R_{ \left[ R \right] }+G_{ \left[ G \right] }+B_{ \left[ B \right] }
よくよく見ると、なにやらこの $ R, G, B $ 、空間のベクトルに見えてきます。3次元のベクトルとして色を捉えることができそうです。
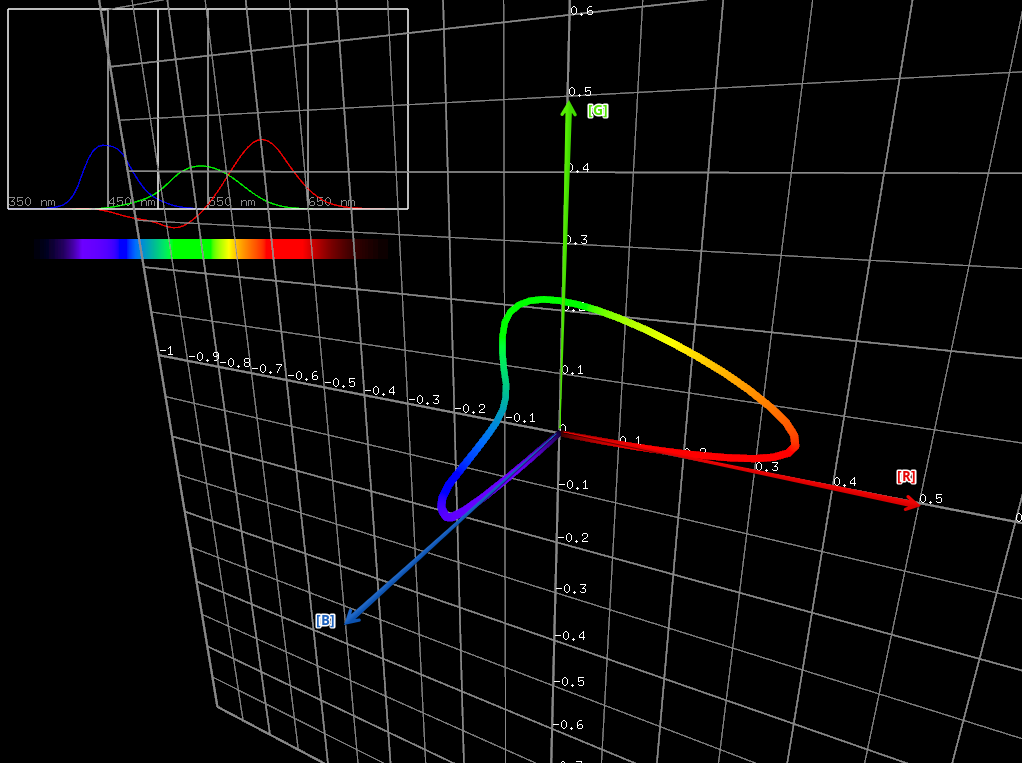
せっかくですので、先の等色実験によって得られた単スペクトルの光はどういう軌跡を描くのかを見てみましょう。
確かに空間の点-ベクトルが色を表していることがわかります。それぞれの軸が原刺激と対応していることをイメージできます。
また、この空間を等色実験と結びつけ、CIE 1931 色空間と呼びます。
平面的解釈
しかしながら、空間的に広がっているのでイメージしずらいことや、色にフォーカスして見たい場合には、3次元的な表現はやや向いていいないと言えます。
そこで、$ R + G + B = 1 $ という制限を加えてあげることでイメージをつかみやすくする工夫がよくなされます。$ R + G + B = 1 $ というのは実際の所平面の方程式で、色と一緒にプロットしてみると、
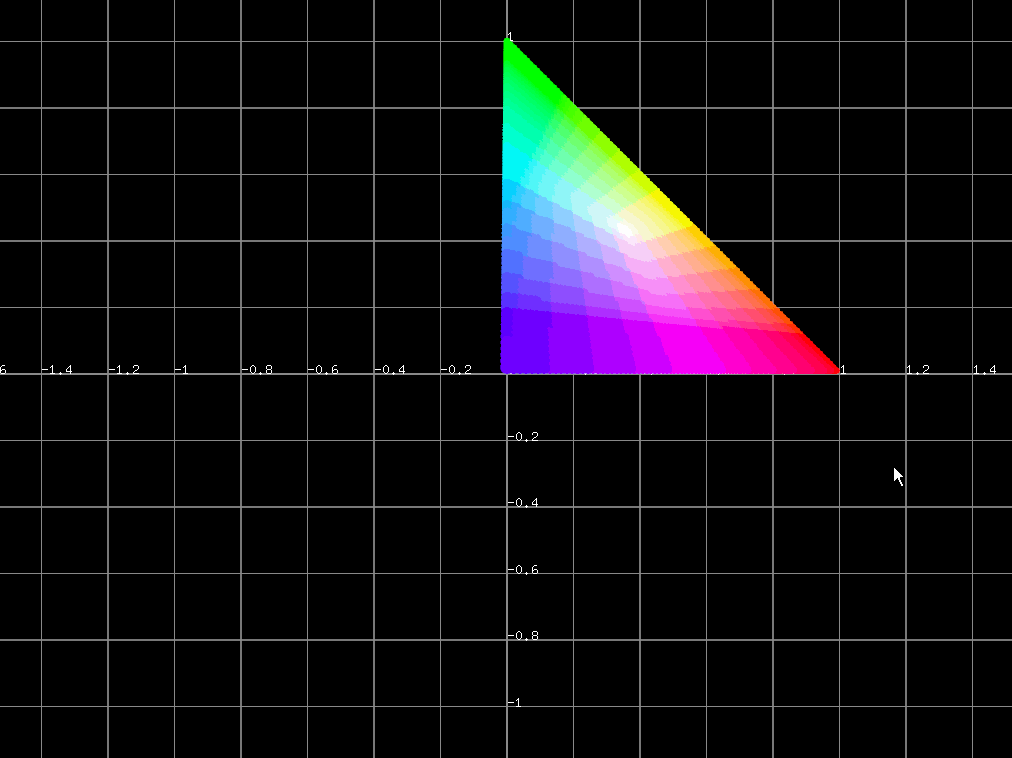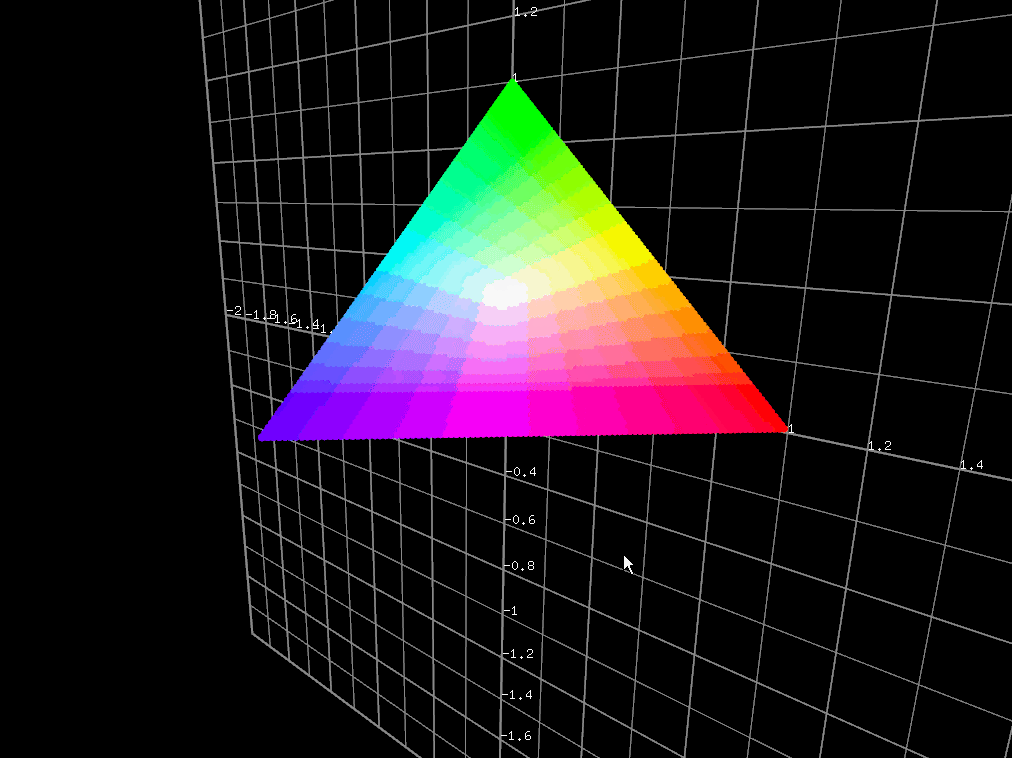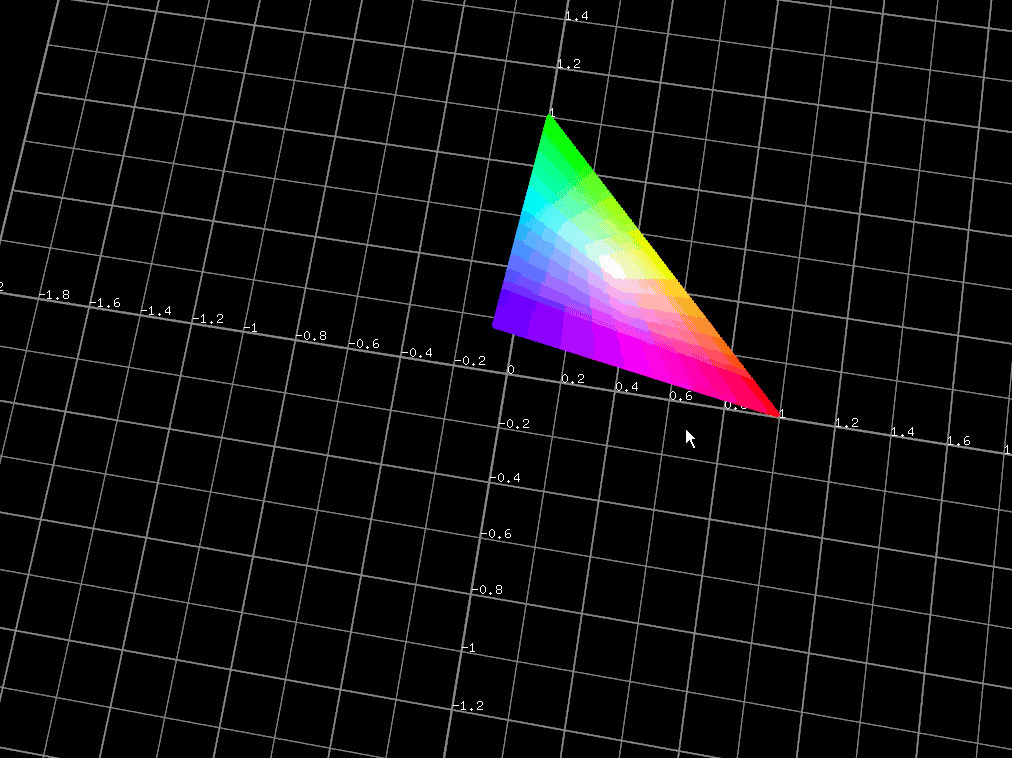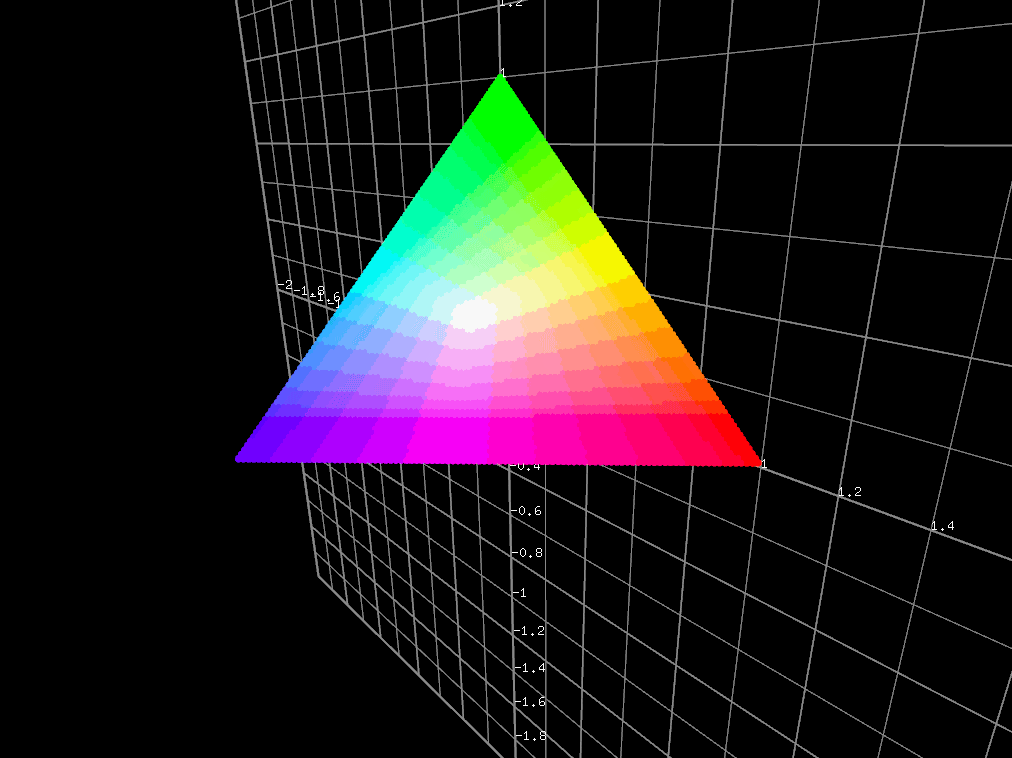
※みやすさを優先して、プロットはR,G,Bが全て正のところに限りました。
GIFの関係で色が段になってますので、以下にスクリーンショットも貼っておきます。
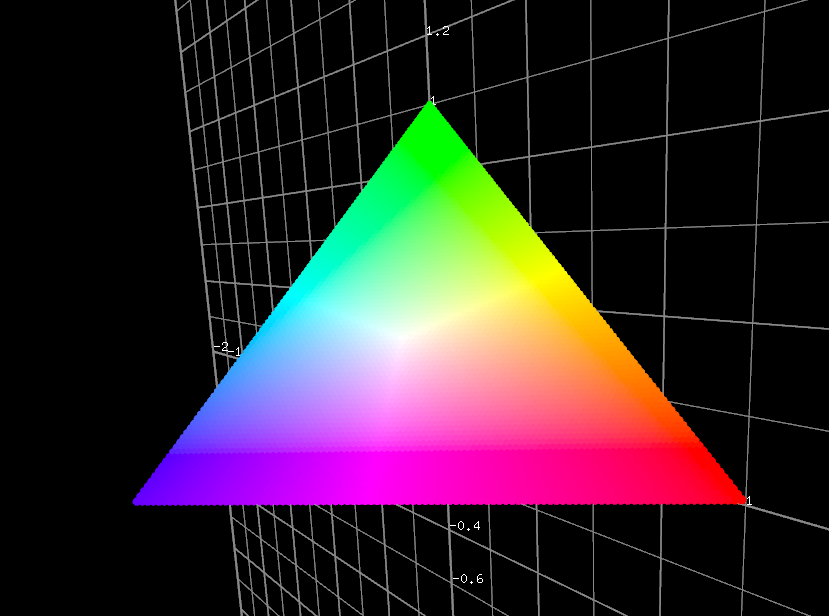
先程の等色関数も、$ R + G + B = 1 $ の制約のもと、プロットしてみたいです。でも等色関数は通常これを満たしません。どうするかというと、
\acute { R } =\frac { R }{ R+G+B } \\ \acute { G } =\frac { G }{ R+G+B } \\ \acute { B } =\frac { B }{ R+G+B }
と変換してあげます。これがなぜかといえば、
\acute { R } +\acute { G } +\acute { B } =1\\ \frac { R }{ R+G+B } +\frac { G }{ R+G+B } +\frac { B }{ R+G+B } =\frac { R+G+B }{ R+G+B } =1
となるためです。
このように変換した $ \acute { R }, \acute { G }, \acute { B } $を色度といいます。とするともはや $ \acute { R }, \acute { G } $ の二次元座標により色が定まる状態になります。なので $ \acute { B } $の軸については思い切って潰してしまってよさそうです。
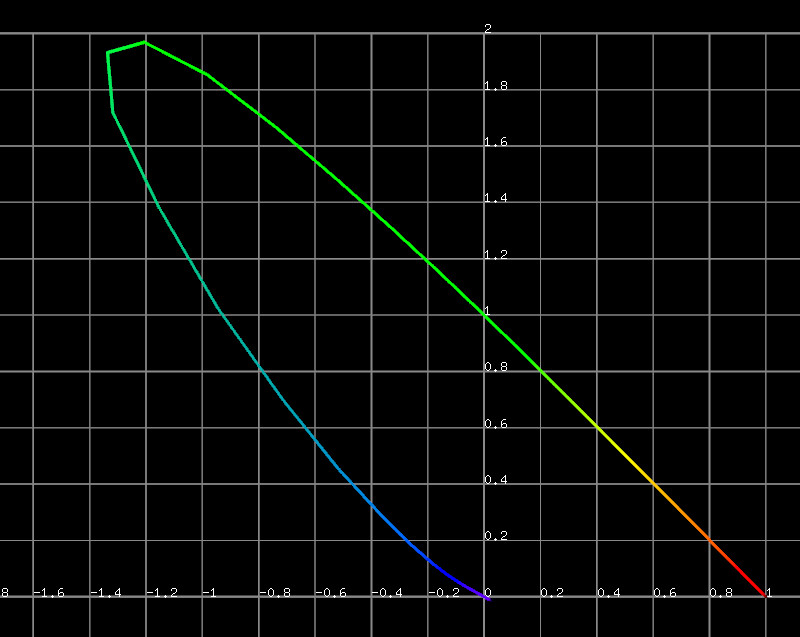
すると、先程の等色関数の軌跡は、
となり、このような図をrg色度図とよび、等色関数の軌跡をスペクトル軌跡と呼びます。
CIE 1931 色空間とは別の空間になるため、注意してください。
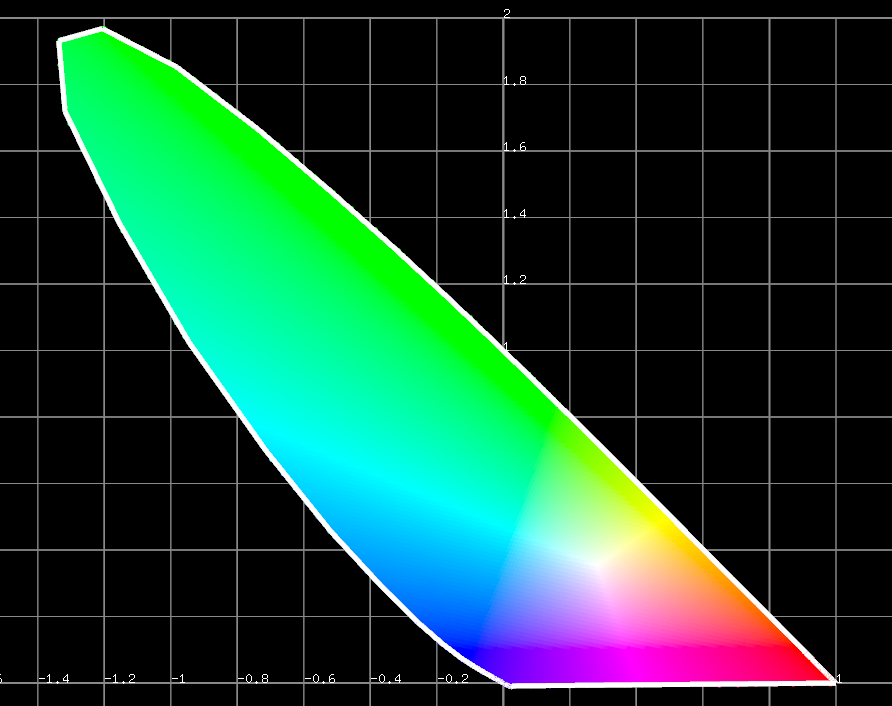
とこのように内側に色を塗ったバージョンもあります。
つづく
ちょっと1記事が膨らみすぎたため、XYZ色空間に迫る(2)に続きます。
ようやくXYZ色空間の話です。
[1] Isaac Newton, The Project Gutenberg EBook of Opticks, by Isaac Newton
[2] refractiveindex.info
[3] 色彩工学入門
[4] 立命館大学文学部人文学科心理学専攻(心理学域) 北岡 明佳 見えない色、見えてしまう色 ~脳が感じる色のふしぎ~
[5] 視覚光学 L, M, S錐体 L, M, S-cone
[6] 感覚の生理と心理 ヘリングの反対色説
[7] カラー画像工学の基礎と応用 (第1回) 視覚と色 矢口 博久
謝辞
@alt さん
表記ミスの修正していただきました。
@scivola さん @7of9 さん
プリズムの絶対屈折率のパートの不適切な表現を指摘と修正の提案、ならびにそれにまつわる議論をしていただきました。
感謝申し上げます